Sequence analysis of the gliding protein Gli349 in Mycoplasma mobile

Abstract

The motile mechanism of Mycoplasma mobile remains unknown but is believed to differ from any previously identified mechanism in bacteria. Gli349 of M. mobile is known to be responsible for both adhesion to glass surfaces and mobility. We therefore carried out sequence analyses of Gli349 and its homolog MYPU2110 from M. pulmonis to decipher their structures. We found that the motif “YxxxxxGF” appears 11 times in Gli349 and 16 times in MYPU2110. Further analysis of the sequences revealed that Gli349 contains 18 repeats of about 100 amino acid residues each, and MYPU2110 contains 22. No sequence homologous to any of the repeats was found in the NCBI RefSeq non-redundant sequence database, and no compatible fold structure was found among known protein structures, suggesting that the repeat found in Gli349 and MYPU2110 is novel and takes a new fold structure. Proteolysis of Gli349 using chymotrypsin revealed that cleavage positions were often located between the repeats, implying that regions connecting repeats are unstructured, flexible and exposed to the solvent. Assuming that each repeat folds into a structural domain, we constructed a model of Gli349 that fits well the shape and size of images obtained with electron microscopy.

Mycoplasmas are gram-positive bacteria and some species such as Mycoplasma mobile, M. pulmonis, M. gallisepticum, M. pneumoniae and M. genitalium have an ability to glide on solid surfaces1. The mechanism for such gliding is thought to differ from other known mechanisms of movement, such as the flagella motor in bacteria or actin-myosin complexes in myocytes and other cell types, since no protein homologous to flagellin, myosin, actin or any other known motor protein has ever been found in mycoplasmas2–6.

M. mobile, which glides at an average velocity of about 2.0 to 4.5 µm/s, or about ten times faster than the other four species mentioned above7,8, expresses two large proteins, Gli349 and Gli521, that are known to be responsible for the gliding: destructive mutation of either gli349 or gli521 eliminates the ability to glide from the organisms9–12. Gli349 is required for M. mobile to adhere to glass, and it is believed that it forms a spike that protrudes from the cell surface and in some way transduces the energy needed for motion9,11,13,14. Beyond this, however, little is known about the gliding mechanism of M. mobile.

In the present study, therefore, we carried out analyses of Gli349 from M. mobile and its homologue MYPU2110 from M. pulmonis to characterize their sequences and decipher the structures of these proteins, which we found not to be homologous to any other known protein. Based on our findings, we propose a structural model in which Gli349 is composed mostly of tandem repeats of homologous domains.

Materials and methods

Hidden Markov model for repeat sequence searches

Comparison of the sequence of Gli349 with itself in a dot matrix plot suggested that several weak repeats exist and that each contains the motif YxxxxxGF (where x denotes any amino acid residue, and hereafter referred to as the YGF motif). To further analyze the structures, we then manually extracted all the subsequences of 120 amino acid residues containing the YGF motif from Gli349 (11 subsequences) and MYPU2110 (16 subsequences) and examined the similarity among the subsequences. Out of the 27 (=11+16) subsequences, four subsequences (1 from Gli349 and 3 from MYPU2110) have no similarity to any of the 27 sequences with an E-value less than 10 using BLAST pairwise alignment15. Note that we have used a relatively high E-value threshold because we have noticed that the subsequences having the YGF motif were highly diverse but tried to include potential repeats in the initial data set as much as possible. In fact, no subsequences other than the 23 repeats were detected by BLAST with an E-value less than 10.0 for each of the 23 repeats as queries (the effective length of database was set so that the size of the database could be the same as the NCBI RefSeq non-redundant database, Release 9). Even using an E-value of 1,000, we have not found any subsequences other than the 27 subsequences having the YGF motif. We excluded four subsequences out of 27 which had an E-value larger than 10.0. We used the remaining 23 subsequences to construct a hidden Markov model (HMM)16–18, which was then used to search for new repeats within Gli349 and MYPU2110 that were similar to the input training data (i.e., repeat subsequences containing the YGF motif).

We used the HMMER package (http://hmmer.wustl.edu/)19 to implement the HMM, which took as input a multiple sequence alignment (MSA), which serves as training data, together with the entire sequence of Gli349 or MYPU2110. The output was comprised of subsequences that match the profile obtained from the MSA. The HMM is composed of one “begin state,” several “match states” (i.e., matches to one of the amino acid residues), several “insert states,” several “delete states” and one “end state.” The transition probabilities between states are trained by the input MSA. Once the model is trained, we can use it to detect new repeats that match the profile within a given sequence, the best starting and end points of each repeat, and the reliability of each repeat (E-value).

Statistical significance of motif occurrences in one sequence

The statistical significance of the number of YGF motif occurrences in a sequence was evaluated as follows. Suppose that the amino acid residues within a sequence were shuffled to make any possible sequence under a fixed residue composition. If the number of chance occurrences of the motif in the shuffled sequence was sufficiently smaller than N_motif times, then the number of the motif occurrences in one sequence would be considered statistically significant. For example, the probability of the occurrence of the motif AxxBxC is written

$$P(\mathit{motif})\equiv f(\text{A})f(\text{B})f(\text{C})$$ (1)

where A, B and C are particular amino acid residues that characterize the motif, and f(A) is the frequency of the amino acid residue A in the original sequence. When the motif length is much smaller than the sequence length, the probability that a shuffled sequence contains the motif N_motif times is given by

$${\left(P(\mathit{motif})\right)}^{N_{\mathit{motif}}}\times {\left(1-P(\mathit{motif})\right)}^{L-(l-1)-N_{\mathit{motif}}}\times \left(\begin{array}{c}L-(l-1)\\ N_{\mathit{motif}}\end{array}\right)$$ (2)

where L is the sequence length, l is the motif length and $\left(\begin{array}{c}a\\ b\end{array}\right)$ is a!/((a−b)!×b!). When a motif length is considered, the probability becomes smaller than that given by equation (2)20, so that the probability P that one shuffled sequence has the motif more than N_motif times is given by the equation

$$\begin{array}{ll}P<\hfill & \sum _{i=N_{\mathit{motif}}+1}^{L-(l-1)}{\left(P(\mathit{motif})\right)}^i\hfill \\ \hfill & \times {\left(1-P(\mathit{motif})\right)}^{L-(l-1)-i}\times \left(\begin{array}{c}L-(l-1)\\ i\end{array}\right)\hfill \\ \hfill & =1-\sum _{i=0}^{N_{\mathit{motif}}}{\left(P(\mathit{motif})\right)}^i\hfill \\ \hfill & \times {\left(1-P(\mathit{motif})\right)}^{L-(l-1)-i}\times \left(\begin{array}{c}L-(l-1)\\ i\end{array}\right)\hfill \end{array}$$ (3)

Note that the use of a binominal distribution allows the overlap of motifs and gives a larger probability than when we use a scan static. When we say that the 11 occurrences of the YGF motif are significant using the binomial distribution, this holds when using a scan static. In that sense, the use of a binominal distribution is a rather rough approximation but we consider it good enough to show the significance.

Results

Finding repeat sequences in Gli349 and MYPU2110

Through visual inspection, we found that the YGF motif appears 11 times in Gli349 and 16 times in MYPU2110, which are significantly greater numbers of occurrences than one would expect from chance. BLAST pair-wise alignment shows that 10 motifs for Gli349 and 13 for MYPU2110 were located in regions which were mutually similar. Using the amino acid residue fractions for Y, G and F in Gli349 (1.8%, 5.0% and 5.6%, respectively), the approximate probability that the YGF motif would appear at least 10 times within the 3,183 amino acid residues of Gli349 was calculated to be 2.8×10⁻¹⁵ using equation (3):

$$\begin{array}{l}1-\sum _{i=0}^9{\left(0.018\times 0.05\times 0.056\right)}^i\\ \hspace{0.17em}\times {\left(1-0.018\times 0.05\times 0.056\right)}^{3176-i}\times \left(\begin{array}{c}3176\\ i\end{array}\right)\end{array}$$ (4)

A similar analysis showed the probability of the YGF motif occurring at least 13 times by chance within MYPU2110 to be 1.1×10⁻²⁰. To test the significance of these numbers, we should consider two types of multiplicity. One is the multiplicity of the amino acid ordering. The order of Y, G, F and X can be YGxxxxxF, YxGxxxxF and so on. The number of the ordering is 6. The other is the multiplicity of amino acid types, that is, Y, G and F can be one of the 20 amino acid types. The number of patterns is 8,000 (= 20 × 20 × 20). Finally, the number of statistical tests required is 6×8,000. By multiplying this number with the probability of the YGF motif occurring at least 10 times within Gli349 and at least 13 times within MYPU2110, we obtained 1.3×10⁻¹⁰ for Gli349 and 5.3×10⁻¹⁶ for MYPU2110. These sufficiently low numbers show the frequency of the occurrence of the YGF motif to be statistically significant.

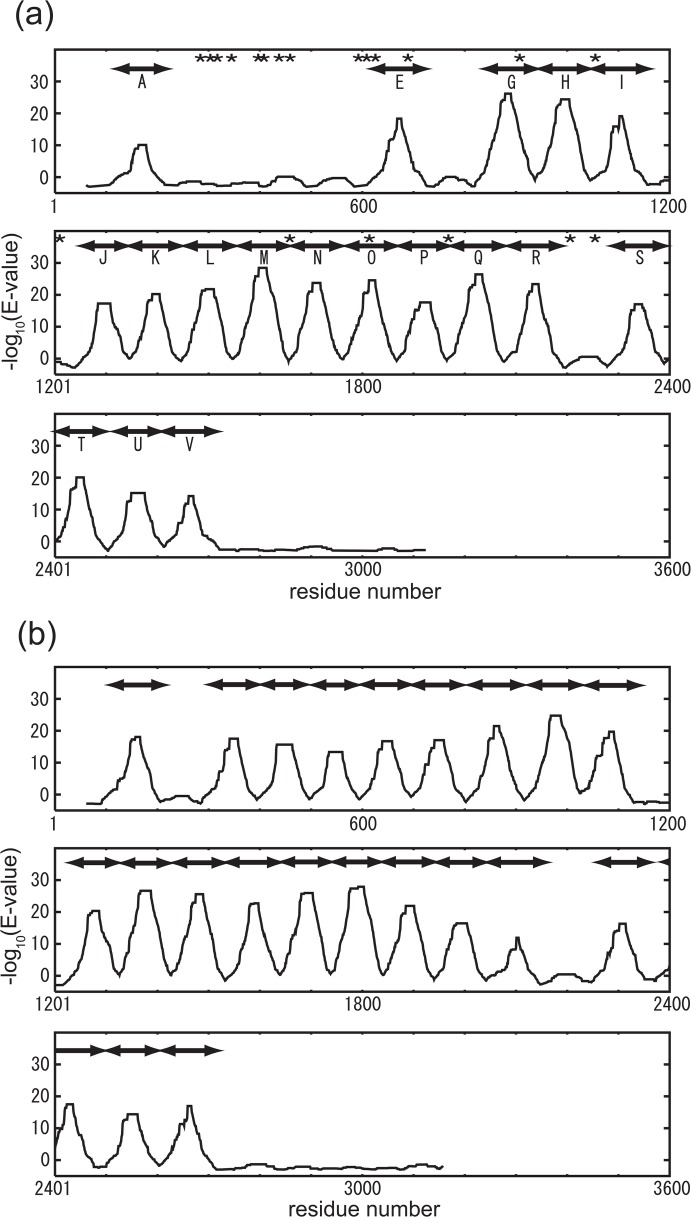
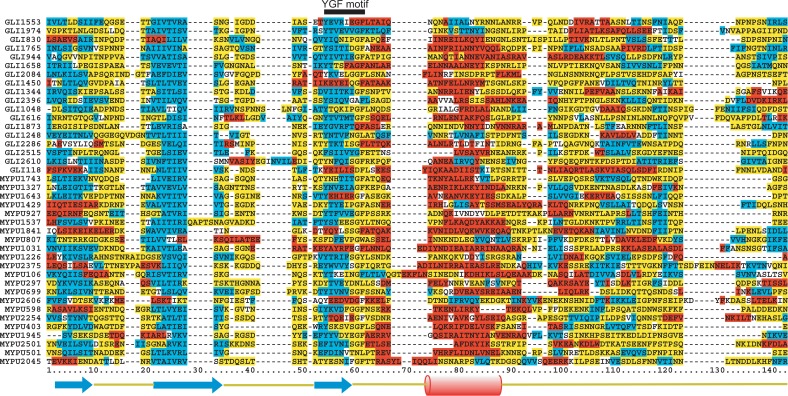
Notably, the positions of the Y within the YGF motif in Gli349 are 867, 979, 1087, 1588, 1694, 1801, 2009, 2123, 2322 and 2653; those in MYPU2110 are 138, 962, 1066, 1363, 1464, 1679, 1775, 1872, 1977, 2081, 2289, 2415 and 2640. Thus each YGF motif is separated by a multiple of about 100 (100, 200, 300 ...) amino acid residues, which implies the existence of a repeat whose length is a multiple of 100. When we took the greatest common measure (i.e., 100) as the repeat length, we found there to be 10 subsequences of about 100 residues in Gli349 and 13 subsequences in MYPU2110 that were well aligned and had several conserved sites in addition to the YGF motif. E-values of each pair-wise alignment of the sequences in Table 1 range from 1×10⁻⁶ to 3.4. Figure 1 shows the MSA of the 10 subsequences in Gli349 generated using clustalW21,22. Note that the region around the YGF motif is conserved best.

Table 1.

Positions of the repeats in repeat Sets #1 and #2

Set #1		Set #2
Gli349	MYPU2110	Gli349	MYPU2110
	86–205	91–210	86–205
806–925		806–925	786–905
916–1035	911–1030	916–1035	911–1030
1026–1145	1011–1130	1026–1145	1011–1130
	1311–1430	1321–1440	1311–1430
	1411–1530	1421–1540	1411–1530
1526–1645		1526–1645	1531–1650
1631–1750	1631–1750	1631–1750	1631–1750
1741–1860	1731–1850	1741–1860	1731–1850
	1829–1948	1841–1960	1829–1948
1946–2065	1931–2050	1946–2065	1931–2050
2061–2180	2031–2150	2061–2180	2031–2150
2261–2380	2231–2350	2261–2380	2231–2350
	2371–2490	2371–2490	2371–2490
2591–2710	2591–2710	2591–2710	2591–2710

Figure 1.

Multiple sequence alignment of 10 subsequences of Gli349 containing a YGF motif is shown. The start and end positions of each repeat are denoted in the first column. Colors on the sequences denote as follows: yellow, 100% conserved residues; cyan, >50% conserved residues; orange, sites that are >70% conserved for D, N, S and T; green, sites that are >70% conserved for A, I, L and V.

It is difficult to determine the start and end of a repeat when the amino acid residues are so weakly conserved among the repeats23. Furthermore, most of the repeats in Gli349 and MYPU2110 appear in tandem. Bearing this in mind, supposed repeats composed of 100 amino acid residues were situated contiguously at positions 1 to 100, 101 to 200 and 201 to 300 and so on; or they could be shifted 50 residues and start at positions 51 to 150, 151 to 250, 251 to 350, and 351 to 450 and so on. In this way, any position can be the starting point of a repeat if contiguous tandem repeats exist. Here, we assumed the boundaries (the start and end) of the repeats to be one of the residues in the least conserved region. We named this repeat set as Set #1 (Table 1). To exclude starting-point dependency in the alignment, we also employed another alignment in which the starting points were shifted by 50 residues. In this case, the YGF motif was again best conserved, and the least conserved region also agreed with the least conserved region in the prior alignment, demonstrating that the least conserved region is unaffected by the starting point of the alignments.

We then searched for subsequences of Gli349 and MYPU2110 that are distantly homologous to the repeats in Set #1. Using the knowledge that Gli349 is orthologous to MYPU21101,3,24, we conjectured that there might be a distantly homologous subsequence in Gli349 that could be aligned to one of the repeats in Set #1 of MYPU2110 and vice versa. In this way, we found an additional five repeats within Gli349 and two within MYPU2110. Then using the MSA of the 30 (23+7) subsequences prepared using clustal W, which we call Set #2, we searched for additional repeat subsequences, and a profile was built using the hidden Markov model with HMMER15. When a repeat search using this profile found new repeats, they and the repeats in Set #2 were aligned to build a new profile based on Set #2 (updating the profile), and then the procedure returned to the starting point in the cycle of iterations (see Fig. 2). The cycle was repeated until the alignment at the i-th iteration and the new alignment at the (i+1)-th iteration had the same alignment score. After seven iterations, we finally obtained additional repeats, three in Gli349 and four in MYPU2110, whose positions are shown in Table 2. This last repeat set containing 40 repeat sequences was called Set #3. The similarities of all the repeats in Set #3 were statistically significant (E-value of each repeat in Set #3 was smaller than 2.6×10⁻¹⁴ against the profile). And as shown in Fig. 3, the peaks of the alignment scores correspond well to the positions of the repeats. The scores were calculated using a 120-residue long window so that the window would contain the entire repeat. Hereafter, “repeat” denotes repeat sequences in Set #3.

Figure 2.

Procedure for detecting repeats using the hidden Markov model.

Table 2.

Positions of the repeats in repeat Set #3

repeat ID	Gli349	MYPU2110	repeat ID	Gli349	MYPU2110
A	118–222	106–216	L	1450–1546	1429–1534
B		297–400	M	1553–1657	1537–1641
C		403–492	N	1658–1762	1643–1740
D		501–594	O	1765–1872	1743–1836
E	616–727	598–698	P	1873–1972	1841–1944
F		699–800	Q	1974–2080	1945–2043
G	830–938	807–916	R	2084–2191	2045–2160
H	944–1047	927–1027	S	2286–2391	2254–2361
I	1048–1161	1031–1141	T	2396–2501	2375–2498
J	1248–1343	1226–1324	U	2515–2608	2501–2601
K	1344–1449	1327–1426	V	2610–2720	2606–2718

Figure 3.

Alignment scores of subsequences of 120 residues against the profile of repeat Set #3. Plotted are the scores at the center position of the subsequences of Gli349 (a) and MYPU2110 (b). Scores were calculated using HMMER19. The unit on the vertical axis is the negative logarithm of the E-value of the alignment. The bars above the line denote repeats detected by HMMER19. Most of the repeats were found to be in tandem form. For Gli349, experimentally determined chymotrypsin susceptible sites are shown by asterisks (a).

Characteristics of the repeat

We calculated sequence identities among the repeats using pairwise alignments generated with clustalW21,22 and found them to fall in a range of 13.6∼36.2% for Gli349 and 11.3∼35.7% for MYPU2110. The degree of sequence conservation in each column of the MSA of the 40 repeats is shown in the form of a sequence logo25 in Fig. 4. The YGF motif is the most conserved region within repeats, and there are three regions having high information values: 1 to 8, 21 to 36 and 54 to 63 (Fig. 4). These regions all contain a binary pattern of hydrophobic and hydrophilic residues, suggesting that the regions form amphipathic β strands and are located on the surface of the protein. Note that, in addition to these regions, there are several conserved amino acid residues: Gly at 38, Ser or Thr at 50, Asn at 76, Tyr at 83, Phe at 117 and Ile at 119.

Figure 4.

The degree of residue conservation at each position in the repeat is shown as information content. The information content of amino acid residue “a” at position “i” is calculated by the equation, I(a, i)=−p(a, i) log₂ p(a, i), where p(a, i) is the fractional content comprised by an amino acid residue. $\sum _{a}p(a,i)=1$ at each position. As $\left({\text{log}}_{2}20-\sum _{a=1}^{20}I(a,i)\right)$ becomes larger, the position “i” is regarded as more conserved. The three black bars indicate well conserved regions.

The predicted secondary structure of each repeat, determined using the NPS server (http://npsa-pbil.ibcp.fr/cgi-bin/npsa_automat.pl?page=/NPSA/npsa_seccons.html)26, was found to be βββα with the second β-strand being well conserved among all repeats (Fig. 5). The locations of the predicted β-strands are particularly consistent with the binary pattern, which suggests the existence of three β-strands. The most highly conserved residues in the YGF motif, Gly and Phe, are found in the region extending from the middle of the third β-strand to the beginning of the following α-helix. Both the primary and secondary structures of the region are well conserved, which may suggest that those regions are important for determining the structure of Gli349. The secondary structure near the C-terminus is less conserved (Fig. 5), suggesting this region may be a linker between domains. The characteristics of the predicted secondary structures of the repeats in MYPU2110 are similar to those of Gli349.

Figure 5.

MSA of repeat Set #3. Residues are colored according to the predicted secondary structures: red, α-helix; blue, β-strand; yellow, coil; and white, ambiguous. The consensus secondary structure is βββα shown at the bottom. The subsequences are listed in order of their E-values. The YGF motif is denoted by a black bar on the top line. GLI and MYPU denote Gli349 and MYPU2110, respectively, and the following number denotes the repeat start position in each subsequence. Residue numbering is the same as in Fig. 4.

Gli349 is comprised of 3,183 amino acid residues; the last repeat starts at position 2,607 and ends at 2,729. The N-terminal 86% of Gli349 is mostly composed of repeats, suggesting the C-terminal region takes a different structure than the rest of the molecule. Repeats G to I, J to R and S to V form three contiguous tandem repeats (Fig. 3). Interestingly, the gap lengths between repeats I and J and between repeats R and S are about 100 amino acid residues long (86 between repeats I and J, and 94 between repeats R and S), or about as long as one repeat. This suggests to us that the gaps are also repeats, but have become too divergent for detection of sequence similarity using currently available methods.

Search for homologous proteins using repeat profiles

Using HMMER with a profile based on the MSA of repeat Set #3, we searched for sequences homologous to both Gli349 and MYPU2110 repeats in the NCBI reference sequence (RefSeq) database (Release 9)27,28 (http://www.ncbi.nlm.nih.gov/RefSeq/), which is a non-redundant protein sequence dataset, but no homologous sequences with E-values less than 0.1 were found. We also checked whether either Gli349 or MYPU2110 matches any profile of known repeat sequences compiled in the REP database23. Neither Gli349 nor MYPU2110 matched any profile in the REP database, suggesting that the repeat in Gli349 and MYPU2110 is novel.

Chymotrypsin treatment

Chymotrypsin breaks the C-terminal peptide bonds of aromatic residues that are exposed to solvent and are flexible and could, therefore, be used to discover exposed flexible regions in Gli349. A knowledge about such regions would provide a hint as to the structure of the entire protein, as well as to the structure of each repeat. Based on the experimentally obtained molecular weights of the fragments of Gli349 (unpublished data) and our understanding of the peptide bonds targeted by chymotrypsin, we estimated the positions of 20 cleavage sites (shown in Fig. 3a and Table 3). Of those, 17 fell within either the non-repeat region or the boundary region of the repeats (Fig. 3a), suggesting that these areas are exposed to solvent and are flexible. We suggest that these regions might be the linkers between domains, which is consistent with our assumption that each repeat sequence folds into a structural domain. The remaining three sites fell within the repeats: one was on the second β-strand and two were on the α-helix. We expect that these areas are exposed to the solvent, as their sequences appear to form an amphipathic β-strand or α-helix.

Table 3.

Positions cleaved by chymotrypsin

molecular weight	position	molecular weight	position
32.0	292	69.4	631
34.7	316	73.4	667
35.8	326	98.5	893
37.1	337	115.0	1052
43.4	392	131.6	1206
44.7	405	181.4	1665
48.5	438	197.1	1816
49.8	450	215.6	1982
65.5	594	241.3	2219
67.5	613	245.0	2253

The positions were calculated based on the molecular weight (kDa) and the known target sites of chymotrypsin.

Discussion

Proteins with tandem repeat sequences

We have found that Gli349 is a protein comprised of tandem repeats, most of which are marked by a YGF motif. Structures with tandem repeats are known to occur either in linear arrays or superhelical structures with repeats arranged around a common axis, as is seen in the β-propeller structure29. Either of the structures presents an extensive surface that is well suited for interaction with other molecules. Indeed, so far the best-known function of the proteins with known repeats is the binding of other proteins29. We suggest that Gli349 also provides an extensive surface with which it interacts with other molecules.

This is the first description of the YGF motif, which was situated within each repeat. When we searched the SWISS-PROT database30 for proteins containing repeat sequences with the YGF motif, we only found kelch-like protein 10 from Homo sapiens31. The kelch repeat has the superhelical structure of a six-bladed β-propeller in which the repeats each consist of about 40 amino acid residues and are arranged around a common axis32. Gli349 is unlikely to assume a structure similar to kelch, because 1) the YGF motif is not conserved in any kelch repeats, 2) the length of repeats differs from the kelch repeat, and 3) electron microscopy (EM) of Gli349 (discussed later) shows an overall rod-shaped structure. We also note that a search of the Pfam database33,34 using Gli349 as a query provided six trusted matches against Pfam-A and three matches against Pfam-B. None of them, however, corresponds to the repeat and has a YGF motif.

Proteins with an Ig-fold repeat are often found on cell surfaces and mediate interactions with other cells, as is the case with a filamin, which contains six Ig-folds in a chain and functions to cross-link pairs of F-actin chains35. The size of the Ig-fold is about 100 residues, which resembles the size of the YGF-containing repeat in Gli349, and is also an all-β structure. We therefore used PSIPRED36 and FORTE37 to thread the repeat sequences of Gli349 and MYPU2110 in the known Ig-fold structures to test whether the repeat sequences are compatible with the Ig-fold. No repeat in Gli349 or MYPU2110 fits into any known Ig-fold structure, however. Apparently, the YGF-containing repeat does not assume an Ig-fold structure, but we will need further structural determination to confirm this speculation.

Implications for richness of Asparagine

One of the characteristics of the Gli349 sequence is that it is rich in Asn residues, which accounts for 12.0% of the residues making up Gli349, or about three times more than the average fraction (4.3%) of Asn residues in all the protein sequences in SWISS-PROT30. There are also Asn-rich proteins in Plasmodium falciparum, which is responsible for malaria in humans. It has been suggested that the Asn-rich proteins in P. falciparum may be useful for avoiding host immunogenic responses38. Gli349 may have similar features. M. mobile lives as a parasite in the gill organ of freshwater fish, which are exposed to water. Almost all of Gli349 is predicted by TMHMM to be outside the cell membrane39. In addition, P1 adhesin from M. pneumoniae, known to be responsible for binding to animal cells and glass surfaces40–43 and to be related with avoiding immunogenic responses, was recently suggested to directly participate in the gliding44. Taken together, these results suggest that Gli349 may also play a role in enabling M. mobile to escape host immunogenic responses.

Structural model based on sequence analysis and EM imaging

Under the assumption that each repeat sequence folds into a structural domain, we speculated on the tertiary structure of Gli349. By predicting the repeat structure using the ROBETTA server (http://robetta.bakerlab.org) and the ROSETTA algorithm45,46, we estimated the size of the domain. ROSETTA is one of the most successful methods for predicting ab initio tertiary structures. We predicted the structures of repeats K and N because they had the highest scores in the alignment used for the HMM profile. Ten predicted tertiary structures per input sequence were obtained with ROBETTA. The sizes of the predicted structures were similar (the average size was 4.2±0.5 nm, where the length is defined as the farthest distance between two Cα atoms), though they exhibited a large variety of folds.

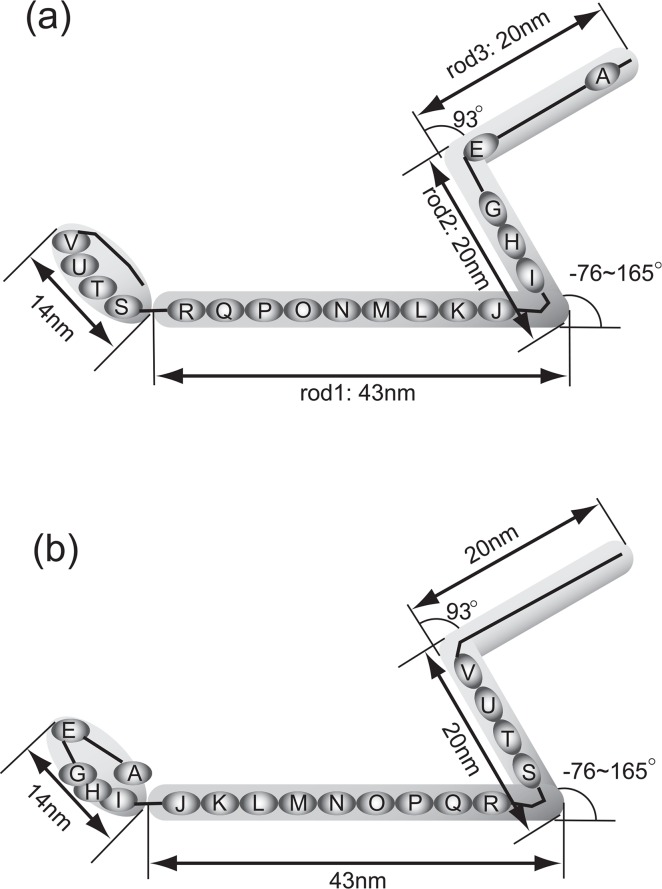
A preliminary EM image of Gli349 shows the shape of Gli349 to have an inverted Z-like structure and to be composed of at least four parts (Fig. 6). It also showed that the joint between rods 1 and 2 is very flexible, whereas the joint between rods 2 and 3 is very rigid (Fig. 6). We then tried to place the predicted structure of the repeat sequences on the image of Gli349, taking into account the rough estimation of the length of Gli349, and assuming that the lengths of the three rods are proportional to the number of residues and that the entire structure is a string-like filament. We found that there are two ways to place the repeats on the image: the N-terminus of Gli349 can be assigned to either the tip (model 1, Fig. 6a) or the base of the body of M. mobile (model 2, Fig. 6b). In both assignments, there are nine repeats and two non-repeat regions within the 43-nm rod 1 (Fig. 6). We can estimate that the length of one repeat is shorter than 4.8 nm (=43/9), which agrees well with the average size of the predicted repeat structures. Because Gli349 is predicted to have a transmembrane region near the N-terminus11 and with the mutation of Ser to Leu at 2770 (Uenoyama, A., Seto, S. and Miyata, M., unpublished data), where the mutation is to be located in the oval region in model 1, Gli349 cannot adhere to glass12, we propose that model 1 more accurately depicts the true structure of Gli349, though in both models the non-repeat regions correspond well to the flexible joints.

Figure 6.

Model of Gli349. Low resolution image of Gli349 obtained with electron microscopy (EM) is shown in gray shade. Repeat regions shown in ovals connected by lines are assigned into the EM image of Gli349. The N-terminus is placed at the far right side in (a), and at the far left side in (b). The length of each rod and angles between two rods are the average values over EM images (unpublished data).