Abstract
The ability to control nonlinear interactions of suspended mechanical structures offers a unique opportunity to engineer rich dynamical behavior that extends the dynamic range and ultimate device sensitivity. We demonstrate a displacement sensing technique based on resonant frequency monitoring of curved, doubly clamped, bistable micromechanical beams interacting with a movable electrode. In this configuration, the electrode displacement influences the nonlinear electrostatic interactions, effective stiffness and frequency of the curved beam. Increased sensitivity is made possible by dynamically operating the beam near the snap-through bistability onset. Various in-plane device architectures were fabricated from single crystal silicon and measured under ambient conditions using laser Doppler vibrometry. In agreement with the reduced order Galerkin-based model predictions, our experimental results show a significant resonant frequency reduction near critical snap-through, followed by a frequency increase within the post-buckling configuration. Interactions with a stationary electrode yield a voltage sensitivity up to ≈ 560 Hz/V and results with a movable electrode allow motion sensitivity up to ≈ 1.5 Hz/nm. Our theoretical and experimental results collectively reveal the potential of displacement sensing using nonlinear interactions of geometrically curved beams near instabilities, with possible applications ranging from highly sensitive resonant inertial detectors to complex optomechanical platforms providing an interface between the classical and quantum domains.
1. Introduction
In many sensors based on micro- and nanoelectromechanical systems (MEMS/NEMS) various physical stimuli are converted into displacements, which are in turn transduced into electrical signals. For instance, pressure sensors monitor deflection of a membrane [1], force sensors measure displacement of a structure acting as a spring [2], and inertial sensors extract angular acceleration from a proof mass displacement [3,4]. Whatever the application, small forces, that yield sub-nanometer displacements, present particular measurement challenges. Efforts are generally devoted to robust design of signal processing circuitry to overcome stringent displacement sensing requirements.
One of the more promising and intensively researched approaches for sensitivity enhancement of miniaturized mechanical systems is based on monitoring device spectral characteristics instead of direct quasi-static displacement measurements. For example, with atomic force microscopy-based frequency (or phase) sensing, non-contact interactions allow topographic, localized-charge and electromagnetic-field imaging at the nanoscale [5,6]. While most of the current resonant MEMS/NEMS architectures are devoted to biochemical mass sensing [7–10] with mass sensitivities ranging from attogram [11] to zeptogram [8], several configurations of resonant accelerometers [12–23], pressure [24] and angular rate [25–28] sensors were reported. Recently, monitoring modal amplitudes [29] and mode localizations of coupled resonating elements [30] showed an increased displacement sensitivity of resonant force and acceleration sensors.
The most common resonant accelerometers consist of a beam connected to a movable proof mass. The beam is either stretched [14,19,24] or compressed axially [28,31,32] by the moving proof mass. These axial forces affect the effective stiffness of the beam and, as a result, its resonant frequency. However, generally small forces induce negligible effective stiffness changes, where the resulting minimal frequency changes are difficult to detect. In this scenario, required device sensitivity is often achieved using complex force amplification mechanisms [14,16,18,19]. Reduction of the resonant sensing element dimensions to the nanoscale represents an alternative method for sensitivity enhancement [32,33].
Another approach allowing effective stiffness reduction and therefore enhancement of the frequency sensitivity to the applied forces is based on electrostatic softening. This is a well-known phenomenon in MEMS that stems from the nonlinear electrostatic force dependence on the distance between the structure and an electrode. Since the electrostatic force also depends on the applied voltage, electrostatic softening is widely used for voltage-based frequency tuning and for structural stress compensation [12,33–36]. The softening effect manifests itself through a decrease of the device’s resonant frequency with an increasing applied voltage [30,33]. The voltage-controlled frequency method is routinely implemented in high-end sensors such as micromachined angular rate sensors (micro gyroscopes) [3,4]. The use of the electrostatic softening for scale factor enhancement in accelerometers was reported by several authors [13,17]. One of the distinguishing features of electrostatic actuation by a close-gap electrode is the presence of the pull-in instability. This buckling instability occurs at a critical voltage above which the device collapses to the electrode. Near the critical point, a region where effective device stiffness and frequency changes are extremely steep, maximal loading sensitivity is achieved. Device operation in close proximity to the pull-in instability is therefore attractive [30,33]. However, the possibility of device collapse and consequent irreversible damage cannot be ignored. For this reason, the operating regime should be chosen far enough from the instability to provide an acceptable dynamic displacement range [21]. Sensing based on critical instability fields was suggested for accelerometers [37,38] and threshold sensors [39,40].
In this work, we demonstrate an approach for safely exploiting electrostatic softening effects while eliminating the dangers of the pull-in collapse. Our approach is based on a combination of electrostatic and intrinsic mechanical nonlinearities of curved, doubly-clamped, bistable micromechanical beams. In-plane curved beam is lithographically-defined from a stress-free, single-crystal silicon structure. In general, the behavior of such a beam is controlled by the initial elevation, which is defined as the distance between the midpoint of the beam and an imaginary straight line connecting the ends of the beam [41–43]. Specifically, the beam is bistable when the initial elevation exceeds a certain threshold value, referred hereafter as the bistability onset or threshold. In contrast to an electrostatically actuated straight beam prone only to a pull-in instability, a curved beam actuated with a stationary, close-gap electrode could manifest two sequential instabilities: snap-through and pull-in instabilities [41,44]. The effective stiffness and consequent resonant frequency of such a beam are influenced by the electrostatic loading.
Device actuation using a steady state DC voltage that is quasi statically increasing from zero to the snap-though value is accompanied by a resonant frequency decrease, reaching zero at the critical snap-through point. Actuation above the critical value gives rise to a sharp frequency increase within the post-buckling state [41,42,44]. Our results show a similar behavior when the DC voltage is held constant while the distance between the beam and the movable electrode decreases. Since snap-through switching to a second stable equilibrium configuration does not involve contact with the electrode, the process is fully reversible. Furthermore, by choosing the initial elevation at the bistability onset, the snap-through collapse is completely eliminated. In this scenario, the slope of the voltage-deflection curve can be tailored such that frequency sensitivity to electrode displacement is optimized. Unlike complex comb-type electrode architectures [45,46], our devices can be easily scaled to the nanometer regime or, if necessary, combined into large arrays of sensors.
In this work we explore, theoretically and experimentally, the dynamic range of voltage-based frequency tuning of curved micromachined beams. For beams of varying geometry interacting with stationary electrodes, we demonstrate non-monotonic voltage-frequency dependence with voltage values exceeding the snap-through point. While electrostatic behavior of curved structures was investigated theoretically [47], numerically [30], and experimentally [48], a systematic experimental study of spectral characteristics during the snap-through transition has not been conducted. We also demonstrate frequency tuning using curved beam interactions with a movable electrode. In this case, we measure the resonant frequency of the beam as a function of the electrode displacement. Our experimental results further show the applicability of geometrically non-linear structures as potential displacement and acceleration sensor platforms.
2. Formulation
The suspended beam is described in the framework of the Euler-Bernoulli theory combined with the shallow arch approximation. As shown in Figure 1(a), we consider a flexible, initially-curved, double-clamped prismatic beam of length L, with a rectangular cross-section of width b and thickness d. The cross sectional moment of inertia and area are I and A, respectively. We assume that the beam is composed from a homogeneous, isotropic, linearly-elastic material with a density ρ and the plane-strain Young’s modulus E/(1 − ν2), where ν is Poisson’s ratio. The lithographically-defined curved beam shape is described by the function z0(x) < 0. For simplicity, we neglect fringing fields and assume that a distributed electrostatic loading can be modeled using the simplest parallel-plate capacitor approximation [37,42]. Here, the electrode is initially located at a distance g0 and allowed to move as a rigid body constrained to the z-direction. In this scenario, the electric field is solely along the z direction.
Figure 1.
(a) Schematic illustration of a curved, doubly clamped beam actuated using a parallel plate electrode architecture. The electrode is allowed to move as a rigid body in the z direction, the displacement u of the electrode is positive in the direction toward the beam. (b) Lumped model results equilibrium curves (the dependence between the midpoint deflection of the beam and the applied voltage) of beams with varying h (h1 = 0, h2 = 2.5 μm, h3 = 3.5 μm). Negative slope corresponds to an unstable equilibrium whereas the positive slope refers to the stable branch. The curve corresponding to the bistability onset (h2) is distinguished by a low stiffness region with highly sensitive deflection to voltage change. (c) Natural frequency of the beam (eq. (10)) with varying h (h1 = 0, h2 = 2.5 μm, h3 = 3.5 μm). The low-tangent stiffness region is discerned by either a steep frequency decrease or increase. Furthermore, since the beam is bistable at h3, the curve is not continuous ([47,49]).
The undamped motion of the beam is described by the following equation [41]
| (1) |
where z(x) is the elevation of the beam above its ends, ε0 is the permittivity of the free space, V is the voltage difference between the beam and the electrode and u is the displacement of the electrode toward the beam. The gap between the beam’s ends and the electrode is g0 − u. Equation (1) accounts for the initial axial force N0 and for the nonlinear stretching force. For simplicity, our formulation neglects residual stresses and assumes N0 = 0. Residual stress in highly doped single crystal silicon, however, could affect buckling behavior [37,42]. We further assume that u is an enforced parameter that is unaffected by V and beam displacement.
3. Reduced order model
In order to analyze the dynamics of the beam, a single degree of freedom, reduced order model was built using the Galerkin method. The details of this development can be found in [42,43,48]. While a multi degree of freedom model can be employed, the single degree of freedom model describes leading static and dynamic effects of these types of devices with satisfactory accuracy [42,43,49]. We define w(x) = z0(x) − z(x) to be the deflection of the beam and set
| (2) |
where wm and h are the deflection and the initial elevation of beam at x=L/2, respectively and
| (3) |
is the fundamental buckling mode of the straight beam. While various functions can be used as the base function (starting from the linear modes of vibrations of straight [41,42,47,48,50], curved [41,51] or statically pre-loaded beams and up to expressions obtained using advanced proper orthogonal decomposition (POD) based algorithms [52,53]), the use of equation (3) allows for closed form, analytic evaluation of the integral associated with the generalized electrostatic force [42,43]. Previous studies [37,43,48,51] showed that the reduced order (RO) models based Eq. (3) capture leading effects of the beam behavior and describe the static and dynamic responses with good accuracy. In accordance with Eq. (2), Eq. (3) is used here as the initial shape of the curved beam and as an approximation of the beam deflection. Since the initial shape of the beam is defined by lithography, the structures of basically any initial configuration can be fabricated. The function form of Eq. (3), which represents the actual fabricated bell-shaped configuration of the beam [38], is chosen here due to its convenience for analysis.
As a result of the common Galerkin procedure, we obtain the nonlinear ordinary differential equation of motion in terms of the deflection, wm
| (4) |
where is the gyration radius and
| (5) |
is the approximate first linear natural frequency of a straight, doubly clamped beam. Hereafter, (·)=∂/∂t denotes derivatives with respect to time. Since the buckling mode was used as a base function rather than the first vibrational mode, the numerical value of the coefficient in Eq. (5) slightly differs from the exact eigenvalue of 4.73.
4. Small vibrations around a deformed equilibrium
For convenience, we re-write Eq. (4) in the form [49]
| (6) |
where
| (7) |
are associated with the mechanical and the electrostatic terms, respectively. We let be a fixed point of Eq. (6) for a given steady state DC voltage Vdc such that . The fundamental mode frequency of small vibrations around the deformed configuration corresponding to Vdc is obtained by linearization of Eq. (6) around the fixed point . We set in Eq. (6) , where wd(t) is the dynamic component of the midpoint deflection, and expand the resulting expression into the first order Taylor series for wd ≪ 1 to obtain
| (8) |
Here
| (9) |
The frequency of small free vibrations around a fixed point is given by the expression
| (10) |
Among other parameters, equation (10) shows a strong frequency dependence on Vdc and u. Frequency sensitivities, SV and Su, with respect to Vdc (at a constant u) and u (at a constant Vdc) are given by
| (11) |
We emphasize that the RO model, Eqs. (6)–(11), has an approximate character and is implemented here for the sake of transparency of the development. Furthermore, the RO model provides a closed form dependency between the frequency on the dc voltage and the displacement of the electrode.
5. Reduced Order Model Results
Parameters used in calculations are detailed in Table 1. Figure 1(b) shows equilibrium curves of beams for several values of h. The equilibrium curve for a straight beam (h1) has a single maximum that corresponds to the electrostatic pull-in instability. For a beam shape described by eq. (3) and h above a certain threshold given by [42,43],
Table 1.
Device parameters used in calculations
| Parameter | Value [μm] |
|---|---|
| L | 1000 |
| d | 3 |
| b | 20 |
| g0 | 10 |
| (12) |
the suspended beam becomes bistable. The equilibrium equation (static counterpart of Eq. (6)) has three real roots, corresponding to two maxima and one minimum. Although in this case the behavior of the beam is influenced by both mechanical and electrostatic nonlinearities, the first local maximum represents the snap-through instability whereas the second maximum is associated with the electrostatic pull-in instability [42]. In this perspective, the softening associated with the snap-through is mainly due to the mechanical nonlinearity rather than the electrostatic force, responsible for the pull-in instability. In the vicinity of the snap-through onset, figure 1(b) shows a monotonic voltage-displacement relationship. Consequently, this region is free from dangers of beam collapse. Using equation (10), figure 1(c) shows the calculated natural frequency as a function of Vdc for various h values with u = 0. Regions near critical points are characterized by a strong stiffness decrease and therefore, a consequent frequency decrease. For values of h slightly below hmin, the equilibrium curve is distinguished by a low stiffness and a low frequency region. At the onset of the snap-through instability, small voltage changes result in significant changes in wm and f. Figure 1(c) further shows two distinct regions characterized by a steeply sloped voltage-frequency curve where a frequency change results in an increased SV. The first, observed at a lower voltage, is in the vicinity of the snap-through. The second, at a higher voltage, is associated with electrostatic softening and corresponds to the pull-in instability.
We now consider the case when the electrostatic force and consequently the effective stiffness and the frequency of the beam are parameterized by the electrode displacement. We emphasize that the displacement of the electrode u is considered as an externally enforced parameter, which is unaffected by the voltage actuating the beam. As an example, one can mention a scenario when a bulky proof mass of an accelerometer is used as the movable electrode, which is significantly larger than the curved beam serving as a sensing element. The sensor is operated by first applying a static voltage, Vdc, to deflect the beam to the optimal working position. The value of Vdc is held constant for the duration of the experiment. Since beam deflection depends on both the applied voltage and electrode displacement, electrode motion induces changes in the electrostatic loading and the natural harmonic. To excite vibrational dynamics, a small, time harmonic AC voltage is applied to the electrode in addition to the DC voltage.
Our lumped model results in figure 2 show the relation between the electrode displacement and resonant frequency of the suspended structure. To evaluate device performance and sensitivity, we estimate the relative frequency change per, both, nanometer of electrode displacement (Δf/f0)/(Δu and relative gap change (Δf/f0)/(Δu/g0). Using h = 2.5 μm and beam parameter values from Table 1, our model results show (Δf/fo)/u > 10−3 nm−1, which corresponds to (Δf/f0)/(u/g0)=O(10). This sensitivity is maintained over a wide range of displacements spanning hundreds of nanometers. It is instructive to compare this result with the capacitive sensing, which is probably the most common interrogation approach in displacement and inertial sensors [4,5,54]. For the quasi-static capacitive-sensing case, the relative capacitance change is linearly proportional to the relative displacement and is (ΔC/C0)/(u/g0)=O(1)[54]. As a result, for the beams with the dimensions detailed in Table 1 and for u = 1 nm, the relative capacitance change is of order of 10−4, which is ten times smaller than the relative frequency change under the same conditions. Using beam geometries from Table 1, our calculations show device capacitance change in the aF range. Detection of absolute capacitance change in this regime is challenging due to noise and influence of much larger parasitic capacitances. Consequently, our sensing approach provides an order of magnitude sensitivity amplification gain. Furthermore, changes in frequency are generally easier to detect, for example, by a heterodyne method.
Figure 2.
Lumped model results for h = 2.5 μm near the bistability onset. (a) Equilibrium curves for beam deflection resulting from electrode displacements at varying Vdc. (b) Effective natural frequency (solid line) as a function of the electrode displacement, for Vdc = 94 V. The dashed line shows the relative sensitivity per nm of electrode motion, (Δf/f0)/nm.
6. Numerical verification
The model results presented above are based on an approximate single degree of freedom, lumped reduced order model of the Euler-Bernoulli beam. Furthermore, the frequency is calculated by using the linearized equation (8). To verify the model results and estimate the level of error caused by these approximations, numerical analysis was performed. First, static, three-dimensional finite element analysis was carried out in order to verify the reliability of the reduced order and the Euler-Bernoulli beam models. A commercial package was used, which implements the finite element method for the description of the elastic domain (the beam) and the boundary elements method for the analysis of the electrostatic field. The volume of the beam was subdivided into 70×4×4 three-dimensional solid brick elements, each with 20 nodes, while the surface of the beam was meshed using electrostatic two-dimensional panel elements. The voltage was increased incrementally from zero to a value close to the snap-through point (voltage control). At each value of the voltage, the electrostatic solver yields the electrostatic pressure distributed on the surface of the beam; the mechanical solver analyzes elastic deformations of the beam loaded by the electrostatic pressure. The mechanical and the electrostatic problems were solved sequentially using a nonlinear iterative solver until convergence and the deformed configuration of the beam was obtained [32]. Figure 3a shows good agreement between the finite element and reduced order model results.
Figure 3.
(a) Static equilibrium curves showing the finite element (markers) and reduced order model results (solid line). (b) Reduced order model results show resonant frequency as a function of the electrode displacement. Markers correspond to the numerical solution of the nonlinear ordinary differential equation (eq. (6)) and solid line corresponds to the linearized frequency (eq. (8)). In both cases, h = 2.5 μm was used near the bistablity onset.
To understand the influence of linearization used for calculation of f, Eq. (10), we numerically solved the nonlinear ordinary differential equation (6) using an integration time long enough to obtain a steady-periodic response. In our simulations, the micromechanical beam was actuated using a combination of Vdc = 94 V and Vac = 5 mV. The excitation frequency was swept from values below to above resonance. Our spectral simulations employed a simple continuation technique [55]. The dependence of the resonant frequency on the electrode displacement was built from the calculated frequency spectra at varying gap values. Since the system is non-linear, the spectral maximum value differs from the linear natural harmonic. For small vibrational amplitudes, however, this approach provides a good approximation. Figure 3(b) shows the comparison between the linearized (equation (8)) and the full nonlinear (equation (6)) results.
7. Experiment
Two separate experiments were conducted, using devices with stationary and movable electrodes. First, micromechanical beams were fabricated from single crystal silicon using a silicon on insulator wafer. Devices were lithographically defined and etched using deep reactive ion etching (Figure 4). Thickness of the device layer, buried silicon dioxide layer and substrate were ≈30 μm, ≈4 μm and ≈400 μm, respectively. The structures were actuated under ambient conditions. A constant DC bias was applied to the suspended beam, while an AC field was delivered to the electrode using an amplified output of a network analyzer. Device motion was monitored using a single beam laser Doppler vibrometer (LDV). In this scenario, the laser was focused at the midpoint of the beam with the LDV output fed back into the network analyzer. While the non-scanning, single-point LDV is unsuitable for the quantitative measurement of the in-plane vibrational amplitudes, the vibrometer’s output can be used for measuring the spectral characteristics of the beam. Here, the modulation of the reflected optical power, resulting from the coupled in-plane and out-of-plane motion, was used to measure the spectral response of the system [45]. This approach can be viewed in a sense as an example of a situation when frequency based sensing is advantageous when compared to the direct amplitude measurement.
Figure 4.
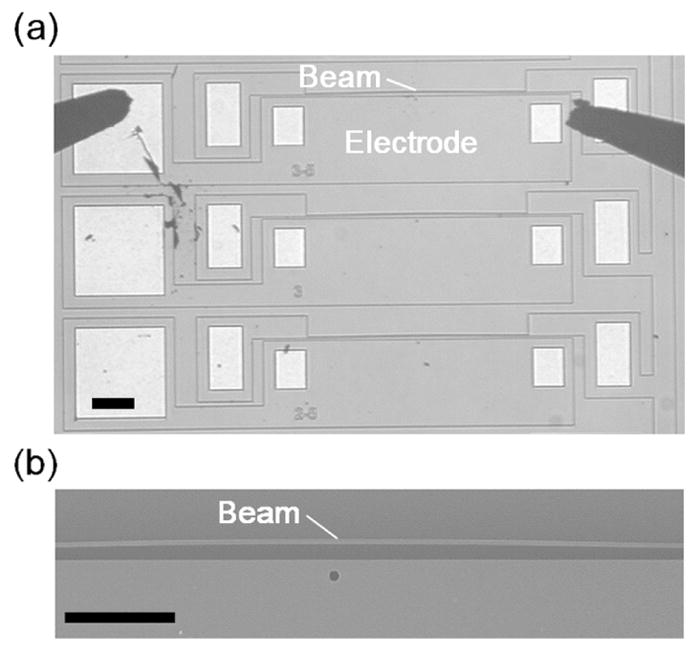
Optical (a) and scanning electron (b) micrographs of the fabricated devices. The dark circular dot in (b) is located at the midpoint of the beam. Scale bars in (a) and (b) correspond to ≈ 200 μm and ≈ 100 μm, respectively.
We measured the dynamic response of curved beams with varying h. Vdc was varied while keeping the magnitude of Vac constant and small enough to ensure linear operating conditions. Frequency spectra were measured for several values of Vdc. We used the maximum amplitude from the frequency spectra as an approximation of the natural frequency. Figure 4(a) and (b) respectively show optical and scanning electron microscope micrographs of the beams used in the experiments.
Figure 5 shows frequency tuning using various values of Vdc. Spectral characteristics of the curved beams with h ≈ 3 μm are shown in figure 5(b) for the Vdc above and below the snap-through value. The frequency behavior of both straight and curved beams observed in experiments is consistent with model predictions. Fabrication errors typically associated with micromachining processes give rise to uncertainties in device dimensions. These geometric uncertainties, coupled with the possible residual stresses within the device layer may explain the discrepancies between the model and experimental data. In order to estimate the influence of geometric uncertainties on the spectral characteristics of the device, structural harmonics were calculated for beam thickness and electrostatic gap values varying by ± 0.3 μm, and h varying by ± 0.1 μm from the respective nominal values [37]. Our experimental results fall within the bounding values predicted by the model. Specifically, the calculated snap-through voltages varied between ≈ 55 V and ≈ 80 V while the minimum point (at the snap-through) of the experimental voltage-frequency curve was at ≈ 60 V, Fig 5(d). Due to an increase in the effective stiffness associated with the axial stretching of the beam, our model and experimental results show that for beams with h ≈ 0, the resonant frequency increases with increasing Vdc. For curved beams, with increasing Vdc, the resonant frequency first decreases as the beam approaches the bistability threshold zone, above which frequency increases. We estimate frequency sensitivity using the slope of the voltage-frequency curves obtained as a fit of the experimental set of values. Our calculations show that at Vdc ≈ 80 V in figure 5(d), the sensitivity is SV ≈ 560 Hz/V, whereas at a higher voltage of Vdc ≈ 100 V, it is SV ≈ 487 Hz/V. These experiments illustrate the non-monotonic dependence of resonant frequency on Vdc during the snap-through transition. Furthermore, the experiments elucidate the accuracy of the reduced order model and its ability to predict the dynamic behavior of curved beams.
Figure 5.
Measured frequency spectra of beam with (a) h ≈ 0 and (b) h ≈ 3 μm. For h ≈ 3 μm, Vdc ≈ 40 V was below snap-through, whereas Vdc values of 65 V and 90 V were above snap-through. Measured resonant frequency (diamonds) as a function of the DC voltage for (c) h ≈ 0 and (d) h ≈ 3 μm beams. Solid lines correspond to the results provided by the reduced order model for the nominal geometry of the beams, Table 2. The statistical uncertainties based on repeated measurements are smaller than the data markers. In the case of a straight beam h ≈ 0 the hardening effect due to the nonlinear stretching of the beam axially constrained by unmovable anchors is observed in both experimental ((a) and (c)) and to theoretical (c) results.
Second set of experiments were conducted using a device with a movable electrode. We investigated the nonlinear interactions between the electrode displacement and the vibrational dynamics of the curved beam. The results overall demonstrate reliable operation of curved beams near snap-through. In this light, these micromechanical, geometrically nonlinear devices could be used as highly sensitive displacement detectors. The schematics of the device are shown in figure 6(a). Figure 6(b) shows an optical micrograph of the fabricated system. Table 3 details nominal and measured device parameters. We find that reactive ion etching and optical proximity effects cause variations in critical device dimensions. For instance, over-etching results in thinner beams and consequently larger gaps between the beam and the electrode.
Figure 6.

(a) Schematic illustration of the coupled beam-electrode device configuration. A truss-shaped movable electrode is separated from the curved beam by a narrow gap and connected to a suspended mass using a folded spring. (b) Optical micrograph of the fabricated displacement sensing devices. Scale bar corresponds to ≈ 200 μm.
Table 3.
Nominal (as designed) and measured (mean ± standard deviation) device parameters for displacement sensing. The estimated measurement error was based on pixel to μm conversion factor of the optical (L) and scanning electron micrographs (d, g0) [37].
| Parameter | Nominal value [μm] | Measured value [μm] |
|---|---|---|
| L | 1000 | ≈ 1000± 2.30 |
| d | 2.8 | ≈ 2.1 ± 0.06 |
| b | 30 | - |
| h | 2.4 | - |
| g0 | 10 | ≈ 11.0 ± 0.06 |
Analogously to experiments with stationary electrodes, DC and AC voltages were applied to the beam. Frequency was swept around resonance at constant Vdc ≈ 20 V on the beam and Vac ≈ 50 V on the electrode. Relatively high AC voltages were requited to achieve measurable amplitudes of low quality factor vibrations in air. The electrode displacement was controlled manually using probes. The distance between the beam and the electrode was measured using optical microscopy. Even though the distance is affected by electrostatic forces impinging on the electrode, we estimate this effect as negligible due to high device stiffness. We measured vibrational spectra using the LDV. Figure 7(c) shows the measured frequency dependence on electrode displacement. The frequency measurement absolute error was estimated to be ≈ 75 Hz and is based on the Lorentzian functional fit to the measured spectra. Electrode displacement measurement error bars were ≈ 90 nm [56]. The error emanates from the pixel to μm conversion ratio determined from the camera resolution and represent one standard deviation. In order to estimate the beam sensitivity to electrode displacement, the reduced order model was used to fit the experimental data. Specifically, the model results shown in figure 7(c) were obtained for h ≈ 1.7 μm, which was considered as a free parameter used for best fitting of experimental data. The reason for this choice of h stems from the fact that lithographically defined beam curvature is also affected by residual and thermal stresses [42]. The slope of the fitting curve in figure 7(c) represents the frequency sensitivity to electrode displacement. Our calculations show that at u ≈ 4 μm, the sensitivity is ≈ 1.5 Hz/nm, whereas for a smaller displacement of u ≈ 2 μm, Su ≈ 0.68 Hz/nm. Note that the working point value of Vdc ≈ 20 V used in the experiment is not optimal. By an appropriate choice of the working point voltage Vdc the sensitivity can be further improved. Specifically, our calculations suggest that for beams with optimal geometry corresponding to the bistablity onset, figure 2, relative sensitivity can reach ≈ 2 × 10−3 nm−1, which, for the adopted parameters, is equivalent to Su ≈ 25 Hz/nm.
Figure 7.

Device with different gaps between the beam and the movable electrode (a) u ≈ 0, (b) u ≈ 4.75 μm. (c) Measured resonant frequency (diamond markers) as a function of electrode displacement. The statistical uncertainties based on repeated measurements are smaller than the data markers. Solid line corresponds to the results provided by the reduced order model for the initial elevation of h ≈ 1.7 μm providing the best fit with the experimental result. Scale bars in (a) and (b) correspond to ≈ 100 μm. The frequency measurement absolute error was estimated to be ≈ 75 Hz. Electrode displacement measurement error bars were ≈ 90 nm [56].
8. Conclusions
Dynamics of curved, doubly clamped MEMS beams near critical snap-through are presented. The model results indicate that optimized h values near the bistability onset provide a mechanism for enhancing sensitivity to both changes in voltage and electrode displacement. Our numerical and experimental results are consistent with these model predictions. While previous groups have reported frequency decrease following snap-through, to our knowledge this work represents the first systematic experimental demonstration of the pre-buckling decrease and post-buckling increase of the in-plane natural harmonic. The ability to exploit the resonant behavior of curved beams shows that micromechanical resonators are promising candidates for displacement sensing. With non-optimized bistability values, we estimate displacement sensitivity (calculated as a slope of a curve fitting the experimental data) of ≈ 1.5 Hz/nm. The performance of the displacement sensor can be enhanced using optimized parameters (Table 1), yielding sensitivities of ≈25 Hz/nm, corresponding to an order of magnitude amplification (Δf/f0)/(u/g0)=O(10). Although electrostatic softening can be achieved with more complex designs and electrode configurations, the simpler single beam devices allow for compact, robust architectures, with potential for nanoscale downsizing and integration with large arrays of frequency based displacement sensors.
Table 2.
Nominal (as designed) and measured (mean ± standard deviation) beam parameters used in experiments. The estimated measurement error was based on pixel to μm conversion factor of the optical (L) and scanning electron micrographs (d, g0) [37].
| Parameter | Nominal value [μm] | Measured value[μm] |
|---|---|---|
| L | 1500 | ≈ 1500± 2.30 |
| d | 4 | ≈ 3.7 ± 0.06 |
| b | 20 | - |
| g0 | 14 | ≈ 14.3 ± 0.06 |
Acknowledgments
The devices were fabricated and tested at the Center for Nanoscale Science & Technology Facility (CNST) at the National Institute of Standards and Technology and at the Tel Aviv University Micro and Nano central characterization & fabrication facility (MNCF). The authors would like to thank Dr. Alexander Gurevich for his help with fabrication, Stella Lulinski and Lior Medina for the help with experiments and Dr. Yoav Linzon for the help with signal processing.
References
- 1.Eaton WP, Smith JH. Micromachined pressure sensors: review and recent developments. Smart Mater Struct. 1997;6:530–9. [Google Scholar]
- 2.Bell DJ, Lu TJ, Fleck NA, Spearing SM. MEMS actuators and sensors: observations on their performance and selection for purpose. J Micromech Microeng. 2005;15:S153. [Google Scholar]
- 3.Acar C, Shkel A. MEMS Vibratory Gyroscopes: Structural Approaches to Improve Robustness. New York: Springer Science & Business Media; 2008. [Google Scholar]
- 4.Kempe V. Inertial MEMS: Principles and Practice. Cambridge: Cambridge University Press; 2011. [Google Scholar]
- 5.Sarid D. Scanning Force Microscopy: with Applications to Electric, Magnetic, and Atomic Forces. New York: Oxford University Press; 1994. [Google Scholar]
- 6.Jalili N, Laxminarayana K. A review of atomic force microscopy imaging systems: application to molecular metrology and biological sciences. Mechatronics. 2004;14:907–45. [Google Scholar]
- 7.Hansen KM, Thundat T. Microcantilever biosensors. Methods. 2005;37:57–64. doi: 10.1016/j.ymeth.2005.05.011. [DOI] [PubMed] [Google Scholar]
- 8.Boisen A, Dohn S, Keller SS, Schmid S, Tenje M. Cantilever-like micromechanical sensors. Rep Prog Phys. 2011;74:36101. [Google Scholar]
- 9.Waggoner PS, Craighead HG. Micro- and nanomechanical sensors for environmental, chemical, and biological detection. Lab Chip. 2007;7:1238. doi: 10.1039/b707401h. [DOI] [PubMed] [Google Scholar]
- 10.Southworth DR, Bellan LM, Linzon Y, Craighead HG, Parpia JM. Stress-based vapor sensing using resonant microbridges. Appl Phys Lett. 2010;96:163503. [Google Scholar]
- 11.Ilic B, Craighead HG, Krylov S, Senaratne W, Ober C, Neuzil PJ. Attogram detection using nanoelectromechanical oscillators. J Appl Phys. 2004;95:3694–703. [Google Scholar]
- 12.Jiao H, Xie B, Wang J, Chen D, Chen J. Electrostatically driven and capacitively detected differential lateral resonant pressure microsensor. Micro Nano Lett. 2013;8:650–3. [Google Scholar]
- 13.Caspani A, Comi C, Corigliano A, Langfelder G, Tocchio A. Compact biaxial micromachined resonant accelerometer. J Micromech Microeng. 2013;23:105012. [Google Scholar]
- 14.Caspani A, Comi C, Corigliano A, Langfelder G, Zega V, Zerbini S. A Differential Resonant Micro Accelerometer for Out-of-plane Measurements. Proc Eng. 2014;87:640–3. [Google Scholar]
- 15.Comi C, Corigliano A, Ghisi A, Zerbini S. A resonant micro accelerometer based on electrostatic stiffness variation. Meccanica. 2013;48:1893–900. [Google Scholar]
- 16.Ding H, Zhao J, Ju B-F, Xie J. A high-sensitivity biaxial resonant accelerometer with two-stage microleverage mechanisms. J Micromech Microeng. 2015;26:15011. [Google Scholar]
- 17.He L, Xu YP, Palaniapan M. A CMOS Readout Circuit for SOI Resonant Accelerometer With 4-Bias Stability and 20-Resolution. IEEE J Solid-State Circuits. 2008;43:1480–90. [Google Scholar]
- 18.Lee B-L, Oh C, Lee S, Oh Y-S, Chun K-J. A vacuum packaged differential resonant accelerometer using gap sensitive electrostatic stiffness changing effect. The 13th Annual Int. Conf. on Micro Electro Mechanical Systems, 2000. MEMS; 2000; IEEE; 2000. pp. 352–7. [Google Scholar]
- 19.Park U, Rhim J, Jeon JU, Kim J. A micromachined differential resonant accelerometer based on robust structural design. Microelectron Eng. 2014;129:5–11. [Google Scholar]
- 20.Seshia A, Palaniapan M, Roessig T, Howe RT, Gooch RW, Schimert TR, Montague S. A vacuum packaged surface micromachined resonant accelerometer. Microelectromech Syst J. 2002;11:784–93. [Google Scholar]
- 21.Su SXP, Yang HS, Agogino AM. A resonant accelerometer with two-stage microleverage mechanisms fabricated by SOI-MEMS technology. IEEE Sens J. 2005;5:1214–23. [Google Scholar]
- 22.Wang J, Shang Y, Tu S, Liu L, Chen D. Micro-machined resonant accelerometer with high sensitivity. 2011 IEEE Int. Conf. on Nano/Micro Engineered and Molecular Systems (NEMS); IEEE; 2011. pp. 527–30. [Google Scholar]
- 23.Yang B, Wang X, Dai B, Liu X. A New Z-axis Resonant Micro-Accelerometer Based on Electrostatic Stiffness. Sensors. 2015;15:687–702. doi: 10.3390/s150100687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Joe DJ, Linzon Y, Adiga VP, Barton RA, Kim M, Ilic B, Krylov S, Parpia JM, Craighead HG. Stress-based resonant volatile gas microsensor operated near the critically buckled state. J Appl Phys. 2012;111:104517. [Google Scholar]
- 25.Zhu R, Zhang G, Chen G. A novel resonant accelerometer based on nanoelectromechanical oscillator. IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS); 2010; IEEE; 2010. pp. 440–3. [Google Scholar]
- 26.Effa D, Abdel-Rahman E, Yavuz M. Cantilever beam microgyroscope based on Frequency modulation. IEEE/ASME Int. Conf. on Advanced Intelligent Mechatronics (AIM); 2013; IEEE; 2013. pp. 844–9. [Google Scholar]
- 27.Seshia AA, Howe RT, Montague S. An integrated microelectromechanical resonant output gyrcosope. The 15th IEEE Int. Conf. on Micro Electro Mechanical Systems; 2002; IEEE; 2002. pp. 722–6. [Google Scholar]
- 28.Weinberg MS, Kourepenis A. Error sources in in-plane silicon tuning-fork MEMS gyroscopes. Microelectromech Syst J. 2006;15:479–91. [Google Scholar]
- 29.Zotov S, Trusov A, Shkel AM. High-range angular rate sensor based on mechanical frequency modulation. Microelectromech Syst J. 2012;21:398–405. [Google Scholar]
- 30.Thiruvenkatanathan P, Yan J, Woodhouse J, Seshia A. Enhancing parametric sensitivity in electrically coupled MEMS resonators. Microelectromech Syst J. 2009;18:1077–86. [Google Scholar]
- 31.Zhao C, Wood GS, Xie J, Chang H, Pu SH, Kraft M. A force sensor based on three weakly coupled resonators with ultrahigh sensitivity. Sensors Actuators A. 2015;232:151–62. [Google Scholar]
- 32.Ya’akobovitz A, Krylov S, Hanein Y. A MEMS nano-extensometer with integrated de-amplification mechanism. Microsyst Technol. 2011;17:337–45. [Google Scholar]
- 33.Muoth M, Chikkadi K, Liu Y, Hierold C. Suspended CNT-FET piezoresistive strain gauges: Chirality assignment and quantitative analysis. IEEE 26th Int. Conf. on Micro Electro Mechanical Systems (MEMS); 2013; IEEE; 2013. pp. 496–9. [Google Scholar]
- 34.Azgin K, Akin T, Valdevit L. Ultrahigh-dynamic-range resonant MEMS load cells for micromechanical test frames. Microelectromech Syst J. 2012;21:1519–29. [Google Scholar]
- 35.Hajjaj AZ, Ramini A, Younis MI. Experimental and analytical study of highly tunable electrostatically actuated resonant beams. J Micromech Microeng. 2015;25:125015. [Google Scholar]
- 36.Kafumbe SMM, Burdess JS, Harris AJ. Frequency adjustment of microelectromechanical cantilevers using electrostatic pull down. J Micromech Microeng. 2005;15:1033. [Google Scholar]
- 37.Medina L, Gilat R, Ilic B, Krylov S. Experimental investigation of the snap-through buckling of electrostatically actuated initially curved pre-stressed micro beams. Sensors Actuators A. 2014;220:323–32. [Google Scholar]
- 38.Tang WC. Digital capacitive accelerometer. 5,353,641 US Patent No. 1994
- 39.Yang H, Yu Z, Li X, Wang Y. 2005 IEEE Sensors. IEEE; 2005. A novel pull-in accelerometer based on cantilever beam mass structure; p. 4. [Google Scholar]
- 40.Rabanim S, Amir E, Schreiber D, Krylov S. Bistability under tension and its use in a threshold force sensor. IEEE 25th Int. Conf. on Micro Electro Mechanical Systems (MEMS); 2012; IEEE; 2012. pp. 1137–40. [Google Scholar]
- 41.Ouakad HM, Younis MI. The dynamic behavior of MEMS arch resonators actuated electrically. Int J Non-Linear Mech. 2010;45:704–13. [Google Scholar]
- 42.Krylov S, Ilic BR, Schreiber D, Seretensky S, Craighead H. The pull-in behavior of electrostatically actuated bistable microstructures. J Micromech Microeng. 2008;18:55026. [Google Scholar]
- 43.Medina L, Gilat R, Krylov S. Symmetry breaking in an initially curved pre-stressed micro beam loaded by a distributed electrostatic force. Int J Solids Struct. 2014;51:2047–61. [Google Scholar]
- 44.Medina L, Gilat R, Krylov S. Bouncing and dynamic trapping of a bistable curved micro beam actuated by a suddenly applied electrostatic force. Commun Nonlinear Sci Numer Simul. 2015;36:273–84. [Google Scholar]
- 45.Zohar OE, Maimon R, Vashdi O, Gerson Y, Berko H, Krylov S. Investigation of energy losses in different vibrational modes of tactical grade micro gyroscope. 2014 Int. Symp. on Inertial Sensors and Systems (ISISS); IEEE; 2014. pp. 1–4. [Google Scholar]
- 46.Lee KB, Cho Y-H. A triangular electrostatic comb array for micromechanical resonant frequency tuning. Sensors Actuators A. 1998;70:112–7. [Google Scholar]
- 47.Das K, Batra RC. Pull-in and snap-through instabilities in transient deformations of microelectromechanical systems. J Micromech Microeng. 2009;19:35008. [Google Scholar]
- 48.Younis MI. MEMS Linear and Nonlinear Statics and Dynamics. Vol. 20. Berlin: Springer; 2011. [Google Scholar]
- 49.Krylov S, Dick N. Dynamic stability of electrostatically actuated initially curved shallow micro beams. Contin Mech Thermodyn. 2010;22:445–68. [Google Scholar]
- 50.Krylov S. Lyapunov exponents as a criterion for the dynamic pull-in instability of electrostatically actuated microstructures. Int J Non Linear Mech. 2007;42:626–42. [Google Scholar]
- 51.Ouakad HM, Younis MI, Alsaleem FM, Miles R, Cui W. The static and dynamic behavior of MEMS arches under electrostatic actuation. ASME 2009 Int. Design Engineering Technical Conf. and Computers and Information in Engineering Conf; American Society of Mechanical Engineers; 2009. pp. 607–16. [Google Scholar]
- 52.Liang YC, Lin WZ, Lee HP, Lim SP, Lee KH, Sun H. Proper orthogonal decomposition and its applications – part II: model reduction for MEMS dynamical analysis. J Sound Vib. 2002;256:515–32. [Google Scholar]
- 53.Kerschen G, Golinval J, Vakaktis AF, Bergman A. The Method of Proper Orthogonal Decomposition for Dynamical Characterization and Order Reduction of Mechanical Systems: An Overview. Nonlinear Dyn. 2005;41:147–69. [Google Scholar]
- 54.Boser BE. Electronics for micromachined inertial sensors. Proc Int Solid State Sensors Actuators Conf (Transducers ’97) 1997;2:1169–72. [Google Scholar]
- 55.Krylov S, Gerson Y, Nachmias T, Keren U. Excitation of large-amplitude parametric resonance by the mechanical stiffness modulation of a microstructure. J Micromech Microeng. 2009;20:15041. [Google Scholar]
- 56.Medina L, Gilat R, Robert Ilic B, Krylov S. Experimental dynamic trapping of electrostatically actuated bistable micro-beams. Appl Phys Lett. 2016;108:73503. doi: 10.1063/1.4941731. [DOI] [PMC free article] [PubMed] [Google Scholar]






