Synchronized chaotic targeting and acceleration of surface chemistry in prebiotic hydrothermal microenvironments

Significance

We describe a physical mechanism capable of achieving simultaneous mixing and focused enrichment in hydrothermal pore microenvironments. Microscale chaotic advection established in response to a temperature gradient paradoxically promotes bulk homogenization of molecular species, while at the same time transporting species to discrete targeted locations on the bounding sidewalls where they become highly enriched. This process delivers an order of magnitude acceleration in surface reaction kinetics under conditions naturally found in subsea hydrothermal microenvironments, suggesting a new avenue to explain prebiotic emergence of macromolecules from dilute organic precursors—a key unanswered question in the origin of life on Earth and elsewhere.

Abstract

Porous mineral formations near subsea alkaline hydrothermal vents embed microenvironments that make them potential hot spots for prebiotic biochemistry. But, synthesis of long-chain macromolecules needed to support higher-order functions in living systems (e.g., polypeptides, proteins, and nucleic acids) cannot occur without enrichment of chemical precursors before initiating polymerization, and identifying a suitable mechanism has become a key unanswered question in the origin of life. Here, we apply simulations and in situ experiments to show how 3D chaotic thermal convection—flows that naturally permeate hydrothermal pore networks—supplies a robust mechanism for focused accumulation at discrete targeted surface sites. This interfacial enrichment is synchronized with bulk homogenization of chemical species, yielding two distinct processes that are seemingly opposed yet synergistically combine to accelerate surface reaction kinetics by several orders of magnitude. Our results suggest that chaotic thermal convection may play a previously unappreciated role in mediating surface-catalyzed synthesis in the prebiotic milieu.

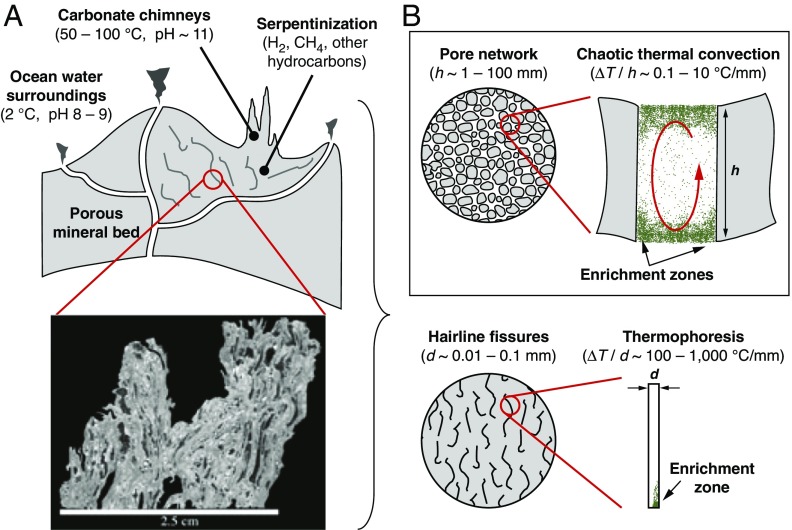
Subsea hydrothermal microenvironments uniquely embed catalytically active mineral surfaces in the presence of thermal and chemical gradients, establishing disequilibrium pathways essential for emergence of biochemical complexity (1–3). Synthesis of organic monomers, for example, can be supported in these systems via pH conditions that favor hydrogen-dependent redox processes similar to the CO₂ reducing acetyl-CoA biochemical pathway (4). The recent discovery of alkaline vent systems [e.g., Lost City vent, mid-Atlantic ridge (5, 6)] has generated particular excitement because geochemical serpentinization yields surroundings abundant in hydrogen at moderate temperatures (150–200 °C) (Fig. 1A). These attributes, combined with the excess hydrogen’s ability to exothermically reduce carbon dioxide into methane, have fueled interest in elucidating the role of alkaline vents in orchestrating synthesis of prebiotic chemical precursors critical to the origin of life (4, 7).

Fig. 1.

Hydrothermal conveyor based on chaotic thermal convection. (A) Mineral formations near off-ridge alkaline hydrothermal vents lining the ocean floor contain embedded pore networks with microenvironments that impose thermal and geometric conditions robustly capable of sustaining internal convective flow fields. Image below depicts a cross-section of material retrieved from the Lost City vent illustrating its internal void morphology. (Scale bar, 2.5 cm.) Reproduced with permission from ref. 18. (B) These vent systems embed characteristic porosity and thermal gradients aligned with chaotic thermal convection. Length scales and thermal gradients associated with thermophoretic focusing are illustrated for comparison.

But, a favorable chemical environment alone is not sufficient to drive macromolecular synthesis owing to the extremely dilute concentrations of precursor compounds in the prebiotic ocean (8–11). Recent studies have explored the combined action of laminar (2D) thermal convection and thermophoresis as a physical enrichment mechanism, albeit in hairline-sized fissures (diameter d ≤ 100 µm) under steep thermal gradients (100–1,000 °C/mm) (12–15). In contrast, surprisingly complex 3D flows characterized by chaotic thermal convection (16, 17) emerge over a broader pore size range [millimeters to centimeters, consistent with porosities in young active carbonate chimneys (18)] and under moderate temperature gradients (0.1–10 °C/mm) (19, 20) (Fig. 1A and SI Appendix). Here we apply simulations and in situ experiments to show how chaotic thermal convection under conditions mimicking those in microscale hydrothermal microenvironments promotes synchronized mixing of chemical species in the bulk while simultaneously accelerating enrichment at discrete sidewall locations (Fig. 1B), thereby enhancing surface reaction kinetics by several orders of magnitude.

Results

Targeted Enrichment.

We first wanted to ascertain where dispersed chemical species are likely to encounter the surface, and how the distribution of these surface encounter sites changes with flow conditions. This was achieved by using 3D computational simulations to quantify surface enrichment in cylindrically shaped pores across a range of size scales representative of hydrothermal microenvironments in off-ridge vent systems. Under these conditions, accessible states of fluid motion under thermal convective transport can be mapped in terms of the pore geometry (aspect ratio, h/d) and thermal gradient [expressed in terms of the dimensionless Rayleigh number, Ra = [g β (T₂ – T₁) h³]/ν α, where β is the fluid’s thermal expansion coefficient, g is gravitational acceleration, T₁ and T₂ are the temperatures of opposing top (cold) and bottom (hot) surfaces, respectively, h and d denote the height and diameter of the cylindrical pore space, α is the thermal diffusivity, and ν is the kinematic viscosity] (16). An aqueous dispersion of precursor molecular species at 10⁻⁷ M (representative of prebiotic concentrations, SI Appendix) was subjected to a vertical temperature gradient (bottom 95 °C, top 55 °C).

To map the distribution of surface adsorption sites, an ensemble of 300 randomly distributed Lagrangian passive tracers was tracked in 3D during 5 min of flow, and the location where each tracer’s trajectory penetrated a 50-µm adsorption boundary layer adjacent to the sidewalls was recorded to obtain surface distribution profiles. These profiles were characterized in terms of a focusing index $f=\langle {\left(I-\langle I\rangle \right)}^2\rangle$, where I represents the local surface adsorption density relative to the average value over the entire sidewall domain $\langle I\rangle$ (SI Appendix, Fig. S2), enabling a parametric map to be constructed depicting the extent of targeted enrichment achievable across a broad range of thermal and geometric conditions (Fig. 2A).

Fig. 2.

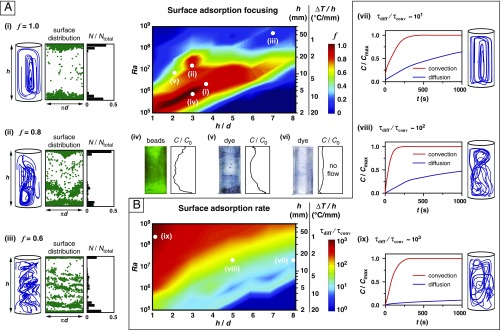
Regimes of targeted surface enrichment and accelerated adsorption kinetics. (A) Computational simulations enable enrichment, quantified in terms of a focusing index f, to be parametrically plotted in terms of the Ra, h/d, and thermal gradient. (A, i–iii) Depiction of representative flow trajectories (Left) and sidewall adsorption profiles corresponding to 300 tracers randomly dispersed in the bulk (Center, individual realizations; Right, vertical distribution histogram). Images below the parametric plot display experimentally obtained sidewall adsorption profiles with (A, iv) fluorescently tagged 1-µm-diameter carboxylated microspheres, and (A, v and vi) methylene blue dye [Left, side-view photograph of cylindrical pore; Right, vertical intensity profile of normalized (A, iv) green and (A, v and vi) blue color channel intensity]. (B) Computational simulations incorporating a kinetic surface adsorption model enable the time-resolved surface accumulation of chemical species on the pore sidewalls to be quantified. Adsorption kinetics are accelerated by up to 1,000-fold in the presence of thermal convection compared with molecular diffusion alone, and this enhancement correlates with a transition from periodic to disordered flow trajectories (B, vii–ix). Pore geometries in A and B are not depicted to scale to facilitate comparison between them.

The results of these simulations can be broadly classified into three characteristic regimes based on the combination of Ra and h/d values (representative states are shown in Fig. 2 A, i–iii). Periodic flow trajectories promote tightly focused enrichment profiles (Fig. 2 A, i), as evident by pronounced surface accumulation bands located near the upper and lower pore boundaries. These profiles become distorted at higher Ra as the flow trajectories undergo a transition to chaos (16) (Fig. 2 A, ii), but preferential accumulation near the upper and lower pore boundaries is retained. Targeted enrichment does not occur beyond Ra > 10⁸ as the increasingly distorted flow trajectories promote uniformly distributed surface adsorption profiles (Fig. 2 A, iii); all flows remain inertially laminar with characteristic values of the Reynolds number in the vicinity of 1∼500).

Experiments reveal that targeted sidewall enrichment is observed in species at both the micrometer scale (1-μm-diameter carboxylated microspheres, Fig. 2 A, iv) and molecular-scale (methylene blue dye, Fig. 2 A, v). In all cases where flow is present, nearly complete transport of material from the bulk to the surface is observed, whereas only a small fraction of the bulk species present near the solid boundaries becomes adsorbed under stagnant conditions (i.e., in the absence of flow when the process is diffusion-dominated, Fig. 2 A, vi). Taken together, these results suggest a robust mechanism for discretely focused surface adsorption under hydrothermally relevant conditions.

Adsorption Kinetics.

We broadened our 3D flow simulations to adopt a kinetic model incorporating both adsorption and desorption to track the time-resolved surface concentration of species at the sidewall boundaries. Adsorption at the pore sidewalls was modeled by coupling the flow equations with a first-order liquid-phase kinetic model, and adsorption rate constants were estimated from adsorption isotherms of prebiotically relevant reactions (SI Appendix, Fig. S3 and Table S1). In this context, our simulation results necessarily explore fast, nearly irreversible, kinetic pathways (forward rates ∼100-fold higher than reverse rates). These data closely resemble response to a step input of first-order C/C_max = (1 – exp(– t/τ)), where C and C_max are the instantaneous and final equilibrium (i.e., corresponding to saturation of active sites) surface concentrations, respectively, t is time, and τ is a time constant. We also determined time-resolved surface concentrations associated with purely diffusive transport by analytically solving the transient 2D diffusion equation in cylindrical coordinates, from which time constants associated with convection (flow; τ_conv) and diffusion (the “null” no-flow condition; τ_diff) were obtained. These simulations reveal that the slowest adsorption rates occur under conditions where flow trajectories display periodicity (Fig. 2 B, vii and viii). Conversely, pore spaces displaying the fastest adsorption rates are characterized by disordered states where homogenization in the bulk continually replenishes adsorbed species near the sidewall boundaries, inhibiting formation of a depletion zone (Fig. 2 B, ix).

The Role of Chaotic Advection.

The results in Fig. 2 appear to indicate that simultaneous localized surface enrichment and accelerated interfacial transport are mutually exclusive. Periodic flow states favor targeted surface adsorption but accumulation occurs slowly, whereas disordered flow states yield rapid surface accumulation but adsorption is not localized. This interplay can be quantified by a figure of merit defined by the product f × (τ_diff/τ_conv), a quantity that can also be plotted in terms of a parametric map (Fig. 3A). Paradoxically, this analysis reveals a relatively broad “sweet spot” at intermediate Ra and h/d where synchronized targeted enrichment and accelerated adsorption is achievable. Corresponding midplane Poincaré plots display Kolmogorov–Arnold–Moser loci with disrupted boundaries within this regime, suggesting divergence of neighboring flow paths consistent with a transition to chaos (21).

Fig. 3.

Chaotic thermal convection synchronizes targeted and accelerated surface enrichment. (A) Computationally simulated parametric plot of the figure of merit f × (τ_diff/τ_conv) reveals a regime at intermediate Ra and h/d, and at modest thermal gradients, where simultaneous targeted and accelerated surface enrichment is achievable (f is scaled such that its magnitude ranges from zero to unity). This sweet spot, spanning orders of magnitude in thermal and geometric conditions, is characterized by chaotic advection. The expanded panel at the left depicts the chaotic nature of the flow at h/d = 2, both qualitatively in terms of midplane Poincaré sections (Left), and quantitatively in terms of Lyapunov exponent spectra (Right). Symbols at the left of each panel match the corresponding states in the parametric plot. (B) Simulations also quantify the strength of the chaotic flow component by increased values of the Lyapunov exponent λ within the sweet-spot regime, compared with states at lower Ra or higher h/d where periodic trajectories predominate.

We used our 3D simulation data to quantify the chaotic nature of these flow states in terms of the Lyapunov exponent (λ)—a parameter representing the rate of divergence experienced by flow trajectories initially in close proximity (SI Appendix). An ensemble of 500 randomly distributed trajectories was analyzed to generate Lyapunov exponent spectra (shown in Fig. 3A for h/d = 2), from which the average values plotted in Fig. 3B were obtained. These data indicate that the figure of merit sweet-spot regime coincides with emergence of chaos (the Péclet number Pe >> 1 over the entire parameter space and increases with Ra, SI Appendix, Fig. S6). Notably, these conditions correspond to modest thermal gradients characteristic of hydrothermal vent systems. We remark that although flow states in the sweet-spot regime are predominantly chaotic (and therefore can be considered globally ergodic), they also embed a small fraction of dispersed periodic trajectories [quantitatively evident by a shift in the Lyapunov exponent spectra toward greater values (22) with increasing Ra in Fig. 3A]. But, coexistence of these periodic “islands” does not impose a significant transport barrier because the broader chaotic nature of the flow field dominates (SI Appendix, Fig. S5).

Interfacial Transport.

Chaotic advection in the pore-mimicking system considered here retains the global periodicity desirable for targeted surface accumulation, but because the corresponding flow trajectories are not closed (i.e., as evident by the midplane Poincaré plots in Fig. 3A), transport from the bulk to the surface can be sustained for an extended time. This interplay can be quantified by examining the time evolution of the Sherwood number Sh = – d(ln(C_b))/dZ, a parameter expressing the relative contributions of convection and diffusion to interfacial mass transfer (C_b is the bulk species molar concentration and Z is a dimensionless distance from the bounding surface). We performed 3D flow simulations incorporating coupled surface reaction across the upper bounding surface (values we report, Sh_av, are averaged over a reaction interface imposed at the top surface of the pore, SI Appendix). Results are presented as a function of a dimensionless residence time t* = t U/h, where t is time, U is the average velocity magnitude, and h is the pore height.

These simulations show that Sh_av evolves much differently under chaotic and periodic flows (Fig. 4A; simulated flows were validated experimentally by visualization of fluorescent tracer beads, Fig. 4B and Movie S1). Periodic states (i.e., small λ) are characterized by a continuous decrease in Sh_av as the species depletion layer adjacent to the upper reaction surface grows progressively larger owing to inefficient molecular exchange among closed flow trajectories in the bulk. Chaotic states (i.e., high λ), on the other hand, display significantly less decay in Sh_av, achieving an asymptotic plateau value an order of magnitude greater than in the periodic case. This sustained enhancement in Sh_av associated with the chaotic regime is maintained over long times t* when compared against periodic flows of varying strength (expressed in terms of Ra, Fig. 4A). Oscillations in Sh_av reflect time-dependent fluctuations in the flow field, particularly at large Ra [similar observations have been reported in studies of chaotic heat and mass transport involving open pore systems (23)].

Fig. 4.

Chaotic advection accelerates interfacial transport under hydrothermally relevant conditions. (A) Computationally simulated interfacial Sherwood number averaged across a reaction interface spanning the top pore surface (Sh_av) continually decays under periodic flow but achieves an order of magnitude greater plateau value under chaotic advection [h/d = 2, Ra = 1.2 × 10⁵ (periodic); h/d = 2, Ra = 1.2 × 10⁷ (chaotic); and h/d = 6, Ra = 1.2 × 10⁷ (periodic)]. (B) Experimental observations obtained by recording motion of 10-µm fluorescent microspheres are in agreement with simulated flow trajectories under both chaotic (d = 6.4 mm) and periodic (d = 1.4 mm) states at h/d = 2 (Movie S1). (C) Simulated projections of the solute mass fraction x_f,A along a midvertical plane in each pore geometry (arrows indicate that the reaction interface is located at the upper surface) reveal that chaotic advection (Top) enables a thin interfacial boundary layer to be maintained as solute species are continually homogenized in the bulk. Molecular diffusion (no flow, Bottom) is also depicted as a control. Symbols match the flow states depicted in Fig. 3.

We also mapped the reacting species concentration distributions within the bulk of the pore as a function of residence time t* (Fig. 4C). Under chaotic conditions, bulk homogenization enables a species concentration gradient to be maintained near the upper reaction surface so that efficient interfacial transport occurs throughout the entire residence time, whereas periodic flow states are characterized by a growing depletion layer that imposes a barrier to interfacial transport. Microscale chaotic advection has been previously explored as a means to enhance bulk mixing in steady-state axial flows involving continuous transport of species from inlet to outlet (24). In contrast to our observations, results of these studies suggest that enhanced mixing in the bulk does not necessarily augment transport to the sidewall surfaces because chaotic and nonchaotic flow states act similarly to inhibit growth of near-wall species depletion zones over the timescale of residence within the microchannel (25), leading to a generally accepted conclusion that chaotic advection does not appreciably enhance interfacial transport in these scenarios (26). This regime is evident at residence times below t* ∼ 10 in our pore-mimicking system, where the data in Fig. 4A show comparable values of Sh_av, among all flow states.

But, axial microchannel flows do not optimally represent prebiotic conditions where sustained interfacial transport over a prolonged period is needed to catalyze synthesis and/or assembly from extremely dilute chemical precursors. This requirement points to a need for operation on the right-hand side of the parameter space in Fig. 4A (t* > 10), where the enhanced plateau value of Sh_av attained under chaotic advection confers a distinct advantage over nonchaotic flows where Sh_av continues to decrease.

In Situ Experiments.

Interfacial transport and surface reactions are challenging to dynamically probe in situ at pore-like size scales, with the majority of experimental approaches focusing on characterization by periodic removal and analysis of reaction products (with limited temporal resolution) or by fluorescence-based methods (with limited and often nonlinear dynamic range). We addressed these limitations by using an electrochemically based technique whereby the upper surfaces of pore-mimicking cylindrical cells were patterned with addressable 100-nm-thick microfabricated copper electrodes (Fig. 5A). In this way, surface-mediated reactions within a pore can be represented by electrochemical dissolution of the electrodes, an easily observable process that occurs slowly at neutral pH but becomes rapid in alkaline surroundings (Fig. 5B). These conditions mirror those encountered in alkaline off-ridge vent environments (27) that embed surface charge densities favoring biomolecular adsorption (28).

Fig. 5.

In situ probe reveals accelerated surface electrochemistry under chaotic thermal convection. (A) Addressable Cu electrodes patterned on a glass substrate affixed to the top surface of a pore-mimicking cylindrical flow cell enable electrochemical dissolution to be viewed from above (drawing not to scale). (B) Anodic dissolution occurs slowly at neutral pH, but is accelerated under alkaline conditions (images of the anode taken after a 3-V potential was applied for 1 min, no convective flow imposed). (C) In the absence of convection, the anode surface is not visibly changed when a 3-V potential is applied in an aqueous solution containing a 100-base-pair double-stranded DNA ladder (1 μg/mL, pH = 7). (D) But, dissolution progresses rapidly when a convective flow is imposed that continuously transports negatively charged DNA toward the anode where the electrophoretically compacted film stabilizes a local pH gradient, favoring Cu dissolution. (E) Experimentally obtained video recordings of the electrodes were analyzed to quantify anodic dissolution at the upper pore surface as a function of time (symbols). These data were used as inputs to a simulated kinetic predictive model (lines). (Insets) Images of the anode corresponding to each condition. A control experiment under convective flow (Ra = 3.4 × 10⁵, h = 4 mm) in the absence of DNA is also shown (open green symbols). Scale: all electrodes are 500 µm wide. (F) Kinetic model of electrode dissolution yields predicted values of τ_diff/τ_conv (G) in agreement with the parametric map in Fig. 2B.

We used these phenomena to spontaneously establish a pH gradient localized at the anode. Pore-mimicking test cells matching the simulation conditions in Fig. 3A (h/d = 2; h = 2.8–12.8 mm) were loaded with an aqueous solution containing a mixture of double-stranded DNA fragments with lengths in the 100–1,000 base-pair range (SI Appendix) (29, 30). The resulting electrophoretically confined DNA film imposes a membrane-like barrier against transport of electrochemically generated OH^– ions into the surroundings, leading to a local increase in pH that acts to accelerate the rate of copper dissolution (Fig. 5 C and D) (31). The convective flow’s ability to mediate surface reaction kinetics can then be monitored in situ by analyzing video recordings of the electrodes to quantify the dissolved mass of Cu as a function of time. These experiments reveal that dissolution progresses slowly under quiescent conditions but becomes dramatically accelerated when a convective flow is established (Fig. 5E), owing to enhanced transport of DNA from the bulk solution to the anode.

We simulated electrochemical dissolution of the copper anode using a simplified mass action kinetic model based on experimentally determined rate constant inputs (SI Appendix). This model (Fig. 5F) captures the sidewall surface adsorption kinetics in Fig. 2B, validating our analysis in terms of a framework chiefly governed by transport from the bulk to the solid interface (the Ra range covered in simulation is broader than in experiments because Cu dissolution at high Ra occurred so rapidly that the applied potential was disrupted within a few seconds; SI Appendix, Fig. S4). We used our kinetic model to compute time constants corresponding to the same range of flow states at h/d = 2 where Lyapunov exponents were determined in Fig. 3A (Fig. 5G). These data reveal that chaotic thermal convection generates nearly a 1,000-fold enhancement in τ_diff/τ_conv. Finally, plotting the Cu dissolution rate data in terms of the residence time t* (SI Appendix, Fig. S7) reveals behavior consistent with the interfacial transport model in Fig. 4, confirming that chaotic advection delivers accelerated surface reaction kinetics under conditions where sustained interfacial transport is needed.

Conclusions

Chaotic thermal convection provides a mechanism to explain prebiotic emergence of complex biomacromolecules from dilute organic precursors—a key unanswered question in the origin of life on Earth and in exobiological scenarios [e.g., the Jovian moon Europa and the Saturnian moon Enceladus (32)]. Of particular note is the potential to enable assembly of oligomers into membrane-like films capable of sustaining pH gradients (Fig. 5D), a precursor to establishment of basic metabolic processes (33). Finally, we remark that a diverse array of processes beyond prebiotic biochemistry can be catalyzed in hydrothermal microenvironments. Porous submarine mineral formations play a key role in geothermal conversion of CO₂ into stable carbonates and partial reduction to formate, carbon monoxide, and methane (34, 35), suggesting a compelling role for the thermal convection phenomena described here in mediating transport and reaction of CO₂ along pathways not captured in existing climate models.

Materials and Methods

Computational Simulations.

Simultaneous flow, interfacial transport, and reaction were simulated using the finite-volume solver of STAR-CCM+ (CD-adapco). A complete description of the models used is provided in the SI Appendix.

Electrochemical Dissolution Experiments.

Materials and methods associated with construction of convective flow cells with embedded Cu electrodes and complete experimental procedures are provided in the SI Appendix.