Objective Assessment of the Evolutionary Action Equation for the Fitness Effect of Missense Mutations Across CAGI Blinded Contests

Abstract

A major challenge in genome interpretation is to estimate the fitness effect of coding variants of unknown significance (VUS). Labor, limited understanding of protein functions, and lack of assays generally limit direct experimental assessment of VUS, and make robust and accurate computational approaches a necessity. Often, however, algorithms that predict mutational effect disagree amongst themselves and with experimental data, slowing their adoption for clinical diagnostics. To objectively assess such methods, the Critical Assessment of Genome Interpretation (CAGI) community organizes contests to predict unpublished experimental data, available only to CAGI assessors. We review here the CAGI performance of Evolutionary Action (EA) predictions of mutational impact. EA models the fitness effect of coding mutations analytically, as a product of the gradient of the fitness landscape times the perturbation size. In practice, these terms are computed from phylogenetic considerations as the functional sensitivity of the mutated site and as the magnitude of amino acid substitution, respectively, and yield the percentage loss of wild-type activity. In five CAGI challenges, EA consistently performed on par or better than sophisticated machine learning approaches. This objective assessment suggests that a simple differential model of evolution can interpret the fitness effect of coding variations, opening diverse clinical applications.

INTRODUCTION

Numerous computational methods seek to predict the impact of genetic variations on fitness (Jordan et al. 2010; Katsonis et al. 2014; Cardoso et al. 2015). Most of them focus on protein coding variants, which are single nucleotide substitutions that change an amino acid in the encoded protein. Although protein coding genes only constitute less than 2% of the human genome, it is estimated that they harbor 85% of disease-related mutations (Choi et al. 2009). Several methods rely purely on homology information, estimating whether a given substitution fits with the amino acid differences observed in other species at that same residue position (Ng and Henikoff 2001; Stone and Sidow 2005; Reva et al. 2007; Reva et al. 2011; Choi et al. 2012). However, the vast majority of the methods also apply machine learning techniques, trained over large datasets and numerous features that may include sequence conservation, functional site information, solvent accessibility, secondary structure, crystallographic B factors, local sequence environment, and intrinsic disorder, amongst others (Karchin et al. 2005; Yue and Moult 2006; Bromberg and Rost 2007; Li et al. 2009; Adzhubei et al. 2010; Liu et al. 2011; Capriotti et al. 2013; Carter et al. 2013; Wei et al. 2013; Kircher et al. 2014; Schwarz et al. 2014; Fariselli et al. 2015; Niroula et al. 2015). Although some studies support clinical value (Chan et al. 2007), the performance of these methods is generally mixed with limited agreement to each other (Castellana and Mazza 2013) and with clinical or experimental data (Tchernitchko et al. 2004; Flanagan et al. 2010; Miosge et al. 2015; Walters-Sen et al. 2015). A common problem, for example, is that performance is sensitive to the availability of sufficient protein homology and structure information (Marini et al. 2010; Hicks et al. 2011). A deeper problem is that the integrative modeling of the multiscale impact of a mutation from the protein to the pathway, to the network and on to a cell, a tissue, and an organism appears far too complex for current tools. In search of an alternative approach that focuses on overall fitness effect, we derived an Evolutionary Action (EA) equation for the fitness effect of coding genetic changes (Katsonis and Lichtarge 2014). EA is the product between the functional sensitivity (i.e. importance) of the mutated protein sequence position and the size of the mismatch introduced by the amino acid switch. As such, EA requires no specific training. Its performance was evaluated against large mutagenesis study datasets (Katsonis and Lichtarge 2014), but the CAGI challenges provided a unique opportunity for independent, objective assessment.

The community of Critical Assessment of Genome Interpretation (CAGI) aims to objectively assess computational methods for predicting the phenotypic impact of genomic variations. Until now, CAGI has organized 4 contests in 2010, 2011, 2013, and 2015 that involved a total of 37 challenges. Only 9 of these challenges asked predictors to estimate the fitness effect of single genetic variants and were suited for EA. The rest of the challenges focused on whole exome sequencing data interpretation of complex traits or on specific tasks that a fitness impact predictor can not address directly, such as case-control distributions and activity restoration, among others. We applied EA to 7 of these fitness effect challenges, as the EA method was unavailable during the first CAGI experiment and a deadline for the NPM-ALK challenge in CAGI 4 was missed. Here, we report on 5 challenges, after we excluded two. First, the BRCA challenge of CAGI 3 (2013) because the variant classification was not robust, leaving 52 of 62 missense variants (more than 80%) annotated as variants of unknown significance, and then the SCN5A challenge of CAGI 2 (2011) because it only involved 3 variants, too few to drive conclusions. In order to assess the methods objectively, CAGI assigned independent assessors to each challenge, often from the team that provided the experimental data. Assessors had freedom to choose any assessment tests and strategy. Most often, assessors used multiple tests that evaluate either the rank of the predictions or their proximity to experimental values. Predictions that perform well in tests of the first type may not necessarily perform well in the tests of the other type, and vice versa. Also, there may be tradeoff between some tests, such as between precision and recall (Buckland and Gey 1994), since the choice of a cutoff may favor performance in one test at the expense of the performance in the other test. Therefore, integrating multiple tests into one overall score has been a common practice in CAGI challenges. Some assessors avoided highlighting one of the methods as the winner, but they rather presented a comprehensive view of the strengths and weaknesses of the submitted methods, often of those with the best performances.

We used our EA method to address CAGI challenges that asked for predictions of the functional and clinical impact of missense mutations. Specifically, we participated in three challenges of CAGI 4 (SUMO ligase, Pyruvate kinase, and NAGLU), in one challenge of CAGI 3 (p16), and one challenge of CAGI 2 (CBS). In each case, the EA scores ranked the amino acid substitutions by their predicted impact on fitness, so that substitutions with larger fitness changes had high scores (see Methods). Since EA scores have already been shown to correlate with the fraction of deleterious mutations in four different experimental systems (Katsonis and Lichtarge 2014), these EA scores, here, were treated as the probability of a substitution to be deleterious for the protein function. The final predicted values were modified specifically to match the experimental scales of each challenge with simple linear transformations. This last choice is simple, but potentially introduces errors if the assay sensitivity was non-linear.

Briefly, the EA method was based on the hypothesis that protein evolution proceeds in infinitesimal fitness steps (Fisher 1930; Orr 2005) and so can be described by a continuous and differentiable evolutionary function that links genotype and phenotype. If so, a mutation can be viewed as a perturbation of the genotype and its effect on the phenotype should be given by differentiating the evolutionary function. This leads to the action of a single missense mutation as a product of the gradient of the evolution function and the magnitude of the mutation. The gradient can be understood as the sensitivity of a protein sequence position to amino acid substitution, i.e. the importance of the genotype position as measured by the Evolutionary Trace algorithm (Lichtarge et al. 1996; Mihalek et al. 2004; Lichtarge and Wilkins 2010). The magnitude of the amino acid change can be approximated with context-dependent log-odds. Together these terms yield the EA scores. Of note, the Evolutionary Trace algorithm, aka the gradient of the evolutionary function, has been used in broad applications, such as to identify functional sites and allosteric pathway residues (Yao et al. 2003), guide mutations that block or reprogram function (Rodriguez et al. 2010), and define structural motifs that predict function on large-scale (Ward et al. 2009; Erdin et al. 2010), such as substrate specificity (Amin et al. 2013). Also, the use of amino acid substitution log-odds is a well-established measure of amino acid similarity (Henikoff and Henikoff 1992) and its context dependence is well-known (Overington et al. 1992), although a dependence on predicted functional importance was first used in calculating the EA scores (Katsonis and Lichtarge 2014). In that same study, EA was predictive on large data sets of experimental assays of molecular function, clinical associations with human disease, and population allelic frequency of human polymorphisms, so that the EA equation matched positive controls and was validated across multiple biological scales.

Here, we reviewed the performance of EA on the CAGI challenges. For each challenge, first, we examined qualitatively the relationships between the experimental values and the EA scores by binning the data points according to the experimental or the predicted values, respectively. Then, we presented the objective assessments of the CAGI assessors and provided details on what assessment tests were used and whether an overall ranking that weighs multiple tests have been provided by the assessor. Last, for all challenges, we showed the performance of the submissions according to Pearson’s Correlation Coefficient and Receiver Operating Characteristic plots that were performed by the authors in order to compare performance between different challenges. We also calculated these two tests for two well-established methods, PolyPhen2 (Adzhubei et al. 2010) and SIFT (Ng and Henikoff 2001), as points of reference (details on using these predictors can be found in Methods). Depending on the dataset availability, we also examined whether the submitted predictions performed better on subsets of mutations that had low standard deviation of experimental replicates and therefore higher confidence for the experimental values.

Evolutionary Action Approach

In order to assess the impact of mutations, we considered a sequence space (Smith 1970) that mapped onto a fitness landscape (Wright 1932). There, each mutation should cause a small displacement away from an idealized equilibrium position for the species, defined as an average over the fitness landscape position of all individuals for that species. Let (r₁, r₂, …, r_i, …, r_n)_P be the genotype, γ, of the protein of interest, P, and φ be the fitness phenotype that integrates all the structural, dynamic, and functional attributes that affect the survival and reproduction of the organism. Our hypothesis is that γ and φ are coupled to each other by a continuous and differentiable evolutionary fitness function f, which implicitly accounts for all selection constraints and their variations over time. If so, a small genotype perturbation dγ will change the fitness phenotype by dφ, which will be given by:

$$d\phi =\mathit{\nabla }f•d\mathit{\gamma },$$ (1)

where ∇f is the gradient of f and • denotes the scalar product. For a single amino acid change at sequence position i, from X to Y, the genotype perturbation becomes the magnitude of the substitution (Δr_i,X→Y) and the gradient becomes the partial derivative of f for its i^th component (∂f/∂r_i). Neglecting higher order terms arising from epistatic interactions with co-occurring mutations (Marks DS et al. 2011; Breen et al. 2012), the phenotypic change, or action, of the amino acid substitution becomes:

$$\mathrm{\Delta }\phi \approx \frac{\partial f}{\partial r_i}•\mathit{\Delta }{r}_{i,X\to Y}.$$ (2)

This is the Evolutionary Action equation, which states that a missense mutation displaces fitness from its equilibrium position by an amount that is proportional to the evolutionary fitness gradient at that site and the magnitude of the amino acid change. Critically, although the function f is unknown, the terms of expression (2) may nevertheless be approximated from empirical data on protein evolution.

We approximated the evolutionary fitness gradient ∂f/∂r_i with the relative importance ranks of the Evolutionary Trace (ET) method (Lichtarge et al. 1996; Mihalek et al. 2004; Lichtarge and Wilkins 2010). The gradient represents the displacement of the fitness phenotype for an elementary genotype change. We hypothesized that evolution proceeds in infinitesimal steps (Orr 2005), so any spontaneous amino acid change in protein evolution is an elementary genotype change that adapts fitness in the genetic and environmental context the protein operates (Coyne and Orr 1998). We also hypothesized that f is continuous and differentiable, so, the gradient equals to the difference in fitness phenotype caused by an elementary genotype change. Together, these two hypotheses suggest that the gradient can be measured by quantifying the correlation of amino acid variation and phylogenetic branching, such as the ET algorithm does (Lichtarge et al. 1996). In the extreme cases, invariant sequence positions yield the maximum evolutionary fitness gradient because any genotypic change can displace fitness beyond any homologous protein, while positions that vary even between the closest homologous sequences yield the minimum evolutionary fitness gradient.

To measure the magnitude of a substitution (Δr_i,X→Y), we used the odds of observing each substitution in homologous proteins (Henikoff and Henikoff 1992; Overington et al. 1992). For example, the amino acid alanine is substituted to serine more often than to aspartate, in line with greater biophysical and chemical similarities to the former. However, we found that the substitution odds also depend on the evolutionary gradient of the substituted position. For example, the alanine to valine substitution odds form a bell-shaped distribution as the evolutionary gradient at the mutated position varies from maximum to minimum; those of alanine to threonine begin flat then tail off, whereas those of alanine to aspartate decay steadily (Katsonis and Lichtarge 2014). Similarly, differences in the substitution odds were found depending on structural features (Overington et al. 1992). Therefore, we approximated Δr_i,X→Y by substitution odds that depend on the evolutionary importance and on protein structure features of the residue.

METHODS

Calculation of the Evolutionary Action (EA)

The EA scores were calculated according to the public web server available for non-profit use at the URL: mammoth.bcm.tmc.edu/uea, where the human protein name and the amino acid substitution may be used as input. Briefly, the evolutionary action Δφ of each mutation was the product of the evolutionary gradient ∂f/∂r_i and the perturbation magnitude of the substitution, Δr_i,X→Y. These two terms, ∂f/∂r_i and Δr_i,X→Y, were measured by percentile ranks of Evolutionary Trace scores and of amino acid substitution odds, respectively, as described previously (Katsonis and Lichtarge 2014). All terms, including the EA scores, have been used in the form of percentile ranks, such that high or low scores indicated high or low impact of the genetic variation, respectively. For example, an EA of 68 implied that the impact was higher than 68% of all possible amino acid substitutions in a protein.

Calculation of other predictors of mutation impact

SIFT predictions were obtained using “SIFT BLink” (http://sift.jcvi.org/), where we provided the GI number of the query protein. Specifically, we used the GI numbers of 4557415 (CBS), 4502749 (p16), 4507785 (SUMO ligase), 32967597 (Pyruvate kinase), and 66346698 (NAGLU). The result was a score between 0 (deleterious) and 1 (neutral) for each possible amino acid substitution within the sequence. SIFT scores were treated as the fraction of the remaining protein function over the wild-type function of the protein (0 means 0% and 1 means 100% function).

PolyPhen2 predictions were obtained using the default parameters (HumDiv classifier) of the batch query tab of PolyPhen2 server (http://genetics.bwh.harvard.edu/pph2/), where we provided the NP identifier of the query protein, the protein residue number, and the wild-type and substitute amino acids. We used the NP identifiers of NP_000062 (CBS), NP_000068 (p16), NP_003336 (SUMO ligase), NP_870986 (Pyruvate kinase), and NP_000254 (NAGLU). We used the “pph2_prob” value as the prediction score, which ranges between 0 (neutral), and 1 (deleterious), to scale it between 0% and 100% loss of the wild-type function of the protein, respectively.

Statistical tests

AUC of ROC

The Area Under the Curve of the Receiver Operating Characteristic plots were calculated using in-house algorithms. The experimental values were transformed to binary values (0 or 1). Typically, the cutoff value was set to 50% of the wild-type protein function, while for the p16 challenge we used a cutoff of 75 (experimental values ranged from 50 to 100), as suggested by the bimodal distributions of the experimental values. Multiple cutoffs were also studied when the challenge provided a sufficient number of experimental values of experimental values.

Pearson's Correlation Coefficient

It was calculated using the built-in function of Microsoft Office Excel.

RESULTS

The EA method to estimate the functional and clinical impact of missense mutations was evaluated in five CAGI challenges. In each one, we tested whether the experimental and the predicted values were correlated linearly, or through a more complex dependence, by plotting the average experimental values as a function of the EA scores and the average EA scores as a function of the experimental values. In order to calculate these relationships we binned the data, often by every 20 or 10 variants when the dataset had more or less than 200 variants, respectively. Datasets with less than 20 variants were not binned, while coarse binning was used when the experimental values were unevenly distributed. Then, we presented the independent and unbiased assessment of the performance of each submitted prediction, according to the summary of the CAGI assessor. Finally, we presented two widely-used statistical tests (the Receiver Operating Characteristic (ROC) curves and Pearson's Correlation Coefficient test), as calculated by the authors, in order to provide common ground on comparing performances across different CAGI challenges. We also applied these two tests on predictions from the two most cited mutation impact prediction methods, PolyPhen2 (Adzhubei et al. 2010) and SIFT (Ng and Henikoff 2001).

SUMO ligase (CAGI 4 – 2016)

A large library of missense mutations in human SUMO ligase was assessed for competitive growth in a high-throughput yeast-based complementation assay, by the laboratory of Professor F. Roth at University of Toronto (Weile J et al. in preparation). The challenge was to predict the effect of mutations on ligase activity, experimentally determined by the change in fractional representation of each mutant clone in the competitive yeast growth assay relative to wild-type clones. Specifically, predictors were asked to submit scores between 0 (no growth) and 1 (wild-type growth) for detrimental mutations, and more than 1 for mutants with better than wild-type growth. The data was divided into three subsets of mutants. Subset 1 contained 219 single amino acid variants, each represented by at least three independent barcoded clones and therefore they were assessed with high accuracy (each barcoded clone represented an individual mutant yeast strain). Subset 2 contained 463 additional single amino acid variants, each represented by fewer than three independent barcoded clones. Subset 3 contained 4,427 alleles corresponding to clones containing two or more amino acid variants.

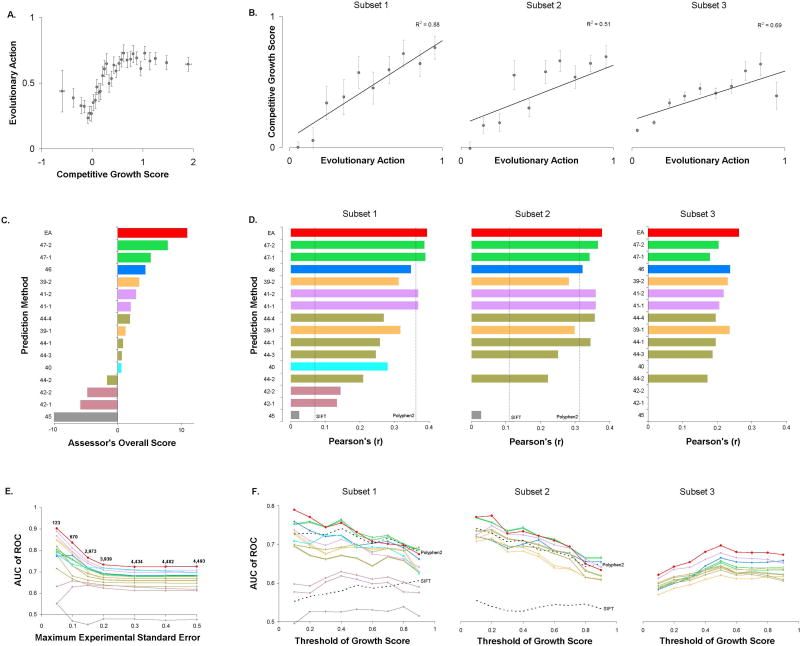
The EA submission (one prediction attempt) treated EA scores as fitness differences. A priori, these differences were assumed to be mostly detrimental, consistent with the nearly neutral theory of molecular evolution (Ohta 1992). To account for gain of function (GOF) variants however, we then hypothesized that substitute amino acids seen more often than the wild-type amino acid in the homolog sequences alignment could be beneficial, so we assigned negative (“not detrimental”) sign of EA scores for those variants. Since EA scores vary between 0 (wild-type) and 100 (loss of function), the activity of SUMO ligase mutants we submitted to CAGI was: submit_EA = 1−EA/100. Next, to combine the effect of multiple mutations (M₁, M₂, …, M_N) on the same allele we multiplied the effect of each mutation, as: submit_EA = (1−EA_M1/100)·(1−EA_M2/100)·…·(1−EA_MN/100). When we plotted the average EA scores for bins of 20 variants with similar experimental growth scores (Fig. 1A), we noted that i) GOF variants had similar EA scores to variants with nearly wild type activity, ii) variants with experimental growth score between 0 and 1 showed a good correlation with EA scores, and iii) variants with negative experimental growth scores had lower EA impact than variants with zero growth scores, suggesting that these variants may have some activity against the function measured by the assay. On the other hand, when we plotted the average experimental growth scores for decile bins of EA scores (Fig. 1B), we noted linear correlations for each subset, the best of which was for the subset 1 (R²=0.88) that had the highest experimental growth accuracy. This correlation was consistent to the correlations in E.coli lac repressor (Markiewicz et al. 1994), HIV-1 protease (Loeb et al. 1989), and human p53 (Kato et al. 2003) mutations, that were used to validate the performance of EA (Katsonis and Lichtarge 2014).

Figure 1. SUMO ligase: Competitive growth of 5,109 alleles in a high-throughput yeast-based complementation assay.

(A) The average EA score for the 682 alleles that each carries a single amino acid variant (subsets 1 and 2), in groups of 20 alleles with similar growth scores. The error bars note the standard error of the mean. (B) The average competitive growth score of the SUMO ligase alleles, in deciles of EA score. The data were divided in three subsets, according to the CAGI 4 challenge description. Subset 1 was the high-accuracy subset of 219 single amino acid variants for which at least three independent barcoded clones were represented. Subset 2 was the remaining 463 single amino acid variants. Subset 3 was 4,427 alleles corresponding to clones containing two or more amino acid variants. The error bars note the standard error of the mean. (C) The performance of the 16 submitted predictions, according to the overall score calculated by the CAGI assessor. The assessor calculated 54 primary scores for each submission, which included Kendall rank, Spearman's rank, Pearson's, and Matthews Correlation Coefficients, F-score, value differences, Root-Mean-Square Deviation, and Receiver Operating Characteristic, amongst others, for the three subsets. The assessor integrated those scores to rank the original predictions, the ranks of the predictions, and a transformation guided by experimental values for each of the three subsets. The CAGI assessor calculated the overall score based on these 9 values. (D) The Pearson's Correlation Coefficients for each subset, calculated by the authors. In addition to the submitted predictions which are shown as colored bars, we calculated Pearson's Correlation Coefficients for the methods PolyPhen2 and SIFT, which are shown as dashed lines. We did not used PolyPhen2 and SIFT in subset 3, since integrating the effect of multiple mutations per allele is ambiguous and submissions followed different approaches. (E) The area under the Receiver Operating Characteristic curve (AUC) as function of the maximum experimental standard error, for all 5,109 alleles (subsets 1, 2 and 3). The variants were divided into deleterious and neutral if they had competitive growth scores less and more than 50, respectively. (F) The AUC as function of the threshold of the competitive growth score to separate deleterious and neutral variants, for each subset. The dashed lines correspond to predictions from PolyPhen2 and SIFT. The lines of the plots in (E) and (F) were colored according to the colors of the bars in (C) and (D).

The CAGI assessor for this challenge carefully examined the results by using 18 different assessment metrics to compare the performance of the submissions in each subset. These metrics measured correlations of the experimental growth scores with i) the original prediction values, ii) the ranks of the predicted values, and iii) a transformation guided by experimental values for the submitted values. Then, as an overall assessment, the CAGI assessor calculated an integrative score for each of these groups of tests and for each data subset, which yielded an overall sum and an overall rank for each method. By this process to define an overall performance score, EA ranked at the top (Fig. 1C). To be clear, the difference between EA and the second best method was small and not necessarily significant. However, all the other methods relied on machine learning and training sets, whereas EA used only the Evolutionary Action equation. Moreover, EA was the only submission with a better overall performance score than a simple conservation-based model developed by the CAGI assessor as a standard of success. To better understand performance, we calculated the Pearson's Correlation Coefficient and the Receiver Operating Characteristic (ROC) curves. EA’s Pearson’s Correlation Coefficients were only 0.39, 0.38, and 0.26 for the subsets 1, 2, and 3, respectively (Fig. 1D). But these were the best in each data set, including compared to SIFT and PolyPhen2 (which did not participate in the challenge). We note that the area under the ROC curve (AUC) for EA in the three subsets of this challenge was 0.73, 0.72, and 0.70, respectively, for experimental value cutoff of 0.5. These AUC values were also better than the other prediction methods, but they were below the AUC of EA in other datasets (Katsonis and Lichtarge 2014). To understand this discrepancy, we tested whether the low performance in the ROC metric could be due to experimental uncertainty (Gallion and Koire et al. 2003). Indeed, when we restricted the analysis to only account for alleles, in any subset, that had low standard error (SE < 0.05) in the experiments, the AUC rose dramatically, reaching up to AUC of 0.9 (Fig. 1E). We also calculated the AUC of all predictions for nine different thresholds of the growth scores, between 0 and 1. For single mutants, the AUC of most methods increased for low thresholds, suggesting that the computational prediction could separate the partial-function variants from non-functional variants better than from the variants with wild-type activity (Fig. 1F). For the multi-variant alleles of the subset 3, the cutoff of 0.5, appears to be optimum in separating functional from non-functional variants for most submitted predictions.

Pyruvate kinase (CAGI 4 – 2016)

A large set of amino acid changing mutations of the pyruvate kinase had been assayed in E. coli extracts for their effect on the enzymatic activity and the allosteric regulation of the liver isozyme (L-PYK), by the laboratory of Professor Aron W. Fenton at University of Kansas Medical Center. One sub-challenge was to predict the effect of mutations on L-PYK enzyme activity, which was measured as a binary assay result (0=inactive or 1=active). A second sub-challenge was to predict the ratios of equilibrium constants for the inhibition of the enzyme by alanine and of the activation of the enzyme by Fructose 1,6 bisphosphate. While the first sub-challenge is directly relevant to predictions made by EA, addressing the second challenge may require computational analysis beyond the scope of EA. Therefore, here, we focus on predicting the enzymatic activity of L-PYK. The data was split into two experiment subsets: i) 113 substitutions in 9 residue positions, and ii) 430 alanine-scanning mutations.

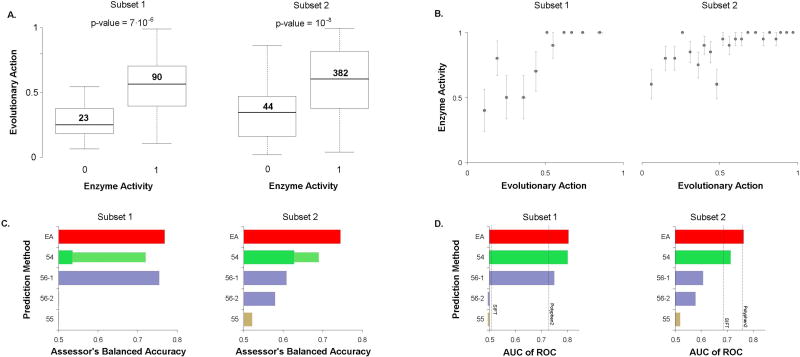
We used EA to address the enzymatic activity of L-PYK and we submitted one prediction file. EA scores vary between 0 (wild-type) and 100 (loss of function), so we treated EA as the probability for a variant to be inactive and we submitted scores calculated as: submit_EA = 100−EA. The average activity predicted by EA for active and inactive variants was 30 versus 54 for subset 1 (Mann–Whitney U p-value=7·10⁻⁶) and 34 versus 59 for subset 2 (Mann–Whitney U p-value=10⁻⁸), respectively (Fig. 2A). When we binned every 20 mutants with similar EA scores, we noted that variants with EA predicted activity of more than half of the wild-type activity were active in their vast majority, while for the rest bins the fraction of active mutants changed almost linearly with the EA prediction (Fig. 2B). This dependence is similar to that of the T4 lysozyme dataset, which we had attributed to sensitivity of the experimental assay (Katsonis and Lichtarge 2014).

Figure 2. Liver pyruvate kinase: Enzymatic activity of 543 missense variants measured in a binary assay in E. coli.

(A) Whisker diagram of the distributions of EA scores for non-functional (0) and functional (1) mutants, divided into two subsets according to the challenge description. The horizontal lines note the median values, the box dimensions note the quartiles, and the error bars note the extremes. The number of variants in each box is shown above its median. Four variants had no enzymatic activity data available. The p-values for the significance of the median differences between non-functional and functional mutants were calculated using the Mann-Whitney U test. (B) The fraction of enzymatic active pyruvate kinase mutants, when every 20 mutants were binned sorted by EA, for each subset. The error bars note the standard error of the mean. (C) The performance of the 5 submitted predictions in the two subsets of pyruvate kinase mutations, according to the balanced accuracy score, which was used by the CAGI assessor to rank the performance of the predictions. The thinner bars correspond to the improvement gained when the CAGI assessor optimized the separation cutoffs. (D) The area under the Receiver Operating Characteristic curve (AUC) for each subset of pyruvate kinase mutations, calculated by the authors. In addition to the submitted predictions which are shown as colored bars, we calculated AUC for PolyPhen2 and SIFT, which are shown as dashed lines.

The CAGI assessor of this challenge used the Balanced Accuracy (BACC) metric to compare the performance of the submitted predictions, for each experimental set. The BACC is given by the average of sensitivity (true positive rate) and specificity (true negative rate), which require to set a cutoff for the submitted predictions. The CAGI assessor tested either using as cutoff the value of 0.5, or they calculated the optimum cutoff for each method. For the EA submitted prediction the value of 0.5 was found to be the optimum cutoff. For each of the two experimental sets, the CAGI assessor found that EA had the top performance according to BACC, even when they optimized the cutoff for the other submitted predictions (Fig. 2C). We reached ourselves the same conclusion when we calculated the AUC of ROC, where EA had AUC of 0.8 and 0.76 in the two subsets, respectively, which were higher than the AUC values of the other submitted predictions as well as of SIFT and PolyPhen2, which did not participated in the challenge (Fig. 2D).

NAGLU (CAGI 4 – 2016)

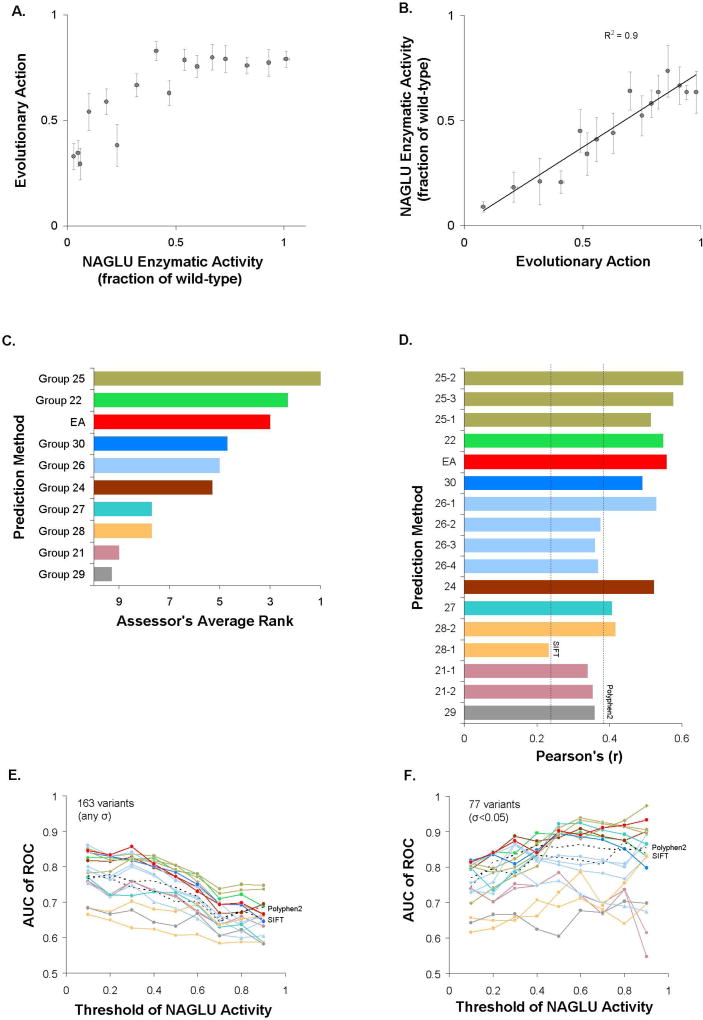
The enzymatic activity of N-acetyl-glucosaminidase (NAGLU) for 165 missense mutations, which were exclusively found in the ExAC dataset (Lek et al. 2016), was assessed as the percentage of the wild-type NAGLU activity by BioMarin Pharmaceutical, Inc. The challenge was to predict NAGLU activity, submitting scores between 0 (no activity) and 1 (wild-type level of activity), or higher than 1, when the mutation effect was predicted to be detrimental or beneficial, respectively. Similar to the pyruvate kinase challenge, we used EA and we submitted one prediction file with scores calculated as: submit_EA = 1−EA/100. When we binned every 10 variants with similar enzymatic activity, small enzymatic activities (less than half of the wild-type) correlated with the average EA prediction values, but large enzymatic activities (more than half of the wild-type) had similar EA scores (Fig. 3A). On the other hand, when we binned every 10 variants with similar EA scores, the average enzymatic activity correlated linearly (R²=0.90) with EA scores (Fig. 3B).

Figure 3. N-acetyl-glucosaminidase (NAGLU): 165 missense mutants were transfected into HEK293 cells and the NAGLU activity was assessed using a fluorogenic substrate.

(A) The average EA scores for groups of 10 mutants with similar NAGLU activity. Two of the 165 mutants had no experimental assessment and they were omitted. The error bars note the standard error of the mean. (B) The average enzymatic activity of NAGLU for groups of 10 mutants with similar EA scores. The error bars note the standard error of the mean. (C) The performance of the submitted predictions, according to the overall rank of the CAGI assessor. The assessor used three tests for the overall assessment, the Root-Mean-Square Deviation, the Pearson's Correlation Coefficient, and the Spearman's Rank Correlation Coefficient. The CAGI assessor reported only the best performing method from each research group, since often multiple submissions from the same groups were based on the same original values using different scaling factors. This choice may favor groups with multiple submissions. (D) The Pearson's Correlation Coefficients for each submission, calculated by the authors. In addition to the submitted predictions which are shown as colored bars, we calculated Pearson's Correlation Coefficients for PolyPhen2 and SIFT, shown as dashed lines. (E) The area under the Receiver Operating Characteristic curve (AUC) for the submitted predictions as function of the threshold of NAGLU activity to separate into deleterious and neutral all 163 mutations or (F) the 77 mutations with an experimental standard deviation of σ=0.05 and less. The AUC values were calculated by the authors and they were colored according to the colors of the bars in (D). The dashed lines correspond to predictions from PolyPhen2 and SIFT.

The CAGI assessor of the NAGLU challenge used three tests to compare the performance of the submissions, the Root-Mean-Square Deviation (RMSD), the Pearson Product-Moment Correlation Coefficient, and the Spearman's Rank Correlation Coefficient. The assessor did not use the well-established ROC test in their overall rank calculation, because they found that the top five submissions, which included EA, had essentially identical performance with AUC values slightly greater than 0.8. In the overall rank, the assessor included only the best performing submission from each predictor group when a group submitted multiple versions, due to redundancy. According to this overall rank, EA had the third best performance (Fig. 3C). The Pearson's Correlation Coefficient of EA was 0.54, which was the second highest and better than SIFT and PolyPhen2 (Fig. 3D). We also calculated the AUC of ROC for nine different threshold values of the enzymatic activity between 0 and 1 (Fig. 3E). Most predictions had their maximum AUC at small thresholds, where EA did particularly well with AUC of 0.86 for the threshold of enzymatic activity at 0.3, which was the highest AUC value achieved by any prediction method at any cutoff. We also tested the ROC performance when the analysis was limited to variants with small experimental standard deviations (77 variants had SD below 0.05). Indeed, there was improvement in AUC for almost all predictions, but only for large enzymatic activity thresholds, since variants with low enzymatic activity very often had low standard deviations (Fig. 3F). EA reached a maximum AUC of 0.93 for the threshold of enzymatic activity at 0.9, suggesting strong performance when the experimental measurements were very consistent. The facts that no method had consistently the best AUC of ROC at each threshold and that the relative ranks changed when the analysis was restricted to variants with consistent experimental measurements, support the conclusion of the CAGI assessor that the AUC performance was indistinguishable for the top performing methods.

P16 (CAGI 3 – 2013)

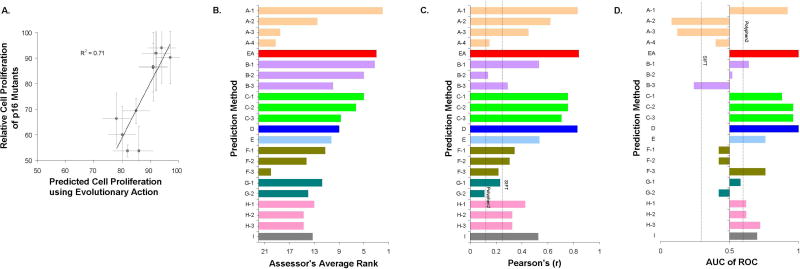
The ability of 10 p16 variants (CDKN2A gene) to block cell proliferation was tested by Maria Chiara Scaini, at Veneto Institute of Oncology of Padova (Scaini et al. 2014). The p16 variants, like the controls of wild-type p16 (negative) and EGFP vector (positive), were expressed in a p16-null-human osteosarcoma cell line and their proliferation rate was recorded for 9 days. The challenge was to predict the proliferation rate of each p16 mutant cell line relative to the positive control, given that the proliferation rate of the wild-type p16 cells was approximately 50% of the proliferation rate of the positive control cells. We used EA to estimate the impact of p16 mutations and then we predicted the proliferation rate will be: submit_EA = 50+EA/2. Although the correlation of the experimental and predicted values was very strong, with a Pearson's r of 0.84 (Fig. 4A), the formula we used to calculate the proliferation rate from the EA scores was subpar. Setting submit_EA = EA would have yielded a much better agreement to the experimentally measured values.

Figure 4. p16 tumor suppressor protein: The proliferation rate of 10 p16-null human cell lines transfected with p16 mutant proteins was estimated relative to the proliferation of cell with wild-type p16.

(A) The experimentally determined proliferation of the 10 cells as function of the EA scores for the 10 p16 variants. The y-axis error bars note the experimental standard deviation and the x-axis error bars correspond to a fixed confidence range of 10 EA score units. (B) The performance of the 22 submitted predictions, according to the overall score calculated by the CAGI assessor. This score was the average rank of the performance of the submissions in 4 tests: Kendall's tau Coefficient, Root-Mean-Square Deviation, Receiver Operating Characteristic, and the count of mutants within 10% overlap between experimental and predicted values. (C) The Pearson's Correlation Coefficients calculated by the authors. In addition to the submitted predictions which are shown as colored bars, we calculated Pearson's Correlation Coefficients for PolyPhen2 and SIFT, shown as dashed lines. (D) The area under the Receiver Operating Characteristic curve (AUC). The variants were divided into deleterious and neutral if they had cell proliferation rate more and less than 50, respectively. The dashed lines correspond to predictions from PolyPhen2 and SIFT.

The CAGI assessor of this challenge used 4 tests to compare the performance of the submitted predictions: Kendall's tau Coefficient (τ), Root-Mean-Square Deviation (RMSD), Receiver Operating Characteristic (ROC), and Overlap within 10%. The CAGI assessor calculated an overall score from the average rank of these four tests, where EA ranked second out of 22 submissions (Fig. 4B). Of note is that the best submission came from a machine learning method trained with evolutionary and structural features, but the same research group submitted three additional predictions on the same challenge that were trained on different combination of features, and these submissions had intermediate or very poor performance. The EA submission had higher Pearson's Correlation Coefficient (r=0.84) than the other submissions and than SIFT and PolyPhen2 (Fig. 4C). Also, the EA submission had perfect ROC, with AUC=1 in separating the proliferation rate of the variants that had a bimodal distribution (Fig. 4D). The poor performance of SIFT and PolyPhen2 in this challenge was due to predicting maximum impact for almost all of these variants. The best performance of EA on Pearson’s coefficient and ROC metrics was consistent between our calculations and the calculations of the CAGI assessor.

Cystathionine beta-Synthase (CAGI 2 – 2011)

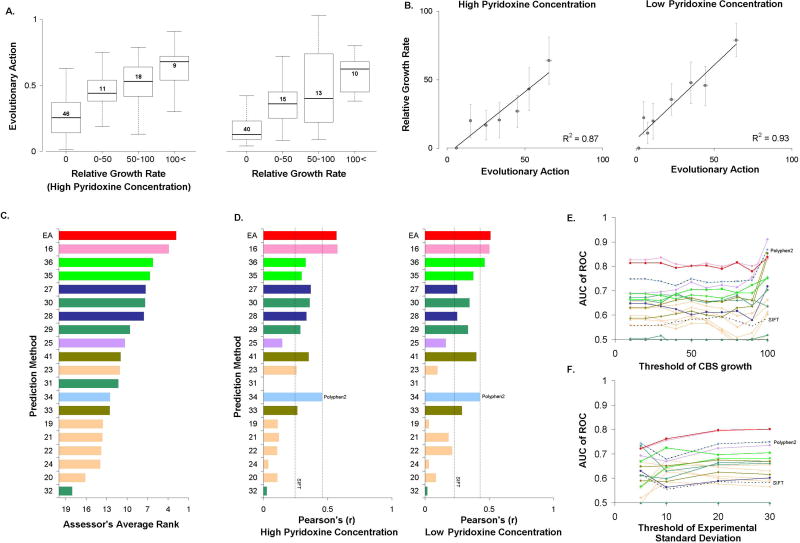
The functionality of 84 single amino acid Cystathionine beta-Synthase (CBS) variants, found in homocystinuria patients, was tested in an in vivo yeast complementation assay, by the laboratory of Professor J. Rine, at UC Berkeley. The human CBS clone was expressed and functionally complemented in yeast cells that had the orthologous yeast gene CYS4 removed from the chromosome. In that assay, growth was dependent upon the level of mutant human CBS function, and the rates were expressed as a percentage relative to wild type (human protein) growth. Two concentrations of pyridoxine, high (400 ng/ml) and low (2 ng/ml), were used. The challenge was to submit predictions on the effect of the variants in the function of CBS in both co-factor concentrations. To address this challenge, we used EA to estimate the loss of CBS activity. At high co-factor concentration, we simply set: submit_EA = 100−EA. At low co-factor concentration, we scaled the EA scores to yield lower CBS activities, guided by the test data, such that an EA of 70 will yield 10% CBS activity instead of 30% (linear scaling without changing the extremes, so, EA of 0 and 100 will still yield 100% and 0% CBS activity, respectively). Since most CBS variants were found to be experimentally inactive, we binned the variants into those with 0, 0–50%, 50–100%, and more than 100% of the wild-type activity. As expected, the average EA score was higher for the bins of the higher relative growth rate (Fig. 5A). On the other hand, binning every 10 CBS variants by their EA scores yielded strong linear correlations between growth rate and EA (Fig. 5B; R² was 0.87 and 0.93 for high and low co-factor concentration, respectively).

Figure 5. Cystathionine beta-Synthase (CBS): The function of 84 mutants of the human CBS was measured in vivo as the growth rate, relative to wild-type, in a yeast complementation assay in high and low co-factor concentrations.

(A) Whisker diagrams of the distributions of EA scores for four functional groups of the CBS mutations, at the two co-factor concentrations. The functional groups were defined as mutants with a relative growth rate of null (0), detectable but less than 50% (0–50), between 50% and 100% (50–100), and more than 100% (100<) of the wild-type growth rate. The horizontal lines note the median values, the box dimensions note the quartiles, and the error bars note the extremes. The number of variants in each box is shown above or below its median. Six mutants had non-defined growth rate at low co-factor concentration. (B) The average relative growth rate for groups of 10 CBS mutants with similar EA score, for each co-factor concentration. The error bars note the standard error of the mean. (C) The performance of the 20 submitted predictions, according to the average rank in all nine statistical tests used by the CAGI assessor to judge the performance of the predictions to match the experimental data at each co-factor concentration. Amongst others, these tests included Precision, Recall, Accuracy, Root-Mean-Square Deviation, Spearman's Rank Correlation Coefficient, F-score, and Receiver Operating Characteristic. The average rank was calculated by the authors, since the assessor did not provide an overall rank of the submitted predictions. (D) The Pearson's Correlation Coefficients for each subset, calculated by the authors. In addition to the submitted predictions which are shown as colored bars, we calculated Pearson's Correlation Coefficients for SIFT, shown as dashed lines. The PolyPhen2 dashed line (in panels D, E, and F) corresponds to a submission by PolyPhen2 developer group at the time of submission. An up-to-date PolyPhen2 calculation yielded equivalent performance, but slightly different predictions from the submitted version (data not shown) (E) The area under the Receiver Operating Characteristic curve (AUC) as function of the threshold of CBS growth rate to separate deleterious and neutral variants, at low co-factor concentration. (F) The AUC as function of the maximum experimental standard deviation, for the 84 CBS mutants at low co-factor concentration. The lines of panels (E) and (F) were colored according to the colors of the bars in (C) and (D), while the dashed lines correspond to predictions from PolyPhen2 and SIFT.

The CAGI assessor of this challenge used 9 different tests for each subset of high and low pyridoxine concentration to compare the performance of the submitted predictions, including Precision, Recall, Accuracy, Root-Mean-Square Deviation (RMSD), Spearman's Rank Correlation Coefficient, F-score, and Receiver Operating Characteristic (ROC), amongst others. Out of 20 submissions, the EA submission had the best performance in nine of the 18 tests, including those of accuracy, RMSD, and F-score, in both datasets. EA was also the best method according to the average rank of all 18 metrics used by the CAGI assessor (Fig. 5C). According to our calculations of the Pearson's Correlation Coefficients, the EA predictions were the best and the second best method at low and high cofactor concentrations, respectively (Fig. 5D). According to our calculation the ROC test, EA was the second best method at both co-factor concentrations, with only a marginal difference from the top method (Fig. 5E). When the analysis was restricted to variants with low thresholds of standard deviation, to our surprise, the AUC for almost all predictions dropped, suggesting that lower standard deviations do not imply more accurate experimental measurements in this particular data set (Fig. 5F).

DISCUSSION

Following objective assessments across diverse challenges, these data demonstrate that the Evolutionary Action is a robust, state-of-the-art method to estimate the mutational harm of protein coding variations with consistent tendency to perform best, or nearly so. Out of the five CAGI challenges EA participated in predicting the impact of genetic variations, three times EA was ranked as the top submission as measured by overall score or by the average rank of metrics chosen by the independent CAGI assessors. The other two times, EA ranked as second and third best out of 16 submitted predictions per challenge, on average. Of note, the CAGI challenges were very competitive, with many submissions performing better than PolyPhen2 and SIFT, which are well-known methods, routinely used in the literature to estimate the impact of genetic variations, but which did not participate in the recent CAGI contests. The typical ROC performance of EA was AUC higher than 0.8. An EA AUC below 0.8, seemed to associate with experimental inaccuracies. Conversely, highly accurate experimental data was associated with AUC values above 0.9. This is consistent with the view that experimental gold standards can themselves be fraught with uncertainties, as discussed elsewhere (Gallion and Koire et al. 2003).

Whether a method achieves a top ranking or not may often be over-interpreted. Of equal or greater value is whether a method adds orthogonal information and techniques that enrich the domain. In that respect, it is critical to stress that EA is far different from other submissions. It follows a compact and simple mathematical logic, lifted directly from elementary calculus. In so doing it factors in homology and phylogenetic information, explicitly. It sets its parameters (the magnitude of a substitution) over the evolutionary history of all proteins, and reflects the specific protein and residue of interest through the evolutionary gradient, which is computed through a set algorithm and requires no training. Still, EA tended to perform on par or better than most machine learning approaches. These approaches, in contrast to EA, were trained on mutation data, structural stability information, physicochemical properties, and functional site annotation (e.g. known functional motifs, interaction sites, and allosteric sites) in addition to homology data. Moreover, many machine learning approaches trained to further integrate the combined outputs from many stand-alone mutation impact predictors.

The good performance of the EA equation in CAGI challenges therefore supports the fundamental hypotheses underlying the EA theory. That is, genotype-phenotype evolution in the fitness landscape may be described by a fundamental differential equation, reminiscent of those seen in physics. This is surprising for many reasons. Clearly, the genetic code changes discretely, not smoothly. Also, far from being “infinitesimal,” some mutations bring a heavy toll on patients. More broadly, EA hinges on an evolutionary function f that is never explicitly defined. Lastly, EA is an essentially untrained expression that apparently is unaware of important details, such as a protein’s structure, functions or interactions. Despite this, CAGI objectively shows through its blind contests assessed by independent judges that EA is an effective, accurate, robust, and generally that performs on par or better than sophisticated and powerful statistical and artificial intelligence techniques trained on large data sets.

These apparent paradoxes can be resolved, however, by examining the formal variables EA uses. First, EA models the impact of genetic variations—the central feature of evolution—by applying basic calculus to Sewall’s fitness landscape: a mutation causes a fitness displacement equal to the perturbation size times the local fitness sensitivity, i.e. the gradient of the mutated position. To estimate this gradient, EA looks at evolutionary history: when this position varied among species did their fitness change much or little? The answer is taken directly from evolutionary trees, or more accurately from the fundamental equivalence between sequence distances and fitness distance between their species (Lichtarge et al. 1996). Thus, only the evolutionary tree and its record of distances between sequences are needed to estimate f’; f itself is never required. Critically, f’ implicitly accounts for structural, dynamical, functional, and other interaction constraints that guide fitness response to point mutations. Although no statistical training is present, the gradient f’ is specific to each protein and its context. Finally, the EA equation reflects the perturbation on the species, since the evolutionary tree comparisons are between species. As such, a mutation that is deadly to an individual is in fact absent from the evolutionary records of species. By the same token discrete mutations among individuals become melded into a slow continuous diffusion process along an evolutionary trajectory over geological time scale.

EA currently uses only first-order terms which were approximated by terms that imply the context. The higher order terms of the EA equation would account for the epistatic interactions of the residues within a protein or across different proteins and they may well improve predictions, so residue coupling information would be a valuable improvement in future developments of computing EA (Marks et al. 2011). However, for now, the first differential term of the evolutionary equation by itself has broad practical applications in identifying key functional determinants with which to predict, redesign, or mimic function and specificity (Yao et al. 2003; Rodriguez et al. 2010; Amin et al. 2013). Now, when used as part of the evolutionary action equation, it helps interpret the impact of genetic variations to prioritize mutations (Rababa'h et al. 2013; Mullany et al. 2015), assess the quality of exomic data (Koire et al. 2016), stratify head and neck cancer patient outcome (Neskey et al. 2015) and predict their response to treatment (Osman et al. 2015a; Osman et al. 2015b).

In summary, CAGI is an important community exercise that objectively compares and illustrates the relative contribution of diverse methods to interpret mutations. In that light, it appears that the performance of EA is as good on prospective datasets as it was on retrospective datasets (Katsonis and Lichtarge 2014). Arguably, strengths of the EA approach are its simplicity combined with its generality. That is, EA is not trained, but rather relies on first principles of protein evolution. As such, EA differs profoundly from other CAGI submissions and leading methods to evaluate mutations. Moreover, it is widely applicable to any proteins, since it is impervious to differences between de novo mutations and polymorphisms, to the eukaryotic, prokaryotic, or viral origin of the proteins, and to the enzymatic or multi-functional proteins. As with all homology-based methods, the number and diversity of the available homologous sequences necessary to build a sufficiently deep evolutionary tree remain a limitation, as is the absence, for now, of the second order terms in the computation of EA. However, the mathematical framework of EA is universal and robustly recognizes the telltale patterns of evolutionary constraints. This robustness, which was shown in the CAGI contests, should make Evolutionary Action, and the associated server, a valuable tool for the functional and clinical interpretation of genetic variations.