Assessing the accuracy and stability of variable selection methods for random forest modeling in ecology

Abstract

Random forest (RF) modeling has emerged as an important statistical learning method in ecology due to its exceptional predictive performance. However, for large and complex ecological data sets there is limited guidance on variable selection methods for RF modeling. Typically, either a preselected set of predictor variables are used, or stepwise procedures are employed which iteratively remove variables according to their importance measures. This paper investigates the application of variable selection methods to RF models for predicting probable biological stream condition. Our motivating data set consists of the good/poor condition of n = 1365 stream survey sites from the 2008/2009 National Rivers and Stream Assessment, and a large set (p = 212) of landscape features from the StreamCat data set as potential predictors. We compare two types of RF models: a full variable set model with all 212 predictors, and a reduced variable set model selected using a backwards elimination approach. We assess model accuracy using RF’s internal out-of-bag estimate, and a cross-validation procedure with validation folds external to the variable selection process. We also assess the stability of the spatial predictions generated by the RF models to changes in the number of predictors, and argue that model selection needs to consider both accuracy and stability. The results suggest that RF modeling is robust to the inclusion of many variables of moderate to low importance. We found no substantial improvement in cross-validated accuracy as a result of variable reduction. Moreover, the backwards elimination procedure tended to select too few variables, and exhibited numerous issues such as upwardly biased out-of-bag accuracy estimates and instabilities in the spatial predictions. We use simulations to further support and generalize results from the analysis of real data. A main purpose of this work is to elucidate issues of model selection bias and instability to ecologists interested in using RF to develop predictive models with large environmental data sets.

Introduction

Ecological processes are complex, and often involve high-order interactions and nonlinear relationships among a large collection of variables (De’ath and Fabricius, 2000; Cutler et al., 2007; Evans et al., 2011). In traditional regression modeling, the relationships between the response and explanatory variables need to be pre-specified, and many assumptions are commonly made (e.g., normality, independence, and additivity) which are rarely satisfied in an ecological context (Prasad et al., 2006; Evans et al., 2011). When the number of explanatory variables is large, regression models can overfit the data unless information criteria such as the Akaiki information criterion or hypothesis testing are employed to reduce the number of parameters (Burnham and Anderson, 2002). Moreover, when there are as many parameters as data points, a multiple regression model will fit the data exactly, but fail to generalize well on new samples (Babyak, 2004; Faraway, 2005). Because of these limitations, more flexible nonparametric and algorithmic approaches are gaining traction amongst ecologists; random forest (RF) modeling (Breiman, 2001), in particular, has recently emerged as a compelling alternative to traditional methods.

Multiple studies have demonstrated that RF models often perform remarkably well in comparison to other methods for ecological prediction. In an application to predictive mapping of four different tree species in the eastern United States, Prasad et al. (2006) found that RF modeling outperformed three other statistical modeling approaches (regression tree analysis, bagging trees, and multivariate regression splines) in terms of the correlations between the actual and predicted species distributions. In their seminal article, Cutler et al. (2007) applied RF classifiers to a wide range of ecological data sets on invasive plant species, rare lichen species, and cavity nesting bird habitats. Using cross-validation, they demonstrated that the RF models outperformed other commonly used classification methods such as logistic regression, classification trees, and linear discriminant analysis. The RF models generally demonstrated the most substantial improvement over linear methods for data sets with strong interactions among variables (e.g., invasive species). In Freeman et al. (2015), RF was compared with stochastic gradient boosting for modeling tree canopy cover over diverse regions in the United States. They found that both models performed similarly in terms of independent test set error statistics (e.g., mean-squared error); although, there were advantages to the RF approach since it was less sensitive to tuning parameters and less prone to overfitting.

While RF modeling has shown exceptional performance on a variety of ecological data sets (Gislason et al., 2006; Prasad et al., 2006; Cutler et al., 2007), insights and guidance on variable selection techniques for RF models of ecological processes are limited. Typically, either a preselected set of predictor variables are used in the RF model (Prasad et al., 2006; Cutler et al., 2007; Carlisle et al., 2009), or a reduced set of variables is selected to improve model interpretability and performance (Evans and Cushman, 2009; Evans et al., 2011; Rehfeldt et al., 2012; Hill et al., 2013). For instance, in Cutler et al. (2007) no variable selection was carried out; instead the authors claimed that one of the strengths of RF modeling is its ability to characterize high-dimensional data with many collinear variables. In other works, stepwise procedures have been proposed whereby a sequence of RF models are estimated by iteratively adding or removing variables according to their importance measures, and the model with optimal performance is selected. For instance, this type of approach has been implemented by Evans and Cushman (2009) to select RF models for predicting occurrence probabilities for conifer species in northern Idaho; Rehfeldt et al. (2012) to reduce the number of predictors for RF models of the geographic distribution of biomes under various climate change scenarios; and Hill et al. (2013) to select a RF model of reference condition stream temperature with a small set of optimally performing natural and anthropogenic predictor variables.

With the growing popularity of RF modeling among ecologists, and the availability and refinement of large environmental data sets, questions about model selection need to be more throughly addressed. Along these lines, we investigate the application of variable selection methods to RF models of stream condition with many landscape features generated from a Geographic Information System (GIS). Our motivating covariate data set is the StreamCat data set of Hill et al. (2016), which contains over 200 natural and anthropogenic landscape variables, readily available for predictive modeling of stream catchment attributes (e.g., estimating the probability of good stream condition for a particular catchment). Using these data, we seek to address the following questions:

• How can we reliably evaluate accuracy for RF modeling when performing variable selection? Is external validation necessary?

• How can we measure and assess the stability of RF models to changes in the number of predictor variables (i.e., landscape features)?

• What effect does variable selection have on the spatial predictions generated by RF models at new, unsampled locations?

For the stability analysis we focus on spatial patterns (i.e., prediction maps) and statistical summaries of the RF predictions of stream condition, in addition to commonly used measures of model performance. Lastly, a common incentive for using RF over other modeling techniques is that it can handle many noisy variables, and is ostensibly robust to overfitting (Breiman, 2001). Thus, another question which we posit is whether variable reduction necessarily improves the predictive accuracy of RF models with large ecological data sets such as StreamCat. While we focus on a particular applied data set for this study, we also use simulations to further generalize and support results.

Methods

Random forest modeling of stream condition

RF modeling is a statistical learning method that builds many decision trees from bootstrap samples of a data set. Predictions are made by averaging over the predictions made by each tree in the forest. Since individual trees often overfit the training data and result in noisy predictions, averaging is a way to reduce the variance of the model and improve prediction accuracy. Additionally, when building each tree, the RF algorithm selects a random subset of predictors as candidates for splitting at each node. This has the effect of decorrelating the trees since no single predictor variable is allowed to dominate the top splits of trees in the forest. As a special case, RF also includes bagging trees, which use all predictors as candidates for splitting (Breiman, 1996a). Many empirical and simulation studies have demonstrated that RF and bagging trees out-perform single tree models (Breiman, 1996a, 2001; Lawrence et al., 2006; Strobl et al., 2009). RF can be used for both regression and classification problems, however in this paper we only focus on classification tasks. For a more in-depth introduction to RF and relevant theory please see Hastie et al. (2009).

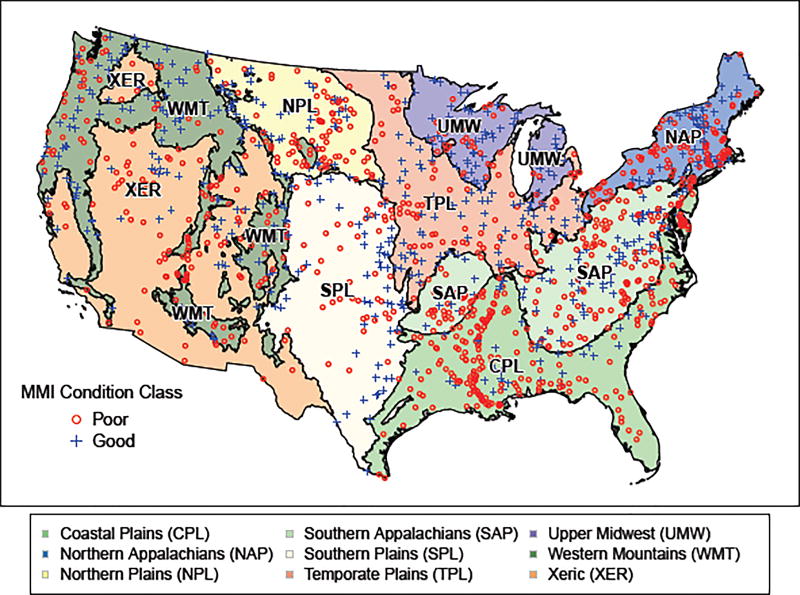
For this study, we train a RF model using data from the U.S. Environmental Protection Agency’s 2008/2009 National Rivers and Stream Assessment (NRSA; U.S. Environmental Protection Agency, 2016a). NRSA uses a spatially balanced sampling design to provide an assessment of the ecological condition of rivers and streams in the conterminous United States (CONUS), and the extent to which they support healthy biological condition. The response data of interest for the RF model is the categorization of n = 1365 NRSA sites (Figure 1) as being in good or poor condition according to the benthic macroinvertebrate Multimetric Index (MMI). Macroinverabrate assemblages provide one of the most reliable indicators of a stream’s biological condition, and the MMI score is a standardized sum of metrics indicative of the health of the macroinvertebrate community (Stoddard et al., 2008; U.S. Environmental Protection Agency, 2016a). A detailed description of the development of the macroinvertebrate MMI for the 2008/2009 NRSA survey is provided in U.S. Environmental Protection Agency (2016b).

Fig. 1.

Locations of 1365 stream sites from the 2008/2009 National Rivers and Stream Assessment and their good/poor condition class according to the benthic macroinvertebrate Multimetric Index (MMI)

The predictor data for the RF model consist of p = 212 variables from the StreamCat data set (Hill et al., 2016). This data set contains natural and anthropogenic landscape features for approximately 2.6 million stream reaches within the CONUS. Variables are at the local catchment (i.e. local drainage area for an individual reach, excluding upstream drainage area) and full watershed (catchment plus upstream catchments) scales (Hill et al., 2016), and can be linked to the National Hydrography Dataset Plus Version 2 (NHDPlusV2; McKay et al., 2012).

Using the estimated RF model we can predict the probability that a stream at a new, unsampled location is in good (or conversely poor) condition. The predicted probability is computed as the proportion of trees in the forest that vote that the new stream site is in good condition. If the predicted probability is greater than 0.5 the stream is classified as being in good condition, and poor condition otherwise. Note, since the NRSA sample frame is limited to perennial streams, we can only make valid predictions on approximately 42% of the catchments in StreamCat (i.e., approximately 1.1 million stream reaches; Hill et al., 2017, 2016).

Moreover, RF also provides an internal way to assess model performance. When building a RF model, a portion of the data (approximately 1/3) is not contained in the bootstrap sample used to form an individual tree; this is referred to as the out-of-bag (OOB) data for that tree. In the context of modeling stream condition, RF can predict the good/poor condition of site i for each tree in the forest where i is OOB, and take the majority vote as the OOB predicted condition, and the proportion of good votes as the OOB predicted probability for that site. We can then repeat this procedure to obtain the OOB predicted condition for each of the i = 1, ⋯, n stream sites. Measures of model performance can be computed using these OOB predictions. In this study, we focus on the following measures: percent of sites correctly classified (PCC; accuracy), percent of good sites correctly classified (PGCC; sensitivity), percent of poor sites correctly classified (PPCC; specificity), and the area under the receiver operating character curve (AUC; Hosmer and Lemeshow, 2000, pp. 160–164). Note that the AUC makes use of the OOB predicted probabilities, and is not dependent on selecting a probability threshold.

In this work, we implement RF in the R computing language (R Core Team, 2014) using the randomForest package of Liaw and Wiener (2002). The two main tuning parameters for estimating a RF model with this package, and in general, are: ntree, the number of trees used to build the model, and mtry, the number of variables randomly selected at each node. For classification tasks the defaults are ntree = 500 and $\text{mtry}=\sqrt{p}$, where p is the number of predictor variables (Liaw and Wiener, 2002). RF models are relatively insensitive to choice of tuning parameters, and the defaults perform well on most data sets (Liaw and Wiener, 2002; Cutler et al., 2007; Freeman et al., 2015). Ideally, ntree should be chosen so that multiple runs of RF produce consistent results, and it is suggested to use more trees than the default when the number of predictor variables is large (Strobl et al., 2009; Boulesteix et al., 2012). Generally, when the number of noise variables far exceeds the number of informative variables mtry values larger than the default will perform better, since the informative predictors are more likely to get sampled at each split (Goldstein et al., 2011). However, when there are many informative variables of varying strengths, small values of mtry tend to perform well since moderately important predictors are given a chance of being selected for each split, thereby preventing the most important predictors from having too much influence in the forest (Boulesteix et al., 2012).

A sensitivity analysis demonstrated that the RF models of stream condition were insensitive to the selection of mtry (i.e., a wide range of candidate values performed similarly), and that values of ntree greater than the default produced more consistent results over multiple runs of RF (Supplement 1). Thus we adopt the default $\text{mtry}=\sqrt{p}$ and ntree = 3000 for this study.

Overview of modeling decisions

Throughout this paper we adhere to the modeling decisions listed below. A comprehensive discussion of each of these decisions is provided in Hill et al. (2017).

• A separate RF model is built for each of the 9 aggregated ecoregions (Figure 1; Omernik, 1987). Separate models are used instead of one national model since the reference sites used to create the MMI are specific to each ecoregion (U.S. Environmental Protection Agency, 2016a,b).

• The 2008/2009 NRSA classified the condition of each sampled stream site as good, fair, or poor according to the MMI score. However, we build the RF models using only the good/poor sites with fair sites removed. To empirically justify this decision we compared the predictive performance of a three-class (good/fair/poor) multinomial RF model with a two-class (good/poor) binomial RF model (Supplement 2). The fair sites were difficult to discriminate with a multinomial RF model (percent of fair sites correctly classified < 25%), and the binomial model had substantially better predictive performance in terms of the various accuracy rates (PCC, PGCC, and PPCC). The multinomial RF modeling results suggest that the fair sites do not stand out as a true intermediate (medium-level) class, but rather as an indeterminate class with a great deal of uncertainty associated with sampled MMI scores.

• RF modeling is known to be sensitive to class imbalances (Chen et al., 2004; Khoshgoftaar et al., 2007; Evans and Cushman, 2009; Khalilia et al., 2011; Freeman et al., 2012). The response data considered in the study is moderately imbalanced: 60% of sampled sites are in poor condition, and 40% are in good condition. In certain ecoregions class imbalances are more severe (e.g., in the Coastal Plains only 16% of sites are in good condition). To deal with this issue we use a down-sampling approach (Chen et al., 2004; Evans and Cushman, 2009): each tree in the ensemble is built by drawing a bootstrap sample with the same number of cases from the majority and minority classes; in practice, the number of cases drawn from each class is set to the size of the minority class. Without balancing, the RF model had much lower predictive accuracy on the less prevalent good class than the more prevalent poor class. Balancing the RF model with the down-sampling approach improved predictive accuracy on the good class, without substantially affecting overall model performance (Supplement 2).

Variable importance

RF provides measures of variable importance (VI) which can be used to rank the 212 predictors in our model of stream condition. In this paper, we use the permutation VI measure, which is computed as follows: For each tree b in the RF model keep the misclassification error rate using the OOB data (i.e., percentage of sites in the OOB data incorrectly classified by tree b). Then randomly permute the values for predictor variable j in the OOB data and recompute the misclassification rate for each tree. The difference in classification rates, averaged over all trees in the RF model, is the permutation VI measure (Hastie et al., 2009).

Formally, using the notation of Genuer et al. (2010), we can define the importance of each variable j as:

$$\mathit{\text{VI}}(X_j)=\frac{1}{\mathit{\text{ntree}}}\sum _{b=1}^{\mathit{\text{ntree}}}({\mathit{\text{errOOB}}}_b-\mathit{\text{err}}{\stackrel{\sim }{\mathit{\text{OOB}}}}_{b,j}),$$ (1)

where errOOB_b is the OOB misclassification rate for tree b, and $\mathit{\text{err}}{\stackrel{\sim }{\mathit{\text{OOB}}}}_{b,j}$ is the OOB misclassification rate for tree b when the values for predictor X_j are randomly permuted in the OOB data. While other measures of VI are provided by RF (e.g., the Gini VI measure gives the total decrease in the Gini index due to splits of a given predictor, averaged over all trees), we focus on the permutation VI since it is directly based on the change in the predictive accuracy. Moreover, the permutation VI measure has been used in the context of variable selection (Díaz-Uriarte and De Andres, 2006; Evans and Cushman, 2009; Genuer et al., 2010). Note, since a separate RF model is estimated for each of the 9 ecoregions, the VI measures for the p = 212 StreamCat predictor variables are also region specific (i.e., a separate VI ranking is computed for each ecoregion). Descriptive statistics on the regional VI measures for the StreamCat predictors can be found in Supplement 3.

Stepwise model selection

The VI measure (Equation 1) for RF can be used for the purpose of model selection. In this paper, we use the following stepwise selection procedure, which we refer to as backwards variable elimination (BVE):

1. Rank predictors according to their VI from the RF model fit to the full set of p predictor variables. Average VI scores over multiple runs of RF to get a stable ranking.

2. Build a stepwise sequence of p RF models by discarding, at each step, the least important remaining variable according to the initial VI ranking. That is, start with a RF model with all p predictors, then remove the least important predictor and estimate a RF model with p − 1 predictors; continue this process until a sequence of RF models with p, p − 1, …, 1 predictors is constructed. Use a standard metric to evaluate the OOB performance of the RF model at each step.

3. Select the model which performs best according to the metric (e.g., model with highest accuracy).

In practice, we average the VI scores over 10 runs of RF to get an initial ranking, and use the PCC (accuracy) as the performance metric for selection. Additionally, since we fit a separate RF model to each of the 9 ecoregions, we apply this model selection procedure separately to each ecoregion. This results in 9 different variable reduced RF models, each containing a different set of variables. Note that for the remainder of this article RF models selected by BVE will be referred to as ‘reduced’ set models, while RF models that use all predictor variables will be referred to as ‘full’ set models. We will also refer to the 9 ecoregions by their acronyms defined in Figure 1.

This type of iterative approach for selecting variables using the VI rankings has been discussed previously in Díaz-Uriarte and De Andres (2006) and Goldstein et al. (2010) for applications to gene selection problems; Evans and Cushman (2009) for species distribution modeling; and Genuer et al. (2010) for more general applications to high-dimensional data sets. Note that in some of these works variables are removed in batches (instead of one at a time), and VI measures are standardized.

Cross-validation

Multiple studies have emphasized the necessity for external validation when applying a variable selection method to a predictive model (Ambroise and McLachlan, 2002; Svetnik et al., 2003; Hastie et al., 2009, pp. 245–247). Ambroise and McLachlan (2002) describe how a ‘selection bias’ can be introduced when the data used to select variables for a model is not independent of the data used to assess the performance of that model. Using two well known genomic data sets, Ambroise and McLachlan (2002) demonstrate that an over-optimistic error rate is obtained when the validation data is not external to the variable selection procedure.

As a correction for selection bias we apply the following K-fold cross-validation (CV) method described in Ambroise and McLachlan (2002) to the BVE procedure for selecting a RF model:

1. Divide the data into K disjoint sets (folds), with roughly the same number of observations in each fold; in practice take K = 10.

2. For each fold k = 1, ⋯, K:

   1. Take out fold k as an independent test set.
   2. Using the remaining K − 1 folds, select a RF model using the BVE procedure.
   3. Use the selected model to make predictions on the withheld fold k (i.e., for each stream site in fold k evaluate the predicted probability of good condition using the RF model selected in (b)).

3. Accumulate the predictions made over the withheld folds k = 1, ⋯, K at each iteration; call these the CV predictions.

4. Use the CV predictions to compute performance measures (e.g., accuracy, sensitivity, specificity, and AUC).

An important point to emphasize about the above CV procedure is that, at each iteration in step 2, all variable selection and estimation is performed using the training data (K − 1 folds), while all predictions are made on data on the external validation fold k. In contrast, when relying on RF’s OOB predictions to assess model performance, the same data used to rank predictor variables, according to their VI measures, is also used to estimate the accuracies of the RF models in the BVE procedure. Hence, the CV predictions provide a more honest assessment of model performance than the OOB predictions.

Note that in step 2(b), the OOB accuracy is still used as the criterion to select a model on the K − 1 folds. Thus, we only use CV to evaluate the performance of the BVE procedure, and to detect whether the OOB accuracy of the selected model is biased.

As an additional level of model validation, 71 NRSA sites (approximately 5% of the data) were withheld, prior to any model fitting and selection, as an independent test set. We use this test data by first selecting a model with BVE using all the training data (1365 NRSA sites; Figure 1); then we evaluate the performance of the selected RF model on the 71 withheld sites. Due to the small size of the test set, the performance metrics are aggregated nationally; that is, performance metrics (PCC, AUC, etc.) are computed with all 71 test set predictions, and not reported for each ecoregion separately. Note that we only withheld a small portion of the data so that most of the data could be used for estimation. A larger withheld set would compromise model performance for validation purposes. We also use 10-fold CV to avoid just relying on one test/training split to externally validate the RF models.

Stability of predictions

To illustrate the stability of the predictions generated by RF, we examine the coefficient of determination (R²) and root-mean-square deviation (RMSD) between the predicted probabilities from the full 212 predictor RF model and each of the k = 1, ⋯, 211 predictor RF models estimated during the BVE procedure. The RMSD and R² values are computed with the predictions made on the population of approximately 1.1 million catchments in the 2008/2009 NRSA sampling frame.

Let u_i for i = 1, ⋯, N be the predicted probabilities from the full set RF model with all 212 predictors, where N is the number of catchments. Let υ_i,k for i = 1, ⋯, N be the predicted probabilities from the RF model with k ∈ {1, ⋯, 211} predictor variables from the BVE algorithm. The Pearson correlation is then given by

$$\frac{{\sum }_{i=1}^N(u_i-\overline{u})({\upsilon }_{i,k}-{\overline{\upsilon }}_k)}{\sqrt{{\sum }_{i=1}^N{(u_i-\overline{u})}^2{\sum }_{i=1}^N{({\upsilon }_{i,k}-{\overline{\upsilon }}_k)}^2}},$$ (2)

where $\overline{u}=\frac{1}{N}{\sum }_{i=1}^N{u}_i$ and ${\overline{\upsilon }}_k=\frac{1}{N}{\sum }_{i=1}^N{\upsilon }_{i,k}$. The coefficient of determination (R²) is defined as the Pearson correlation (Equation 2) squared. In this context, R² can be interpreted as a standardized measure (between 0 and 1) of linear association between the probabilities from the full and k variable RF models, with values close to 1 indicating strong association and values close to 0 indicating weak association. Geometrically, the R² value can be thought of as measuring deviation from the least-squares regression line in the scatter plot between the predicted probabilities from the full and k variable RF models.

The root-mean-square deviation is given by

$$\sqrt{\frac{1}{N}\sum _{i=1}^N{({\upsilon }_{i,k}-u_i)}^2}.$$ (3)

Since u_i and υ_i,k are probabilities, the RMSD is between 0 and 1; an RMSD value close to 0 indicates close agreement between the predictions made by the two RF models. Geometrically, the RMSD can be thought of as measuring deviation from the 1-1 line in the scatter plot between the predicted probabilities from the full and k variable RF models. Note, since the RF models are fit separately to each ecoregion, the R² and RMSD values are also evaluated regionally.

Simulation study

We use simulated data to further generalize properties of RF modeling investigated in the real data analysis. Specifically, we use simulations to: (1) evaluate the robustness of RF modeling to including a large number of predictor variables which are unrelated to the response; and (2) compare the performance of reduced variable RF models, selected using the BVE procedure, with RF models which use a full set of predictor variables. In the simulations we emulate the dimensions of large environmental data sets such as StreamCat.

For this study we use a standard simulated data set named threenorm which was proposed in Breiman (1998) and used in several articles on RF modeling (e.g., Breiman, 2001; Segal, 2004). This simulated data consist of a 2-class (binary) response and d relevant predictors. The response data is balanced: half of the points are labeled class 1, and the other half are labeled class 2. Predictor values for each class are generated from d-dimensional multivariate normal distributions with unit covariance matrix. Specifically, predictor values for class 1 are generated with equal probability from a multivariate normal distribution with mean (a, a, …, a) and from a multivariate normal distribution with mean (−a, −a, …, −a); predictor values for class 2 are generated from a multivariate normal distribution with mean (a, −a, a, −a…, a); and $a=2/\sqrt{d}$. We implement this simulation using the function mlbench.threenorm from the R package mlbench (Leisch and Dimitriadou, 2010).

For the first simulation design we evaluate the robustness of RF modeling to including a large number of irrelevant features by adding noise predictor variables to simulated threenorm data sets with d = 20 relevant predictors. We use d = 20 since this was the dimension used in Breiman (1998, 2001). The noise predictors are generated from independent normal distributions with mean 0 and variance 1. Seven simulation cases are considered by setting the number of noise predictors k to 0, 50, 100, 150, 200, 250, and 300. This gives p = 20 + k total predictors for each case. The dimensions of the StreamCat data set are emulated by generating training sets of size 1000 for each simulation case. Test sets of size 1000 are also generated for each case, and the performance of the RF models are quantified using the same metrics as the stream condition models (PCC, sensitivity, Specificity, and AUC). All performance metrics are averaged over 20 repeated simulation runs.

The second simulation design considers two cases where we generate threenorm data sets and vary the proportion of relevant predictors. For the first case, there are d = 50 relevant predictors and k = 150 noise predictors (i.e., 25% of predictors are relevant). For the second case, there are d = 150 relevant predictors and k = 50 noise predictors (i.e., 75% of predictors are relevant). For each case we compare the performance of full RF models which use all 200 predictors with reduced RF models selected using the BVE procedure. Again, we generate training and test sets of size 1000, and average the performance metrics (PCC, sensitivity, Specificity, and AUC) over 20 repeated simulations runs. For all simulations we also use ntree = 1000 and the default $\text{mtry}=\sqrt{p}$.

Results

Stepwise model selection

The accuracy curves for the BVE procedure applied to each ecoregion show that the OOB accuracy of the RF models remains steady until a small portion of predictor variables remain (Figure 2). For example, the OOB accuracy for the NAP ecoregion fluctuates steadily between 76–80% until about 25 variables remain, at which point there is an increase in accuracy followed by a sharp decline as additional variables are removed. This general pattern, i.e., a bump in OOB accuracy once a large portion of variables are removed, is present in the accuracy curves for most other ecoregions as well. Moreover, the OOB accuracies of the RF models tend to degrade rapidly near the optimums (vertical lines in Figure 2, which indicate the reduced variable model selected by BVE). The only exceptions are the UMW ecoregion, which shows a sudden increase in OOB accuracy for the univariate RF model, and the SAP ecoregion, which shows a gradual decline in OOB accuracy once less than 75 variables remain. Since RF is generally known to perform well with a large number of predictor variables many of the effects in the OOB accuracy curves produced by BVE are unexpected.

Fig. 2.

Percent of sites correctly classified (PCC) versus number of predictor variables at each step of the backwards elimination procedure. PCC is computed on the out-of-bag data for each random forest model. The vertical line in each panel denotes the random forest model with optimal PCC. Ecoregion codes: Coastal Plains (CPL), Northern Appalachians (NAP), Northern Plains (NPL), Southern Appalachians (SAP), Southern Plains (SPL), Temperate Plains (TPL), Upper Midwest (UMW), Western Mountains (WMT), and Xeric (XER)

Table 1 further quantifies the results by displaying the OOB performance metrics for the full and reduced variable set RF models. For all ecoregions the selection procedure substantially reduces the number of variables. Variable reduction also leads to sizable increases in OOB accuracy (up to about 10 percentage points) and AUC for some ecoregions (e.g., SPL, WMT, and XER). Although for other ecoregions, such as NPL and SAP, the full and reduced models perform similarly in terms of the OOB performance metrics. Again, the UMW ecoregion is unusual since the reduced model contains only one variable, watershed area in square kilometers, and has much higher accuracy than any of the other models estimated during the stepwise procedure.

Table 1.

Out-of-bag performance metrics for the full and reduced variable random forest models for each ecoregion. Reduced model variables were selected to optimize out-of-bag accuracy using a backwards variable elimination approach. Nvars is the number of variables, PCC is the percent of sites correctly classified (accuracy), PGCC is the percent of good sites correctly classified (sensitivity), PPCC is the percent of poor sites correctly classified (specificity), and AUC is the area under the receiver operating characteristic curve. Ecoregion codes: Coastal Plains (CPL), Northern Appalachians (NAP), Northern Plains (NPL), Southern Appalachians (SAP), Southern Plains (SPL), Temperate Plains (TPL), Upper Midwest (UMW), Western Mountains (WMT), and Xeric (XER)

Region	Model	Nvars	PCC	PGCC	PPCC	AUC
CPL	Full	212	0.80	0.68	0.83	0.83
	Reduced	11	0.84	0.81	0.84	0.87
NAP	Full	212	0.77	0.67	0.82	0.85
	Reduced	9	0.84	0.76	0.89	0.87
NPL	Full	212	0.82	0.80	0.83	0.86
	Reduced	16	0.85	0.86	0.85	0.89
SAP	Full	212	0.76	0.66	0.81	0.81
	Reduced	86	0.78	0.70	0.82	0.83
SPL	Full	212	0.72	0.74	0.69	0.80
	Reduced	13	0.81	0.81	0.81	0.86
TPL	Full	212	0.78	0.78	0.78	0.86
	Reduced	12	0.86	0.85	0.87	0.91
UMW	Full	212	0.71	0.74	0.63	0.73
	Reduced	1	0.79	0.82	0.73	0.81
WMT	Full	212	0.71	0.70	0.72	0.81
	Reduced	22	0.82	0.77	0.88	0.84
XER	Full	212	0.68	0.58	0.74	0.80
	Reduced	11	0.79	0.74	0.82	0.84

Table 1 suggests choosing the reduced models since they have higher OOB accuracy. However, Figure 2 also shows that the reduced set RF models, selected to optimize OOB accuracy, generally occur in places on the accuracy curves that are unstable. That is, small changes in the number of predictors around the reduced set models (either by decreasing or increasing) results in models that have very different OOB accuracies. The full set RF models, on the other hand, occur on much more stable places on the accuracy curves. Moreover, in the next section we show that when data external to the variable selection process are used to assess accuracy, there is no significant difference in performance between the full and reduced set models.

Cross-validation

The full and reduced set RF models perform similarly in terms of the 10-fold CV performance metrics (Table 2). For instance, the full RF models perform as well or better than the reduced models in terms of CV accuracy and AUC for most ecoregions (NAP, NPL, SAP, SPL, TPL, and XER). For the other ecoregions (CPL, UMW, and WMT), the difference in CV accuracy between the reduced and full RF models is marginal (maximum difference is approximately 4%). In contrast, when using RF’s internal OOB data to measure model performance (Table 1), the difference in accuracy and AUC between the reduced and full models can be substantial (over 10%). Hence, the OOB accuracy estimates are upwardly biased, and give an over-optimistic impression of how well the reduced RF models are performing.

Table 2.

Cross-validation (CV) performance metrics for the full and reduced variable random forest models for each ecoregion. Performance metrics are computed using 10-fold CV with validation folds external to the variable selection process. The average number of predictor variables (AvgNvars) is provided since at each iteration of the CV procedure a different portion of the data is used as the training set for selecting a random forest model. PCC is the percent of sites correctly classified (accuracy), PGCC is the percent of good sites correctly classified (sensitivity), PPCC is the percent of poor sites correctly classified (specificity), and AUC is the area under the receiver operating characteristic curve. Ecoregion codes: Coastal Plains (CPL), Northern Appalachians (NAP), Northern Plains (NPL), Southern Appalachians (SAP), Southern Plains (SPL), Temperate Plains (TPL), Upper Midwest (UMW), Western Mountains (WMT), and Xeric (XER)

Region	Model	AvgNvars	PCC	PGCC	PPCC	AUC
CPL	Full	212.0	0.78	0.62	0.81	0.82
	Reduced	17.9	0.79	0.70	0.80	0.84
NAP	Full	212.0	0.77	0.69	0.82	0.83
	Reduced	8.8	0.77	0.62	0.86	0.82
NPL	Full	212.0	0.82	0.78	0.85	0.87
	Reduced	39.9	0.77	0.71	0.80	0.82
SAP	Full	212.0	0.74	0.62	0.80	0.80
	Reduced	61.1	0.69	0.51	0.78	0.76
SPL	Full	212.0	0.75	0.79	0.69	0.80
	Reduced	12.4	0.75	0.76	0.73	0.80
TPL	Full	212.0	0.79	0.79	0.79	0.87
	Reduced	21.6	0.79	0.81	0.78	0.86
UMW	Full	212.0	0.67	0.71	0.57	0.73
	Reduced	12.0	0.71	0.77	0.57	0.74
WMT	Full	212.0	0.71	0.71	0.70	0.79
	Reduced	20.8	0.75	0.71	0.79	0.80
XER	Full	212.0	0.69	0.62	0.74	0.80
	Reduced	22.1	0.68	0.64	0.70	0.75

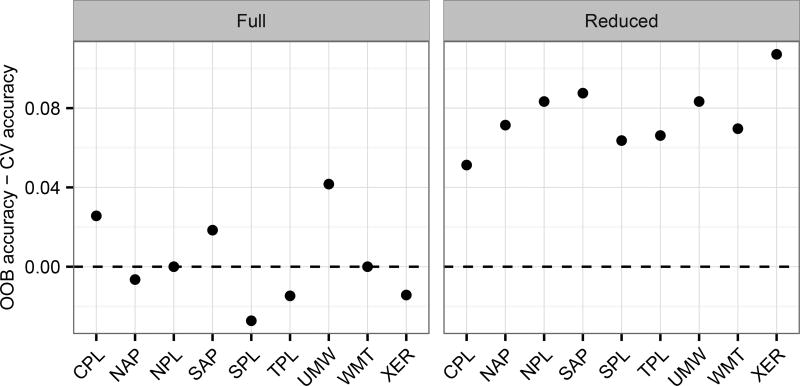
To further illustrate this issue of selection bias, Figure 3 shows the difference in the OOB accuracies (Table 1; PCC) and CV accuracies (Table 2; PCC) for the full and reduced RF models for each ecoregion. For the reduced set models, a clear bias is apparent as the OOB accuracy is between 4%–10% higher than the CV accuracy for each ecoregion RF model. For the full set models, on the other hand, no such bias is apparent since the difference in accuracies fluctuates around 0%.

Fig. 3.

Difference between out-of-bag (OOB) and 10-fold cross-validation (CV) accuracies (percent of sites correctly classified) for the full and reduced variable random forest models for each ecoregion. Ecoregion codes: Coastal Plains (CPL), Northern Appalachians (NAP), Northern Plains (NPL), Southern Appalachians (SAP), Southern Plains (SPL), Temperate Plains (TPL), Upper Midwest (UMW), Western Mountains (WMT), and Xeric (XER)

The nationally aggregated performance metrics also provide evidence of selection bias (i.e., the aggregated OOB metrics are over-optimistic for the RF models selected using BVE). Table 3 shows the performance results for the full and reduced RF models on the test data (71 withheld NRSA sites); nationally aggregated OOB and 10-fold CV performance metrics are also shown for comparison (PCC, PGCC, PPCC, and AUC are calculated on the combined set of 1365 OOB and CV predictions generated from the 9 regional models). The full and reduced RF models perform similarly on the withheld test data, and in terms of aggregated CV metrics; only the aggregated OOB metrics show a gain in performance due to variable reduction. While the test set is small, this perhaps suggests that the OOB accuracy estimates for the reduced model will fail to generalize to new locations.

Table 3.

Nationally aggregated model performance metrics for the full and reduced variable random forest models. For comparisons, performance metrics are computed using the test set of 71 withheld stream sites (Test), the 1365 out-of-bag (OOB) predictions, and the 1365 10-fold cross-validation (CV) predictions. PCC is the percent of sites correctly classified (accuracy), PGCC is the percent of good sites correctly classified (sensitivity), PPCC is the percent of poor sites correctly classified (specificity), and AUC is the area under the receiver operating characteristic curve

	Model	PCC	PGCC	PPCC	AUC
Test	Full	0.746	0.613	0.850	0.812
	Reduced	0.775	0.613	0.900	0.803
OOB	Full	0.753	0.707	0.783	0.835
	Reduced	0.820	0.787	0.841	0.865
CV	Full	0.749	0.707	0.776	0.828
	Reduced	0.745	0.693	0.779	0.815

Model comparisons and stability assessment

Several important distinctions stand out between the maps of the predicted probability of good stream condition for the full and reduced variable set RF models (Supplement 4). First, while the overall patterns are similar, the predicted probabilities appear more intense in the map for the reduced set model. That is, when compared to the full set model, sites predicted to be in good condition (blue) appear to have higher probabilities (closer to 1), and sites predicted to be in poor condition (red) appear to have lower probabilities (closer to 0). The histogram densities of predicted probabilities (Figure 4) support this comparison, since the probabilities from the reduced set models are more uniformly distributed and have greater density around 0 and 1 than the full set model. Second, the predictions for UMW are unusual in the map for the reduced set model, since this model only has one predictor variable (watershed area), and the spatial patterns in the predicted probabilities are very different than the full set model. Note that the prediction sites in both maps are only made for perennial streams (as designated in NHDPlusV2) since the 2008/2009 NRSA sample frame is limited to these types of streams.

Fig. 4.

Histogram density plots of the random forest predicted probabilities of good stream condition from the full and reduced variable set models. The predicted probabilities in each density plot are on the population of 1.1 million catchments within the sampling frame for the 2008/2009 National Rivers and Streams Assessment

While the intensity of the probability scales between the two models are different, many of the overall spatial trends are still similar for most ecoregions. One explanation for the different intensity scales is that the reduced set RF models focus on only the most important variables, and therefore tend to predict probabilities that are closer to 1 or 0 than would be when other, less important, variables are taken into account.

Even though the overall spatial trends appear similar, the (binned) scatter plots (Figure 5) reveal substantial differences in the values for the predicted probabilities for the full versus reduced set RF models. In particular, the predicted probabilities for the reduced set UMW model shows almost no association with the full set model. Only the SAP ecoregion shows strong correspondence between the two models; not surprisingly, the reduced SAP model has 86 predictors, which is substantially more than any other reduced ecoregion model (Table 1).

Fig. 5.

Scatter plots of the predicted probabilities of good stream condition from random forest RF) models with full versus reduced variable sets. Since there are a very large number of prediction sites within each ecoregion, points are binned in the scatter plots. The black line in each panel is the 1-1 line. The prediction sites for the RF models are all 1.1 million catchments within the sampling frame for the 2008/2009 National Rivers and Streams Assessment. Ecoregion codes: Coastal Plains CPL), Northern Appalachians (NAP), Northern Plains (NPL), Southern Appalachians (SAP), Southern Plains (SPL), Temperate Plains (TPL), Upper Midwest (UMW), Western Mountains WMT), and Xeric (XER)

To illustrate the stability of the models, we examine the coefficient of determination (R²) and RMSD between the predicted probabilities from the full set model and each RF model estimated during the BVE procedure (Figures 6 and 7, respectively). The R² curves (Figure 6) reveal that models with less than 25 predictor are, generally, substantially different than the full set model in terms of R². Interestingly, models with more than 50 predictors are, generally, very similar to the full set model in terms of R² values. This is consistent with the claim that RF is robust to adding many noisy variables (Breiman, 2001), since the 75 variable RF models, for example, are similar to the full 212 predictor variable models in terms of the associations between the predicted probabilities. The R² plots also suggest that the models selected by BVE (vertical lines) generally occur in places on the R² curves that are unstable. That is, although these model optimize OOB accuracy, small changes in the number of predictors around the selected model tend to result in substantial changes in the predicted probabilities as quantified by R². The RMSD curves (Figure 7) reveal similar patterns in the RF predictions as the R² curves (Figures 6). That is, RF models with more than 50 variables have small RMSDs (< 0.08), and are thus similar to the full set model, while RF models with less than 25 variables have substantially larger RMSD values and show instabilities.

Fig. 6.

Coefficient of determination (R²; Equation 2) versus number of predictor variables from the backwards elimination procedure. The R² values in each panel are between the predicted probabilities from the random forest model with the full set of predictor variables, and the predicted probabilities generated by the random forest models as variables are removed stepwise. The predicted probabilities used to compute the R² values are on the population of 1.1 million catchments within the sampling frame for the 2008/2009 National Rivers and Streams Assessment. The vertical line in each panel denotes the random forest model selected to optimize out-of-bag accuracy (Figure 2). Ecoregion codes: Coastal Plains (CPL), Northern Appalachians (NAP), Northern Plains (NPL), Southern Appalachians (SAP), Southern Plains (SPL), Temperate Plains (TPL), Upper Midwest (UMW), Western Mountains (WMT), and Xeric (XER)

Fig. 7.

Root-mean-square deviation (RMSD; Equation 3) versus number of predictor variables from the backwards elimination procedure. The RMSD values in each panel are between the predicted probabilities from the random forest model with the full set of predictor variables, and the predicted probabilities generated by the random forest models as variables are removed stepwise. The predicted probabilities used to compute the RMSD values are on the population of 1.1 million catchments within the sampling frame for the 2008/2009 National Rivers and Streams Assessment. The vertical line in each panel denotes the random forest model selected to optimize out-of-bag accuracy (Figure 2). Ecoregion codes: Coastal Plains (CPL), Northern Appalachians (NAP), Northern Plains (NPL), Southern Appalachians (SAP), Southern Plains (SPL), Temperate Plains (TPL), Upper Midwest (UMW), Western Mountains (WMT), and Xeric (XER)

Simulation study

The performances of RF on the simulated threenorm data sets were robust to inclusion of many irrelevant features (Table 4). That is, the RF models which contained k = 50, ⋯, 300 noise predictors retained test set performance comparable to the baseline case with just the 20 relevant predictors and no noise (k = 0). Inclusion of up to 300 noise predictors resulted in test set performance rates (PCC, sensitivity, Specificity, and AUC) which were within 1–3% of the baseline case (k = 0). Moreover, performance rates computed with the OOB data were generally within 1% of those computed with independently generated test data. Thus, for all simulation cases, RF’s internal OOB metrics closely approximated the true test set performance metrics.

Table 4.

Performance summary of random forest models on simulated threenorm data sets with 20 relevant predictors and k noise predictors. Performance metrics were computed using independent test sets of size 1000 (Test) and the out-of-bag data (OOB), and averaged over 20 simulation runs. PCC is the percent of observations correctly classified, sensitivity is the percent of observations in class 1 correctly classified, specificity is the percent of observations in class 2 correctly classified, and AUC is the area under the receiver operating characteristic curve

	k	PCC	Sens.	Spec.	AUC
Test	0	0.857	0.854	0.861	0.936
OOB	0	0.862	0.862	0.862	0.937
Test	50	0.849	0.841	0.858	0.929
OOB	50	0.848	0.832	0.864	0.927
Test	100	0.844	0.835	0.853	0.926
OOB	100	0.847	0.842	0.850	0.925
Test	150	0.843	0.835	0.852	0.924
OOB	150	0.833	0.827	0.838	0.915
Test	200	0.837	0.831	0.843	0.920
OOB	200	0.834	0.827	0.840	0.912
Test	250	0.836	0.843	0.831	0.917
OOB	250	0.829	0.833	0.825	0.909
Test	300	0.834	0.827	0.842	0.918
OOB	300	0.828	0.822	0.832	0.909

Simulation results comparing the full and reduced variable RF models are presented in Table 5. There was not a substantial difference between the test set performances (PCC, sensitivity, Specificity, and AUC) of the full and reduced models. However, when 25% of the variables were relevant (d = 50, k = 150), the reduced model performed slightly better on the test data; and when 75% of the variables were relevant (d = 150, k = 50), the full model performed slightly better on the test data. The OOB performance metrics for the reduced RF models, selected using BVE, were over-optimistic for both cases (i.e., the OOB performance metrics were higher than those computed with independent test data). This bias in the OOB performance metrics was more severe for the case when 75% of the variables were relevant (e.g., there was a 4% difference in the PCC computed using the OOB and test data). The OOB metrics for the full RF model, on the other hand, were slightly conservative and more closely approximated the true test set performance metrics.

Table 5.

Performance summary of full and reduced variable random forest models on simulated threenorm data sets with d relevant predictors and k noise predictors. Performance metrics were computed using independent test sets of size 1000 (Test) and the out-of-bag data (OOB), and averaged over 20 simulation runs. PCC is the percent of observations correctly classified, sensitivity is the percent of observations in class 1 correctly classified, specificity is the percent of observations in class 2 correctly classified, and AUC is the area under the receiver operating characteristic curve

	d	k	Model	PCC	Sens.	Spec.	AUC
Test	50	150	Full	0.805	0.807	0.806	0.893
OOB	50	150	Full	0.794	0.793	0.793	0.877
Test	50	150	Reduced	0.828	0.829	0.828	0.909
OOB	50	150	Reduced	0.840	0.838	0.842	0.909
Test	150	50	Full	0.768	0.763	0.777	0.859
OOB	150	50	Full	0.748	0.739	0.753	0.833
Test	150	50	Reduced	0.755	0.755	0.757	0.838
OOB	150	50	Reduced	0.795	0.798	0.790	0.865

Discussion

Comparison with other studies

A major result of this work is that the RF models of stream condition showed no significant improvement in predictive performance as a result of variable selection using the backwards elimination approach. Studies with other data sets have also suggested that robustness to overfitting, and the ability to handle many noise variables without the need for variable selection, are more general properties of RF modeling. Below we list several examples:

• Svetnik et al. (2003) applied RF modeling to classify 186 drug compounds (as P-gp substrates or non-substrates) with a set of 1522 atom pair descriptors. Using an extensive cross-validation approach, they found no improvement in the performance of the RF classifier as a result of variable selection. However, the results suggested that the number of variables could be cut down to about 190 without degradation of performance.

• Díaz-Uriarte and De Andres (2006) applied RF modeling to multiple high-dimensional genetic data sets, each with thousands of genes (predictor variables) and typically less than 100 patients (observations). On all data sets, the performance of RF when performing variable selection was comparable to RF without variable selection. Moreover, RF with no variable selection and minimal tuning also performed comparably with alternative classifiers (e.g., support vector machines, k-nearest neighbors, etc.).

• Biau (2012) provided analytic and simulation results suggesting that with a sufficiently large sample size the performance of RF does not depend on the number of pure noise variables.

Note that the performance metrics in these studies are reliable since selection bias was accounted for by running the variable selection process separately from the data used to validate the model. Thus, empirical results on a variety of data sets suggest that variable selection procedures for RF models generally do not improve predictive performance, and that RF has built in mechanisms which allow it to perform well with high-dimensional data sets (e.g., by probing the predictor space at each split and averaging over many trees).

Our study has also provided several unique methodological contributions not addressed in the previously mentioned works. First, we assessed variable selection for RF modeling using a large environmental data set, which has dimensions and properties different than the high-dimensional data sets analyzed in Svetnik et al. (2003) and Díaz-Uriarte and De Andres (2006). Second, since the StreamCat predictors are spatially referenced, we had the opportunity to produce maps of the predicted probabilities. Assessment of the prediction maps revealed instabilities in the variable selection procedure which previous works had not addressed; for instance, we found that in certain ecoregions (e.g., UMW), the predictions maps were surprisingly different between the full and reduced RF models, even though CV accuracy was similar. Third, we demonstrated that RF’s OOB metrics can be misleading when applying a stepwise variable selection procedure, and we provided empirical evidence supporting the need for external validation for reduced variable RF models.

We also believe that our study is the first to demonstrate that there is actually a cost to variable selection in RF models, at least when using the OOB accuracy as a selection criterion. Specifically, predictions from the selected models are unstable, that is, small changes in the number of predictor variables have substantial effects on the predicted probabilities once variables have been reduced to a small proportion of the original set. Further, the R² and RMSD curves (Figures 6 and 7) reveal that larger sets of predictor variables are necessary to obtain predicted probabilities which have values similar to the full set RF model, and most other RF models estimated in the sequence. The 10-fold CV and test set results also indicate that the predictor variables selected by optimizing OOB accuracy are biased towards the sample; thus the selection routine may fail to retain many predictors which are important to retain when making predictions at unsampled locations.

Preselection of predictor variables

While StreamCat is large for an environmental data set, predictors were selected to be indicative of stream condition based on two criteria: First, a literature review of natural and anthropogenic watershed characteristics that had been linked to instream biological and habitat condition (e.g., soils, lithology, runoff, topography, roads, dams, mines, urban and agricultural land use, and imperviousness of man-made surfaces; Hill et al., 2016, p. 123). Second, a search for publicly available landscape layers hypothesized to also characterize watersheds (e.g., air temperature and precipitation, N and P sources, and forest cover change; Hill et al., 2016, p. 123). Many of these explanatory variables are correlated with each other; for instance, StreamCat contains eight temperature variables with pairwise correlations exceeding 0.77. Each of the eight temperature variables provide slightly different information covering different spatial scales (watershed versus catchment) and time durations (30 year average versus 2008/2009 NRSA sampling period). For traditional regression modeling, including many collinear predictors can cause serious issues in parameter estimation and statistical inferences (Faraway, 2005). However, since RF averages over many trees and randomly selects variables for each split, the influence of groups of correlated variables gets spread out over the forest (Cutler et al., 2007). Including all 212 StreamCat variables thus provides the RF algorithm with an opportunity to comprehensively explore the predictor space and model complex interactions between variables that simpler models, with fewer variables, would not be able to exploit.

Model validation and computational considerations

One appealing feature of RF modeling is that the OOB data provide a convenient way to assess model performance, without the need for external validation (either by K-fold CV or a withheld test set). However, the results of this study demonstrated that external validation is necessary when applying variable selection for RF models with the VI rankings. The OOB performance metrics gave the misleading impression that variable reduction significantly improved the RF models; whereas, the 10-fold CV performance metrics, which used validation data (folds) completely external to the variable selection process, showed no such improvements as a result of variable reduction (Figure 3). Nevertheless, for the full set model, the OOB and CV performance metrics agreed closely, suggesting that the OOB performance metrics are reasonable as long as no variable reduction is performed using the VI rankings.

The CV procedure of Ambroise and McLachlan (2002), which corrects for selection bias when assessing model performance, is also computationally expensive since it requires completely embedding variable selection within the model validation procedure. For our implementation, we estimated p = 212 RF models for each of the 10 training folds (i.e, 19080 RF models total for the 9 ecoregions). With parallelization over 5 cores this task took 1.7 hours. The 9 ecoregion RF models without variable selection, on the other hand, took only 1.3 minutes to estimate without any parallelization. Hence, variable selection imposed additional computational costs on RF modeling that limited reproducibility and resulted in negligible changes in performance.

Robustness of random forests to overfitting

Simulations provided empirical evidence suggesting that RF models are robust to overfitting when using data sets with similar dimensions as StreamCat. A statistical model which overfits will adapt too closely to random characteristics in a sample, and fail to generalize to new samples from the population (Babyak, 2004; Strobl et al., 2009). That is, overfit models have low error on the training set, but high error on test sets (Breiman, 1996b). Simulations are ideal for investigating this issue since models can be validated using large, independently generated test sets. The simulations demonstrated that the test set performance of the full RF model was not substantially affected by including many random noise variables (Table 4). There was also no substantial difference between the test set performance of the full and reduced RF models (Table 5). Furthermore, in all simulations, the OOB performance metrics for the full RF model closely approximated performance metrics computed using the test data. This distinguishes RF from other modeling approaches such as linear regression where in-sample performance measures such as the coefficient of determination (R²) can be misleading for models with a large number of parameters, and other measures (e.g., adjusted-R², AIC) are needed to correct for model complexity.

Conclusions

In this paper we compared two types of RF models for good/poor biological stream condition in each ecoregion: a full set model, which used all 212 landscape predictors from the StreamCat data set; and a reduced set model, which was selected to optimize OOB accuracy by removing variables stepwise according to their importance measures. We validated RF models using a 10-fold CV procedure with validation folds external to the variable selection process. According to standard metrics (e.g., PCC and AUC), we found no substantial difference between the CV performance of the full and reduced RF models. In fact, in most ecoregions, the CV performance of the full RF model was equivalent to or slightly better than the reduced model. For the stability assessment, we investigated how variable reduction affected the maps of the RF predicted probabilities on the population of approximately 1.1 million perennial stream reaches within the CONUS. With various statistics (R², RMSE) we evaluated deviations between the predicted probabilities from the full RF model, and each RF model estimated during the stepwise variable reduction procedure. According to these diagnostics, we found that the RF models with no variable reduction and minimal tuning were surprisingly robust. The results suggested that many noisy predictors (i.e., predictors with moderate to low VI measures) could be included in a RF model without substantially affecting the predicted probabilities (e.g., the 75 variable and 212 variable RF models produced similar predictions). The reduced RF models, on the other hand, which were selected to optimize OOB accuracy, tended to contain too few variables; hence, adding or removing a small number of variables around the selected model often resulted in substantial fluctuations in the predicted probabilities.

The assessment of both the StreamCat and simulated data sets demonstrated that a stepwise variable selection procedure for RF models can cause over-optimistic OOB performance metrics. In the analysis of the StreamCat data set, we found that the OOB metrics for the reduced models were substantially higher than those computed using 10-fold CV, with validation folds external to the variable selection procedure. In the analysis of large simulated data sets, we also found that the OOB metrics for the reduced RF models were higher than those computed using independently generated test sets. Thus, if a stepwise algorithm is used to select variables for a RF model, we recommend externally validating that RF model (e.g., by withholding an independent validation set, or using the K-fold CV procedure discussed in this study).

While variable selection is often an essential part of developing a statistical model in a traditional linear regression framework, in this study we found the application of variable selection methods for RF models unnecessary. However, while the full set RF model performed well with our data set, we do not advocate including as many variables as possible as a general strategy for RF modeling. The preselection of variables of hypothesized relevance to the ecological process at hand may be a very important step in developing an adequate RF model. Indeed, the results of this study demonstrate that the application of a variable selection method to a RF model needs to be carefully examined, as we found numerous issues when evaluating the accuracy and stability of the RF models selected with the backwards elimination approach. When considering this, however, accuracy alone should not be the sole criterion; rather, trade-offs between accuracy and stability need to be considered.