Here, we report the first minimally invasive in vivo measurements of the relationship between lymphangion chain length and lymphatic pumping pressure. We also provide the first in vivo validation of lumped parameter models of lymphangion chains previously developed through data obtained from isolated vessel testing.
Keywords: lymph transport, contractility, microstructure-constitutive models, lymphedema
Abstract
The intrinsic contraction of collecting lymphatic vessels serves as a pumping system to propel lymph against hydrostatic pressure gradients as it returns interstitial fluid to the venous circulation. In the present study, we proposed and validated that the maximum opposing outflow pressure along a chain of lymphangions at which flow can be achieved increases with the length of chain. Using minimally invasive near-infrared imaging to measure the effective pumping pressure at various locations in the rat tail, we demonstrated increases in pumping pressure along the length of the tail. Computational simulations based on a microstructurally motivated model of a chain of lymphangions informed from biaxial testing of isolated vessels was used to provide insights into the pumping mechanisms responsible for the pressure increases observed in vivo. These models suggest that the number of lymphangions in the chain and smooth muscle cell force generation play a significant role in determining the maximum outflow pressure, whereas the frequency of contraction has no effect. In vivo administration of nitric oxide attenuated lymphatic contraction, subsequently lowering the effective pumping pressure. Computational simulations suggest that the reduction in contractile strength of smooth muscle cells in the presence of nitric oxide can account for the reductions in outflow pressure observed along the lymphangion chain in vivo. Thus, combining modeling with multiple measurements of lymphatic pumping pressure provides a method for approximating intrinsic lymphatic muscle activity noninvasively in vivo while also providing insights into factors that determine the extent that a lymphangion chain can transport fluid against an adverse pressure gradient.
NEW & NOTEWORTHY Here, we report the first minimally invasive in vivo measurements of the relationship between lymphangion chain length and lymphatic pumping pressure. We also provide the first in vivo validation of lumped parameter models of lymphangion chains previously developed through data obtained from isolated vessel testing.
INTRODUCTION
The primary function of the lymphatic system is to transport interstitial fluid, protein, and waste back to the blood circulation to maintain physiological homeostasis (17, 64). The lymphatic system also serves to transport macromolecules, dietary lipids from the gut, and antigens and immune cells to facilitate the immune response. To achieve these vital functions, lymph flow is driven by both extrinsic pumps (e.g., skeletal muscle contraction by surrounding tissues) (29, 41, 51, 61, 67) and intrinsic pumps (e.g., phasic contraction of smooth muscle cells wrapped around collecting lymphatic vessels) (14, 47, 72). The network of collecting lymphatic vessels is composed of intrinsic contractile units (lymphangions) separated by one-way valves that are arranged in series. The major function of lymphatic valves is to provide unidirectional movement of lymph through the vessels against an adverse pressure gradient. The majority of the collecting vessels ultimately converge to the thoracic duct, where fluid is returned to the venous circulation. Pump dysfunction (e.g., due to valve failure or loss of smooth muscle contractility) may play a significant role in the pathogenesis and progression of lymphatic pathologies, such as lymphedema (62). Mechanisms driving the delayed onset seen in many forms of secondary lymphedema remain elusive, attributable in part to limited diagnostic tools clinically available (18); however, the disease progression is likely intimately linked with changes in the existing vessel network structure and/or function.
Significant strides have been made toward our understanding of the intrinsic lymphatic pump through recently developed computational models of chains of lymphatic vessels (2, 3, 8, 30, 31, 36). The development of these models has been populated with data informed from functional testing of isolated lymphatic vessels (25, 35, 52, 57). These computational studies have predicted that a longer lymphangion chain can pump against higher opposing pressure gradients (30, 31), a phenomenon that has also been reported in isolated vessel studies (21, 22). However, most of the predictions made through these computational models have yet to be verified in vivo. Additionally, although isolated vessel studies have been crucial to reveal the molecular regulation and mechanosensitivity of lymphatic contractility, the techniques remove the vessel from their native tissue environment and thus change the mechanical support of the vessel, remove the influence of surrounding biological tissues such as immune cells, and eliminate the effects of the extrinsic pump (39, 44). Thus, although computational models and isolated vessel studies have been in good agreement, there is a pressing need to translate the insights gained from these studies into in vivo measurements of lymphatic function.
One approach used heavily in vivo is to image lymphatic function through tracking the clearance of a tracer. The primary metrics that are measured in vivo are either a rate of tracer clearance of a large-molecular-weight dye (32, 46) or contraction frequency, which is inferred by either counting fluorescent fluctuations in a vessel (termed “packets”) as dye is ejected during each contraction (10) or directly visualizing contraction in fluorescently labeled vessels (39, 40). Dye clearance rate captures a measure of total interstitial fluid clearance, but this measure does not allow one to parse the separate contributions of interstitial fluid pressure, lymph formation, extrinsic tissue contractility, and intrinsic vessel pumping. The frequency of passing packets of dyes through the field of view (packet frequency), on the other hand, is not necessarily indicative of intrinsic pumping capacity, as lymphatic vessels are known to inhibit contraction when other factors (e.g., lymph formation) are sufficient to drive lymphatic flow. Thus, there is a pressing need for improved techniques that can directly measure the contractile health of the lymphatic smooth muscle, thus improving our basic understanding of lymphatic physiology in vivo.
We recently reported on an imaging method to measure the pumping pressure of a chain of lymphatics in the rat tail (45). In the present study, we sought to use this in vivo imaging technique, combined with computational modeling, to test the hypothesis that the increase in maximum pressure generation along a chain of lymphangions correlates with lymphangion number and active tension of lymphatic smooth muscle cells. To bridge the gap between the precise functional measurements that can be made in isolated vessels with the physiological relevance of in vivo approaches, we applied a computational model of lymphatic pumping that was derived from experimental data of lymphatic vessel biomechanics taken from isolated vessels. We then challenged this model in vivo using near-infrared imaging (NIR) of lymphatic pump function under normal conditions and with treatment by a dermally delivered nitric oxide (NO) donor. By combining both computational modeling and the new NIR imaging approach, in which we measured lymphatic pumping pressure at multiple locations along a lymphangion chain, we established an approach to approximate lymphatic muscle force generation in vivo.
METHODS
In Vivo Assessment of Lymphatic Pumping Pressure
The pressure measurement system.
To evaluate the maximal pressure generation of lymphangion chains in vivo, we used a previously described method to quantify lymphatic pumping pressure (45). Briefly, these methodologies involve a closed-loop lymphatic pressure measurement system that was designed using a commercially available pressure cuff (Kent Scientific, Torrington, CT). The pressure cuff was attached to a 5-ml BD luer-lock syringe via plastic tubing and to a precalibrated pressure transducer (Honeywell Sensing and Control, Morristown, NJ). The pressure transducer was connected to a data-acquisition device (National Instruments, Austin, TX), and pressure values were read into a LabView virtual instrument (LabView 2014 32-bit, National Instruments). These real-time pressure readings were used to control the serial command output to the syringe pump (PHD 2000 Infusion/Withdraw 70–2001, Harvard Apparatus, Holliston, MA). The difference between the desired pressure and the sampled pressure was used to control the flow rates on the syringe pump to subsequently inflate or deflate the pressure cuff.
To determine the presence or absence of lymph flow at various occlusion pressures, vessels were imaged with a lymphatic NIR imaging system as previously described (45, 70). In brief, a diode driver and temperature control box powered a 1-W 808-nm laser diode and a 20° beam diffuser (Thorlabs, Newton, NJ), which provided excitation light. This achieved a uniform excitation field of ~75 cm2 with <1.9 mW/cm2. An Infinity K2/SC video ×2.15 magnification microscope lens (Edmund Optics, Barrington, NJ) and a bandpass filter (center wavelength: 840 nm, full-width half-maximum: 15 nm, Omega Optical, Brattleboro, VT) were attached to a PIXIS 1024B back-illuminated charge-coupled device camera (Princeton Instruments, Trenton, NJ) to capture fluorescence emission centered at 840 nm. The excitation light source was positioned ~24 cm from the tails at a 60° angle from the imaging surface. Animals were positioned such that the right and left vessels received symmetrical illumination from the excitation light source.
Experimental protocol.
All animal procedures were carried out at the Georgia Institute of Technology (Atlanta, GA) and were reviewed and approved by the Georgia Institute of Technology Institutional Animal Care and Use Committee. A standardized procedure to quantify pumping pressure was carried out on 9-wk-old male Sprague-Dawley (Charles River, Wilmington, MA) rats (45). To minimize light scattering, a depilatory lotion was used to remove hair in the region of interest (ROI) on the tail 1 day before experimentation. Rats were anesthetized with an intramuscular injection of diazepam (2.5 mg∕kg) followed by a cocktail of fentanyl (0.12 mg∕kg) and droperidol (6 mg∕kg). After ~10 min for the anesthetics to take effect, the rat was positioned under the camera. Animals in the NO treatment group received a topical application of 500 mg glyceryl trinitrate ointment [GTNO; 0.2% (wt∕wt), Rectogesic, Care Pharmaceuticals, Bondi Junction, NSW, Australia) applied to the entirety of the tail.
The proximal edge of the pressure cuff was placed 4, 8, or 12 cm from the distal tip of the tail. The rat was positioned so that the field of view was immediately proximal to the cuff (Fig. 1). A mixture of 30 µl of indocyanine green (ICG)-albumin solution (150 µg/ml ICG, Acros Organics, Geel, Belgium) and 60 g/ml BSA (MP Biomedicals, Auckland, New Zealand) dissolved in deionized water was injected intradermally at the tip of the tail.
Fig. 1.
Experimental setup for measuring lymphatic pumping pressure. The pressure cuff is positioned at various locations measured from the tip of the tail. Flow restoration is imaged by capturing the return of fluorescence into the collecting lymphatic vessel (LV) in a region proximal to cuff. The pressure at which flow restoration is observed is reported as the effective lymphatic pumping pressure and compared with barometric pressure in the computational model. ROI, region of interest.
Image acquisition began just before intradermal injection of the dye with a field of view that included the edge of the cuff and the proximal region (Fig. 1). Once steady-state fluorescence was established, a predetermined sequence of pressure cuff applications was administered to the tail. Specifically, the pressure was increased to 80 mmHg for 10 min to allow for the proximal vessel to completely empty its contents. After holding for 10 min at 80 mmHg, pressure was quickly decreased to 55 mmHg and then subsequently decreased in decrements of 2.5 mmHg, holding at each pressure step for 60 s, until the pressure value reached zero.
Images of the tail were captured by the NIR imaging system throughout the experiment at a frame rate of 1 frame/s with a camera exposure time of 50 ms. After the first frame was captured, a ROI was selected that was positioned just proximal to the pressure cuff, over the fluorescent collecting vessel. The mean intensity within the ROI was recorded and used in conjunction with the pressure data to evaluate lymphatic pumping pressure. Effective pumping pressure was calculated using two points as previously described (45), the minimum intensity value during occlusion at 80 mmHg and the maximum intensity value after flow was restored during deflation. The average of these two values was the intensity threshold for flow restoration. The pressure at the time at which the intensity rose to equal this intensity threshold was the effective pumping pressure of the collecting lymphatic vessel. Animals were euthanized at the end of experiments using CO2.
Statistical analysis.
Statistical significance between measurements taken at various locations for control animals was determined through a Kruskal-Wallis test with a post hoc Dunn’s test for multiple comparisons. While the data sets here were not statistically powered to reject the null hypothesis that the data is normally distributed (as determined by the Shapiro-Wilk test), previous measurements of pumping pressure in the rat for larger data sets (45) have demonstrated that the distribution of pumping pressure values across rats is not normal. Therefore, we chose to use the nonparametric Kruskal-Wallis test for this study. Significant difference between the control and GTNO data sets was evaluated using the extra sum of squares F-test on the quadratic best-fit regressions of the data. For this test, the restricted model was a single quadratic regression for both data sets, corresponding to the null hypothesis that the control and GTNO sets can be sufficiently described by a single quadratic regression. The full model was two quadratic equations for control and GTNO, respectively, corresponding to the hypothesis that control and GTNO data sets were best described with two distinct quadratic regressions. The F-statistic was computed from the sequential sum of squares for the two models. To determine statistical significance, a P value was computed from the F-statistic with P < 0.05 corresponding to a rejection of the null hypothesis. All statistical computations were performed in Prism software (GraphPad Software, La Jolla, CA).
Model Theoretical Framework
Our theoretical framework consists of a lump-parameter model for lymph transport (30), a two-dimensional (2-D), nonlinear, elastic, homogeneous, anisotropic model over finite deformations for the passive mechanics of the vessel wall, and a Rachev-Hayashi model for the active, contractile behavior of the vessel wall (8, 9).
Lymph transport and valve function.
Lymph is transported through chains of lymphangions, separated by intraluminal one-way valves (72). Assuming fully developed Newtonian flow, Poiseuille's law is used to calculate flow rate, which has been shown to be a good approximation in regions away from valves (16, 50). The lymphatic valve imposes a variable resistance to flow during leaflet movements. This resistance becomes minimum during valve opening and maximum during closure, whereas the opening/closure behavior is a function of transvalvular pressure. The lumped model of valve resistance originally proposed by Bertram et al. (3) is used to simulate the role of one-way valves. The valve resistance is a sigmoidal curve, which is a function of pressure drop along the valve, defined as follows:
where RVn is the resistance of fully open valve, RVx is the resistance of fully closed valve, so is a parameter associated with the rate of opening and closure of valves, ΔpV is the pressure drop across the valve, and Δpo is the pressure drop at which the valve opens or closes.
Passive contribution of the extracellular matrix.
The passive circumferential and axial components of the 2-D Cauchy stress in the framework of 2-D finite elasticity of an incompressible solid are expressed as follows (9):
| (1) |
| (2) |
where Ce is the right Cauchy-Green strain tensor, defined as , where = h/H, = d/D, and = l/L (where h and H are the loaded and unloaded thickness, d and D are the loaded and unloaded diameter, and l and L are the loaded and unloaded length of the lymphangion, respectively). W is the strain energy density function that was adapted from the four-fiber family strain energy density function as follows (28):
| (3) |
where b is a constant associated with elastin-dominated amorphous matrix; is the first invariant of Ce; and are material parameters associated with locally parallel collagenous fibers, , and αk is the direction of kth fiber. In this framework, the average circumferential and axial stresses are
| (4a) |
and
| (4b) |
where P and f are transmural pressure and axial force, respectively.
Active contribution of smooth muscle cells.
Lymphatic smooth muscle cells modulate contractile force generation in response to changes in transmural pressure of the vessels (27, 42). A modified length-active tension relationship, which was originally proposed for arteries by Rachev and Hayashi, was adapted as previously described (9, 48). In this framework, active circumferential stress is expressed as follows:
| (5) |
where Tact(t) is the activation parameter as a function of time that depends on the degree of muscle activation in response to variation in intensity of stimuli (e.g., intracellular Ca2+), which contributes to phasic contraction and tonic constriction, λθ is elastic circumferential stretch, λM is the stretch at which force generation is maximum, and λ0 is the stretch at which force generation ceases.
Assuming a cosine function for time dependency of stimulation (e.g., intracellular Ca2+ response) during phasic contraction and a constant parameter for contribution to tonic contractions, Tact(t) is written as follows:
| (6a) |
and
| (6b) |
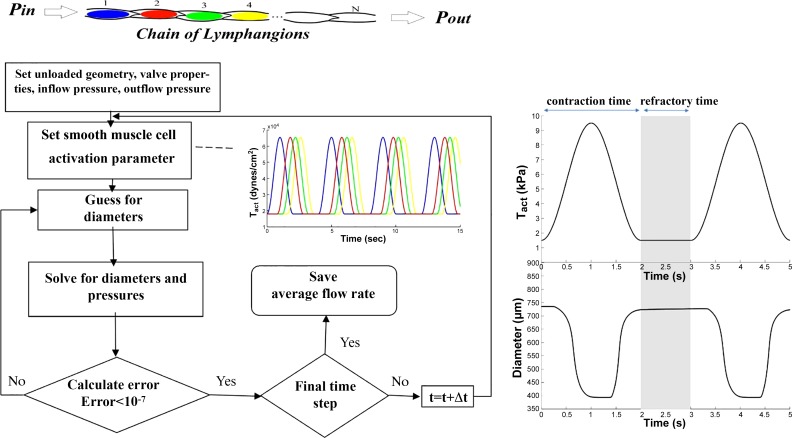
where Tphasic and Ttonic regulate the magnitude of maximum phasic contractions and tonic constrictions, respectively, t is time, and tc is the period of contraction. Additionally, the parameter tr is defined as the refractory period to separate consecutive contractions (i.e., the time period of tonic constriction as defined in Eq. 6b and shown in Fig. 3).
Fig. 3.
Schematic of the solving routine for computational framework used to model a chain of lymphangions in a series arrangement. Tact, activation parameter; t, time.
Morphological and biomechanical parameters.
Because circumferential stress depends on the unloaded configuration of lymphangion, the mean unloaded morphological parameters (diameter, thickness, and length) in rat tail lymphatics were quantified from dissected collecting vessels (Fig. 2 and Table 1). Male Sprague-Dawley rats weighing between 300 and 350 g were used for experiments, similar to those used for the in vivo measurement of effective pumping pressure. Rats were anesthetized with a combination of a solution of fentanyl plus droperidol (0.3 ml/kg im) and diazepam (2.5 mg/kg im). To isolate lymphatic vessels from a tail region, an incision was made in the tail skin under the lateral caudal vein at the base of the tail to ligate lymphatic vessels to prevent them from leakage and keep them under pressure for easy identification. Tail skin with attached lateral caudal veins, arteries, and lymphatics was removed from both sides of tail, the bone was discarded, but the tip of the tail was kept intact. Two stripes of skin with the vessel bundle were placed in a petri dish (150 × 15 mm) coated with Sylgard and filled with Dulbecco's-PBS. The skin was pinned down to the bottom of the dish to expose the vessel bundle on top. Lymphatic segments located at 4, 8, and 12 cm from the tip of tail were identified usually lateral to the lateral caudal vein, as vessels were filled with near-transparent fluid inside (lymph). They were then carefully separated from blood vessels and nerves under a stereoscope using microsurgical forceps and scissors and cleaned (with caution not to grab or pinch vessels) from adipose and other connective tissue. The segment of tail lymphatic vessels without branches was cut and transferred to a vessel chamber, where it was cannulated and tied with 11 size of surgical suture to ~200-μm glass cannulas and used for imaging.
Fig. 2.
Geometric and microstructural properties of rat tail lymphatics along various regions of the tail. A–C: cannulated lymphatic vessels isolated from regions 12 cm (A), 8 cm (B), and 4 cm (C) from the tip of the tail, as shown in D. E–G: second harmonic generation images of collagen microstructure of vessels isolated from regions 12 cm (E), 8 cm (F), and 4 cm (G) from the tip of the tail. H: chain of lymphangions showing typical valve spacing along the length of the chain.
Table 1.
Parameters associated with biomechanical properties, geometry, and valve models
| Biomechanical Parameters (Rat Thoracic Duct) |
|||||
|---|---|---|---|---|---|
| Passive parameters | Contractile parameters | Geometric Parameters (Rat Tail) | |||
| b, Pa | 66.16 | Tact, Pa | 10.9 | Unloaded | |
| , Pa | 199.0 | Tphasic/Ttonic | 0.4 | Diameter, μm | 220 |
| , Pa | 0.14624 | λm | 1.4575 | Thickness, μm | 7.85 |
| , Pa | 0.000011 | λ0 | 0.6641 | Length, cm | 0.33 |
| , Pa | 0.48137 | Valve parameters (rat mesentery) | |||
| , Pa | 189.9 | RVn, Pa·ml−1·cm−2 | 60 | ||
| , Pa | 0.46244 | RVx, Pa·ml−1·cm−2 | 12e10 | ||
| α1, ° | 90 | so | 0.01 | ||
| α2, ° | 0 | Δpo | 0 | ||
| α3, ° | 27.7 | Flow parameter | |||
| α4, ° | −27.7 | Viscosity, cP | 0.01 | ||
| λz | 1.1 | ||||
Collagen distribution was imaged with three-dimensional multiphoton imaging using second harmonic generation as described previously (9). Given that the microstructure and collagen distribution in rat tail lymphatics were qualitatively similar to that of the rat thoracic duct, the active and passive parameters were obtained from previously experimentally quantified parameters (9). All parameters are shown in Table 1. The model material properties that were used, specifically the passive parameters associated with collagen and elastin organization in lymph vessels and the active parameters associated with the lymphatic smooth muscle cells, were selected within the range of what has been quantified previously through biaxial testing of rat thoracic duct and are shown in Table 1. The geometry of lymphatic vessels was directly obtained from tail, whereas the measurements for biomechanical properties of lymphatic vessel and lymphatic valves were obtained from thoracic duct and mesenteric lymphatic vessels, respectively (Table 1).
Integrative modeling.
To obtain the flow rate generated by intrinsic contractions of lymphangions, an algorithm in Matlab 2010 was used to simultaneously solve constitutive equations of lymphangion wall mechanics, lymph flow, and intraluminal valve models. This algorithm has been previously discussed in detail (8). In brief, lymphangion constitutive equations of wall mechanics are composed of both a passive model (Eqs. 1−4), which accounts for the structure-function relationship of the lymphatic vessel wall, and an active model, which constitutes a framework to model active force generation of lymphatic smooth muscle cells that incorporates both tonic constrictions and phasic contractions (Eq. 5). Both active and passive model parameters were informed by ex vivo isolated lymphatic vessel experiments in rat thoracic duct (see Table 1). A parameter (Tact) that dictates the contraction and relaxation of lymphatic smooth muscle cells is prescribed to simulate the phasic contractions and tonic contractility of smooth muscle cells (Eqs. 5 and 6). The contractile activity of a lymphangion is regulated by both mechanical stimuli (e.g., stretch response) and biochemical stimuli (e.g., calcium dose response). The stretch dependency of the lymphatic contraction model (Eq. 5) accounts for length-tension relationship of the muscle, whereas cyclic changes in the amplitude of active tension (Tact) prescribes the time-dependent response. Tact can oscillate between basal (diastolic) and maximum (systolic) values that ultimately determine systolic and diastolic diameters, respectively. It should also be noted that Tact only determines the maximum amplitude of active stress (regardless of stretch response) at each time point of contraction. When comparing the model with in vivo data, Tact was changed to find the best fit to experimental measurements. For the purposes of this study, Tact was assumed to be constant along the length of the chain. In addition, parameters associated with the valve and flow models were adopted from previous studies (see Table 1). The solving algorithm is based on an optimization routine to find diameter and pressure that satisfy mass conservation for each lymphangion (see Fig. 3).
Because the computational model was used to recapitulate the in vivo lymphatic pressure-length relationship of a rat tail model, the geometrical parameters were measured from the tail (see Table 1). To determine the number of lymphangions in the tail, the skin was removed from the tail region, and, upon application of trypan blue dye (0.4%) to identify lymphatic vessels, a long chain of lymphangions was observed. Based on the measurement of the distance between two lymphatic valves under a stereomicroscope (Zeiss SteREO Lumar V12) using segments of a lymphangion chain at three different locations (4, 8, and 12 cm from the tip of the tail), the average lymphangion number was approximated to be 3 lymphangions/cm in the rat tail. Because occlusion pressures were measured at three locations from the tip of the tail (4, 8, and 12 cm), three locations along the tail were modeled as chains with 12, 24, and 36 lymphangions based on the average number of lymphangions per centimeter of tail (3 lymphangion/cm), respectively. The pressure at the inlet of chain was set to 6 mmHg (an approximate pressure at the injection site near the tip of the tail), which was based on an approximation of the y-intercept of a curve fitting the experimental data where the number of lymphangions is mathematically zero. The outflow pressure was elevated in the model until the flow rate dropped below 0.01 ml/min (equivalent to the pressure applied through the pressure cuff to occlude lymphatic flow).
RESULTS
Experimental and Computational Modeling Results Show That Pumping Pressure Increases With Chain Length
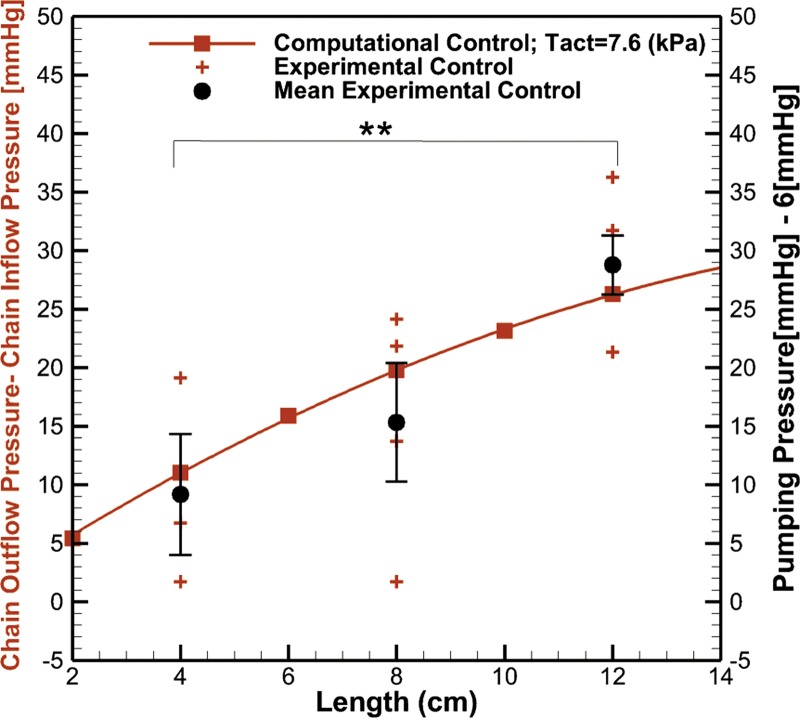
The effective pumping pressure in the rat tail progressively increases along the length of the tail as one moves from the tip of the tail toward the base (Fig. 4). Specifically, the average pumping pressure for each group of rats was 15.02 ± 5.17 mmHg (n = 3), 21.03 ± 5.06 mmHg (n = 4), and 34.80 ± 2.52 mmHg (n = 5) at distances of 4, 8, and 12 cm from the tip of the tail, respectively (P < 0.05). As the length from the tip of tail increases, the maximum occlusion pressure at which flow can be achieved increases. This phenomenon was also observed in the computational model, and optimization of the activation parameter to provide the best fit to the data suggested a value of Tact = 7.64 kPa, which can be converted into a tension by multiplying by the vessel thickness to yield a value of 0.06 mN/mm, which is within the range but smaller than tension values reported in the literature for isolated rat lymphatics from other tissue beds (Table 2). The Pearson correlation coefficient between mean experimental data and computational data was r = 0.914.
Fig. 4.
The maximum outflow pressure at which flow can be achieved as a function of chain length using in vivo near-infrared imaging measurements and computational modeling. The activation parameter (Tact) that is associated with the degree of smooth muscle cell activation is the sum of phasic and tonic activation parameters (see Eq. 7) and was iteratively solved for to provide the best fit for the experimental data. SEs along with the mean at 4 cm (n = 3), 8 cm (n = 4), and 12 cm (n = 5) distance from the tip of tail were plotted. Statistical significance was determined through a Kruskal-Wallis test with a post hoc Dunn’s test for multiple comparisons (**P < 0.05).
Table 2.
Values of maximum active tension and associated geometric properties of lymphangions for various organs in various species
| Species and Organ | Mean Diameter, μm | Mean Thickness, μm | Maximum Active Tension, mN/mm | Reference |
|---|---|---|---|---|
| Human Thoracic Duct | 2,210 | 6.240 ± 0.750 | 65 | |
| Rat Thoracic Duct | 404.500 ± 10.100 | 10.800 ± 0.900 | 0.590 ± 0.030 | 26 |
| Rat Thoracic Duct | 259.700 ± 53.000 | 0.128 ± 0.011 | 60 | |
| Rat Thoracic Duct | 480.000 ± 21.800 | 32.200 ± 1.600 | 0.520 ± 0.140* | 9 |
| Rat Cervical | 236.000 ± 19.500 | 8.100 ± 0.600 | 0.370 ± 0.030 | 26 |
| Rat Femoral | 203.000 ± 10.700 | 7.800 ± 0.500 | 0.390 ± 0.030 | 26 |
| Rat Mesentery | 149.000 ± 14.100 | 6.000 ± 0.700 | 0.340 ± 0.020 | 73 |
| Rat Mesentery | 105.900 ± 0.000 | 0.380 ± 0.020 | 19 |
Active tension was quantified using the wire myograph technique except in Ref. 9, in which biaxial mechanical testing was used.
Parametric Experiments
Contractility strength and number of lymphangions modulate pumping pressure and flow rate.
To explore further how the number of lymphangions in a chain and the stimulation of smooth muscle cells might influence this observed pressure-length relationship, we used the computational model to plot the relationship between flow rate and outflow pressure for a lymphangion chain with different numbers of lymphangions and varying activation parameters (Fig. 5). As the number of working lymphangions within a chain increases (while holding Tact = 10.9 kPa), a nonzero flow rate can be achieved at higher opposing pressure gradients (Fig. 5A). Additionally, an increase in contractile strength via a larger activation parameter in a chain with 36 lymphangions results in sustaining flow at a higher confronting pressure gradient (Fig. 5B). Ultimately, when there are many lymphangions in series, there appears to be a nonlinear relationship between occlusion pressure and the number of lymphangions in a chain [e.g., for a chain with 36 lymphangions and Tact = 8.7 kPa, the empirical fit of occlusion pressure = −0.0089n2 + 1.0431n provides a better fit than a linear one (R2 = 0.9986)]. At a lower lymphangion number, the relationship appears to be reasonably approximated by a linear fit (e.g., for a chain with 6 lymphangions and Tact = 8.7 kPa, R2 = 0.9609) that is dependent on the contractility of smooth muscle cells (Fig. 6). This implies that the lymphangion chain with a higher degree of smooth muscle cell activation is more capable to overcome higher pressure along the chain and that each lymphangion contributes to the build up of pressure to propel flow against an adverse pressure gradient.
Fig. 5.
Flow rate as function of outflow pressure in the lymphangion chains. A: flow rates for different numbers of lymphangions in a chain with an activation parameter (Tact) = 10.9 kPa. B: flow rates for different values of Tact of smooth muscle cells in a chain with 36 lymphangions.
Fig. 6.
Muscle activation (Tact) and the number of lymphangions in a chain both serve to increase the maximum pressure generation capacity of a lymphatic chain. Tact and lymphangion number were both varied over ranges that have been measured in vivo. Tact = 10.9 kPa (y = 1.3733x, R2 = 0.947); Tact = 8.7 kPa (y = 1.0526x, R2 = 0.9609); Tact = 6.6 kPa (y = 0.7026x, R2 = 0.9517); Tact = 4.4 kPa (y = 0.3619x; R2 = 0.908), where x and y denote outflow pressure – inflow pressure and lymphangion number, respectively.
The theoretical maximum flow that can be achieved under the pressure scenarios modeled here occurs when no adverse pressure gradient is present (i.e., the outlet pressure of the chain equals the inlet pressure). Although increased smooth muscle cell activity increases the maximum flow rate that can be achieved through the network, the total number of lymphangions within the chain has very little effect on maximizing flow in the absence of an adverse pressure gradient (Fig. 7). Stated another way, increasing the number of lymphangions within a given length of vessel would enhance the ability of that vessel to overcome adverse pressure gradients but would not have a substantial benefit for enhancing lymphatic flow.
Fig. 7.
Maximum flow rate that can be achieved when there is no adverse pressure gradient present due to the intrinsic contraction of lymphangions with a different number of lymphangions in the chain as a function of lymphatic smooth muscle activation. Tact, activation parameter.
Contractile frequency has little effect on maximum pumping pressure.
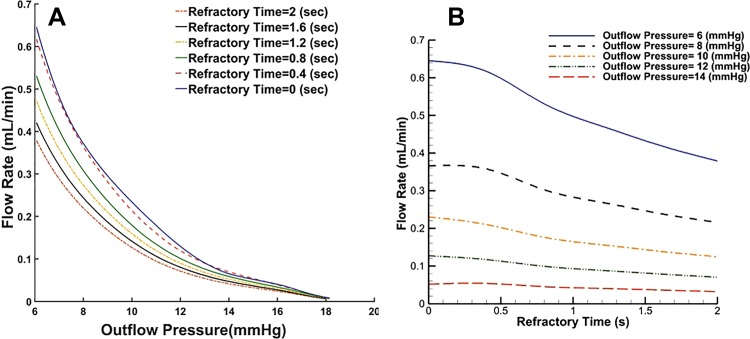
Many in vivo studies that use NIR imaging rely primarily on lymphatic contractile frequency as a measure of lymphatic function (5, 23, 37, 38, 56), yet it is unclear how exactly contractile frequency changes lymphatic drainage in different physiological scenarios. To investigate the effect of lymphatic contractile frequency on both flow rate and maximal pumping pressure, the computational model was used to vary the refractory period between contractions (Fig. 8). A contraction cycle is composed of a contraction time (rhythmic contraction) as well as a refractory time (time at which the diastolic diameter is held constant). Thus, the frequency of contraction is the reciprocal of the sum of these two contraction times (Fig. 2). Under a minimal adverse pressure gradient, increased contraction frequency (i.e., decreased refractory time) enhances lymphatic flow. However, in the presence of an adverse pressure gradient, the benefit of increased pumping frequency is diminished. Increased contraction frequency increases lymphatic pumping pressure for frequency ranges of <10 cpm; however, the benefit of contraction frequency to pumping pressure is diminished at values larger than this (Fig. 9). Interestingly, compared with in vivo data, there is no correlation between the contraction frequency of a lymphatic preocclusion and the resulting pumping pressure. However, it should be noted that the current experimental set-up does not allow one to track packet frequency distal to the occlusion while pumping pressure measurements are being made, making it unclear whether this frequency-pressure generation relationship occurs in vivo.
Fig. 8.
Effect of refractory time on flow rate and maximum pressure in a chain of 8 lymphangions (A) and flow rate generated by intrinsic contraction of lymphangions for chains exposed to different opposing outflow pressures (B).
Fig. 9.
Effect of frequency on maximum pressure that can be overcome by a lymphangion chain to maintain flow rate. A: computational results for a chain of 8 lymphangions (activation parameter = 10.9 kPa). B: experimental results from the rat tail model demonstrate that there was no correlation between the baseline packet frequency and effective pumping pressure.
Experimental and Computational Modeling Results Concur That Dermal NO Donor Diminishes Maximum Pumping Pressure
Given the prediction of the model that the maximum outflow pressure is highly dependent on lymphatic muscle activity, we sought a method to experimentally alter Tact in vivo by treating the tails of rats with a dermal cream (GTNO) containing a NO donor. NO was chosen given its previously documented effects on reducing lymphatic contractile dynamics both in vivo and in isolated vessels (6, 57, 68, 69). Additionally, NO is known to impair Ca2+-dependent activation and cross-bridge kinetics in arteries, thereby reducing smooth muscle tension (12, 13, 54).
The average pumping pressure for each group of rats was found to be 10.30 ± 4.02 mmHg (n = 4), 12.43 ± 5.80 mmHg (n = 3), and 18.54 ± 3.40 mmHg (n = 12) at distances of 4, 8, and 12 cm from the tip of the tail, respectively. Comparison of control and GTNO data sets using the extra sum of squares F-test on the quadratic best-fit regressions of the data revealed that the two groups were statistically different. This lies in the fact that application of NO resulted in the attenuation of the pumping pressure that was more pronounced as one increased the number of lymphangions in the chain. Thus, treatment of the lymphatic chain with dermal NO compromises its capability to maintain flow rate in the presence of a confronting pressure (Fig. 10). Using the computational framework, decreasing contractile strength via a reduction of the activation parameter by ~40% (from 7.6 to 4.4 kPa) could capture these experimental observations (Fig. 10).
Fig. 10.
Effect of dermal nitric oxide (NO) delivery on the relationship between maximum outflow pressure and length from the tip of the tail using in vivo near-infrared imaging pumping pressure measurements and the computational model. The activation parameter associated with the degree of smooth muscle cell activation that best fits the in vivo NO experiments was found to be Tact = 4.4 kPa. SEs along with the mean at 4 cm (n = 4), 8 cm (n = 3), and 12 cm (n = 12) distance from the tip of the tail were plotted. Significant difference between the control and glyceryl trinitrate ointment data sets was determined using an extra sum of squares F-test on the quadratic best-fit regressions of the data (P < 0.05).
DISCUSSION
Although significant advances have been made toward understanding the molecular regulation of lymphatic contractility in both isolated vessels and small animal models, there remains a significant gap in our understanding of how networks of lymphangions work across long distances to move fluid against the unfavorable pressure gradients that exist in vivo. Recent advances by several groups have demonstrated the ability to measure lymphatic pumping pressure in both clinical and animal research settings (7, 11, 43, 45, 53, 63, 66). Similar to blood pressure, which provides a measurement of cardiac pump function, the technique has been suggested to be indicative of the combined capacity of the intrinsic and extrinsic lymphatic pump. However, unlike the cardiovascular system, in the lymphatic system the vessels themselves are the primary source of pressure generation. This would suggest that any measurement of lymphatic pumping pressure will be highly sensitive to the number of lymphangions that are contributing to pressure generation and thus the location on the appendage that the measurement is made. By combining computational modeling built on experimental measurements of lymphatic vessel mechanical properties with in vivo measurements of lymphatic pumping pressure along various locations in the rat tail, we show that pumping pressure changes over the length of the vessel and that this change in pumping pressure depends on both the number of lymphangions engaged in pumping and the contractile force of the muscle generating the contractions. In the rat tail model, this allows one to record a direct measurement of the intrinsic pump, although it remains to be seen whether the intrinsic pumping capacity can be decoupled from the extrinsic pump (e.g., skeletal muscle contraction in a human arm) where extrinsic contractility is thought to significantly contribute to the transport capacity.
In addition to enabling the in vivo measurements of lymphatic muscle contractility, the computational model also allows for the investigation of how various parameters affect the maximum outflow pressure that can be achieved for a given lymphangion chain. This is important because the lymphatic system is typically exposed to hydrostatic pressure gradients that oppose flow from the interstitial space to the venous system, and thus lymphatic smooth muscle cells must impart energy to propel flow through the network (72). Although intrinsic pump activity enables lymphatic vessels to pump over a larger range of transmural or outflow pressures, the further elevation of outlet pressure outside of this range induces pump incompetency (14, 22). The simulations show that flow rate declines with increase in maximal outflow pressure, as exposing a lymphangion chain to higher outflow pressure results in the progressive inability of lymphangions to empty, an observation that is consistent with isolated vessel experiments (15, 21) and is also in agreement with other computational models of lymphangion chains (30). The simulation results suggest that both the degree of smooth muscle cell activation and the number of working lymphangions directly influence this relationship between flow and outflow pressure. In the context of lymphedema, it has been suggested that patients with a higher lymph load are predisposed to disease (1, 11), motivating further studies that explore how prolonged elevated demand on the intrinsic lymphatic pump might drive fatigue of lymphatic muscle force generation and thus lymphedema. Although smooth muscle force generation of lymphatics likely exhibits regional and species variations, the values for the model that best fit the in vivo data are within the range of those measured experimentally from other tissues tested ex vivo (Table 2), but interestingly are lower than rat lymphatics from other tissue beds.
Frequency of lymphatic pumping has become a very common measurement that has been suggested to be indicative of lymphatic function (5, 10, 39, 56, 59, 69, 71). However, if the ultimate function of lymphatics is to generate flow, contraction frequency by itself may not always accurately reflect function. This has been suggested by both in vivo experiments, where flow can be observed in certain situations even when the vessel is not contracting (4, 16, 33, 34, 49), and in isolated vessel experiments, in which imposed flow actually serves to inhibit lymphatic contraction and conserve energy (24, 25, 35). This is also evident through the in vivo experiments reported here, where the baseline contraction frequency of an animal does not necessarily reflect the maximum pressure generation capacity of the lymphangion chain (Fig. 9). The computational model suggests that the benefit of contraction frequency to pressure generation by a lymphangion chain plateaus at values above 10 cpm. These results raise doubt as to whether focusing on contractile frequency as the primary metric of lymphatic dysfunction is a clinically relevant endeavor for explaining lymphatic failure in lymphedema.
It is important to note that isolated vessel studies have demonstrated that contraction frequency increases under an elevated outflow pressure (58). This pressure dependence on the contractile frequency is not incorporated into the present model and would be a valuable feature to include in future iterations. However, the model and in vivo data still support the idea that the generated pressure gradient along a chain confronted with a high adverse pressure is mainly due to the contractile strength of lymphatic smooth muscle cells and the number of lymphangions present. Although Tact contains both the effects of tonic constriction and phasic contractions, the present study assumes that the ratio between these two is constant and thus cannot decouple the independent effects of the two. Although we include intraluminal valve function by modeling variable resistance to lymph flow from opening to closure as a function of the transaxial pressure gradient along the valve, there is a known dependency of the valve resistance behavior on the transmural pressure (or circumferential stretch) (14), which is neglected in this model. Including this feature in future iterations of the model would likely further enhance the benefit of Tact on enhancing the effective pumping pressure, as the elevated myogenic constriction under a large transmural pressure would improve valve function.
This study has several limitations that should be noted. First, although the microstructure-based model captures many of the salient features of pumping function in a lymphangion chain, the comprehensive experimental quantification and validation of model parameters in the specific anatomic ROI are still needed. There is experimental evidence that lymphatic vessels from different regions have adapted their contractile force in line with the particular in vivo pressure experienced by the lymphatic vessel (24, 26). An example in the rat is the femoral lymphatic vessel, which shows the highest capability to adapt its contractile force to withstand high pressure, whereas the thoracic duct exhibits the lowest capacity to overcome elevated pressure (26). In contrast, the thoracic duct is known to be very sensitive to wall shear stress and thereby is able to switch between pump and conduit modes (24). The ideal computational approach requires experimental measurements of valve resistance and biomechanical material properties across a chain of vessels within the tail, as it is unknown how these parameters vary along the length of a chain of lymphangions. Additionally, the extent that the surrounding matrix provides structural support and the mechanical properties of said matrix vary from one tissue bed to another could be salient features to include in future versions of the model. This is particularly important in the context of lymphedema in which fibrosis of the interstitium is known to alter the surrounding matrix. However, in situ biaxial testing of lymphatic vessels currently remains experimentally unavailable to the research community. In the absence of such information, we have invoked experimentally derived parameters from isolated lymphatic tests, including a valve model that has been validated previously in rat mesenteric lymphatic vessels (3) and passive biomechanical properties quantified in the rat thoracic duct. In addition, the heterogeneity of biomechanical properties as well as complex topology of the lymphatic network (e.g., branches in region near the tip of the tail) are neglected in this study. Thus, the direct measurement of model properties along with a better understanding of network properties in the lymphatic vasculature to validate intraspecific (e.g., the tail, mesentery, thoracic duct, limb, and popliteal vessels) and interspecific (e.g., rat, sheep, and human) pressure-length relationships remain areas for future studies.
Finally, it is difficult to narrow down the specific mechanism by which NO is decreasing lymphatic pumping pressure. Previous studies in isolated vessels have shown that excess NO lowers the frequency of contraction, vessel tone, and contraction amplitude (25, 57, 68). In vivo studies involving fluorescent tracers have shown that NO decreases the frequency of contractile events and/or tracer clearance rate (39, 55, 69, 70). However, NO is also known to alter microvascular permeability (20), and thus it is difficult with in vivo experiments to pin down the exact mechanism by which NO is altering function. Our computational model and experimental results show that the reduction in effective pumping pressure is likely not primarily due to its effects on contraction frequency or interstitial fluid pressure but rather captured by its influence on Tact. However, because Tact includes both the combined effects of tonic constrictions and phasic contractions, it is not clear in this study whether NO effects on tone (and indirectly valve function) or contraction amplitude are primarily responsible.
In summary, through computational modeling and a novel implementation of lymphatic pumping pressure measurements using NIR imaging, we show that the maximum outflow pressure that a lymphangion chain can overcome is a function of the number of lymphangions in the chain and the active tension generation by the lymphatic muscle cells. By fitting our computational model to experimental measurements of the pumping pressure at multiple locations along the tail, we can estimate the average force generation for the chain of lymphatics, decoupling the intrinsic function of that vessel from other extrinsic factors such as interstitial fluid pressure at the injection site. Although measurement of the maximum pumping pressure is known to have the potential as a clinical diagnostic approach for lymphedema (11, 63), this study suggests that any measurement of the maximum pumping pressure should be interpreted in the context of chain length; hence, measurements should be performed at multiple locations to provide sufficient information on lymphatic muscle activity in the limb of interest. Because this approach is noninvasive, the potential as a clinical diagnostic in lymphatic health is promising, and future trials in humans are warranted to establish feasibility. The ability to obtain a direct measurement of lymphatic muscle health in a clinically relevant scenario remains lacking and would be a substantial benefit to future diagnostic capabilities.
GRANTS
This work was supported by National Heart, Lung, and Blood Institute Grant R01-HL-113061.
DISCLOSURES
Georgia Tech has licensed technology to LymphaTech that is related to this study and is covered by patent applications for which T.S.N. and J.B.D. are inventors. J.B.D. owns equity in LymphaTech and serves as a scientific advisor. J.B.D. and T.S.N. are eligible to receive royalties under the license agreement with LymphaTech.
AUTHOR CONTRIBUTIONS
M.R., T.S.N., and J.B.D. conceived and designed research; M.R., T.S.N., and Z.N. performed experiments; M.R., T.S.N., Z.N., and J.B.D. analyzed data; M.R., T.S.N., R.L.G., and J.B.D. interpreted results of experiments; M.R., T.S.N., and Z.N. prepared figures; M.R. and T.S.N. drafted manuscript; M.R., T.S.N., Z.N., R.L.G., and J.B.D. edited and revised manuscript; M.R., T.S.N., Z.N., R.L.G., and J.B.D. approved final version of manuscript.
REFERENCES
- 1.Bains SK, Stanton AWB, Cintolesi V, Ballinger J, Allen S, Zammit C, Levick JR, Mortimer PS, Peters AM, Purushotham AD. A constitutional predisposition to breast cancer-related lymphoedema and effect of axillary lymph node surgery on forearm muscle lymph flow. Breast 24: 68–74, 2015. doi: 10.1016/j.breast.2014.11.010. [DOI] [PubMed] [Google Scholar]
- 2.Bertram CD, Macaskill C, Davis MJ, Moore JE Jr. Consequences of intravascular lymphatic valve properties: a study of contraction timing in a multi-lymphangion model. Am J Physiol Heart Circ Physiol 310: H847–H860, 2016. doi: 10.1152/ajpheart.00669.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bertram CD, Macaskill C, Moore JE Jr. Incorporating measured valve properties into a numerical model of a lymphatic vessel. Comput Methods Biomech Biomed Engin 17: 1519–1534, 2014. doi: 10.1080/10255842.2012.753066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Blatter C, Meijer EFJ, Nam AS, Jones D, Bouma BE, Padera TP, Vakoc BJ. In vivo label-free measurement of lymph flow velocity and volumetric flow rates using Doppler optical coherence tomography. Sci Rep 6: 29035, 2016. doi: 10.1038/srep29035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Blum KS, Karaman S, Proulx ST, Ochsenbein AM, Luciani P, Leroux J-C, Wolfrum C, Detmar M. Chronic high-fat diet impairs collecting lymphatic vessel function in mice. PLoS One 9: e94713, 2014. doi: 10.1371/journal.pone.0094713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bohlen HG, Gasheva OY, Zawieja DC. Nitric oxide formation by lymphatic bulb and valves is a major regulatory component of lymphatic pumping. Am J Physiol Heart Circ Physiol 301: H1897–H1906, 2011. doi: 10.1152/ajpheart.00260.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bouta EM, Wood RW, Brown EB, Rahimi H, Ritchlin CT, Schwarz EM. In vivo quantification of lymph viscosity and pressure in lymphatic vessels and draining lymph nodes of arthritic joints in mice. J Physiol 592: 1213–1223, 2014. doi: 10.1113/jphysiol.2013.266700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Caulk AW, Dixon JB, Gleason RL Jr. A lumped parameter model of mechanically mediated acute and long-term adaptations of contractility and geometry in lymphatics for characterization of lymphedema. Biomech Model Mechanobiol 15: 1601–1618, 2016. doi: 10.1007/s10237-016-0785-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Caulk AW, Nepiyushchikh ZV, Shaw R, Dixon B, Gleason RL. Quantification of the passive and active biaxial mechanical behaviour and microstructural organization of rat thoracic ducts. J R Soc Interface 12: 20150280, 2015. doi: 10.1098/rsif.2015.0280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chong C, Scholkmann F, Bachmann SB, Luciani P, Leroux J-C, Detmar M, Proulx ST. In vivo visualization and quantification of collecting lymphatic vessel contractility using near-infrared imaging. Sci Rep 6: 22930, 2016. doi: 10.1038/srep22930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cintolesi V, Stanton AWB, Bains SK, Cousins E, Peters AM, Purushotham AD, Levick JR, Mortimer PS. Constitutively enhanced lymphatic pumping in the upper limbs of women who later develop breast cancer-related lymphedema. Lymphat Res Biol 14: 50–61, 2016. doi: 10.1089/lrb.2016.0005. [DOI] [PubMed] [Google Scholar]
- 12.Collins P, Griffith TM, Henderson AH, Lewis MJ. Endothelium-derived relaxing factor alters calcium fluxes in rabbit aorta: a cyclic guanosine monophosphate-mediated effect. J Physiol 381: 427–437, 1986. doi: 10.1113/jphysiol.1986.sp016336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cornwell TL, Pryzwansky KB, Wyatt TA, Lincoln TM. Regulation of sarcoplasmic reticulum protein phosphorylation by localized cyclic GMP-dependent protein kinase in vascular smooth muscle cells. Mol Pharmacol 40: 923–931, 1991. [PubMed] [Google Scholar]
- 14.Davis MJ, Rahbar E, Gashev AA, Zawieja DC, Moore JE Jr. Determinants of valve gating in collecting lymphatic vessels from rat mesentery. Am J Physiol Heart Circ Physiol 301: H48–H60, 2011. doi: 10.1152/ajpheart.00133.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Davis MJ, Scallan JP, Wolpers JH, Muthuchamy M, Gashev AA, Zawieja DC. Intrinsic increase in lymphangion muscle contractility in response to elevated afterload. Am J Physiol Heart Circ Physiol 303: H795–H808, 2012. doi: 10.1152/ajpheart.01097.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dixon JB, Greiner ST, Gashev AA, Cote GL, Moore JE Jr, Zawieja DC. Lymph flow, shear stress, and lymphocyte velocity in rat mesenteric prenodal lymphatics. Microcirculation 13: 597–610, 2006. doi: 10.1080/10739680600893909. [DOI] [PubMed] [Google Scholar]
- 17.Dixon JB. Lymphatic lipid transport: sewer or subway? Trends Endocrinol Metab 21: 480–487, 2010. doi: 10.1016/j.tem.2010.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dixon JB, Weiler MJ. Bridging the divide between pathogenesis and detection in lymphedema. Semin Cell Dev Biol 38: 75–82, 2015. doi: 10.1016/j.semcdb.2014.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dougherty PJ, Davis MJ, Zawieja DC, Muthuchamy M. Calcium sensitivity and cooperativity of permeabilized rat mesenteric lymphatics. Am J Physiol Regul Integr Comp Physiol 294: R1524–R1532, 2008. doi: 10.1152/ajpregu.00888.2007. [DOI] [PubMed] [Google Scholar]
- 20.Durán WN, Breslin JW, Sánchez FA. The NO cascade, eNOS location, and microvascular permeability. Cardiovasc Res 87: 254–261, 2010. doi: 10.1093/cvr/cvq139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Eisenhoffer J, Elias RM, Johnston MG. Effect of outflow pressure on lymphatic pumping in vitro. Am J Physiol Regul Integr Comp Physiol 265: R97–R102, 1993. [DOI] [PubMed] [Google Scholar]
- 22.Eisenhoffer J, Kagal A, Klein T, Johnston MG. Importance of valves and lymphangion contractions in determining pressure gradients in isolated lymphatics exposed to elevations in outflow pressure. Microvasc Res 49: 97–110, 1995. doi: 10.1006/mvre.1995.1008. [DOI] [PubMed] [Google Scholar]
- 23.Escobedo N, Proulx ST, Karaman S, Dillard ME, Johnson N, Detmar M, Oliver G. Restoration of lymphatic function rescues obesity in Prox1-haploinsufficient mice. JCI Insight 1: e85096, 2016. doi: 10.1172/jci.insight.85096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gashev AA, Davis MJ, Delp MD, Zawieja DC. Regional variations of contractile activity in isolated rat lymphatics. Microcirculation 11: 477–492, 2004. doi: 10.1080/10739680490476033. [DOI] [PubMed] [Google Scholar]
- 25.Gashev AA, Davis MJ, Zawieja DC. Inhibition of the active lymph pump by flow in rat mesenteric lymphatics and thoracic duct. J Physiol 540: 1023–1037, 2002. doi: 10.1113/jphysiol.2001.016642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gashev AA, Zhang R-Z, Muthuchamy M, Zawieja DC, Davis MJ. Regional heterogeneity of length-tension relationships in rat lymph vessels. Lymphat Res Biol 10: 14–19, 2012. doi: 10.1089/lrb.2011.0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gashev AA. Lymphatic vessels: pressure- and flow-dependent regulatory reactions. Ann N Y Acad Sci 1131: 100–109, 2008. doi: 10.1196/annals.1413.009. [DOI] [PubMed] [Google Scholar]
- 28.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast 61: 1–48, 2000. doi: 10.1023/A:1010835316564. [DOI] [Google Scholar]
- 29.Ikomi F, Schmid-Schönbein GW. Lymph pump mechanics in the rabbit hind leg. Am J Physiol 271: H173–H183, 1996. [DOI] [PubMed] [Google Scholar]
- 30.Jamalian S, Bertram CD, Richardson WJ, Moore JE Jr. Parameter sensitivity analysis of a lumped-parameter model of a chain of lymphangions in series. Am J Physiol Heart Circ Physiol 305: H1709–H1717, 2013. doi: 10.1152/ajpheart.00403.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jamalian S, Davis MJ, Zawieja DC, Moore JE Jr. Network scale modeling of lymph transport and its effective pumping parameters. PLoS One 11: e0148384, 2016. doi: 10.1371/journal.pone.0148384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Karlsen TV, McCormack E, Mujic M, Tenstad O, Wiig H. Minimally invasive quantification of lymph flow in mice and rats by imaging depot clearance of near-infrared albumin. Am J Physiol Heart Circ Physiol 302: H391–H401, 2012. doi: 10.1152/ajpheart.00842.2011. [DOI] [PubMed] [Google Scholar]
- 33.Kassis T, Kohan AB, Weiler MJ, Nipper ME, Cornelius R, Tso P, Dixon JB. Dual-channel in-situ optical imaging system for quantifying lipid uptake and lymphatic pump function. J Biomed Opt 17: 086005, 2012. doi: 10.1117/1.JBO.17.8.086005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kassis T, Yarlagadda SC, Kohan AB, Tso P, Breedveld V, Dixon JB. Postprandial lymphatic pump function after a high-fat meal: a characterization of contractility, flow, and viscosity. Am J Physiol Gastrointest Liver Physiol 310: G776–G789, 2016. doi: 10.1152/ajpgi.00318.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kornuta JA, Nepiyushchikh Z, Gasheva OY, Mukherjee A, Zawieja DC, Dixon JB. Effects of dynamic shear and transmural pressure on wall shear stress sensitivity in collecting lymphatic vessels. Am J Physiol Regul Integr Comp Physiol 309: R1122–R1134, 2015. doi: 10.1152/ajpregu.00342.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kunert C, Baish JW, Liao S, Padera TP, Munn LL. Mechanobiological oscillators control lymph flow. Proc Natl Acad Sci USA 112: 10938–10943, 2015. doi: 10.1073/pnas.1508330112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kwon S, Agollah GD, Wu G, Chan W, Sevick-Muraca EM. Direct visualization of changes of lymphatic function and drainage pathways in lymph node metastasis of B16F10 melanoma using near-infrared fluorescence imaging. Biomed Opt Express 4: 967–977, 2013. doi: 10.1364/BOE.4.000967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kwon S, Agollah GD, Wu G, Sevick-Muraca EM. Spatio-temporal changes of lymphatic contractility and drainage patterns following lymphadenectomy in mice. PLoS One 9: e106034, 2014. doi: 10.1371/journal.pone.0106034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liao S, Cheng G, Conner DA, Huang Y, Kucherlapati RS, Munn LL, Ruddle NH, Jain RK, Fukumura D, Padera TP. Impaired lymphatic contraction associated with immunosuppression. Proc Natl Acad Sci USA 108: 18784–18789, 2011. doi: 10.1073/pnas.1116152108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liao S, Jones D, Cheng G, Padera TP. Method for the quantitative measurement of collecting lymphatic vessel contraction in mice. J Biol Methods 1: e6, 2014. doi: 10.14440/jbm.2014.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McGeown JG, McHale NG, Thornbury KD. Arterial pulsation and lymph formation in an isolated sheep hindlimb preparation. J Physiol 405: 595–604, 1988. doi: 10.1113/jphysiol.1988.sp017350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McHale NG, Roddie IC. The effect of transmural pressure on pumping activity in isolated bovine lymphatic vessels. J Physiol 261: 255–269, 1976. doi: 10.1113/jphysiol.1976.sp011557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Modi S, Stanton AWB, Svensson WE, Peters AM, Mortimer PS, Levick JR. Human lymphatic pumping measured in healthy and lymphoedematous arms by lymphatic congestion lymphoscintigraphy. J Physiol 583: 271–285, 2007. doi: 10.1113/jphysiol.2007.130401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Moriondo A, Solari E, Marcozzi C, Negrini D. Diaphragmatic lymphatic vessel behavior during local skeletal muscle contraction. Am J Physiol Heart Circ Physiol 308: H193–H205, 2015. doi: 10.1152/ajpheart.00701.2014. [DOI] [PubMed] [Google Scholar]
- 45.Nelson TS, Akin RE, Weiler MJ, Kassis T, Kornuta JA, Dixon JB. Minimally invasive method for determining the effective lymphatic pumping pressure in rats using near-infrared imaging. Am J Physiol Regul Integr Comp Physiol 306: R281–R290, 2014. doi: 10.1152/ajpregu.00369.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.García Nores GD, Cuzzone DA, Albano NJ, Hespe GE, Kataru RP, Torrisi JS, Gardenier JC, Savetsky IL, Aschen SZ, Nitti MD, Mehrara BJ. Obesity but not high-fat diet impairs lymphatic function. Int J Obes 40: 1582–1590, 2016. doi: 10.1038/ijo.2016.96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Quick CM, Venugopal AM, Gashev AA, Zawieja DC, Stewart RH. Intrinsic pump-conduit behavior of lymphangions. Am J Physiol Regul Integr Comp Physiol 292: R1510–R1518, 2007. doi: 10.1152/ajpregu.00258.2006. [DOI] [PubMed] [Google Scholar]
- 48.Rachev A, Hayashi K. Theoretical study of the effects of vascular smooth muscle contraction on strain and stress distributions in arteries. Ann Biomed Eng 27: 459–468, 1999. doi: 10.1114/1.191. [DOI] [PubMed] [Google Scholar]
- 49.Rahbar E, Akl T, Coté GL, Moore JE Jr, Zawieja DC. Lymph transport in rat mesenteric lymphatics experiencing edemagenic stress. Microcirculation 21: 359–367, 2014. doi: 10.1111/micc.12112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rahbar E, Moore JE Jr. A model of a radially expanding and contracting lymphangion. J Biomech 44: 1001–1007, 2011. doi: 10.1016/j.jbiomech.2011.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Reddy NP, Palmieri V, Cochran GV. Subcutaneous interstitial fluid pressure during external loading. Am J Physiol Regul Integr Comp Physiol 240: R327–R329, 1981. [DOI] [PubMed] [Google Scholar]
- 52.Sabine A, Bovay E, Demir CS, Kimura W, Jaquet M, Agalarov Y, Zangger N, Scallan JP, Graber W, Gulpinar E, Kwak BR, Mäkinen T, Martinez-Corral I, Ortega S, Delorenzi M, Kiefer F, Davis MJ, Djonov V, Miura N, Petrova TV. FOXC2 and fluid shear stress stabilize postnatal lymphatic vasculature. J Clin Invest 125: 3861–3877, 2015. doi: 10.1172/JCI80454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Saito T, Unno N, Yamamoto N, Inuzuka K, Tanaka H, Sano M, Sugisawa R, Katahashi K, Konno H. Low lymphatic pumping pressure in the legs is associated with leg edema and lower quality of life in healthy volunteers. Lymphat Res Biol 13: 154–159, 2015. doi: 10.1089/lrb.2014.0015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sandoo A, van Zanten JJCSV, Metsios GS, Carroll D, Kitas GD. The endothelium and its role in regulating vascular tone. Open Cardiovasc Med J 4: 302–312, 2010. doi: 10.2174/1874192401004010302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Saul ME, Thomas PA, Dosen PJ, Isbister GK, O’Leary MA, Whyte IM, McFadden SA, van Helden DF. A pharmacological approach to first aid treatment for snakebite. Nat Med 17: 809–811, 2011. doi: 10.1038/nm.2382. [DOI] [PubMed] [Google Scholar]
- 56.Savetsky IL, Albano NJ, Cuzzone DA, Gardenier JC, Torrisi JS, García Nores GD, Nitti MD, Hespe GE, Nelson TS, Kataru RP, Dixon JB, Mehrara BJ. Lymphatic function regulates contact hypersensitivity dermatitis in obesity. J Invest Dermatol 135: 2742–2752, 2015. doi: 10.1038/jid.2015.283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Scallan JP, Davis MJ. Genetic removal of basal nitric oxide enhances contractile activity in isolated murine collecting lymphatic vessels. J Physiol 591: 2139–2156, 2013. doi: 10.1113/jphysiol.2012.250662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Scallan JP, Wolpers JH, Davis MJ. Constriction of isolated collecting lymphatic vessels in response to acute increases in downstream pressure. J Physiol 591: 443–459, 2013. doi: 10.1113/jphysiol.2012.237909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sharma R, Wang W, Rasmussen JC, Joshi A, Houston JP, Adams KE, Cameron A, Ke S, Kwon S, Mawad ME, Sevick-Muraca EM. Quantitative imaging of lymph function. Am J Physiol Heart Circ Physiol 292: H3109–H3118, 2007. doi: 10.1152/ajpheart.01223.2006. [DOI] [PubMed] [Google Scholar]
- 60.Shirasawa Y, Benoit JN. Stretch-induced calcium sensitization of rat lymphatic smooth muscle. Am J Physiol Heart Circ Physiol 285: H2573–H2577, 2003. doi: 10.1152/ajpheart.00002.2003. [DOI] [PubMed] [Google Scholar]
- 61.Skalak TC, Schmid-Schönbein GW, Zweifach BW. New morphological evidence for a mechanism of lymph formation in skeletal muscle. Microvasc Res 28: 95–112, 1984. doi: 10.1016/0026-2862(84)90032-3. [DOI] [PubMed] [Google Scholar]
- 62.Stanton AWB, Modi S, Bennett Britton TM, Purushotham AD, Peters AM, Levick JR, Mortimer PS. Lymphatic drainage in the muscle and subcutis of the arm after breast cancer treatment. Breast Cancer Res Treat 117: 549–557, 2009. doi: 10.1007/s10549-008-0259-z. [DOI] [PubMed] [Google Scholar]
- 63.Sugisawa R, Unno N, Saito T, Yamamoto N, Inuzuka K, Tanaka H, Sano M, Katahashi K, Uranaka H, Marumo T, Konno H. Effects of compression stockings on elevation of leg lymph pumping pressure and improvement of quality of life in healthy female volunteers: a randomized controlled trial. Lymphat Res Biol 14: 95−103, 2016. doi: 10.1089/lrb.2015.0045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Swartz MA. The physiology of the lymphatic system. Adv Drug Deliv Rev 50: 3–20, 2001. doi: 10.1016/S0169-409X(01)00150-8. [DOI] [PubMed] [Google Scholar]
- 65.Telinius N, Drewsen N, Pilegaard H, Kold-Petersen H, de Leval M, Aalkjaer C, Hjortdal V, Boedtkjer DB. Human thoracic duct in vitro: diameter-tension properties, spontaneous and evoked contractile activity. Am J Physiol Heart Circ Physiol 299: H811–H818, 2010. doi: 10.1152/ajpheart.01089.2009. [DOI] [PubMed] [Google Scholar]
- 66.Unno N, Nishiyama M, Suzuki M, Tanaka H, Yamamoto N, Sagara D, Mano Y, Konno H. A novel method of measuring human lymphatic pumping using indocyanine green fluorescence lymphography. J Vasc Surg 52: 946–952, 2010. doi: 10.1016/j.jvs.2010.04.067. [DOI] [PubMed] [Google Scholar]
- 67.Webb RC Jr, Starzl TE. The effect of blood vessel pulsations on lymph pressure in large lymphatics. Bull Johns Hopkins Hosp 93: 401–407, 1953. [PMC free article] [PubMed] [Google Scholar]
- 68.von der Weid PY, Zhao J, Van Helden DF; Weid von der P. Nitric oxide decreases pacemaker activity in lymphatic vessels of guinea pig mesentery. Am J Physiol Heart Circ Physiol 280: H2707–H2716, 2001. [DOI] [PubMed] [Google Scholar]
- 69.Weiler M, Dixon JB. Differential transport function of lymphatic vessels in the rat tail model and the long-term effects of Indocyanine Green as assessed with near-infrared imaging. Front Physiol 4: 215, 2013. doi: 10.3389/fphys.2013.00215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Weiler M, Kassis T, Dixon JB. Sensitivity analysis of near-infrared functional lymphatic imaging. J Biomed Opt 17: 066019, 2012. doi: 10.1117/1.JBO.17.6.066019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zawieja DC, Davis KL, Schuster R, Hinds WM, Granger HJ. Distribution, propagation, and coordination of contractile activity in lymphatics. Am J Physiol 264: H1283–H1291, 1993. [DOI] [PubMed] [Google Scholar]
- 72.Zawieja DC. Contractile physiology of lymphatics. Lymphat Res Biol 7: 87–96, 2009. doi: 10.1089/lrb.2009.0007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zhang R-Z, Gashev AA, Zawieja DC, Davis MJ. Length-tension relationships of small arteries, veins, and lymphatics from the rat mesenteric microcirculation. Am J Physiol Heart Circ Physiol 292: H1943–H1952, 2007. doi: 10.1152/ajpheart.01000.2005. [DOI] [PubMed] [Google Scholar]