Integrative Sparse Principal Component Analysis of Gene Expression Data

Abstract

In the analysis of gene expression data, dimension reduction techniques have been extensively adopted. The most popular one is perhaps the PCA (principal component analysis). To generate more reliable and more interpretable results, the SPCA (sparse PCA) technique has been developed. With the “small sample size, high dimensionality” characteristic of gene expression data, the analysis results generated from a single dataset are often unsatisfactory. Under contexts other than dimension reduction, integrative analysis techniques, which jointly analyze the raw data of multiple independent datasets, have been developed and shown to outperform “classic” meta-analysis and other multi-datasets techniques and single-dataset analysis. In this study, we conduct integrative analysis by developing the iSPCA (integrative SPCA) method. iSPCA achieves the selection and estimation of sparse loadings using a group penalty. To take advantage of the similarity across datasets and generate more accurate results, we further impose contrasted penalties. Different penalties are proposed to accommodate different data conditions. Extensive simulations show that iSPCA outperforms the alternatives under a wide spectrum of settings. The analysis of breast cancer and pancreatic cancer data further shows iSPCA’s satisfactory performance.

1 Introduction

Gene expression studies have been extensively conducted, providing valuable molecular information for a wide variety of biomedical problems. With sample and cost limitations, gene expression studies usually have the “small sample size, high dimensionality” characteristic. Dimension reduction and variable selection techniques have been routinely applied in gene expression data analysis. With dimension reduction techniques, as represented by PCA (principal component analysis), PLS (partial least squares), ICA (independent component analysis), and others, a small number of linear combinations of gene expressions are used to represent signals in all genes. The most popular dimension reduction technique is perhaps PCA, which has a wide spectrum of applications. For example, in some studies (Zhong et al., 2009), PCA has been used to facilitate regression analysis, where only a small number of PCs (principal components), as opposed to the original measurements, are used as covariates. In other studies, PCA has been used as the basis of clustering (Yeung & Ruzzo, 2001) and to assist in understanding the biological functionalities of genes (Ma & Kosorok, 2009). In such studies, PCs have been referred to as metagenes, super genes, eigen-genes, latent genes, among others. We refer to the literature (Ma & Dai, 2011) for comprehensive reviews and discussions.

With the standard PCA, the loadings (coefficients of genes in the PCs) are dense. When a large number of genes are measured, some are expected to be “noises”. In addition, PCs with dense loadings are difficult, if not impossible, to interpret. For the analysis of high-dimensional data including gene expressions, to remove noises and generate more interpretable and more reliable results, the SPCA (sparse PCA) approach has been developed (Zou, Hastie, & Tibshirani, 2006). It applies regularization especially penalization to generate sparse loadings. Extensive methodological, theoretical, and numerical studies on the SPCA have been conducted (Lee, Epstein, Duncan, & Lin, 2012; D. Shen, Shen, & Marron, 2013; H. Shen & Huang, 2008), demonstrating its superior performance over the standard PCA. It is noted that the PCA and SPCA techniques have also been applied to omics data other than gene expressions and generated interesting findings (Langfelder & Horvath, 2007).

In the analysis of gene expression and other omics data, it has been well noted that results generated from analyzing a single dataset are often unsatisfactory (Guerra & Goldstein, 2009). Although multiple factors may contribute, the most important one is perhaps the small sample size. For scientific problems of common interest, there are often multiple independent studies with similar designs, making it possible to pool data, increase sample size, and generate better results. As a relatively recent technique, integrative analysis, which jointly analyzes the raw data of multiple independent studies, has been shown to outperform the classic meta-analysis (which analyzes multiple studies separately and pools summary statistics) and other multi-datasets techniques and single-dataset analysis. In the literature, most of the integrative analysis developments have been in the context of regression analysis with variable selection (Zhao et al., 2015).

Considering the importance of PCA in the analysis of gene expression and other omics data and limitations of single-dataset analysis, in this study, we develop the iSPCA method, which conducts the integrative analysis of multiple independent datasets based on the SPCA technique. The analysis goal is to more accurately identify relevant genes and estimate loadings. The sparse PCs so generated can be used in the same way as described above. This study advances from the existing literature in the following aspects. Advancing from the existing single-dataset PCA/SPCA, the integrative analysis of multiple independent datasets is conducted. With the successes of integrative analysis under other contexts, it is reasonable to expect that the proposed analysis can generate better results than single-dataset analysis and alternative multi-datasets analysis. Different from the existing integrative analysis studies, our analysis is based on the PCA technique, which conducts dimension reduction as opposed to variable selection. In addition, to take advantage of the similarity across datasets and further improve analysis, we propose imposing contrasted penalties. Tailored penalties are developed to accommodate different data conditions. Overall, this study provides a practically useful venue for analyzing gene expression and other omics data.

2 Methods

2.1 SPCA with a single dataset

For completeness, we first briefly review analyzing a single dataset using the SPCA. We refer to the existing literature for detailed discussions on methodology (D. Shen et al., 2013; H. Shen & Huang, 2008; Zou et al., 2006) and applications (Hsu, Huang, & Chen, 2015). Assume that standard data pre-processing, which may include normalization, accommodation of missing data, and centralization, has been properly conducted. Denote X as the n × p data matrix of gene expressions, where n is the number of samples and p is the number of genes. In published studies (H. Shen & Huang, 2008), PCA and SPCA have been achieved with the assistance of SVD (singular value decomposition). Specifically, with the standard PCA, to obtain the first PC, consider

$${\mathit{min}}_{{\mathbf{u}}_1,{\mathbf{v}}_1}{\Vert \mathbf{X}-{\mathbf{u}}_1{\mathbf{v}}_1^T\Vert }_F^2,$$ (1)

where the subscript F denotes the Frobenius norm, u₁ is a n × 1 vector with a unit norm, v₁ is a length p × 1 vector, and T denotes transform. ${\mathbf{u}}_1{\mathbf{v}}_1^T$ so obtained provides the best rank-one approximation of the data matrix. Elements in v₁ are the loadings of the first PC.

Directly optimizing (1) leads to a dense estimate. That is, all components of v₁ are nonzero. SPCA generates a sparse estimate of loadings with the assistance of penalization (or another type of regularization). Specifically, consider

$${\mathit{min}}_{{\mathbf{u}}_1,{\mathbf{v}}_1}\left\{{\Vert \mathbf{X}-{\mathbf{u}}_1{\mathbf{v}}_1^T\Vert }_F^2+\mathit{pen}({\mathbf{v}}_1)\right\},$$ (2)

where pen(·) is the penalty function. The most popular choice of penalty is Lasso with $\mathit{pen}({\mathbf{v}}_1)=\lambda {\mathrm{\sum }}_{j=1}^p\mid v_{1j}\mid$, where λ > 0 is a data-dependent tuning parameter and v_1j is the jth component of v₁. Other penalty functions have also been adopted. The estimation in (2) generates the first PC. The consecutive PCs can be generated in a similar way.

2.2 iSPCA

Consider the scenario where there are multiple datasets from independent studies with comparable designs. The most straightforward approach is to pool all data together and “pretend” there is just a single dataset. With the differences across independent studies, this simple approach is often inferior, as can be partly seen from our simulation. A more sensible approach is to analyze each dataset separately using SPCA and then combine the analysis results. This is a meta-analysis strategy (which is investigated numerically in simulation and data analysis). Under other contexts especially “regression analysis + variable selection”, it has been shown that integrative analysis outperforms simple data-pooling, meta-analysis, and other multi-datasets analysis. The intuition is that integrative analysis does not need stringent conditions on data comparability, borrows information across datasets earlier on, and hence can be more effective. Below we develop the SPCA-based integrative analysis.

Consider M independent gene expression datasets. To simplify notations, consider the scenario where the same set of genes is measured in all datasets. With the maturity of gene profiling techniques, matching gene sets across datasets is usually feasible. Following the literature, unmatched gene sets can be accommodated by setting the corresponding loadings as zero and adjusting the penalty using weights (Shi et al., 2014). Assume that the M datasets have undergone proper preprocessing, which may include imputation of missing measurements, centralization, and normalization. As integrative analysis does not assume full comparability across datasets, pre-processing can be conducted for each dataset separately. Use the superscript (m) to denote the mth dataset. In dataset m, the n^(m) × p data matrix is denoted as X^(m). For estimating the first PCs, consider the penalized objective function:

$$\left\{\sum _{m=1}^M\frac{1}{2n^{(m)}}{\Vert {\mathbf{X}}^{(m)}-{\mathbf{u}}_1^{(m)}{\mathbf{v}}_1^{(m)T}\Vert }_F^2\right\}+\mathit{pen}({\mathbf{v}}_1^{(1)},\dots ,{\mathbf{v}}_1^{(M)}),$$ (3)

where we normalize using the sample sizes to avoid the analysis being dominated by large datasets, and pen(·) is the penalty function. The definition of ${\mathbf{u}}_1^{(m)}’\mathrm{s}$ and ${\mathbf{v}}_1^{(m)}’\mathrm{s}$ is similar to that in (2).

With SPCA, sparsity – the selection of important genes with nonzero loadings – is emphasized. In integrative analysis, when the sparsity structures of multiple datasets need to be considered, two models have been proposed (Zhao et al., 2015). In this study, we focus on the homogeneity model, under which the M first PCs share the same sparsity structure. That is, if a gene has a nonzero loading in one dataset, it has nonzero loadings in all M datasets. The homogeneity model is reasonable when the M studies have comparable designs. We refer to the literature (Y. Huang, Huang, Shia, & Ma, 2012; Ma, Huang, & Song, 2011; Ma, Huang, Wei, Xie, & Fang, 2011) for more detailed discussions on the homogeneity model. In multi-datasets analysis, the selection of comparable datasets is non-trivial. However, it has been carefully studied in the literature and will not be reiterated here.

Consider the penalty

$$\mathit{pen}({\mathbf{v}}_1^{(1)},\dots ,{\mathbf{v}}_1^{(M)})={\lambda }_1\sum _{j=1}^p{\left\{{(v_{1j}^{(1)})}^2+\dots +{(v_{1j}^{(M)})}^2\right\}}^{1/2}.$$ (4)

λ₁ > 0 is a data-dependent tuning parameter. This is a Group Lasso (GLasso) penalty, where we treat the loadings corresponding to the same gene in the M datasets as a group. With the “all in or all out” property of GLasso, if a group is selected, then all loadings within this group have nonzero estimates, and so the corresponding gene is concluded as important for the first PC in all datasets. Otherwise, all M loadings of this gene are zero. Here we adopt the Lasso-based group penalty for the satisfactory numerical performance of Lasso and computational simplicity. This penalty can be replaced with other group penalties.

2.3 Contrasted penalization

In the iSPCA approach described above, the GLasso ensures that the PCs of the M datasets have the same sparsity structure. However, it does not sufficiently account for the relationships among multiple datasets. Our exploratory analysis, which is partly described in simulation study below, suggests that although this approach can outperform the pooled analysis, classic meta-analysis, and single-dataset analysis, there may still be room for improvement. To this end, we further propose iSPCA based on the contrasted penalization.

2.3.1 Magnitude-based contrasted penalization

When the study designs of multiple datasets are “similar enough” (which can be determined by analyzing metadata (Grutzmann et al., 2005; Guerra & Goldstein, 2009)), it may be reasonable to expect that the first PCs not only share the same sparsity structure but also have loadings with similar magnitudes. Here it is noted that it is extremely rare that multiple datasets are generated under the same protocol. Thus, differences are expected across datasets. Without being too stringent (as in the pooled analysis), it is only assumed that the loadings of the first PCs are similar but not the same. Relevant discussions have been provided in the context of “regression analysis + variable selection” (Shi et al., 2014).

When the loadings of the first PCs are expected to have similar magnitudes, we propose further imposing the following magnitude-based contrasted penalty to the objective function in (3):

$$\frac{{\lambda }_2}{2}\sum _{j=1}^p\sum _{1\le m^{\prime }<m\le M}{(v_{1j}^{(m)}-v_{1j}^{(m^{\prime })})}^2,$$ (5)

where λ₂ > 0 is a data-dependent tuning parameter. We refer to this approach as iSPCA_M, where the subscript M standards for magnitude.

This approach involves two penalties. The first GLasso has the same interpretation as described above. For gene j(= 1, …, p), the newly added penalty (5) encourages its loadings in different datasets to have similar magnitudes. The degree of encouragement is adjusted by λ₂. Shrinking the differences between parameters has been considered in other contexts in the literature. The most popular are perhaps the fused penalization (Tibshirani, Saunders, Rosset, Zhu, & Knight, 2005) and Laplacian penalization (Liu, Huang, & Ma, 2013). Different from the fused penalization which shrinks differences only between adjacent parameters, the proposed approach considers all (m,m′) pairs. In addition, the ℓ₂ penalty, which is computationally simpler, is adopted as opposed to ℓ₁. The Laplacian penalization adjusts penalties using the “degrees” of connections, which is not sensible with independent datasets. The most relevant existing approach is that in (Shi et al., 2014), which considers a similar contrasted penalty but under the “regression analysis + variable selection” framework.

2.3.2 Sign-based contrasted penalization

iSPCA_M encourages the M first PCs to have quantitatively similar loadings. When the degree of similarity of the M datasets is only moderate, expecting quantitative similarity can be overly strong. For the scenario where the datasets are moderately similar, we propose further imposing the following sign-based contrasted penalty to the objective function in (3):

$$\frac{{\lambda }_2}{2}\sum _{j=1}^p\sum _{1\le m^{\prime }<m\le M}{(\mathit{sign}(v_{1j}^{(m)})-\mathit{sign}(v_{1j}^{(m^{\prime })}))}^2,$$ (6)

where λ₂ > 0 is a data-dependent tuning parameter. The sign function is defined as sign(a) = 1, 0, −1 for a > 0,= 0, and < 0. We refer to this approach as iSPCA_S, where the subscript S refers to sign. The sign function is not continuous, leading to challenges in optimization. To improve computational feasibility, we further propose approximating sign(a) with $\frac{a}{\sqrt{a^2+\tau }}$, where τ takes a small positive value.

With this approach, we encourage the first PCs in the M datasets to have qualitatively similar results. That is, if a gene has a positive loading in a dataset, we encourage its loadings in other datasets to also have a positive sign. Encouraging qualitative similarity is weaker than quantitative similarity. Note that the proposed approach is flexible in that it only encourages but does not force the signs to be the same. Penalties based on the sign function have been considered in the literature for the analysis of a single dataset (Chiquet, Grandvalet, & Ambroise, 2011), where the analysis goal is fundamentally different from the present study. To the best of our knowledge, sign penalties have not been well adopted in integrative analysis, especially not in the context of dimension reduction. We conjecture that the ℓ₂ norm in (6) can be replaced with the ℓ₁ and other norms. In our exploration, we find that the ℓ₂ norm may be computationally simpler. In addition, the ℓ₂ norm is “consistent” with that in (5).

For both iSPCA_M and iSPCA_S, computation of the other PCs can be conducted consecutively in a similar manner by keeping updating the data matrices.

2.4 Computation

For iSPCA_M and iSPCA_S, the proposed computational algorithms share the same strategy and have been motivated by the sPCA-rSVD procedure (H. Shen & Huang, 2008). They are iterative, optimize over ${\stackrel{\sim }{\mathbf{v}}}_1^{(m)}$ for a fixed ${\stackrel{\sim }{\mathbf{u}}}_1^{(m)}$, optimize over ${\stackrel{\sim }{\mathbf{u}}}_1^{(m)}$ for a fixed ${\stackrel{\sim }{\mathbf{v}}}_1^{(m)}$ under the unit ℓ₂-norm constraint $\Vert {\stackrel{\sim }{\mathbf{u}}}_1^{(m)}\Vert =1$, and then repeat. When optimizing over ${\stackrel{\sim }{\mathbf{v}}}_1^{(m)}$, since the objective function is separable, we can optimize over each ${\stackrel{\sim }{v}}_{1j}^{(m)}$, j = 1, …, p separately. The above optimizations can be realized using the coordinate descent (CD) technique, which has been extensively adopted for penalized estimation, optimizes with respect to a single parameter at a time, and cycles through all parameters. For both iSPCA_M and iSPCA_S, the proposed computational algorithms are as follows.

Algorithm

1. Initialize. For m = 1, …, M:

   1. Apply the standard SVD to X^(m) and obtain the best rank-one approximation of X^(m) as $d_1^{(m)}{\mathbf{u}}_1^{\ast (m)}{\mathbf{v}}_1^{\ast (m)T}$, where ${\mathbf{u}}_1^{\ast (m)}$ and ${\mathbf{v}}_1^{\ast (m)}$ are vectors with unit norms.

   2. Set l = 0, ${\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}=d_1^{(m)}{\mathbf{v}}_1^{\ast (m)}$, and ${\stackrel{\sim }{\mathbf{u}}}_{1[l]}^{(m)}={\mathbf{u}}_1^{\ast (m)}$.

      Denote ${\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}={({\stackrel{\sim }{v}}_{11[l]}^{(m)},{\stackrel{\sim }{v}}_{12[l]}^{(m)},\dots ,{\stackrel{\sim }{v}}_{1p[l]}^{(m)})}^T,{\stackrel{\sim }{\mathbf{u}}}_{1[l]}^{(m)}={({\stackrel{\sim }{u}}_{11[l]}^{(m)},{\stackrel{\sim }{u}}_{12[l]}^{(m)},\dots ,{\stackrel{\sim }{u}}_{1n^{(m)}[l]}^{(m)})}^T$.

2. Update l=l+1. For m = 1, …, M:

   1. (a) Optimize over ${\stackrel{\sim }{\mathbf{v}}}_1^{(m)}$ with ${\stackrel{\sim }{\mathbf{u}}}_1^{(m)}$ fixed at ${\stackrel{\sim }{\mathbf{u}}}_{1[l-1]}^{(m)}$, and obtain ${\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}$.

   2. Optimize over ${\stackrel{\sim }{\mathbf{u}}}_1^{(m)}$ with ${\stackrel{\sim }{\mathbf{v}}}_1^{(m)}$ fixed at ${\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}$. Specifically, calculate ${\stackrel{\sim }{\mathbf{u}}}_{1[l]}^{(m)}={\mathbf{X}}^{(m)}{\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}/\Vert {\mathbf{X}}^{(m)}{\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}\Vert$.

3. Repeat Step 2 until convergence. In numerical study, we take the ℓ₂ norm of the difference between two consecutive estimates smaller than 10⁻⁴ as the criterion of convergence.

iSPCA_M and iSPCA_S differ in Step 2(a). Specifically,

Step 2(a) for iSPCA_M can be realized iteratively as follows. For m = 1, …, M:

1. Initialize k=0 and ${\stackrel{\sim }{\mathbf{v}}}_{1[k]}^{(m)}={\stackrel{\sim }{\mathbf{v}}}_{1[l-1]}^{(m)}$.

2. Update k=k+1. Compute

   $${\stackrel{\sim }{v}}_{1j[k]}^{(m)}=\frac{{(\Vert S_{1j[k]}\Vert -{\lambda }_1)}_{+}{S}_{1j[k]}^{(m)}}{c\Vert S_{1j[k]}\Vert },$$

   where $S_{1j[k]}^{(m)}=\frac{1}{n^{(m)}}{\sum }_{i=1}^{n^{(m)}}{x}_{ij}^{(m)}{\stackrel{\sim }{u}}_{1i[l-1]}^{(m)}+{\lambda }_2\left({\sum }_{m^{\prime }\ne m}{\stackrel{\sim }{v}}_{1j[k-1]}^{(m^{\prime })}\right),\Vert S_{1j[k]}\Vert =\sqrt{{\sum }_{m=1}^M{S_{1j[k]}^{(m)}}^2}$, and $c=\frac{1}{n^{(m)}}{\sum }_{i=1}^{n^{(m)}}{(x_{ij}^{(m)})}^2+{\lambda }_2(M-1)$.

3. Repeat Step 2 until convergence. The estimate at convergence is ${\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}$.

Step 2(a) for iSPCA_S can be realized iteratively as follows. For m = 1, …, M:

1. Initialize k=0 and ${\stackrel{\sim }{\mathbf{v}}}_{1[k]}^{(m)}={\stackrel{\sim }{\mathbf{v}}}_{1[l-1]}^{(m)}$.

2. Update k=k+1. Compute

   $${\stackrel{\sim }{v}}_{1j[k]}^{(m)}=\frac{{(\Vert S_{1j[k]}\Vert -{\lambda }_1)}_{+}{S}_{1j[k]}^{(m)}}{c\Vert S_{1j[k]}\Vert },$$

   where $S_{1j[k]}^{(m)}=\frac{1}{n^{(m)}}{\sum }_{i=1}^{n^{(m)}}{x}_{ij}^{(m)}{\stackrel{\sim }{u}}_{1i[l-1]}^{(m)}+{\lambda }_2\left({\sum }_{m^{\prime }\ne m}\frac{{\stackrel{\sim }{v}}_{1j[k-1]}^{(m^{\prime })}}{\sqrt{{({\stackrel{\sim }{v}}_{1j[k-1]}^{(m^{\prime })})}^2+{\tau }^2}}\right)\frac{1}{\sqrt{{({\stackrel{\sim }{v}}_{1j[k-1]}^{(m)})}^2+{\tau }^2}},\Vert S_{1j[k]}\Vert =\sqrt{{\sum }_{m=1}^M{S_{1j[k]}^{(m)}}^2}$, and $c=\frac{1}{n^{(m)}}{\sum }_{i=1}^{n^{(m)}}{(x_{ij}^{(m)})}^2+\frac{{\lambda }_2(M-1)}{{({\stackrel{\sim }{v}}_{1j[k-1]}^{(m^{\prime })})}^2+{\tau }^2}$.

3. Repeat Step 2 until convergence. The estimate at convergence is ${\stackrel{\sim }{\mathbf{v}}}_{1[l]}^{(m)}$.

With closed-form simple updates, the proposed algorithms are much affordable. They are based on the CD technique, which enjoys satisfactory convergence properties. For all of our simulations, convergence is achieved with a small to moderate number of iterations. The proposed methods involve tuning parameters λ₁ and λ₂. In our simulation and data analysis, we select them using the five-fold cross validation, which has been extensively adopted with penalization methods. As the proposed algorithms have affordable computational cost, it is feasible to conduct a grid search of tunings. Other tuning parameter selection methods may be also applicable. Another parameter is τ in the sign function approximation. Interestingly, we do not need a very accurate approximation to the sign function. The proposed methods behave well as long as τ is small enough (compared to the values of nonzero loadings) and can reasonably quantify sign inconsistency. In our numerical study, we set τ = 0.1 and observe satisfactory results. In practice, we suggest examining numerical results under a few τ values and use the smallest one that generates stable estimates. To facilitate data analysis, we have developed R code, which is publicly available at www.github.com/shuanggema.

3 Simulation

Simulation is conducted to assess performance of the proposed integrative analysis and compare with alternatives. As in the published PCA and SPCA studies, focus is on the first PCs. Our simulation settings mimic those in the literature to a certain extent. We set M = 4 or 8, n^(m) = 25, and p = 500. In data generation, we first construct the population covariance matrices

$${\mathbf{\sum }}^{(m)}={\mathbf{V}}^{\ast (m)}{\mathbf{D}}^{(\mathbf{m})}{\mathbf{V}}^{\ast (m)T},$$

where ${\mathbf{D}}^{(\mathbf{m})}=\mathit{diag}\left\{d_1^{(m)},d_2^{(m)},\dots ,d_p^{(m)}\right\}$ is the eigenvalue matrix, and ${\mathbf{V}}^{\ast (m)}=({\mathbf{v}}_1^{\ast (m)},{\mathbf{v}}_2^{\ast (m)},\dots ,{\mathbf{v}}_p^{\ast (m)})$ is the eigenvector matrix. Following the literature (D. Shen et al., 2013), we consider the spike model where $d_1^{(m)}=p^{\alpha },d_2^{(m)}=\dots =d_p^{(m)}=1$ and α is the spike index. With the emphasis on the first PCs, generation of the first eigenvectors is especially important and described in detail below. Once the first eigenvectors are generated, we then generate the nonzero values of the rest eigenvectors from unif[1, 2]. Normalization and orthogonalization are conducted to generate V^*(m)’s. The data matrices X^(m)’s are generated from the multivariate normal distributions.

For the first eigenvectors, denote the number of nonzero entries as p^β where β is the sparsity index. Published SPCA studies suggest the critical role of α and β. Especially, in single-dataset analysis, when α ∈ (0, 1] and α ≤ β, the SPCA estimation is not consistent (D. Shen et al., 2013). As shown in Tables 1–3 and 5–7 (Appendix), we consider a wide spectrum of settings. For β, we consider 0.3 (0.4 in Tables 3 and 7), 0.5, and 0.8, which correspond to 6 (12), 22, and 144 nonzero entries per dataset. For the combination of β and α, under the first three settings in Table 1, the four datasets have the same α values; Under the next three settings, different datasets have different spike indexes; Under the last three settings, one dataset has α < β. This setting is designed to examine whether the one dataset can be “saved” by borrowing information from other datasets.

Table 1.

Simulation results for Scenario 1 (M=4). In each cell, mean (MAD).

β	α	Method	Angle	TP	FP	Sign
0.3	(0.5, 0.5, 0.5, 0.5)	meta-PCA	45.46(2.9)	6(0)	494(0)	0.01(0)
		meta-SPCA	8.19(2.06)	6(0)	3(1.6)	0.99(0.01)
		pooled-SPCA	82.78(3.77)	6(0)	8(6)	0.98(0.01)
		iSPCA	5.69(1.29)	6(0)	0(0)	1(0)
		iSPCAM	2.93(0.68)	6(0)	0(0)	1(0)
		iSPCAS	5.69(1.29)	6(0)	0(0)	1(0)
0.5	(0.6, 0.6, 0.6, 0.6)	meta-PCA	36.77(2.57)	22(0)	478(0)	0.05(0)
		meta-SPCA	13.39(2.37)	22(0)	15.5(3.2)	0.97(0.01)
		pooled-SPCA	88.32(0.92)	20(2)	46(29)	0.9(0.07)
		iSPCA	8.82(1.22)	22(0)	3(1)	0.99(0)
		iSPCAM	4.51(0.65)	22(0)	2(1)	1(0)
		iSPCAS	8.83(1.23)	22(0)	3(1)	0.99(0)
0.8	(1, 1, 1, 1)	meta-PCA	11.86(1.17)	144(0)	356(0)	0.29(0)
		meta-SPCA	7.89(0.96)	144(0)	42.3(5.8)	0.92(0.01)
		pooled-SPCA	89.65(0.08)	144(0)	139.5(34.5)	0.72(0.07)
		iSPCA	6.48(0.65)	144(0)	2.5(1)	1(0)
		iSPCAM	3.15(0.15)	144(0)	1(0.8)	1(0)
		iSPCAS	6.48(0.65)	144(0)	2.5(1)	1(0)
0.3	(0.7, 0.5, 0.6, 0.8)	meta-PCA	27.86(3.21)	6(0)	494(0)	0.01(0)
		meta-SPCA	3.99(1.05)	6(0)	1.8(1)	1(0)
		pooled-SPCA	80.26(1.3)	6(0)	4(3)	0.99(0.01)
		iSPCA	3.07(0.76)	6(0)	3(1)	0.99(0)
		iSPCAM	1.31(0.28)	6(0)	2(1)	1(0)
		iSPCAS	3.07(0.78)	6(0)	2.2(1.6)	0.99(0.01)
0.5	(0.6, 0.6, 1, 1.5)	meta-PCA	20.22(1.76)	22(0)	478(0)	0.05(0)
		meta-SPCA	6.84(1.23)	22(0)	7.4(2.4)	0.98(0.01)
		pooled-SPCA	89.36(0.64)	16(4)	79.5(75)	0.82(0.14)
		iSPCA	4.72(0.76)	22(0)	3.5(1.7)	0.99(0)
		iSPCAM	1.04(0.17)	22(0)	2.3(1.2)	0.99(0)
		iSPCAS	4.73(0.76)	22(0)	2(1.7)	0.99(0)
0.8	(0.9, 0.9, 1.5, 1.5)	meta-PCA	11.3(1.36)	144(0)	356(0)	0.3(0)
		meta-SPCA	6.85(0.81)	144(0)	34.3(6.6)	0.93(0.01)
		pooled-SPCA	89.75(0.15)	141.5(2)	345(5.5)	0.3(0.08)
		iSPCA	5.34(0.53)	144(0)	1.8(0.8)	1(0)
		iSPCAM	1.4(0.13)	144(0)	1(0.8)	1(0)
		iSPCAS	5.34(0.53)	144(0)	1.7(1)	1(0)
0.3	(0.5, 0.2, 0.5, 0.5)	meta-PCA	56.7(3.62)	6(0)	494(0)	0.01(0)
		meta-SPCA	36.59(1.81)	4(0)	5.5(2.7)	0.98(0.01)
		pooled-SPCA	81.68(3.11)	6(0)	6(4)	0.98(0.01)
		iSPCA	10.53(2.81)	6(0)	4(1)	0.99(0.01)
		iSPCAM	4.08(0.86)	6(0)	3(1)	0.99(0)
		iSPCAS	10.51(2.78)	6(0)	3(1)	0.99(0)
0.5	(0.4, 0.6, 0.6, 0.7)	meta-PCA	27.7(2.25)	22(0)	478(0)	0.05(0)
		meta-SPCA	20.52(3.65)	21.2(0.8)	21.1(4.3)	0.95(0.01)
		pooled-SPCA	89.76(0.24)	13(6.5)	119.5(89.5)	0.73(0.18)
		iSPCA	10.86(1.55)	22(0)	3(1.6)	0.99(0)
		iSPCAM	4.86(0.6)	22(0)	2(1)	0.99(0)
		iSPCAS	10.86(1.54)	22(0)	3(1.2)	0.99(0)
0.8	(0.7, 0.9, 0.9, 1)	meta-PCA	11.6(0.98)	144(0)	356(0)	0.29(0)
		meta-SPCA	13.8(1.8)	143.8(0.3)	79.3(9.3)	0.84(0.02)
		pooled-SPCA	65.34(8.2)	140(4)	245.5(108.5)	0.36(0.13)
		iSPCA	10.41(1.18)	144(0)	4(1.3)	0.99(0)
		iSPCAM	6.07(0.53)	144(0)	2.8(1)	0.99(0)
		iSPCAS	10.41(1.18) 19	144(0)	3.5(1.3)	0.99(0)

Table 3.

simulation results for Scenario 3 (M=4). In each cell, mean(MAD).

β	α	Method	Angle	TP	FP	Sign
0.4	(0.5, 0.5, 0.5, 0.5)	meta-PCA	45.46(2.9)	12(0)	488(0)	0.03(0)
		meta-SPCA	18.7(2.64)	12(0)	37.5(7.2)	0.92(0.01)
		pooled-SPCA	82.43(0.45)	8.2(1)	5.8(3)	0.98(0.01)
		iSPCA	11.91(1.65)	12(0)	8.08(1.1)	0.98(0)
		iSPCAM	10.94(1.61)	12(0)	8(1)	0.98(0)
		iSPCAS	11.25(1.69)	12(0)	7(1)	0.99(0)
0.5	(0.6, 0.6, 0.6, 0.6)	meta-PCA	36.77(2.57)	22(0)	478(0)	0.05(0)
		meta-SPCA	16.49(2.01)	22(0)	39.9(4.2)	0.92(0.01)
		pooled-SPCA	86.91(0.67)	19.33(2.7)	13.2(11)	0.95(0.03)
		iSPCA	11.88(1.32)	22(0)	13(1)	0.97(0)
		iSPCAM	10.96(1.38)	22(0)	13(1.2)	0.97(0)
		iSPCAS	11.24(1.37)	22(0)	11(1)	0.98(0)
0.8	(1, 1, 1, 1)	meta-PCA	11.86(1.17)	144(0)	356(0)	0.29(0)
		meta-SPCA	8.94(0.82)	144(0)	136.6(6.5)	0.73(0.01)
		pooled-SPCA	55.87(2.2)	143.5(0.5)	340.1(2.5)	0.31(0.01)
		iSPCA	8.79(0.68)	144(0)	71(1)	0.86(0)
		iSPCAM	8.12(0.79)	144(0)	71(1)	0.86(0)
		iSPCAS	8.3(0.66)	144(0)	64.58(2.1)	0.87(0)
0.4	(0.7, 0.5, 0.6, 0.8)	meta-PCA	27.86(3.21)	12(0)	488(0)	0.03(0)
		meta-SPCA	10.06(1.6)	12(0)	29.4(12.9)	0.94(0.03)
		pooled-SPCA	83.22(0.48)	11.2(0)	7.8(5)	0.98(0.01)
		iSPCA	6.51(0.99)	12(0)	8.1(1.1)	0.98(0)
		iSPCAM	6.21(1.03)	12(0)	8.1(1.1)	0.98(0)
		iSPCAS	6.11(0.98)	12(0)	6.17(1)	0.99(0)
0.5	(0.6, 0.6, 1, 1.5)	meta-PCA	2.53(0)	22(0)	478(0)	0.06(0)
		meta-SPCA	9.28(0)	22(0)	40(3.4)	0.92(0.01)
		pooled-SPCA	79.13(0)	22(0)	449(5)	0.09(0.02)
		iSPCA	6.86(1.06)	22(0)	12.67(1)	0.97(0)
		iSPCAM	6.86(1.06)	22(0)	12.67(1)	0.97(0)
		iSPCAS	6.54(1.04)	22(0)	9.83(1)	0.98(0)
0.8	(0.9, 0.9, 1.5, 1.5)	meta-PCA	2.41(0.61)	144(0)	356(0)	0.3(0.01)
		meta-SPCA	7.1(0.72)	144(0)	133.8(7.4)	0.73(0.02)
		pooled-SPCA	66.83(12.79)	143(1)	352(4)	0.26(0.02)
		iSPCA	7.63(0.85)	144(0)	70(1)	0.86(0)
		iSPCAM	7.69(0.85)	144(0)	70(1)	0.86(0)
		iSPCAS	7.25(0.82)	144(0)	57.25(2.4)	0.88(0)
0.4	(0.5, 0.3, 0.5, 0.5)	meta-PCA	56.7(3.62)	12(0)	488(0)	0.02(0)
		meta-SPCA	26.31(3.56)	9.58(0.8)	17.4(4.7)	0.96(0.01)
		pooled-SPCA	82.71(0.47)	9.17(1)	6.8(3)	0.98(0.01)
		iSPCA	17.56(2.85)	12(0)	8.17(1.2)	0.98(0)
		iSPCAM	16.69(2.8)	12(0)	8.92(1.1)	0.98(0)
		iSPCAS	16.71(2.99)	12(0)	7.33(1)	0.98(0)
0.5	(0.4, 0.6, 0.6, 0.7)	meta-PCA	27.7(2.25)	22(0)	478(0)	0.05(0)
		meta-SPCA	21.03(2.49)	19.17(1.1)	39.7(4.3)	0.91(0.01)
		pooled-SPCA	87.6(1.45)	7(5.6)	15.5(12.8)	0.94(0.03)
		iSPCA	15.74(2.05)	22(0)	13.5(1)	0.97(0)
		iSPCAM	15.24(2.08)	22(0)	13.42(1)	0.97(0)
		iSPCAS	15.05(2.11)	22(0)	11.5(1)	0.98(0)
0.8	(0.7, 0.9, 0.9, 1)	meta-PCA	11.6(1.01)	144(0)	356(0)	0.29(0.01)
		meta-SPCA	14.04(1.88)	140.8(1.5)	136.6(5.6)	0.7(0.03)
		pooled-SPCA	66.15(8.03)	141.5(2.5)	341.8(12.3)	0.27(0.01)
		iSPCA	14.84(1.54)	144(0)	71.33(1)	0.85(0)
		iSPCAM	14.57(1.52)	144(0)	71.33(1)	0.86(0)
		iSPCAS	14.15(1.45) 21	144(0)	64.17(1.8)	0.87(0)

In integrative analysis, we pay special attention to the similarity/difference across datasets. The following three scenarios are considered: (Scenario 1) The first eigenvectors have the same sparsity structure and same values of loadings; (Scenario 2) The first eigenvectors have the same sparsity structure but different values of loadings; (Scenario 3) 10% of the nonzero loadings have different locations across datasets, and the values of loadings are different. Under Scenario 1, the nonzero entries of the first eigenvectors are constant; Under Scenarios 2 and 3, the nonzero entries are randomly generated from a normal distribution. Scenarios 1 and 2 satisfy the homogeneity model and represent different levels of similarity across datasets. Scenario 3 violates the homogeneity model assumption and is designed to test performance of the proposed analysis under model misspecification.

To better gauge performance of the proposed analysis, we compare with (a) meta-PCA and meta-SPCA, which conduct the PCA and SPCA for each dataset separately and then combine the analysis results, and (b) pooled-SPCA, which pools data together and then applies the SPCA. In the literature, multi-datasets dimension reduction analysis is still lacking. It is sensible to compare with meta-analysis, which is the default multi-datasets approach. The simulate data have comparability higher than practically encountered, and thus the pooled analysis may be a viable approach. To compare different analyses, we consider the following measures: Angle (which is the acute angle between the estimated and true first eigenvector), TP/FP (which is the number of true/false positives), and Sign (which is the percentage of the loading’s signs that are correctly estimated). In addition, to “eliminate” effects of tuning parameter selection on identification evaluation, we also present the ROC curves in Appendix. With meta-PCA, which generates dense estimates, we compute the norm of loadings for each variable and apply thresholding for selection. With multiple datasets, average measures are computed.

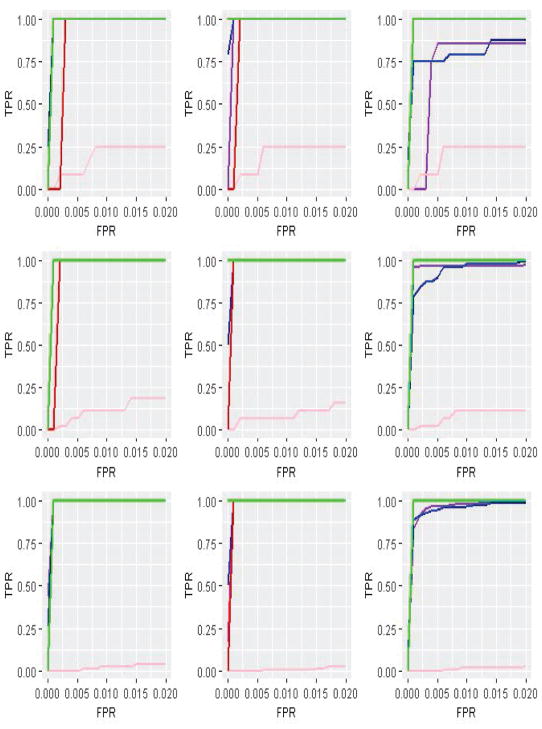
Summary statistics based on 200 replicates are provided in Tables 1–3 and 5–7 (Appendix). The ROC plots are provided in Figures 1–6 in Appendix. The proposed integrative analysis is observed to have competitive performance across the whole spectrum of simulation. For example, in Table 1, when the magnitudes of loadings are the same for all four datasets, iSPCA_M has the most competitive performance, as expected. For example under the first setting, the Angle measures are 45.46 (meta-PCA), 8.19 (iSPCA), 82.78 (pooled-SPCA), 5.69 (iSPCA), 2.93 (iSPCA_M), and 5.69 (iSPCA_S), respectively. When the nonzero loadings take different values across datasets, the advantage of iSPCA_S becomes prominent. For example under the second setting in Table 2, all integrative analysis methods can accurately identify the TPs, while iSPCA_S has the smallest number of FPs (2, compared to 478, 22.4, 44, 3.5, and 3.5 of the alternatives). In addition, for the settings with one dataset having β > α, the merit of integrative analysis is clearly seen: by borrowing information across datasets, integrative analysis methods have smaller Angle and FP and higher TP and Sign. Tables 3 and 7 suggest that under the violation of the homogeneity model assumption, the proposed analysis still has competitive performance. The ROC plots clearly demonstrate the competitive identification performance of the proposed integrative analysis.

Table 2.

Simulation results for Scenario 2 (M=4). In each cell, mean(MAD).

β	α	Method	Angle	TP	FP	Sign
0.3	(0.5, 0.5, 0.5, 0.5)	meta-PCA	45.41(1.19)	6(0)	494(0)	0.01(0.01)
		meta-SPCA	10.48(1.19)	5(2.9)	8.1(6.6)	0.98(0.02)
		pooled-SPCA	87.67(0.03)	4(19)	12(67.5)	0.97(0.12)
		iSPCA	6.15(1.05)	6(0.6)	3(1.1)	0.99(0.01)
		iSPCAM	6.1(1.02)	6(0.4)	3(1.2)	0.99(0)
		iSPCAS	5.97(0.98)	6(0.8)	2(1)	0.99(0)
0.5	(0.6, 0.6, 0.6, 0.6)	meta-PCA	36.9(3.27)	22(0)	478(0)	0.04(0)
		meta-SPCA	13.35(1.81)	16.3(1)	22.4(4.2)	0.94(0.01)
		pooled-SPCA	89.59(0.41)	15(2)	44(18)	0.9(0.03)
		iSPCA	9.53(1.46)	22(0)	3.5(1.5)	0.99(0)
		iSPCAM	9.51(1.44)	22(0)	3.5(1.5)	0.99(0.01)
		iSPCAS	9.38(1.46)	22(0)	2(1)	0.99(0)
0.8	(1, 1, 1, 1)	meta-PCA	11.64(1.06)	144(0)	356(0)	0.28(0)
		meta-SPCA	7.98(0.74)	124.4(2.2)	84.8(7.6)	0.78(0.02)
		pooled-SPCA	89.82(0.16)	131(12)	225.5(67.5)	0.51(0.07)
		iSPCA	6.95(0.61)	144(0)	2(1)	0.98(0)
		iSPCAM	6.95(0.62)	144(0)	2(1)	0.98(0)
		iSPCAS	6.84(0.6)	143.8(0.2)	0(0)	0.99(0)
0.3	(0.7, 0.5, 0.6, 0.8)	meta-PCA	28.6(2.56)	6(0)	494(0)	0.01(0.01)
		meta-SPCA	6.1(1.02)	5.3(0)	9.4(2.3)	0.98(0.01)
		pooled-SPCA	87.38(2.41)	5(1)	31(11)	0.93(0.02)
		iSPCA	3.61(0.95)	6(0)	3.7(1.8)	0.99(0.01)
		iSPCAM	3.63(0.97)	6(0)	3.7(1.7)	0.99(0.01)
		iSPCAS	3.54(0.94)	6(0)	2.8(1.1)	0.99(0.01)
0.5	(0.6, 0.6, 1, 1.5)	meta-PCA	21.14(2.04)	22(0)	478(0)	0.05(0)
		meta-SPCA	7.59(0.94)	18.5(0.8)	26(4.8)	0.94(0.01)
		pooled-SPCA	89.99(0.01)	9.5(5)	37.5(35)	0.89(0.06)
		iSPCA	5.27(0.77)	22(0)	3.5(1)	0.99(0)
		iSPCAM	5.25(0.77)	22(0)	3.5(1)	0.99(0)
		iSPCAS	5.21(0.79)	22(0)	1.6(0.8)	1(0)
0.8	(0.9, 0.9, 1.5, 1.5)	meta-PCA	11.01(1.06)	144(0)	356(0)	0.29(0)
		meta-SPCA	6.86(0.75)	126.8(2)	86.9(6.5)	0.79(0.01)
		pooled-SPCA	89.92(0.08)	107(19)	207.5(72.5)	0.52(0.1)
		iSPCA	5.9(0.6)	144(0)	1.7(1)	0.98(0)
		iSPCAM	5.91(0.61)	144(0)	1.7(1)	0.98(0)
		iSPCAS	5.8(0.58)	143.7(0.3)	0.5(0.5)	1(0)
0.3	(0.5, 0.2, 0.5, 0.5)	meta-PCA	56.83(4.11)	6(0)	494(0)	0.01(0)
		meta-SPCA	36.76(2.49)	3.7(0.4)	9.5(2.9)	0.97(0.01)
		pooled-SPCA	87.8(2.2)	4.5(0.5)	14.5(8)	0.97(0.01)
		iSPCA	11.45(2.75)	6(0)	4(1)	0.99(0)
		iSPCAM	11.18(2.87)	6(0)	4(1)	0.99(0)
		iSPCAS	11.2(2.92)	6(0)	3.3(1)	0.99(0.01)
0.5	(0.4, 0.6, 0.6, 0.7)	meta-PCA	27.31(2.65)	22(0)	478(0)	0.04(0)
		meta-SPCA	16.73(2.2)	15.3(1)	21.4(3.8)	0.94(0.01)
		pooled-SPCA	89.99(0.01)	8.5(2.5)	63.5(50.5)	0.85(0.1)
		iSPCA	11.39(1.59)	22(0)	3.9(1.1)	0.99(0)
		iSPCAM	11.31(1.61)	22(0)	3.9(1.1)	0.99(0)
		iSPCAS	11.09(1.63)	22(0)	2.5(1)	0.99(0)
0.8	(0.7, 0.9, 0.9, 1)	meta-PCA	11.22(1.19)	144(0)	356(0)	0.27(0.01)
		meta-SPCA	13.23(1.19)	115.9(2.9)	85.1(6.6)	0.77(0.02)
		pooled-SPCA	89.97(0.03)	102.5(19)	217(67.5)	0.47(0.12)
		iSPCA	11.63(1.05)	143.4(0.6)	2.3(1.1)	0.97(0.01)
		iSPCAM	11.55(1.02)	143.6(0.4)	2.2(1.2)	0.98(0)
		iSPCAS	11.39(0.98) 20	142.8(0.8)	1.3(1)	0.99(0)

4 Data analysis

4.1 Breast cancer data

We collect three breast cancer gene expression datasets from GEO (Gene Expression Omnibus) (Gene Expression Omnibus., 2017), which have IDs GSE9574, GSE21947, and GSE5364, respectively. These datasets have gene expression measurements on 20,995 probes and sample sizes 31, 32, and 198, respectively. We refer to the original publications (Graham, Ge, De, Tripathi, & Rosenberg, 2011; Tripathi et al., 2008; Yu et al., 2008) for detailed information on the study design and data collection. These datasets have been jointly analyzed in published studies, which, based on the analysis of meta-data and expert’s opinion, suggest that it is reasonable to expect a certain degree of similarity (and so to assume the homogeneity model).

Prior to analysis, normalization is conducted for each dataset separately. We match genes across datasets using the Unigene Cluster IDs. Although the proposed analysis can accommodate partially matched gene sets, to generate more reliable results, we focus on genes that are measured in all three datasets. With limited sample sizes, to improve reliability, we conduct a screening using the coefficient of dispersion, which results in 1,583 genes for downstream analysis. Centralization of gene expressions is then conducted for each dataset separately.

We analyze data using the integrative analysis methods as well as the meta-analysis and pooled analysis methods described above. As in published studies, we focus on the first PCs. As shown in Table 4, different methods lead to different results. Meta-PCA generates dense estimates. Meta-SPCA and pooled-SPCA identify 409 and 67 nonzero loadings, respectively. The proposed integrative methods identify 147, 165, and 165 nonzero loadings, respectively. The three integrative analysis methods generate similar results, with iSPCA_M and iSPCA_S identifying the same set of important genes. In Table 8 (Appendix), we provide the top 20 genes with the largest norms of loadings under integrative analysis. Note that our analysis is conducted at the probe level, and there are multiple probes that correspond to the same genes. More detailed estimation results are available from the authors. Interestingly, the top four genes are all involved in the encoding of immunoglobulins, which are generated by the body’s immune system in response to cancer cells, bacteria, viruses, fungus, and others. Breakdown of the immune system has been identified as a major risk factor for breast and other cancers. Pathway analysis suggests that the top genes are involved in the following pathways: immunoregulatory interactions, inflammatory response, TGF-signaling, complement cascade, signaling by the B cell receptor, metabolism of carbohydrates, and others, all of which have been implied in breast cancer development. With practical data, it is impossible to directly assess identification accuracy. We conduct the following evaluations, which may provide some indirect support to the proposed analysis. We first evaluate stability by computing the observed occurrence index (OOI) (J. Huang & Ma, 2010). In particular, we randomly sample 75% of the subjects and conduct the proposed analysis. This step is repeated 100 times, and the probability of a gene identified with nonzero loadings is computed and referred to as the OOI. We observe that for the genes identified using the integrative analysis methods, the OOIs are close to 100%, indicating satisfactory stability. In contrast, the meta-SPCA and pooled-SPCA OOIs are considerably lower. We also evaluate prediction performance. Each dataset is randomly split into a training and a testing set with sizes 3:1. We compute the first PCs using the training sets and make prediction for the testing sets. iSPCA_S has a prediction MSE about 4% lower than iSPCA and iSPCA_M but over 10% lower than meta- and pooled analysis. This result may suggest that there may exist considerable differences across datasets and that the less stringent sign contrasted penalty may be more sensible.

Table 4.

Data analysis: numbers of overlapping genes identified by different methods.

	Breast cancer data
	meta-PCA	meta-SPCA	pooled-SPCA	iSPCA	iSPCAM	iSPCAS
meta-PCA	1583	409	67	147	165	165
meta-SPCA		409	67	146	164	164
pooled-SPCA			67	67	67	67
iSPCA				147	147	147
iSPCAM					165	165
iSPCAS						165
	Pancreatic cancer data
	meta-PCA	meta-SPCA	pooled-SPCA	iSPCA	iSPCAM	iSPCAS
meta-PCA	1258	486	150	241	310	311
meta-SPCA		486	150	241	310	311
pooled-SPCA			150	150	150	150
iSPCA				241	241	241
iSPCAM					310	310
iSPCAS						311

4.2 Pancreatic cancer data

We collect two pancreatic cancer gene expression datasets from GEO, and the IDs are GSE16515 and GSE19650. These datasets have gene expression measurements on 41,632 and 41,642 probes and sample sizes 54 and 24, respectively. We refer to the original publications (Hiraoka et al., 2011; Pei et al., 2009) for more information on data. These two datasets have also been previously jointly analyzed. Similar data processing as described above is conducted, leading to 1,258 genes for downstream analysis. The analysis results using the proposed and alternative methods are summarized in Table 4. The observed patterns are similar to those for the breast cancer data. Specifically, meta-SPCA identifies more genes than the integrative analysis methods, while pooled-SPCA identifies fewer. The identification results using iSPCA_M and iSPCA_S are almost identical. Different from the breast cancer data, the iSPCA results have larger difference from those using the contrasted penalties. The top 20 genes with the largest loadings under integrative analysis are listed in Table 9 (Appendix). More detailed results are available from the authors. Gene AMY2B is in the cluster of amylase genes that are expressed at high levels in either salivary gland or pancreas. Gene PNLIP encodes a member of the lipase family of proteins. The encoded enzyme is essential for the efficient digestion of dietary fats. Multiple CELA genes, which belong to the chymotrypsin like elastase family, are identified. Elastases are secreted from the pancreas as zymogens. Gene PRSS1 encodes a trypsinogen. Mutations in this gene are associated with hereditary pancreatitis. Gene CPA1 encodes a member of the carboxypeptidase A family of zinc metalloproteases. Mutations in this gene may be linked to chronic pancreatitis, while elevated protein levels may be associated with pancreatic cancer. The top-ranking genes are involved in the following pathways: angiogenesis, lipid digestion, mobilization, and transport, AGE/RAGE, metabolism of carbohydrates, metabolism of water-soluble vitamins and cofactors, and others, which are cancer-related or specific to pancreatic cancer. In the evaluation of stability, the integrative analysis methods again have close to perfect OOIs. Prediction performance is evaluated as described above. iSPCA_M and iSPCA_S have comparable prediction MSEs, which are about 3% lower than iSPCA, 8% lower than meta-analysis, and over 10% lower than pooled-SPCA.

5 Discussion

In the analysis of gene expression data, PCA, SPCA, and other dimension reduction techniques have been extensively adopted. In this study, built on SPCA, we have developed the iSPCA approach and conduct the jointly analysis of raw data from multiple independent studies. The proposed analysis can more accurately identify relevant genes and estimate their loadings. This study significantly extends the novel integrative analysis paradigm to dimension reduction analysis. To effectively and comprehensively accommodate the similarity across datasets, we have developed two contrasted penalties based on the magnitude and sign respectively. The sign-based contrasted penalty has not been well adopted in the literature, especially not under similar contexts. It makes less stringent assumptions and can be useful for many practical situations. It can be potentially extended to other integrative analysis settings. The proposed methods can be effectively realized. Under a wide spectrum of simulation settings, the proposed integrative analysis outperforms meta-analysis and pooled analysis. It is observed that performance of the magnitude and sign penalizations depends on data settings, neither dominates the other, and hence both are needed in practice. In data analysis, integrative analysis generates results different from meta-analysis. The stability and prediction evaluation provides some support to the validity of integrative analysis. In data analysis, it is also observed that the contrasted penalization identifies more genes. Similar observations have also been made in the regression and variable selection context. It may be noted that the sample sizes of the analyzed datasets are small. Integrative analysis is more sensible with smaller sample sizes (and hence there is a stronger need for increasing sample size). Although the cost of profiling keeps going down, with sample and other constraints, even some recent studies still have limited sample sizes, and so integrative analysis is needed.

This study can be potentially extended in multiple directions. Beyond PCA, there are quite a few other dimension reduction techniques (PLS, ICA, etc.). It will be of interest to develop their integrative analysis counterparts. For selection, the group Lasso penalty is adopted and can be potentially replaced with other group penalties. The sign-based contrasted penalty has not been well adopted, provides a useful alternative to the magnitude-based, and can have applications far beyond this study. The stability and prediction evaluation provides some support to the integrative analysis results. More confirmation may be needed (although it is noted that in the literature there is still a lack of good approaches for evaluating SPCA results).

Appendix

Table 5.

Simulation results for Scenario 1 (M=8). In each cell, mean(MAD).

β	α	Method	Angle	TP	FP	Sign
0.3	(0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5)	meta-PCA	44.94(3.54)	6(0)	494(0)	0.01(0)
		meta-SPCA	8.18(2.04)	6(0)	3(1.4)	0.99(0.01)
		pooled-SPCA	51.49(18.16)	6(0)	19.5(18)	0.96(0.03)
		iSPCA	5.68(1.33)	6(0)	9.4(5.6)	0.98(0.01)
		iSPCAM	2.24(0.58)	6(0)	7.7(1.9)	0.98(0.01)
		iSPCAS	5.57(1.35)	6(0)	7.1(2.3)	0.98(0.01)
0.5	(0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6)	meta-PCA	35.91(2.09)	22(0)	478(0)	0.05(0)
		meta-SPCA	13.31(2.31)	22(0)	16.6(3.3)	0.97(0.01)
		pooled-SPCA	56.27(17.2)	20(2)	46.5(34.5)	0.9(0.06)
		iSPCA	8.64(1.2)	22(0)	12(2.1)	0.98(0.01)
		iSPCAM	3.73(0.41)	22(0)	6.6(1.8)	0.99(0)
		iSPCAS	8.56(1.2)	22(0)	8.3(2)	0.98(0)
0.8	(1, 1, 1, 1, 1, 1, 1, 1)	meta-PCA	11.55(1.13)	144(0)	356(0)	0.29(0)
		meta-SPCA	7.87(0.95)	144(0)	51.1(6.2)	0.9(0.01)
		pooled-SPCA	27.72(8.76)	144(0)	119.5(27)	0.76(0.05)
		iSPCA	6.37(0.63)	144(0)	8(1.9)	0.98(0)
		iSPCAM	2.64(0.11)	144(0)	1.6(1)	1(0)
		iSPCAS	6.37(0.63)	144(0)	4.1(2.1)	0.99(0)
0.3	(0.7, 0.5, 0.6, 0.8, 0.8, 0.7, 0.6, 0.5)	meta-PCA	35.14(2.99)	6(0)	494(0)	0.01(0)
		meta-SPCA	4.72(1.19)	6(0)	2(1)	1(0)
		pooled-SPCA	13.93(6.69)	6(0)	5(4)	0.99(0.01)
		iSPCA	3.53(0.89)	6(0)	0(0)	0.99(0.01)
		iSPCAM	1.21(0.25)	6(0)	6(2)	0.99(0.01)
		iSPCAS	3.51(0.87)	6(0)	4.3(2.3)	0.99(0.01)
0.5	(0.6, 0.6, 1, 1.5, 0.8, 0.8, 1, 1.5)	meta-PCA	2.41(0.21)	22(0)	478(0)	0.06(0)
		meta-SPCA	5.54(1)	22(0)	8.1(2.6)	0.98(0.01)
		pooled-SPCA	76.4(6.26)	15(7)	107(89)	0.77(0.16)
		iSPCA	3.88(0.62)	22(0)	0(0)	1(0)
		iSPCAM	0.62(0.11)	22(0)	4.3(1.9)	0.99(0)
		iSPCAS	3.88(0.62)	22(0)	2.5(1.3)	0.99(0)
0.8	(0.9, 0.9, 1.5, 1.5, 1, 1, 1.2, 1.2)	meta-PCA	6.11(0.61)	144(0)	356(0)	0.3(0)
		meta-SPCA	6.15(0.72)	144(0)	32.2(6.8)	0.94(0.01)
		pooled-SPCA	60.48(12.79)	136(8)	266(44.5)	0.42(0.1)
		iSPCA	4.83(0.47)	144(0)	6.5(1.5)	0.99(0)
		iSPCAM	1.18(0.08)	144(0)	1.8(1)	1(0)
		iSPCAS	4.83(0.47)	144(0)	1.6(0.9)	1(0)
0.3	(0.5, 0.2, 0.5, 0.5, 0.2, 0.4, 0.2, 0.4)	meta-PCA	56.44(4.61)	6(0)	494(0)	0.01(0)
		meta-SPCA	39.38(3.04)	3.9(0.1)	6.6(3.4)	0.98(0.01)
		pooled-SPCA	33.44(15.86)	6(0)	7(7)	0.98(0.01)
		iSPCA	11.32(2.89)	6(0)	9.6(4.1)	0.98(0.01)
		iSPCAM	3.79(0.72)	6(0)	9.1(2)	0.98(0.01)
		iSPCAS	11.04(2.94)	6(0)	8.4(2)	0.98(0.01)
0.5	(0.4, 0.6, 0.6, 0.7, 0.4, 0.7, 0.4, 0.7)	meta-PCA	27.1(2.38)	22(0)	478(0)	0.05(0)
		meta-SPCA	21.22(3.78)	21.1(0.8)	23.4(4.7)	0.94(0.02)
		pooled-SPCA	80.77(3.7)	13(8)	214.5(168)	0.54(0.34)
		iSPCA	10.92(1.55)	22(0)	11.3(2)	0.98(0.01)
		iSPCAM	4.11(0.46)	22(0)	6.8(1.9)	0.98(0.01)
		iSPCAS	10.88(1.57)	22(0)	8(2)	0.98(0.01)
0.8	(0.7, 0.9, 0.9, 1, 0.7, 1, 0.7, 1)	meta-PCA	11.48(1.01)	144(0)	356(0)	0.29(0)
		meta-SPCA	15.15(1.88)	143.6(0.4)	73.6(8.3)	0.85(0.02)
		pooled-SPCA	64.2(8.03)	132.5(11.5)	279(75.5)	0.37(0.11)
		iSPCA	10.55(1.15)	144(0)	7.8(2.1)	0.98(0)
		iSPCAM	4.02(0.29)	144(0)	2.6(1.1)	0.99(0)
		iSPCAS24	10.55(1.15)	144(0)	7.4(2)	0.99(0)

Table 6.

Simulation results for Scenario 2 (M=8). In each cell, mean(MAD).

β	α	Method	Angle	TP	FP	Sign
0.3	(0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5)	meta-PCA	44.94(3.54)	6(0)	494(0)	0.01(0)
		meta-SPCA	10.39(1.81)	5(0)	8.1(2.1)	0.98(0.01)
		pooled-SPCA	53.01(9.28)	4(1)	12(7)	0.97(0.02)
		iSPCA	5.96(1.39)	6(0)	12(2.8)	0.97(0.01)
		iSPCAM	5.93(1.36)	6(0)	12(2.9)	0.97(0.01)
		iSPCAS	5.65(1.36)	6(0)	8.5(2.6)	0.98(0.01)
0.5	(0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6)	meta-PCA	35.91(2.09)	22(0)	478(0)	0.04(0)
		meta-SPCA	13.48(1.77)	16.1(1)	22.2(3.8)	0.94(0.01)
		pooled-SPCA	55.4(4.82)	14(2)	45(23)	0.89(0.05)
		iSPCA	9.13(1.27)	22(0)	12.1(2.4)	0.97(0.01)
		iSPCAM	9.09(1.24)	22(0)	12(2.4)	0.97(0.01)
		iSPCAS	8.8(1.21)	22(0)	6.3(1.9)	0.99(0)
0.8	(1, 1, 1, 1, 1, 1, 1, 1)	meta-PCA	11.55(1.13)	144(0)	356(0)	0.28(0)
		meta-SPCA	8.08(0.83)	123.4(2.2)	83.8(6.6)	0.79(0.02)
		pooled-SPCA	49.7(2.3)	143(1)	353(3)	0.28(0.01)
		iSPCA	6.7(0.66)	144(0)	7.1(2.1)	0.97(0.01)
		iSPCAM	6.69(0.67)	144(0)	7.1(2.1)	0.97(0.01)
		iSPCAS	6.56(0.66)	144(0)	1.1(0.9)	1(0)
0.3	(0.7, 0.5, 0.6, 0.8, 0.8, 0.7, 0.6, 0.5)	meta-PCA	35.14(2.99)	6(0)	494(0)	0.01(0)
		meta-SPCA	6.88(1.16)	5.3(0)	9.6(2.8)	0.98(0.01)
		pooled-SPCA	46.97(8.36)	5(0)	20.5(13)	0.96(0.02)
		iSPCA	3.71(0.85)	6(0)	10.8(2.4)	0.98(0.01)
		iSPCAM	3.69(0.82)	6(0)	10.7(2.3)	0.98(0.01)
		iSPCAS	3.59(0.84)	6(0)	6.5(2.1)	0.98(0.01)
0.5	(0.6, 0.6, 1, 1.5, 0.8, 0.8, 1, 1.5)	meta-PCA	2.41(0.21)	22(0)	478(0)	0.05(0.01)
		meta-SPCA	6.21(0.74)	19.1(0.7)	26.8(3.6)	0.94(0.01)
		pooled-SPCA	72.4(6.8)	10(3)	40.5(35.5)	0.89(0.06)
		iSPCA	4.13(0.62)	22(0)	9.4(2)	0.98(0.01)
		iSPCAM	4.13(0.59)	22(0)	9.4(2)	0.98(0.01)
		iSPCAS	4(0.57)	22(0)	2.9(1.1)	0.99(0)
0.8	(0.9, 0.9, 1.5, 1.5, 1, 1, 1.2, 1.2)	meta-PCA	6.11(0.61)	144(0)	356(0)	0.29(0)
		meta-SPCA	6.21(0.63)	127.6(1.8)	87.6(6.3)	0.79(0.01)
		pooled-SPCA	63.95(8.2)	108.5(14)	181(27)	0.54(0.06)
		iSPCA	5.15(0.48)	144(0)	6.3(1.6)	0.97(0)
		iSPCAM	5.14(0.48)	144(0)	6.3(1.6)	0.97(0)
		iSPCAS	5.03(0.48)	143.8(0.3)	0.8(0.5)	1(0)
0.3	(0.5, 0.2, 0.5, 0.5, 0.2, 0.4, 0.2, 0.4)	meta-PCA	56.44(4.61)	6(0)	494(0)	0.01(0)
		meta-SPCA	31.68(8.3)	3.5(0.6)	9(3.1)	0.97(0.01)
		pooled-SPCA	51.05(8.19)	4(1)	14(10)	0.97(0.02)
		iSPCA	11.98(3.11)	6(0)	12.7(2.9)	0.97(0.01)
		iSPCAM	11.69(2.76)	6(0)	12.8(2.7)	0.97(0.01)
		iSPCAS	11.31(3.09)	6(0)	9(2.1)	0.98(0.01)
0.5	(0.4, 0.6, 0.6, 0.7, 0.4, 0.7, 0.4, 0.7)	meta-PCA	27.1(2.38)	22(0)	478(0)	0.04(0)
		meta-SPCA	17.98(2.47)	15.4(1.1)	21.9(4.1)	0.94(0.01)
		pooled-SPCA	80.19(5.2)	10.5(4.5)	123.5(114)	0.74(0.21)
		iSPCA	11.61(1.71)	22(0)	11.9(1.9)	0.97(0.01)
		iSPCAM	11.34(1.65)	22(0)	11.8(1.6)	0.97(0.01)
		iSPCAS	11.06(1.53)	22(0)	7(1.6)	0.98(0.01)
0.8	(0.7, 0.9, 0.9, 1, 0.7, 1, 0.7, 1)	meta-PCA	11.48(1.01)	144(0)	356(0)	0.27(0)
		meta-SPCA	13.47(1.48)	116.1(3.3)	84.1(7.3)	0.77(0.02)
		pooled-SPCA	70.1(6.74)	95(28.5)	171.5(55)	0.55(0.05)
		iSPCA	11.08(1.08)	144(0)	8.4(1.9)	0.96(0.01)
		iSPCAM	10.94(1.04)	144(0)	8.4(1.9)	0.97(0.01)
		iSPCAS25	10.7(1.03)	144(0)	2.9(1)	0.99(0)

Table 7.

Simulation results for Scenario 3 (M=8). In each cell, mean (MAD).

β	α	Method	Angle	TP	FP	Sign
0.4	(0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5)	meta-PCA	44.94(3.54)	12(0)	488(0)	0.03(0)
		meta-SPCA	18.27(2.88)	12(0)	37.8(6.4)	0.92(0.01)
		pooled-SPCA	78.3(4.92)	11.1(0.9)	5.8(3)	0.5(0.48)
		iSPCA	11.27(1.56)	12(0)	18.9(2)	0.96(0)
		iSPCAM	10.73(1.65)	12(0)	18.8(2.1)	0.96(0)
		iSPCAS	10.14(1.6)	12(0)	11.9(1.6)	0.98(0)
0.5	(0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6, 0.6)	meta-PCA	35.91(2.09)	22(0)	478(0)	0.05(0)
		meta-SPCA	16.55(1.98)	22(0)	40.4(3.9)	0.92(0.01)
		pooled-SPCA	71.58(2.28)	22(0)	13.2(11)	0.04(0)
		iSPCA	11.69(1.32)	22(0)	25.1(2.8)	0.95(0.01)
		iSPCAM	11.2(1.41)	22(0)	25.1(2.9)	0.95(0.01)
		iSPCAS	10.53(1.26)	22(0)	17.6(1.5)	0.96(0)
0.8	(1, 1, 1, 1, 1, 1, 1, 1)	meta-PCA	11.55(1.13)	144(0)	356(0)	0.29(0)
		meta-SPCA	8.9(0.96)	144(0)	136(6.2)	0.73(0.01)
		pooled-SPCA	63.17(1.04)	144(0)	349.9(2.1)	0.03(0.01)
		iSPCA	8.65(0.77)	144(0)	102.8(1.9)	0.79(0)
		iSPCAM	8.33(0.84)	144(0)	102.9(1.9)	0.79(0)
		iSPCAS	7.8(0.68)	144(0)	89.2(2.1)	0.82(0)
0.4	(0.7, 0.5, 0.6, 0.8, 0.8, 0.7, 0.6, 0.5)	meta-PCA	44.81(3.16)	12(0)	488(0)	0.03(0)
		meta-SPCA	11.18(1.88)	12(0)	34(12)	0.93(0.02)
		pooled-SPCA	62.89(1.72)	11.1(0)	121.2(26.4)	0.76(0.05)
		iSPCA	7.46(1.22)	12(0)	18.3(2)	0.96(0)
		iSPCAM	7.37(1.17)	12(0)	18.2(1.9)	0.96(0)
		iSPCAS	6.66(1.24)	12(0)	10.4(1.1)	0.98(0)
0.5	(0.6, 0.6, 1, 1.5, 0.8, 0.8, 1, 1.5)	meta-PCA	2.41(0.21)	22(0)	478(0)	0.06(0)
		meta-SPCA	7.29(1.05)	21.9(0.1)	38.8(4)	0.92(0.01)
		pooled-SPCA	77.52(3.71)	15.4(4.8)	127.9(85.6)	0.72(0.16)
		iSPCA	6.07(0.77)	22(0)	23.4(1.9)	0.95(0)
		iSPCAM	6.07(0.77)	22(0)	23.4(1.9)	0.95(0)
		iSPCAS	5.66(0.76)	22(0)	13.4(1)	0.97(0)
0.8	(0.9, 0.9, 1.5, 1.5, 1, 1, 1.2, 1.2)	meta-PCA	6.11(0.61)	144(0)	356(0)	0.3(0)
		meta-SPCA	6.83(0.73)	144(0)	134.4(6.1)	0.73(0.01)
		pooled-SPCA	70.51(3.22)	143(1)	342.1(2.5)	0.27(0.03)
		iSPCA	7.04(0.76)	144(0)	101.1(1.9)	0.8(0)
		iSPCAM	7.07(0.75)	144(0)	101.2(1.8)	0.8(0)
		iSPCAS	6.5(0.71)	144(0)	78.6(2.8)	0.84(0.01)
0.4	(0.5, 0.3, 0.5, 0.5, 0.3, 0.4, 0.3, 0.6)	meta-PCA	35.24(3.02)	12(0)	488(0)	0.02(0)
		meta-SPCA	25.71(3.29)	9.3(0.9)	15.9(3.8)	0.96(0.01)
		pooled-SPCA	77.28(4.08)	7.1(4)	1.9(1)	0.98(0.01)
		iSPCA	17.44(2.89)	12(0)	18(2.4)	0.96(0.01)
		iSPCAM	16.86(2.92)	12(0)	18(2.9)	0.96(0.01)
		iSPCAS	15.72(2.85)	12(0)	13.2(2)	0.97(0)
0.5	(0.4, 0.6, 0.6, 0.7, 0.4, 0.7, 0.4, 0.7)	meta-PCA	27.1(2.38)	22(0)	478(0)	0.04(0)
		meta-SPCA	21.18(2.56)	19.2(0.8)	39.9(3.9)	0.91(0.01)
		pooled-SPCA	80.1(2.58)	12.3(4.1)	126.2(62.9)	0.72(0.12)
		iSPCA	16.07(2.48)	22(0)	25.9(1.9)	0.94(0.01)
		iSPCAM	15.72(2.32)	22(0)	26.1(2.1)	0.94(0.01)
		iSPCAS	14.68(2.34)	22(0)	18.4(1.8)	0.96(0.01)
0.8	(0.7, 0.9, 0.9, 1, 0.7, 1, 0.7, 1)	meta-PCA	11.48(1.01)	144(0)	356(0)	0.29(0)
		meta-SPCA	15.06(1.56)	139.4(1.8)	136.8(6.5)	0.71(0.02)
		pooled-SPCA	71.7(2.15)	135.3(8.8)	316.3(39.7)	0.27(0.07)
		iSPCA	15.43(1.65)	144(0)	102.4(1.1)	0.79(0)
		iSPCAM	15.24(1.67)	144(0)	102.4(1.3)	0.79(0)
		iSPCAS26	14.08(1.56)	144(0)	87.9(2.8)	0.82(0.01)

Figure 1.

ROC curves for Scenario 1 (M=4). meta-PCA: purple; meta-SPCA: blue; pooled-SPCA: pink; iSPCA: red; iSPCA_M: orange; iSPCA_S: green.

Figure 2.

ROC curves for Scenario 2 (M=4). meta-PCA: purple; meta-SPCA: blue; pooled-SPCA: pink; iSPCA: red; iSPCA_M: orange; iSPCA_S: green.

Figure 3.

ROC curves for Scenario 3 (M=4). meta-PCA: purple; meta-SPCA: blue; pooled-SPCA: pink; iSPCA: red; iSPCA_M: orange; iSPCA_S: green.

Figure 4.

ROC curves for Scenario 1 (M=8). meta-PCA: purple; meta-SPCA: blue; pooled-SPCA: pink; iSPCA: red; iSPCA_M: orange; iSPCA_S: green.

Figure 5.

ROC curves for Scenario 2 (M=8). meta-PCA: purple; meta-SPCA: blue; pooled-SPCA: pink; iSPCA: red; iSPCA_M: orange; iSPCA_S: green.

Figure 6.

ROC curves for Scenario 3 (M=8). meta-PCA: purple; meta-SPCA: blue; pooled-SPCA: pink; iSPCA: red; iSPCA_M: orange; iSPCA_S: green.

Table 8.

Analysis of breast cancer data: top 20 genes with the largest norms of loadings under integrative analysis.

Rank	iSPCA	iSPCAM	iSPCAS
1	IGLV1-44	IGLV1-44	IGLV1-44
2	IGLC1	IGLC1	IGLC1
3	IGHA1	IGHA1	IGHA1
4	IGHG1	IGHG1	IGHG1
5	CSN1S1	IGLL5	CSN1S1
6	IGLL5	CTA-246H3.1	IGLL5
7	CTA-246H3.1	CSN1S1	CTA-246H3.1
8	PIP	PIP	PIP
9	IGKC	IGKC	IGKC
10	IGKC	IGKC	IGKC
11	CSN3	CSN3	CSN3
12	SCGB2A2	SCGB2A2	SCGB2A2
13	IGKC	IGKC	IGKC
14	LOC651629	LOC651629	LOC651629
15	IGKV1D-13	IGKV1D-13	IGKV1D-13
16	LOC391427	APOD	LOC391427
17	APOD	LOC391427	APOD
18	IGLC1	IGLC1	IGLC1
19	LALBA	LALBA	LALBA
20	ATF3	ATF3	ATF3

Table 9.

Analysis of pancreatic cancer data: top 20 genes with the largest norms of loadings under integrative analysis.

Rank	iSPCA	iSPCAM	iSPCAS
1	AMY2B	AMY2B	AMY2B
2	PNLIP	PNLIP	PNLIP
3	CTRB2	CTRB2	CTRB2
4	CELA2A	CELA2A	CELA2A
5	PRSS1	CPA1	PRSS1
6	CPA1	PRSS1	CPA1
7	PLA2G1B	PLA2G1B	PLA2G1B
8	CPB1	CPB1	CPB1
9	CTRC	CTRC	CTRC
10	PRSS1	PRSS1	PRSS1
11	PRSS2	PRSS2	PRSS2
12	CTRB2	CTRB2	CTRB2
13	CLPS	CLPS	CLPS
14	REG1A	REG1A	REG1A
15	CELA2B	CELA2B	CELA2B
16	CEL	CEL	CEL
17	CELA3A	CELA3A	CELA3A
18	CELA3A	CELA3A	CELA3A
19	CPA2	CPA2	CPA2
20	PNLIPRP2	PNLIPRP2	PNLIPRP2