Preference option randomized design (PORD) for comparative effectiveness research: Statistical power for testing comparative effect, preference effect, selection effect, intent-to-treat effect, and overall effect

Abstract

Comparative effectiveness research trials in real-world settings may require participants to choose between preferred intervention options. A randomized clinical trial with parallel experimental and control arms is straightforward and regarded as a gold standard design, but by design it forces and anticipates the participants to comply with a randomly assigned intervention regardless of their preference. Therefore, the randomized clinical trial may impose impractical limitations when planning comparative effectiveness research trials. To accommodate participants’ preference if they are expressed, and to maintain randomization, we propose an alternative design that allows participants’ preference after randomization, which we call a “preference option randomized design (PORD)”. In contrast to other preference designs, which ask whether or not participants consent to the assigned intervention after randomization, the crucial feature of preference option randomized design is its unique informed consent process before randomization. Specifically, the preference option randomized design consent process informs participants that they can opt out and switch to the other intervention only if after randomization they actively express the desire to do so. Participants who do not independently express explicit alternate preference or assent to the randomly assigned intervention are considered to not have an alternate preference. In sum, preference option randomized design intends to maximize retention, minimize possibility of forced assignment for any participants, and to maintain randomization by allowing participants with no or equal preference to represent random assignments. This design scheme enables to define five effects that are interconnected with each other through common design parameters—comparative, preference, selection, intent-to-treat, and overall/as-treated—to collectively guide decision making between interventions. Statistical power functions for testing all these effects are derived, and simulations verified the validity of the power functions under normal and binomial distributions.

1. Introduction

Translation to practice phase 3 translational, or T3, research is often conducted as comparative effectiveness research (CER) in real-world settings.^1,2 CER studies usually involve treatments or interventions with proven efficacy in controlled research settings³ for which double-blind parallel-group randomized designs are a gold standard experimental design for establishing treatment efficacy. However, it may be difficult to carry out such rigorous controlled designs in real-world settings, where treatments are often unmasked and participants have strong preferences.^4,5 The traditional parallel randomized design forces a randomly assigned intervention regardless of participants’ preference, and anticipates that the participants will comply with the assigned intervention. Therefore, this design may impose impractical limitations when planning CER trials where such compliance may not be realistic. Herein, we consider CER trial designs that primarily aims to test two interventions, denoted in general by A and B. Two examples of such CER trials that compare two efficacious interventions for delivering a medicine or a program in real-world settings are described. In these examples, the effectiveness of the medicine or program on clinical outcome depends on successful delivery for patients’ intake or uptake, thus accommodation of patient preference may be important.

One example is a CER trial that aims to test the effectiveness of two delivery models of a very powerful medication for treating hepatitis C virus (HCV) infection with >90% sustained viral response (SVR) rate.⁶ The treatment requires a three-month daily regimen to result in SVR, making patient adherence a critical issue.⁷ To this end, directly observed therapy (DOT)⁸ has been shown effective to both increase adherence to antiviral medications and improve viral outcomes in HIV-infected patients receiving medicines at a clinic.^9,10 It is often very challenging to administer a classic DOT at a clinic in real-world settings where HCV medications may be taken multiple times each day, and when patients do not attend the clinic daily. Therefore, DOT has often been modified (mDOT) with a less intensive mode to meet such challenges.¹¹ Another alternative way of delivering and monitoring the intake of the medicine to increase adherence is utilization of patient navigators (PN) who coordinate treatments, assist the participants to overcome logistical barriers, and provide health education and psychosocial support.¹² To compare effectiveness of mDOT vs. PN on the SVR endpoint outcome, the CER may need to allow participants to choose their preferred delivery method.

Another example is a CER trial evaluating different ways to deliver the Diabetes Prevention Program (DPP). DPP has been shown to be effective in reducing the incidence of diabetes among high-risk individuals; when compared to placebo and metformin, the intensive lifestyle modification intervention reduced the incidence by 58% and 39%, respectively.¹³ The DPP trial informed the creation of the National DPP program, implemented by the Centers for Disease Control and Prevention (CDC). The CDC’s National DPP includes a 16-week core curriculum with follow-up maintenance classes thereafter. Evaluation criteria include reporting of attendance and reporting of physical activity, and weight loss (https://www.cdc.gov/diabetes/prevention/pdf/dprp-standards.pdf). Maintaining recognition from the CDC requires that programs observe an average weight loss greater than 5%. DPP has been implemented in community, faith-based, workplace and healthcare-settings.^14,15 Similar to the DOT case, it is challenging for many participants to attend enough sessions to successfully reduce their body weight and subsequent risk of developing diabetes.¹⁶ There are a number of virtual DPP (vDPP) apps, implemented either online using a desktop computer or with a smart-phone based app¹⁷ that may help increase engagement. Therefore, allowing participants’ preference, a CER trial might want to compare the effectiveness of DDP vs. vDPP on attendance, weight change, and downstream outcomes such as glycated hemoglobin (HbA1C) reduction.

There have been a variety of designs that accommodate participants’ preference.^18–20 For example, the Zelen’s double consent randomized trial design^21,22 involves two stages to accommodate preference. First, it randomizes participants, and then it seeks participants’ consent to preferred or randomly assigned treatments by asking whether or not participants consent to the assigned intervention. If they do not, the design allows them to switch treatment. For this reason, Zelen’s design might raise ethical concerns because participants are not informed of treatments before randomization.²³ Apart from this concern, we suspect that it is likely that inquiring directly about preference after randomization might cause unintended crossover perhaps influenced by the query itself.

Wennberg et al.’s²⁴ or Rucker’s²⁵ preference clinical trial design, on the other hand, also involves two or more stages but it seeks consent before initial randomization. First, consented participants are randomly assigned to a randomization arm or a choice arm. Then, participants assigned to the randomization arm will be randomly assigned to a treatment whereas those assigned to the choice arm will either choose their preferred treatment or, if they have no preference, further be randomized. Although this type of design has been widely implemented in diverse research areas,^20,26 the participants in the randomization arm should comply with the randomly assigned treatments and, are neither queried as to nor allowed to switch over to their preferred treatments. In addition, variations of the two-stage designs such as fully or partially randomized preference design have also been adopted.^20,27

To the best of our knowledge, however, there is no design which can collectively encompass all desirable features that we believe are pertinent to the CER paradigm that: (1) minimize forced assignment and influenced switch; (2) maintain and compare randomized groups; (3) administer single randomization; (4) accommodate preference; (5) and thus maximize retention, adherence or compliance. To this end, building upon existing preference designs,^20,28 we propose a novel simpler study design, referred to herein as the “preference option randomized design” (PORD), which allows participants to switch to their preferred interventions only if they actively express preference after randomization. PORD design components including that process are introduced in Section 2. Under this design, the following diverse effects that are inter-connected through common design parameters can be defined, estimated, and tested: comparative effect; preference effect; selection effect; intent-to-treat (ITT) effect; overall/as-treated (AT) effect. Definitions of all of these effects are detailed in Section 3, and their sample estimates are derived in Section 4. Statistical power function for testing each effect is derived and verified by simulation examinations in Section 5. Followed is discussion in Section 6.

2. PORD design components

2.1. Study population

We do not attempt to make any inferences about the population that would not participate in trials even though strong preferences, expressed or not, for certain interventions might be present among this group. We do, however, attempt to make inferences about the population who would participate in trials that meet their needs and accommodate their preferences with appropriate interventions. We assume there are three mutually exclusive and exhaustive classes of participants in this population. They are participants who: (1) prefer and choose intervention A whichever intervention is assigned; (2) prefer and choose intervention B whichever intervention is assigned; or (3) prefer A or B equally or with no particular preference by taking whichever intervention is assigned. All of these three classes are assumed to have a sizable number of participants.

2.2. Informed consent process

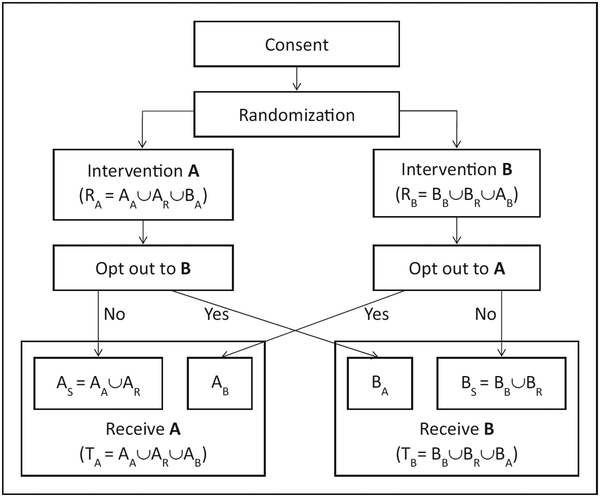
A key component of a PORD is its informing participants about their preference options during the consent process prior to randomization (Figure 1). As usual during a consent process, intervention properties are fully explained to the participants. However, the unique features of the PORD consent process are that participants will be informed and instructed that: (1) they will have the opportunity to express their intervention preference after randomization. Participants will be informed to clearly express their preference after randomization only if their randomly assigned intervention is not their preferred intervention; and (2) if they do not express an intervention preference after randomization they will be assumed to accept randomization.

Figure 1.

Illustration diagram of preference option randomized design.

Participants will not be asked about their preferred interventions. Rather, they will have to volunteer their preferences independently. This feature intends to prevent participants from influenced or unintended crossover if they are prompted to consider their preference when asked post-randomization. It also intends to avoid participant forced assignment and to keep participants who would refuse to take a randomly assigned intervention from dropping out because it is not their preferred intervention. To ensure that a participant fully understands the contents and intents of the interventions, the random assignment and the opt-out process, research staff may ask the participant to explain back those crucial elements. In sum, all of these instructions during the PORD informed consent process are intended to maximize retention, minimize possibility of forced assignment or to influence a switch among participants with no preference who otherwise represent those who comply with random assignment.

2.3. Randomization

Once it is clear that participants fully understand the interventions and the preference- or choice-based opt-out process, they will be randomly assigned. There will be only a single randomization process (Figure 1). The specific randomization strategy depends on the study settings. For example, unbalanced allocations might occur due to potentially non-symmetric preferences and might require implementation of adaptive randomization such as urn randomization.²⁹ Discussion of various strategies is nevertheless beyond the scope of the present study.

2.4. Opt-out process

PORD will allow a participant to cross over to his/her preferred intervention only when the participant actively expresses the preference after randomization (Figure 1), as informed during the consent process. The length of time interval between randomization and opt-out based on choice should be flexible depending on the nature of interventions, study settings, resources, and characteristics of target populations. Especially when the time interval is relatively long, a reminder of the opt-out process might minimize possibility of participant crossing over later during the study period.

2.5. Participant compositions

We denote by A_S (a group or set of) participants who tacitly opt in to stay in intervention arm A when A is assigned. The components of A_S are those (A_A) for whom A is their preference, and those (A_R) who have no or equal preference but would be willing to comply with the assigned intervention A, that is, A_S = A_A∪A_R. We further denote by A_B participants who actively switch to A from B. Therefore, the combination of A_A and A_B represents participants who prefer A. In a similar fashion, when B is assigned, we denote by B_S (a group or set of) participants who tacitly opt in to stay in intervention arm B_S. The components of B_S are those (B_B) for whom B is their preference, and those (B_R) who have no or equal preference but would be willing to comply with the assigned intervention B, that is, B_S = B_B∪B_R. Group B_A represents participants who actively switch to B from A. Therefore, the combination of B_B and B_A represents participants who prefer B. Collectively, we denote by R_A and R_B participants who are randomly assigned to interventions A and B, respectively, that is, R_A=A_A∪A_R∪B_A and R_B=B_B∪B_R∪A_B. We also denote by T_A and T_B participants who are treated with interventions A and B, respectively, that is, T_A=A_A∪A_R∪A_B and T_B=B_B∪B_R∪B_A. All these participant compositions are presented in Figure 1.

2.6. Identifiability of groups

When a PORD study is completed, although both A_s and B_s are identifiable by design, their components are unidentifiable. First, both A_R and B_R are unidentifiable but will represent participants who are randomly assigned interventions A and B, respectively with no or equal preference. Likewise, both A_A and B_B are unidentifiable but will represent participants who prefer the randomly assigned interventions A and B, respectively. All the other groups—A_B, B_A, R_A, R_B, T_A, and T_B—are identifiable by design.

2.7. Study outcome distribution

The outcome variable for the ith participant will be denoted by Y_i, distributions of which we herein consider independent normal or binomial/Bernoulli. However, distributions of Y_i can be flexible as long as a large sample theory could be applied for constructing asymptotically normally distributed test statistics such as a Wald test that we adopted below.

2.8. Group size

n(Ω) will denote the group or sample size of participants in set Ω, i.e. n(Ω)=#{i|Y_i∈Ω}.

2.9. Assumptions

2.9.1. Assumption 1 (A1)

We assume exclusion restriction (ER)³⁰ that the expected outcomes to be the same between those who actively cross over or opt out to an intervention arm of their preferences and those who stay in the randomly assigned intervention arm because the assigned intervention is their preference. That is

$$E(Y|A_A)=E(Y|A_B)\text{and}E(Y|B_B)=E(Y|B_A)$$

2.9.2. Assumption 2 (A2)

We also assume no selection bias from randomization (NSBR)¹⁹ that preference rate of a intervention in a stay group will be equal to that of the intervention in the other randomly intervention assigned arm, that is

$$P(A_A|A_s)=P(A_B|R_B)\text{and}P(B_B|B_S)=P(B_A|R_A)$$

And thus accordingly

$$P(A_R|A_s)=1-P(A_B|R_B)\text{and}P(B_R|B_S)=1-P(B_A|R_A)$$

2.9.3. Assumption 3 (A3)

We assume equal variances (EVs), that is, variance of Y does not depend on any subgroups Ω, i.e. Var(Y |Ω=Var(Y)=σ² for all Ω For normal distributions, a residual variance or a pooled within-group variance may serve as an equal σ². However, this assumption does not hold for a non-normal outcome Y whose variance depends on its expectation. Nevertheless, for a binary outcome, an EV could be estimated based on average of hypothesized probabilities of all groups. This approach is applied for simulation studies below.

3. Definitions of effects

3.1. Comparative effect

Let us first denote: ξ_A=E(Y|A_R) and ξ_B=E(Y|B_R), representing outcome expectations among participants with no or equal preferences to randomly assigned interventions. Then, the comparative effect ξ can be defined as

$$\xi ={\xi }_A-{\xi }_B$$

This effect represents the difference in expectations of outcome Y between participants who were randomly assigned to A or B. Therefore, this effect is equivalent to a potential effect that could be obtained from a parallel randomized clinical trial (RCT). For this reason, the randomization features in RCTs can be preserved in a PORD study.

Nonetheless, both ξ_A and ξ_B are unidentifiable because both the corresponding sets of participants A_R and B_R are unidentifiable by design. Owing to the ER (A1) and NSBR (A2) assumptions, however, both ξ_A and ξ_B can be derived from identifiable expectations such as E(Y|A_S) and E(Y|A_B). First, note that

$$E(Y|A_S)=E(Y|A_A)P(A_A|A_S)+E(Y|A_R)P(A_R|A_S)$$ (1)

$$=E(Y|A_B)P(A_A|A_S)+E(Y|A_R)P(A_R|A_S)$$ (2)

$$=E(Y|A_B)P(A_B|R_B)+E(Y|A_R)(1-P(A_B|R_B))$$ (3)

Equation (1) holds due to a law of total expectation; the second equation (2) due to the ER (A1) assumption; and the last (3) due to the NSBR (A2) assumption. Therefore, the unidentifiable ξ_A=E(Y|A_R) can be estimated as

$${\xi }_A=(E(Y|A_S)-E(Y|A_B)P(A_B|R_B))/(1-P(A_B|R_B))$$

Likewise, ξ_B=E(Y|B_R) can be estimated in a similar fashion as

$${\xi }_B=(E(Y|B_S)-E(Y|B_A)P(B_A|R_A))/(1-P(B_A|R_A))$$

3.2. Preference effect

Extending the notions of the preference effect proposed by Turner et al.,²⁸ we define the preference effect λ as

$$\text{λ}\text{=}\text{(}{w}_A{\text{λ}}_A+w_B{\text{λ}}_B\text{)}/(w_A+w_B)$$

where λ_A=E(Y|A_A∪A_B)–E(Y|A_R) and λ_B=E(Y|B_B∪B_A)–E(Y|B_R), and w′s are the inverses of the variances of the corresponding estimates. λ_A and λ_B represent the effects of active preference to interventions A and B over equal or no preference, respectively, and λ is a weighted average of λ_A and λ_B representing an overall preference effect. We note that since P(A_A∩A_B)=0 and it is assumed that E(Y|A_A)=E(Y|A_B), it is immediate that E(Y|A_A∩A_B)=E(Y|A_B) and E(Y|B_B∪B_A)=E(Y|B_A). Thus, λ_A and λ_A can be reduced to: λ_A=E(Y|A_B)–ξ_A and λ_B=E(Y|B_A)–ξ_B.

3.3. Selection effect

A selection effect ς can be defined as

$$\varsigma =(w_A{\text{λ}}_A-w_B{\text{λ}}_B)/(w_A+w_B)$$

This quantity represents the effect of selecting intervention A over intervention B. That is, it quantifies the extent of benefit or harm for participants who prefer A over those who prefer B when compared to their respective counterparts with no or equal preference.

3.4. ITT effect

Participants randomly assigned to interventions A and B were intended to be treated with the assigned interventions. Therefore, ITT effect can be defined as

$$\eta ={\eta }_A-{\eta }_B$$

where η_A=E(Y|R_A) and η_B=E(Y|R_B). These expectations can be derived as follows

$$E(Y|R_A)=E(Y|A_s)P(A_S|R_A)+E(Y|B_A)(1-P(A_S|R_A))$$

and

$$E(Y|R_B)=E(Y|B_s)P(B_S|R_B)+E(Y|A_B)(1-P(B_S|R_B))$$

3.5. Overall/As-treated (AT) effect

Overall intervention effect τ is defined as difference in outcome expectations between those who are actually treated with A and B. Thus, it is the same as “as-treated” effect and can be quantified as

$$\tau ={\tau }_A-{\tau }_B$$

Where τ_A=E(Y|T_A) and τ_B=E(Y|T_B). These expectations can be derived as follows.

$$E(Y|T_A)=E(Y|A_S)P(A_S|T_A)+E(Y|A_B)(1-P(A_S|T_A))$$

and

$$E(Y|T_B)=E(Y|B_S)P(B_S|T_B)+E(Y|B_A)(1-P(B_S|T_B))$$

where

$$P(A_S|T_A)=\frac{n(R_A)P(A_S|R_A)}{n(R_A)P(A_S|R_A)+n(R_B)P(A_B|R_B)}$$

and

$$P(B_S|T_B)=\frac{n(R_B)P(B_S|R_B)}{n(R_B)P(B_S|R_B)+n(R_A)P(B_A|R_A)}$$

4. Sample estimates

In what follows, sample estimates are in general denoted by $\tilde{E}$ or $\tilde{P}$, in the form of $\tilde{E}(Y|\Omega )={\displaystyle {\sum }_{i\in \Omega }{Y}_i/n(\Omega )}$ and $\tilde{P}({\Omega }_1|{\Omega }_2)=n({\Omega }_1)/n({\Omega }_2)$ where Ω₁ ⊂ Ω₂

4.1. Comparative effect estimate

Sample estimates of both unidentifiable ξ_A and ξ_B can be derived as follows. First, observe that

$${\tilde{\xi }}_A=\tilde{E}(Y|A_R)=\frac{\tilde{E}(Y|A_S)-\tilde{E}(Y|A_B)\tilde{P}(A_B|R_B)}{1-\tilde{P}(A_B|R_B)}=\frac{{\displaystyle {\sum }_{i\in A_S}{Y}_i/n(A_S)}-{\displaystyle {\sum }_{i\in A_B}{Y}_i/n(R_B)}}{1-n(A_B)/n(R_B)}=\frac{{\displaystyle {\sum }_{i\in A_S}{Y}_i/n(A_S)}-{\displaystyle {\sum }_{i\in A_B}{Y}_i/n(R_B)}}{n(B_S)/n(R_B)}=\left(n(R_B){\displaystyle {\sum }_{i\in A_S}{Y}_i/n(A_s)}-{\displaystyle {\sum }_{i\in A_B}{Y}_i}\right)/n(B_S)$$

since $\tilde{E}(Y|A_S)={\displaystyle {\sum }_{i\in A_s}{Y}_i/n(A_S)}$, $\tilde{E}(Y|A_B)={\displaystyle {\sum }_{i\in A_B}{Y}_i/n(A_B)}$, $\tilde{P}(A_B|R_B)=n(A_B)/n(R_B)$, and n(R_B) = n(A_B)+n(B_S). It can similarly be shown that

$${\tilde{\xi }}_B=\tilde{E}(Y|B_R)=\left(n(R_A){\displaystyle {\sum }_{i\in B_S}{Y}_i/n(B_s)}-{\displaystyle {\sum }_{i\in B_A}{Y}_i}\right)/n(A_S)$$

It is now straightforward to derive variance estimates based on the EV (A3) assumption as follows

$$Var\left({\tilde{\xi }}_A\right)={\sigma }^2(n(A_B)+n^2(R_B)/n(A_S))/n^2(B_S)$$

and

$$Var\left({\tilde{\xi }}_B\right)={\sigma }^2(n(B_A)+n^2(R_A)/n(B_S))/n^2(A_S)$$

Finally, we have $\tilde{\xi }={\tilde{\xi }}_A-{\tilde{\xi }}_B$ and $Var\left(\tilde{\xi }\right)=Var\left({\tilde{\xi }}_A\right)+Var\left({\tilde{\xi }}_B\right)$.

4.2. Preference effect estimate

First, a sample estimate of E(Y|A_A∪A_B) can be expressed as follows

$$\tilde{E}(Y|A_A\cup A_B)=\frac{{\displaystyle {\sum }_{i\in A_A\cup A_B}{Y}_i}}{n(A_A)+n(A_B)}=\frac{(n(A_S)/n(R_B)+1){\displaystyle {\sum }_{i\in A_B}{Y}_i}}{n(A_B)(n(A_S)/n(R_B)+1)}=\frac{{\displaystyle {\sum }_{i\in A_B}{Y}_i}}{n(A_B)}=\tilde{E}(Y|A_B)$$

since the unidentifiable n(A_A) and ${\displaystyle {\sum }_{i\in A_A\cup A_B}{Y}_i}$ can be estimated as

$$n(A_A)=n(A_S)P(A_A|A_S)=n(A_S)P(A_B|R_B)=n(A_S)n(A_B)/n(R_B)$$

and

$${\displaystyle {\sum }_{i\in A_A\cup A_B}{Y}_i}={\displaystyle {\sum }_{i\in A_B}{Y}_i}+{\displaystyle {\sum }_{i\in A_A}{Y}_i}={\displaystyle {\sum }_{i\in A_B}{Y}_i}+n(A_S){\displaystyle {\sum }_{i\in A_B}{Y}_i}/n(R_B)=(1+n(A_S)/n(R_B)){\displaystyle {\sum }_{i\in A_B}{Y}_i}$$

Similarly, $\tilde{E}(Y|B_B\cup B_A)=\tilde{E}(Y|B_A)={\displaystyle {\sum }_{i\in B_A}{Y}_i/n(B_A)}$. It follows that

$${\tilde{\lambda }}_A\text{=}\tilde{E}(Y|A_A\cup A_B)-\tilde{E}(Y|A_R)=\tilde{E}(Y|A_B)-{\tilde{\xi }}_A=(1/n(A_B)+1/n(B_S)){\displaystyle {\sum }_{i\in A_B}{Y}_i}-n(R_B){\displaystyle {\sum }_{i\in A_S}{Y}_i}/(n(A_S)n(B_S))$$

and

$${\tilde{\lambda }}_B\text{=}\tilde{E}(Y|B_B\cup B_A)-\tilde{E}(Y|B_R)=\tilde{E}(Y|B_A)-{\tilde{\xi }}_B=(1/n(B_A)+1/n(A_S)){\displaystyle {\sum }_{i\in B_A}{Y}_i}-n(R_A){\displaystyle {\sum }_{i\in B_S}{Y}_i}/(n(A_S)n(B_S))$$

And, thus $\tilde{\lambda }=(w_A{\tilde{\lambda }}_A+w_B{\tilde{\lambda }}_B)/(w_A+w_B)$, where $w_A=1/Var({\tilde{\lambda }}_A)$, $w_B=1/Var({\tilde{\lambda }}_B)$, with

$$Var({\tilde{\lambda }}_A)={\sigma }^2\left[n(A_B){\left(\frac{1}{n(A_B)}+\frac{1}{n(B_S)}\right)}^2+\frac{n^2(R_B)}{n(A_S)n^2(B_S)}\right]$$

and

$$Var({\tilde{\lambda }}_B)={\sigma }^2\left[n(B_A){\left(\frac{1}{n(B_A)}+\frac{1}{n(A_S)}\right)}^2+\frac{n^2(R_A)}{n(A_S)n(B_S)}\right]$$

due to the EV (A3) assumption. Finally, we have $Var(\tilde{\lambda })=1/(w_A+w_B)$.

4.3. Selection effect estimate

It is immediate that $\tilde{\varsigma }=(w_A{\tilde{\lambda }}_A-w_B{\tilde{\lambda }}_B)/(w_A+w_B)$, and $Var(\tilde{\varsigma })=Var(\tilde{\lambda })$.

4.4. ITT effect estimate

A sample estimate of the ITT effect can be obtained as follows: $\tilde{\eta }={\tilde{\eta }}_A-{\tilde{\eta }}_B=\tilde{E}(Y|R_A)-\tilde{E}(Y|R_B)={\displaystyle {\sum }_{i\in R_A}{Y}_i/n(R_A)}-{\displaystyle {\sum }_{i\in R_B}{Y}_i/n(R_B)}$, and due to the EV (A3) assumption, $Var(\tilde{\eta })={\sigma }^2(1/n(R_A)+1/n(R_B))$.

4.5. Overall/AT effect

A sample estimate of the overall/AT effect can be obtained as follows: $\tilde{\tau }={\tilde{\tau }}_A-{\tilde{\tau }}_B=\tilde{E}(Y|T_A)-\tilde{E}(Y|T_B)={\displaystyle {\sum }_{i\in T_A}{Y}_i/n(T_A)}-{\displaystyle {\sum }_{i\in T_B}{Y}_i/n(T_B)}$, and due to the EV (A3) assumption, $Var(\tilde{\tau })={\sigma }^2(1/n(T_A)+1/n(T_B))$, where n(T_A) = n(A_S) + n(A_B) and n(T_B) = n(B_S) + n(B_A).

5. Power functions

5.1. Test statistic

Once sample estimates and their variances are derived, a Wald test statistic D_θ for testing H₀: θ=0 vs. H_a: θ ≠ 0, where θ represents any of the five effect parameters, can be constructed as follows

$$D_{\theta }=(\tilde{\theta }-\theta )/\sqrt{\text{Var}(\tilde{\theta })}$$ (4)

5.2. Statistical power

As the distributions of D_θ under both H₀ and H_a are asymptotically normal due to a large sample theory, its statistical power φ_θ with a two-sided significance level α can be expressed as

$${\phi }_{\theta }={\Phi }^{-1}\left(\theta /\sqrt{\text{Var}(\tilde{\theta })}-z_{1-\alpha /2}\right)+{\Phi }^{-1}\left(-\theta /\sqrt{\text{Var}(\tilde{\theta })}-z_{1-\alpha /2}\right)$$ (5)

where Φ⁻¹ is the inverse of the cumulative distribution function Φ of a standard normal variable, and z_1−α/2 = Φ⁻¹ (1 − α/2). However, depending on the sign or direction of θ either term of the right hand side is often negligible for power analysis, and thus the statistical power φ_θ is usually expressed as

$${\phi }_{\theta }={\Phi }^{-1}\left(|\theta |/\sqrt{Var(\tilde{\theta })}-z_{1-\alpha /2}\right)$$

5.3. Required parameters

As all aforementioned effects are inter-connected with each other through the following parameter values, to compute power for cohesively testing the significance of their individual effects, one needs to pre-specify:

• (1)Stay-in (or equivalently opt-out) rates: P(A_S|R_A) (or P(B_A|R_A)=1–P(A_S|R_A)) and P(B_S|R_B) (or P(A_B|R_B)=1–P(B_S|R_B));
• (2)Four outcome expectations: E(Y|A_S), E(Y|B_S), E(Y|A_B), and E(Y|B_A);
• (3)Sample sizes: n(R_A) and n(R_B);
• (4)The variance σ² of Y and a two-sided significance level α.

Once all of these values are specified, the assumption A2 enables one to compute expected sizes of all sets or groups as follows: n(A_S) = (1–P(B_A|R_A))n(R_A), n(A_R)=(1–P(A_B|R_B))n(A_S), n(A_A)=P(A_B|R_B)n(A_S), n(A_B)=P(A_B|R_B)n(R_B), n(T_A)=n(A_S)+n(A_B), n(B_S)=(1 P(A_B|R_B), n(B_R)=(1–P(B_A|R_A))n(B_S), n(B_B)=P(B_A|R_A)n(B_S), n(B_A)=P(B_A|R_A)n(R_A), and n(T_B)=n(B_s)+n(B_A). In addition, magnitudes of all the effects (i.e. comparative effect ξ = ξ_A − ξ_B, preference effect λ = (w_Aλ_A + w_Bλ_B)/(w_A + w_B), selection effect ς = (w_Aλ_A − w_Bλ_B)/(w_A + w_B), ITT effect η = η_A − η_B, and overall/AT effect τ = τ_A − τ_B) and their variances can be derived as shown above in Section 3 and 4.

5.4. Closed-form power functions

When all of those effects and sample sizes are determined, all corresponding power functions can be derived using the effect and variance estimates presented above in Section 4. For instance, with the determined ξ = ξ_A − ξ_B, the statistical power for testing a comparative effect, H₀: ξ = 0 vs. H₀: ξ ≠ 0, can be expressed as

$${\phi }_{\xi }={\Phi }^{-1}\left(|\xi |{\sigma }^{-1}/\sqrt{\frac{n(A_B)+n^2(R_B)/n(A_S)}{n^2(B_S)}+\frac{n(B_A)+n^2(R_A)/n(B_S)}{n^2(A_S)}}-z_{1-\alpha /2}\right)$$

Likewise, for testing a preference effect, H₀: λ=0 vs. H_a: λ≠0, we have

$${\phi }_{\lambda }={\Phi }^{-1}(|\lambda |\sqrt{w_A+w_B}-z_{1-\alpha /2})$$

for testing a selection effect, H₀: ζ = 0 vs. H₀: ζ ≠ 0, we have

$${\phi }_{\varsigma }={\Phi }^{-1}(|\varsigma |\sqrt{w_A+w_B}-z_{1-\alpha /2})$$

for testing a ITT effect, H₀: η = 0 vs. H₀: η ≠ 0, we have

$${\phi }_{\eta }={\Phi }^{-1}\left(|\eta |{\sigma }^{-1}/\sqrt{1/n(R_A)+1/n(R_B)}-z_{1-\alpha /2}\right)$$

and finally for testing an AT/overall effect, H₀: τ = 0 vs. H₀: τ ≠ 0, we have

$${\phi }_{\tau }={\Phi }^{-1}\left(|\tau |{\sigma }^{-1}/\sqrt{\frac{1}{n(A_S)+n(A_B)}+\frac{1}{n(B_S)+n(B_A)}}-z_{1-\alpha /2}\right)$$

5.5. Example for power computation

Investigators who plan to conduct the hepatitis C treatment trial example comparing mDOT (intervention A) and PN (intervention B) in terms of continuous log₁₀ viral load outcome (instead of a binary SVR outcome for the sake of example) standardized by a standard deviation (SD) might take into account for power analysis at the design stage the following considerations made based on clinical experiences, literature search, or pilot study results: (1) the stay-in rate will be lower, or the opt-out rate will be higher, in the mDOT arm than the PN arm since mDOT requires more frequent regular visit to a clinic, P(A_S|R_A)=0.65 and P(B_S|R_B)=0.80; (2) therefore, the randomization should be unbalanced with a heavier weight to mDOT arm, n(R_A)=400 and n(R_B)=200, to result in approximately equal numbers of participants treated with between mDOT and PN; (3) the standardized outcome of mDOT might be better than that of PN among participants who stay in their randomly assigned arms, E(Y|A_S)=0.9 and E(Y|B_S)=0.4; (4) the standardized outcome of participants who opt out to mDOT from PN might also be better than that of those who opt out to PN from mDOT, E(Y|A_B)=1.2 and E(Y|B_A)=0.7; (5) (residual) outcome variance will be σ²=1 across all groups as the outcome is standardized without loss of generality; and (6) test will be two-sided with α=0.05 significance level.

Under this hypothesized parameter setting, the investigators will expect that: (1) sample sizes of participants who opt out to A from B and to B from A will be n(A_B)=40 and n(B_A)=140, respectively; (2) sample sizes of participants who stay in A and B will be n(A_S)=260 and n(B_S)=160, respectively; and (3) sample sizes of participants who are treated with A and B will be n(T_A)=(T_B)=300. And, the following parameter values will be expected: (1) for comparative effect, ξ_A=0.83, ξ_B=0.24, ξ=0.59; (2) for preference effect, λ_A=0.38, λ_B =0.46, w_A=22.2, w_B=31.5, λ=0.43; (3) for selection effect, ς=−0.12; (4) for ITT effect, η_A=0.83,η_B=0.56, η=0.27; and (5) for AT effect, τ_A=0.94, τ_A=0.54, and τ=0.40. Finally, the statistical power for each effect under the specifications above is computed as follows: φ_ξ=0.96, φ_λ=0.88, φ_ς=0.14, φ_η=0.88, and φ_τ>0.99. An R code for computations of all of these quantitates along with theoretical power (5) and simulation-based empirical power in equation (6) below is provided in Supplementary Material.

5.6. Special case

For a special case in which n(R_A)=n(R_B)=n(R) and P(A_S|R_A)=P(B_S|R_B)=π_S, we have: n(A_S)=n(B_S)=π_Sn(R), n(A_B)=n(B_A)=(1–π_S)n(R), n(T_A)=n(T_B)=n(R), w_A=w_B, λ=(λ_A+λ_B)/2, and ς = (λ_A − λ_B)/2 Furthermore all power functions listed above can be simplified to

$$\begin{array}{lll}{\phi }_{\xi }\hfill & =\hfill & {\Phi }^{-1}\left({\pi }_S|\xi |{\sigma }^{-1}\sqrt{n(R)/2(1/{\pi }_S+1-{\pi }_S)}-z_{1-\alpha /2}\right)\hfill \\ \text{}{\phi }_{\lambda }\hfill & =\hfill & {\Phi }^{-1}\left(|\lambda |{\sigma }^{-1}\sqrt{n(R)(1-{\pi }_S^2)/2}-z_{1-\alpha /2}\right)\text{}\hfill \\ {\phi }_{\varsigma }\hfill & =\hfill & {\Phi }^{-1}\left(|\varsigma |{\sigma }^{-1}\sqrt{n(R)(1-{\pi }_S^2)/2}-z_{1-\alpha /2}\right)\hfill \\ {\phi }_{\eta }\hfill & =\hfill & {\Phi }^{-1}\left(|\eta |{\sigma }^{-1}\sqrt{n(R)/2}-z_{1-\alpha /2}\right)\hfill \end{array}$$

and

$${\phi }_{\tau }={\Phi }^{-1}\left(|\tau |{\sigma }^{-1}\sqrt{n(R)/2}-z_{1-\alpha /2}\right)$$

Note that, although it appears that all of these power functions are a monotone function of π_S under the special case, they are not necessarily so since all of ξ, λ, ς, η, and τ are also an implicit function of π_S, and so are their variance estimates.

Table 1 displays effects of π_S on all effects and their variance under a special case of: n(R_A) n(R_B)=n(R)=300, E(Y|A_S)=0.9, E(Y|B_S)=0.4, E(Y|A_B)=1.2, E(Y|B_A) 0.6, and σ²=1 As can be seen, the comparative decreases effect ξ and increases but its variance with increasing π_S. On the other hand, both preference effect λ and selection effect ς decrease with increasing π_S but their variances are the same and non-monotonic over π_S. The ITT effect η increases with increasing π_S whereas the overall/AT effect τ decreases. Their variances are the same but remain constant over π_S. Figure 2 presents impact of π_S on all power functions under the same special case of the design parameters. The magnitude of power for comparative effect ξ increases π_S whereas those for preference effect λ and selection effect ς are exactly symmetric about π_S = 50%, and ITT effect η is roughly symmetric about π_S ≈55%. On the other hand, overall/AT effect τ and selection effect ς are almost constant at > 0.99% and 5–10%, respectively. If π_S≈80%, then all effects except for the preference and selection effects will be detected with > 90% statistical power.

Table 1.

Derived effects and their variances over varying stay-in rates π_S = P(A_S|R_A) = P(B_S|R_S) under n(R_A) = n(R_B) = n(R) = 300, E(Y|A_S) = 0.9, E(Y|B_S) = 0.4, E(Y|A_B) = 1.2, E(Y|B_A) = 0.6, and σ² = 1.

Stay-in rate	Comparative effect		Preference effect		Selection effect		ITT effect		Overall/AT effect
πS	ξ	$\text{Var}\text{(}\tilde{\xi }\text{)}$	λ	$\text{Var}\text{(}\tilde{\lambda }\text{)}$	ς	$\text{Var}\text{(}\tilde{\zeta }\text{)}$	η	$\text{Var}\text{(}\tilde{\eta }\text{)}$	τ	$\text{Var}\text{(}\tilde{\tau }\text{)}$
1%	−9.40	6732.7	25.00	1683.2	5.00	1683.2	−0.59	0.007	0.60	0.007
10%	−0.40	7.267	2.50	1.852	0.50	1.852	−0.49	0.007	0.59	0.007
20%	0.10	0.967	1.25	0.260	0.25	0.260	−0.38	0.007	0.58	0.007
30%	0.27	0.299	0.83	0.088	0.17	0.088	−0.27	0.007	0.57	0.007
40%	0.35	0.129	0.63	0.043	0.13	0.043	−0.16	0.007	0.56	0.007
50%	0.40	0.067	0.50	0.027	0.10	0.027	−0.05	0.007	0.55	0.007
60%	0.43	0.038	0.42	0.019	0.08	0.019	0.06	0.007	0.54	0.007
70%	0.46	0.024	0.36	0.016	0.07	0.016	0.17	0.007	0.53	0.007
80%	0.48	0.015	0.31	0.016	0.06	0.016	0.28	0.007	0.52	0.007
90%	0.49	0.010	0.28	0.023	0.06	0.023	0.39	0.007	0.51	0.007
99%	0.50	0.007	0.25	0.172	0.05	0.172	0.49	0.007	0.50	0.007

Figure 2.

Comparisons of statistical power across five effects with varying stay-in rates π_S=P(A_S|R_A)=P(B_S|R_S) under a special case of: n(R_A)=n(R_B)=n(R)=300, E(Y|A_S)=0.9, E(Y|B_S)=0.4, E(Y|A_B)=1.2, E(Y|B_A) 0.6, and σ²=1. A: theoretical statistical power: B: empirical statistical power based on 10,000 simulations. Black and gray lines represent theoretical and empirical power, respectively.

5.7. Simulation verification

Simulations were conducted with normal and binomial distributions of outcome Y. Simulation-based empirical power is defined as

$${\tilde{\phi }}_{\theta }={\displaystyle {\sum }_{k=1}^{K}1\{p_k(\tilde{\theta })<\alpha \}/K}$$ (6)

where 1{.} is an indicator function; $p_k(\tilde{\theta })$ is the p value from testing significance of $\tilde{\theta }$ for the kth simulation with estimated sample variance of Y; and K is the total number of simulations. For the same specifications used for Table 1 and Figure 2, the magnitudes of empirical power (presented in gray lines in Figure 2) based on K=10,000 simulations for each specification are virtually identical to those of the theoretical power. In addition, under unbalanced sample sizes and various differential preference rates, Table 2 shows that both theoretical and empirical power, under normal distributions are again virtually identical to each other in view of $\text{max}|{\phi }_{\theta }-{\tilde{\phi }}_{\theta }|$ in equations (5) and (6). Table 3 shows that simulation results even under binomial distributions are also very close to each other in view of $\text{max}|{\phi }_{\theta }-{\tilde{\phi }}_{\theta }|$, even if this quantity is in general slightly greater than that under the normal distributions. The asymptotic distributions of the test statistic D_θ (4) based on large sample theory are shown to be useful for binomial outcomes when an EV is estimated based on average of given probabilities under the parameter specification considered in Table 3. Furthermore, the type I error rates of D_θ (4) under both normal and binomial distributions appear to be preserved since the empirical power is close to the theoretical power even when it is near 0.05 meaning a null effect. With all the other parameters held fixed, effects of unbalanced stay-in rates between arms on statistical power appear to be greater for comparative and preference effects compared to that for the other effects for both normal and binomial outcomes (Tables 2 and 3).

Table 2.

Comparisons between theoretical and empirical power under normal distributions over varying sample sizes and sty-in rates with fixed E(Y|A_S) = 0.9, E(Y|B_S) = 0.4, E(Y|A_B) = 1.2, E(Y|B_A) = 0.6, σ² = 1, two-sided α = 0.05, and number of simulations = 10,000.

Sample size		Stay-in rate		Comparative effect		Preference effect		Selection effect		ITT effect		Overall/AT effect
n(RA)	n(RB)	P(AS|RA)	P(BS|RB)	φξ	${\tilde{\phi }}_{\xi }$	φλ	${\tilde{\phi }}_{\lambda }$	φζ	${\tilde{\phi }}_{\varsigma }$	φη	${\tilde{\phi }}_{\eta }$	φτ	${\tilde{\phi }}_{\tau }$
250	150	20%	40%	0.185	0.186	0.578	0.571	0.118	0.125	0.568	0.567	0.999	0.999
		30%	30%	0.067	0.070	0.623	0.614	0.103	0.103	0.744	0.736	0.999	1.00
		40%	20%	0.081	0.090	0.564	0.558	0.081	0.078	0.873	0.863	0.999	0.999
200	200	20%	40%	0.198	0.196	0.586	0.581	0.086	0.087	0.595	0.595	1.00	1.00
		30%	30%	0.068	0.074	0.630	0.626	0.074	0.075	0.770	0.764	1.00	1.00
		40%	20%	0.082	0.091	0.566	0.561	0.061	0.062	0.893	0.883	1.00	1.00
150	250	20%	40%	0.194	0.189	0.549	0.542	0.062	0.062	0.568	0.574	1.00	1.00
		30%	30%	0.067	0.074	0.589	0.581	0.056	0.051	0.744	0.735	1.00	1.00
		40%	20%	0.079	0.088	0.524	0.520	0.051	0.054	0.873	0.862	1.00	1.00
250	150	60%	80%	0.796	0.795	0.556	0.557	0.051	0.049	0.568	0.563	0.995	0.995
		70%	70%	0.654	0.657	0.589	0.587	0.056	0.057	0.377	0.386	0.997	0.998
		80%	60%	0.418	0.420	0.597	0.590	0.081	0.089	0.213	0.228	0.997	0.997
200	200	60%	80%	0.822	0.823	0.594	0.595	0.052	0.051	0.595	0.598	0.999	0.998
		70%	70%	0.682	0.680	0.630	0.627	0.074	0.078	0.398	0.404	1.00	1.00
		80%	60%	0.439	0.447	0.642	0.633	0.121	0.125	0.224	0.242	1.00	1.00
150	250	60%	80%	0.798	0.797	0.584	0.586	0.065	0.064	0.568	0.564	1.00	0.999
		70%	70%	0.654	0.647	0.623	0.617	0.103	0.108	0.377	0.382	1.00	1.00
		80%	60%	0.416	0.423	0.639	0.635	0.164	0.171	0.213	0.222	1.00	1.00
$\text{max}|{\phi }_{\theta }-{\tilde{\phi }}_{\theta }|$				0.009		0.008		0.008		0.018		0.001

Table 3.

Comparisons between theoretical and empirical power under binomial distributions over varying sample sizes and sty-in rates with fixed E(Y|A_S) = 0.7, E(Y|B_S) = 0.5, E(Y|A_B) = 0.8, E(Y|B_A) = 0.6, two-sided α = 0.05, and number of simulations = 10,000.

Sample size		Stay-in rate		Comparative effect		Preference effect		Selection effect		ITT effect		Overall/AT effect
n(RA)	n(RB)	P(AS|RA)	P(BS|RB)	φξ	${\tilde{\phi }}_{\xi }$	φλ	${\tilde{\phi }}_{\lambda }$	φζ	${\tilde{\phi }}_{\varsigma }$	φη	${\tilde{\phi }}_{\eta }$	φτ	${\tilde{\phi }}_{\tau }$
250	150	20%	40%	0.217	0.227	0.418	0.415	0.060	0.050	0.230	0.229	0.963	0.971
		30%	30%	0.093	0.094	0.464	0.462	0.054	0.050	0.369	0.378	0.962	0.964
		40%	20%	0.052	0.057	0.422	0.416	0.051	0.060	0.528	0.533	0.946	0.951
200	200	20%	40%	0.234	0.242	0.438	0.437	0.051	0.042	0.242	0.246	0.990	0.993
		30%	30%	0.096	0.096	0.485	0.473	0.050	0.047	0.380	0.404	0.987	0.990
		40%	20%	0.052	0.049	0.438	0.434	0.051	0.052	0.554	0.565	0.976	0.980
150	250	20%	40%	0.228	0.235	0.422	0.413	0.051	0.045	0.230	0.232	0.998	0.998
		30%	30%	0.093	0.090	0.464	0.466	0.054	0.054	0.369	0.375	0.996	0.998
		40%	20%	0.052	0.045	0.418	0.414	0.060	0.057	0.528	0.535	0.989	0.991
250	150	60%	80%	0.716	0.710	0.457	0.462	0.073	0.064	0.528	0.536	0.946	0.949
		70%	70%	0.580	0.587	0.464	0.463	0.054	0.044	0.369	0.366	0.962	0.964
		80%	60%	0.383	0.385	0.451	0.454	0.051	0.043	0.230	0.233	0.963	0.965
200	200	60%	80%	0.744	0.749	0.474	0.474	0.058	0.049	0.554	0.568	0.976	0.979
		70%	70%	0.607	0.605	0.485	0.484	0.050	0.039	0.389	0.384	0.987	0.987
		80%	60%	0.403	0.413	0.474	0.475	0.058	0.052	0.242	0.254	0.990	0.991
150	250	60%	80%	0.718	0.731	0.451	0.454	0.051	0.039	0.528	0.541	0.989	0.990
		70%	70%	0.580	0.576	0.464	0.466	0.054	0.045	0.369	0.373	0.996	0.995
		80%	60%	0.381	0.383	0.457	0.463	0.073	0.062	0.230	0.235	0.998	0.998
$\text{max}|{\phi }_{\theta }-{\tilde{\phi }}_{\theta }|$				0.013		0.012		0.012		0.024		.008

6. Discussion

The PORD design is a simplified version of existing preference trial designs which involve multiple steps of randomizations or consent processes. However, it has many aforementioned desirable features including those which other designs might not have. For example, although it does not have a randomization arm, a PORD includes by design randomized groups who willingly, as opposed to potentially reluctantly, accept randomly assigned intervention. In addition, it enables CER investigators to estimate and test diverse effects. It might be convenient to determine sample sizes, n(R_A) and n(R_A), for a primary effect in a routine iterative fashion since inversions of power functions to sample size formulas are complicated, albeit possible, especially when opt-out rates and randomizations are unbalanced. We recommend the simulation approach ${\tilde{\phi }}_{\theta }$ (6) for binary outcomes in particular since the asymptotic normality of D_θ (4) might not always be reliable especially for small sample sizes and very low or high success probabilities. Definite thresholds of sample sizes and probabilities for reliable normal approximations are unknown although the conventional “np > 5” rule for all identifiable and unidentifiable groups may serve as a criterion for the purpose of using the theoretical power function φ_θ (5) for binary outcomes. Nonetheless, it takes only a few seconds to estimate simulation-based empirical power by running 10,000 simulations for a combination of pre-specified parameters using the R code provided in Supplementary Material.

We stress that power calculations for all five effects need to be conducted through the common design parameters since they will all be inter-connected. In other words, if one computes power for one effect independently from the other effects, then the power calculations may not be cohesive under a PORD design. Since the PORD involves five effects, proper adjustment of the significance level for multiple testing would be an issue for computing power or sample sizes. If a PORD study is aimed to test a single primary effect, then any adjustment may not be necessary for testing the primary effect. However, if a PORD aims to find any significant effect among the five effects, then a multiplicity adjustment (e.g. Bonferroni correction) to the significance level should be applied for computing power.

Use of PORD or any other types of preference design might not be suitable when a vast majority of participants are expected to have clear preference. In this case, willingness to be randomized might be diminished.³¹ If a PORD study was implemented in such a case, the NSBR (A2) assumption in particular would not consequently hold since it is highly likely that almost all participants in the stay-in groups would be those who preferred the assigned interventions. It follows that there would be disproportionately very few A_R(B_R) participants in A_S(B_s). For this reason, estimates of the comparative effect, preference effect, and selective effect following the PORD analytic strategies would be biased. Furthermore, even if the NSBR assumption could be relaxed so that A_S(B_s) is treated as the same as A_B(B_A), AT effect would be confounded by the preference effect. Therefore, application of PORD would be useful when an adequate size of participants is anticipated to have equal or no preferences.

When a PORD study is successfully implemented and completed, all five effect estimates could collectively or specifically guide treatment or intervention decision making at the individual patient or clinician level, and at the organization level such as hospitals and community-based organizations. For example, if the preference effect is significant but comparative effect is not, then clinicians would ask for patient’s preferences and prescribe accordingly. If the preference effect is not significant but comparative or overall effect is, then clinicians would recommend the more effective intervention to patients even if patients might prefer the less effective intervention. Per the selection effect, patients who choose more convenient delivery methods such as app-aided DPP might have less motivation than those who choose more demanding conventional delivery methods. Therefore, it is likely that their outcome might be even worse on average than those who do not have preference and thus that the selection effect of choosing conventional methods would be significant. In this case, the recommendation of convenient delivery methods might be discarded at an organizational level. If all effects are not significant and the outcomes are equivalently effective between interventions, then an optimal intervention approach can be implemented considering individual patient-level and clinician preferences, considering also practical constraints such as cost and insurance reimbursement.

The following limitations should be taken into account for implementing a PORD. First, especially when the opt-out rate is unbalanced, it is likely that the covariate profiles balance among participants between A_S and B_S may be compromised. For the comparisons of identifiable groups such as ITT or AT effect, these effects can be adjusted for differential characteristics applying multivariable regression analysis. However, for comparisons between unidentifiable groups, post-hoc adjustment to the comparative, preference and selection estimates will be difficult and we believe that additional assumptions on covariate profiles for unidentifiable groups would be necessary. Examination of this potential post-randomization selection bias would be a valuable future research undertaking. Second, if the opt-out rate is anticipated to be high, then the power for testing for the comparative effect in particular will be small. Therefore, if the comparative effect is of the primary interest, then a large sample size would be required. In such case, it might be more reasonable to have preference or selection effect as the primary aim. Third, the effect of violations of assumptions (A1)–(A3) on the statistical analysis is not examined in the present paper. These assumptions, albeit well-accepted, are rather ideal and may not hold in the real world situations. At the analysis stage, however, it will be possible to test the EV assumption (A3) between identifiable groups and if rejected, an appropriate test with unequal variances can be applied to testing significance of effects. For comparison of unidentifiable groups, testing EV is not possible, and thus a pooled variance from identifiable groups (e.g. A_s, A_B, B_s, and B_A) can be used for constructing test statistics D_θ (4) as demonstrated in the simulation R code in Supplementary Material.

In conclusion, we believe that the PORD is an ideal design to address many challenges arising from CER to accommodate participants’ preferences in real-world settings while effectively estimating and testing diverse effects without compromising randomization.