Abstract
Cell types in cell populations change as the condition changes: some cell types die out, new cell types may emerge and surviving cell types evolve to adapt to the new condition. Using single-cell RNA-sequencing data that measure the gene expression of cells before and after the condition change, we propose an algorithm, SparseDC, which identifies cell types, traces their changes across conditions and identifies genes which are marker genes for these changes. By solving a unified optimization problem, SparseDC completes all three tasks simultaneously. SparseDC is highly computationally efficient and demonstrates its accuracy on both simulated and real data.
INTRODUCTION
Multicellular organisms function through cohesive and dynamic interactions among billions of highly heterogeneous cells. Precisely identifying diverse cell types and delineating how cells evolve over the course of tissue development and disease progression are fundamental quests in modern biology (1–4). Single-cell RNA-sequencing (scRNA-seq), which measures the transcriptome of hundreds to thousands of individual cells in a single run, provides a highly efficient tool to reveal cellular identity from the transcriptome perspective which has led to unprecedented biological insights (5–11).
With transcriptome measurements from many cells, cell types may be discovered computationally by clustering cells with similar transcriptome profiles together. For cancer cells and some other cells, it is more accurate to call these cell types ‘cell clones’ or ‘cell subpopulations’, but for simplicity we will use ‘cell types’ for all of them for the remainder of the text. The single-cell transcriptome profile reflects both cellular identity (lineage or cell type) and intracellular response to given extrinsic micro-environmental stimuli. As tissue develops or disease progresses, or after drug treatment (we call these ‘condition changes’ herein), the micro-environment changes and the cell types also change. An example of what happens when the condition changes is illustrated in Figure 1. We call the condition before and after the change ‘condition A’ and ‘condition B’, respectively. In condition A, there are three types of cells (denoted by different colors, red, blue and green). As the condition changes to B, the green type dies out, while a new cell type, purple, emerges. The red type and the blue type survive under the condition change, although their relative proportions in the whole cell population change. The red type decreases from 50 to 25% in the cell population, and the blue type increases from 25 to 50%. Moreover, the red and the blue types are not exactly the same cell types as those in condition A, as their expression profiles have changed to adapt to the micro-environmental change. In the figure, we added white stars to the red and blue cells to highlight this difference.
Figure 1.
A toy example of cell type changes and different categories of marker genes. (A and B) The composition of the cell population changes as the condition changes. Different colors denote different cell types. The blue and red cells are preserved in condition B but have changed as indicated by the stars. On the other hand, the green cells have died out and a new purple cell type has emerged. The proportion of cell types present in the population has also changed. (C and D) different categories of marker genes for the red cell type. A marker gene for a cell type is a gene whose expression is consistent in cells of this type and also different from the background. In the plot, the background expression is shown in dark red, and expression higher than the background is shown in yellow. The brighter the yellow is, the higher the expression is. Gene 1 is a housekeeping marker gene. Gene 2 is a condition-dependent marker gene, since although it is a marker gene in both conditions, its expression is lower (less bright yellow) in condition B. Gene 3 is not a marker gene in condition B anymore as its expression in condition B is the same as the background; it is thus a condition-A-specific marker gene. Gene 4 is a condition-B-specific marker gene. Gene 5 is a null gene.
In this paper, we focus on solving the problem of, based on scRNA-seq data under two biological conditions, discovering cell types in both conditions and describing how the transcriptome profile of the cell types change as the condition changes. We call this problem ‘differential clustering analysis’ or DC analysis for short. It is worth noting that DC analysis considers the cells in the two biological conditions as being sampled from independent populations (that is, not longitudinal); this is the case for the majority of real scRNA-seq data, since current scRNA-seq protocols cannot generate multiple expression measurements for the same cell (12). In DC analysis, the discovery of cell types is ‘unbiased’/unsupervised: it is not assumed that cells come from known cell types in either condition; all cell types are discovered and defined computationally based on the data. Besides cell type discovery, DC analysis emphasizes computationally linking the cell types discovered in the two conditions to determine, in response to the condition change, which cell types die out, emerge or survive. An obvious difficulty in linking the inferred cell types is that no cell types remain the same across the conditions. Even cells of the ‘same’ cell type may display differences in their transcriptomic profile, as genes which are sensitive to or responding to the condition changes may have altered their expression significantly. To overcome this difficulty, it is preferable to use a one-step approach which discovers and links cell types simultaneously, instead of a two-step approach that attempts to link the cell types across the conditions after they have been discovered.
With the increasing popularity of scRNA-seq in recent years, several clustering algorithms have been developed for cell type discovery in a single biological condition (11,13–20), supplementing and improving upon classical clustering methods such as K-means and hierarchical clustering. However, the area of DC analysis has been much less explored. A relevant problem is inferring the developmental trajectories of single cells by estimating the pseudo temporal ordering (pseudotime). The differences between these pseudotime-estimation methods (see e.g. (16,17,21–25)) and DC analysis are distinct, including the type of data they take as input, the scientific question they seek to answer and the approach they use. Pseudotime-estimation methods often take as input expression measurements for a single cell type (23), while DC analysis requires two cell populations under different conditions that contain multiple cell types. Pseudotime-estimation methods seek to describe the developmental path of one cell type, while DC analysis aims to discover multiple cell types in each condition and characterize the differences of each cell type across conditions. Pseudotime-estimation methods find a position for each cell along a continuous trajectory, DC analysis instead clusters cells into a small number of disjoint clusters. (See Supplementary Materials for a more detailed discussion of their differences and ideas on how they may be used in tandem). The first, and still the only, algorithm for DC analysis was proposed by Huang et al. (26) to model time variant clusters. It is based on a Bayesian parametric model using a binary branching process, which is designed for DC analysis for cells coming from multiple time points. For data with only two conditions, this model is too constrained for describing various scenarios of cell type changes across conditions. Moreover, the method is computationally expensive and unstable and its applicability on data with more than 45 genes is unexplored (26).
In this paper, we have proposed the first algorithm for DC analysis that is suitable for data with thousands or tens of thousands of genes. Our algorithm, called SparseDC (a sparse algorithm for differential clustering analysis), is a variation of the classic K-means clustering algorithm that inherits many of its advantages: it is a non-parametric method, has an interpretable target function and is computationally very fast. Furthermore, by including 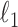 penalties in the target function, SparseDC generates a sparse solution, allowing it to largely overcome the ‘curse of dimensionality’ and making it suitable for very high-dimensional data.
penalties in the target function, SparseDC generates a sparse solution, allowing it to largely overcome the ‘curse of dimensionality’ and making it suitable for very high-dimensional data.
SparseDC has a crucial additional feature: it not only discovers cell types and traces their changes, but also identifies marker genes for each cell type and for the changes of each cell type across conditions. Identifying marker genes can be of great biological interest as it gives insight on the biological functions of the cell type and provides targets for further investigation. Generally, a marker gene for a cell type can be defined as a gene whose expression is consistent in cells of this type and also different from cells of other types. When considering cell types present in both condition A and condition B, we propose that a marker gene can be classified to one of the following three categories: (i) ‘housekeeping marker gene’: a gene that is a marker in both conditions and its expression is the same in both conditions. The classic T-cell lineage markers CD4 and CD8 are examples of housekeeping marker genes (27); (ii) ‘condition-dependent marker gene’: a gene that is a marker in both conditions, but its expression is different in the two conditions, such as stem cell markers NES (28) and SOX2 (29) where expression of the stem cell marker genes decreases once cells undergo differentiation; (iii) ‘condition-specific marker gene’: a gene that is a marker in only one condition but not the other, such as cytokine expression in response to inflammation. We call a gene a ‘condition-A-specific marker gene’ if it is a marker only in condition A, and a ‘condition-B-specific marker gene’ if it is a marker only in condition B. Figure 1(C and D) shows an example of each type of marker gene, as well as a ‘null gene’, a gene that is not a marker gene for any cell type. SparseDC is able to identify marker genes for each cell type, and for cell types that are present in both conditions it identifies all three types of marker gene and distinguishes between them.
In summary, we have developed SparseDC, a computational algorithm which completes the following three tasks: (i) clustering cells in each condition into cell types in an unsupervised manner, (ii) identifying the correspondence between cell types in the two conditions and (iii) detecting marker genes for each cell type. SparseDC completes all three tasks by solving a single optimization problem and is computationally highly efficient. The performance of SparseDC is studied on simulated data representing a range of potential cell type and population changes in scRNA-seq data. SparseDC is also applied to four real scRNA-seq datasets to demonstrate its ability to describe cell type changes and identify biologically meaningful marker genes.
MATERIALS AND METHODS
SparseDC is designed to minimize the within-cluster sum of squared errors of gene expression, while penalizing the differences across clusters and across conditions. This penalization is done by adding several different  penalties, which overall form a fused-lasso type of penalty (30). The penalization drives similar clusters from the two conditions together, revealing the correspondence between clusters present in both conditions. The
penalties, which overall form a fused-lasso type of penalty (30). The penalization drives similar clusters from the two conditions together, revealing the correspondence between clusters present in both conditions. The 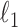 penalties, due to their nature (31), also generate a ‘sparse’ solution, that is, only a small fraction of genes are involved in determining the cell-type identities. This sparsity not only makes SparseDC highly applicable to high-dimensional problems, but also automatically identifies marker genes for each cell type. Below, we give details about the algorithm.
penalties, due to their nature (31), also generate a ‘sparse’ solution, that is, only a small fraction of genes are involved in determining the cell-type identities. This sparsity not only makes SparseDC highly applicable to high-dimensional problems, but also automatically identifies marker genes for each cell type. Below, we give details about the algorithm.
Notations and settings
Suppose, we have scRNA-seq data from two conditions, A and B, and the expression of p genes is measured in N cells in condition A, and the same set of p genes is measured in 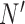 cells in condition B. For condition A, we have data matrix X of dimension
cells in condition B. For condition A, we have data matrix X of dimension  , with
, with 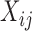 being the expression of gene i in cell j. Similarly, we can define
being the expression of gene i in cell j. Similarly, we can define  and
and  for data from condition B. Generally, we use notations without superscripts for quantities from condition A, and use notations with superscript ‘prime’ for quantities from condition B.
for data from condition B. Generally, we use notations without superscripts for quantities from condition A, and use notations with superscript ‘prime’ for quantities from condition B.
We assume that the gene expression has been properly normalized for the sequencing depth, which is often estimated by pooled deconvolution (32), methods based on spike-ins (33,34) or methods developed for bulk-based RNA-seq data (35–37). We also recommend taking proper transformations such as  or
or 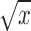 to stabilize variances.
to stabilize variances.
For clustering, we let  indicate the indices of the cells in condition A that are contained in cluster k. That is,
indicate the indices of the cells in condition A that are contained in cluster k. That is,  means cell j in condition A is in cluster k,
means cell j in condition A is in cluster k, 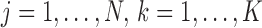 . Let
. Let 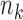 be the size of
be the size of 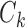 ; surely we have
; surely we have 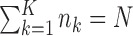 . Let
. Let 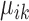 be the (regularized) cluster mean, or cluster center, for cluster k and gene i in condition A. We define
be the (regularized) cluster mean, or cluster center, for cluster k and gene i in condition A. We define 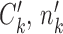 and
and 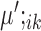 correspondingly, for condition B. Note that cells in
correspondingly, for condition B. Note that cells in  and
and 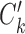 are considered to be the same ‘type’ of cells, and thus this notation not only defines the individual clustering of the two conditions, but also defines the correspondence between the cell types from the two conditions. When
are considered to be the same ‘type’ of cells, and thus this notation not only defines the individual clustering of the two conditions, but also defines the correspondence between the cell types from the two conditions. When  and
and 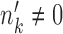 , cell type k survives the condition change. When
, cell type k survives the condition change. When  and
and  , cell type k dies out as the condition changes. When
, cell type k dies out as the condition changes. When  and
and 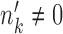 , cell type k is a new cell type that emerges in condition B.
, cell type k is a new cell type that emerges in condition B.
The optimization problem that SparseDC proposes
Prior to clustering, the expression of each gene is centralized, that is, the mean expression of each gene is subtracted such that 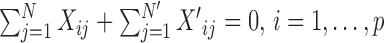 .
.
SparseDC proposes solving the following optimization problem: find 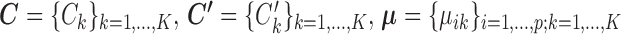 and
and  that minimize
that minimize
 |
where 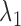 and
and 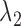 are pre-specified positive constants.
are pre-specified positive constants.
The first two terms in the target function minimize the within-cell-type variance, the last three terms are  penalties on
penalties on 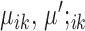 , and the difference between
, and the difference between  and
and  , respectively. Without these three terms, the solution will be the same as doing K-means clustering for condition A and condition B independently. These three terms add a ‘fused-lasso’ (30) type of penalty, which affects the solution in two ways: (i) penalizing
, respectively. Without these three terms, the solution will be the same as doing K-means clustering for condition A and condition B independently. These three terms add a ‘fused-lasso’ (30) type of penalty, which affects the solution in two ways: (i) penalizing 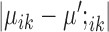 pushes similar cells across conditions together and thus gives the correspondence between cell types in the two conditions; and (ii) penalizing
pushes similar cells across conditions together and thus gives the correspondence between cell types in the two conditions; and (ii) penalizing 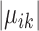 and
and 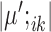 makes most genes null genes (having the same expression as the background) and lets the marker genes stand out.
makes most genes null genes (having the same expression as the background) and lets the marker genes stand out.
With properly chosen 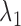 and
and 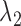 values, the solution will be very ‘sparse’ because of the nature of
values, the solution will be very ‘sparse’ because of the nature of 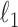 penalties (31): most
penalties (31): most  and
and 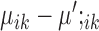 will be exactly zero. Therefore, marker genes can be identified based on the solution:
will be exactly zero. Therefore, marker genes can be identified based on the solution:
Null genes: genes with
 for all
for all 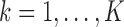 . These genes have uniform expression in both conditions and all clusters. These genes do not contribute to the clustering, and they are not marker genes of any kind. The majority of the genes will be null genes when
. These genes have uniform expression in both conditions and all clusters. These genes do not contribute to the clustering, and they are not marker genes of any kind. The majority of the genes will be null genes when  and
and 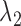 are properly chosen.
are properly chosen.Housekeeping marker genes: genes with
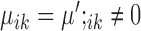 are housekeeping marker genes for cell type k. These genes are expressed differently in cluster k compared to the ‘background’ expression, and their expression stays the same across conditions.
are housekeeping marker genes for cell type k. These genes are expressed differently in cluster k compared to the ‘background’ expression, and their expression stays the same across conditions.Condition-dependent marker genes: genes with
 but
but 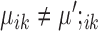 are condition-dependent marker genes for cell type k. These genes are marker genes for cluster k in both conditions, but their expression changes when the condition changes.
are condition-dependent marker genes for cell type k. These genes are marker genes for cluster k in both conditions, but their expression changes when the condition changes.Condition-specific marker genes: genes with
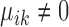 and
and 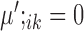 , or
, or 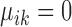 and
and 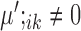 are condition-specific marker genes for cell type k in condition A or B, respectively. These genes are marker genes for cell type k in one condition but not the other.
are condition-specific marker genes for cell type k in condition A or B, respectively. These genes are marker genes for cell type k in one condition but not the other.
Based on the values of 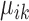 and
and 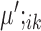 , the upregulation or downregulation of a gene can be defined. If
, the upregulation or downregulation of a gene can be defined. If 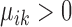 or
or 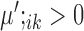 , then gene i is ‘upregulated in cell type k’ compared to other cell types, since the overall expression of all cells has been centralized to 0. Similarly, if
, then gene i is ‘upregulated in cell type k’ compared to other cell types, since the overall expression of all cells has been centralized to 0. Similarly, if 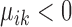 or
or 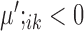 , then gene i is ‘downregulated in cell type k’. Upregulation or downregulation can also be defined across conditions. If
, then gene i is ‘downregulated in cell type k’. Upregulation or downregulation can also be defined across conditions. If 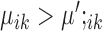 , then gene i is ‘upregulated in condition A’ or ‘downregulated in condition B’. Similarly, if
, then gene i is ‘upregulated in condition A’ or ‘downregulated in condition B’. Similarly, if 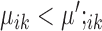 , then gene i is ‘downregulated in condition A’ or ‘upregulated in condition B’.
, then gene i is ‘downregulated in condition A’ or ‘upregulated in condition B’.
The target function of SparseDC contains two tuning parameters ( and
and 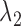 ), which control the number of marker genes in the solution and which in turn can influence the accuracy of the clustering. Selecting tuning parameters for unsupervised clustering settings is known to be a notoriously difficult problem and methods such as the gap statistic often exhibit mixed results (38,39). Notably, we have found that the performance of the gap statistic is highly unstable for this problem and thus we have instead devised a new ad hoc approach (See Supplementary Materials). Simulation has also shown that the results of SparseDC appear to be robust to minor departures of
), which control the number of marker genes in the solution and which in turn can influence the accuracy of the clustering. Selecting tuning parameters for unsupervised clustering settings is known to be a notoriously difficult problem and methods such as the gap statistic often exhibit mixed results (38,39). Notably, we have found that the performance of the gap statistic is highly unstable for this problem and thus we have instead devised a new ad hoc approach (See Supplementary Materials). Simulation has also shown that the results of SparseDC appear to be robust to minor departures of  and
and 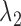 from the values given by our approach (See Supplementary Materials for details).
from the values given by our approach (See Supplementary Materials for details).
Notice that we also add weights ( and
and 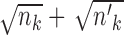 ) to make the
) to make the 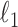 penalties adaptive to the cluster sizes. The choice of these weights was inspired by the group lasso (40). We have also tried other sets of weights, such as
penalties adaptive to the cluster sizes. The choice of these weights was inspired by the group lasso (40). We have also tried other sets of weights, such as  and
and  , or no weights at all, and found that they lead to inferior performance.
, or no weights at all, and found that they lead to inferior performance.
The algorithm that SparseDC uses to solve the optimization problem
Given 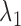 and
and  , SparseDC relies on the following observations to find
, SparseDC relies on the following observations to find 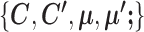 that minimize
that minimize 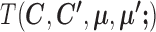 :
:
When
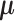 and
and  are given,
are given,  is equivalent to
is equivalent to 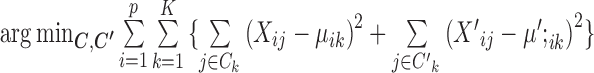 , whose solution is given by assigning each cell to its nearest centroid.
, whose solution is given by assigning each cell to its nearest centroid.- When C and
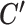 are given, T is separable on i and k, and thus
are given, T is separable on i and k, and thus 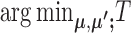 can be calculated by solving
can be calculated by solving
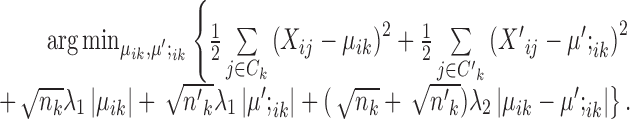
This problem is quite like the fused lasso (30) or the total variance minimization (41) problem, although they are not the same because of the different forms of the weights and existing algorithms do not directly apply. However, the solution can be computed as follows (See Supplementary Materials for full derivations), where 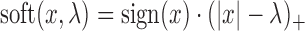 is the soft thresholding operator.
is the soft thresholding operator.
If
 , the solution is given by
, the solution is given by 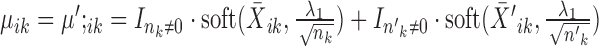 , where
, where 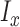 is the indicator function that equals 1 if condition x is satisfied and 0 otherwise.
is the indicator function that equals 1 if condition x is satisfied and 0 otherwise.Else if
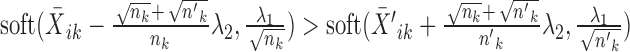 , the solution is given by
, the solution is given by  and
and 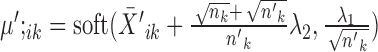 .
.Else if
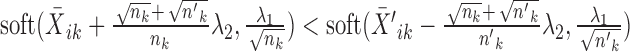 , the solution is given by
, the solution is given by 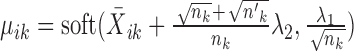 and
and 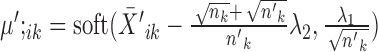 .
.Else, the solution is given by
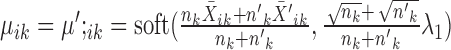 .
.
Given these observations, SparseDC initializes C and 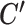 by randomly assigning cells to clusters, and then iteratively updates
by randomly assigning cells to clusters, and then iteratively updates  and
and 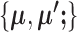 until the clustering solution does not change. We have found that convergence is usually achieved within 20 iterations. This alternative optimization strategy is quite similar to that of regular K-means clustering. And just like regular K-means, SparseDC is guaranteed to converge, but only to a local optimum. In regular K-means, multiple initial values are used to increase the chances of achieving the global optimum. We have found that a similar strategy also works for SparseDC: we assign multiple sets of random initial values to C and
until the clustering solution does not change. We have found that convergence is usually achieved within 20 iterations. This alternative optimization strategy is quite similar to that of regular K-means clustering. And just like regular K-means, SparseDC is guaranteed to converge, but only to a local optimum. In regular K-means, multiple initial values are used to increase the chances of achieving the global optimum. We have found that a similar strategy also works for SparseDC: we assign multiple sets of random initial values to C and  , iterate to get the solution for each set of initial values, and the final solution is chosen as the one that gives the smallest T among all solutions. Our simulation and real data results were obtained by using 50 sets of initial values.
, iterate to get the solution for each set of initial values, and the final solution is chosen as the one that gives the smallest T among all solutions. Our simulation and real data results were obtained by using 50 sets of initial values.
The computational load of our algorithm is generally at a similar level to regular K-means. Given  , updating
, updating 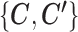 is the same as K-means. Given
is the same as K-means. Given 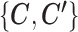 , updating
, updating 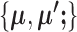 is not done by calculating the centroids, but they still have a closed-form solution and thus the update is still very fast, making the optimization of SparseDC highly efficient and scalable to high-dimensional datasets.
is not done by calculating the centroids, but they still have a closed-form solution and thus the update is still very fast, making the optimization of SparseDC highly efficient and scalable to high-dimensional datasets.
Simulated data
To study the performance of SparseDC under different compositional changes of cell populations between different biological conditions, data were simulated under a range of scenarios, listed in Table 1. For example, in scenario 6, cell types 1 and 2 are present in condition A, while cell types 2, 3 and 4 are present in condition B. Thus, in this scenario, there is one cell type (type 1) dying out and two cell types (type 3 and 4) emerging. The seven scenarios can be classified into three categories, from least to most challenging: (i) Scenario 1: there are no cell types dying out/emerging. (ii) Scenarios 2 and 3: there are cell types dying out. Since the target function of SparseDC is symmetric for the two conditions, these scenarios are equivalent to cell types emerging if the condition labels of A and B are exchanged. (iii) Scenarios 4–7: there are both cell types dying out and cell types emerging.
Table 1. The cell type composition of the simulation scenarios.
| Cluster scenario | Cell types in condition A | Cell types in condition B |
|---|---|---|
| 1 | (1,2,3) | (1,2,3) |
| 2 | (1,2,3) | (2,3) |
| 3 | (1,2,3,4) | (2,3,4) |
| 4 | (1,2) | (2,3) |
| 5 | (1,2,3) | (2,3,4) |
| 6 | (1,2) | (2,3,4) |
| 7 | (1,2,3,4) | (3,4,5) |
For each scenario, a proportion (10, 3 or 1%) of genes were assigned as marker genes. This proportion denotes the ‘sparsity’ of marker genes among all genes and thus hereafter we refer the proportions as ‘abundant’, ‘sparse’ or ‘very sparse’ marker genes. The sparser the marker genes are, the more challenging the clustering problem is likely to be.
For each of the simulation scenarios and levels of sparsity we first generated datasets where all of the marker genes are housekeeping marker genes. We then generated data, where half of the marker genes are condition-specific marker genes and half are housekeeping marker genes. Compared with setting all marker genes as housekeeping marker genes, this provides an additional challenge for SparseDC to correctly identify the condition-specific genes as well as increasing the difficulty of linking the clusters across conditions.
In summary, we simulated seven scenarios of cell population changes as shown in Table 1; for each scenario, we simulated data with three levels of sparsity; and for each level of sparsity, we simulated data with two different configurations of marker genes. For each of these 42 combinations of scenario, sparsity and marker-gene configuration, we simulated 100 datasets, each containing expression levels for 1000 genes and 100 cells in each biological condition. Details about how the expression levels were simulated are provided in Supplementary Materials.
Overview of four real datasets
ScRNA-seq data with cells from two biological conditions are quite common in the literature and two of them were used to evaluate the performance of SparseDC. They are ‘Real dataset 3: Llorens–Bobadilla data’ and ‘Real dataset 4: Shalek data’; detailed descriptions are given in the following sections.
A shortcoming of real datasets with cells from two conditions, such as the Llorens–Bobadilla data and the Shalek data, is that the biological truth of cell type changes is usually unknown, and thus the ability of SparseDC to link clusters of cells of the same type across conditions and identify cell types that have emerged or died out cannot be accurately tested on them. To overcome this, two other real datasets, ‘Real dataset 1: Pollen data’ and ‘Real dataset 2: Biase data’ (details given in the following sections), were also used. Each of these two datasets contains cells from a single condition, but we have proposed a process to modify them to create datasets that contain cells from two conditions with known changes of cell types. These known cell type changes will then be used as the gold standard to test SparseDC’s clustering accuracy. Below brief descriptions are given about the four real datasets we have used, and then the process of modifying the Pollen data and the Biase data is described in the section ‘Modifying real datasets for known cluster changes’.
Real dataset 1: Pollen data
This real scRNA-seq dataset was created by Pollen et al. (42), who captured single cells from a range of tissues composed of an assortment of cell types. Ten of the cell types were selected to be used in the analysis (See Supplementary Materials) giving a dataset with 286 cells. The cells contained in the data for analysis were 37 BJ (dermal, from human foreskin), 22 CRL-2338 (epithelial), 17 CRL-2339 (lymphoblastoid), 26 fetal cortex GW16 (neural, gestational week 16), 16 fetal cortex GW21 (neural, gestational week 21), 8 fetal cortex GW21 + 3 (neural, gestational week 21 + cultured for 3 weeks), 24 hiPSC (pluripotent), 54 HL-60 (myeloid, acute leukemia), 42 K562 (myeloid, chronic leukemia) and 40 Kera (epidermal, foreskin keratinocyte) cells. After filtering out lowly expressed genes, total Transcripts Per Kilobase Million (TPM) <10 and genes expressed in three or fewer cells, there were 18 206 genes remaining. The data were transformed as 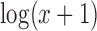 prior to analysis.
prior to analysis.
Real dataset 2: Biase data
This scRNA-seq dataset was created by Biase et al. (43) and contains 49 cells from nine one-cell, ten two-cell and five four-cell mouse embryos. This gives 9 one-cell cells, 20 two-cell cells and 20 four-cell cells. The data were collected to study cell fate inclination in mouse embryos. The dataset contains Fragments Per Kilobase Million (FPKM) measurements for 25 737 genes, of which 16 514 remained after filtering out genes which were expressed in <3 cells or whose total FPKM expression across all the cells was <10. The data were transformed as  prior to analysis.
prior to analysis.
Real dataset 3: Llorens–Bobadilla data
This real scRNA-seq dataset was created by Llorens–Bobadilla et al. (44) to study the progression and activation of neural stem cells (NSCs) under both normal conditions and after ischemic injury. They created scRNA-seq libraries for 130 naïve cells and 57 cells taken after ischemic injury. A total of 104 of the naïve cells were GLAST+/Prom1+, while the other 26 were PSA-NCAM+, a marker for neuroblast cells. For each cell, there were trimmed mean of M values (TMM) normalized FPKM measurements for 43 309 genes. Genes with a total TMM-FPKM expression <10 or expressed in <3 cells were filtered out, leaving 16 630 genes for analysis. Cells which expressed <15% of these genes were removed from the analysis, leaving 128 naïve cells and 56 ischemic injured cells. The data were transformed as  prior to analysis.
prior to analysis.
Real dataset 4: Shalek data
Shalek et al. (45) created scRNA-seq expression measurements for mouse bone-marrow-derived dendritic cells exposed to one of three pathogenic components, lipopolysaccharide (LPS), a synthetic mimic of bacterial lipopeptides (PAM) or viral-like double-stranded RNA (PIC). For each group of stimulated cells, samples were taken at 1, 2, 4 and 6 h. The two largest groups of cells exposed to stimulus, LPS and PAM, were selected for analysis by SparseDC. Prior to analysis, non-viable cells and cluster disrupted dendritic cells were removed, using the same process as the original authors, leaving 258 LPS cells and 159 PAM cells. The dataset contains TPM expression measurements for 27723 genes for each cell. Prior to analysis, any genes with total TPM expression <10 or expressed in <3 cells were filtered out of the analysis leaving 14 343 genes. The data were transformed as 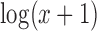 prior to analysis.
prior to analysis.
Modifying real datasets for known cluster changes
To create gold standard datasets where the true cell type changes are known, we took datasets that contain cells from one condition and assigned the cells into two conditions. For example, the original Biase data contain three types of cells: zygote, two-cell embryo and four-cell embryo. We assigned the cells into two groups by putting all zygote cells and half of the two-cell embryo cells into condition A and putting the rest of the two-cell embryo cells and all four-cell embryo cells into condition B. This created a two-condition dataset with known cell types and known changes in the composition of cell types: as the condition changes from A to B, one cell type (zygote) dies out, one cell type (four-cell embryo) emerges and one cell type (two-cell embryo) is present in both conditions. This corresponds to simulation scenario 4 in Table 1.
RESULTS
SparseDC was applied to each simulated and real dataset, with all of its parameters automatically determined by the algorithm (See Supplementary Materials) with the exception of the number of clusters, K, for which the true value is used. As in many clustering algorithms, this K is practically important, although its value is often given by ideas and algorithms that are not directly related to the proposed clustering algorithm (39,46), or in many cases set according to researchers’ experience or their understanding of the problem.
Measurement of performance
The performance of SparseDC is summarized using three statistics: classification rate, sensitivity and specificity. The classification rate is the proportion of samples (cells) that have been correctly classified. While it is usually used for classification, a supervised problem, it is well defined in our unsupervised clustering problem since in our simulations the true cluster labels are known. The classification rate ranges from 0 to 100%, and a high value means that the algorithm accurately discovers cell types in both conditions and also links the clusters correctly across conditions.
Sensitivity and specificity are used to describe the accuracy of detecting marker genes. Sensitivity is the proportion of marker genes that are successfully detected as marker genes, and specificity is the proportion of non-marker genes that are correctly identified as non-markers. They also range from 0 to 100%, and higher values indicate superior performance.
Performance on simulation data
The detailed results of the performance of SparseDC on simulation data are given in Supplementary Table S1. SparseDC was able to cluster the cells with an average classification rate of >99% and track them across conditions for all of the 42 simulation settings (Figure 2A and B; Supplementary Table S1). The classification rate of SparseDC is almost unchanged when half of the marker genes are condition-specific marker genes and the marker genes are abundant or sparse in the data, only scenario 3 sees a 0.205% decrease. When the marker genes are very sparse the classification rate of SparseDC declines by an average of 0.253% across the different scenarios, but is still above 99%.
Figure 2.
The average classification rates from the simulation tests. The cluster scenario refers to the cell composition in each condition as displayed in Table 1. Different levels of marker gene sparsity are represented by the different shades. The error bars represent the standard error of the results from the 100 simulations. (A) All marker genes are housekeeping marker genes. (B) Half of the marker genes are condition-specific marker genes.
When all of the marker genes are housekeeping marker genes, SparseDC had an average sensitivity and specificity of over 97 and 98%, respectively (Figure 3A and B; Supplementary Table S1). When half of the marker genes are condition-specific marker genes, the sensitivity declines by an average of 8%, while the specificity of SparseDC is almost unchanged (Figure 3C and D; Supplementary Table S1).
Figure 3.
The average sensitivity and specificity from the simulation tests. The cluster scenario refers to the cell composition in each condition as displayed in Table 1. Different levels of marker gene sparsity are represented by the different shades. The error bars represent the standard error of the results from the 100 simulations. (A and B) Sensitivity and specificity for simulations with all housekeeping marker genes. (C and D) Sensitivity and Specificity for simulations with half condition-specific marker genes.
Comparison with Huang et al. Method
We tried to compare the performance of SparseDC to the time-variant clustering (TVC) algorithm presented by Huang et al. (26), which is the only other algorithm currently available for DC analysis. The algorithm was developed for single-cell quantitative reverse transcriptase-polymerase chain reaction (qRT-PCR) data, which often contains no more than a few dozen genes. It is based on a Bayesian model and relies on a computationally expensive recursive jump Markov chain Monte Carlo that requires from 100 000 (default setting of the software) up to 1 000 000 iterations (suggested setting). In the original paper, the TVC algorithm was applied to datasets with 21 and 23 genes, and encountered convergence problems in a significant proportion of the realizations of Monte Carlo (26).
We applied the TVC algorithm to a single dataset simulated under scenario 1 of Table 1, which contains 1000 genes and 100 cells in each condition, and it would take more than a month to complete the suggested 1 000 000 iterations. When using a smaller number of iterations (100 000 iterations), it took >3 days to complete but did not give any meaningful clustering results (all cells were clustered into a single cluster). We also tried to apply the TVC algorithm on a much smaller simulated dataset that contained only 100 genes. With 1 000 000 iterations, the TVC algorithm took 7.85 h to run and still did not generate any meaningful clustering of the cells. See Supplementary Materials for details.
Through simulation, it is clear to us that the TVC algorithm is not suitable for DC analysis via scRNA-seq data, either in the sense of computational speed or performance. Comparatively, on both of the above datasets (1000 and 100 genes), SparseDC finished within 15 s and achieved a classification rate no less than 98%.
Performance on Pollen data
The first real dataset to which SparseDC was applied is the Pollen Data. The 10 cell types which we use in this analysis are drawn from four different tissue types, blood (CRL-2339, HL-60, K562), dermal or epidermal (BJ, CRL-2338, Kera), neural (GW16, GW21, GW21 + 3) and pluripotent (hiPSC). The three neural cell types are all taken from the fetal cortex and differ only in gestational week, either 16, 21 or 21 and then cultured for 3 weeks. The difference between these three neural cell types is smaller than the difference between GW and other cell types. We split the data such that the GW16 cells are in condition A and the GW21 and GW21 + 3 cells are in condition B. Ideally, SparseDC should be able to detect that the GW16, GW21 and GW21 + 3 cells should be in the same cluster, GW; at the same time, it should recognize the differences between them by identifying meaningful sets of condition-dependent and condition-specific marker genes. In this sense, this dataset provides an ideal situation to comprehensively evaluate SparseDC’s ability.
Using the idea described in the section titled ‘Modifying real datasets for known cluster changes’, three (HL-60, K562, Kera) of the remaining seven cell types were split amongst the conditions so that overall seven cell types are present in condition A (CRL-2338, CRL-2339, GW, hiPSC, HL-60, K562 and Kera) and five are present in condition B (BJ, GW, HL-60, K562 and Kera). Moreover, there are different marker gene types present in the split data: (i) All the marker genes for the HL-60, K562 and Kera cell types should be housekeeping marker genes, as cells from these types were randomly assigned to the two conditions. (ii) Marker genes for the GW cell type should include both housekeeping marker genes and condition-specific/condition-dependent marker genes, as the three subtypes of GW (GW16, GW21 and GW21 + 3) were non-randomly assigned to the two conditions.
SparseDC was applied to the divided data and achieved a 100% classification rate. This means that SparseDC correctly identified all cell types in both conditions, connected the cell types across conditions, and assigned all cells to their respective cell types, without an error. Notably, it was able to link the four cell types present in both conditions (GW, HL-60, K562 and Kera) across the conditions, including the neural cluster which has a different set of marker genes in each condition.
For the HL-60, K562 and Kera clusters, the marker gene selection and mean values were the same in each condition, indicating SparseDC correctly specified all the marker genes as housekeeping marker genes. For the neural cluster, SparseDC instead identified several condition-specific and condition-dependent marker genes (Figure 4). These genes indicate differences that have arisen from the additional gestational weeks and allow us to track the changes in gene expression in the fetal cortex over time. Of the five condition-specific marker genes for the GW16 cells, three are known to be related to neuronal development, CSRP2 (47), GAP43 (48) and PLXNA4 (49–51). Upon examining the condition-dependent marker genes, there were several genes which were upregulated for the neural cluster in condition A, made up of the GW16 cells, compared to the neural cluster in condition B, made up of the GW21 and GW21 + 3 cells. Among these genes CXADR has previously been shown to be highly expressed in the mouse brain during synapse formation with declining expression during maturation (52,53). Several other condition-dependent genes are also known to be related to neuronal development, including GNG3 (54), MIR100HG (55), MLLT11 (56) and TSPAN7 (57). Thus, we have seen that for this dataset SparseDC successfully detected that there were intracellular transcriptome changes for the neural cells across the conditions but that all the other cell types retained the same transcriptome profile across the conditions.
Figure 4.
Heatmaps of the gene expression of condition-specific and condition-dependent marker genes for the neural cluster (GW), detected by SparseDC in the Pollen data. (A) Condition A and (B) condition B correspond to how the data was split into two conditions as described in the text. For the plot labels, 2338 and 2339 represent the cell types CRL-2338 and CRL-2339, respectively. The color bars at the top of the plots represents the cell type of each of the cells. The top five genes are condition-specific marker genes for the neural cluster in condition A (‘AS’ was added to the gene names to denote this type of marker gene). The next nine genes are condition-dependent marker genes for the neural cluster which are upregulated in condition A (‘AD’ was added to the gene names to denote this type of marker gene). The last gene is a condition-dependent marker gene for the neural cluster in condition B (‘BD’ was added to the gene name to denote this type of marker gene).
The marker genes identified by SparseDC show clear differences in expression for the cell types for which they are marker genes compared to the other cell types, as is clear from the block pattern of expression seen in the heatmaps (Figure 5A and B), indicating that the marker genes identified by SparseDC are capable of characterizing the cell types in this dataset. To determine if the marker genes are also biologically relevant to the cell type, we examined the top 10 upregulated marker genes for each of the clusters (genes with the 10 largest positive 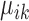 or
or 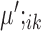 values for each
values for each  ; the names of these genes are given in Table 2, and the total numbers of marker genes identified in real datasets are given in Supplementary Tables S2–5) by examining their expression levels in different tissues as determined by the Genotype-Tissue Expression Project (GTEx) (58) (Table 2). The GTEx measured RNA expression in 53 different human tissues, and we considered a gene known to be upregulated in a tissue if it was among the top three tissues that express that gene. For the CRL-2339, HL-60 and K563 cells, the majority of the top 10 marker genes have all been shown to be upregulated in blood tissue types (Table 2). Many of the top marker genes for the dermal or epidermal cell types were also shown to be upregulated for those tissues (Table 2). While there are differences between the center vectors of the GW cluster in each condition, the top 10 marker genes are the same and again many of these marker genes have previously been shown to be upregulated in neural tissues (Table 2). For the pluripotent cell type, hiPSC, literature survey revealed that many of the top 10 marker genes have previously been shown to be related to the function of stem cells (59–65) (Table 2). Overall, we have seen that for this dataset the housekeeping marker genes for each of the cell types, as well as the condition-specific and condition-dependent marker genes for the GW cells (described in the last paragraph), agree well with existing gene annotations.
; the names of these genes are given in Table 2, and the total numbers of marker genes identified in real datasets are given in Supplementary Tables S2–5) by examining their expression levels in different tissues as determined by the Genotype-Tissue Expression Project (GTEx) (58) (Table 2). The GTEx measured RNA expression in 53 different human tissues, and we considered a gene known to be upregulated in a tissue if it was among the top three tissues that express that gene. For the CRL-2339, HL-60 and K563 cells, the majority of the top 10 marker genes have all been shown to be upregulated in blood tissue types (Table 2). Many of the top marker genes for the dermal or epidermal cell types were also shown to be upregulated for those tissues (Table 2). While there are differences between the center vectors of the GW cluster in each condition, the top 10 marker genes are the same and again many of these marker genes have previously been shown to be upregulated in neural tissues (Table 2). For the pluripotent cell type, hiPSC, literature survey revealed that many of the top 10 marker genes have previously been shown to be related to the function of stem cells (59–65) (Table 2). Overall, we have seen that for this dataset the housekeeping marker genes for each of the cell types, as well as the condition-specific and condition-dependent marker genes for the GW cells (described in the last paragraph), agree well with existing gene annotations.
Figure 5.
The heatmaps display the expression measurements for the top 10 upregulated marker genes detected by SparseDC in the Pollen data for each of the cell types in each condition. For a cell type k, the top 10 upregulated marker genes are the genes with the ten largest positive  or
or 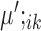 values. (A) Condition A and (B) condition B correspond to how the data was split into two conditions as described in the text. The color bars above the heatmaps indicate the cell type of each of the cells, while the color bars along the left side of the heatmaps indicate which of the cell types each of the genes was detected as a marker for. For the plot labels, 2338 and 2339 represent the cell types CRL-2338 and CRL-2339, respectively. In the heatmap for condition A, there are clear blocks of similar expression for the marker genes of all the present cell types. Similar blocks can be seen in the heatmap for condition B for the cell types which are present. For example, there are clear blocks of high expression for the Kera marker genes in both heatmaps as this type is present in both conditions, while there is only a block for the BJ marker genes in the heatmap for condition B since the BJ cells are only present in condition B.
values. (A) Condition A and (B) condition B correspond to how the data was split into two conditions as described in the text. The color bars above the heatmaps indicate the cell type of each of the cells, while the color bars along the left side of the heatmaps indicate which of the cell types each of the genes was detected as a marker for. For the plot labels, 2338 and 2339 represent the cell types CRL-2338 and CRL-2339, respectively. In the heatmap for condition A, there are clear blocks of similar expression for the marker genes of all the present cell types. Similar blocks can be seen in the heatmap for condition B for the cell types which are present. For example, there are clear blocks of high expression for the Kera marker genes in both heatmaps as this type is present in both conditions, while there is only a block for the BJ marker genes in the heatmap for condition B since the BJ cells are only present in condition B.
Table 2. Top 10 upregulated marker genes for each of the cell types in the Pollen data.
| Cell type | Tissue type | Top 10 marker genes |
|---|---|---|
| CRL-2339 | Blood | CD48(58), CD52(58), CD74(58), ELK2AP, HLA-DPA1(58), HLA-DRA(58), HLA-DRB1(58), HLA-DRB5(58), IGJ, MS4A1(58) |
| HL-60 | Blood | AIF1(58), ARHGDIB(58), CST7(58), CTSG(58), LAT2(58), MPO(58), MS4A3(58), PRG2(58), PRTN3(58), SRGN(58) |
| K562 | Blood | GAGE4(58), GATA1(58), HBA2(58), HBG1(58), HBG2(58), PRAME, RHAG(58), RHOXF2, SNAR-A10, SNAR-A5, SNAR-A6, SNAR-A9 |
| BJ | Dermal or epidermal | COL1A2(58), CRYAB, DCN(58), DKK1(58), GREM1(58), LUM, PSG5(58), SERPINE1(58), TAGLN, TNFRSF11B |
| CRL-2338 | Dermal or epidermal | IFI27, KRT15(58), KRT81, LCN2, RARRES1, S100A8, S100A9, S100P, SLPI, STEAP4(58) |
| Kera | Dermal or epidermal | AREG, C19orf33(58), FGFBP1(58), KRT14(58), KRT17(58), KRT5(58), KRT6A(58), S100A14(58), S100A2(58), SERPINB5(58) |
| GW | Neural | C1orf61(58), DCX(58), FXYD6(58), GPM6A(58), MAP1B(58), NNAT(58), RTN1(58), SOX11(58), STMN2(58), TUBA1A(58) |
| hiPSC | Pluripotent | CRABP1, DPPA4(59), ESRG(60), PHC1(61), SFRP2(62), SHISA2, SLC7A3(63), TDGF1(64), VSNL1, ZIC2(65) |
Underlined genes have been previously shown to be upregulated in the tissue of interest or in the case of the stem cell cluster, related to the functioning of stem cells.
Performance on Biase data
When applied to the Biase data, SparseDC clustered the cells and linked them across conditions with a classification rate of 100%. See Supplementary Materials for a detailed description of the results.
Performance on Llorens–Bobadilla data
The third real dataset analyzed by SparseDC is the Llorens–Bobadilla data. During their analysis of the data, the original authors used successive rounds of principal component analysis (PCA) and hierarchical clustering and manually incorporated knowledge of known gene markers to detect subpopulations in the data. They finally inferred the existence of four likely subpopulations in the data, corresponding to oligodendrocytes, quiescent NSCs (qNSCs), activated NSCs (aNSCs) and neuroblasts. As such, SparseDC was applied to the dataset with the number of clusters set to four.
Most of the clusters detected by SparseDC contain a mixture of ischemic injured and naïve cells (Table 3). All of the cells in cluster 4 are naïve PSA-NCAM+ cells. This mirrors the result of the original authors who found that the PSA-NCAM+ and GLAST+/Prom1+ cells had distinct transcriptomes, with the PSA-NCAM+ cells corresponding to neuroblasts (44). The authors of the original paper clustered genes highly correlated with the first four principal components of the data into seven modules using hierarchical clustering. They then associated each of the modules with subpopulations of cells using their expression levels; module 1 was associated with oligodendrocyte cells, modules 2 and 3 were associated with both qNSCs and aNSCs, modules 4, 5 and 6 were associated with aNSCs, and module 7 was associated with neuroblast cells. These modules can be used to validate the results of SparseDC by examining the housekeeping up- and downregulated genes and calculating the proportion of the detected marker genes in each module for each cluster.
Table 3. The clustering solution from the application of SparseDC to the Llorens–Bobadilla data.
| Condition | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Ischemic injured | 20 | 11 | 25 | 0 |
| Naive | 63 | 12 | 28 | 25 |
The ischemic injured cells are in the first condition, while the naïve cells are in the second. For example, cluster 1 contains 20 cells in the first condition, ischemic injured cells and 63 naïve cells from the second condition.
For cluster 1, 62% of the upregulated housekeeping marker genes are from module 3 and 10% are from module 2, both of which are associated with qNSCs and aNSCs, while the downregulated housekeeping genes are mainly found in module 4 (38%) and module 5 (30%), both of which are expressed for aNSCs (Table 4). As cluster 1 expresses upregulated genes for qNSCs and aNSCs and downregulated genes for aNSCs, the cluster likely contains the qNSC cells.
Table 4. The percentage of housekeeping up and downregulated genes detected by SparseDC on the Llorens–Bobadilla data contained in each of the modules from the original paper.
| 1-Up | 1-Down | 2-Up | 2-Down | 3-Up | 3-Down | 4-Up | 4-Down | |
|---|---|---|---|---|---|---|---|---|
| # of Genes | 208 | 158 | 350 | 124 | 726 | 39 | 194 | 703 |
| Module 1 | 0% | 4% | 65% | 0% | 0% | 8% | 4% | 2% |
| Module 2 | 10% | 0% | 2% | 0% | 0% | 28% | 0% | 15% |
| Module 3 | 62% | 0% | 0% | 57% | 0.50% | 51% | 0% | 25% |
| Module 4 | 0% | 38% | 3% | 1% | 48% | 0% | 0% | 3% |
| Module 5 | 0% | 30% | 0% | 3% | 10% | 0% | 7% | 0% |
| Module 6 | 0% | 3% | 0% | 0% | 13% | 0% | 0% | 0% |
| Module 7 | 0% | 9% | 0% | 4% | 1% | 0% | 55% | 0% |
‘1-Up’/‘1-Down’ stands for up/downregulated in cluster 1 and so forth. Housekeeping genes are defined as those which have the same center value in the SparseDC solution for a cluster in both conditions. upregulated genes are those which have a positive center value in the SparseDC solution while downregulated genes have a negative center value.
For cluster 2, the module containing oligodendrocyte markers, module 1, contains 65% of the upregulated genes. The downregulated genes are mainly contained in module 3 (57%), which is expressed in both qNSCs and aNSCs. This indicates that cells in cluster 2 are likely to be oligodendrocyte cells.
For cluster 3, the majority (71%) of the upregulated markers are contained in modules 4, 5 and 6, which are expressed in aNSCs. While the majority, 79%, of the downregulated markers for cluster 3 are from modules 2 and 3, which are expressed in qNSCs and aNSCs. This provides an indication that the cells contained in cluster 3 are the aNSCs. While the downregulated genes for this cluster are from modules that are expressed in both qNSCs and aNSCs, it is important to note there are only a few genes detected as downregulated for cluster 3 (Table 4) and the high expression of modules 2 and 3 by cluster 1 has led to them being detected as downregulated for almost all other clusters.
Module 7, which is associated with neuroblast markers, contains 55% of the upregulated housekeeping genes for cluster 4. As previously discussed, all of the cells in cluster 4 are naïve PSA-NCAM+ cells, and thus it is likely that the cells in cluster 4 are neuroblast cells.
On this dataset, SparseDC detected subpopulations of cells in the data and identified relevant marker genes which provide an indication as to the cell type of each cluster. A heatmap of the top 10 upregulated marker genes for each condition is displayed in Figure 6. The top 10 upregulated genes are those genes with the 10 largest positive center values for each cluster. It is clear from the plot that these marker genes do a good job of separating this dataset, with clear blocks of expression visible relating to each cluster and its marker genes.
Figure 6.
Heatmaps of the expression of the top 10 upregulated housekeeping marker genes detected by SparseDC for the Llorens–Bobadilla data. The top 10 housekeeping marker genes are identified as the 10 genes which have the largest positive center value, 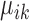 , in both conditions, ischemic injured (A) and naive (B). The color bars at the top represent the clusters of the cells, while the color bars at the side represent the marker genes for each cluster. The numbers on the plot correspond to the clusters found in the data, where cluster 1 contains the likely qNSC cells, cluster 2 contains the likely oligodendrocyte cells, cluster 3 contains the likely aNSC cells and cluster 4 contains the likely neuroblast cells. For all of the cell clusters there are clear blocks relating to the marker genes for the cluster.
, in both conditions, ischemic injured (A) and naive (B). The color bars at the top represent the clusters of the cells, while the color bars at the side represent the marker genes for each cluster. The numbers on the plot correspond to the clusters found in the data, where cluster 1 contains the likely qNSC cells, cluster 2 contains the likely oligodendrocyte cells, cluster 3 contains the likely aNSC cells and cluster 4 contains the likely neuroblast cells. For all of the cell clusters there are clear blocks relating to the marker genes for the cluster.
SparseDC detected several genes as either condition-specific or condition-dependent for cluster 1 and cluster 3 (Table 5), and some of them are known to be biologically relevant from the literature. Gfap, which is a condition-specific gene for the injured cells in cluster 1, has previously been shown to be important in repair after a brain injury, particularly in the formation of glial scars (66) and has been found to have increased expression after an ischemic stroke (67). Stmn1 was a condition-dependent gene with higher expression in the injured cells and is known to be upregulated following ischemic injury (68,69). Fos was detected as a downregulated condition-specific gene for the naïve cells in cluster 1 and an upregulated condition-dependent gene for the injured cells in cluster 3, and its expression has previously been shown to be upregulated after injury (70). Fos may not have been detected as an upregulated gene for the injured cells in cluster 1, as it also plays a role in the normal development of NSCs (71). Fxyd6 was also detected as a downregulated condition-specific gene for the naïve cells in cluster 1 and has previously been shown to respond to hypoxia (72). Condition-specific genes for the naïve cells in cluster 1 include genes involved in differentiation, Cntfr (73), targets of Notch signaling, Fjx1 (74) and genes involved in warding off neuronal disorders, Tpp1 (75,76). Some condition-dependent genes for the naïve cells in cluster 1 have also been shown to play a role in the functioning and differentiation of NSCs such as Fgfr3 (77), Sparcl1 (78–80) and Aqp4 (81), while Gpc5 has been shown to activate Hedgehog signaling (82), which plays a role in determining stem cell positional identity (83). For cluster 3 there was also one condition-specific upregulated gene, Junb, which has been shown to be related to ischemic injury (84,85). No condition-specific or condition-dependent markers were detected for cluster 2. Cluster 4 only contains cells from a single condition and so all of its marker genes are housekeeping marker genes.
Table 5. Condition-specific and condition-dependent genes identified by SparseDC for the clusters in the Llorens–Bobadilla data.
| Cluster | Naïve CS | Naïve CD | Injured CS | Injured CD |
|---|---|---|---|---|
| 1-Up | Tril, Cntfr, Tlcd1, Fjx1, Tpp1, AI464131 | Fgfr3, Grm3, Gpc5, Slc39a12, Ephx2, Aqp4, Dhrs7, Sparcl1 | Gfap | Stmn1 |
| 1-Down | Fos, Fxyd6 | |||
| 3-Up | Junb | Fos |
Definitions of the different types of marker genes can be found in the section ‘The optimization problem that SparseDC proposes’. There were no condition-specific or condition-dependent genes detected for cluster 2 and cluster 4 contains cells from only a single condition. In the table CS stands for condition-specific genes while CD stands for condition-dependent genes, so for example, naïve CS means condition-specific genes for the naïve cells.
SparseDC also tracks changes in the proportion of cell types present in each condition, and for this dataset it agrees with the findings of the original authors. Leaving out cluster 4, which contains the PSA-NCAM+ cells, there is a larger proportion of the naïve cells in cluster 1 (61.2%), which expresses qNSC markers, compared to the injured cells (35.7%). Conversely, cluster 3, which expresses aNSC markers, contains 27.2% of the naïve cells and 44.6% of the injured cells. Llorens–Bobadilla et al. found that injury led to the activation of a larger proportion of the NSCs.
Performance on Shalek data
The fourth real dataset analyzed by SparseDC is the Shalek data, which contains scRNA-seq measurements for mouse bone-marrow-derived dendritic cells exposed to different pathogenic components and taken at different time points (45). In their analysis, Shalek et al. clustered the genes into 12 modules, four of which were significantly correlated with the first three principal components of the single cell gene expression profiles. These four modules are the core anti-viral module, the maturity module, the peaked inflammatory module and the sustained inflammatory module. See the original paper for additional details on the modules and the genes contained in each. Their analysis showed that there was significant variation within each stimulus and time point, with some cells responding to the stimulus faster than the others.
The 258 LPS cells used for analysis in SparseDC consist of 75, 65, 60 and 58 cells from 1, 2, 4 and 6 h times points, respectively, and the 159 PAM cells used for analysis in SparseDC consist of 48, 41, 35 and 35 cells from the four time points, respectively. Shalek et al. empirically determined the number of clusters present in the data to be four, which was used as the cluster number for SparseDC.
SparseDC detected two common subpopulations present in both datasets and a subpopulation unique to each of the groups (Table 6). Using the time each cell was captured to analyze the clustering result, it can be seen that cluster 1 corresponds to an early state containing all of the 1 h cells for both conditions, with additional 2 h cells from both conditions and some 4 h PAM cells (Table 6). On the other hand, cluster 3 corresponds to a later state containing all the LPS cells from the 4 and 6 h time points and the majority of the 6 h PAM cells. Cluster 2 is unique to the PAM cells and contains mostly 2 and 4 h cells, while cluster 4, which is unique to the LPS cells, contains samples solely from 2 h.
Table 6. Breakdown of the SparseDC clustering result for the Shalek data by time point.
| Cluster | 1 h | 2 h | 4 h | 6 h |
|---|---|---|---|---|
| 1 | 75, 48 | 15, 23 | 0, 3 | 0, 0 |
| 2 | 0, 0 | 0, 17 | 0, 23 | 0, 5 |
| 3 | 0, 0 | 7, 1 | 60, 9 | 58, 30 |
| 4 | 0, 0 | 43, 0 | 0, 0 | 0, 0 |
The first value in each entry is the number of samples from the LPS data in each cluster, while the second value is the number of samples from the PAM data. For example, in cluster 1, there are 75 LPS cells and 48 PAM cells from the 1 h time point, 15 LPS and 23 PAM cells from the 2 h time point and 3 PAM cells from the 4 h time point
One way of investigating the biological relevance of each of the clusters is to compare the marker genes detected by SparseDC to the gene modules found by the original authors. This is done by looking at the proportion of housekeeping up- and downregulated genes contained in each module for each cluster.
For cluster 1, many of the downregulated marker genes come from either the core anti-viral module (43.4%), or the sustained inflammatory module (35.2%), both of which showed limited expression at early time points in the original paper (Table 7). This cluster appears to be composed of cells which are not yet responding to or just beginning to respond to the stimulus.
Table 7. Percentage of SparseDC detected housekeeping up/downregulated genes present in each module for each cluster in the Shalek data.
| Module | 1-Up | 1-Down | 2-Up | 2-Down | 3-Up | 3-Down | 4-Up | 4-Down |
|---|---|---|---|---|---|---|---|---|
| Core anti-viral | 0% | 43.41% | 0% | 47.27% | 52.27% | 0% | 5.26% | 18.75% |
| Maturity | 0% | 6.04% | 2.90% | 1.81% | 2.84% | 0% | 5.26% | 0% |
| Peaked inflammatory | 0% | 1.10% | 20.29% | 0% | 0% | 0% | 17.54% | 6.25% |
| Sustained inflammatory | 0% | 35.16% | 31.88% | 1.81% | 22.16% | 0% | 7.02% | 25% |
‘1-Up’/‘1-Down’ stands for up/downregulated in cluster 1 and so forth. Up/downregulated housekeeping marker genes are defined as those which have a positive/negative center value in the SparseDC solution and the same value in both conditions.
Cluster 2 contains only cells stimulated by PAM from either 2, 4 or 6 h and many of the upregulated housekeeping genes are from the peaked inflammatory module (20.3%), or the sustained inflammatory module (31.9%), while 47% of the downregulated marker genes are from the core anti-viral module. This cluster is then most likely composed of PAM cells responding to the stimulus. The upregulation of inflammatory related modules and the downregulation of the core anti-viral module make sense since there are only PAM cells in this cluster and Shalek et al. found that the PAM cells did not begin to express the core anti-viral module until late after stimulation.
The largest cluster detected by SparseDC, cluster 3, contains 125 LPS cells and 40 PAM cells all from 2 h onward. This cluster contains all of the LPS cells from the 4 and 6 h time points. Upregulated housekeeping marker genes for this cluster come from either the core anti-viral module (52.3%) or the sustained inflammatory module (22.2%). This mirrors the findings of Shalek et al. (45), who found that the core anti-viral response genes were detectable in only some LPS cells early on but turned on in most cells between 2 and 4 h.
The LPS specific cluster, cluster 4, contains only LPS cells from the 2 h time point. The module with the most upregulated genes for cluster 4 is the peaked inflammatory module. Again, this is similar to the findings of Shalek et al., who identified a rapid rise in expression of the peaked inflammatory module for the LPS cells and then a decrease in expression as time progressed.
The heatmap of the top 10 upregulated housekeeping marker genes, reveals blocks of similar expression present in each condition for each of the clusters (Supplementary Figure S1). The top 10 upregulated housekeeping marker genes are the genes which have the largest common positive center value. The blocks in the heatmap for this dataset are less distinct than for other datasets, which is most likely due to the cells being of the same type at different time points, with many of the cells transitioning from state to state and as such may be expressing the marker genes of the state they are transitioning into.
There were several marker genes detected as condition-specific and condition-dependent for cluster 1 and cluster 3. For cluster 1, there were six condition-specific genes for the LPS cells and 10 for the PAM cells, along with 15 condition-dependent genes. There were five condition-specific genes for the LPS cells in cluster 3, 34 condition-specific genes for the PAM cells and 32 condition-dependent genes. Among these, TNF, which has previously been shown to be induced by both LPS and PAM (86), was detected as a condition-specific downregulated gene for the PAM cells in cluster 1 and the LPS cells in cluster 3, possibly indicating differences in the reaction times to the stimulus as previously LPS was shown to induce a greater increase in TNF expression. CXCL10, which has previously been shown to be promoted by LPS (87), was detected as a condition-dependent upregulated gene for the LPS cells in both cluster 1 and cluster 3. Several genes that have previously been identified as sensitive to LPS were detected as upregulated for the LPS cells (88), such as IFIT2, IFIT3, IFIH1, IFI44, NT5C3, RSAD2 and ISG15, which are condition-dependent upregulated genes for the LPS cells in cluster 3, and OAS2, which is a condition-specific upregulated gene for the LPS cells in cluster 3.
DISCUSSION
We have proposed the concept of differential clustering analysis, and we have presented SparseDC, a powerful tool which effectively clusters cells from two conditions, links the clusters between conditions, identifies a set of marker genes for each cluster and determines which of the marker genes change between the two conditions. We have also proposed classifying marker genes in DC analysis into three categories.
SparseDC has demonstrated its applicability and efficiency across a range of simulated data, as well as four real datasets. In simulation data, SparseDC was able to achieve high accuracy in both discovering cell types and identifying marker genes. In real datasets where the cell types are known, we developed a strategy to create two-condition data where the true changes of cell types are known. On both modified datasets, SparseDC achieved high accuracy in discovering cell types and linking them across conditions, and for the Pollen data it identified marker genes for each cell type that are highly consistent with known gene annotations and was able to differentiate between the three different types of marker genes. On the real two-condition datasets, SparseDC was able to identify clusters with biologically relevant marker genes including condition-dependent and condition-specific marker genes that are relevant to the condition change.
SparseDC is highly computationally efficient. As shown in Supplementary Materials, the computing time increases roughly linearly as the number of cells increases. The memory requirement is also linear with respect to the size of the data matrix. This makes SparseDC especially suitable for scRNA-seq datasets with large numbers of cells.
SparseDC is the first algorithm that is suitable for DC analysis of scRNA-seq data. It may be useful for researchers working on a vast array of problems, such as examining the differences in diseased versus healthy cells, determining the effect of a treatment on cancer cells or studying the effects of experimental stress on healthy cells. While we have focused on scRNA-seq data in this paper, SparseDC is applicable to many other forms of single-cell data such as single-cell qRT-PCR data, and applicable to bulk-based RNA-seq/microarray data. For example, if in two hospitals/countries, two groups of patients with a particular disease have their transcriptome profile measured by bulk-based RNA-seq or microarrays, SparseDC can be used to discover the composition of patients with different (unknown) subtypes of the disease. Some of these subtypes may be present in the two hospitals/countries, while some others may not. Additionally, as a general algorithm that detects shared/distinct clusters for two groups of samples, SparseDC may also be applied to problems outside the field of biology.
At present, there are several limitations to SparseDC. First, the current version of SparseDC relies on the user to set the value of K, the total number of clusters. In the Supplementary Materials, we have shown how SparseDC performs when the value of K is set incorrectly for the Pollen data. In the immediate future, we will work on developing a method to computationally determine the value of K. We have tried to adapt the popular ‘gap statistic’ approach for selecting K automatically, and it seemed to work properly on a simulated dataset (See Supplementary Materials for details). We have included this implementation in our R package to serve as a rudimentary option for choosing K.
Second, SparseDC takes normalized gene expression data as input, and does not explicitly take into consideration the count nature of sequencing data or the excess zeros partly due to ‘dropouts’ (89,90) in the data. Additional analysis was performed on simulated data with excess zeros or generated from the negative binomial distribution (See Supplementary Materials for details), and we found that SparseDC shows some deterioration in its performance, although this deterioration seems quite affordable. While the current model of SparseDC is largely nonparametric and has displayed satisfactory performance on both simulation data and real data, we will explore possible ways to specifically deal with excess zeros and determine if this increases the power of SparseDC, as some current literature shows that modeling these dropouts explicitly may improve the power of statistical inference (14,91–93).
Finally, the current version of the SparseDC algorithm can only be applied to data with cells from two biological conditions. In the future, we will extend it to data from more than two conditions, which can be done by modifying the target function. However, work will be needed to derive the closed-form solution for each iteration of the multiple condition model.
DATA AVAILABILITY
SparseDC has been implemented in R and is available as an R package from CRAN (‘https://cran.r-project.org/web/packages/SparseDC/index.html’). A vignette is also available at ‘https://cran.r-project.org/web/packages/SparseDC/vignettes/SparseDC.html’. The scRNA-Seq data from Pollen et al. (42) are available from the NCBI Sequence Read Archive under accession number SRP041736. The scRNA-seq data from Llorens–Bobadilla et al. (44) are available under GEO accession number GSE67833. The scRNA-seq data from Biase et al. (43) are available from the additional files for the article. The scRNA-seq data from Shalek et al. (45) are available under GEO accession number GSE48968.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Dr Nicholas Navin at The University of Texas MD Anderson Cancer Center for valuable discussions about the methods and real data analysis of the paper.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Institutes of Health [R03CA212964 to J.L., R01CA194697 to S.Z., J.L., R01CA197128 to J.L.]. Funding for open access charge: National Institutes of Health [R03CA212964 to J.L., R01CA194697 to S.Z., J.L., R01CA197128 to J.L.].
Conflict of interest statement. None declared.
REFERENCES
- 1. Arendt D., Musser J.M., Baker C.V.H., Bergman A., Cepko C., Erwin D.H., Pavlicev M., Schlosser G., Widder S., Laubichler M.D. et al. The origin and evolution of cell types. Nat. Rev. Genet. 2016; 17:744–757. [DOI] [PubMed] [Google Scholar]
- 2. Saadatpour A., Lai S., Guo G., Yuan G.-C.. Single-cell analysis in cancer genomics. Trends Genet. 2015; 31:576–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Gawad C., Koh W., Quake S.R.. Single-cell genome sequencing: current state of the science. Nat. Rev. Genet. 2016; 17:175–188. [DOI] [PubMed] [Google Scholar]
- 4. Kuipers J., Jahn K., Beerenwinkel N.. Advances in understanding tumour evolution through single-cell sequencing. Biochim. Biophys. Acta. 2017; 1867:127–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Patel A.P., Tirosh I., Trombetta J.J., Shalek A.K., Gillespie S.M., Wakimoto H., Cahill D.P., Nahed B.V., Curry W.T., Martuza R.L. et al. Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma. Science. 2014; 344:1396–1401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Dalerba P., Kalisky T., Sahoo D., Rajendran P.S., Rothenberg M.E., Leyrat A.A., Sim S., Okamoto J., Johnston D.M., Qian D. et al. Single-cell dissection of transcriptional heterogeneity in human colon tumors. Nat. Biotech. 2011; 29:1120–1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Shapiro E., Biezuner T., Linnarsson S.. Single-cell sequencing-based technologies will revolutionize whole-organism science. Nat. Rev. Genet. 2013; 14:618–630. [DOI] [PubMed] [Google Scholar]
- 8. Macosko E.Z., Basu A., Satija R., Nemesh J., Shekhar K., Goldman M., Tirosh I., Bialas A.R., Kamitaki N., Martersteck E.M. et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell. 2015; 161:1202–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Wu A.R., Neff N.F., Kalisky T., Dalerba P., Treutlein B., Rothenberg M.E., Mburu F.M., Mantalas G.L., Sim S., Clarke M.F. et al. Quantitative assessment of single-cell RNA-sequencing methods. Nat. Methods. 2014; 11:41–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Buettner F., Natarajan K.N., Casale F.P., Proserpio V., Scialdone A., Theis F.J., Teichmann S.A., Marioni J.C., Stegle O.. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat. Biotech. 2015; 33:155–160. [DOI] [PubMed] [Google Scholar]
- 11. Xu C., Su Z.. Identification of cell types from single-cell transcriptomes using a novel clustering method. Bioinformatics. 2015; 31:1974–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Stegle O., Teichmann S.A., Marioni J.C.. Computational and analytical challenges in single-cell transcriptomics. Nat. Rev. Genet. 2015; 16:133–145. [DOI] [PubMed] [Google Scholar]
- 13. Grün D., Lyubimova A., Kester L., Wiebrands K., Basak O., Sasaki N., Clevers H., van Oudenaarden A.. Single-cell messenger RNA sequencing reveals rare intestinal cell types. Nature. 2015; 525:251–255. [DOI] [PubMed] [Google Scholar]
- 14. Pierson E., Yau C.. ZIFA: dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biol. 2015; 16:241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. žurauskienė J., Yau C.. pcaReduce: hierarchical clustering of single cell transcriptional profiles. BMC Bioinformatics. 2016; 17:140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Trapnell C., Cacchiarelli D., Grimsby J., Pokharel P., Li S., Morse M., Lennon N.J., Livak K.J., Mikkelsen T.S., Rinn J.L.. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014; 32:381–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Setty M., Tadmor M.D., Reich-Zeliger S., Angel O., Salame T.M., Kathail P., Choi K., Bendall S., Friedman N., Pe’er D.. Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat. Biotech. 2016; 34:637–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zeisel A., Muñoz-Manchado A.B., Codeluppi S., Lönnerberg P., Manno G.L., Juréus A., Marques S., Munguba H., He L., Betsholtz C. et al. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science. 2015; 347:1138–1142. [DOI] [PubMed] [Google Scholar]
- 19. Grün D., Muraro M.J., Boisset J.-C., Wiebrands K., Lyubimova A., Dharmadhikari G., van den Born M., van Es J., Jansen E., Clevers H. et al. De Novo prediction of stem cell identity using single-cell transcriptome data. Cell Stem Cell. 2016; 19:266–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Li H., Courtois E.T., Sengupta D., Tan Y., Chen K.H., Goh J.J.L., Kong S.L., Chua C., Hon L.K., Tan W.S. et al. Reference component analysis of single-cell transcriptomes elucidates cellular heterogeneity in human colorectal tumors. Nat. Genet. 2017; 49:708–718. [DOI] [PubMed] [Google Scholar]
- 21. Coifman R.R., Lafon S., Lee A.B., Maggioni M., Nadler B., Warner F., Zucker S.W.. Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps. Proc. Natl. Acad. Sci. U.S.A. 2005; 102:7426–7431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Marco E., Karp R.L., Guo G., Robson P., Hart A.H., Trippa L., Yuan G.-C.. Bifurcation analysis of single-cell gene expression data reveals epigenetic landscape. Proc. Natl. Acad. Sci. U.S.A. 2014; 111:E5643–E5650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Shin J., Berg D.A., Zhu Y., Shin J.Y., Song J., Bonaguidi M.A., Enikolopov G., Nauen D.W., Christian K.M., Ming G. et al. Single-cell RNA-seq with waterfall reveals molecular cascades underlying adult neurogenesis. Cell Stem Cell. 2015; 17:360–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Welch J.D., Hartemink A.J., Prins J.F.. SLICER: inferring branched, nonlinear cellular trajectories from single cell RNA-seq data. Genome Biol. 2016; 17:106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Matsumoto H., Kiryu H.. SCOUP: a probabilistic model based on the Ornstein–Uhlenbeck process to analyze single-cell expression data during differentiation. BMC Bioinformatics. 2016; 17:232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Huang W., Cao X., Biase F.H., Yu P., Zhong S.. Time-variant clustering model for understanding cell fate decisions. Proc. Natl. Acad. Sci. U.S.A. 2014; 111:E4797–E4806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Mocellin S., Provenzano M., Rossi C.R., Pilati P., Nitti D., Lise M.. Use of quantitative real-time PCR to determine immune cell density and cytokine gene profile in the tumor microenvironment. J. Immunol. Methods. 2003; 280:1–11. [DOI] [PubMed] [Google Scholar]
- 28. Mohammad M.H., Al-shammari A.M., Al-Juboory A.A., Yaseen N.Y.. Characterization of neural stemness status through the neurogenesis process for bone marrow mesenchymal stem cells. Stem Cells Cloning. 2016; 9:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Brazel C.Y., Limke T.L., Osborne J.K., Miura T., Cai J., Pevny L., Rao M.S.. Sox2 expression defines a heterogeneous population of neurosphere-forming cells in the adult murine brain. Aging Cell. 2005; 4:197–207. [DOI] [PubMed] [Google Scholar]
- 30. Tibshirani R., Saunders M., Rosset S., Zhu J., Knight K.. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. B. 2005; 67:91–108. [Google Scholar]
- 31. Hastie T., Tibshirani R., Wainwright M.. Statistical learning with sparsity: the lasso and generalizations. 2015; Chapman & Hall/CRC. [Google Scholar]
- 32. L. Lun A.T., Bach K., Marioni J.C.. Pooling across cells to normalize single-cell RNA sequencing data with many zero counts. Genome Biol. 2016; 17:75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Ding B., Zheng L., Zhu Y., Li N., Jia H., Ai R., Wildberg A., Wang W.. Normalization and noise reduction for single cell RNA-seq experiments. Bioinformatics. 2015; 31:2225–2227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Katayama S., Töhönen V., Linnarsson S., Kere J.. SAMstrt: statistical test for differential expression in single-cell transcriptome with spike-in normalization. Bioinformatics. 2013; 29:2943–2945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Anders S., Huber W.. Differential expression analysis for sequence count data. Genome Biol. 2010; 11:R106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Bullard J.H., Purdom E., Hansen K.D., Dudoit S.. Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics. 2010; 11:94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Robinson M.D., Oshlack A.. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2010; 11:R25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Witten D.M., Tibshirani R.. A framework for feature selection in clustering. J. Am. Stat. Assoc. 2010; 105:713–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Tibshirani R., Walther G., Hastie T.. Estimating the number of clusters in a data set via the gap statistic. J. Royal Stat. Soc. B. 2001; 63:411–423. [Google Scholar]
- 40. Simon N., Friedman J., Hastie T., Tibshirani R.. A sparse-group lasso. J. Comput. Graph. Stat. 2013; 22:231–245. [Google Scholar]
- 41. Chambolle A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004; 20:89–97. [Google Scholar]
- 42. Pollen A.A., Nowakowski T.J., Shuga J., Wang X., Leyrat A.A., Lui J.H., Li N., Szpankowski L., Fowler B., Chen P. et al. Low-coverage single-cell mRNA sequencing reveals cellular heterogeneity and activated signaling pathways in developing cerebral cortex. Nat. Biotech. 2014; 32:1053–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Biase F.H., Cao X., Zhong S.. Cell fate inclination within 2-cell and 4-cell mouse embryos revealed by single-cell RNA sequencing. Genome Res. 2014; 24:1787–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Llorens-Bobadilla E., Zhao S., Baser A., Saiz-Castro G., Zwadlo K., Martin-Villalba A.. Single-cell transcriptomics reveals a population of dormant neural stem cells that become activated upon brain injury. Cell Stem Cell. 2015; 17:329–340. [DOI] [PubMed] [Google Scholar]
- 45. Shalek A.K., Satija R., Shuga J., Trombetta J.J., Gennert D., Lu D., Chen P., Gertner R.S., Gaublomme J.T., Yosef N. et al. Single-cell RNA-seq reveals dynamic paracrine control of cellular variation. Nature. 2014; 510:363–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Chiang M.M.-T., Mirkin B.. Intelligent choice of the number of clusters in k-means clustering: an experimental study with different cluster spreads. J. Classif. 2010; 27:3–40. [Google Scholar]
- 47. Ling K.-H., Hewitt C.A., Beissbarth T., Hyde L., Banerjee K., Cheah P.-S., Cannon P.Z., Hahn C.N., Thomas P.Q., Smyth G.K. et al. Molecular networks involved in mouse cerebral corticogenesis and spatio-temporal regulation of Sox4 and Sox11 novel antisense transcripts revealed by transcriptome profiling. Genome Biol. 2009; 10:R104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Benowitz L.I., Routtenberg A.. GAP-43: an intrinsic determinant of neuronal development and plasticity. Trends Neurosci. 1997; 20:84–91. [DOI] [PubMed] [Google Scholar]
- 49. Haklai-Topper L., Mlechkovich G., Savariego D., Gokhman I., Yaron A.. Cis interaction between Semaphorin6A and Plexin-A4 modulates the repulsive response to Sema6A. EMBO J. 2010; 29:2635–2645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Suto F., Ito K., Uemura M., Shimizu M., Shinkawa Y., Sanbo M., Shinoda T., Tsuboi M., Takashima S., Yagi T. et al. Plexin-A4 mediates axon-repulsive activities of both secreted and transmembrane semaphorins and plays roles in nerve fiber guidance. J. Neurosci. 2005; 25:3628–3637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Yaron A., Huang P.-H., Cheng H.-J., Tessier-Lavigne M.. Differential requirement for Plexin-A3 and -A4 in mediating responses of sensory and sympathetic neurons to distinct class 3 Semaphorins. Neuron. 2005; 45:513–523. [DOI] [PubMed] [Google Scholar]
- 52. Gonzalez-Lozano M.A., Klemmer P., Gebuis T., Hassan C., van Nierop P., van Kesteren R.E., Smit A.B., Li K.W.. Dynamics of the mouse brain cortical synaptic proteome during postnatal brain development. Sci. Rep. 2016; 6:35456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Honda T., Saitoh H., Masuko M., Katagiri-Abe T., Tominaga K., Kozakai I., Kobayashi K., Kumanishi T., Watanabe Y.G., Odani S. et al. The coxsackievirus-adenovirus receptor protein as a cell adhesion molecule in the developing mouse brain. Mol. Brain Res. 2000; 77:19–28. [DOI] [PubMed] [Google Scholar]
- 54. Leypoldt F., Lewerenz J., Methner A.. Identification of genes up-regulated by retinoic-acid-induced differentiation of the human neuronal precursor cell line NTERA-2 cl.D1. J. Neurochem. 2001; 76:806–814. [DOI] [PubMed] [Google Scholar]
- 55. Huynh N.P.T., Anderson B.A., Guilak F., McAlinden A.. Emerging roles for long noncoding RNAs in skeletal biology and disease. Connect Tissue Res. 2017; 58:116–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Yamada M., Clark J., Iulianella A.. MLLT11/AF1q is differentially expressed in maturing neurons during development. Gene Expr. Patterns. 2014; 15:80–87. [DOI] [PubMed] [Google Scholar]
- 57. Bassani S., Cingolani L.A., Valnegri P., Folci A., Zapata J., Gianfelice A., Sala C., Goda Y., Passafaro M.. The X-linked intellectual disability protein TSPAN7 regulates excitatory synapse development and AMPAR trafficking. Neuron. 2012; 73:1143–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. GTEx Consortium The genotype-tissue expression (GTEx) project. Nat. Genet. 2013; 45:580–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Maldonado-Saldivia J., van den Bergen J., Krouskos M., Gilchrist M., Lee C., Li R., Sinclair A.H., Surani M.A., Western P.S.. Dppa2 and Dppa4 Are Closely Linked SAP Motif Genes Restricted to Pluripotent Cells and the Germ Line. Stem Cells. 2007; 25:19–28. [DOI] [PubMed] [Google Scholar]
- 60. Wang J., Xie G., Singh M., Ghanbarian A.T., Raskó T., Szvetnik A., Cai H., Besser D., Prigione A., Fuchs N.V. et al. Primate-specific endogenous retrovirus-driven transcription defines naive-like stem cells. Nature. 2014; 516:405–409. [DOI] [PubMed] [Google Scholar]
- 61. Chen C., Morris Q., Mitchell J.A.. Enhancer identification in mouse embryonic stem cells using integrative modeling of chromatin and genomic features. BMC Genomics. 2012; 13:152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Alfaro M.P., Pagni M., Vincent A., Atkinson J., Hill M.F., Cates J., Davidson J.M., Rottman J., Lee E., Young P.P.. The Wnt modulator sFRP2 enhances mesenchymal stem cell engraftment, granulation tissue formation and myocardial repair. Proc. Natl. Acad. Sci. U.S.A. 2008; 105:18366–18371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Kim J.J., Khalid O., Namazi A., Tu T.G., Elie O., Lee C., Kim Y.. Discovery of consensus gene signature and intermodular connectivity defining self-renewal of human embryonic stem cells. Stem Cells. 2014; 32:1468–1479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Minchiotti G. Nodal-dependant Cripto signaling in ES cells: from stem cells to tumor biology. Oncogene. 2005; 24:5668–5675. [DOI] [PubMed] [Google Scholar]
- 65. Luo Z., Gao X., Lin C., Smith E., Marshall S., Swanson S.K., Florens L., Washburn M.P., Shilatifard A.. Zic2 is an enhancer-binding factor required for embryonic stem cell specification. Mol. Cell. 2015; 57:685–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Paetau A., Elovaara I., Paasivuo R., Virtanen I., Palo J., Haltia M.. Glial filaments are a major brain fraction in infantile neuronal ceroid-lipofuscinosis. Acta Neuropathol. 1985; 65:190–194. [DOI] [PubMed] [Google Scholar]
- 67. Huang L., Wu Z.-B., ZhuGe Q., Zheng W., Shao B., Wang B., Sun F., Jin K.. Glial scar formation occurs in the human brain after ischemic stroke. Int. J. Med. Sci. 2014; 11:344–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Li L., Wadia P., Chen R., Kambham N., Naesens M., Sigdel T.K., Miklos D.B., Sarwal M.M., Butte A.J.. Identifying compartment-specific non-HLA targets after renal transplantation by integrating transcriptome and “antibodyome” measures. Proc. Natl Acad. Sci. U.S.A. 2009; 106:4148–4153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Koo D.D.H., Welsh K.I., Roake J.A., Morris P.J., Fuggle S.V.. Ischemia/reperfusion injury in human kidney transplantation. Am. J. Pathol. 1998; 153:557–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Gass P., Katsura K.-I., Zuschratter W., Siesjö B., Kiessling M.. Hypoglycemia-Elicited Immediate Early Gene Expression in Neurons and Glia of the Hippocampus: Novel Patterns of FOS, JUN, and KROX Expression following Excitotoxic Injury. J. Cereb. Blood Flow Metab. 1995; 15:989–1001. [DOI] [PubMed] [Google Scholar]
- 71. Velazquez F.N., Prucca C.G., Etienne O., D’Astolfo D.S., Silvestre D.C., Boussin F.D., Caputto B.L.. Brain development is impaired in c-fos −/− mice. Oncotarget. 2015; 6:16883–16901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Wang S., Zhou Y., Seavey C.N., Singh A.K., Xu X., Hunt T., Hoyt R.F., Horvath K.A.. Rapid and dynamic alterations of gene expression profiles of adult porcine bone marrow-derived stem cell in response to hypoxia. Stem Cell Res. 2010; 4:117–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Murata T., Tsuboi M., Koide N., Hikita K., Kohno S., Kaneda N.. Neuronal differentiation elicited by glial cell line-derived neurotrophic factor and ciliary neurotrophic factor in adrenal chromaffin cell line tsAM5D immortalized with temperature-sensitive SV40 T-antigen. J. Neurosci. Res. 2008; 86:1694–1710. [DOI] [PubMed] [Google Scholar]
- 74. Rock R., Heinrich A.C., Schumacher N., Gessler M.. Fjx1: A notch-inducible secreted ligand with specific binding sites in developing mouse embryos and adult brain. Dev. Dyn. 2005; 234:602–612. [DOI] [PubMed] [Google Scholar]
- 75. Lojewski X., Staropoli J.F., Biswas-Legrand S., Simas A.M., Haliw L., Selig M.K., Coppel S.H., Goss K.A., Petcherski A., Chandrachud U. et al. Human iPSC models of neuronal ceroid lipofuscinosis capture distinct effects of TPP1 and CLN3 mutations on the endocytic pathway. Hum. Mol. Genet. 2014; 23:2005–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Tracy C.J., Whiting R.E.H., Pearce J.W., Williamson B.G., Vansteenkiste D.P., Gillespie L.E., Castaner L.J., Bryan J.N., Coates J.R., Jensen C.A. et al. Intravitreal implantation of TPP1-transduced stem cells delays retinal degeneration in canine CLN2 neuronal ceroid lipofuscinosis. Exp. Eye Res. 2016; 152:77–87. [DOI] [PubMed] [Google Scholar]
- 77. Stevens H.E., Smith K.M., Rash B.G., Vaccarino F.M.. Neural stem cell regulation, fibroblast growth factors, and the developmental origins of neuropsychiatric disorders. Front. Neurosci. 2010; 4:59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Wilczynska K.M., Singh S.K., Adams B., Bryan L., Rao R.R., Valerie K., Wright S., Griswold-Prenner I., Kordula T.. Nuclear factor I isoforms regulate gene expression during the differentiation of human neural progenitors to astrocytes. Stem Cells. 2009; 27:1173–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Singh S.K., Wilczynska K.M., Grzybowski A., Yester J., Osrah B., Bryan L., Wright S., Griswold-Prenner I., Kordula T.. The unique transcriptional activation domain of nuclear factor-I-X3 is critical to specifically induce marker gene expression in astrocytes. J. Biol. Chem. 2011; 286:7315–7326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Magistri M., Khoury N., Mazza E.M.C., Velmeshev D., Lee J.K., Bicciato S., Tsoulfas P., Faghihi M.A.. A comparative transcriptomic analysis of astrocytes differentiation from human neural progenitor cells. Eur. J. Neurosci. 2016; 44:2858–2870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Cavazzin C., Ferrari D., Facchetti F., Russignan A., Vescovi A.L., La Porta C.A.M., Gritti A.. Unique expression and localization of aquaporin-4 and aquaporin-9 in murine and human neural stem cells and in their glial progeny. Glia. 2006; 53:167–181. [DOI] [PubMed] [Google Scholar]
- 82. Li F., Shi W., Capurro M., Filmus J.. Glypican-5 stimulates rhabdomyosarcoma cell proliferation by activating Hedgehog signaling. J. Cell Biol. 2011; 192:691–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Ihrie R.A., Shah J.K., Harwell C.C., Levine J.H., Guinto C.D., Lezameta M., Kriegstein A.R., Alvarez-Buylla A.. Persistent sonic hedgehog signaling in adult brain determines neural stem cell positional identity. Neuron. 2011; 71:250–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Chang N.-J., Weng W.-H., Chang K.-H., Liu E.K.-W., Chuang C.-K., Luo C.-C., Lin C.-H., Wei F.-C., Pang S.-T.. Genome-wide gene expression profiling of ischemia-reperfusion injury in rat kidney, intestine and skeletal muscle implicate a common involvement of MAPK signaling pathway. Mol. Med. Rep. 2015; 11:3786–3793. [DOI] [PubMed] [Google Scholar]
- 85. Alfonso-Jaume M.A., Bergman M.R., Mahimkar R., Cheng S., Jin Z.Q., Karliner J.S., Lovett D.H.. Cardiac ischemia-reperfusion injury induces matrix metalloproteinase-2 expression through the AP-1 components FosB and JunB. Am. J. Physiol. Heart Circ. Physiol. 2006; 291:H1838–H1846. [DOI] [PubMed] [Google Scholar]
- 86. Hauber H.P., Karp D., Goldmann T., Vollmer E., Zabel P.. Comparison of the effect of lps and pam3 on ventilated lungs. BMC Pulm. Med. 2010; 10:20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Re F., Strominger J.L.. Toll-like receptor 2 (TLR2) and TLR4 differentially activate human dendritic cells. J. Biol. Chem. 2001; 276:37692–37699. [DOI] [PubMed] [Google Scholar]
- 88. Øvstebø R., Olstad O.K., Brusletto B., Møller A.S., Aase A., Haug K.B.F., Brandtzaeg P., Kierulf P.. Identification of genes particularly sensitive to lipopolysaccharide (LPS) in human monocytes induced by wild-type versus LPS-deficient Neisseria meningitidis strains. Infect. Immun. 2008; 76:2685–2695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Liu S., Trapnell C.. Single-cell transcriptome sequencing: recent advances and remaining challenges. F1000Res. 2016; 5:doi:10.12688/f1000research.7223.1. eCollection 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Bacher R., Kendziorski C.. Design and computational analysis of single-cell RNA-sequencing experiments. Genome Biol. 2016; 17:63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Kharchenko P.V., Silberstein L., Scadden D.T.. Bayesian approach to single-cell differential expression analysis. Nat. Methods. 2014; 11:740–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Korthauer K.D., Chu L.-F., Newton M.A., Li Y., Thomson J., Stewart R., Kendziorski C.. A statistical approach for identifying differential distributions in single-cell RNA-seq experiments. Genome Biol. 2016; 17:222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Finak G., McDavid A., Yajima M., Deng J., Gersuk V., Shalek A.K., Slichter C.K., Miller H.W., McElrath M.J., Prlic M. et al. MAST: a flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol. 2015; 16:278. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
SparseDC has been implemented in R and is available as an R package from CRAN (‘https://cran.r-project.org/web/packages/SparseDC/index.html’). A vignette is also available at ‘https://cran.r-project.org/web/packages/SparseDC/vignettes/SparseDC.html’. The scRNA-Seq data from Pollen et al. (42) are available from the NCBI Sequence Read Archive under accession number SRP041736. The scRNA-seq data from Llorens–Bobadilla et al. (44) are available under GEO accession number GSE67833. The scRNA-seq data from Biase et al. (43) are available from the additional files for the article. The scRNA-seq data from Shalek et al. (45) are available under GEO accession number GSE48968.








