Ensemble Docking in Drug Discovery

Abstract

Ensemble docking corresponds to the generation of an “ensemble” of drug target conformations in computational structure-based drug discovery, often obtained by using molecular dynamics simulation, that is used in docking candidate ligands. This approach is now well established in the field of early-stage drug discovery. This review gives a historical account of the development of ensemble docking and discusses some pertinent methodological advances in conformational sampling.

Main Text

History

Computational structure-based drug design has a long history dating back at least to the late 1970s. Soon after the first crystallographic protein structures were derived, it was realized that “rational” drug design would mimic the process nature takes by docking potential ligands to protein targets in three dimensions and ranking the results. However, success in these endeavors in the early days was limited by the lack of experimental structures for most targets, relatively poor computational methods, and weak computer power. Hence, the field of early stage drug discovery pivoted somewhat to the combination of combinatorial chemistry and experimental high-throughput screening.

Nowadays, computational structure-based design appears to be enjoying a renaissance. Using comparative (homology) modeling, it has become possible to derive useful three-dimensional (3D) structures for the majority of proteins associated with human and pathogen genomes (1). Indeed, the procedure of structure generation has begun to become automated. For example, the Ensembler code takes any set of sequences and shepherds them through various stages of modeling and refinement to produce docking-ready structures (2). Further, our understanding of ligand binding thermodynamics and corresponding methods for modeling and simulating targets and ranking compounds and predicting binding poses have improved. Finally, the computer power available has increased dramatically.

Early docking studies were performed with static target crystal structures and rigid ligands. These were quite successful in some cases, such as in the discovery of antivirals for HIV and influenza (3, 4). The subsequent inclusion of ligand flexibility was relatively straightforward, given the comparatively limited conformational space of small molecules. However, molecular dynamics (MD) simulations had also shown that considering proteins as rigid structures would fail to take into account the thermal fluctuations of atoms that lead to proteins exploring a multitude of complex “conformational substates” (5), and that these substates might correspond to different shapes of binding sites. Hence, well before the late 1990s it was already appreciated that important conformational changes in proteins are often associated with ligand binding. However, even though it was recognized that incorporating target flexibility into drug discovery protocols can improve the drug discovery process, still at that time it was standard practice to dock libraries of molecular fragments or small molecules to a single conformation of the target molecule, often derived from crystallography.

Ensemble docking of small probe molecules for flexible pharmacophore modeling was introduced in 1999 (6). The authors of this seminal paper had conducted extensive MD simulations of the catalytic domain of HIV integrase, including a modeled active-site loop region that was not resolved crystallographically, and noted particularly large fluctuations in the binding site. This suggested that docking to an ensemble of the target molecule structures would be useful. The 1999 paper showed that consensus pharmacophore models, based on multiple MD structures or on multiple crystallographic structures, were more successful than models based on single conformations in yielding successful predictions of binding. Application of this ensemble docking method using molecular fragments showed that the resulting “dynamic pharmacophores” were better able to predict binding of known inhibitors than pharmacophore models based on single target structures. Subsequent docking of a library of available small molecules led to the discovery of new inhibitors of the HIV-1 integrase that were confirmed in subsequent experimental work (7).

In 2002, the “relaxed complex scheme” (RCS) was introduced for flexible binding site modeling and ensemble docking of drug-like compound libraries (8). In RCS, MD simulation is first applied to sample different conformations of the target receptor in the ligand-free form. Then, rapid docking of mini-libraries of drug-like molecules to a large ensemble of the receptor’s MD snapshots is performed to identify candidate inhibitors. The use of many MD snapshots was able to account for the receptor flexibility but also increased the cost for molecular docking. To address this issue, novel structural clustering techniques based on the root mean-square deviation of the receptor and the “QR-factorization” were introduced to construct receptor ensembles from the MD snapshots (9). This greatly increased the efficiency of ensemble docking of small-molecule compound libraries.

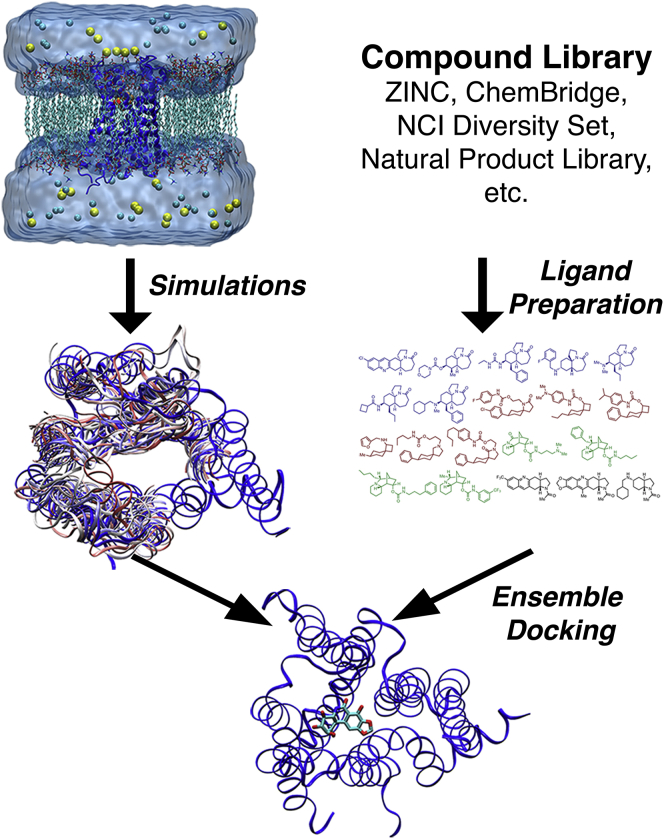
With the RCS approach, a novel binding trench was discovered near the active site of the HIV-1 integrase (10). Multiple protein snapshots were extracted from a 2 ns MD trajectory. Ensemble docking of ligands with a single key tetrazole group revealed that they are able to bind the protein active site and the trench in different poses. So-called “butterfly compounds” with two such groups were predicted to access two different tetrazole-binding subsites in the enzyme simultaneously, leading to higher affinity. The discovery was influential in leading to the first US Food and Drug Administration-approved drug for the HIV-1 integrase. Ensemble docking, the process of which is illustrated in Fig. 1, is now widely used for small molecule hit discovery. Space restrictions preclude listing more examples.

Figure 1.

Schematic workflow of ensemble docking using the M₂ muscarinic G-protein-coupled receptor as a model receptor: computer simulations using MD are performed to construct structural ensembles of different receptor conformations that can account for the receptor flexibility. Meanwhile, a compound library can be prepared from chemical databases, e.g., ZINC, ChemBridge, National Cancer Institute (NCI) Diversity Set, Natural Product Library, etc. Finally, molecular docking to the receptor ensembles (i.e., ensemble docking) are carried out to identify top-ranked compounds for experimental testing. To see this figure in color, go online.

Protein:protein interaction modulation

An important, more recent application of docking that extends its use well beyond just that of discovering enzyme catalytic modulators is to identify small molecules modulating protein-protein interactions either by disrupting them or enhancing them (i.e., acting as a “molecular glue” between the protein species). Protein-protein interaction modulators most frequently bind to the surface of proteins (although allosteric mechanisms also exist). In addition, modulating protein-protein interactions that occur through the stabilization of otherwise flexible loops requires an extensive sampling of the conformational space accessible to the loops. Notwithstanding, it is nowadays possible to design modulators even in the absence of either experimental structures for the complex or one of the partner proteins. For example, a recent docking campaign was successful in identifying novel molecular effectors of the coagulation cascade, targeting the interactions between Factor Xa and Factor Va in the absence of the Va structure (11). Indeed, in this case, the conformations of Xa surface loops were found to be an important factor and led to the discovery of ligands that would not have been predicted to bind on a static model of the protein surface. Likewise, the first inhibitors of the FRFR:FGF23:α Klotho endocrine signaling complex were found by a similar ensemble docking protocol to a homology model of FGF23 (12), as were inhibitors designed to block efflux pump assembly that have been found to be effective in the fight against antibiotic resistance (13).

Conformational sampling problem

MD suffers from the key drawbacks of force field errors and sampling problems. The former, together with methods for performing docking, will not be discussed here in detail, although we note that progress is being made in improving force fields, such as by including electronic polarization (14), and that the alternative of incorporating quantum mechanical simulation methods is also being pursued (15). The sampling problem, which will be assessed here, refers to the insufficient sampling of target configurational space, due to a large gap between the timescales reachable by simulation (usually microseconds) and slow target conformational changes, which can be many orders of magnitude longer. Moreover, a converged simulation would not only visit all the relevant conformations but also visit them sufficiently to establish Boltzmann occupancy statistics for each state. The relative free energies of each complex could then be accessible and would be used to weight the relative ligand-binding propensities. The construction of special purpose computers, such as ANTON (16), has allowed MD simulations of proteins to now be extended to the millisecond timescale. However, even a millisecond may not be enough for convergence of a single MD trajectory. Indeed, it has recently been shown that the internal dynamics of a single protein is nonequilibrium and nonergodic, aging over 13 decades in time, from the picosecond up to the second timescales (17). Thus, sampling still represents a severe problem.

Selecting conformations

The above historical small-molecule ensemble docking examples implicitly assumed the “conformational selection” model of ligand binding (18), in which the ligand “selects” from among the conformations sampled by the apo-protein that to which it can bind the strongest. This model thus assumes that the relevant conformation of the target will be sampled in the unbound species. However, even within the conformational selection paradigm, obtaining an accurate, statistically converged set of MD binding site conformations is daunting.

Given that a single trajectory will not statistically converge with current computer power, practically researchers have either taken random snapshots of the protein configurations and docked to them or clustered the configurations obtained (e.g., by root mean-square deviation) and docked to representatives of each cluster. However, lacking a method to identify a subset of conformational states that effectively segregates active and inactive small molecules, ensemble docking may result in the recommendation of a large number of false positives. The question arises, then, as to whether, in an unconverged set of conformations of a protein, those that will be selected by potential ligands can nevertheless be empirically identified. Even sampling to a small degree outside of the frozen crystal structure minimum—i.e., MD simulation for 10 s of nanoseconds—has been shown to be effective in sampling unseen, druggable pockets for multiple targets (19, 20). However, there is no known set of rules that has been shown to correlate structural or energetic properties of a protein conformation with the selection by ligands of this conformation. Furthermore, the conformation(s) selected may be ligand-dependent. However, identifying protein properties that render an apo-structure likely to be “selectable” would reduce the computational effort needed for ensemble docking in addition to possibly providing important fundamental knowledge on the mechanism of conformational selection. Recently, machine learning methods involving an oversampling and a binary classification procedure were trained on a set of nuclear receptor conformations, each of which was labeled with a virtual screening enrichment measure (21). This kind of approach may provide a methodology to identify pharmaceutically interesting conformations for targets. In related work, knowledge-based methods that construct structural ensembles and evaluate their virtual screening success were examined (22). Each knowledge-based method selects best-performing ensembles by optimizing an objective function calculated by using the receiver operating characteristic curve.

There is, however, another fundamental issue with a quest for “selectable” apo-protein conformations: conformational selection acts by lowering the free energy of the protein:ligand complex. Any property of the apo-target conformation will, by definition, be a property of the apo free energy hypersurface and not of the free energy hypersurface of the complex, which is the surface that, ideally, one would wish to sample. The alternative model to conformational selection, which is related to “induced fit” arguments, assumes that conformation of the target when bound is not sampled in the unbound form; in other words, it is induced by ligand binding. Local ligand-induced rearrangements can be accommodated by “induced fit docking” procedures. However, larger-scale binding pocket changes are problematic for simulation-based ensemble docking because, in principle, this would require exhaustive simulations for each trial ligand. This is challenging to do in a computationally efficient manner, although methods are being actively developed (23). Nonetheless, target ensembles generated with a bound ligand, which is then removed before docking, have proved useful, as in the HIV integrase work.

A possible approach to this problem might be to determine the free energy surface of a protein:ligand complex and of the corresponding apo-protein and to identify which conformations of the apo-target are structurally proximal to the conformation with the free energy minimum in the protein:ligand complex. Protein properties that are unique (if any) to this apo- conformation could then be identified. However, until such an approach is performed, it is useful to remember that protein:ligand complexes may follow a law of mass action: often-sampled protein conformations may also be more represented in the ensemble of protein:ligand complexes than apo-structures that are rarely sampled. Thus, clustering a population of apo-protein conformations and focusing on the most populated clusters of conformation is a priori a reasonable empirical approach to follow.

To address the overall MD sampling problem, many enhanced sampling techniques have been developed during the last several decades (24, 25). These methods greatly improve sampling of receptor configurations, but they require predefined collective variables (CVs) and often suffer from hidden energy barriers (25). Furthermore, there exists a second class of enhanced sampling methods that do not require predefined system-dependent CVs and as such do not suffer from the hidden barrier problem, such as replica exchange (26, 27) or parallel tempering (28), self-guided molecular/Langevin dynamics (29, 30, 31), essential energy space random walk (32, 33, 34), and accelerated MD (aMD) (35, 36). In contrast to the CV-biasing enhanced sampling methods, these methods can explore protein configurations without the need for a priori knowledge, providing unconstrained enhanced sampling of proteins to identify possible unknown intermediate conformational states. This is valuable for exploring different receptor conformations used in ensemble docking.

In one illustrative example, aMD simulations were incorporated into ensemble docking to design novel allosteric modulators of the M₂ muscarinic acetylcholine receptor, a G-protein-coupled receptor (37). Long-timescale aMD simulations were performed to construct structural ensembles that account for the receptor flexibility and were used for induced-fit ensemble docking. It was found that 12 compounds with affinities ≤30 μM were identified, of which four were confirmed as novel negative allosteric modulator and one as a positive allosteric modulator of agonist-mediated response at the M₂ muscarinic acetylcholine receptor. Such approaches should be useful for future drug design efforts targeting many other important and flexible receptors (38).

Eroom’s law

The sampling problem can also be potentially addressed by examining computational methods that can be used optimally with modern-day computer hardware technology in mind. Moore’s Law—the observation that the number of transistors in a dense integrated circuit doubles approximately every 2 years—contrasts with Eroom’s Law in drug discovery, which states that the cost of developing a drug doubles every 9 years (39). Moore’s Law appears nowadays to be in some danger insofar as it translates into processor speeds. However, massively parallel supercomputing has advanced, and, whereas the first MD simulation of a protein in the mid-1970s was performed on an IBM System/370 Model 168 machine running at ∼5 megaflops, there has since been a 10¹⁰-fold increase in supercomputer power, to the point that the first exaFLOP machines will be expected to be built within 5 years’ time.

Exascale supercomputing may not permit ready lengthening of single, individual classical MD trajectories, but the massively parallel nature of modern supercomputers will certainly allow running many shorter simulations of the same system in parallel. The challenge, then, is to use multiple simulations that are shorter than the timescales of interest to build a model capable of describing long-time statistical dynamics. If these simulations can be judiciously chosen and then related to each other in a meaningful way, the sampling problem may well be overcome. This can, in principle, be accomplished by using Markov state models (MSMs) (40, 41, 42) or related methods such as milestoning (43). In this Biophysical Perspective, we focus on MSMs because they allow the identification of metastable structural states of drug targets (receptors) that can be subsequently used in structure-based computer-aided drug design approaches.

MSMs

MSMs require a discretization of the configurational space explored in the MD into “microstates,” which are subsequently merged into clusters. The resulting clusters represent approximations to ideal metastable states, i.e., the number of transitions between clusters is minimized, and, equivalently, the lifetimes of the clusters are maximized. Stochastic transitions between these discrete states are described by a matrix of conditional transition probabilities estimated from the simulation trajectories. The transitions between states are Markovian if their probability does not depend on past states. It is thus required that the states are not chosen arbitrarily but rather according to a local metastability criterion that guarantees that the equilibration time of the dynamics within each state is less than the expected exit time from the state, thus validating the memoryless model for the dynamics. The initial MSM can then be improved through adaptive sampling in which rarely sampled configurations are used as starting configurations for subsequent MD simulations to reduce statistical error (44). An MSM correctly recovers the equilibrium thermodynamic and kinetic properties of the system even if the short trajectories used to construct it were not initiated from equilibrium. The model hierarchy yields a qualitative understanding of the multiple time- and length scales in the dynamics of macromolecules.

MSMs do have inherent limitations. Errors can be introduced when decomposing the state space and there is a compromise to make: a longer lag time provides models of higher fidelity but coarser resolution (45). MSMs can introduce significant biases in the computation of reaction rates, which depend on the boundaries selected for the metastable states, and weighted ensemble methods have been proposed as an alternative (23). When trajectories spend most of their time in kinetic traps, MSM approaches can become inefficient. Path-sampling methods can alleviate these problems since they sample unbiased rare trajectories between stable states and hence can sample transitions in which high barriers are encountered without losing any kinetic information (46).

Nevertheless, MSMs and related technologies promise to provide a complete description of the conformations accessed by drug targets together with their relative free energies. This is in harmony with the principle historically followed in drug design of finding inhibitors with maximal binding affinity to the target. Moreover, with increasing simulation power, the possibility of determining conformational changes of native proteins associated with function—which often have timescales in the microsecond to millisecond range or longer—have become possible through the use of MSMs. For example, intrinsic fluctuations of β-lactamase in its native state revealed a multitude of potential allosteric binding sites that could potentially be exploited in the design of allosteric modulators of activity (47). MSM studies of the activation pathways of kinases and G-protein-coupled receptors similarly revealed possible allosteric binding sites as well as the possibility of distinguishing between agonists and antagonists by using structural information from MSM-derived putative functional pathways (48, 49). Among the related questions that have been examined is how to compute free energy differences from samples obtained from multiple equilibrium states (50). This has been tackled by using results from statistical inference to construct a statistically optimal estimator for computing free energy differences and equilibrium expectations at arbitrary thermodynamic states by using equilibrium samples from multiple thermodynamic states.

Drug-binding kinetics

A complete description of drug binding requires not only binding free energies but also determination of the target-drug kinetics. A direct strategy for exploiting kinetics is the maximization of the ligand residence time at the receptor (51). Protein-ligand kinetics may involve more than two kinetically relevant states due to different ligand binding poses, different protein conformations, or their coupling. Although this multistate nature is not always apparent in ensemble kinetics experiments, accounting for it may help in multiple stages of the drug design process. MSMs are useful in this regard as they can provide estimates of both equilibrium free energies and the kinetics of drug binding.

By combining high-throughput MD simulations with MSMs, the complete binding pathway and kinetics of the benzamidine inhibitor to trypsin protein was reconstructed in (52). In a follow-up study, it was found that trypsin possesses multiple conformational states whose kinetics are coupled to the binding kinetics (53). Seven metastable conformations with different binding pocket structures were found that interconvert at timescales of tens of microseconds. These conformations differed in their substrate-binding affinities and binding/dissociation rates. For each metastable state, corresponding solved structures of trypsin mutants or similar serine proteases are contained in the Protein Data Bank. Thus, the wild-type simulations explore a space of conformations that can be individually stabilized by adding ligands or making suitable changes in protein sequence.

Recently, it has also been possible for the first time to simulate the association and dissociation of a protein-protein complex, the archetypal enzyme barnase to its natural inhibitor barstar, with all-atom MD (54). The association was simulated with 2 ms of adaptive MD simulations and MSMs, with which the timescale of hours could be reached, on which the two proteins dissociate (55). The resulting model revealed details of the binding and dissociation pathways, allowed the effects of protein mutations to be probed, and suggested key residues that may be affected by drugs (54). However, despite this encouraging success in sampling, this approach still requires considerable computational effort to sample the rare dissociation events, and these are still subject to large statistical uncertainties.

To compute binding and unbinding kinetics more efficiently and with higher precision, it has proven useful to combine the advantages of enhanced sampling methods and MSMs. For this, the concept of multiensemble Markov models (MEMMs) was developed (56). MEMMs combine unbiased simulations of fast events (such as rapid binding) with efficient sampling of the rare events in biased ensembles (such as biased unbinding) within a reweighting framework that can extract full and unbiased kinetics. The MEMM framework has been recently exploited to compute full protein-peptide binding kinetics of the oncoprotein fragment Mdm2 and the nanomolar inhibitor peptide PMI (57). In using this system, direct estimates of kinetics beyond the seconds timescale was achieved by using simulations of an all-atom MD model, with high accuracy and precision. These results only required explicit simulations on the submilliseconds timescale. The overall strong binding was found to arise from a variety of conformations with different hydrophobic contact surfaces that interconvert on the milliseconds timescale.

Due to force field uncertainties, the accuracy of any empirical MD model is fundamentally limited. Therefore, we expect that integrating simulation and experimental data in order to reweight the model obtained from the MD simulation is a key technique toward accurate models (58, 59). This approach has been formulated for MSM estimation (60) and is thus now amenable to integrate swarms of short off-equilibrium MD trajectories with experimental equilibrium observables. The results of (60) suggest that correcting the probabilities/free energies of conformations by incorporating experimental equilibrium data can improve both the equilibrium and kinetic estimates of the simulation. Recently, this approach has been extended to also incorporate dynamical observables directly (61).

Specialized software

A number of software packages have been developed for the construction, validation, and interpretation of MSMs, including MSMBuilder (http://msmbuilder.org/) (62) and PyEMMA (http://pyemma.org), which provide accurate and efficient algorithms for kinetic MSM model construction (63). Moreover, analysis tools adapted to ensemble docking are becoming available, such as the open-source POVME binding pocket analysis software, which maps binding pocket flexibility by employing a voxel/grid-based 3D pocket representation (64) and is useful for the visualization of binding pocket dynamics and the selection of representative structures for ensemble docking efforts. With the drive toward high throughput MD simulations involving ever-greater numbers of simulation replicates run for longer, biologically relevant timescales (microseconds), the need for improved computational methods that facilitate fully automated MD workflows gains more importance. To this end, an automated workflow tool has been developed to reduce the user input time for submitting multistep AMBER graphics processing unit MD simulations to local and remote computers as well as generating a detailed report of the simulation protocol (65).

Computational advances

The use of MSMs combined with massively parallel supercomputing (including cloud resources) promises to greatly increase the usefulness of MD in ensemble docking drug discovery. An MSM-based “parallel ensemble” hierarchical multiscale MD approach should, in principle, scale to exaflop machines. For this, however, a parallelization strategy must be developed. Current MD parallelization strategies are based on distributing either subsets of the system, e.g., groups of atoms, or workload units (e.g., energy and force terms) to different nodes. This strategy has intrinsic limitations as, in principle, each atom communicates with every other atom via long-range electrostatic forces. An alternative approach is to efficiently partition the configurational space itself into grid cells such that communication occurs only between cells that are spatially adjacent. To enable this, the simulation-space distribution is in the 3N-dimensional state space of the molecule rather than in the 3D geometrical space of each of the N individual atoms. Instead of simulating the time history of an individual molecule, the approach would therefore be to simulate the evolution of a molecular ensemble.

In macromolecules, there may be a few metastable states that have many neighbors and many that have few neighbors; the distribution of the number of neighbors typically follows a power law. This is in conflict with supercomputer architecture in which each node can efficiently “talk” to a fixed number (n) of neighbors (n may be 4, 6, 8… depending on the network topology, e.g., two-dimensional or 3D mesh or hypercube). The optimal assignment of computer nodes to metastable states could therefore be determined by solving the corresponding optimization problem, taking into account the number of nodes, the interconnection topology, and the bandwidth. This optimization problem can be solved in parallel in a similar fashion to the parallel determination of metastable states. The scheme results in an efficient parallelization of MD adapted to whatever supercomputer architecture is used.

The efficient parallelization of docking programs is also necessary to perform the sometimes massive docking calculations needed in ensemble docking. An incorrect view of docking is that it is an embarrassingly parallel process that can easily be scaled on supercomputers. A massive amount of data is produced, processed, read, and written, and I/O issues become rapidly intractable for massive docking campaigns. Nonetheless, a parallelized version of the AutodockVina docking engine has been established that is efficient on supercomputers (66). In addition to the MPI parallelization of I/O activities, load balancing and workers’ communications strategies were found to be essential to scaling on massive computing platforms. Such parallelization techniques will continue to be important, and as the architectures of supercomputers continue to evolve, parallelization for both MD and docking will likely have to be fine-tuned for each new machine. In addition to I/O parallelization, leveraging the power of graphics processing units is needed for optimal use of the power of the next generation of supercomputers.

Conclusions

The field of virtual drug discovery and design is undergoing an important rebirth. Fueled by a large number of derivable target structures, improved methodology and massive computer power it is now possible to dock ∼1 M trial compounds to a target structure in less than an hour. From the timescale of picoseconds reachable in the first MD simulations in the 1970s, we can, via MSMs and related techniques, now estimate processes on the seconds timescale and anticipate fully statistically converged ensembles of flexible target structures for use in ensemble docking. One can envisage similar approaches to be of use in the structure-based design of vaccines against pathogenic diseases and cancers, and the possibility also exists of structure-based toxicity prediction via the calculation of off-target binding of drug candidates, which, even if only partly accurate, could greatly aid in overcoming Eroom’s Law. Moreover, the rapidity of modern-day genome sequencing combined with increased computer power may permit the calculation of personalized protein structure libraries, which might then be able to be used for the prediction of drug efficacy and toxicity in individuals.

Editor: Tamar Schlick.