Abstract
Background and Aims
As a major evolutionary transition in seed plants, the evolution of plant mating systems has been much debated in evolutionary ecology. Over the last 10 years, well-established patterns of evolution have emerged. On the one hand, experimental studies have shown that self-fertilization is likely to evolve in a few generations (microevolution) as a response to rapid environmental change (e.g. pollinator decline), eventually rescuing a population. On the other, phylogenetic studies have demonstrated that repeated evolution towards self-fertilization (macroevolution) leads to a higher risk of lineage extinction and is thus likely to be disadvantageous in the long term.
Scope
In either case – the short-term or long-term evolution of self-fertilization (selfing) – these findings indicate that a mating system is not neutral with respect to population or lineage persistence. They also suggest that selfing can have contrasting effects depending on time scale. This raises the question of whether mating system evolution can rescue populations facing environmental change. In this review, empirical and theoretical evidence of the direct and indirect effects of mating systems on population demography and lineage persistence were analysed. A simple theoretical evolutionary rescue model was also developed to investigate the potential for evolutionary rescue through selfing.
Key Findings
Demographic studies consistently show a short-term advantage of selfing provided by reproductive assurance, but a long-term disadvantage for selfing lineages, suggesting indirect genomic consequences of selfing (e.g. mutation load and lower adaptability). However, our theoretical evolutionary rescue model found that even in the short term, while mating system evolution can lead to evolutionary rescue, it can also lead to evolutionary suicide, due to the inherent frequency-dependent selection of mating system traits.
Conclusions
These findings point to the importance of analysing the demographic consequences of self-fertilization in order to predict the effect of selfing on population persistence as well as take into account the indirect genomic consequences of selfing. The pace at which processes such as inbreeding depression, purging, reproductive assurance and genomic rearrangements occur after the selfing transition is the key to clarifying whether or not selfing will result in evolutionary rescue.
Keywords: Self-fertilization, evolutionary rescue, microevolution and macroevolution
INTRODUCTION
In the tree of life of plants, mating system transitions are frequent. These have been widely studied, especially in seed plants, including gymnosperms and angiosperms. Seed plants can have a variety of mating systems (Yampolsky and Yampolsky, 1922). A majority of seed plants bear hermaphroditic flowers that allow the practice of self-fertilization and/or outcrossing. Self-fertilization encompasses modifications in a set of traits, including inconspicuous flowers, a reduced pollen–ovule ratio, cleistogamy and reduced anther–stigma distance: this is known as the selfing syndrome (Duncan and Rausher, 2013). Whatever the mechanism, the selfing rate, defined as the ratio of selfed ovules over the total number of fertilized ovules, provides a synthetic measure of hermaphroditic mating systems.
In evolutionary ecology, the selective advantage of selfing vs. outcrossing has a long history. Early hypotheses for the evolution of selfing were proposed by Darwin (1876), who considered that while selfing was deleterious as a result of the reduced performance of progeny (inbreeding depression), it allowed seed set without the aid of pollinators (reproductive assurance; see also Baker, 1955). With the rise of population genetics, mating system theory has enjoyed a major advance, especially with the seminal work of Ronald Fisher (1941). Population geneticists view self-fertilization from the gene perspective, in which self-fertilization is a question of gene transmission. So a selfing plant transmits two copies of its genes in its seeds, while an outcrossing plant transmits only one. Assuming that selfing does not impede pollen export (i.e. no pollen discounting; Nagylacki, 1976), this results in a 3/2 transmission advantage for selfing genes compared with outcrossing genes (cost of outcrossing).
The modern theory of mating system evolution was developed by Lloyd in the 1970s (Lloyd, 1977, 1979, 1980). Evolutionary models have allowed the key parameters in the evolution of self-fertilization to be identified (namely reproductive assurance, pollen discounting and inbreeding depression), which empiricists have then gone on to estimate. This high level of research activity has resulted in the accumulation of a substantial amount of both field data (Vogler and Kalisz, 2001; Ashman et al., 2006) and experimental data (Winn et al., 2011). In this regard, plant mating systems are exemplary cases for articulating theory, estimating mating systems in the field and experimentally measuring key parameters (e.g. inbreeding depression and reproductive assurance) via floral manipulation or experimental crosses (Eckert et al., 2010). Since the 1970s, modern theories of mating system evolution have become a major field of research in evolutionary biology, yet the ecological impact of a mating system on population demography is less well studied. While many studies have focused on reduced seed set in circumstances of pollen limitation (reviewed in Burd, 1994), there have been few on the demographic parameters of a plant’s entire life cycle and the impact of this on the population growth rate. The few studies that have been conducted on the impact of a mating system on population demography (e.g. growth rate and time to extinction) have been in the field of conservation biology and, to a certain extent, lie outside traditional mating system studies. In short, most studies of plant mating systems have focused on how self-fertilization evolves (in supposedly viable populations), but not on how it may condition population demography.
Yet in the current context of environmental change, there has been renewed interest in the role of mating systems in population persistence. In particular, the decline in pollinators in many parts of the world (Winfree et al., 2011; Thomann et al., 2013; Hallmann et al., 2017) has led to a realization that insect-pollinated plants could be under threat. In the UK and The Netherlands, Biesmeijer et al. (2006) showed a parallel decline in pollinators and insect-pollinated plants in the second half of the 20th century, demonstrating a link between a decrease in pollinators and population extinctions of insect-pollinated plants. This has led evolutionary ecologists to study the possibility of short-term adaptations to changes in pollination regimes (Roels and Kelly, 2011; Thomann et al., 2013; Gervasi and Schiestl, 2017).
As a rule of thumb, a plant’s ability to self-fertilize is considered a way to avoid extinction in an impoverished pollinator environment. This view is somewhat inconsistent with the longer term perspective of Stebbins (1957), who considered selfing an evolutionary dead end (Takebayshi and Morell, 2001). Recent studies using well-resolved phylogeny have provided results supporting Stebbins (Goldberg et al., 2010). Yet while they may seem inconsistent, these contrasting theories both underline that a mating system is not neutral with respect to population demographics or lineage persistence. They are not necessarily mutually exclusive, but could suggest that while the evolution of selfing may optimize population persistence in the short term, it might be detrimental to the lineage in the long term. This would imply that selective advantages at play in the short term in a population are not necessarily consistent with the success of a lineage in the long term (Igic and Busch, 2013).
At the intersection between genetics and demography, the evolutionary rescue theory (Gomulkiewicz and Holt, 1995) has proposed a general framework to analyse the ability of evolution to rescue populations. This theory puts forward that in the context of environmental change, adaptation could allow populations to avoid extinction. In the absence of adaptation, extinction could be caused either (1) by a population vital rate that is <1 (deterministic extinction) or (2) by a low population size (below a critical value), making extinction very likely through demographic stochasticity. Recent environmental changes such as habitat fragmentation and a decline in pollinators have been identified as affecting the mating system traits in plants (Eckert et al., 2010). Empirical data suggest that outcrossing strategies directly or indirectly affect individual performance and population viability, which makes this mating system a good candidate to investigate using the evolutionary rescue framework. To date, mating system evolution and the impact of a mating system on population demography have not been considered in a single framework. The aim of this review was to examine patterns of evolution at various time scales in light of theoretical and empirical data to analyse how the evolutionary rescue framework may help determine the ability of mating system evolution to rescue populations.
MICRO- AND MACROEVOLUTION OF SELFING TRAITS
Adaptability of mating system traits and microevolution
The ability of plant mating systems to adapt to changes in response to selection pressures requires substantial genetic variance in traits associated with self-fertilization. Because of the impact of these traits on fitness, genetic variance would be expected to erode as the result of stabilizing selection. However, a compilation of data has revealed that floral traits exhibit coefficients of variation between 15 and 30 %, reaching up to 55 % for reward traits. In a set of 41 hermaphroditic species, Ashman and Majetic (2006) showed that populations exhibit substantial heritability for floral traits associated with mating systems (e.g. average h2 = 0.40 for anther–stigma separation and positioning) and pollinator attraction at the flower level (e.g. average h2 = 0.45 for corolla size; average h2 = 0.20 for nectar production). These data reveal that mating system traits can respond to selection over a short time scale (i.e. microevolution). In line with the heritability of selfing traits, the substantial among-population variation for outcrossing rates (Whitehead et al., 2018) is likely to be due in part to adaptation to local ecological conditions.
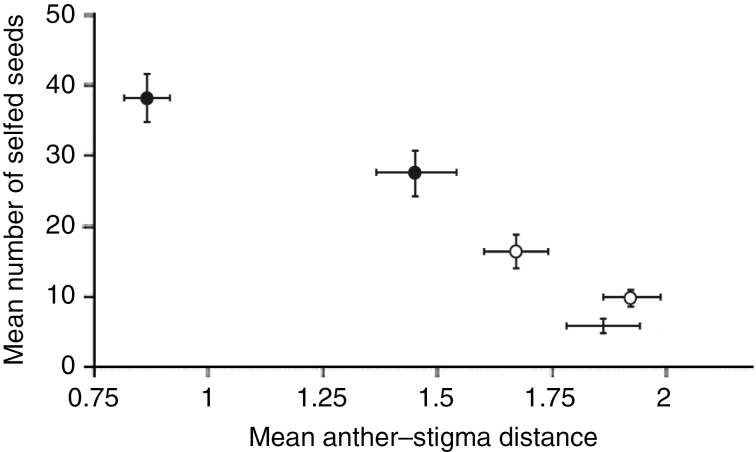
The context of pollinator decline in Europe and America (Winfree et al., 2011) has provided the ideal context to test the ability of mating systems to adapt to global changes. To investigate this, Roels and Kelly (2011) conducted an elegant experiment using the species Mimulus guttatus as a model system. The authors measured changes in anther–stigma distance (herkogamy) and a plant’s ability to set seeds without pollinators over five generations at two pollination levels. In the experimental populations, plants without pollinators evolved an improved ability to self-fertilize, associated with a reduced anther–stigma distance and increased autogamous seed set (Roels and Kelly, 2011), while plants with pollinators exhibited few changes (Fig. 1). Notably, the evolutionary potential was not limited in this study; surprisingly, the heritability of anther–stigma distance was even higher after selection than before selection. This type of evolution towards selfing has also been reported in natural populations of Centaurium erythraea by Brys and Jacquemyn (2012). In that study, the authors compared fragmented urban populations where pollinators were scarce to non-fragmented rural populations with high pollinator activity. They found that plants from fragmented environments exhibited less herkogamy and a higher capacity for autonomous selfing than plants from non-fragmented populations, results that provide a convincing demonstration that mating systems in natural contexts can evolve rapidly in the face of environmental change.
Fig. 1.
Shifts in anther–stigma distance in four experimental populations of Mimulus guttatus evolving with pollinators (white dots) or without pollinators (black dots) over five generations from initially equivalent populations (no dot). Reduced herkogamy is associated with the increase of selfed seed production. Error bars show standard errors (modified from Roels and Kelly, 2011, with permission).
However, the evolution of self-fertilization may not be the unique evolutionary response to pollinator scarcity. In the self-incompatible species Centaurea cyanus (Asteraceae), Thomann et al. (2015) reported the opposite trend, i.e. the evolution of increased attractiveness. In their resurrection ecology study, using seeds sampled 18 years apart in a location in the north of France where pollinator decline has been reported, they showed that the old population exhibited smaller capitula and a lower floral display than the more recent population. At the same time, the flowering date had advanced by 3 d. As the species remained self-incompatible, these data suggest that the rarity of pollinators selected for traits that allowed better pollinator attraction. While these findings appear to be inconsistent with previous results, increased attractiveness may be a way to respond to pollinator impoverishment in self-incompatible systems. Self-incompatibility is indeed not known to evolve to self-compatibility on a very short time scale. While such examples of microevolution are still scarce, findings such as these show that plant mating systems are likely to respond to fragmentation, pollinator decline and climate change through adaptation.
Patterns of macroevolution
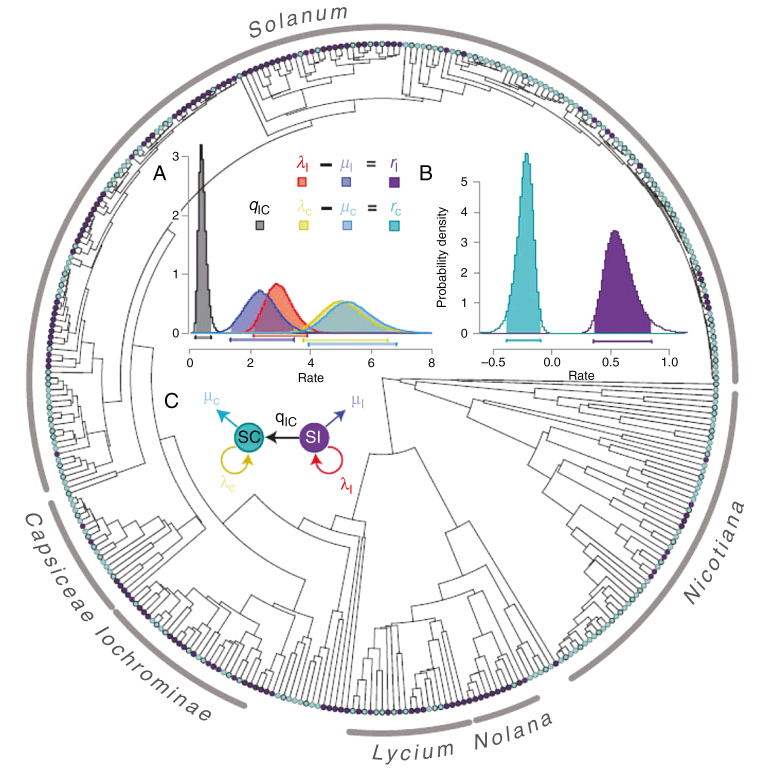
Beyond microevolutionary processes, the evolution of selfing in outcrossing ancestors has been considered a frequent transition in angiosperms (Takebayshi and Morell, 2001). While the transition from outcrossing to selfing was hypothesized by Stebbins decades ago (1950), unequivocal results have only been published in the last 10 years regarding the loss of self-incompatibility. Goldberg et al. (2010) analysed the loss of self-incompatible systems in 616 Solanaceae species and modelled the diversification and extinction rates of lineages. Their estimation revealed a higher speciation rate for self-compatible species, but this apparent advantage was counteracted by a much higher extinction rate. As a consequence, self-incompatible lineages exhibited a higher net diversification rate than selfing lineages (Fig. 2). While Goldberg et al. (2010) did not directly consider the evolution of selfing but rather the evolution of self-compatibility, several other studies have revealed the same pattern on selfing rates (Armbruster, 1988; Schoen et al., 1997; Goodwillie, 1999). Goldberg et al. (2010) were, however, one of the first to describe the long-term disadvantage of self-compatibility or the ‘evolutionary dead end’ of self-compatible lineages (Takebayshi and Morell, 2001). As Goldberg et al. (2010) noted, this pattern is compatible with selection operating at the group level. In another study, Igic et al. (2006) provided a solid demonstration of the irreversible evolution from self-incompatibility to self-compatibility in Solanaceae. Based on the population-genetic properties that self-incompatible alleles will be less subject to drift than neutral markers (because of balancing selection operating on self-incompatible alleles), the authors showed that self-incompatible alleles are conserved from ancestors through speciation. The findings revealed that the loss of self-incompatible alleles is irreversible, providing more evidence for the directional transition from outcrossing to selfing.
Fig. 2.
Phylogenetic relationships in the Solanaceae species (356 species). Self-incompatibility (SI) and self-compatibility (SC) are depicted by purple and turquoise tips, respectively. Probability distribution of transitions (and 95 % credibility intervals) between characters. (A) Estimates of transition (q), extinction (μ) and speciation (λ) are given for SI species (I subscript) and SC species (C subscript). (B) The net diversification rate is the difference between speciation and extinction rates. (C) Summary of estimated parameters (taken from Goldberg et al., 2010, with permission).
Overall, micro- and macroevolution patterns suggest that selfing can easily evolve and seems likely to be advantageous in the short term, but not in the long term. This suggests that the selective advantage of self-fertilization may differ depending on the time scale.
MATING SYSTEM STRATEGIES AND POPULATION PERSISTENCE/DEMOGRAPHY
Empirical evidence for the effect of mating systems on population demography
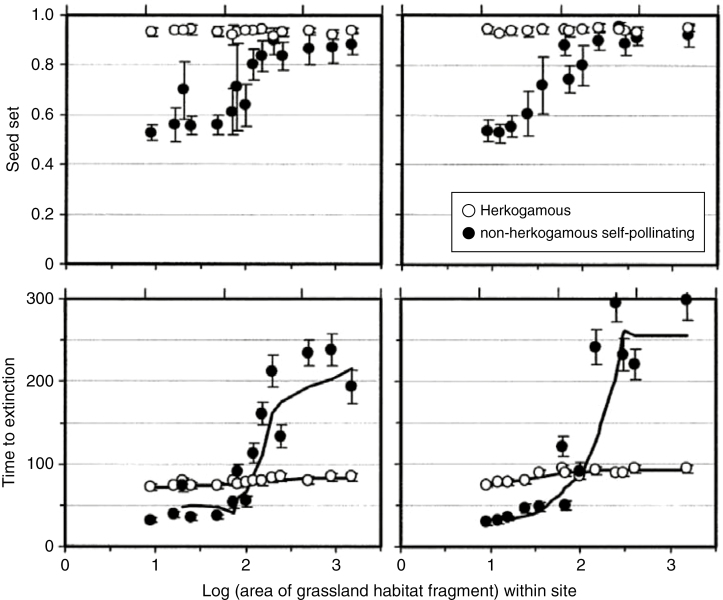
The idea that selfing may favour population demography through increased seed set goes back to Darwin (1876). It is also central in the seminal model of Baker (1955), who wrote: ‘with a self-compatible individual a single propagule is sufficient to start a sexually reproducing colony, making its establishment much more likely than if the chance growth of two self-incompatible yet cross-compatible individuals sufficiently close together spatially and temporally is required’. Yet very few experimental studies have investigated the role of mating systems in population demography. One meta-analysis comparing fragmented and non-fragmented habitats has revealed that seed set is lower in fragmented contexts, specifically in self-incompatible species, which the authors interpret as the consequence of reduced pollinator abundance (Aguilar et al., 2006). A few demographic studies have measured the direct impact of a selfing strategy on population demography parameters. In the insect-pollinated species Clarkia concinna, Groom (1998) showed that pollen limitation due to low census population sizes caused increased patch extinction within 5–6 years. Such a deterministic threat is caused by the Allee effect (Stephens, 1999), i.e. the fact that the population growth rate is negatively related to the population size in outcrossing plants. Because selfing individuals do not require mates in order to reproduce, such an Allee effect is not expected in selfing plants. In another study comparing non-herkogamous (i.e. selfing) plants and herkogamous (i.e. outcrossing) plants of the species Gentianella campestris, Lennartsson (2002) demonstrated that pollen limitation affects both seed set and time to extinction, resulting in a positive relationship of these parameters to population size in herkogamous plants. In contrast, the relationship is flat in non-herkogamous plants (Fig. 3). Interestingly, while seed set in selfing plants was higher than that in outcrossing plants, extinction in outcrossing plants was much lower than that in selfing plants in large populations. This implies a demographic advantage of outcrossing plants in the absence of pollen limitation. An advantage of outcrossing over selfing is likely to be caused by inbreeding depression. Because inbred progeny have lower performance, inbreeding depression would be expected to impede population demography (Saccheri et al., 1998). As outcrossing plants avoid inbreeding depression, outcrossing may provide a demographic advantage in terms of offspring survival.
Fig. 3.
Seed set and time to extinction in herkogamous and non-herkogamous plants of the species Gentianella campestris (from Lennartsson, 2002). The percentage of grassland in the landscape was 2–6 % for left panels and 12–15 % for right panels. Top: mean seed set (and standard deviation) in six populations along gradients of local fragmentation. Bottom: mean time to extinction for each local habitat fragment estimated from a stochastic matrix population model (see Lennartsson, 2002 for methodology, with permission).
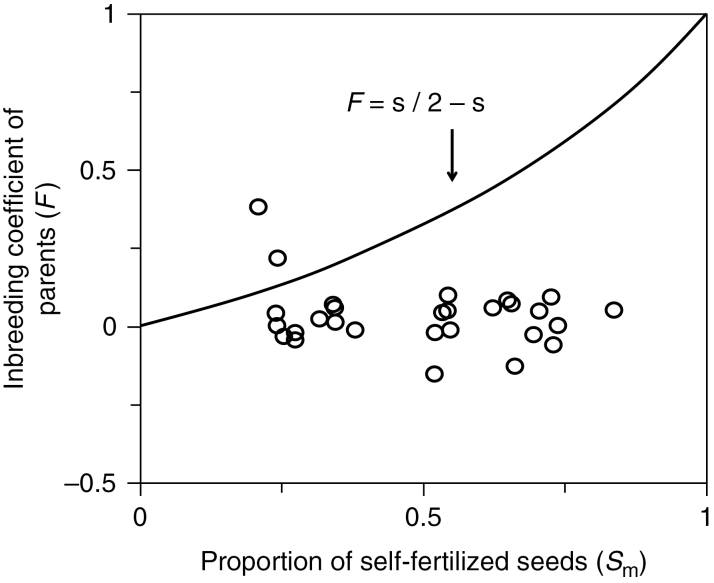
While few studies have tested the demographic effects of inbreeding depression in plant populations, there is indirect evidence that such an effect must be strong. For instance, by comparing inbreeding in seed and adult plants in the mixed selfer Rhododendron ferrugineum, Delmas et al. (2014) showed that about 90 % of selfed progeny died before adulthood (relative to outcrossed progeny), while the species produced more than half of its seeds through selfing (Fig. 4). These few examples illustrate that, while pollen limitation can impede population demography in outcrossing populations, inbreeding depression is likely to affect the population growth rate in selfing populations. Importantly, because inbreeding depression potentially affects demographic parameters over the entire life cycle (seed set and survival; see Husband and Schemske 1996), whereas pollen limitation only affects seed set, we would expect inbreeding depression to have more impact on the population growth rate than pollen limitation. Theoretical demography has indeed demonstrated that the sensitivity of the population growth rate to fertility (seed set) is much lower than the sensitivity to survival as an organism’s longevity increases (Caswell, 1982).
Fig. 4.
Inbreeding depression estimates from the variation between self- fertilization in progeny (s =1− t) and the inbreeding coefficient (F) of adult R. ferrugineum individuals in 24 patches. The solid line indicates the relationship between s and F in patches at equilibrium in the absence of inbreeding depression. From the deviation of the curve, inbreeding depression expressed during the life cycle can be inferred, resulting in a mean (s.e.) life time estimate of ID in natura of 0.9±0.03 (see Delmas et al., 2014 for more details, with permission)
Deterministic vs. stochastic sources of extinction
Conservation biology studies have established various sources of variation in population vital rates. At the population level, vital rates can be reduced deterministically or stochastically (Holsinger, 2000). The demography of selfing vs. outcrossing can be qualitatively classified according to these categories. When pollen limitation is caused by low mate density (Courchamp et al., 1999), the vital rate of outcrossing populations varies deterministically with population density; such an Allee effect constitutes a source of extinction for outcrossers. In selfing populations, inbreeding depression can deterministically decrease the population growth rate. These deterministic threats are expected to occur at the demographic scale, i.e. on a short time scale. In theory, such a disadvantage for selfers is expected to be cancelled out by the purging process (Charlesworth et al., 1991; but, for empirical data, see Byers and Waller, 1999; Winn et al., 2011). However, the purging process is expected to occur on a longer time scale than the demographic effects of selfing. The time scale of purging crucially depends on the properties of deleterious mutations. Highly deleterious mutations can be purged in a few generations, while weakly deleterious mutations may last for thousands of generations in populations.
Regarding stochastic threats, three sources of stochasticity have been defined in conservation biology (Holsinger, 2000). Environmental stochasticity refers to a situation in which vital rates vary randomly over time as a consequence of the temporal heterogeneity of the environment. The pollination environment is typically considered to vary over time and is expected to impact the reproductive success of outcrossing plants (Kalisz et al., 2004). In contrast, self-fertilization is expected to dampen environmental stochasticity caused by the temporal variation in pollinator services. Genetic stochasticity refers to the increased effect of random genetic processes in populations. Because selfing is expected to impact effective population size, we would expect a selfing population to be more affected by genetic drift, leading to lower selection efficiency (fixation of deleterious mutations) and loss of adaptive potential in the long term. Finally, because demographic stochasticity is the consequence of randomness in demographical processes without any variation between individuals, it is the consequence uniquely of population size, which is not expected to vary in a systematic way as a result of a selfing strategy.
EVOLUTIONARY RESCUE THROUGH MATING SYSTEM ADAPTATION
The extinction of selfing lineages in the long term and the evolution of selfing in the face of pollen limitation in the short term suggest that selfing may be advantageous in contemporary evolution (e.g. in the face of global change), but not at the macroevolution scale. The common view is that microevolution is driven by the dynamics of selfing genes within a population, whereas the macroevolution of selfing would be driven at the level of the lineage and operate at species level (species selection; Goldberg et al., 2010) as a result of the indirect genomic consequences of selfing. However, as explained in the next sections, such a view must be nuanced by the fact that evolution towards extinction can occur, even in the context of microevolution.
Optimization vs. invasion criteria
The seminal evolutionary rescue model (Gomulkiewicz and Holt, 1995) assumes that adaptation to a new environmental context can help recover a viable population. This is not necessarily the case. Whether or not the evolution of a trait will optimize population demography depends on the type of selection (Maynard-Smith, 1982). When selection is frequency dependent (i.e. when individual fitness depends on traits in the population), invasion criteria apply, and the issue of selection does not necessarily optimize population demography. In contrast, when selection is not frequency dependent, adaptation is expected to improve the population growth rate (Ferriere and Legendre, 2013). An important consequence of this is that frequency-dependent selection may eventually not only fail at rescuing a population, but actually cause evolutionary suicide. In a mating system, the success of an individual depends on mating strategies. For example, in dioecious species, the success of a male is directly related to the number of females available to sire, i.e. the sex ratio. However, the evolutionarily stable sex ratio of 50:50 (Charnov, 1976) does not maximize the population growth rate, since a higher proportion of females would increase it. Regarding the evolution of selfing, selfing traits are typically driven by frequency-dependent selection because selfers gain fitness by siring ovules in the population (Fisher’s automatic advantage). As a consequence, the fitness gain of a selfing genotype decreases with the opportunity to sire available ovules in the population, i.e. with the population selfing rate. The next sub-section shows how the evolution of selfing does not always improve the population growth rate using the standard model devised by Lloyd (1979).
Evolutionary rescue models for mating system traits must consider a two-phase model: (1) evolutionary dynamics and (2) demographic properties at a given selfing rate. The few models that have introduced demography in evolutionary models of self-fertilization (Cheptou, 2004; Abu Awad and Billiard, 2017) have studied the impact of selfing on population demography. These models have not fundamentally modified the criteria for the evolution of selfing defined by Lloyd (1979) (but see Cheptou and Dieckmann, 2002). As a rule of thumb, modifiers of selfing rates are driven by the traditional Fisherian benefits of selfing, inbreeding depression and reproductive assurance in a given demographic state.
Evolutionary rescue in a context of pollen limitation
To illustrate the discrepancy between evolutionary process and demography optimization, let us take the most intuitive situation, in which potential rescue is driven by the evolution of self-fertilization in a context of pollen limitation; for instance, after a pollinator crash (contemporary evolution). The evolutionary dynamics of selfing are captured by the fitness of a rare mutant practising a selfing rate sʹ in a population practising s (Lloyd, 1979; Lande and Schemske, 1985). The fitness of a focal individual can be estimated as the sum of selfed ovules, outcrossed ovules and pollen export, that is:
| (1) |
(where f is the number of ovules per plant, δ is inbreeding depression and e the rate of pollination of ovules available for outcrossing). Frequency dependence in eqn (1) is captured by the fact that pollen export depends on mating opportunities in the population, i.e. the population outcrossing rate (1 – s). The growth rate of a population practising s is given by:
| (2) |
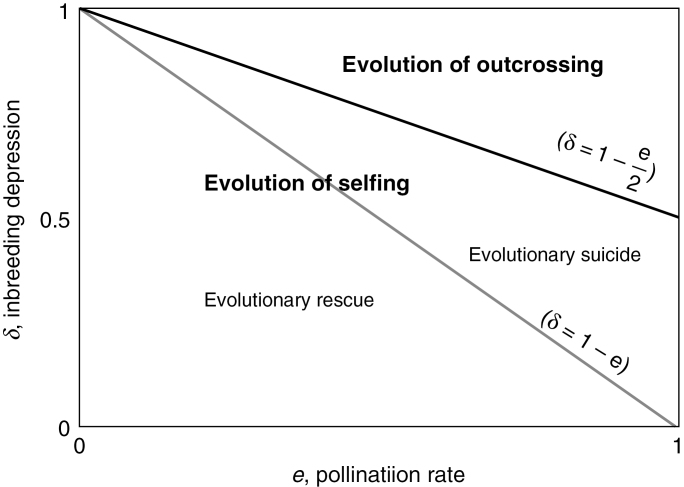
From eqn (1), it appears that higher selfing rates evolve as far as (1 – δ) >e/2, but the vital rate is maximized through higher selfing if (1 – δ) >e [eqn (2)]. Thus, when (1 – δ) >e, the evolution of self-fertilization will rescue a population (evolutionary rescue, Fig. 5), but when e >(1 – δ) >e/2, self-fertilization will potentially lead a population to deterministic extinction (evolutionary suicide, Fig. 5). This simple scenario highlights that the dynamics of individual plants (demography) does not equate to the dynamics of the genes driving evolution (Cheptou and Schoen, 2007).
Fig. 5.
The evolution of self-fertilization towards a non-optimal population growth rate in a context of pollen limitation assuming that the evolution is driven by the Fisherian cost of outcrossing and inbreeding depression (δ) (without purging) and the pollination rate of outcrossed ovules (e). Complete self-fertilization evolves for the set of parameters below the solid line and complete outcrossing evolves for the set of parameters above the solid line. Increased growth by selfing occurs below the thin line, resulting in evolutionary rescue, and decreased growth by selfing occurs above the thin line, resulting in evolutionary suicide.
In Cheptou (2004) this model was extended by introducing density-dependent pollen limitation (Allee effect) and density regulation. This model showed that the evolution of selfing does not always rescue populations, and that evolutionary suicide by selfing can happen. This occurs only when inbreeding depression is high, i.e. when its effect on the population growth rate is strong. This model also highlighted an unexpected effect of inbreeding depression: increasing inbreeding depression can select for selfing because density is so low that mate limitation makes pollen transfer for outcrossing very difficult. Importantly, the model indicates that evolutionary suicide by outcrossing is never possible. However, the evolution of outcrossing in the model led to populations sensitive to density variation, which can in turn lead to population extinction (demographic bistability), which was termed ‘ecological extinction’ (Cheptou, 2004).
Evolutionary rescue through the genomic consequences of selfing
Genomic consequences are typically considered to be acted out on a long time scale; through lower adaptability or the dynamics of deleterious mutations. A major impact of self-fertilization is the 2-fold reduction of effective population size (Ne) due to non-independent gamete sampling during reproduction (Pollack, 1987). The effect of genetic drift is expected to increase in selfing populations, leading to less efficient selection. As a consequence, weakly deleterious mutations may become effectively neutral. An empirical test comparing the ratio of synonymous vs. non-synonymous mutations in selfing and outcrossing species did not, however, reveal a reduction of purifying selection in selfers (Wright et al., 2002).
There are two types of models that have addressed the genomic consequences of selfing on population demography or population persistence: (1) models that study the ability of a population to adapt to a new environment and (2) models that study the effect of deleterious mutations and their impact on the genetic load. Glemin and Ronfort (2013) conducted a theoretical study of the impact of self-fertilization (considered as a fixed trait) on the fate of a beneficial mutation at a single locus that rescued a population after an environmental change. Their model allowed the rate of adaptation to be broken down into two components: (1) the waiting time until the appearance of the beneficial mutation and (2) the fixation time of the mutation. Selfers always have a shorter fixation time than outcrossers. However, the effect of the mating system on waiting time depends on standing variation and on the dominance of mutations. Selfers typically exhibit less standing variation than outcrossers as a consequence of lower effective population size, which tends to increase waiting time (genetic stochasticity), but the reverse can be true when mutations are partly recessive. Overall, the authors concluded that selfing slows down the rate of adaptation only when effective population sizes are reduced by much more than half (Glemin and Ronfort, 2013). Such a reduction could be due to life history traits linked to selfing (e.g. low colonization ability), which remains to be empirically demonstrated.
The effects of a mating system on genetic load and inbreeding depression have been widely studied in population genetics since the 1980s (Lande and Schemske, 1985; Charlesworth and Charlesworth, 1990; Charlesworth et al., 1990), but the role of mating systems in population demography has been investigated only recently. Generally, inbreeding is expected to purge deleterious mutations and lower inbreeding depression and genetic load, which, in the long term, should have a positive impact on population demography. Yet empirical results are not totally compatible with such predictions (Winn et al., 2011). In particular, highly selfing populations have sometimes revealed high inbreeding depression (e.g. Herlily and Eckert, 2002). Recently, Abu Awad and Billiard (2017) developed a simulation model with recurrent deleterious mutations in which selfing was allowed to evolve. Overall, their findings showed that evolutionary rescue by selfing does not always occur, and that evolutionary suicide sometimes results. The authors identified two major components for the possibility of evolutionary rescue. First, properties of deleterious mutations condition the possibility of purging. When mutations are weakly deleterious and selfing evolves in large steps, purging has a major demographic effect, leading to a high probability of extinction during the outcrossing–selfing transition. Some lineages accumulate by chance a large amount of deleterious mutations (due to genetic stochasticity). However, when selfing evolves in small steps and mutations are more deleterious, the evolution of selfing can provide evolutionary rescue.
CONCLUSIONS
Does self-fertilization rescue populations or is it an evolutionary dead end?
Taken together, evolutionary patterns show that plant mating systems are labile and have evolved in response to environmental changes at various temporal scales. However, the evolutionary trends provide a contrasting picture of whether selfing is advantageous or not. The microevolution of selfing would tend to support the argument that this mating system can rescue populations, in particular in the context of global environmental change. In contrast, macroevolutionary patterns are more consistent with Stebbins, i.e. self-fertilization is not advantageous in the long term. In many studies, the evolutionary dead end of selfing in the long term is traditionally interpreted as an indirect genomic consequence of this strategy, while the short-term advantage of selfing is viewed as the direct demographic advantage of higher seed production. While this view makes sense, it may need to be more nuanced. The model above shows that extinction through selfing is possible even in the short term when it is driven by inbreeding depression, the cost of outcrossing and reproductive assurance. This suggests that the distinction between the indirect genomic effects of selfing operating over the long term and the direct beneficial effects in the short term should be treated with caution. The key is the pace at which each process acts. The long-term patterns are somewhat paradoxical with regard to the purging process on the genome by selfing (Charlesworth et al., 1991), which should decrease the genetic load at equilibrium, resulting in higher mean fitness. As suggested by several authors (e.g. Glemin and Ronfort, 2013), the lower adaptability of selfers could be one of the causes of extinction of selfing lineages, but the theoretical conditions leading to this explanation are restrictive. Interestingly, a recent study on organisms with haploid-dominant life cycles (green algae) found no evidence of an ‘evolutionary dead end’ in the phylogeny (Hanschen et al., 2018). The authors propose that the dominant haploid phase exposing deleterious mutations to selection may be the reason for this discrepancy between seed plants and algae. Analysing the macroevolution of self-fertilization in organisms with various life cycles may be the key to understanding the evolutionary dead end in seed plants. Moreover, the irreversibility of selfing evolution has mainly been tested on genera possessing a self-incompatibility system (but see Armbruster, 1988). The argument for this irreversibility relies on the genomic constraint of self-incompatibility machinery, which, once dissolved, has little chance of reverting to functional self-incompatibility. An interesting direction for future studies would be to explore the ‘dead end’ hypothesis using non-self-incompatible species. Anther–stigma distance would be a good candidate to test if the irreversibility of selfing evolution is due to genomic constraint or selection.
Can models predict the impact of selfing on population persistence?
While traditional models simulating the evolution of selfing (and including inbreeding depression, the transmission advantage and reproductive assurance) provide compelling arguments for short-term evolution, most have not considered the impact of selfing on population demography or persistence. The reason is that these standard evolutionary models of self-fertilization rely on relative fitness. By assumption, such models cannot make predictions about population viability (Cheptou and Donohue, 2011). The first step to improve our understanding of this question is to consider two-phase models that couple evolutionary and demographic models; these can result in non-trivial outcomes. As illustrated in a very simple model (see above), the evolution of a mating system may sometimes lead to evolutionary rescue, and sometimes to evolutionary suicide. Since the advantages and disadvantages of selfing do not play out on the same temporal scale, it is crucial to pay particular attention to the pace of evolution in models.
The discrepancy between long-term and short-term processes may also underline that selection operates at different levels at these two time scales. Goldberg et al. (2010) argue that the extinction of selfing lineages in the long term is consistent with group selection. This idea was developed by Williams (1992) who stated that ‘The prevalence of outcrossing in flowering plants may result from selection for selfing within gene pools often being countered by selection for outcrossing between gene pools. Exclusively outcrossed plants may thus be favoured by clade selection over those that rely partly on selfing.’ However, most current mating system theory is based on gene level selection and cannot make predictions for higher selection levels. There is thus a crucial need to develop models in which selection potentially operates at various levels to evaluate the relevance of such an argument. From an empirical perspective, it is worth noting that macroevolution patterns may mask population variations and can only be processed at the level of the lineage. Thus it is important to keep in mind that our understanding of the processes at work may be limited by a lack of knowledge on population variation in macroevolutionary studies.
Mating system evolution as a case study for evolutionary rescue models
It is widely accepted that mating systems are key in responding to environmental change. This can occur through direct effects on a mating system, e.g. a crash in pollinators, or through indirect effects on the adaptability of a population to a new environment. Mating systems are thus good candidates for studying the possibility of rescue through adaptation. The large amount of existing data on the evolution of self-fertilization at various scales makes it a particularly relevant case study. As discussed in this review, evolutionary rescue through selfing cannot be considered simply as optimization because of the frequency-dependent selection inherent to mating system traits. We know from evolutionary ecology theory that many life history traits (e.g. dispersal, resource allocation, etc.) are driven by frequency-dependent selection (Stearns, 1992). In this respect, mating system traits may help to generalize evolutionary rescue theory.
ACKNOWLEDGEMENTS
I would like to thank the three reviewers and Jeffrey Karron for their helpful comments. This study was supported by the SEAD Project (How Selfing Affects Adaptation) funded by the French National Research Agency (ANR).
LITERATURE CITED
- Abu Awad D, Billiard S. 2017. The double edged sword: the demographic consequences of the evolution of self-fertilization. Evolution 71: 1178–1190. [DOI] [PubMed] [Google Scholar]
- Aguilar R, Ashworth L, Galetto L, Aizen MA. 2006. Plant reproductive susceptibility to habitat fragmentation: review and synthesis through a meta-analysis. Ecology Letters 9: 968–980. [DOI] [PubMed] [Google Scholar]
- Armbruster WS. 1988. Multilevel comparative-analysis of the morphology, function, and evolution of Dalechampia blossoms. Ecology 69: 1746–1761. [Google Scholar]
- Ashman TL, Majetic CJ. 2006. Genetic constraints on floral evolution: a review and evaluation of patterns. Heredity 96: 343–352. [DOI] [PubMed] [Google Scholar]
- Baker HG. 1955. Self-compatibility and establishment after ‘long distance’ dispersal. Evolution 9: 347–348. [Google Scholar]
- Biesmeijer JC, Roberts SP, Reemer M, et al. . 2006. Parallel declines in pollinators and insect-pollinated plants in Britain and the Netherlands. Science 313: 351–354. [DOI] [PubMed] [Google Scholar]
- Brys R, Jacquemyn H. 2012. Effects of human-mediated pollinator impoverishment on floral traits and mating patterns in a short-lived herb: an experimental approach. Functional Ecology 6: 189–197. [Google Scholar]
- Burd M. 1994. Bateman’s principle and plant reproduction: the role of pollen limitation in fruit and seed set. Botanical Review 60: 83–139. [Google Scholar]
- Byers DL, Waller DM. 1999. Do plant populations purge their genetic load? Effects of population size and mating system history on inbreeding depression. Annual Review of Ecology and Systematics 30: 479–513. [Google Scholar]
- Caswell H. 1982. Life history theory and the equilibrium status of populations. American Naturalist 120: 317–339. [Google Scholar]
- Charlesworth B, Morgan MT, Charlesworth D. 1991. Multilocus models of inbreeding depression with synergistic selection and partial self-fertilization. Genetical Research Cambridge 57: 177–194. [Google Scholar]
- Charlesworth D, Charlesworth B. 1990. Inbreeding depression with heterozygote advantage and its effect on selection for modifiers changing the outcrossing rate. Evolution 44: 870–888. [DOI] [PubMed] [Google Scholar]
- Charlesworth D, Morgan MT, Charlesworth B. 1990. Inbreeding depression, genetic load, and the evolution of outcrossing rates in a multilocus system with no linkage. Evolution 44: 1469–1489. [DOI] [PubMed] [Google Scholar]
- Charnov EL, Maynard-Smith J, Bull JJ. 1976. Why be an hermaphrodite?Nature 263: 125–126. [Google Scholar]
- Cheptou PO. 2004. Allee effect and self-fertilisation in hermaphrodites: reproductive assurance in demographically stable populations. Evolution 58: 2613–2621. [DOI] [PubMed] [Google Scholar]
- Cheptou PO, Dieckmann U. 2002. The evolution of self-fertilization in density-regulated populations. Proceedings of the Royal Society B: Biological Sciences 269: 1177–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheptou PO, Donohue K. 2011. Environment-dependent inbreeding depression: its ecological and evolutionary significance. New Phytologist 189: 395–407. [DOI] [PubMed] [Google Scholar]
- Cheptou PO, Schoen DJ. 2007. Combining population genetics and demographical approaches in evolutionary studies of plant mating systems. Oikos 116: 271–279. [Google Scholar]
- Courchamp F, Clutton-Brock T, Grenfell B. 1999. Inverse density dependence and the Allee effect. Trends in Ecology and Evolution 14: 405–410. [DOI] [PubMed] [Google Scholar]
- Darwin CR. 1876. The effects of cross and self fertilization in the vegetable kingdom. London: Murray. [Google Scholar]
- Delmas CE, Cheptou PO, Escaravage N, Pornon A. 2014. High lifetime inbreeding depression counteracts the reproductive assurance benefit of selfing in a mass-flowering shrub. BMC Evolutionary Biology 14: 243. doi: 10.1186/s12862-014-0243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan TM, Rausher MD. 2013. Evolution of the selfing syndrome in Ipomoea. Frontiers in Plant Science 4: 301. doi: 10.3389/fpls.2013.00301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert CG, Kalisz S, Geber MA, et al. . 2010. Plant mating systems in a changing world. Trends in Ecology & Evolution 25: 35–43. [DOI] [PubMed] [Google Scholar]
- Ferriere R, Legendre S. 2013. Eco-evolutionary feedbacks, adaptive dynamics and evolutionary rescue theory. Philosophical Transactions of the Royal Society B: Biological Sciences 368: 20120081. doi: 10.1098/rstb.2012.0081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. 1941. Average excess and average effect of a gene substitution. Annals of Eugenics 11: 53–63. [Google Scholar]
- Gervasi DDL, Schiestl FP. 2017. Real-time divergent evolution in plants driven by pollinators. Nature Communications 8: 14691. doi: 10.1038/ncomms14691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glemin S, Ronfort J. 2013. Adaptation and maladaptation in selfing and outcrossing species: new mutations versus standing variation. Evolution 67: 225–240. [DOI] [PubMed] [Google Scholar]
- Goldberg EE, Kohn JR, Lande R, Robertson KA, Smith SA, Igić B. 2010. Species selection maintains self-incompatibility. Science 330: 493–495. [DOI] [PubMed] [Google Scholar]
- Gomulkiewicz R, Holt RD. 1995. When does evolution by natural selection prevent extinction. Evolution 49: 201–207. [DOI] [PubMed] [Google Scholar]
- Goodwillie C. 1999. Multiple origins of self-compatibility in Linanthus section Leptosiphon (Polemoniaceae): phylogenetic evidence from internal-transcribed-spacer sequence data. Evolution 53: 1387–1395. [DOI] [PubMed] [Google Scholar]
- Groom MJ. 1998. Allee effects limit population viability of an annual plant. American Naturalist 151: 487–496. [DOI] [PubMed] [Google Scholar]
- Hallmann CA, Sorg M, Jongejans E, et al. . 2017. More than 75 percent decline over 27 years in total flying insect biomass in protected areas. PLoS One 12: e0185809. doi: 10.1371/journal.pone.0185809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanschen ER, Herron MD, Wiens JJ, Nozaki H, Michod RE. 2018. Repeated evolution and reversibility of self-fertilization in the volvocine green algae. Evolution 72: 386–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herlihy CR, Eckert CG. 2002. Genetic cost of reproductive assurance in a self-fertilizing plants. Nature 416: 320–323. [DOI] [PubMed] [Google Scholar]
- Holsinger KE. 2000. Demography and extinction in small populations. In: Young AG, Clarke GM, eds. Genetics, demography and viabiolity of fragmented populations. Cambridge: Cambridge University Press, 55–74. [Google Scholar]
- Husband B, Schemske DW. 1996. Evolution of the magnitude and timing of inbreeding depression in plants. Evolution 50: 54–70. [DOI] [PubMed] [Google Scholar]
- Igic B, Busch JW. 2013. Is self-fertilization an evolutionary dead end?New Phytologist 198: 386–397. [DOI] [PubMed] [Google Scholar]
- Igic B, Bohs L, Kohn JR. 2006. Ancient polymorphism reveals unidirectional breeding system shifts. Proceedings of the National Academy of Sciences, USA 103: 1359–1363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalisz S, Vogler DW, Hanley KM. 2004. Context-dependent autonomous self-fertilisation yields reproductive assurance and mixed mating. Nature 430: 884–886. [DOI] [PubMed] [Google Scholar]
- Lande R, Schemske DW. 1985. The evolution of self fertilization and inbreeding depression in plants. I. Genetic models. Evolution 39: 24–40. [DOI] [PubMed] [Google Scholar]
- Lennartsson T. 2002. Extinction threshold and disrupted plant–pollinator interactions in fragmented plant populations. Ecology 83: 3060–3072. [Google Scholar]
- Lloyd DG. 1977. Genetic and phenotypic models of natural selection. Journal of Theoretical. Biology 69: 543–560. [DOI] [PubMed] [Google Scholar]
- Lloyd DG. 1979. Some reproductive factors affecting the selection of self-fertilization in plants. American Naturalist 113: 67–79. [Google Scholar]
- Lloyd DG. 1980. Demographic factors and mating patterns in Angiosperms. In: Solbrig OT, ed. Demography and evolution in plant populations. Berkeley, CA: University of California Press, 67–88. [Google Scholar]
- Maynard Smith J. 1982. Evolution and the theory of games. Cambridge: Cambrige University Press. [Google Scholar]
- Nagylaki T. 1976. A model for the evolution of self-fertilization and vegetative reproduction. Journal of Theoretical Biology 58: 55–58. [DOI] [PubMed] [Google Scholar]
- Pollack E. 1987. On the theory of partially inbreeding finite populations. I. Partial selfing. Genetics 117: 353–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roels SAB, Kelly JK. 2011. Rapid evolution caused by pollinator loss in Mimulus guttatus. Evolution 65: 2541–2552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saccheri I, Kuussaari M, Kankare M, Vikman P, Fortelius W, Hanski I. 1998. Inbreeding and extinction in a butterfly population. Nature 392: 491–494. [Google Scholar]
- Schoen DJ, Johnston MO, L’Heureux AM, Marsolais JV. 1997. Evolutionay history of the mating system in Amsinckia (Boraginaceae). Evolution 51: 1090–1099. [DOI] [PubMed] [Google Scholar]
- Stearns SC. 1992. The evolution of life histories. Oxford: Oxford University Press. [Google Scholar]
- Stebbins GL. 1957. Self-fertilization and population variability in higher plants. American Midland Naturalist 91: 337–54. [Google Scholar]
- Stephens PA. 1999. Consequences of the allee effect for behavior, ecology and conservation. Trends in Ecology and Evolution 14: 401–405. [DOI] [PubMed] [Google Scholar]
- Takebayshi N, Morell PL. 2001. Is self-fertilization an evolutionary dead end? Revisiting an old hypothesis with genetic theories and macroevolutionary approach. American Journal of Botany 88: 1143–1150. [PubMed] [Google Scholar]
- Thomann M, Imbert E, Devaux C, Cheptou PO. 2013. Flowering plants under global pollinator decline. Trends in Plant Science 18: 353–359. [DOI] [PubMed] [Google Scholar]
- Thomann M, Imbert E, Engstrand RC, Cheptou PO. 2015. Contemporary evolution of plant reproductive strategies under global change is revealed by stored seeds. Journal of Evolutionary Biology 28: 766–778. [DOI] [PubMed] [Google Scholar]
- Vogler DW, Kalisz S. 2001. Sex among the flowers: the distribution of plant mating systems. Evolution 55: 202–204. [DOI] [PubMed] [Google Scholar]
- Whitehead MR, Lanfear R, Mitchell RJ, Karron JD. 2018. Plant mating systems often vary widely among populations. Frontiers in Ecology and Evolution 6: 38 doi.org/10.3389/fevo.2018.00038. [Google Scholar]
- Williams GC. 1992. Natural selection: domain, levels and challenges. New York: Oxford University Press. [Google Scholar]
- Winfree R, Bartomeus I, Cariveau DP. 2011. Native pollinators in anthropogenic habitats. Annual Review of Ecology, Evolution, and Systematics 42: 1–22. [Google Scholar]
- Winn AA, Elle E, Kalisz S, et al. . 2011. Analysis of inbreeding depression in mixed-mating plants provides evidence for selective interference and stable mixed mating. Evolution 65: 3339–3359. [DOI] [PubMed] [Google Scholar]
- Wright SI, Lauga B, Charlesworth D. 2002. Rates and patterns of molecular evolution in inbred and outbred Arabidopsis. Molecular Biology and Evolution 19: 1407–1420. [DOI] [PubMed] [Google Scholar]
- Yampolsky C, Yampolsky H. 1922. Distribution of sex forms in the phanerogamic flora. Bibliotheca Genetica 3: 1–62. [Google Scholar]