Electromagnetic simulation for diagnosing damage to femoral neck vasculature: A feasibility study

Abstract

Background

Femoral neck fractures are common injuries managed by orthopedic surgeons across the world. From pediatrics to geriatrics, disruption of the blood supply to the femoral neck is a well-recognized source of morbidity and mortality, oftentimes resulting in avascular necrosis of the femoral head. This devastating complication occurs in 10–45% of femoral neck fractures. Therefore, it is vital for orthopedic surgeons provide efficient treatment of this injury, in order to optimize the patient's potential outcome and prevent long-term sequelae.

Methods

In this study, the anatomy of the proximal femur, including femoral metaphysis, femoral neck, vasculature, and femoral head, were simulated in COMSOL Finite Element Analysis (FEA) software. Electric fields were generated in a fashion that exploited disruptions within the vasculature of the femoral neck. This study was aimed at developing an alternative imaging modality for narrowing or disrupting the femoral neck's vasculature. The variables used for investigation included: frequency, penetration depth, and magnitude of the electrical energy. These variables, when combined, allowed for enhanced simulated visualization of the vasculature of the femoral neck and theoretically expedited diagnosis of obvious, or occult, femoral neck injury.

Results

Simulated blood vessels were developed in two-dimensions: the phi direction (circular), and z-direction. Two different frequencies, 3 GHz, and 5 GHz were considered, with 100-J energy pulses within blood vessels of 2.54 mm in diameter. The fat surrounding the bone to the outside surface body was simulated at 0.25 inch (0.65 cm). An additional model, with layered fat and skin above the vessels, was simulated at 2000J and successfully able to visualize the femoral neck's blood vessels. Results showed a distinguished E field across the blood boundary of nearly 170 V/M.

Conclusions

The electric field simulation data within the Phi and Z directions promises the feasibility of a subsequent practical model.

1. Introduction

Femoral neck fractures are a challenge routinely faced by orthopedic surgeons. With an aging population, there is an increasing incidence of low-energy femoral neck fractures from a ground level fall. Furthermore, some femoral neck fractures are often the result of high-energy trauma in younger patients, as a result of shear forces across the patient's femoral neck. These injuries are particularly complex given their notoriously fragile blood supply.

The blood supply to the femoral head is the result of three main arterial sources and their branches: the medial femoral circumflex artery, lateral femoral circumflex artery, and terminal branches of the obturator artery.⁸ Fractures, most commonly in elderly with osteoporotic bone and comorbidities, results in direct disruption of this blood flow. The result of this disruption of blood flow is avascular necrosis (AVN) of the femoral head and neck if anatomic reduction is not immediately restored through surgical intervention.⁴ Various classifications by Garden² and Pauwels³ have been developed in order to aid clinicians in the swift diagnosis and ideal management of this challenging patient population. Nonetheless, Current literature have identified that nearly 7% of all femur fractures have an ipsilateral femoral neck fracture.⁷ These injuries are frequently missed amongst trauma patients and advancing protocols have been developed to aid clinicians in this diagnosis.⁵

The increased concern around this injury aims at preventing the known sequelae of avascular necrosis of the femoral head. While current literature has found an increased rate of AVN with the severity of displacement, non-displaced or occult fractures can also lead to osteonecrosis. The elevated risk of avascular necrosis and the high rates of non-union^1,6 make the management of this injury a challenge for all parties involved in the patient's care.

Currently, trauma patients are triaged and imaged, most commonly, using preliminary X-rays to visualize a patient's injuries. Radiographic images are often all that is needed to confirm the diagnosis of a femoral neck fracture—though advanced imaging is oftentimes utilized for inconclusive cases. CT scanner and MRI are useful tools for challenging diagnostic cases. However, CT scans subject patients to elevated levels of radiation while MRIs are unfavorable from a time and cost standpoint—being one of the more expensive imaging options for patients. Alternative imaging methods are challenging the current “gold standard” for evaluation of femoral neck fractures, in hopes of finding an efficient, reliable, and fiscally responsible modality. In this study, an alternative approach is proposed using electrical fields. With an electric field scan, transmission properties of simulated arteries, bone, and surrounding fat/skin can be used to evaluate an alternative imaging option. This paper details the control parameters of such an investigation.

2. The EM models

The wave equation used in the determination of the E distribution is given below:

∇ x (∇xE) = ∇ (∇.E) - ∇²E

From Gauss ‘law, ∇. D = ρ_v, then ∇. E = ρ_v/ɛ.

Using ρ_v = 0, the wave equation becomes:

∇ x (∇x E) = - ∇²E

The electric field is given in the form:

E = E₀ e^−γz

where γ = Propagation constant determined from:

γ² = - ω²μɛ̂

Where ɛ̂ is the complex permittivity given as:

ɛ̂ = ε(1-jσ/ωε)

Where ε = ε₀ε_r, the radian frequency, ω = 2πf, and σ is the conductivity.

The propagation constant, γ, is given by:

γ = α + jβ, where α is the attenuation constant, and β is the phase shift constant. The electric field is then given by:

E = E_o e^−αz e^-jβz

The magnitude of the field is given by:

E = E_o e^−αz

The boundary conditions used in this analysis was based on matching the tangential components of the electric fields at the interfaces, fat/vessels/bone boundaries. That is nxE = 0 at the interfaces.

The COMSOL mesh models for both the z and phi directions are given in Fig. 1.

Fig. 1.

The z and phi Blood Vessels Used for the Simulation: (a) for the z-direction, and (b) for the phi direction.

3. Results and discussions

Though not anatomically accurate, for simplicity of the investigation, all simulated vessels in this study had variable diameters for addressing the normal, narrowing, and blocking cases. Table 2 gives the diameter sizes for all cases. Initially 3 Ghz signals simulation was used to detect the presence of the vessels and measure the anatomic thicknesses of the blood vessels. Table 1 gives the material properties used in the simulation. The investigation of the blood vessels narrowing inside the human femur was addressed via electric field pulse applications with the solution of wave equation inside multiple layer structure. The wavelength, λ, the penetration depth, δ, the energy in joules, and the multiple layer (fat, bone, and blood vessels) widths were of important considerations. The transmission properties of the materials have led to distinguishing the blood vessel sizes within the femur neck. Two different frequencies were considered for the investigation; 3 GHz (λ = 0.1) and 5 GHz (λ = 0.06). The frequencies used in this investigation were appropriate with the material transmission properties within the COMSOL software. The energy levels range from 100 J to 2000 J, where the high energy pulse was important to transmit a pulse through the multiple layers (3D structure), and skin/fat/blood vessels). The low energy pulses were appropriate for the study of the transmission properties and layer interface within 2D structure. Layer thicknesses range between 0.05 (blood vessels) and 0.25 inches. The data were then processed to transform it in the digital format, where the blood vessel sizes can be identified. The following cases were investigated for the best image quality within the simulation resulting from the electric transmission parameters. The impact of the parameters were addressed as follows:

• A.
  Impact of the frequency (or wavelength)

  • i.
    At 3 GHz in 2D simulation for normal and narrow blood vessels at 100 J energy pulse in the phi direction
  • ii.
    At 5 GHz in 2D simulation for normal and narrow blood vessels at 100 J energy pulse in the phi direction
• B.
  Impact of the energy

  • i.
    At 3 GHz in 2D for normal and narrowing blood vessels at 500 J and 1000 J energy pulses
  • ii.
    At 5 GHz in 2D for normal and narrowing blood vessels at 500 J and 1000 J energy pulses
• C.Impact of the skin/fat/blood vessels, 3D simulation
• i.At 3 GHz within the skin/fat/blood vessels at 1000 J, and 200 J in both Phi and Z directions
• ii.At 5 GHz within the skin/fat/blood vessels at 1000 J, 1000 J and 2000J in both Phi and Z directions
• D.The digital formatted data to identify the blood vessel widths
• i.At 3 GHz for the 2D simulation case
• ii.At the 5 GHz for the 3D simulation case

Table 2.

Vessel sizes used in the simulation.

Dimension	Normal	Small	Big	Closed
Z	0.075	0.035	0.1	0.01
Phi	0.05	0.025	0.1	0.01

Table 1.

Material properties used in the simulation.

Material	Frequency	Relative permittivity	Conductivity (mho/m)
Bone	2 Ghz	4.9	0.15
	5 Ghz	0.8	0.21
Muscle	2 Ghz	55.4	1.45
	5 Ghz	49.6	2.56
Fat	2 Ghz	15	0.35
	5 Ghz	12	0.82

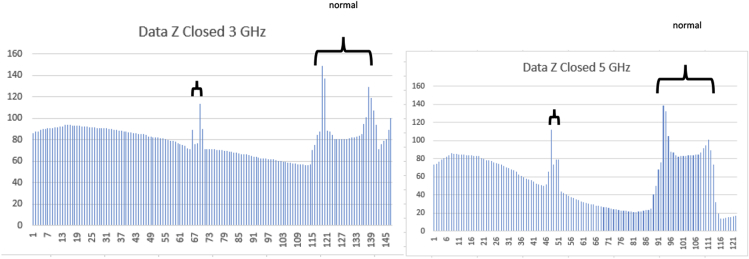
The selection of the frequency 3 GHz and 5 GHz were based on the availability of the practical model where the size of the antenna used for this purpose is manageable and readily available. Different simulation results were obtained in response to the penetration depths of the tissue materials. Fig. 2 shows the COMSOL model with respect to the actual anatomical model used in the simulation. The blood vessels were altered to investigate the feasibility study of diagnosing their thicknesses in 2D and 3D models. The COMSOL model were made close to the anatomical model seen in Fig. 2b. It shows the head, neck, and leg of the femur. Fig. 3 shows the blood vessels with the bone rapture case that may result from further blood vessel narrowing. Fig. 4, Fig. 5 show the impact of both energy levels and frequency. At 3 GHz for instance, the 100 J response in Fig. 3 does not exhibit enough information about the size of the vessels, while the 500 J for the same frequency shows better response. Likewise, the case of the 5 GHz in both Fig. 4, Fig. 5. Within these data, it is observed that the 3 GHz data were more indicative to the vessel sizes than that of the 5 GHz. This may be attributed to the less penetration depth at the higher frequency operation. The 3D model uses 0.6 cm fat region covering the femur. This reflects the actual model when diagnosis is determined from outside (non-invasive). Fig. 6 gives the field response within the phi direction, while Fig. 7 gives the response in the z-detection. In the practical model, the analog signal can be converted into digital form. This can be implemented via comparator circuitries. Fig. 8 shows the simulation for the narrow arteries for 3 and 5 Ghz. The blocked arteries were simulated as negligible diameter (.01in). The simulation for both 3 Ghz and 5 Ghz are given in Fig. 9. Fig. 10 shows the concept of the comparator circuit and the expected output voltages. As it is clear, the energy pulse was increased in order to overcome the power absorbed by the fat/skin materials. After a number of simulation efforts, the 1000 and 2000 J energy levels seem to be producing effective data for determining the blood vessel thicknesses. Apparently, very little difference between the two responses were observed, and therefore, the 1000 J is more feasible for the practical model. This is due to the appropriate antenna system that may be applied for transmitting this level of energy. The material properties used in the simulation is given in Table 1, and the dimensions considered for normal, small, and big size vessels are given in Table 2.

Fig. 2.

The Femur with compoents and blood vessels: (a) the COMSOL Model, (b) the Femur components.

Fig. 3.

Blood Vessels showing rapture in the femur.

Fig. 4.

2D simulation for the 3 Ghz and 5 GHz field response.

Fig. 5.

2D simulation for the 5 GHz Field response.

Fig. 6.

3D Field response in the Phi direction for two different frequencies and two different energy levels with fat depth of nearly 0.6 cm.

Fig. 7.

3D Field response in the Z-direction for two different frequencies (3 GHz and 5 GHz) and two different energy levels; 1000 J and 2000J with fat depth of nearly 0.6 cm.

Fig. 8.

Narrowing arteries at 3 GHz and 5 GHz.

Fig. 9.

Closed (or blocked) at 3 Ghz and 5 Ghz

Fig. 10.

The concept of comparator circuits for generating the output voltages given at different frequencies for both the Z- and Phi directions.

4. Conclusion and future work

The study conducted in this research proved the concept of detecting blood vessels inside the femur bone. The findings may serve the non-invasive approach for diagnosing the status of the blood vessels. The received numbers from the transmitted and reflected fields as determined from the finite element simulation by COMSOL are within the existing sensor technology for MEMS (micro-electro-mechanical systems.⁹ The Hall Effect sensors may be built on flexible substrates in order to shape up the sensors around the waist for better measurements. Fig. 11 (a) shows a comparator circuit that may be used to provide a digitized formatted output as shown in Fig. 10. The function v should be the reference potential while the input is the signal coming from the sensors. Buffering circuitries may be necessary for better interfacing the sensor to the circuit as shown in Fig. 11. Fig. 12 shows the proposed 2D and 1D Hall Effect sensors on flexible substrate that may be utilized for the practical model. In case if 1D array sensors is used, a servomechanism system or movable hardware system may be needed to track the field distribution around the femur bone. Fig. 13 proposes an idea of wearing hardware with 1D array movable sensors to track the field data.

Fig. 11.

The proposed electronic circuits for the practical model of the proposed system:(a) The top circuit is the comparator circuit for generating the digitized output, the bottom circuit (b) is the sample and hold off circuit to store the data within the capacitance.

Fig. 12.

Proposed sensor array in 2D (a) and 1D array (b).

Fig. 13.

Proposed 3D holder system with 1D array that may rotate to track the field distribution inside the Femur.