Simulations Reveal Multiple Intermediates in the Unzipping Mechanism of Neuronal SNARE Complex

Abstract

The assembling of the soluble N-ethylmaleimide-sensitive factor attachment protein receptor protein complex is a fundamental step in neuronal exocytosis, and it has been extensively studied in the last two decades. Yet, many details of this process remain inaccessible with the current experimental space and time resolution. Here, we study the zipping mechanism of the soluble N-ethylmaleimide-sensitive factor attachment protein receptor complex computationally by using a coarse-grained model. We explore the different pathways available and analyze their dependence on the computational model employed. We reveal and characterize multiple intermediate states, in agreement with previous experimental findings. We use our model to analyze the influence of single-residue mutations on the thermodynamics of the folding process.

Introduction

Soluble N-ethylmaleimide-sensitive factor attachment protein receptor (SNARE) proteins are fundamental catalysts for vesicle-membrane fusion (1, 2, 3). This is in turn a fundamental step in several biological processes, as for instance signal transmission in neurons.

Neuronal exocytosis is driven by the formation of a four-helix complex, composed by one vesicle-SNARE protein (VAMP2 or synaptobrevin) and two target-SNARE (t-SNARE) proteins, syntaxin and SNAP25. Synaptobrevin (Sb) and syntaxin (Sx) both contribute to this complex with one α-helix, whereas SNAP25 consists of two α-helical motifs connected by an unstructured linker loop. These four helices assemble parallel to each other in a coiled-coil bundle composed of 15 hydrophobically stacked layers (4). This folding process provides the free energy necessary to trigger vesicle-membrane fusion (5, 6). Fig. 1 shows a schematic representation of the structure of the SNARE complex, its domains, and its layers. A conserved layer, formed by the positively charged residue ARG56 of Sb and the three polar residues GLN226 of Sx and GLN53 and GLN174 of SNAP25, divides the four helices into their N-terminal domains (NTDs) and C-terminal domains (CTDs). This layer is usually referred to as the ionic layer and is numbered as layer 0, and positive increasing indexes are assigned to C-terminal layers and negative indexes to N-terminal ones. Sx and Sb also contain each a linker domain (LD) connecting their CTDs to the respective transmembrane domains.

Figure 1.

Schematic view of the SNARE complex. The four parallel helices of synaptobrevin (Sb), syntaxin (Sx), and SNAP25 form the core bundle of the complex. One arginine and three glutamine residues constitute the ionic layer, which divides the C-terminal domain (CTD; layers +1 to +8) from the N-terminal domain (NTD; layers −7 to −1). The linker domain (LD) of Sx and Sb and the linker loop of SNAP25 are also shown. Dashed colored lines schematically indicate the anchoring points on Sx, Sb, and SNAP25 to the lipid membranes. These are also the residues used in the definition of the pulling coordinates.

In the last decade, biologists have discovered several details about the function of this protein complex, about its structure, and about the mechanism that enables the lipid bilayers fusion. Specifically, several experiments have shown that a partially assembled SNARE complex exists as an intermediate state during vesicle exocytosis (7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20). The presence of such an intermediate state is critical for the kinetic of exocytosis. In vitro studies of de novo SNARE assembly have revealed rates of hundreds of milliseconds (14, 15), much slower than in vivo action potential transmission, which occurs at submillisecond timescales. It is thus believed that SNARE preassembles in this intermediate state and that a calcium influx triggers its final, quick folding (7, 8, 10, 11).

Recent single-molecule pulling experiments with optical (14) and magnetic tweezers (15) revealed important structural, energetic, and kinetic details of such a half-zipped intermediate, showing that it corresponds to an unzipping of the CTD of Sb up to the ionic layer. The optical tweezers measurements reported in (14) also identified the unzipping of the LD as the first step of SNARE unfolding. The half-zipped SNARE intermediate has been further analyzed by means of single-molecule Förster resonance energy transfer (FRET) experiments (16), which interestingly revealed the presence of an additional intermediate state. This additional step of fusion, corresponding to the zipping of the domain surrounding the ionic layer, was later confirmed and characterized by means of optical tweezers experiments (19). Analogous half-zipped intermediates were also observed with optical tweezers in different SNARE complexes (21) as well as in the t-SNARE binary complex zipping (22). The influence of regulator proteins Munc18 and α-SNAP on the SNARE zipping mechanism was also studied with optical tweezers and single-molecule FRET (19, 23, 24).

However, many questions on the SNARE zipping mechanism and its role in exocytosis remain still unanswered. Here, we address some of these questions. Specifically, we investigate the role of the ionic layer in the formation of the intermediate states and the precise structure of the intermediates and their functional role. To provide possible answers to these questions, we make use of a computational model that enables us to characterize structural details of the complex unzipping with atomic-scale resolution.

Molecular dynamics (MD) simulations are an extremely convenient tool to investigate the dynamics of biological macromolecules at the nanometer scale. Thanks to the methodological advances (25, 26, 27, 28) of the last decades, as well as the ever-growing computational resources available (29), it is nowadays possible to perform informative simulations of small proteins (30, 31, 32) or nucleic acids (33) at biologically relevant timescales. Nevertheless, atomistic, explicit-solvent simulations still have a high computational cost, making it extremely challenging to simulate long-timescale processes for large systems, even with special-purpose hardware (29). For this reason, several alternative models have been proposed that aim at reducing the complexity of computations by simplifying the description of the molecules of interest. Common simplifications are, for instance, avoiding explicit simulation of solvent molecules or grouping together several atoms in a single bead in what is usually referred to as coarse graining. The so-called structure-based models (SBMs) are an interesting candidate in this sense (34, 35, 36).

The idea of SBMs is to simplify the protein force field by eliminating all non-native interactions and explicitly considering only interactions between residues that are in contact in the native, minimal-energy structure (plus excluded volumes and bond/angle/dihedral potentials along the protein chain). This simplification is justified by the principle of minimal frustration (37), a tenet of the energy landscape theory of protein folding (38, 39), which posits that naturally occurring proteins have evolved to minimize frustration so that non-native interactions are overall much weaker than the native ones and play a minimal, often negligible role on the folding dynamics (40). Despite their apparent simplicity, SBMs have been repeatedly shown to be able to successfully characterize several details of protein folding (34, 41, 42, 43, 44, 45, 46, 47, 48, 49), showing significant consistency with experimental findings (50, 51, 52, 53). SBMs have also been used to study protein binding (54) and conformational transitions (55, 56, 57, 58, 59, 60, 61, 62, 63) in proteins and nucleic acids.

It is worth commenting that the success of SBMs and other coarse-grained models in general lies not only in their lower computational cost but most importantly in the fact that by reducing the complexity of the model, they allow us to focus on the effect of specific physicochemical features, disregarding details that are considered not important for the specific case of study. SBMs, for example, provide information about the overall properties of the system that are “encoded” in the topological details of the native structure while ignoring non-native frustration and the fast, small fluctuations during the protein dynamics.

The dynamics of the SNARE folding-unfolding mechanism have been previously studied with MD simulations (64), both using all-atom explicit-solvent models (65, 66, 67, 68, 69) and coarse-grained potentials (70, 71, 72). However, given the large size of the SNARE complex ($\simeq 300$ amino acids), explicit-solvent MD simulations are limited to very short timescales and very few trajectories. In particular, if used to simulate the effect of mechanical pulling on a protein complex such as SNARE, the high computational cost limits the simulations to non-biologically fast pulling and poor statistics. Considering these limitations, Tekpinar et al. (68) observed the two unzipping steps of LD and CTD unfolding using an atomistic explicit-solvent model.

Coarse-grained models, on the other hand, are more efficient, enabling more exhaustive analysis of the unzipping process. Zheng et al. (71) showed that steered MD simulations of a C^α-only SBM of SNARE were not able to capture the correct unfolding mechanism, whereas a reparametrized C^α SBM qualitatively identified the CTD unzipping step. Other computational studies focused on the interaction of SNARE with the membrane (69, 70) or its cofactor complexin (66, 67).

Here, we employ an atomistic SBM (44, 73) of the SNARE complex to investigate the formation of intermediate states and their possible functional role at atomistic resolution with reduced computational cost with respect to all-atom explicit-solvent simulations. Such an approach is known to provide a good understanding of the folding mechanism of proteins, correctly predicting the presence of intermediates and giving insights on their structural details (34, 35, 42, 43, 44, 45, 46, 49, 54, 74, 75). The reduced number of degrees of freedom of the model enables us to perform hundreds of relatively long simulations, providing statistically significant results.

We perform MD simulations to characterize the mechanism of mechanical unfolding of the SNARE complex with the goal of gluing together findings coming from different, independent experiments, providing a unifying model able to explain all evidence. We do so by simulating the unzipping of SNARE under the action of a mechanical force as well as its rezipping when such force is released. We note that the analysis of the rezipping phase is missing in all previous computational studies. This computational investigation allows us to identify and characterize multiple intermediate states during the mechanical unzipping that can be directly compared with the results of several different experiments (14, 15, 16). Moreover, we perform a free-energy analysis that enables us to 1) identify the preferred unzipping pathway and 2) study the effect of single-point mutations on the stability of the different intermediates.

Materials and Methods

Initial structure

The x-ray structure of the SNARE complex was obtained from the Protein Data Bank (1SFC) (4). As the linker loop of SNAP25 is missing in the deposited structure, we modeled it using the robotics-inspired kinematic closure algorithm for loop closure implemented in the Rosetta software (76, 77, 78). We used the algorithm to produce an ensemble of 50 possible conformations for the loop and defined the parameters of the SBM force field to reproduce such ensemble. Details are provided in the Supporting Materials and Methods. To prevent the complete separation of Sb from the rest of the complex, we modeled a disulfide bridge between the N-terminals of Sx and Sb, introducing a harmonic distance restraint (see details in the Supporting Materials and Methods).

SBM

The all-atom SBM (73) of SNARE was generated using the SMOG web server (79). Details of the model are given in the Supporting Materials and Methods. Simulations were performed using a modified version of GROMACS 4.5 (80), which implements the Gaussian-well potential described in (81). In all simulations, the temperature was fixed at T = 105 K (GROMACS external units). This temperature was chosen after computing the folding temperature of the system ($\simeq 135$–140 K). See Fig. S1 for a more detailed discussion. It is important to notice that the units used in the SBM simulations are simply internal units of the model (see Supporting Materials and Methods for a more detailed explanation) and do not represent real physical values. Indeed, for the SBM of SNARE, 105 K represent a temperature close to physiological temperature, being around 20% lower than its melting temperature. This is a convention generally used for SBM simulations (36). For this specific reason, we reported all our results as function of k_BT, which makes a comparison with experimental quantities more intuitive.

Steered MD

To mimic the experimental setup of a typical single-molecule pulling experiment and the in vivo unzipping mechanism, we performed two sets of 100 steered MD simulations (82). We simulated two different pulling protocols using two different reaction coordinates. The first reaction coordinate (RC1, used in the first set of simulations) consists of the distance between the C^α atoms of residues SER141 and LEU69, which are at the C-terminals of Sx and Sb, respectively (see also Fig. 1). This mimics the setup used in previous optical/magnetic tweezers experiments (14, 15, 19, 22). The second reaction coordinate (RC2, used in the second set of simulations) is defined as the distance between the C^α atom of LEU69 and the center of mass of the C^α atoms of SER141 (C-terminal of Sx), and CYS221, CYS224, CYS226, and CYS228 (lipid anchors tethering points on SNAP25, see Fig. 1) (83). RC2 is designed to resemble the in vivo mechanism of SNARE unzipping because both Sx and SNAP25 are anchored to the cell membrane during exocytosis, and they are thus bound to move together.

During steered MD simulations, a pulling force is applied on either RC1 or RC2 (depending on the set of simulations) by adding a time-dependent term to the potential energy in the form of

$$U\left(\mathbf{r},t\right)=U_0\left(\mathbf{r}\right)+\frac{1}{2}k{\left[d\left(t\right)-\left(d_0+vt\right)\right]}^2,$$ (1)

where U₀ is the unbiased potential energy, k is the elastic constant of the moving harmonic restraint, v is the pulling speed, d(t) is the instantaneous value of the reaction coordinate considered, and d₀ is its initial value. After an initial equilibration of 5 ns at a fixed length of 1.70 nm, the restraint was increased with a rate v = 0.4 nm/ns for 150 ns. Preliminary analysis showed no significant difference when performing steered MD with a reduced speed of v = 0.08 nm/ns. We used k = 0.5 kJ/mol/nm for the simulations with RC1 and k = 1.0 kJ/mol/nm for those with RC2. The pulling force resulting from this harmonic constraint is always parallel to the direction connecting the two residues (or groups of residues) that are being pulled apart.

We simulated the rezipping of the SNARE complex using two different procedures. We used as starting configurations the ensembles of unzipped structures obtained from the pulling trajectory at times t = 125 ns and t = 150 ns (restraint distance of 51.70 and 61.70 nm, respectively). Different hysteresis behaviors were observed (see Results and Supporting Materials and Methods for more information). After a short equilibration of 5 ns leaving the restraint fixed, we reduced the restraint distance with a rate of v = −0.4 nm/ns for 125 ns.

The two sets of steered MD trajectories were analyzed using the Density Peak clustering algorithm (84, 85) to identify intermediate states in the folding/unfolding process.

Umbrella sampling analysis

To reconstruct the equilibrium free-energy of the system, we performed two independent sets of umbrella sampling (US) simulations (86) using the two different collective variables introduced above: RC1 and RC2. In both cases, we defined 71 umbrellas (either along RC1 or RC2) with an elastic constant k = 5 kJ/mol and a separation of 0.436 nm. The initial configurations for the US simulations were selected from the steered MD trajectories. US simulations were combined by using the TRAM algorithm (87) as implemented in the PyEmma software package (88). TRAM assigns to each MD frame its optimal Boltzmann weight in the absence of any bias potential. These weights can be rescaled to simulate the presence of a constant force F acting on the C-terminals’ distance, using the rescaling factor

$$\mu \left(d_i\right)=e^{-\beta F{d}_i},$$ (2)

where d_i is the distance between Sx and Sb C-terminals in the i-th frame and $\beta =\frac{1}{k_{B}T}$ is the inverse temperature.

Virtual mutations

To compare our model with the results of single-point substitution experiments, we mimicked the effect of a mutation in a given layer of SNARE by removing all the attractive interactions between residues of that layer. The effect of this virtual mutation on the free-energy can be estimated by means of perturbation theory (44) by reweighting each configuration x by the factor

$$w_x=\frac{e^{-\beta H\left(x\right)}}{e^{-\beta H^{\ast }\left(x\right)}}=e^{-\beta {\sum }_{i,j\in L_k}\mathit{\Delta }{V}_{ij}\left(x\right)},$$ (3)

where $\beta =\frac{1}{k_{B}T}$ is the inverse temperature and i,j ∈ L_k are the indexes of all the native contact pairs belonging to the k-th layer. ΔV_ij corresponds to the Gaussian attractive term of the nonbonded interaction between atoms i and j, given by

$$\mathit{\Delta }{V}_{ij}=-A\exp \left[-\frac{{\left(r-\mu \right)}^2}{2{\sigma }^2}\right],$$ (4)

where A is the depth of the well, μ is the native contact distance, and σ is the width of the Gaussian well.

This procedure will provide exact results in the limit of perfectly sampled phase space. Here, we rely on the assumption that the relevant regions of the phase space of the mutated system are sampled already in the unperturbed simulations.

Results and Discussion

Unzipping mechanism

To model the process of unzipping of SNARE in a setup comparable to single-molecule pulling experiments, we performed steered MD simulations pulling on RC1. Fig. S2 shows the results of this set of simulations. We observed that the most likely (83%) unzipping pathway corresponds to the detachment of Sx from the SNAP25-Sb complex. In a living cell, as SNAP25 and Sx are attached to the same membrane, they are not expected to separate. Moreover, results of previous single-molecule pulling experiments performed in a setup that closely resembles our computational model (14) suggest that Sb detaches from the SNAP25-Sx complex also when the unzipping force is applied only to the C-terminals of Sb and Sx, when the experiments are performed on the SNARE complex alone in the absence of membrane. This is consistent with experiments showing that the binary SNAP25 + Sx complex is more stable than the SNAP25 + Sb one (89). This difference in stability has been attributed to the larger number of salt bridges between Sx and SNAP25 (4). We hypothesize that the inconsistency of the results from our computational model with the experimental data arises from the pulling speed used (0.4 nm/ns), which is much faster compared to in vivo and experimental timescales even if we take into account the speedup that is known to be introduced in an SBM by the smoothing of the folding landscape and can be as large as four orders of magnitude (90).

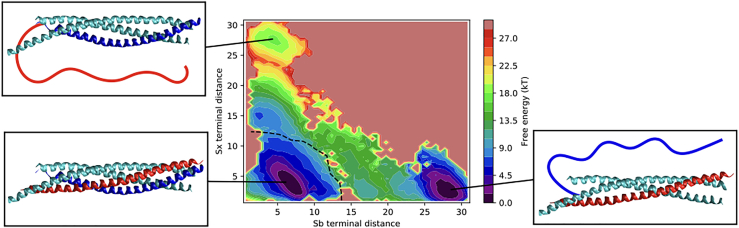
To test this hypothesis, we performed US simulations of the unzipping process of SNARE using RC1. These simulations allow us to estimate the equilibrium properties of the system, i.e., the behavior at infinitely slow pulling speed. Fig. 2 shows the free-energy landscape associated with the SNARE unzipping process as obtained by means of US simulations on RC1, projected on the distances between the C-terminals of SNAP25 and either Sx or Sb. The free-energy profile is rescaled using Eq. 2 to model the effect of a constant force equilibrating the folded (zipped) and unfolded (unzipped) states. This free-energy landscape clearly reveals a strong preference for the Sb detachment from the SNAP25-Sx complex with respect to the detachment of Sx from the SNAP25-Sb complex, with a free-energy difference between the two alternative unzipped states of $\mathit{\Delta }F\simeq 18$ k_BT.

Figure 2.

Free-energy landscape of SNARE unzipping as obtained from US simulations on the collective variable RC1, rescaled to model the effect of a constant pulling force F = 10.6 k_BT/nm. The free energy is plotted as a function of the distances between the C-terminal of the first helix of SNAP25 and the C-terminals of, respectively, Sb and Sx. The dashed black line indicates the opening of the ionic layer. Schematic representations of the structure of SNARE in the three main free-energy minima (folded, Sx unfolded, and Sb unfolded) are shown.

These results suggest that the atomistic SBM here used can capture the unzipping pathway of the SNARE complex observed in the experiments, and the inconsistencies in the unzipping pathway observed in the steered MD can be most probably attributed to the unrealistically fast pulling speed. Interestingly, if a similar analysis is performed on a C^α-only (rather than all-atom) SBM, we find that such a simple model is not accurate enough to capture the experimentally observed unfolding pathway even at infinitely slow pulling speed. Details of this analysis are provided in Fig. S3. Such a different unzipping pathway was also previously reported for a C^α-only model simulated with out-of-equilibrium steered MD simulations (71). The equilibrium analysis performed here, by means of US simulations, confirms that the preference of the C^α-only model to unzip through the alternative pathway is not due to the fast pulling speed used in the steered MD as for the all-atom model but is caused by the lack of details in the C^α model, and it is preserved even at infinitely slow pulling speed.

Intermediates

The analysis of the subset of pulling simulations that follow the pathway with Sb detaching from the rest of SNARE identifies multiple intermediates during the process (see Fig. S2). The structure of these intermediates is investigated by means of additional simulations, pulling on the distance between the Sb C-terminal, and the center of mass of both Sx and SNAP25 terminals (RC2, as described in the Materials and Methods). This setup mimics a more realistic situation, analogous to what happens during real vesicle exocytosis. As can be seen in the force-extension plot in Fig. 3 A, seven different states are revealed, each corresponding to a different phase on the unzipping/zipping process. We used the Density Peak clustering algorithm (84, 85) to precisely assign trajectory frames to these states (see Fig. S4). Each of the 100 pulling simulations along RC2 visited all of these seven states. The different steps of the unzipping mechanism predicted by our model are schematically represented in Fig. 3 B and can be summarized as follows: the SNARE complex starts from its folded conformation (state 1); the LD is the first to open up during mechanical unzipping (state 2), followed by a second step in which the Sb helix is detached from the SNAP25 + Sx complex up to layer +5 (state 3); the unzipping proceeds until all residues of Sb up to right before the ionic layer (layers +2/+3) are detached (state 4); when the pulling force becomes large enough, the ionic layer breaks, and the complex unzips further up to layer −2 (state 5); finally, Sb reaches a completely open conformation (state 6) before its complete detachment from the rest of the complex (state 7). More detailed images for these states, together with contact maps for states 3, 4, and 5, are provided in Fig. S5.

Figure 3.

Intermediate states observed in the MD simulation of the SNARE complex mechanical unzipping. (A) A force-extension plot is shown. The force exerted by the virtual spring is shown as a function of the linear separation between the terminals during the pulling (blue) and unpulling (red) phases. Different states are marked by dashed orange lines. (B) A schematic view of the structure of the intermediates is shown. The LD and layers +5, +3, −2, and 0 (ionic) are outlined in the relevant states; nonreversible transitions from states 6–7 to 7–3 are represented by a single arrow.

Hysteresis

As the process biologically relevant for exocytosis is the zipping of SNARE, it is important to check if the observed mechanism is conserved in the rezipping phase. For this reason, we performed unpulling simulations to characterize the rezipping from the unfolded state populated upon pulling. We gradually reduced the length of the restraint on the C-terminals’ distance to simulate the refolding of the complex. When unpulling was initiated starting from the final state 7, in which Sb is linked to Sx only through the disulfide bridge, a strong hysteresis was observed (see Fig. S6): instead of progressively retracing the intermediate states 6, 5, and 4, the complex folds directly into state 3. When the unpulling is initiated from state 6, with Sb still docked to the t-SNARE complex, all intermediate states 2–5 are visited during the refolding of the complex (Fig. 3 A). Interestingly, this behavior is in agreement with what was previously observed experimentally with optical tweezers pulling and unpulling of the SNARE complex (14, 19). In those experiments, strong hysteresis was detected if the unpulling was started with Sb completely detached from the t-SNARE complex, whereas the hysteresis disappeared if a cross-linker between Sb and Sx was inserted at layer −6, thus keeping Sb docked to the rest of the complex. According to our model, such a cross-linker removes the hysteresis simply by preventing the system from transitioning from state 6 to state 7.

We notice that in realistic in vivo and in vitro exocytosis process, the thermodynamics and kinetics of the transition from state 6 to the completely unbound state 7 is mainly governed by the diffusion of Sx with respect to Sb. This effect cannot be realistically captured by our simulations because the disulfide bridge between the N-terminals of Sx and Sb hinders this diffusion, and state 7 will not be further discussed in the rest of our analysis.

Comparison with experiments

The results of our simulations can be used to recapitulate in a unifying picture the pieces of information from several different and independent experimental observations.

The first step of our proposed unzipping model is the unfolding of the LD (see Figs. 1 and 3 C). This state has been experimentally observed using optical tweezers in (14, 19). A similar result was also previously reported from short steered MD simulations in explicit solvent (68).

In the later steps of unzipping, our model of SNARE visits three distinct intermediate states. Fig. 4 A shows representations of the structures of states 3, 4, and 5, highlighting the positions of the ionic layer and the residues (V241 on Sx and A72 on Sb) marked with FRET dyes by Shin et al. (16). Fig. 4 B shows the distribution of the distance between these two residues. The distribution of the same distance observed in state 4 in our simulations peaks around a value of $\simeq 4-6$ nm, compatible with a Förster radius of $\simeq 6$ nm associated with the Cy3-Cy5 dyes used in the FRET experiment (91, 92, 93). Therefore, state 4 is consistent with the first intermediate state reported by Shin et al. (16), associated with a FRET efficiency of $\simeq 0.4$. Moreover, in this state, Sb is completely unfolded up to layer +3, consistent with what was observed with optical tweezers by Zhang and co-workers (19).

Figure 4.

Details of intermediate states 3, 4, and 5. (A) A schematic view of the structure of the three states is shown; residues V241 on Sx and A72 on Sb are highlighted in purple, and the ionic layer is highlighted in yellow. (B) The distribution of distance between residues V241 of Sx and A72 of Sb is shown. (C) The unstructured fraction for residues of Sb is shown in the different intermediates: left y axis represents the fraction of structures in which residue i is “unstructured,” i.e., has broken its native contacts (empty squares) or is not assuming an α-helix conformation (filled circles); the dashed yellow line indicates the position of the ionic layer; red triangles (right y axis) report the unstructured fraction as experimentally measured with EPR by Shin et al. (16).

State 5, observed in our simulations, shows unfolding of Sb up to layer −2, compatible with results from optical tweezers measurements in which this second intermediate state was estimated to be unzipped up to around the ionic layer (14, 19). In Fig. 4 C, we compare the fraction of broken native contacts (see Supporting Materials and Methods for details on the calculation) for each residue of Sb in the different states as observed in our simulations with the results of the electron paramagnetic resonance (EPR) experiment performed by Shin et al. (16). We observe a significant agreement of state 5 with the EPR results. This intermediate was also previously reported in two computational studies using an explicit-solvent atomistic model (68) and an ad hoc parametrized SBM (71).

Our simulation model predicts an additional (earlier) intermediate step in the unzipping of SNARE (state 3). To our knowledge, no experimental result related to the presence of such intermediate have been reported so far. This could be explained as an overestimation of the stability of the conformations in state 3 by our SBM simulation or by limits of resolution of single-molecule experimental techniques (94).

Energetics and mutations

Fig. 5 A shows the results of the US analysis of the Sb zipping pathway along the collective variable RC2. The reconstructed free energy is plotted as a function of the Sx-Sb C-terminal distance and rescaled using Eq. 2 to model the effect of force of 13.4 k_BT/nm applied to the terminals. All seven intermediate states identified with steered MD are visited during the US simulations (see Fig. S7 for additional details), enabling us to study the energetics of the zipping/unzipping mechanism.

Figure 5.

Effects of modifications on the SBM potential energy on the SNARE free-energy profile. (A) Free energy as a function of the Sx-Sb terminal distance is shown rescaled with F = 13.4 k_BT/nm for noncharged SBM, F = 14.4 k_BT/nm for charged SBM; vertical dashed lines indicate the boundaries of the seven intermediate states (the exact value of each boundary is also reported next to each line). (B–D) Effects on the energetics of the intermediate states for mutations of different layers in the NTD (B), MD (C), and CTD (D) of the SNARE complex are shown.

Consistent with the results presented above, at this intermediate level of force, the highest free-energy barrier corresponds to the detachment of the ionic layer (terminal distance $\simeq 15$ nm).

To compare the prediction of our model with single-point substitution experiments, we performed virtual mutations of residues at each layer of the SNARE complex. We do this using Eq. 3 to evaluate the free-energy change of every intermediate state under the effect of a virtual mutation. Fig. 5 shows the results of this analysis. The definition of states in the US simulations was based on the Sx-Sb terminal distance. The limits of each state were manually identified by looking at the free-energy profile (as shown in Fig. 5 A). Fig. 5 B shows that mutations in any layer in the NTD (−5 to −1) result in a reduction of SNARE stability. Mutations of the ionic layer and layers +1 and +2 (Fig. 5 C) also decreased the complex stability, as well as all mutations in the CTD of layers +3 to +6 (Fig. 5 D), with the exception of layer +7, at which a simulated single alanine substitution leads to a slight increase of the stability of state 2 (Fig. 5 C). This finding reflects the experimental results reported in (19), in which the substitution of residue T251 in layer +7 with isoleucine was the only mutation increasing the folding energy of the CTD. Notably, mutation of layer +5 significantly stabilizes the intermediate states 3 and 4, although it does not stabilize the folded state.

It has been speculated that the charges in the conserved ionic layer play an important role in the SNARE zipping mechanism. To test the effect of these charges, we have performed additional simulations with electrostatic interactions explicitly added to the SBM potential. Interestingly, the results of these simulations show that the structure of the intermediate states is not affected by the introduction of charges in the model (see Fig. S8 for details of the analysis and the results). Indeed, we observe no significant difference between the results of pulling simulations of the model with and without charges. All seven intermediates are visited (Fig. S8 A), and they present no evident structural difference, as discussed in the Supporting Materials and Methods. The main effect of the charges appears to be a strong stabilization of the zipped SNARE (state 1), i.e., the difference in free energy of the complex upon folding is enhanced by the electrostatic interactions. An additional effect observed in the model with explicit electrostatic is a decrease in the stability of the intermediate states with respect to the zipped and the unzipped conformations. Combined, these effects increase the energy stored in the prefusion half-zipped SNARE complex, that is, the energy that can be released by SNARE to power the final stage of membrane fusion.

Conclusions

We report the results from simulated single-molecule pulling of the SNARE complex using an atomistic SBM and present a detailed comparison with the available experimental data for this system. The simplifications in the energy function introduced by the model enable us to simulate hundreds of pulling and unpulling events while maintaining all-atom resolution. This allows us to obtain statistically robust results, bearing in mind the qualitative nature of the predictions that such a model can produce.

The free-energy analysis of the pulling simulations of the C-terminals of Sb and Sx shows that, in the limit of infinitely slow pulling speed, Sb unzips from the complex while the other three helices remain intact. This result is in agreement with experimental data (4, 14, 89) and previous explicit-solvent steered MD simulations (68). We notice that if a simplified C^α-only model is used, a preference for Sx detachment (71) is observed instead.

The SBM of the SNARE complex unzipping predicts that the breaking of the ionic layer represents the highest free-energy barrier for SNARE unfolding, suggesting that it is a rate-determining factor for vesicle-membrane fusion. It is interesting to notice that although our model does not explicitly take into account charges, it is still able to capture the functional importance of the ionic layer in the zipping/unzipping process. The role of the ionic layer may be related to structural details of the folded complex, which are in turn indirectly determined by the charge distribution. Indeed, the addition of explicit electrostatic interactions to our model does not show any effect on the structure of the intermediates. This result supports the idea that the SNARE zipping/unzipping pathways are not directly influenced by the charge distribution, which instead plays a strong role in the energetics of the process.

This simulation study allows us to obtain a complete picture of the several intermediates present in the free-energy landscape of the SNARE zipping/unzipping process. Such a picture reconciles the findings from several different previous studies. Our model reveals multiple intermediate states in the unzipping of the SNARE complex. Specifically, we confirm the LD unzipping as the first step and the critical step of the ionic layer disruption, as predicted by previous computational models (68, 71) and observed experimentally (14, 15, 16). We also observe an additional intermediate state, corresponding to a partially unzipped CTD (state 4), that is consistent with experimental evidence from different sources (16, 19). We predict an additional early intermediate (state 3) that, to our knowledge, has not been reported experimentally. This work may thus provide a reference for future experiments aimed at measuring the presence of intermediate states in the unzipping of the CTD of Sb.

Virtual mutations performed on our model partially confirm results obtained by optical tweezers experiments (19) and predict that a mutation of layer +5 might stabilize state 3 with respect to the folded state. We expect that future experiments might exploit this information to investigate the presence of this additional intermediate.

It is important to note that an exact quantitative comparison of our simulations with experimental data is challenging not only because of the simplifications introduced by the SBM, but also because of the multiple sources of experimental uncertainties, as well as the lack of knowledge of the exact functional form of the force exerted on SNARE in the experimental setup. However, despite the limitation of the model, the results presented here provide a good framework to integrate different sources of experiment and characterize the mechanism of unzipping of the SNARE complex.

At the level presented here, our model lacks additional details that play important roles in the process of SNARE folding, namely the membrane itself and other interacting proteins such as MUNC proteins, complexin, and synaptotagmin. These proteins interact with SNARE at different stages of exocytosis, and therefore the knowledge of the structural details of the SNARE intermediates is of primary importance to the understanding of the mechanism. Our study provides predictions for the SNARE intermediate structures that can be further investigated in the presence of interaction partners. The study of these additional factors by means of simulations will be the aim of future work.

Author Contributions

G.P., A.K., J.C., and C.C. designed the research. G.P. and G.C. carried out all simulations and analyzed the data. G.P. and C.C. wrote the article.

Editor: Alan Grossfield.