Using population surfaces and spatial metrics to track the development of deprivation landscapes in Glasgow, Liverpool, and Manchester between 1971 and 2011

Abstract

Measuring change in the spatial arrangement of deprivation over time, and making international, inter-city comparisons, is technically challenging. Meeting these challenges offers a means of furthering understanding and providing new insights into the geography of urban poverty and deprivation. In this paper, we introduce a novel approach to mapping and analysing spatio-temporal patterns of household deprivation, assessing the distribution at the landscape level. The approach we develop has advantages over existing techniques because it is applicable in situations where i) conventional approaches based on choropleth mapping are not feasible due to boundary change and/or ii) where spatial relationships at a landscape level are of interest. Through the application of surface mapping techniques to disaggregate census count data, and by applying spatial metrics commonly used in ecology, we were able to compare the development of the spatial arrangement of deprivation between 1971 and 2011 in three UK cities of particular interest: Glasgow, Manchester and Liverpool. Applying three spatial metrics – spatial extent, patch density, and mean patch size – revealed that over the 40 year period household deprivation has been more spatially dispersed in Glasgow. This novel approach has enabled an analysis of deprivation distributions over time which is less affected by boundary change and which accurately assesses and quantifies the spatial relationships between those living with differing levels of deprivation. It thereby offers a new approach for researchers working in this area.

Highlights

• •A novel approach to mapping and analysing spatio-temporal patterns of household deprivation.
• •Surface mapping techniques and spatial metrics used to compare the spatial arrangement of deprivation in three UK Cities.
• •Methods used allow for more complete analyses of deprivation distributions over time.

1. Introduction

Measuring change in the spatial arrangement of deprivation over time, and making international inter-city comparisons (i.e. comparing cities from different countries), is technically challenging. To meet these challenges, this study created and tested a new approach by drawing together two existing techniques not applied to this field before. Combing these techniques facilitated a comparison of the spatial distribution of deprivation in three UK cities, Glasgow, Liverpool, and Manchester, over a 40 year period (1971–2011). The approach could, however, be applied to any situation in which there is a need to examine the spatial distribution of population or population characteristics at landscape level over time, where boundary changes have occurred which preclude using the same areal units over time, and/or where the nature of the areal units for which data are available differs between study areas. In the paper, we briefly explain our motivation for this methodological development, justify the need for a new approach, explain the approach itself, and then use comparisons of the distributions of deprived populations in Glasgow, Liverpool and Manchester over time to demonstrate its application. Finally, we consider the strengths and weaknesses of our approach.

2. Background

Maps have been used to enhance studies of poverty in urban Britain since the work of Charles Booth in London and Seebohm Rowntree in York during the late 19th and early 20th centuries (Dorling & Pritchard, 2010). Whilst conceptions and measures have evolved since then, producing and analysing maps of both poverty and deprivation remains highly relevant. The methods used to conduct spatial analysis of poverty and deprivation have also evolved; however, a key feature of such maps remains that they demonstrate that poverty and deprivation are not randomly distributed across urban areas – they are spatially arranged. Examining this spatial arrangement has furthered understanding of deprivation and poverty and, importantly, their impact on urban populations. The spatial configuration of the poorest people has implications for many aspects of society and has the potential to influence a number of social and health outcomes.

2.1. Study motivation

Our focus on methods resulted from an interest in examining the impact of the spatial distribution of deprivation on population health. Specifically, we were interested in comparing the spatial distribution of poverty in Glasgow, Scotland with two other cities in England: Manchester and Liverpool. These cities have been compared many times in the literature (Livingston & Lee, 2014; Mccartney, Collins, Walsh, & Batty, 2012; Walsh, Bendel, Jones, & Hanlon, 2010; Walsh, Mccartney, Collins, Taulbut, & Batty, 2017) because of two particular features. First, on many dimensions the three cities are incredibly alike, having a similar population size, socio-economic history, and current levels of socio-economic deprivation. Second however, Glasgow differs markedly in one particular respect; it has very much worse population health (Walsh et al., 2010). Between 2003 and 2007 for example, Glasgow's all-cause premature mortality was 30% higher than Liverpool and Manchester. Yet, Glasgow's high level of mortality relative to the other two English cities has not always been present; it emerged in the 1970s (Walsh et al., 2010), suggesting that ‘something changed’ to cause its adverse position. Understanding what ‘changed’ between the 1970s and subsequent time periods was the driving force behind our methodological innovation.

One theory is that the cities developed differing spatial patterns of deprivation in the 1970s or subsequently, and that this explains the disparities in their population health (Livingston & Lee, 2014; McCartney et al., 2012; Walsh et al., 2017). It is important to emphasise the focus is not levels of deprivation – the cities have almost identical levels of, and temporal trends in these. Instead, the theory is that the cities differed in the development of where more and less deprived people live within each city. This theory is underpinned by previous research which showed that the health of urban residents can be influenced not only by their individual and neighbourhood levels of deprivation, but also by those in both proximal areas, and the wider urban area as a whole. The entire city's spatial pattern of deprivation is thus a possible contributor to population health there (Allender, Scarborough, Keegan, & Rayner, 2012; Cox, Boyle, Davey, Feng, & Morris, 2007; Livingston & Lee, 2014; Maheswaran, Craigs, Read, Bath, & Willett, 2009; Richardson, Moon, Pearce, Shortt, & Mitchell, 2017; Sridharan, Turnstall, Lawder, & Mitchell, 2007; Zhang, Cook, Jarman, & Lisboa, 2011). Testing this theory was the motivation for our methodological development. Choosing to work on Glasgow, Liverpool and Manchester which have been so extensively studied, meant we were could be sure the levels of deprivation in the city were almost identical over time, and our approach could focus on the distribution of that deprivation. We began by exploring the existing literature to see whether and how others had approached tracking spatial arrangements of deprivation over long time periods, and what the issues would be.

2.2. Existing literature and techniques

Others have already examined spatial arrangements of deprivation within Glasgow. The most notable study was by Livingston and Lee (2014) who explored the influence of deprivation levels in neighbouring areal units on the health of residents, making a comparison between Glasgow, Manchester and Liverpool. They found an impact of surrounding deprivation at two different scales on neighbourhood health outcomes in Glasgow and Liverpool but not in Manchester which suggested that they had not discovered the explanation for Glasgow's higher mortality. Their approach used small area measures of deprivation and although it was comparable between the cities, it was a contemporary measure constraining them to a cross-sectional study. Livingston and Lee (2014) also noted the difficulty posed by the fact that the cities from different countries (Scotland and England) used different definitions of the areal units themselves and that unit selection was not straight-forward.

Areal unit definition, consistency over time, and selection are the key challenges in this field. The definition of the areal unit introduces the well-known modifiable areal unit problem (MAUP) (Openshaw, 1984). The MAUP refers to the fact that relationships identified in data aggregated to a set of areal boundaries (such as postcode sectors or output areas) are at least partly dependent on the boundaries used (Flowerdew, Manley, & Sabel, 2008; Norman, 2010; Rae, 2009). Consequently, the data values for each area might be a reflection of the area boundary rather than of the underlying distribution of the data. Thus, if areal units differ between cities in their basis and size, there is a risk that any conclusions about between-city differences in spatial relationships are driven more by the areal units than by true differences on the ground.

When we add the reality of change in areal unit definitions over time, the uncertainties introduced by the MAUP are multiplied massively. A variety of different approaches to minimising the problem of boundary changes have been tested, and we explored each to assess whether they would meet our needs. Menis and Hultgren (2006), for example, advocate the use of dasymetric mapping in conjunction with areal interpolation to adjust census data to a common set of boundaries. Typically, however, the ancillary data used in dasymetric mapping is land use data, usually from remotely sensed satellite images (Holt, Lo, & Hodler, 2004; Menis & Hultgren, 2006; Slocum, McMaster, Kessler, & Howard, 2009). To apply their technique to our problem would have required land use data back to the 1970s; such data were not available. Norman, 2010, Norman, 2016 and Exeter, Boyle, Feng, Flowerdew, and Scheirloh (2005) offer alternative approaches to issues of boundary changes over time which could have been adopted in this study. Norman, 2010, Norman, 2016 converts older census data to recent boundaries by using the population overlap between different boundary systems to apportion data, using weights calculated by postcodes falling in the same source and target area. Disadvantages of this technique include uneven levels of error between any pair of boundary systems (due to some localities experiencing widespread adjustments whilst others experience little or no change), and increasing error over time. Whereas Norman, 2010, Norman, 2016 focussed on (re)creating data for contemporary geographies, Exeter et al. (2005) determined coincidences of boundaries to define a set of fixed areal units (‘Consistent Areas Through Time’ (CATTs)) which could be used to compare data from the 1981, 1991, and 2001 census in Scotland. Such an approach, however, is only feasible in Scotland because of the ways in which census zones were built there. A further disadvantage of this approach is that it results in zones with very uneven physical and population sizes. For the purposes of this study, further limitations of Norman, 2010, Norman, 2016 and Exeter et al.'s (2005) approaches are that they still result in non-uniform areal-unit based zones, suited to choropleth mapping, and do little to minimise the MAUP.

One other approach we identified discarded the use of areal units altogether. Pacione (2004) created maps from successive decennial censuses showing that temporal change in the spatial arrangement of deprivation in Glasgow. However, his approach was limited because he only mapped the centroids of the smallest available areal units at each time point in order to deal with boundary change. This was problematic as it did not provide an indication of the spatial extent of these areas and therefore the spatial relationships between the residents, nor was it able to assess formally whether more or less deprived areas bordered one another. There was no attempt to consider or quantify the distribution of deprivation at a city level.

Even without the problems of areal unit selection and representation however, the use of small area-based data and/or maps for this work poses a further problem which Kwan, 2012a, Kwan, 2012b labels the Uncertain Geographic Context Problem (UGCoP). The UGCoP highlights that whilst an individual may reside within a particular areal unit, this is very unlikely to be the only place they encounter; there are other places, indeed multiple spatial scales, exerting influence on them. This has been highlighted as particularly pertinent to studies examining relationships between health and deprivation (Cummins, 2007) and led to the suggestion that the smallest and most local area possible may not be the most appropriate scale of analysis (Caughy, Hayslett-Mccall, & O'campo, 2007; Cummins, 2007). Perhaps the best way of dealing with this problem is to somehow undertake analyses which are able to examine multiple spatial scales from very fine to whole city. This was an attractive proposition for us since the mechanisms (and hence scale) via which the spatial arrangement of deprivation might exert influence on health was not clear from the literature.

In summary, we required an approach which was able to: accurately model and assess the spatial distribution of deprivation in cities; which minimised problems due to differing small area geographies and differing boundary changes; and which allowed us to pay attention to, and quantify, spatial relations based on both fine and larger spatial scales. Our review of existing literature and techniques found nothing suitable within geography or epidemiology. We did however, find a useful approach in ecology.

2.3. Borrowing from ecology

Ecologists are often interested in understanding the interactions between organisms, and/or between organisms and their host environment. Their unit of analysis is the ‘landscape’, understood to be a unit of space comprised of interacting ecosystems (Leitao, Miller, Ahern, & McGarigal, 2006). A useful understanding of a landscape from an ecological perspective is provided by Arroyo-Rodriguez and Fahrig (2014):2 who define a landscape “as a heterogeneous land area containing a mosaic of patches or land cover types”. We acknowledge that other disciplines use the term differently, particlarly human geography which explores the cultural landscape to understand how individuals and societal groups have modified the land, as well as the meaning ascribed to the land by individuals and groups (Robertson & Richards, 2003).

Ecologists have developed theoretical and empirical approaches to studying landscapes; examining their composition (which different forms of land cover are present within a landscape) and configuration (the spatial arrangement of the composition) (Leitao et al., 2006; McGarigal & Marks, 1995). The spatial scale at which a landscape is studied is usually defined by the organism or ecosystem under study. There are clear parallels between what ecologists do and our own desire to understand deprivation within cities. We wanted to see exactly where deprived populations live within the city, how more and less deprived neighbourhood borders relate to other, and to understand their distribution and spatial relationships across the city. Overall, the landscape approach was attractive to us because it seemed to enable a balance in which the wider context can be studied without losing the finer scale detail; to figuratively see both the trees, and the wood.

It also offered a further important advantage; techniques were available to assess and quantify landscapes which would help us deal with MAUP and that would facilitate working back at least as far as the 1970s. Spatial metrics are defined as “quantitative indices to describe structures and pattern of a landscape” (Herold, Scepan, & Clarke, 2002:34). There has been recent and growing interest in the use of spatial metrics to analyse whole urban environments (Herold, Couclelis, & Clarke, 2005; Zhao & Murayama, 2011). Studies of urban environments using spatial metrics include: models explaining land and housing values in the vicinity of Washington D.C. (Geoghegan, Wainger, & Bockstael, 1997); a framework for modelling how interactions between socio-economic and ecological processes impact upon urban development (Alberti & Waddell, 2000); exploring changes in urban land use (Herold et al., 2002; Wang & Yin, 2011); modelling and analysing urban growth (Herold et al., 2005; Jain, Kohli, Rao, & Bijker, 2011; Li et al., 2014; Pham, Yamaguchi, & Bui, 2011; Thapa & Murayama, 2011; Zhao & Murayama, 2011); and changes in land abandonment in Bucharest (Gradinaru et al., 2013). All these studies used spatial metrics to examine patterns across whole landscapes rather than between, or surrounding, neighbourhoods, and in doing so they enhanced understanding of urban environments. However, no previous study has used spatial metrics to facilitate comparisons of spatial patterns of deprivation.

Most applications of spatial metrics to both ecological or social phenomena use raster (i.e. cell or grid based) data. This holds some advantages in that as ‘building blocks’ of any landscape model, grid cells can be of a uniform size. Many spatial metrics are then based on the concept of the ‘patch’. A patch is an individual homogenous area (in this instance of cells with the same designation, such as the same land cover or habitat type) which can comprise any number of contiguous cells of the same type. A gridded representation of the landscape permits clear demarcation between areas of one habitat or land cover and another in the way a choropleth representation does not unless the boundaries in the choropleth map are precisely designed to delimit the features of interest. Spatial metrics are largely then, quantitative descriptions of the size, distribution and spatial relationships between, patches. Carrying raw information about a landscape in a raster form does not however completely avoid the MAUP, since the grid cell size itself will have influence over the patterns seen and metrics calculated. However, crucially, any landscapes for which data are available at the grid cell scale can be compared and where those data are available over time, longitudinal analysis is possible without the malign influence of boundary change.

2.4. The ability to work with gridded data

Ecology has little problem in finding data available on a gridded basis. Contemporary landscape ecology often draws on secondary satellite imagery in which the raw observations are per pixel. The convention in primary data gathering is to sample by quadrants which also yields cellular data. Measures of socio-economic situation for whole cities however are far more usually available on a small area basis in which census or survey data for the residents of each small area are aggregated. However, there are techniques available for disaggregating these small area-based measures into realistic models of their distribution on a grid basis. In general, these techniques try to recreate the original disaggregated distribution of a variable which was lost in the spatial aggregation process. Gridded data hold other advantages over working with irregular small areal units. By virtue of their need to cover the entire land surface, in urban choropleth maps there are usually i) no ‘gaps’ between areal units (showing open spaces for example) and ii) no good representation of the distribution of socially mixed neighbourhoods unless the areal units are extremely small. With small grid cells representing spatial distributions, both of these are more easily possible.

We selected Martin's surface mapping technique to render data into raster form (Martin, 1989; Martin & Bracken, 1991). Martin's technique attempts to re-create the real population distribution across geographical space from a set of aggregated counts attached to population weighted small area centroids. Explanations of Martin's technique are available elsewhere (for example Martin, 1989; Martin & Bracken, 1991). In brief, Martin's technique takes the count associated with a small areal unit and spatially ‘spreads it out’ into much smaller cellular units. SurfaceBuilder, the software Martin created, uses an algorithm to distribute data from each centroid, based on its spatial relationships with other centroids and the size of their population. Each centroid is examined and the mean inter-centroid distance calculated, this is then used to calculate distance decay and assign weights to the output grid cells (Martin, 1996). Whilst much of Martin's work (for example Martin, 1989, Martin, 1996; Martin & Bracken, 1991) focussed on using this technique to produce surface maps of population and population change from UK decennial censuses, the technique is readily applicable to other types of population counts. As far as we are aware, this is the first time that the technique has been applied to counts of deprived people.

With the identification of Martins' surface modelling technique to produce spatially and temporally comparable gridded representations of the cities, and landscape metrics to quantify and assess them, we next applied these techniques as described below.

3. Methods

3.1. Selecting deprivation indicators

For this study, indicators of deprivation that were comparable between the three cities, could be mapped spatially, and were valid over time were required. We were aware of a substantial and important literature debating the meaning and measurement of deprivation. Within a UK context, the work of Townsend, 1987, Townsend, 1993 has been instrumental in defining deprivation as a relative concept, with individuals classed as relatively deprived if they cannot obtain “the conditions of life” that allow them to participate fully in society (Townsend, 1993:36). Many different indicators have been shown to be effective measures of, or proxies for, relative deprivation in explaining differences in health status between populations (Carstairs & Morris, 1989; Leyland, Dundas, McLoone & Boddy, 2007; Stanners, Walsh & McCartney, 2015) and it was that work we drew most heavily on in indicator selection.

Individual or household level data describing socio-economic situation for the entire populations of the three cities were not available at any time point. Whilst area-based, aggregate measures of multiple deprivation are well established in both Scotland and England, these originated in the 2000s and were thus not suited to the longer time frame required. The only spatially comprehensive and comparable data source extending back further in time is the UK decennial census. These data are collected from every adult in every household, describing their demographic, social and economic situation. For confidentiality reasons, spatially comprehensive census data are only released in aggregate form, providing counts for small-area zones.

There is a general consensus that indicators of deprivation should include indicators of material wealth, unemployment, and housing conditions (Allik, Brown, Dundas, & Leyland, 2016). Following others (Carstairs & Morris, 1991; Mitchell, Dorling, & Shaw, 2000; Norman, 2010; Townsend, 1987) we selected four census variables: male unemployment, households without a car, overcrowded households, and households which were socially rented. Several studies have used the census to track deprivation over time, including Norman, 2010 and Mitchell et al., 2000. As Mitchell et al. (2000) note, the suitability of census variables as indicators of deprivation is period specific. Prior to a policy in the UK called the ‘Right to Buy initiative’ introduced in 1980, social tenancy was widespread and not necessarily associated with deprivation (Jones & Murie, 2006). Hence, whilst male unemployment, households without a car and overcrowded households were used in all census years from 1971 to 2011, households which were socially rented was only used from 1991 to 2011. Overcrowding used the 2001 census definition, applied to all time points.

3.2. Disaggregating the small area measures household deprivation

The aggregate census variables and population weighted centroids for the smallest available areal unit were obtained from the UK Data Service (via Casweb for 1971, 1981, 1991 and 2001, via InFuse for English data in 2011, and via the Scottish Government for Scottish data in 2011). For 1971, the smallest available areal unit was enumeration district (with an average of 200 households and 450 people) in both Scotland and England. Scotland adopted the smaller sized output area (target size of 125 households) for the 1981 census, whilst England continued to use enumeration districts up until the 2001 census. The geographic area covered by these units varied widely reflecting the population density within them. All three cities have experienced changes to their city boundary over the study time period. To ensure consistency we used the 2001 definition of each city boundary.

SurfaceBuilder allows the user to select the search radius and cell size used, both of which affect the model of spatial distribution produced. Others have tested the accuracy of using different cell sizes and search radiuses (for example Martin, 1996 and Martin, Lloyd & Shuttleworth, 2011) and it appears that there is no “ideal” cell size for all purposes. Detailed sensitivity analysis was undertaken by creating surface maps for household data for Glasgow using a combination of available options and then making visual and field-based comparisons of surface maps created with for the ‘ground truth’ in areas of the city well known to the researchers. By comparing the models produced with the actual observed spatial distribution of housing within small areas, paying particular attention to the recreation of open spaces for example, we were able to assess how accurately SurfaceBuilder recreated the settlement pattern under different cell size and search radius scenarios. From this process, we identified that a search radius of 500 m and cell size of 75m² produced models which best replicated the ‘real-world’.

Surface maps for male unemployment, households without a car, and overcrowded households were created for each of the three cities in 1971, 1981, 1991, 2001, and 2011, and for social rented households in 1991, 2001, and 2011. These surfaces provided counts per grid cell of either unemployed males, households without a car, overcrowded households, and social rented households. Population denominator surfaces were then created for each of the indicators so that the counts could be rendered meaningful, relative to the number of households or people in each cell. For male unemployment, the denominator surface was the total number of economically active males. For the other three indicators, the total number of households was used.

The raster surfaces were imported into ArcGIS 10.1. The raster calculator was used to divide numerator surfaces by denominator surfaces, and multiply by 100, producing continous, percentage values for each indicator in each cell. To distinguish between cells with a value of 0% due to no resident population, and cells with a value of 0% because none of the households or people within the cell were classed as deprived, a surface map of count of households was made for each of the time points to act as a ‘mask’, identifying and excluding areas with no resident population from the subsequent calculations.

3.3. Preparing for spatial metrics

As stated, deprivation is widely understood to be a relative concept – an individual's situation should be considered relative to what others in the same society have (Carstairs & Morris, 1989; Gordon & Pantazia, 1997; Townsend, 1993; Vaucher, Bischoff, & Diserens, 2012). Reflecting this, we applied a classification method which identified cells with high values relative to the rest of that city at that time point. Rather than using a method which required the subjective selection of an arbitrary value or proportion of cells to classify as deprived, we used Jenk's natural breaks method to intially classify the cells into five groups. Jenks's method is widely used in geographical information science (de Smith, Goodchild, & Longley, 2009; Henke & Petropoulos, 2013) and is a relative classification method based on the distribution of cell counts. It categorises values into different classes by grouping together similar values, and is designed to maximise the variance between classes, and minimise the variance within a class. The class boundaries are thus meaningful in the sense that they are derived from important aspects of the distribution, and that the classes are designed to contain homogenous values (Henke & Petropoulos, 2013). Sensitivity analyses were undertaken exploring the impacts of different methods of grouping, including quantiles and geometric intervals. We found few substantive differences in results using alternative methods.

Whilst it is possible to apply spatial metrics to grid cells with more than two categories, we opted to then dichotomise the cells into either ‘most deprived’ or ‘other’ groups, ‘most deprived’ was thus defined relative to each city at each time point, with the highest two groups identified by Jenks selected as “most deprived” cells. Working with larger numbers of deprivation categories was not viewed as advantageous in this instance. Our study was interested in the spatial arrangement of areas with high numbers of deprived households relative to the rest of the city and we also wished to minimise complexity in this proof-of-concept study. We consider the limitations of this aspect of our approach in the discussion section.

Finally, reflecting that household deprivation is a multifaceted concept rarely well-captured by one indicator, the last stage of map production was to create summary maps for each city at each time point identifying cells where high levels of all the indicators of household deprivation were observed. The result was 15 maps which highlighted the location of the most deprived cells in each of the cities at each time point relative to the rest of that city at that time point.

3.4. Applying spatial metrics

The summary maps were analysed in ArcGIS 10.1 using Patch Analyst 5.1 for ArGIS 10 (Rempel, Kaukincan, & Carr, 2012). We selected and applied three spatial metrics: spatial extent, mean patch size, and patch density. These metrics were the most appropriate for temporal and cross-city comparisons and quantified spatial extent as well as providing an indication of fragmentation and patch size. The spatial extent metric calculated the percentage of the residential city land surface covered by cells identified as most deprived. Residential land surface was used to allow for the fact that the cities may have varied in the spatial extent of retail, industrial, open and derelict land. This metric enabled us to identify whether the proportion of each city landscape made up of the most deprived cells had increased, decreased, or remained the same over time.

The other two metrics were, as noted in section 2.2, based on the concept of the ‘patch’; an individual homogenous area (in this instance of cells classified as ‘most deprived’) which can comprise any number of contiguous cells of the same type. Patch density is a measure of fragmentation or dispersion within a landscape, with a higher value indicating a higher level of fragmentation. Patch density is calculated by dividing the number of patches of deprivation by the landscape area. Mean patch size is similar to patch density in that it also provides a measure of fragmentation. However, mean patch size is a function of the number of patches within the class, whereas patch density is a function of the total landscape area (McGarigal & Marks, 1995). Mean patch size was selected because it also enabled comparisons to be made between both the size of patches of most deprived households and the level of subdivision. Patch size standard error was used to calculate confidence intervals around the mean patch size and hence ascertain statistical significance of any observed differences.

4. Results

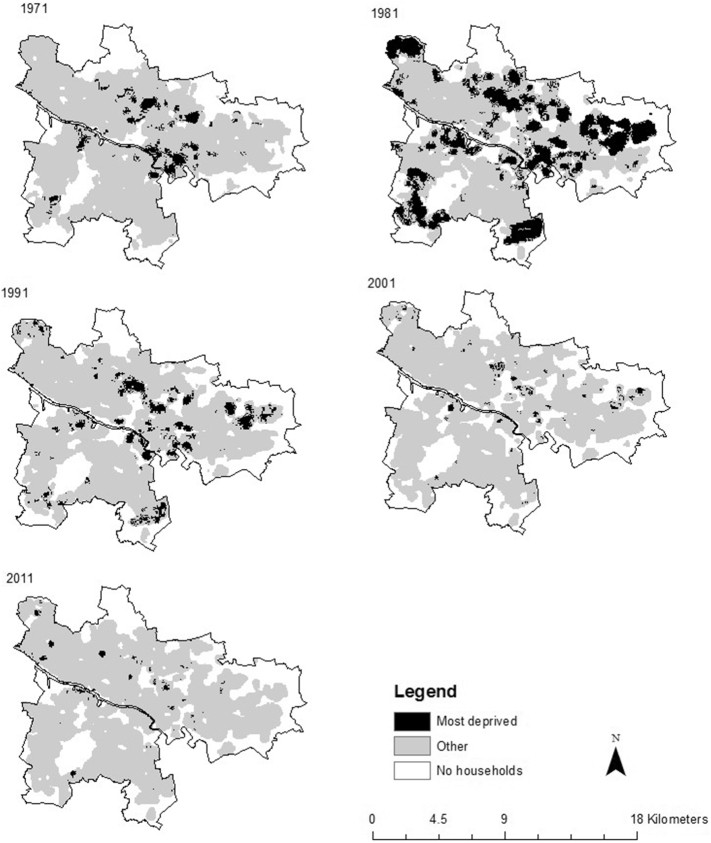
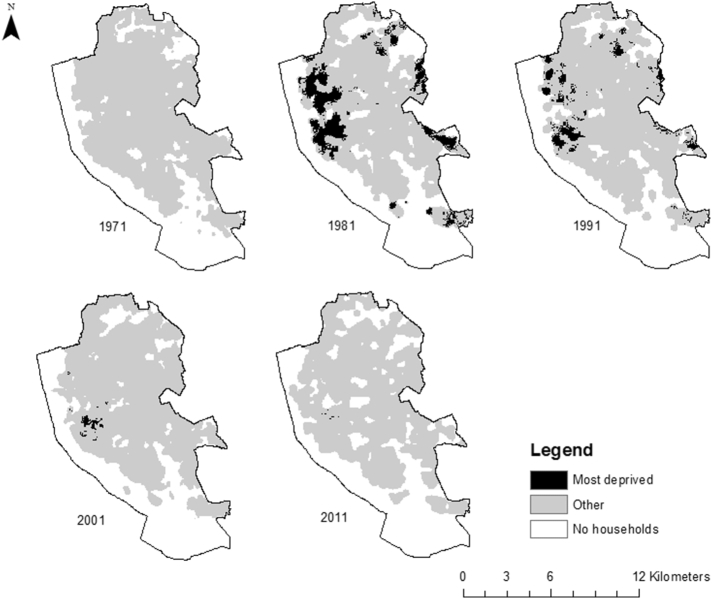
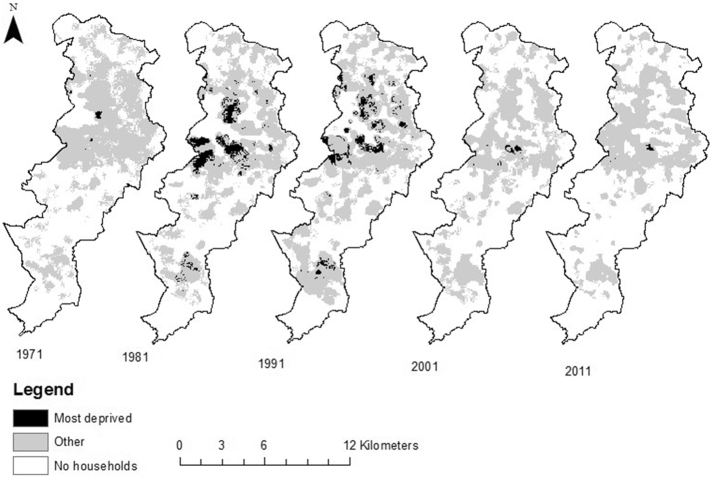
Fig. 1, Fig. 2, Fig. 3 show the most deprived parts of the cities (based on all indicators of deprivation being present) at each of the time periods between 1971 and 2011. They reveal four important results. First, both similarities and differences in spatial pattern of household deprivation were observed between the three cities. Second, the spatial patterning of household deprivation in all three cities varied markedly over time. Third, the spatial extent of household deprivation peaked in 1981, and then steadily decreased to a low in 2011. Fourth, in 1971 Liverpool did not have any areas with high levels of all the indicators. This does not mean that households in Liverpool were exempt from experiencing high levels of household deprivation in 1971; rather it indicates that there were no areas in which all three indicators coincided at a high level.

Fig. 1.

Surface maps showing the most deprived areas of Glasgow at decennial intervals from 1971 to 2011. (source: Based on census data and boundary data provided by General Register Office for Scotland and the National Records for Scotland with the support of the UK Data Service Census Support. Contains National Statistics data © crown copyright and database right 2013. Contains Ordnance Survey data © crown copyright and database right 2013)

Fig. 2.

surface maps showing the most deprived areas of Liverpool at decennial intervals from 1971 to 2011. (source: Based in census data and boundary data provided by English Office for National Statistics and Office for Population Census and Surveys with the support of the UK Data Service Census Support. Contains National Statistics data © crown copyright and database right 2013. Contains Ordnance Survey data © crown copyright and database right 2013)

Fig. 3.

surface maps showing the most deprived areas of Manchester at decennial intervals from 1971 to 2011. (source: Based in census data and boundary data provided by English Office for National Statistics and Office for Population Census and Surveys with the support of the UK Data Service Census Support. Contains National Statistics data © crown copyright and database right 2013. Contains Ordnance Survey data © crown copyright and database right 2013)

4.1. Spatial extent metric

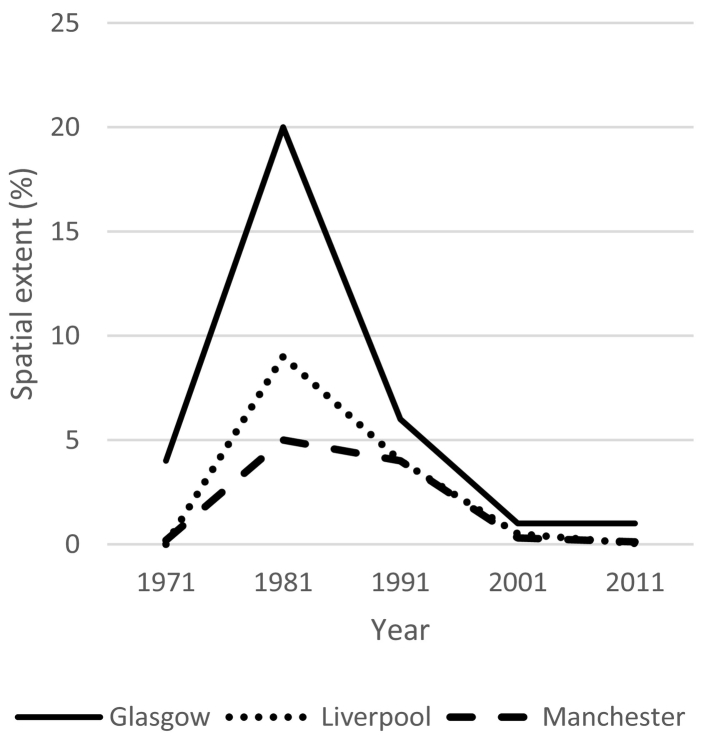
The spatial extent of deprivation varied between the years (Fig. 4), and this confirms the visual impression given in Fig. 1, Fig. 2, Fig. 3. All three cities experienced a similar change over time in the spatial extent of deprivation; a considerable increase between 1971 and 1981, followed by a fall from the peak in 1981 to a low in 2011. Glasgow had the greatest spatial extent of deprivation at all-time points, but most notably in 1971 (4% compared to 0% in Liverpool and 0.2% in Manchester) and 1981 (20% compared to 9% in Liverpool and 5% in Manchester). From 1991 onwards, the differences between the cities reduced. Glasgow also had a much more extreme increase and decrease in spatial extent of deprivation over time.

Fig. 4.

Percent of Glasgow, Liverpool, and Manchester's total area comprised of cells with high levels of household deprivation.

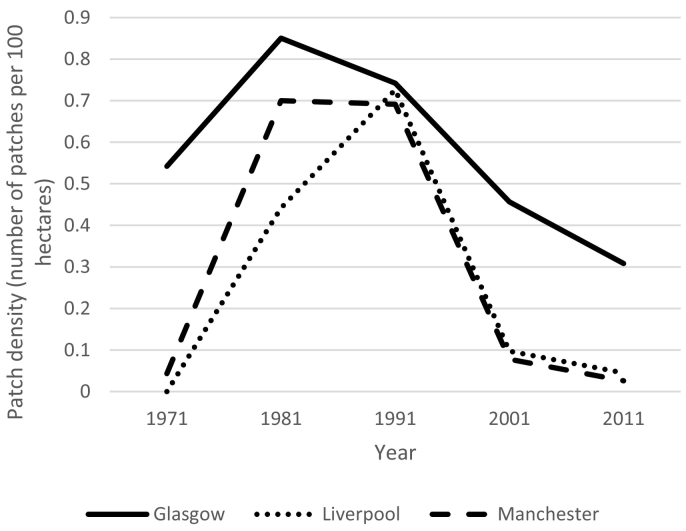
4.2. Patch density metric

Between 1971 and 2011 Glasgow had the highest patch density (Fig. 5). This means that in Glasgow, areas with high levels of all the poverty indicators were more fragmented or dispersed than in Liverpool and Manchester. All three cities experienced temporal change in this metric, with a sharp rise in patch density between 1971 and 1981. This metric peaked in 1981 for Glasgow (0.85 patches per 100 ha) and Manchester (0.7 patches per 100 ha), but in 1991 for Liverpool (0.73 patches per 100 ha). In Glasgow, patch density started to fall from 1981 onwards whereas in Liverpool and Manchester levels remained high until 1991, but then fell sharply. There was a striking similarity in patch density across all three cities in 1991, and the trajectory from then on was almost identical in Manchester and Liverpool.

Fig. 5.

Patch density values for Glasgow, Liverpool, and Manchester 1971–2011.

4.3. Mean patch size metric

Glasgow had the highest mean patch size in 1971, 1981, and 1991 (Table 1). Wide confidence intervals meant that there were no significant differences in mean patch size between the cities at any time point. Considerable variety in patch size is likely to explain the high standard errors and hence, wide confidence intervals. Whilst exercising caution in the interpretation, the trajectories in mean patch size are still interesting. There was a sharp increase in mean patch size for both Glasgow and Liverpool between 1971 and 1981 (also in Fig. 1, Fig. 2), but not for Manchester. In Glasgow and Liverpool, this was followed by a significant decrease in mean patch size between 1981 and 1991 (Glasgow p = 0.03, and Liverpool p = 0.04), and a further significant decrease in Glasgow 1991 to 2001 (p = 0.01). The most striking result is the difference in trajectory for Manchester, where the 1981 peak was essentially absent. Aside from 1981, mean patch size was not dissimilar in all three cities.

Table 1.

Mean patch size (MPS) of patches of areas with high levels of household deprivation in hectares. Confidence intervals (CI) were calculated as MPS ± 1.96 standard error.

Year	Glasgow		Liverpool		Manchester
	MPS (Hectares)	(CI)	MPS (Hectares)	(CI)	MPS (Hectares)	(CI)
1971	8	(3−12)	0	N/A	5	(0−10)
1981	24	(10–37)	20	(3–38)	7	(2−11)
1991	8	(5–10)	6	(2–9)	5	(2–8)
2001	3	(2–4)	6	(0−12)	4	(0–8)
2011	3	(2–4)	1	(0–1)	5	(0−11)

5. Discussion

We were able to combine surface mapping techniques and spatial metrics in order to compare the development of the spatial pattern of deprivation in Glasgow, Manchester, and Liverpool from 1971 to 2011. This approach minimised the influence of MAUP and boundary changes on the comparison, whilst enabling both the finer scale and landscape level spatial patterning of deprivation to be explored. Results revealed the spatial extent of deprivation was higher at all the time points in Glasgow, and considerably so in 1971 and 1981. Glasgow also experienced a more extreme increase and decrease in the spatial extent of deprivation over the study period. At all-time points Glasgow had higher patch density figures, indicating a more fragmented spatial arrangement of deprivation. As discussed in section 2, Livingston and Lee (2014) identified that in the mid-2000s Glasgow's spatial arrangement of income deprivation was more dispersed than that observed in either Liverpool or Glasgow. Our findings therefore, using different measures of deprivation, support this assertion but discover that this is a feature of the city dating back at least as far as 1971. Mean patch size was largely similar across the cities and, whilst there were some differences in values, particularly peak values, the trajectories of change for spatial extent, patch density, and mean patch size were also roughly similar. Future work could assess the extent to which Glasgow's more fragmented spatial arrangement of deprivation is implicated in its poor heath record. For this study, the demonstration of an effective methodology is the end point.

Our background section made much of the inadequacies of existing techniques for tracking and measuring spatial distributions over time. It is therefore important to critically reflect on the strengths and weaknesses of our own methods and how they might be improved in the future.

5.1. Strengths and limitations

A key strength of our technique is using Martin, 1989, Martin, 1996 and Martin and Bracken's (1991) approach to spatially disaggregate census counts to render maps of deprivation from different cities, in different countries, comparable over time. The disaggregation technique effectively minimises the MAUP. Although it draws on aggregate data, which will reflect the small area boundaries specific to the city and time period, the fact that the technique attempts to recreate the ‘real’ distribution of people on the ground means that the biases in aggregation introduced by arbitrary placement of small area boundaries are, as far as possible, removed. If we assume for a moment that the true spatial distribution of deprived households is well replicated at each time point, in each city, it is clear that the boundary change issue is also greatly resolved. However, it is important to note that the problems with MAUP and boundary change are only reduced, not eliminated. Although the census data were disaggregated, the household level distribution of deprivation is not replicated. The models use a very small cell (75m²), but they do still use a cell which is an areal unit. Furthermore, SurfaceBuilder models the disaggregated distributions based on model parameters; bias and error in this model are inevitable and, unquantifiable. Also, where there has been change in small area units within the cities, the location of the population weighted centroids upon which the disaggregation model rests, will alter. Our assumption is that shifts in the location of the centroids, and differing centroid density over time and between cities, will not have unduly affected the replication of the ‘real’ distribution of household deprivation, but this assumption is also untested. Overall however, compared to the existing methods which rely on small area unit analysis, even a critical gaze on our method should concede that the problems of MAUP have been reduced.

The use of spatial metrics enabled the landscape of household deprivation to be quantified and thus facilitated temporal and spatial comparisons without the need to rely on visual judgement. These techniques have not been used in this way before and our application of them to maps of household deprivation is innovative and original. We used three spatial metrics; however, a number of others exist, including shape metrics, nearest neighbour metrics, interspersion metrics, diversity metrics, and core area metrics. These metrics could be used in the future for research on deprivation which has a different focus than this study. Spatial metrics could also be applied to other variables such as affluence, or to assess the spatial relationships between cells of contrasting type (such as affluent and deprived).

It is worth considering whether spatial metrics could have been applied to the small area units, without the need to apply Martin's disaggregation technique. We do not believe they could have been applied appropriately. Given that the areal units have a different basis in the two countries, and they changed differently in each city over time, we would have had no way of knowing whether any differences in metrics at one time point were driven by differences in the nature of the areal units, and/or whether change in the metrics over time were driven by boundary change or by real substantive change in distribution. The common spatial unit provided by SurfaceBuilder was necessary.

Using UK decennial census data allowed comparable measures of relative deprivation over time for cities in Scotland and England. The data are among the highest quality available. However, whilst the four selected census variables have been used in other deprivation indices, they all have limitations. For example, although there is a well-established link between unemployment and both social and material deprivation (Howard, Garnham, Fimister, & Veit-Wilson, 2001), the use of unemployment was problematic. It has been suggested that both economic and political pressures prompted some people out of work to move their status from unemployed to permanently sick, particularly during the 1980s (Beatty and Fothergill (2005) for example). Furthermore, the UK census does not include a specific question on household income. A commonly used surrogate for income is car ownership, with the assumption being that households with one or more cars are likely to have higher incomes than those without. Correlations between car ownership and income support this surrogacy (Johnson, Currie, & Stanley, 2010). However, car ownership remains a lifestyle choice for some that may be influenced by access to public transport and parking facilities (Focas, 1998). The converse can also be true; where public transport is poor, and distances great, owning a car can be a necessity prioritised by those in adverse economic situations. Our approach to dealing with the limitation of each indicator was to create a measure based on all four. The study was also focused on comparing cities over time and, arguably, the weaknesses of each indicator will apply similarly in each city and should not have profoundly affected our overall conclusions. It is feasible that we underestimated the spatial extent of deprivation by setting the criteria for deprived being a cell with all four indicators present. However, analysis conducted on maps of the individual census variables revealed similar overall results. We also acknowledge a much wider debate over what deprivation is and how it is best measured. We were constrained by the availability of variables over time, but recognise that different choices of variables might have produced different results. However, this is not a paper about how to measure deprivation, rather it is a paper about how to use those measures in a spatial comparison over a long time period.

As the focus of this research was on identifying cells with values which were high relative to the rest of the city at specific time points, using Jenk's natural breaks, a classification method which maximises differences between classes, was viewed as advantageous. It was particularly useful for this study because we were attempting to identify areas which differed from other areas by having high numbers of people who are likely to be experiencing high levels of deprivation, relative to the rest of the city. However, a problem with using natural breaks to classify the cells is that the actual class boundary values are specific to that city and time point. Consequently, a cell classified as most deprived in one city and time point, might not be classified as so in others. It could be argued that this makes drawing meaningful comparisons of maps between cities and time points problematic; however, as the purpose of the analysis was to highlight areas with a high levels of deprivation relative to that city at that time point, natural breaks was a valid method. Future work could explore imposing the same class boundaries across all cities, or across time periods. Our sensitivity analysis suggested few substantive differences in results with alternative methods to Jenks and we preferred natural breaks since the cell classes were based on the distribution of the variable, rather than an arbitrary value (or proportion of cells). We were reassured that our main results were not dependent on this choice.

We also dichotomised cells as either ‘highly deprived’ or not. This was both to render the interpretation easier, and to suit the spatial metrics we chose to apply. Some spatial metrics are able to handle multiple classes of patch and future work should explore the use of multiple classes such as quintiles. We acknowledge that our choice means information was lost.

6. Conclusion

We created and demonstrated a novel approach to comparing the spatial distribution of deprivation between cities from different counties, over time. Although none of the individual techniques used were new, the combination of these methods was. We have minimised, but not eliminated, the influences of MAUP stemming from differences in areal unit definition and boundary change. We have demonstrated mapping and analysis techniques which allow both a fine scale and landscape scale assessment of the distributions. We believe these techniques could be usefully applied in other fields of urban studies, geography and epidemiology. We found that Glasgow's household deprivation has been more dispersed and fragmented over a long time period. These results have implications for future research into the excess mortality experienced in Glasgow.

Notes

When initially developed, spatial metrics were referred to as “landscape metrics” and this continues to be the case in disciplines such as ecology, where the natural environment is the focus of studies. However, when used to study urban environments the protocol has been to use the term “spatial metrics”. Spatial metrics is therefore the term used in this study.