Simulation of P2X‐mediated calcium signalling in microglia

Abstract

Key points

• A computational model of P2X channel activation in microglia was developed that includes downfield Ca²⁺‐dependent signalling pathways.

• This model provides quantitative insights into how diverse signalling pathways in microglia converge to control microglial function.

Abstract

Microglia function is orchestrated through highly coupled signalling pathways that depend on calcium (Ca²⁺). In response to extracellular ATP, transient increases in intracellular Ca²⁺ driven through the activation of purinergic receptors, P2X and P2Y, are sufficient to promote cytokine synthesis. Although the steps comprising the pathways bridging purinergic receptor activation with transcriptional responses have been probed in great detail, a quantitative model for how these steps collectively control cytokine production has not been established. Here we developed a minimal computational model that quantitatively links extracellular stimulation of two prominent ionotropic purinergic receptors, P2X4 and P2X7, with the graded production of a gene product, namely the tumour necrosis factor α (TNFα) cytokine. In addition to Ca²⁺ handling mechanisms common to eukaryotic cells, our model includes microglia‐specific processes including ATP‐dependent P2X4 and P2X7 activation, activation of nuclear factor of activated T‐cells (NFAT) transcription factors, and TNFα production. Parameters for this model were optimized to reproduce published data for these processes, where available. With this model, we determined the propensity for TNFα production in microglia, subject to a wide range of ATP exposure amplitudes, frequencies and durations that the cells could encounter in vivo. Furthermore, we have investigated the extent to which modulation of the signal transduction pathways influence TNFα production. Our results suggest that pulsatile stimulation of P2X4 via micromolar ATP may be sufficient to promote TNFα production, whereas high‐amplitude ATP exposure is necessary for production via P2X7. Furthermore, under conditions that increase P2X4 expression, for instance, following activation by pathogen‐associated molecular factors, P2X4‐associated TNFα production is greatly enhanced. Given that Ca²⁺ homeostasis in microglia is profoundly important to its function, this computational model provides a quantitative framework to explore hypotheses pertaining to microglial physiology.

Key points

• A computational model of P2X channel activation in microglia was developed that includes downfield Ca²⁺‐dependent signalling pathways.

• This model provides quantitative insights into how diverse signalling pathways in microglia converge to control microglial function.

Introduction

Microglia reside in the CNS, where they serve roles in neurological development, as well as surveillance of, and mitigate insults to, CNS tissue. In the latter role, microglia respond to an expansive set of molecular stimuli, including foreign matter such as proteolysed bacterial coat sugars (Kettenmann et al. 2011), pro‐inflammatory peptides such as interleukins and tumour necrosis factor α (TNFα), as well as secondary messengers, such as ATP. ATP is particularly significant, given its dual role both in cell‐to‐cell communication and responses to tissue injury (Davalos et al. 2005). Under the latter stimuli, microglia can undergo dramatic changes in activity, gene expression, and morphology to sense and respond to insults (Owens, 2012). Efforts in recent decades to characterize microglial function in response to ATP have identified a variety of intricate signal transduction pathways, of which the mechanisms of some are known in considerable detail (reviewed by Kettenmann et al. 2011). Despite our detailed knowledge of ATP‐triggered pathways in microglia, it is unclear how these mechanisms collectively integrate to encode microglial responses in response to diverse ATP stimuli (Kettenmann et al. 2011).

Although in vivo preparations provide the ideal platform for studying microglia activation under physiological conditions, given the difficulties of characterizing microglia physiology in vivo, the majority of published experimental data have utilized immortalized cell lines or primary cultures. It is recognized that cultured cells present phenotypes that can significantly differ from those of in situ resting microglia (Kettenmann et al. 2011). Nevertheless, ex vivo cell preparations provide substantial information on microglia physiology, despite these phenotypical variations. A primary goal of our study therefore was to develop a quantitative model of P2X‐dependent signalling in microglia, utilizing experimental data largely collected from cultured cells. With such a model, hypotheses regarding microglial function could be quantitatively evaluated complementary to traditional experimental assays and in principle be refined to emulate in vivo conditions and cellular phenotypes.

Computational systems biology has emerged as a powerful tool toward bridging external stimuli with phenotypical outputs (Winslow et al. 2012), through synthesizing diverse models of intracellular functions, including ion channel gating, intracellular signal transduction and gene programming. To our knowledge, such models for ATP‐dependent glial function are scarce and have been limited to the modelling of purinergic receptor gating (P2X) (Garcia‐Guzman et al. 1997; Hide et al. 2000; Kettenmann et al. 2011; Khadra et al. 2012; Kettenmann et al. 2012; Toulme & Khakh, 2012; Ase et al. 2015; North, 2016), as well as IP₃‐mediated Ca²⁺ signalling (Skupin et al. 2008), which can be indirectly modulated by ATP exposure. Our goal was therefore to establish a computational systems biology model of ATP‐dependent signalling pathways in microglia, with which we could probe factors that contribute to cytokine production. The resulting model provides insights into microglia physiology in typical in vitro assays and testable predictions for how intracellular microglial signalling pathways function in vivo.

Our model describes microglial responses to ATP binding at purinoceptors localized to the plasma membrane (PM). Purinoceptor activation is strongly associated with dramatic changes in intracellular Ca²⁺ content and Ca²⁺‐dependent signalling cascades linked to gene expression (Kettenmann et al. 2011). Changes in Ca²⁺ in response to ATP can occur directly through the opening of Ca²⁺ non‐selective ionotropic channels (P2X), or indirectly by metabotropic receptors (P2Y) that utilize second messengers such as IP₃. Of the P2X receptors, P2X4 and P2X7 are the most abundant channels expressed in microglial membrane (Kettenmann et al. 2011), where we have adopted the naming convention of Collingridge et al. (2009). These channels respond most prominently to micromolar and millimolar ATP, respectively (Verkhratsky & Butt, 2007; Kettenmann et al. 2012) although P2X7 presents significant activity even at micromolar ATP (Chessell et al. 1997). The channels also have different rates of deactivation, with P2X4 generally deactivating more rapidly than P2X7 (Coddou et al. 2011). P2X activation by ATP is associated with an increase in production and release of TNFα (Hide et al. 2000). Linking these events are observations that ATP‐dependent TNFα production is strongly correlated with elevated intracellular Ca²⁺ and p38 phosphorylation (Hide et al. 2000). Moreover, Ca²⁺‐dependent nuclear factor of activated T‐cells (NFAT) activation via calcineurin (Cooling et al. 2009; Furman & Norris, 2014) appears to be implicated in TNFα synthesis in microglia (Ferrari et al. 1999; Nagamoto‐Combs & Combs, 2010). We therefore hypothesized that TNFα production following ATP binding to P2X receptors utilizes Ca²⁺ signal transduction mechanisms to invoke cytokine production through calcineurin (CN)/NFAT activation. Toward investigating this hypothesis, we integrated Markov models of P2X4 and P2X7 activation (Khadra et al. 2012; Zemkova et al. 2015), Ca²⁺ homeostasis (Shannon et al. 2004; Saucerman & Bers 2008; Cooling et al. 2009; Bazzazi et al. 2015) and subsequent activation of CN and NFAT.

Microglia utilize diverse mechanisms to control Ca²⁺ homeostasis and Ca²⁺‐dependent responses to external stimuli, many of which are broadly used by nearly all eukaryotic cells. These mechanisms encompass external Ca²⁺ entry, the triggering of intracellular Ca²⁺ release by way of second messengers, Ca²⁺ binding to buffers and effectors, as well as Ca²⁺ clearance via pumps and exchangers (Berridge et al. 2003). The mechanisms of Ca²⁺ homeostasis tested in our model include the Na⁺/Ca²⁺exchanger (NCX), sarcoplasmic/endoplasmic reticulum calcium ATPase (SERCA) and Ca²⁺‐dependent control of TNFα transcription, for which models have been developed for other cell types, such as cardiac cells (Shannon et al. 2004; Winslow et al. 2016). The results of our computational model suggest that short/pulsatile ATP is probably sufficient to invoke production of TNFα via P2X4, whereas long‐duration and high‐amplitude ATP exposure is necessary for production via P2X7. With this computational model, we provide a framework to challenge our current understanding of microglia physiology with the goal of motivating new hypotheses and avenues of experiments.

Methods

Microglial Ca²⁺ model

Our computational model of P2X‐mediated microglial signalling portrayed in Fig. 1 assumes: (1) ATP‐dependent activation of P2X receptors assuming minimal contributions from P2Y receptors is minor as is reported in BV2 microglial cell lines (Gilbert et al. 2016); (2) Ca²⁺‐dependent activation of signalling proteins calmodulin (CaM), CN, NFAT, as well as Ca²⁺ extrusion and uptake mechanisms; and (3) TNFα transcription, translation and exocytosis. For clarity, we numbered these reactions and list their supporting literature in Table S1. Although microglial regulatory mechanisms are complex and involve a great variety of channels, proteins and processes that we neglect here, our minimal model permits quantitative descriptions of P2X‐mediated behaviour with a tractable number of equations and parameters. These equations form the basis of time‐dependent ordinary differential equations that we numerically integrate, subject to a variety of experimental conditions described below. Parameters for these equations are summarized in Sect. A.1 (Supporting Information). Where possible, these parameters were adopted from the literature, although in many cases they were refitted to reproduce experimental data measured in microglia, especially in cases where the parameters or models were drawn from systems unrelated to glia. Because cell‐to‐cell variation and differences in experimental preparations can lead to varied data sets (Hanisch & Kettenmann, 2007; Kongsui et al. 2014), we present sensitivity analyses in our results that indicate the extent to which our fitted parameter choices influence measured observables.

Figure 1. Schematic of the microglial signalling model.

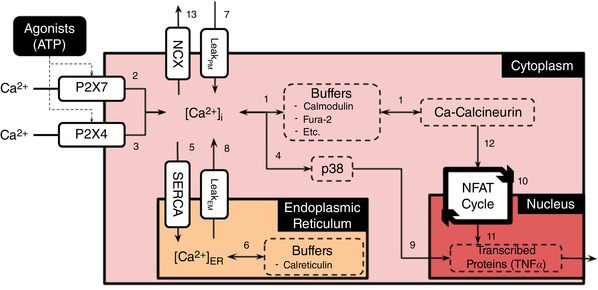
Schematic of the microglial signalling model assumed in this study Table S1 provides a summary of the numbered pathways in this diagram, as well as a link to the corresponding equations in the Supplementary Information. In this schematic, ATP activates the purinoceptors, P2X4 and P2X7, which culminates in the exocytosis of TNFα. [Color figure can be viewed at wileyonlinelibrary.com]

Simulation

Numerical model of Ca²⁺ handling

The microglial model was implemented in the Generalized ODE Translator gotran (https://bitbucket.org/johanhake/gotran) framework as described previously (Stewart et al. 2018). The gotran model was compiled into a Python module to make use of our Python‐based routines for simulation and analysis. In our numerical experiments, the microglia model was numerically integrated by the scipy function ODEINT, which utilizes the LSODA algorithm for stiff ordinary differential equations (ODE; Petzold, 1983) The numerical model was integrated using a timestep of 0.1 ms for a total simulation time of up to 180 min. These simulations provide as output the time‐dependent values of model states, such as intracellular Ca²⁺ or the open gates of the P2X channels. Model fitting proceeded by a genetic algorithm (reviewed by Srinivas & Patnaik, 1994) that iteratively improved parameter values, such as P2X4 conductance and PM Ca²⁺ leak over several generations of progeny. Parameters for the model components are summarized in Sect. A.1 (Supporting Information). Based on these parameterizations, our key model outputs were Ca²⁺ transients with respect to ATP exposure durations and concentrations, as well subsequent changes in NFAT activation and TNFα exocytosis. Experimentally measured outputs, such as Ca²⁺ transient decay time and amplitude, were measured for each of the progeny; those that reduced output error relative to the experimentally measured equivalent were stored for future generations. To validate our implementation, we present comparisons against predicted channel current profiles, intracellular Ca²⁺ content, activation of NFAT and p‐p38, as well as TNFα in the Results section.

Analysis

To examine potential mechanisms that link increased P2X stimulation to TNFα production, we monitored and identified prominent changes in key ‘state’ variables (including total amount of CN, CaM and NFAT, the density of purinoceptors, and the influx capacity) relative to control conditions. These sensitivity analyses were performed to determine relative correlations between model input parameters and predicted outputs (see Supplementary Information). Data processing was performed using SCIPY and the IPython notebooks. All codes written in support of this publication will be publicly available at https://bitbucket.org/pkhlab/pkh-lab-analyses. Simulation‐generated data are available upon request. Supplementary material is provided, which features elaborations of the model components, including parameter sets and equations, as well as supporting figures.

Results

Plasma membrane Ca²⁺ influxes and effluxes

Activation of the P2X7 and P2X4 receptors has been well characterized in the literature, particularly through whole‐cell electrophysiological methods using channels expressed in HEK cells as well as in microglia (Khakh et al. 1999; Egan, 2004; Egan et al. 2006; Coddou et al. 2011; Samways et al. 2011; Zemkova et al. 2015). P2X4 activation is triggered at micromolar ATP (∼100 μM), which culminates in a rapid (<1 s) and sharply peaked current profile that decays within tens of seconds (Toulme et al. 2010). P2X7 receptors, on the other hand, respond to millimolar ATP concentrations (up to 1 mM), but in contrast to P2X4, maintain significant current over prolonged ATP exposures (Chessell et al. 1997; Hide et al. 2000; Yan et al. 2010). As a first step toward the validation of our microglial Ca²⁺ model, we sought to reproduce the unique current profiles for the respective channels over appropriate concentrations and durations of ATP exposure, using a Markov model adapted to microglia P2X activation (Khadra et al. 2012; Zemkova et al. 2015). The Markov model framework assumed in this study captures the time evolution of channel gating states; of these states, the channel current is proportional to the probability of the open state. While Markov models have been reported in the literature (Yan et al. 2010); Khadra et al. 2012; Zemkova et al. 2015; Mackay et al. 2017), including 12‐ and 13‐state models from Khadra et al. and Zemkova et al., for the sake of parsimony we merged gating states that were in rapid equilibrium relative to state transitions that follow much slower kinetics (Smith & Crampin, 2004). In Sect. A.3.1 (Supporting Materials), we summarize the Markov models and their parameterizations for P2X4 and P2X7, respectively. Given the model reformulation, it was essential to ensure that our model reproduced experimentally measured currents attributed to P2X7 and P2X4 in microglia. Here, we validate the fitted P2X4 and P2X7 models by comparing our predicted current profiles against those measured for P2X4 by Toulme & Khakh (2012) and P2X7 by Chessell et al. (1997).

We first present in Fig. 2 A predicted currents vs. recordings conducted using P2X4 transfected into microglia (Toulme & Khakh, 2012). According to their study, the P2X4 channels were expressed and induced inward currents comparable to those previously observed in lipopolysaccharides (LPS)‐activated microglia (Toulme et al. 2010). Namely, the transfected channels exhibited an ∼30‐fold higher current density than those in resting C8–B4 cell lines. For this reason, for validation purposes we fit the P2X4 current profile to the Toulme & Khakh (2012) data, but in the following section, we reduced the current density by ∼30‐fold to validate the model against Ca²⁺ transients measured in primary microglia cultures by Hide et al. (2000). In Fig. 2 A we present two sets of modelling predictions: (1) using the ‘full’ model from Zemkova et al. (2015) and (2) our ‘lumped’ model, for which the open states Q1 and Q2 in the ‘full’ model are consolidated into a single Q12 ‘macro‐state’. At 100 μM, both the full and the lumped models closely follow the currents measured by Toulme et al., namely, they capture the sharp peak of approximately −375 pA in the early phase of ATP pulse, after which the current rapidly decays. A notable distinction between the two model formulations is that the lumped model presents a modestly faster rate of current decay in the presence of ATP, relative to the full model. In supplementary Fig. S2 we demonstrate that our Q12 ‘macro‐state’ mirrors the summation of the Q1 and Q2 states except for the phase after ATP removal, and hence merging of the Q1 and Q2 states introduces some error into the current dynamics. Nevertheless, both model representations yield nearly identical channel current profiles for all but the final seconds of ATP treatment, and thus our reduced model is sufficiently accurate for modelling rates of Ca²⁺ entry following ATP‐dependent P2X4 activation. We also made predictions at 10 μM and 1 mM ATP for comparison (data not shown); as anticipated, the reduced ATP treatment leads to a smaller (125 pA) current maximum, while a 10‐fold increase in ATP is indistinguishable from that reported for 100 μM ATP.

Figure 2. Inward currents via P2X4 and P2X7.

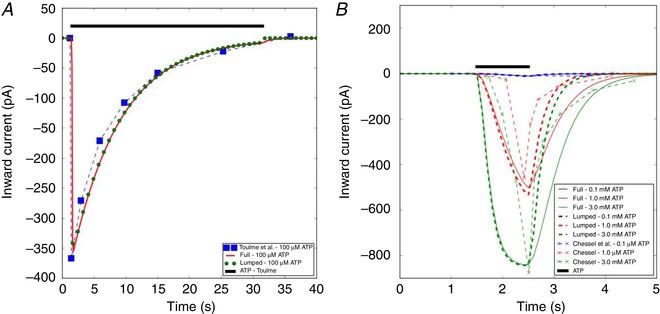
A, inward P2X4 current profile recorded in microglia (blue boxed) by Toulme & Khakh (2012) and the model prediction (red solid and green bead) when subject to 100 μM ATP for 30 s. B, inward P2X7 currents measured in microglia by Chessell et al. (1997) as well as the model predictions, when subject to 100 μM to 3 mM ATP for 0.5 s. Conditions to model the experimental conditions are listed in Table S2 (see also Sect. A.3.1 in Supporting Information). [Color figure can be viewed at wileyonlinelibrary.com]

In Fig. 2 B, we provide analogous current profiles stemming from P2X7 activation, subject to 0.1–3.0 mM ATP for 1 s as reported by Chessell et al. (1997). In contrast to P2X4, the P2X7 current profile exhibits a relatively slower rise to peak and a slower rate of current decay (also see Fig. 3 B). While the full and lumped models adequately capture the experimentally recorded peak current amplitudes, the models modestly overestimate the rate at which peak current increases and underestimate the rate of current decay after extensive fitting. While we could expect better agreement by introducing additional states, we believe the modest error is acceptable in order to reduce the number of variables and parameters in the model. Nevertheless, the high degree of overlap between the model predictions and the measured data suggests that any minor discrepancy will not appreciably impact our estimates of Ca²⁺ entry by these channels. We also report in Fig. 3 B the P2X7 channel profile when subject to 1.0 mM ATP over a 400‐s interval. Under these conditions, the channel exhibits a long‐lived plateau that is sustained over the entire duration of ATP treatment. This extended plateau is a common gating attribute of P2X7 receptors (Coddou et al. 2011) and is speculated to arise from a dilatated open‐pore structure following extended activation (Hide et al. 2000; Egan et al. 2006). Overall, these data suggest that our implementation of the P2X4 and P2X7 Markov models faithfully reproduces Ca²⁺ current profiles across a variety of ATP applications, and moreover, the channel dynamics exhibit vary considerably as a function of ATP exposure amplitude and duration. Unless otherwise noted, all further applications of our model assume both channels to be present.

Figure 3. Predictions of Ca²⁺ increase and its corresponding inward currents via activation of P2X4 and P2X7 by ATP.

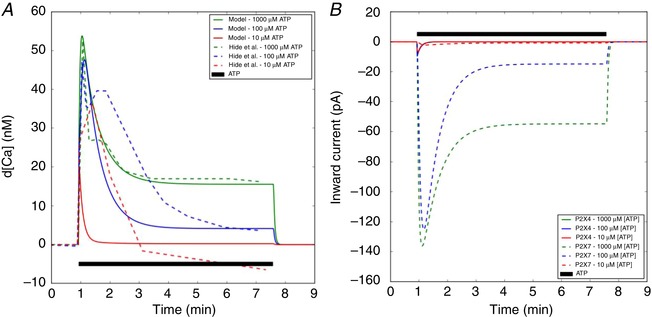
A, predicted free cytosolic Ca²⁺ (solid) with respect to time, subject to ATP treatments of 10–1000 μM ATP for 400 s (black), compared to experimental data from mouse microglia (dashed) (Hide et al. 2000) Complementary ER Ca²⁺ transients are reported in Fig. S5. B, inward current via P2X4 and P2X7 channels. Conditions to model the experimental conditions are listed in Table S2 (see also Sect. A.3.1 in Supporting Information). [Color figure can be viewed at wileyonlinelibrary.com]

Complementary to P2X‐driven Ca²⁺ entry, NCX and the plasma membrane ATPase comprise the primary mechanisms for extruding cytosolic Ca²⁺ and restoring basal Ca²⁺ content in glia (Lencesova et al. 2004; Golovina, 2005) and probably in microglia (Kettenmann et al. 2011). Given the lack of published experimental data on the role of plasma membrane ATPases in microglia Ca²⁺ management (Kettenmann et al. 2011), we neglected their contribution in the model. In addition, a modest PM leak term was incorporated to maintain Ca²⁺ steady state at rest. This addition was necessary to counterbalance a slight NCX Ca²⁺ efflux owing to the negative membrane potential assumed in the model (Boscia et al. 2009). We present in Sect. A.3.2 (Supporting Information) predictions using an NCX model developed for cardiac cells of rabbit origin (Shannon et al. 2004), which we refitted here for microglia Ca²⁺ handling. Because the membrane potential in microglia under normal conditions is generally negative (Kettenmann et al. 2011), it is anticipated that NCX primarily extrudes Ca²⁺. Nevertheless, we validated our model against single‐cell traces reported in fig. 5 of Boscia et al. (2009), for which significant negative NCX currents (−12 to −17 pA) were reported from −60 to −40 mV (see Fig. S3). Here we note that the activity characterized by Boscia et al. (2009) was conducted in Krebs medium solution, the Na⁺ concentration of which was comparable to the 145 mM assumed in our model. Importantly, our data successfully reproduce the experimentally measured currents under the aforementioned solution conditions. We note that our model may overestimate the contribution of NCX to Ca²⁺ extrusion rates, given the omission of PM ATPase activity. Nevertheless, our parameterization appeared sufficient to maintain resting Ca²⁺ levels, as well as restore Ca²⁺ levels following P2X4 stimulation.

Figure 5.

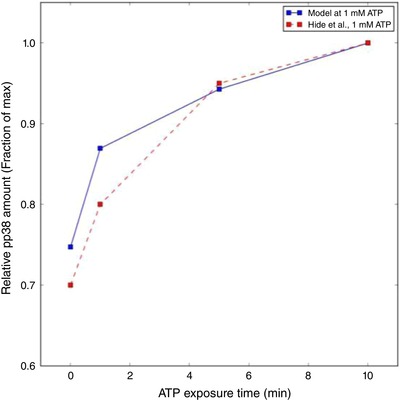
Prediction of activated (phosphorylated) p‐p38 (solid blue) with respect to 1 mM ATP exposure time vs. experimental data collected in mouse microglia by Hide et al. ( 2000 ) (dashed red) [Color figure can be viewed at wileyonlinelibrary.com]

Cytosolic Ca²⁺‐dependent signalling

P2X activation contributes substantial total Ca²⁺ to the cytosol (see Fig. 3 A) depending on the nature of ATP exposure, although free Ca²⁺ generally increases by nanomolar to micromolar levels as assessed by Ca²⁺ indicators (Hide et al. 2000; Toulme & Khakh, 2012). We therefore utilized the ratiometric measurements of Fura‐loaded cells presented by Hide et al. (2000) to estimate the free Ca²⁺ following substantial buffering by Ca²⁺ binding proteins (Berridge et al. 2003). Accordingly, we plot our predictions of Ca²⁺ transients following P2X stimulation in Fig. 3. To obtain reasonable agreement with the Hide et al. measurements, additional refitting of the P2X kinetic constants was performed. The revised P2X7 parameters are summarized in Table S3 and generally involved adjustments to transition parameters, k4_{P 2 X 7}, k6_{P 2 X 7} and H7_{P 2 X 7}, the use of which is further explained in Sect. A.3.1 (Supporting Information). Overall, we were able to reasonably reproduce Ca²⁺ transients measured following 100 μM and 1 mM ATP treatments, although our predicted currents at 100 μM ATP decayed more rapidly than indicated by the experimentally measured Ca²⁺ transient data. It is possible that there exist additional sources of ATP‐dependent Ca²⁺ entry not controlled for in the Hide et al. experiment, such as some level of P2Y‐mediated Ca²⁺ release from internal Ca²⁺ stores. We discuss these matters in greater detail in the Limitations section.

In addition to Ca²⁺ influxes and effluxes mediated by P2X and NCX, we reflect Ca²⁺ exchange with the endoplasmic reticulum (ER). Specifically, we include ER Ca²⁺ uptake via SERCA as well as a concentration‐dependent ER Ca²⁺ leak in order to maintain constant ER Ca²⁺ content of 0.8 mM (Skupin et al. 2008). To our knowledge measurements of SERCA function and effects on ER Ca²⁺ in microglia are not well established, so we utilized the SERCA mathematical model from Shannon et al. (2004). As a reasonable surrogate for microglial cells, we fit our SERCA V _max values to reproduce Ca²⁺ uptake rates following IP₃‐mediated spontaneous intracellular Ca²⁺ release in astrocytes (Schipke et al. 2008). We later demonstrate that the model is relatively insensitive to the choice of SERCA V _max. In principle, the ER Ca²⁺ leak assumed in our model to counterbalance SERCA uptake probably corresponds to spontaneous IP₃‐mediated ER release (Skupin et al. 2008), but including such contributions was beyond the scope of our study. In Fig. S5 we demonstrate that ER Ca²⁺ load is elevated in response to P2X activation with a modest lag relative to the cytosolic Ca²⁺ transient but returns to resting load after termination of the membrane current. In other words, ER Ca²⁺ load is increased only transiently, which indirectly suggests that Ca²⁺ entering through the PM is extruded by another mechanism, namely NCX exchange. Hence, physiologically normal rates of Ca²⁺ entry via PM Ca²⁺ influx were compensated for by NCX extrusion, and therefore were necessary for maintaining ER Ca²⁺ at resting levels when subject to infrequent or low‐amplitude P2X4 stimulation.

Ca²⁺‐dependent NFAT activation constitutes a prominent signal transduction pathway implicated in the release of inflammatory agents (Kataoka et al. 2009; Shiratori et al. 2010) including TNFα (Hide et al. 2000; Hanisch & Kettenmann, 2007; Shieh et al. 2014; Santa‐Cecilia et al. 2016). Of these, Ca²⁺ binding to CaM and CN, as well as subsequent binding of the Ca²⁺‐saturated proteins to NFAT, is an established substrate for activation of this pathway (Cooling et al. 2009). Our implementation of the CaM/CN model was originally developed for cardiomyocytes by Saucerman & Bers (2008), although we utilized parameters adapted by Bazzazi et al. (2015) for HEK cells. Given that time‐dependent CN activation data are not available in glia, we sought qualitative agreement between measurements of CN activation by Bazzazi et al., subject to Ca²⁺ transients that we tuned to be similar in amplitude to their data. Figure S4 summarizes our qualitative comparisons, namely that the predicted CaM/Ca²⁺‐saturated CN at low stimulation frequencies reaches a maximum that lags the peak Ca²⁺ concentration by several seconds, while its decay is less rapid than that of the Ca²⁺ transient. Furthermore, a rapid frequency of pulsatile ATP exposure (1‐s pulses at 0.5 Hz) was sufficient to maintain an elevated CaM/Ca²⁺‐saturated CN (see Fig. S4). Both trends were consistent with the HEK data from Bazzazi et al., although our data reflect slower relaxation kinetics, which we attribute to different rates of Ca²⁺ uptake and extrusion mechanisms in microglia. Hence, we anticipate that transient increases in Ca²⁺ arising from brief P2X stimulation will not lead to sustained CN activation, in contrast to transients of sustained duration.

We next tuned the kinetics of NFAT activation in our microglial model to agree with Western blot‐based measurements of activated (dephosphorylated) NFAT from Ferrari et al. (1999), for which the dephosphorylated factor was reported for several 3 mM ATP exposure durations (15 min). Notably, we adjusted most of the reaction constants associated with NFAT cycle model from Cooling et al. (2009) to reproduce percentage changes in NFAT with respect to ATP exposure time up to 60 min, in accordance with the microglial data from Ferrari et al. (1999). We report good agreement with experiment for the time‐dependent increase in dephosphorylated NFAT at 3 mM ATP (Fig. 4), although our model predicted higher percentages of activated NFAT under steady‐state conditions for ATP treatments below 3 mM. We anticipate that this can be refined with further retuning of the NFAT activation model.

Figure 4. Predictions of dephosphorylated NFAT concentration as a function of ATP exposure time and concentrations.

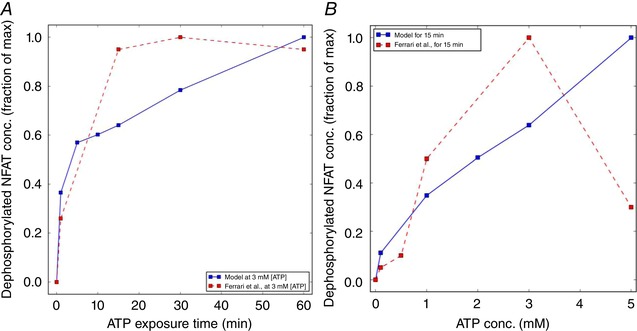
A, activated (dephosphorylated) NFAT following 3 mM ATP treatment for up to 60 min recorded by Ferrari et al. (1999) (dashed) and predicted by the model (solid). B, analogous predictions of activated NFAT, subject to 15‐min treatments of ATP up to 5 mM vs. experiment (Ferrari et al. 1999) Parameters and conditions to model the experimental conditions are listed in Table S2. [Color figure can be viewed at wileyonlinelibrary.com]

Our predictions shown in Fig. 4 are in good agreement with experimental data as exposure time was varied, and for variations of concentrations up until 3 mM ATP. A decline in activated NFAT was reported by Ferrari et al. (1999) that we could not capture in the model. Moreover, assuming that NFAT activation at ATP concentrations below 1 mM arise from P2X4‐mediated Ca²⁺ current and increasing P2X7 contributes Ca²⁺ at and above this concentration, both channels are capable of eliciting NFAT responses.

The MAPK p38 serves as a prominent signalling hub that has been implicated in TNFα release in microglia (Hide et al. 2000). Phosphorylation of p38 follows the activation of P2X channels (Hide et al. 2000; Trang et al. 2009), and non‐specific Ca²⁺ entry via ionophores (Trang et al. 2009), and this apparent Ca²⁺ sensitivity may involve CaMK (Wright et al. 2007) or Ras (Cullen & Lockyer, 2002) activation. Notably, p38 contributes to the regulation of over 60 substrates (Trempolec et al. 2013), converges on c‐Jun N‐terminal kinase (JNK) and is reported to indirectly stabilize transcribed TNFα mRNA (Menon & Gaestel, 2018), complementary to NFAT activation of TNFα translation. Given the complexity of the p38 activation pathway and lack of quantitative data for its Ca²⁺‐dependent activation in microglia, for simplicity we assumed a phenomenological, Ca²⁺‐dependent Hill formulation for p38 phosphorylation as described in Sect. A.3.4 (Supporting Information). We rationalize this functional form based on evidence that p38 in granule cells can be phosphorylated through treatment with the Ca²⁺ ionophore A23187, independent of ionotropic or metabotropic receptor activation (Kawasaki et al. 1997).

To validate this implementation, we utilized Western blot data from Hide et al. (2000), which reported phosphorylated p38 content as a function of time (subject to 1 mM ATP). In Fig. 5, we demonstrate that at low ATP concentrations that are expected to preferentially activate P2X4 over other competing purinergic receptors, p38 is rapidly phosphorylated and in strong agreement with Trang et al. (2009). At 1 mM ATP we slightly overestimate the rate of p38 phosphorylation, which may be attributed to the discrepancy in our predicted cytosolic Ca²⁺ transients relative to experiment. Nevertheless, the model captures the Ca²⁺‐dependent activation of p38, which can be elicited both by P2X4 and by P2X7.

Transcriptional regulation

P2X activation, followed by elevation of cytosolic Ca²⁺ load whereby NFAT and p38 are activated, culminate in cytokine production (Hide et al. 2000; Ji & Suter, 2007; Kettenmann et al. 2011). In our model, we assume that p38 is phosphorylated in a Ca²⁺‐dependent fashion to form p‐p38; concurrently, NFAT is activated by Ca²⁺‐saturated CN. We utilized phenomenological models to couple NFAT and p38 control of TNFα transcription, as summarized in Sect. A.3.5 (Supporting Information). Specifically, we assumed that TNFα mRNA transcription is driven by the formation of an NFAT/DNA complex (Boise et al. 1993), and the transcribed mRNA is partially protected from degradation in a p‐p38‐dependent manner (Menon & Gaestel, 2018), thereby permitting increased rates of TNFα protein translation (Destexhe et al. 1998). It is important to note that additional regulatory mechanisms ultimately control the exocytosis of molecular cargo (Stanley & Lacy, 2010), but are represented only by approximation in this study. In Hide et al. (2000), enzyme‐linked immunosorbent assays (ELISAs) were conducted with 3 h of ATP treatment, the concentration of which varied from 0.01 to 1 mM, as well as at 1‐h interval using 3 mM ATP. The predicted TNFα production rate data were fitted to experimental data provided by Hide et al. (see Fig. 6), primarily through modulating parameters that control mRNA production, its degradation, translation and P2X7‐dependent exocytosis. In our opinion, those regulatory mechanisms following P2X7 activation in microglia in particular are poorly resolved and insufficient for developing a more sophisticated and validatable model. Because we have been unable to identify TNFα production rates solely attributable to P2X7 activation, we assumed for simplicity that TNFα production and release rates were proportional to the cytokine ELISAs performed by Hide et al. (2000). The predicted TNFα production data correlate positively with ATP concentration and duration of exposure, although the model overestimates release rates at 3 mM ATP and is less sensitive to ATP concentration than reported by Hide et al. Although further refinement of the TNFα transcription model could improve agreement with experimental data (see Limitations section), our model demonstrates that even low levels of ATP can trigger TNFα production, thereby suggesting sensitivity to both P2X7 and P2X4 activation.

Figure 6. Predictions of TNFα production as a function of ATP concentration and exposure time.

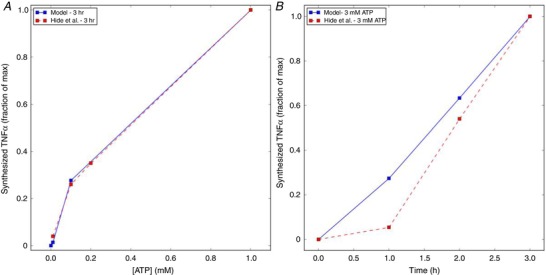
A, predictions (solid) of TNFα production following 3 h of micromolar to 1 mM ATP exposure vs. exocytosed protein collected by Hide et al. (2000) (dashed), assuming that exocytosed TNFα scales proportionally to the total amount of TNFα synthesized. B, TNFα production predictions (solid) as a function of time (h), following 3 mM ATP treatment vs. experiment (dashed). Parameters and conditions to model the experimental conditions are listed in Table S2. [Color figure can be viewed at wileyonlinelibrary.com]

Effects of ATP waveform on intracellular Ca²⁺ dynamics and TNFα production

Our overarching hypothesis in this study was that the duration, frequency and amplitude of ATP stimulation control the dynamics of the intracellular Ca²⁺ transient and, ultimately, the ability to trigger TNFα production. This hypothesis was chiefly motivated by observations that (1) low‐micromolar, high‐frequency (up to 5 Hz) quanta of ATP are released by astrocytes as part of their physiological function (Lalo et al. 2014), and (2) P2X4 and P2X7 present markedly different ATP sensitivities and deactivation kinetics (Coddou et al. 2011). Moreover, non‐P2X‐specific Ca²⁺ entry via ionophores induces TNFα mRNA production in T cells (Tsytsykova et al. 2007) and CCL3 (a chemokine) mRNA via NFAT in microglia (Kataoka et al. 2009), suggesting elevated intracellular Ca²⁺ in cytokine synthesis. To test this hypothesis, we subjected our model to ATP pulses of up to 2 mM, with frequencies of 0.5–5 Hz and consisting of durations of up to 20 s. Here, we first discuss the degree to which these conditions changed the average intracellular Ca²⁺ content from values maintained at rest, after which we phenomenologically relate the Ca²⁺ content to the propensity for TNFα release. Based on data presented in Fig. 7 A, we find that high frequencies of low‐amplitude ATP stimulation (within the range of ATP from 300 μM and above) are sufficient to increase the cytosolic Ca²⁺ load in a manner sufficient to promote TNFα production above resting levels, although to a lesser extent than changes following millimolar ATP concentrations. In contrast, resting Ca²⁺ is rapidly restored at reduced ATP concentrations or stimulation frequencies, as evidenced by the dark region left of the yellow Ca²⁺ = 0.110 μM iso‐contour. Given that P2X4 responds to micromolar ATP, it is apparent that P2X4 contributes most significantly under high‐frequency ATP stimulation, although P2X7 appears to account for the majority of Ca²⁺ entry, especially at higher ATP concentrations.

Figure 7. Predictions of free cytosolic Ca²⁺ (A) and TNFα production (B) following pulsatile ATP exposure for 20 s.

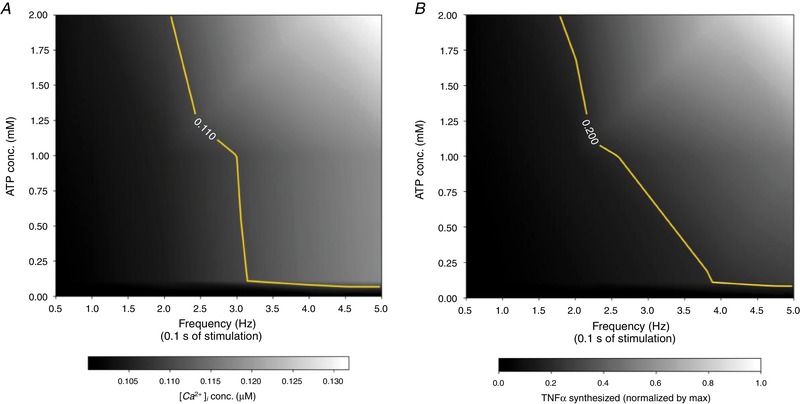
ATP pulse frequency is varied from 0.5 to 5 Hz and concentration is varied up to 2 mM. The TNFα data were normalized by the maximum TNFα production under conditions considered. For reference, thresholds are drawn at Ca²⁺ = 0.110 μM and TNFα = 0.2 to represent above‐resting Ca²⁺ levels and half‐maximal TNFα transcription rates, respectively. Corresponding Ca²⁺ transients are illustrated in Fig. S8. [Color figure can be viewed at wileyonlinelibrary.com]

Second, we demonstrate in Fig. 7 B rates of ATP‐mediated TNFα production under conditions analogous to those in Fig. 7 A. Importantly, we observe (1) significant rates of TNFα production under high‐frequency, low‐amplitude ATP stimulation and (2) that the TNFα production rates correlate with increase Ca²⁺ load, as TNFα production rates appear to decrease more rapidly with decreasing frequency, compared to sustained Ca²⁺ load (see yellow, iso‐contour representing half‐maximal rates of TNFα transcription). Overall, these results appear to establish bounds for the frequency and amplitude capable of evoking transcriptional responses. Shieh et al. (2014) demonstrated that TNFα release was not seen in P2X7 knock‐out microglia under 24 h of ATP treatment. Our interpretation of these data are that the P2X4 channel rapidly desensitized and thus elevated Ca²⁺ loads could not be maintained. An important distinction in our protocol, however, is that we utilize short bursts of ATP that reduce the rate of P2X4 desensitization, which facilitate elevated Ca²⁺ and subsequent TNFα transcription.

Finally, in Fig. 8 we present Ca²⁺ transient maxima and TNFα production rates using baseline (0.3 pA/pF) and elevated (9 pA/pF) P2X4 current densities. The baseline P2X4 density is typical of a resting, immortalized microglial cell line (CB‐8), while the latter is representative of an LPS‐activated cell (Toulme et al. 2010; Toulme & Khakh, 2012). Here we observe that the 30‐fold higher P2X4 density presents substantially larger calcium transients with corresponding increases in TNFα production rates. Interestingly, the elevated P2X4 current densities appear to enable substantial TNFα production, even under low‐micromolar, high‐frequency ATP exposures.

Figure 8. Predicted increase in intracellular Ca²⁺ concentrations (averaged from 10 to 20 s) and TNFα synthesis rates in activated microglia (red) and the cell at rest state (blue).

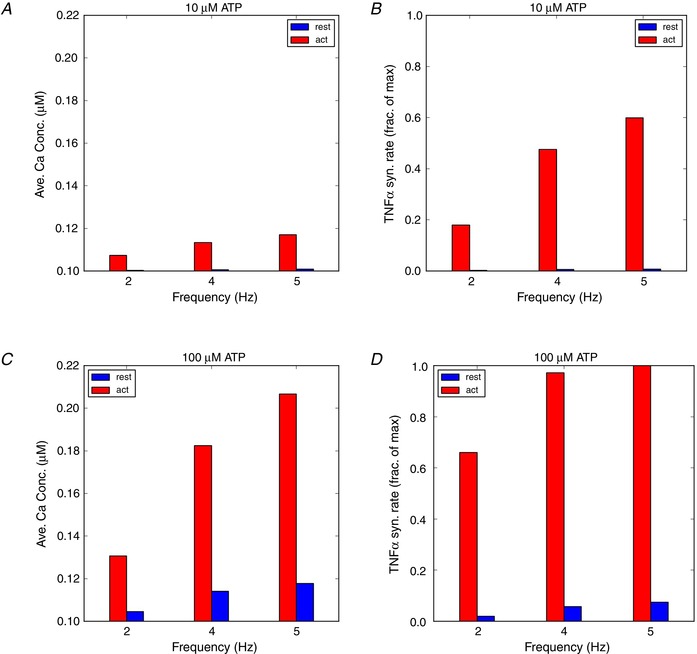
The P2X4 channel density parameters (ρ_{P 2 X}) for cells at rest (1×) and LPS‐activated (30×) are listed in Tables S3 and S4. [Color figure can be viewed at wileyonlinelibrary.com]

Sensitivity analysis and effects of partial (ant)agonism on TNFα production

Lastly, given that TNFα transcription and release are collectively controlled by several Ca²⁺‐dependent compounds in our microglial model, we utilize sensitivity analysis to highlight parameters that most significantly influence the model predictions. Our central goal here was to provide predictions that can be tested with common experimental protocols, such as controlling gene expression, or the application of protein‐specific inhibitors and agonists. Here, parameters modulating activities of a given signal transduction component were varied in order to represent its up‐regulation, down‐regulation, or to a certain extent, partial inhibition or agonism. In Fig. 9, we report the sensitivity of TNFα production as a function of plasma membrane Ca²⁺ entry, as determined by purinoceptor concentration, NCX Ca²⁺ flux, and the rate of inward Ca²⁺ leak, subject to low and high ATP concentrations. Here, each line represents the rate of TNFα production, r _TNFα, relative to control vs. the channel expression relative to control [P]. The slope of a given line, ∆r _TNFα/∆[P], indicates the sensitivity of TNFα production relative to changes in a component's activity. Because the P2X receptors and the Ca²⁺ leak contribute inward Ca²⁺ current, TNFα production is positively correlated with the concentration (P2X) or rate (leak) relative to control values, with greater sensitivity to P2X7 owing to its larger contribution to Ca²⁺ transients. Importantly, the slope increases with increasing channel expression, which suggests that greater rates of TNFα production are realized relative to control. Similarly, higher rates of Ca²⁺ influx via a non‐specific, inward Ca²⁺ leak sensitizes TNFα production, and hence the threshold for TNFα production via P2X stimulation is reduced. Analogously, reducing extracellular Na⁺ decreases and potentially reverses the rate of Ca²⁺ extrusion via NCX, which has the net effect of increasing intracellular Ca²⁺ relative to control. As a result, decreased rates of Ca²⁺ extrusion that arise from decreasing extracellular Na⁺ sensitize TNFα production.

Figure 9.

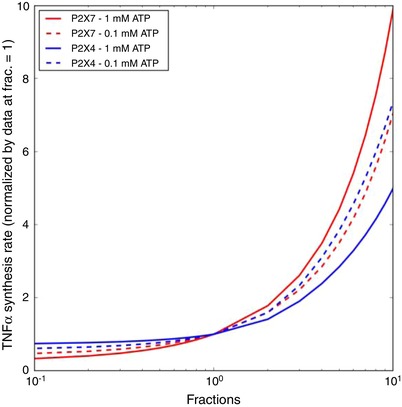
Sensitivity of TNFα production as a function of P2X4 (blue) and P2X7 (red) expression with respect to 1 Hz, 0.1 and 1.0 mM ATP pulses for 300 s [Color figure can be viewed at wileyonlinelibrary.com]

In Fig. 10, we report similar measures of TNFα production sensitivity to variations in CaM, CN and NFAT. Given that the Ca²⁺‐dependent activation of these model components promotes TNFα expression, decreases in concentrations of these proteins depressed TNFα production, and conversely, their increase accelerated TNFα production rates. Of these, TNFα production was most sensitive to the modulation of CaM and CN, with a relatively minor dependence on ATP concentration. Among the proteins considered, CaM is known to increase expression upon activation (Sola et al. 1997), which suggests that TNFα production may be accelerated under these conditions.

Figure 10. Sensitivity of predicted synthesis rate of TNFα to variations in model parameters.

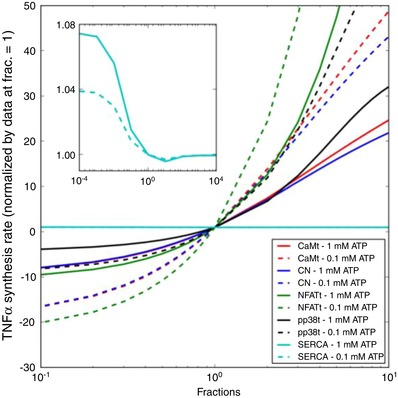
Degree of TNFα synthesized as a function of total CaM (red), CN (blue), NFAT (green), SERCA pump capacity (cyan) or p‐p38 (black) concentration with respect to 1 Hz, 0.1 and 1.0 mM ATP pulses for 300 s. [Color figure can be viewed at wileyonlinelibrary.com]

Discussion

Overarching outcomes

In this study, we have established a quantitative model for TNFα expression following P2X activation via extracellular ATP binding, using a microglia‐specific computational approach. The computational model recapitulates ATP‐dependent activity profiles for two prominent P2X channels, parallel rises in intracellular Ca²⁺, activation of the Ca²⁺‐dependent NFAT pathway, and ultimately cytokine production. With this minimal model, we assess the extent to which the intracellular signalling cascades are coupled to characteristics of extracellular ATP exposure and sensitivity to variations in protein expression and kinetics.

The breadth of ATP signatures considered were intended to be representative of physiological conditions experienced in intact tissue, as well as in cell culture. The variations considered in the sensitivity analyses were reflective of anticipated phenotypical changes in expression during microglial activation, as well as pharmacological or genetic strategies used in a variety of experiments to manipulate and understand microglia physiology. The model we developed integrates both biophysically motivated and phenomenological descriptions of purinergic receptors, NFAT‐ and p38‐mediated gene expression pathways, cytosolic Ca²⁺ handling, as well as provides a framework to link a wide body of experiments probing microglial function (reviewed by Verkhratsky et al. 1998; Kettenmann et al. 2011). With this model we characterized the relative contributions of P2X4 and P2X7 in driving TNFα production across a broad range of ATP exposure concentrations and durations, as well as the sensitivity of this process to changes in protein expression and activity. Most significantly, we provide computational predictions that TNFα mRNA expression is possible from low‐amplitude, short‐duration ATP signals that might be expected within neuronal synapses, while thresholds for mRNA production are reduced under conditions typical of activated microglia, such as increased P2X and CaM expression.

P2X receptor activation

Recently, there has been considerable focus on the modulation of purinergic receptors, including P2X4 and P2X7, in controlling pain and inflammation, as reviewed by Kuan & Shyu (2016). Both P2X receptors are responsive to ATP released from damaged cells (Illes & Ribeiro, 2004; Koizumi et al. 2005; Stogsdill & Eroglu, 2017). Although both channels are activated by ATP, the micromolar vs. millimolar affinities of P2X4 and P2X7, respectively, raise the possibility that the channels have distinctive roles in their responses to extracellular agonists.

Toward addressing this hypothesis, we implemented state‐based models of P2X7 and P2X4 activation that could predict open state probabilities over a broad ranges of ATP exposures. In turn, the current profiles were used to predict rates of intracellular Ca²⁺ entry. The channel models considered in this study were developed in previous works that examined P2X channel activity for endogenous ATP, as well as several pharmacological agonists and antagonists (Yan et al. 2010; Khadra et al. 2012; Zemkova et al. 2015; Mackay et al. 2017). These models consisted of at least eight and as many as 32 states to capture nuances of desensitization and changes in channel gating arising from pharmacological treatment. Our primary objective was to exclusively examine channel responses to ATP over a range of concentrations, durations and frequencies, so we opted for a simplified model with fewer free parameters. Overall, the reduced models, which shared the same number of states but with different gating parameters, reproduced experimentally measured and predicted current profiles with acceptable accuracy. For this reason, the parsimonious model was appropriate for predicting increases in intracellular Ca²⁺ load, assuming that 8% of each channel's predicted current corresponded to Ca²⁺ influx, as suggested by Garcia‐Guzman et al. (1997). We note, however, that further refinement of the model to reflect responses to P2X7 and P2X4 agonists such as 3′‐O‐(4‐benzoyl)benzoyl ATP (BzATP) and ivermectin, respectively, could necessitate additional gating terms as described by Yan et al. (2010) and Zemkova et al. (2015).

To determine the extent to which P2X4 modulation impacted steady‐state Ca²⁺ load and subsequent TNFα production, we utilized a basic sensitivity analyses approach described by Stewart et al. (2018). Our predictions of P2X4 activity indicate that low‐amplitude ATP exposures of short duration (<1 s) across a broad range of frequencies were sufficient to trigger significant Ca²⁺ entry. Microglial P2X4 could thus serve a predominant role in processing small, highly transient, ATP signals arising from normal communication between neural synapses (Stogsdill & Eroglu, 2017), to activate a microglia‐dependent modulation of synaptic function. An exciting possibility that remains to be tested is whether there are lower thresholds for ATP concentration and exposure duration that are sufficient to activate P2X4‐dependent Ca²⁺ signalling in microglia. For instance, how many synapses with elevated ATP would a single microglia cell need to sample during a short duration (milliseconds to seconds) to activate a P2X4‐dependent Ca²⁺ response? Furthermore, because prolonged exposure to ATP is associated with increased membrane trafficking and mobility of P2X4 (Toulme & Khakh, 2012), higher P2X4 activity could prime microglia to have increased sensitivity to ATP, thereby lowering the threshold of ATP needed to induce P2X4‐dependent Ca²⁺ responses. The sensitivity analyses we conducted indeed demonstrate greater propensities for TNFα mRNA production under conditions of multi‐fold higher P2X4 akin to activated microglia. It remains to be determined experimentally the extent to which simultaneous changes in microglial Ca²⁺ handling upon activation, such as increased CaM (Sola et al. 1997) and ionized calcium‐binding adapter molecule 1 (Iba‐1) expression (Bederson et al. 2001), could compensate for larger inward Ca²⁺ currents via increased P2X4 expression. Beyond changes in expression, differences in subcellular localization could additionally counterbalance the effects of increased P2X4 activity, such as the asymmetric distribution and mobility of P2X4 between the microglial soma and the microglial processes (Toulme & Khakh, 2012), as well as the localization of ATP encountered presumably by the microglia process at the synapse. Careful characterization of the subcellular distribution of P2X4 may therefore be important for understanding the channel's ability to prime microglia to increased sensitivity to ATP.

Our computational simulations indicate P2X7 responses predominate over P2X4 at high ATP concentrations and prolonged exposure durations. The computational sensitivity analyses are also in agreement with the role of P2X7 in ATP‐dependent TNFα production from microglia (Hide et al. 2000), and the effects of selective inhibitors of P2X7 such as KHG26792 (Kim et al. 2015; Jin et al. 2018) that suppress TNFα production. The distinct channel activation profiles of P2X4 and P2X7 probably provide microglia with the ability to respond differently to low or high levels of ATP, by activating a neurotrophic (Trang et al. 2009) or cytokine response, respectively. Moreover, selective inhibitors of P2X7 may be useful in the case of pathologically elevated ATP, such as that seen after a traumatic brain injury, while selective agonists or antagonist of P2X4 may be more useful in modulating microglia when subject to physiological levels of ATP.

Maintenance of cytosolic Ca²⁺ content

Activation of microglia and exocytosis of cytokines and chemokines are strongly correlated with increased intracellular Ca²⁺ content. We predict that the sensitivity of ATP‐triggered TNFα production increases at elevated Ca²⁺ inward leak rates (see Fig. 9). The increased cytosolic Ca²⁺ load can arise from an arbitrary source, such as Ca²⁺ selective ionophores, which can increase mRNA expression independent of toll‐like receptor signalling or purinergic receptor activation (Kataoka et al. 2009). A primary goal of our model was therefore to couple the Ca²⁺ current carried by activated P2X receptors to the intracellular Ca²⁺ pool.

Our model found that cytosolic Ca²⁺ is strongly buffered, with as much as 90% of the inward Ca²⁺ buffered within the cytosol. This percentage is estimated by comparing the Ca²⁺ entering the cell via P2X channels vs. measurements of free Ca²⁺ reported in the literature. This high level of buffering is typical of a variety of eukaryotic cells (Berridge et al. 2003). Although we are unable to attribute the buffering to a specific set of Ca²⁺ proteins, candidates for buffering include CaM (Sola et al. 1997) and Iba‐1 (Ito et al. 2001). The Ca²⁺ buffering capacity of these components has not been characterized in microglia, and thus it is unclear if these contributions are sufficient to account for the 90% buffering of cytosolic Ca²⁺ we predict. For instance, intracellular ATP and SERCA may buffer a substantial portion of Ca²⁺ in microglia, as this is typical in cardiac cells (Bers, 2001). Similarly, the plasma membrane in cardiac cells contributes roughly 42 and 15 μM buffering through Ca²⁺ binding to low‐ (micromolar) and high‐affinity (sub‐micromolar) binding sites (Post & Langer, 1992). Given the large surface area to volume ratio in resting microglia (Beck et al. 2008), it is plausible that its plasma membrane exhibits similar buffering properties.

In addition to controlling the free Ca²⁺ inside the cells, mobile (non‐stationary) buffers such as the Ca²⁺ indicator Fura can influence the dynamics of Ca²⁺ fluctuations. Most notably, rapid equilibrium of a Ca²⁺ fluctuation with a mobile indicator can reduce the effective diffusion rate for Ca²⁺ (Wagner & Keizer, 1994), and lead to strongly heterogeneous Ca²⁺ transients, as we have previously shown for cardiomyocytes (Kekenes‐Huskey et al. 2012) For this study, the Fura concentrations we used were relatively low and thus the Ca²⁺ transients were not significantly altered (see Figs S6 and S7). However, it is important to note that the intracellular Fura concentrations are approximate, as it is difficult to quantitatively estimate how much indicator has entered the cell and how it is distributed within the cytoplasm.

We also found that the sensitivity of ATP‐triggered TNFα production increased at elevated Ca²⁺ inward leak rates (see Fig. 9). This behaviour is analogous to the positive correlation between TNFα production sensitivity and P2X expression, except here the change in cytosolic Ca²⁺ load can arise from an arbitrary source, such as treatment of microglial cells with Ca²⁺‐selective (Kataoka et al. 2009) or non‐selective ionophores (Hoffmann et al. 2003). In this regard and to a certain extent, diverse mechanisms that increase cytosolic Ca²⁺ load may comprise a positive feedback process, as the Ca²⁺‐dependent activation of genes that initially promote autocrinic activity or enhance Ca²⁺ channel current in principle can promote further gene expression. This feedback could provide a basis for an integrative activation of immune responses (Shieh et al. 2014), whereby both danger‐associated and pathogen‐associated molecular patterns must be presented to invoke an immune activity. However, such feedback is nuanced, as it has been demonstrated that pathogen‐mimetic LPS treatment blunts ATP‐mediated P2X responses (Hoffmann et al. 2003), and further model development is needed to investigate this hypothesis.

In general, PM Ca²⁺ currents are counterbalanced by Ca²⁺ extrusion mechanisms to maintain constant Ca²⁺ load at rest. In our study, modest levels of Ca²⁺ entry via P2X activation were compensated for by forward mode extrusion of intracellular Ca²⁺ via NCX. Given the slower rate of Ca²⁺ efflux via NCX relative to SERCA uptake, transient increases in ER Ca²⁺ load were apparent in our model (see Fig. S5). While IP₃ receptor‐mediated Ca²⁺ release was beyond the scope of this study, it is possible that the transient increases in ER Ca²⁺ load could lead to more frequent spontaneous or IP₃‐triggered ER Ca²⁺ release events (Kettenmann et al. 2011; Kettenmann et al. 2012). IP₃‐triggered ER Ca²⁺ release could lead to localized regions wherein Ca²⁺ is strongly elevated relative to bulk cytosol, which could disproportionally influence Ca²⁺ signal transduction pathways. Future models that account for the microglial morphology and spatial distribution of important signalling proteins may provide additional insights into microglial function.

Ca²⁺/CaM/CN/NFAT signal transduction

In microglia, CaM is linked to cytoskeletal remodelling (Szabo et al. 2016) and the activation of CN (Furman & Norris, 2014). The CN phosphatase is well established to play a significant role in glial physiological function, as reviewed by Furman & Norris (2014). In response to elevated cytosolic Ca²⁺ levels, CaM and CN activation ensues whereby NFAT is dephosphorylated. The dephosphorylated NFAT translocates to the nucleus, where it modulates transcription. Similar levels of NFAT activation are reported in microglia treated with a Ca²⁺ ionophore (A23187; Kataoka et al. 2009), which suggests that Ca²⁺ alone is sufficient to invoke this response. CN and NFAT activation are known to be dependent on stimulation frequency (Cooling et al. 2009; Bazzazi et al. 2015), thus it would be of interest to understand the relationship of NFAT‐driven TNFα expression in response to transient and sustained ATP stimuli. In this study, we specifically investigated the coupling between CN activation and dephosphorylation of NFAT, for which the latter is a substrate for TNFα transcription (Hide et al. 2000). We assumed in our model that full activation of CN proceeds through binding of Ca²⁺‐saturated CaM, as described by Saucerman & Bers (2008). We found that rates of TNFα production directly correlated with the CaM‐bound CN concentration and NFAT activation. Moreover, P2X stimulation at high frequency that led to sustained increases in cytosolic Ca²⁺ load were sufficient to maintain CN in an activated state capable of driving NFAT‐dependent TNFα production. Our computational model additionally indicated that inhibition of NFAT by nearly 100% substantially suppressed the TNFα mRNA production rate at 1 mM ATP, consistent with reported reductions in TNFα following treatment with the NFAT inhibitor VIVIT (Nagamoto‐Combs & Combs 2010; Rojanathammanee et al. 2015). Furthermore, our computational model showed similar reductions when inhibiting CN activity, which were comparable to reductions reported by Rojanathammanee et al. (2015) following 1 μM treatments of the CN inhibitor FK506. On the one hand, the ability of the computational model to capture both the Ca²⁺‐dependent activation of NFAT and the blunting of TNFα production by CaM, CN or NFAT inhibition exemplifies the exquisite coupling of gene expression in microglia to intracellular Ca²⁺ homeostasis, in addition to establishing the accuracy of the model. However, it is clear that additional regulatory mechanisms complicate this coupling, as pharmacological inhibition of CN and VIVIT does not completely suppress TNFα expression (Nagamoto‐Combs & Combs, 2010; Rojanathammanee et al. 2015).

ATP‐triggered TNFα synthesis

Our study focused on a representative cytokine associated with an activated microglial state. Our model for TNFα expression was phenomenological in form, but captured key stages of mRNA transcription, with phenomenological representations for translation. We assumed deterministic rate expressions for these stages, which were found to qualitatively reproduce TNFα ELISAs following microglia activation (Hide et al. 2000; Martinez‐Martinez & Redondo, 2004; Rojanathammanee et al. 2015), including following treatments with p‐p38, CN and NFAT inhibitors, as well as increased mRNA expression upon increasing PM Ca²⁺ leak in a manner analogous to ionophore treatment (Kataoka et al. 2009). The agreement between the deterministic models assumed here and the experimental measurements suggests that the modelled Ca²⁺‐dependent processes are abundant in number and are frequent. In contrast, we anticipate that measurements performed on an individual cell or perhaps on a subcellular basis would be fewer and less frequent, which advocates for stochastic approaches commonly used for modelling gene expression in other cell types (Gillespie, 1976).

Our model assumed that TNFα mRNA transcription is proportional to the nuclear content of dephosphorylated NFAT. Although it is clear from our analyses that the frequency and concentration of ATP application could modulate NFAT activation and TNFα mRNA transcription, the apparent dependence of TNFα translation and exocytosis on P2X7‐specific activation suggests that parallel regulatory mechanisms are required for microglial immune responses. More generally, it has been suggested that microglial activation is not ‘all or none’ and depends profoundly on the context of the activating stimuli (Hanisch & Kettenmann, 2007). Interestingly, TNFα is known to feedback on TNFα receptors localized to the microglia plasma membrane, thereby contributing to further TNFα biosynthesis and cytokine release (Kuno et al. 2005). It is plausible that transient ATP stimuli lead to brief P2X activation intervals that result in a limited exocytosed TNFα pool insufficient for autocrinic activity, whereas prolonged ATP exposure could promote sufficient TNFα release to active TNFα receptors. The former scenario may be appropriate for regulating synaptic plasticity mediated by TNFα (Stogsdill & Eroglu, 2017), especially given the quantile nature of ATP release exhibited by astrocytes (Lalo et al. 2014). In the latter scenario, however, released cytokines could lead to more robust activation of microglial cytokine receptors, thereby driving phenotypical changes that may represent the tipping point between acute and sustained microglial activation (Kuno et al. 2005).

A novel outcome of the study is the simulation of microglial Ca²⁺ and TNFα responses following pulsatile addition of ATP. These pulsatile ATP packets were intended to represent potential nucleotide concentrations and dynamics in neural synapses. We are aware that the in vivo microglial environment and corresponding microglial phenotype may be quite different to the in vitro conditions from which we derived data for training the model. With regard to the microglial environment, the transient ATP pools in neural synapses are shaped by the activity of ectonucleotidases localized to the synapse. A recent computational model by Sandefur et al. (2017) provides a compelling description of ectonucleotidase activity and corresponding effects on extracellular nucleotide concentrations. Nevertheless, microelectrode recordings reported by Lalo et al. (2014) suggested that the ATP packets were high frequency (>1 Hz) and of low micromolar concentrations (tens of μM), which validates our choice of ATP signatures in our model. Under those conditions we found that resting intracellular Ca²⁺ rose above basal levels and this was sustained for at least 20 s after the onset of those ATP pulses. We note that P2X4 desensitized over that interval, which probably explains why we did not see significant TNFα production over longer duration ATP exposures. In contrast, when we utilize 30‐fold higher P2X4 concentrations typical of LPS‐activated microglia (Toulme et al. 2010), we report significant Ca²⁺ transients and TNFα production. Hence, it is possible that P2X‐driven cytokine responses may be muted under physiological conditions, but upon activation of microglia by triggers similar to LPS upregulated P2X expression primes these cells for ATP‐initiated inflammatory responses.

Limitations

Our computational model used a minimal basis for linking microglial P2X activation with TNFα production. The model provides a starting point for augmentation with additional factors and refinement with new experimental data. Additional factors that could be considered in the model include microglial heterogeneity due to genetics, age and disease, cultured microglia vs. in vivo cells, as well as differences in the neuronal and glia populations in different regions of the CNS that influence the cell‐to‐cell interactions. Our study examined P2X activation given their importance in microglia activation and inflammatory responses. Hence, quantitative assessments of P2X4 and P2X7 expression and their respective contributions to intracellular Ca²⁺ entry in microglia preparations would be invaluable to improve our model. Moreover, P2Y receptors are also highly expressed in resting microglia and respond to micromolar ATP concentrations (Hide et al. 2000). Upon activation, this subfamily of G‐protein coupled receptors promote phospholipidase C activity and subsequent IP₃ production that potentiates IP₃ receptor‐mediated ER Ca²⁺ release. IP₃ receptor‐mediated ER Ca²⁺ release has been described by Skupin et al. (2008), which contributes to stochastic and highly heterogenous oscillatory Ca²⁺ spiking that could augment deterministic transients arising from ionotropic Ca²⁺ channel activation. Furthermore, including such an IP₃ signalling model, Skupin et al. (2008) provided descriptions of receptor activation including that of toll‐like receptors by LPS as a prototypical example of microglial responses to pathogen‐associated molecular patterns (Hu et al. 2014). It is expected that including both P2X‐ and P2Y‐mediated responses, as well as a realistic model of ectonucleotidase activity (Sandefur et al. 2017) and associated regulation of synaptic nucleotide pools, would constitute a significant step toward modelling in vivo microglia activity. It is reported, however, that in some cells lines like BV2 P2Y effects on intracellular Ca²⁺ responses are small, especially compared to those mediated by P2X channels (Gilbert et al. 2016). For this reason, our initial model of microglia Ca²⁺‐dependent function may be particularly applicable to P2X‐specific signalling in commonly used cell lines such as BV2 that have insignificant P2Y activity.

In addition to intracellular IP₃ receptor‐mediated Ca²⁺ production, we omitted store operated Ca²⁺ entry (SOCE). SOCE describes a mechanism by which depletion of ER Ca²⁺ is sensed by Stromal interaction molecule 1 (STIM1), after which activated STIM promotes extracellular Ca²⁺ entry by binding ORAI1 (Kettenmann et al. 2011). SOCE is prominent in microglia and is known to increase steady‐state Ca²⁺ influx following prolonged ATP treatments (Kettenmann et al. 2011). However, under the conditions considered in our model, our predictions demonstrated minimal changes in ER Ca²⁺ load, given the absence of IP₃ receptor‐mediated release. Therefore, we do not anticipate contributions from SOCE that would influence the model predictions under the stimuli we considered. We note that introducing this contribution to cytosolic Ca²⁺ handling in subsequent models would be advantageous for examining how long‐lived elevations in Ca²⁺ load control activated microglial responses, including the release of cytokines, chemokines, nitric oxide as well as reactive oxygen species (Stebbing et al. 2015).

Beyond purinergic receptors, myriad plasma membrane channels have been identified in microglia. Many of these channels, particularly those controlling potassium transmembrane currents (Nguyen et al. 2017), have altered expression levels depending on the maturity and potential pathological state of the microglial cell (Eder, 1998). Given the prominent role of potassium channels in determining the membrane potential, we could expect phenotype‐dependent changes in the electrogenic driving forces governing voltage‐gated channel and exchanger activity. For instance, although our model demonstrates that NCX operates in forward mode to extrude cytosolic Ca²⁺, hyper‐polarization of the membrane potential could induce reverse‐mode NCX activity that would increase intracellular Ca²⁺ load. Overall, inclusion of channels that overwhelmingly control microglia membrane potentials would permit more detailed examinations of microglia activation and phenomena in pathological states.

A limitation of this phenomenological model for the Ca²⁺‐dependent phosphorylation of p38 is that the Ca²⁺ dependency of activation is indirect and probably mediated by upstream kinases for which corresponding quantitative data in microglia are scarce. Wright et al. (2007) demonstrated in skeletal muscle that CaMK inhibition prevented the Ca²⁺‐dependent phosphorylation of p38, and thus similar Ca²⁺‐dependent kinases in microglia upstream of p38 may participate in regulating p‐p38. p38 phosphorylation is strongly associated with a variety of cytokines, most notably interleukins, as well as the neurotrophic factor brain‐derived neurotrophic factor (BDNF) and probably involve pathways independent of Ca²⁺ (Ji & Suter, 2007). For this reason, refinement of these potentially Ca²⁺‐independent pathways in our model would represent an important step toward quantifying chemokine and cytokine responses in microglia.

Our model of TNFα expression assumed NFAT‐dependent mRNA production, followed by degradation (Shiratori et al. 2010) and translation processes that were phenomenologically dependent on p38 phosphorylation. However, there exist a variety of regulatory mechanisms of gene expression and exocytosis that were not considered in this study. For instance, extracellular signal‐regulated kinases (ERKs) and JNK inhibition in microglia has been demonstrated to both reduce CXCL2 mRNA expression and TNFα exocytosis (Hide et al. 2000) following P2X7 activation (Shiratori et al. 2010). Hence, it is plausible that several mitogen‐activated protein kinases (MAPKs) work in tandem to finely control TNFα mRNA expression. Additionally, translation of expressed TNFα mRNA and its eventual exocytosis is tightly regulated by diverse trafficking and secretion pathways, as reviewed by Stanley & Lacy (2010) for TNFα release in macrophages. Refinement of our model to include such pathways, as well as their differential regulation by P2X7 vs. P2X4, could elucidate the cocktail of stimuli required for encoding specific patterns of microglia‐secreted signalling molecules.

Conclusions

In this study, we developed a computational model of Ca²⁺ handling in microglia that links ATP‐dependent activation of P2X4 and P2X7 activation to production of a representative cytokine, TNFα. We validated this model against a wealth of experimental data collected for these purinergic receptors as well as intracellular components that regulate Ca²⁺ homeostasis and gene expression. We have demonstrated using this model how the temporal signature of ATP activation influences the ability to evoke TNFα production. Furthermore, we examined how variation of the expression of microglia proteins considered to this model impacts the ATP‐sensitivity of TNFα production, so as to provide insight into how microglia respond and adapt to their environment. We anticipate that this model will be invaluable in generating and testing hypotheses pertaining to microglial physiology at a systems level, as has been demonstrated in other computational models of mammalian cellular function (Winslow et al. 2012).

Additional information

Preprint Publication Information

This article was first published as a preprint: Chun, B., Stewart, B., Vaughan, D., Bachstetter, A. & Kekenes‐Huskey P. (2018). Simulation of P2X‐mediated calcium signalling in microglia. bioRxiv. https://doi.org/10.1101/354142

Supporting information

Supplementary Table S1. Reactions used in the computational microglia model

Supplementary Table S2. Experimental data and ATP stimuli used for model validation

Supplementary Table S3. Markov State Parameters for P2X4 and P2X7 Receptors used to generate Fig. 3A. The rest of parameters for P2X7 is given in Sect. A.3.1

Supplementary Table S4. Reversal potentials and channel densities used in Markov State models of P2X4 and P2X7 receptors: fitted to individual P2X channels Toulme and Khakh (2012); Chessell et al. (1997) in Fig. 2

Supplementary Table S5. Parameters used in Markov State Models of P2X7 receptor: fitted to inward current measured from P2X7 channels by Chessel et al. (1997) in Fig. 2B

Supplementary Table S6. Parameters for Calculations associated with Buffers Parameter

Supplementary Table S7. Parameters for NCX and SERCA Calculations

Supplementary Table S8. Parameters for p38/NFAT Cycle/TNFα Gene Expression Calculations

Supplementary Table S9. Other Parameters in Calculations

Supplementary Table S10 Initial States in Calculations

Supplementary Figure S1 Markov model used for P2X channels in this study (full), for which the Q1/Q2 and D3/D4 states of Zemkova et al. (2015) model (lumped) are consolidated into the ‘macro states’ Q12 and D34. Predictions of the Q12 ‘macrostate’ relative to the original Q1 and Q2 states is shown in Fig. S2

Supplementary Figure S2 Comparison of model implemented from full Zemkova et al. (2015) model and the lumped model version used in this study. Predicted currents using the full model (red solid) and our reduced model (green bead)

Supplementary Figure S3. Outward Ca²⁺ current from NCX as a function of the cell membrane potentials. Model predictions (solid) compare well with experimental data reported in Boscia et al. (2009) (dashed)

Supplementary Figure S4. Predicted active calcineurin (denoted as active CN) with respect to two distinct stimulation pulses: single pulse and pulse with a frequency of 0.5 Hz. The simulated Ca²⁺ intervals in this figure were chosen to resemble those of Bazzazi et al. but are not quantitatively identical, given that the Bazzazi data was obtained using HEK cells. Given these Ca²⁺ transients, the timescales for rapid Ca²⁺‐dependent CN activation and delayed decline relative to the Ca²⁺ transients are shown and are analogous to comparable measurements from Bazzazi et al. (2015)

Supplementary Figure S5. Predicted Ca²⁺ concentration transients in ER domain, subject to ATP treatment conditions shown in Fig. 3

Supplementary Figure S6. Predicted Ca²⁺ concentration transients with and without Fura2 in cytoplasm, subject to ATP treatment conditions shown in Fig. 3

Supplementary Figure S7. Predicted Ca²⁺ concentration buffered by given compounds in the model, subject to ATP treatment conditions shown in Fig. 3

Supplementary Figure S8. Cytosolic Ca²⁺ transients as a function of ATP pulse frequencies (rows) and ATP concentration (columns) as applied for 20 seconds with TNFa responses shown in the final column

Supplementary Figure S9. Left) Genetic algorithm guesses for P2X4 parameter H2. Right) Predicted current relative to Toulme et al.data (truth)

Biography

Byeongjae Chun is a postdoctoral researcher in the Department of Chemistry at the University of Kentucky. He received his BSc in Chemical Engineering from the University of Texas at Austin in 2011 and PhD in Chemical & Biomolecular Engineering from Georgia Institute of Technology in 2015. His PhD thesis is based on characterizing polymeric materials using molecular dynamics simulation, which led to his first postdoctoral research in computational biophysics at the School of Physics, Georgia Institute of Technology. The current direction of his research is toward correlating calcium cascades to physiological responses in microglial cells.