Partitional calorimetry

Abstract

For thermal physiologists, calorimetry is an important methodological tool to assess human heat balance during heat or cold exposures. A whole body direct calorimeter remains the gold standard instrument for assessing human heat balance; however, this equipment is rarely available to most researchers. A more widely accessible substitute is partitional calorimetry, a method by which all components of the conceptual heat balance equation—metabolic heat production, conduction, radiation, convection, and evaporation—are calculated separately based on fundamental properties of energy exchange. Since partitional calorimetry requires relatively inexpensive equipment (vs. direct calorimetry) and can be used over a wider range of experimental conditions (i.e., different physical activities, laboratory or field settings, clothed or seminude), it allows investigators to address a wide range of problems such as predicting human responses to thermal stress, developing climatic exposure limits and fluid replacement guidelines, estimating clothing properties, evaluating cooling/warming interventions, and identifying potential thermoregulatory dysfunction in unique populations. In this Cores of Reproducibility in Physiology (CORP) review, we summarize the fundamental principles underlying the use of partitional calorimetry, present the various methodological and arithmetic requirements, and provide typical examples of its use. Strategies to minimize estimation error of specific heat balance components, as well as the limitations of the method, are also discussed. The goal of this CORP paper is to present a standardized methodology and thus improve the accuracy and reproducibility of research employing partitional calorimetry.

INTRODUCTION

Calorimetry—the measurement of heat transfer—is an integral tool for thermal physiologists in the assessment of human heat balance. Beginning in the nineteenth century, interest in human metabolic energy expenditure and human-environmental heat exchange led to the development of whole body direct calorimeters, which involved measurements of heat dissipation from a human subject enclosed inside a sealed, insulated chamber (for a thorough historical review of direct calorimetry, see Ref. 54). Although direct calorimetry remains the gold standard for assessing human heat balance, it remains largely inaccessible because of the high costs of construction/maintenance and technical issues. Moreover, certain types of human thermoregulatory research are not best performed in a direct calorimeter, including clothing studies (because of clothing-related alterations in the latent heat of vaporization of sweat), studies requiring the separation of radiant and convective heat exchanges (because of the inability to separate dry heat exchange into its individual components), and assessment of thermoregulatory responses to different physical activities (because of size limitations of typical direct calorimeter chambers). An alternative approach that overcomes these issues is “partitional” calorimetry. First introduced in 1936 by Winslow et al. (94), partitional calorimetry is a method by which each avenue of human heat exchange can be calculated separately based on fundamental physical laws governing dry and latent heat transfer. Such estimations can be performed in laboratory or field settings (i.e., without the need of a chamber) with relatively inexpensive equipment. Over the last 80 years, partitional calorimetry has been used to address a variety of topics in thermal research. Examples include predicting the physiological compensability (i.e., the ability to attain a balance between the rates of internal heat production and net heat dissipation) of a given combination of activity, clothing, and climate, which is a key requirement for predicting human heat strain and heat-illness risk in occupational and sport-related settings (7, 9, 31, 45, 48); determining fluid replacement requirements during prolonged activity and heat stress (31a, 31b, 31c); the accurate quantification of metabolic heat production and the evaporative requirements for human heat balance to compare time-dependent core temperature and sweating responses between different individuals or groups (20, 27, 50); estimating changes in body heat storage and thermoregulatory effector responses attributable to warming or cooling interventions (21, 54, 82); the determination of clothing properties (10); and deriving heat transfer coefficients (95).

For investigators considering the use of partitional calorimetry to assess elements of human heat balance, this Cores of Reproducibility in Physiology (CORP) article provides basic equations to estimate avenues of human-environmental heat exchange, discusses the various sources of error and limitations of partitional calorimetry, and provides some real-world examples that may assist investigators in the use of partitional calorimetry.

HOW TO ASSESS EACH COMPONENT OF THE HEAT BALANCE EQUATION THROUGH PARTITIONAL CALORIMETRY

The fundamental human heat balance equation states

$$\text{S}=\text{M}-\text{Wk}-\text{R}-\text{C}-\text{K}-\text{E\hspace{0.17em}}\left(\text{W}\right)$$ (1)

where S is the rate of body heat storage; M is metabolic rate; Wk is external work rate; R, C, and K represent the rates of dry heat transfer via radiation, convection, and conduction, respectively; and E represents the rate of evaporative heat dissipation. Heat transfer via radiation and conduction occurs solely from the skin surface (R_skin and K_skin), whereas heat transfer via convection and evaporation occurs from the skin surface (C_skin and E_skin) and the respiratory tract during pulmonary ventilation (C_res and E_res). All terms are expressed in watts, which is the SI unit for energy exchange.

Estimating Heat Production

Internal metabolic heat production (H_prod) is determined by subtracting the rate of any external work performed (Wk) from the concurrent rate of metabolic energy expenditure (M):

$${\text{H}}_{\text{prod}}=\text{M}-\text{Wk\hspace{0.17em}}\left(\text{W}\right)$$ (2)

Metabolic energy expenditure.

Although direct calorimetry has been used to estimate human metabolic rate (19), contemporary laboratories estimating human metabolic energy expenditure use indirect calorimetry based on rates of oxygen consumption (V̇o₂) and carbon dioxide production (V̇co₂) and accounting for macronutrient energy equivalents. Expired gases may be captured in Douglas bags, with mean V̇o₂ and V̇co₂ values subsequently estimated with samples analyzed for O₂ and CO₂ content as well as temperature-adjusted volumes. Increasingly common in laboratories across the world has been the use of precision metabolic testing systems to derive these values by analyzing expired gases sampled either breath by breath or from a mixing box.

For every 1 liter of oxygen that is consumed to catabolize carbohydrates, 21.13 kJ (5.05 kcal) of energy is released, whereas the consumption of 1 liter of oxygen to catabolize fat yields 19.62 kJ (4.69 kcal) of energy (16, 61, 97). The proportion of each fuel source used therefore influences M for a given V̇o₂ (Table 1). If carbohydrates are exclusively utilized CO₂ is generated in amounts equal to the volume of O₂ consumed [i.e., a respiratory exchange ratio (RER) of 1.00], whereas a fat-only fuel source returns a RER of 0.70. Thus M can be calculated as

$$\begin{array}{l}\text{M}={\text{VO}}_2\cdot \frac{\left\{\left[\left(\frac{\text{RER}-\text{0.7}}{\text{0.3}}\right)\cdot \text{21.13}\right]\text{+}\left[\left(\frac{\text{1.0}-\text{RER}}{\text{0.3}}\right)\cdot \text{19.62}\right]\right\}}{\text{60}}\cdot \text{1,000\hspace{0.17em}}\left(\text{W}\right)\end{array}$$ (3)

where V̇o₂ is measured in liters per minute. At rest (V̇o₂ ~0.25 l/min), RER values remain low at ~0.75 when fasted (57), increase to ~0.85 in the postprandial state (23, 32), and approach values of 1.00 in clinical conditions such as septic shock (29). With elevations in V̇o₂ from rest (e.g., exercise), RER values of ~0.85 are typical of low-to-moderate work intensities and increase to values approaching ~1.00 at higher intensities (8). Notable exceptions include athletes adapted to high-fat diets (11) or shivering in a glycogen-depleted state (33), which cause substantial elevations in V̇o₂ but RER values that remain closer to 0.70.

Table 1.

Proportion of carbohydrates and fats utilized for different RERs and associated metabolic energy expenditure for different rates of absolute oxygen consumption

Carb %	0	10	20	30	40	50	60	70	80	90	100
Fat %	100	90	80	70	60	50	40	30	20	10	0
RER	0.70	0.73	0.76	0.79	0.82	0.85	0.88	0.91	0.94	0.97	1.00
Metabolic Energy Expenditure, W
V̇o2
0.5 l/min	164	165	166	167	169	170	171	172	174	175	176
1.0 l/min	327	330	332	335	337	340	342	345	347	350	352
1.5 l/min	491	495	498	502	506	510	513	517	521	525	528
2.0 l/min	654	659	664	669	674	679	684	689	694	699	704
2.5 l/min	818	824	830	837	843	849	855	862	868	874	880
3.0 l/min	982	989	997	1,004	1,012	1,019	1,027	1,034	1,042	1,049	1,057

Summary table of proportion of carbohydrates (Carb %) and fats (Fat %) utilized for different respiratory exchange ratios (RERs) and the associated metabolic energy expenditure for different rates of absolute oxygen consumption (V̇o₂)

Estimates of metabolic energy expenditure via indirect calorimetry rely on the assumption that metabolic energy is derived from oxidative rather than nonoxidative (i.e., anaerobic) energy sources. However, this may not be the case during, for example, high-intensity exercise. To maximize the accuracy of indirect calorimetric estimates of metabolic energy expenditure, investigators should consider prescribing experimental conditions that ensure that metabolic energy is overwhelmingly of oxidative origin. This can be achieved by ensuring that workloads do not lead to RER values >1.00 and/or elevations in blood lactate concentration. If RER values >1.00 are observed, the energy equivalent for carbohydrate (21.13 kJ/l O₂) must be used only. Estimates of total metabolic energy expenditure may be improved by adding the estimated nonoxidative contribution, which can be assessed from the calculated oxygen debt by subtracting the cumulative O₂ uptake during 60 min of recovery from the values measured across the same time frame during preexercise rest (5).

Steady-state V̇o₂ values measured with modern metabolic testing systems have been reported to be accurate within ±3% (72). Measurement error is smaller with a mixing chamber compared with a breath-by-breath sampling technique (6). Given that the maximum difference in M between utilizing exclusively carbohydrates or only fats is only 1.5 kJ per liter of O₂ consumed, assuming a fixed energy yield of 21 kJ/l O₂ (equivalent to a RER of ~0.97) or 20.38 kJ/l O₂ (equivalent to a RER of ~0.85) are potentially acceptable options in the event that CO₂ production cannot be sampled. However, such assumptions inflate the potential measurement error for M by as much as an additional ~4–7%.

External workload.

This parameter can be most easily regulated and measured in a laboratory environment with a cycle ergometer. Values for Wk can be calculated for traditional ergometers by multiplying the force generated (in N) to overcome the resistance of the wheel by the speed of the ergometer belt (in m/s). Some modern electromagnetically braked ergometers (e.g., Lode) enable the maintenance of a constant external workload irrespective of pedaling cadence, usually within a given range (e.g., 30–150 rpm). The accuracy of these ergometers is within 3 W for workloads between 7 and 100 W and 3% for workloads between 100 and 500 W.

If treadmill running instead of cycle ergometry is employed as an exercise mode, the proportion of metabolic energy that is converted into mechanical work is much lower. External work is ~0 W when running on a flat surface, as the propulsion and braking forces of gait lead to equal amounts of positive and negative work, respectively (85). The external work performed on a graded treadmill remains relatively small but can be calculated with (28)

$$\text{Wk}=9\text{.}81\cdot m\cdot v_{\text{tr}}\cdot \text{F\hspace{0.17em}}\left(\text{W}\right)$$ (4)

where 9.81 represents gravitational acceleration (m/s²), m is total body mass (kg), v_tr is treadmill belt velocity (m/s), and F is the treadmill gradient defined as the fraction of vertical displacement (in m) for every 100 m of treadmill belt rotation (i.e., % grade/100). Estimation error for this calculation can be largely minimized by calibrating treadmill belt velocity before testing (i.e., measuring the treadmill belt length and then the time required to complete a fixed number of belt cycles) rather than relying on the treadmill console speed setting.

Heat Exchange at the Skin Surface

Heat and mass flows from the skin surface to a surrounding air medium follow the general equation of

$$\text{heat\hspace{0.17em}or\hspace{0.17em}mass\hspace{0.17em}loss}=\text{gradient/resistance\hspace{0.17em}}\left(\text{W}\right)$$ (5)

For dry heat loss, the gradient is a temperature differential between the skin surface and the surrounding environment, and resistance refers to the barrier to dry heat loss imposed by clothing insulation and the adjacent air layer. Under hot conditions in which the ambient temperatures exceed skin temperature, the thermal gradient is negative, and thus convective and/or radiative heat loss will be negative (i.e., heat gain); in other words, heat will flow toward the body rather than away from it. For mass loss and the attendant rate of evaporative heat dissipation, the gradient is the difference in water vapor pressure between the skin and ambient air, and resistance is determined by the permeability of clothing and the surrounding air layers to water vapor. Under extremely humid conditions in which ambient water vapor pressure exceeds that of the saturated skin surface, the vapor pressure gradient is negative, but the rate of evaporative heat dissipation would be zero since heat cannot be gained by evaporation.

Estimating Dry Heat Exchange at the Skin Surface

Dry heat exchange at the skin surface (H_{dry_skin}) can theoretically occur via three different avenues: convection (C_skin), radiation (R_skin) and conduction (K_skin):

$${\text{H}}_{\text{dry}\_\text{skin}}={\text{C}}_{\text{skin}}+{\text{R}}_{\text{skin}}+{\text{K}}_{\text{skin}}\left(\text{W}\right)$$ (6)

Conduction.

For most indoor and outdoor exercise studies conduction is considered negligible, as the surface area of skin in direct contact with a solid surface (e.g., feet with ground) is typically small for the majority of activities, and even these skin surfaces are usually insulated (e.g., footwear). However, conduction may represent a major source of heat gain/loss during prolonged exposures to objects hotter or colder than skin temperature, for example, postoperative warming blankets (30), prerace cooling with ice vests (44), or sleeping outdoors in a poorly insulated sleeping bag.

Internal conductive heat exchange can transiently occur after the ingestion of a hot or cold fluid. The amount of heat energy exchanged between an ingested fluid and the body as it equilibrates with body temperature is determined by the temperature of the fluid relative to core temperature, the ingested volume, and the specific heat capacity of the fluid (e.g., water: 4.184 kJ⋅kg⁻¹⋅°C⁻¹).

Convection and radiation.

Convective and radiative heat losses are driven by a temperature difference between the skin surface (t_sk) and ambient air (t_a) (for convection) and mean radiant temperature (t_r) (for radiation). When t_a and t_r are lower than t_sk, these dry heat transfer avenues transport heat away from the body. Conversely, if t_a and/or t_r exceed t_sk, the direction of these pathways is reversed, with heat driven from the environment toward the body. It is most convenient to collectively calculate combined dry heat transfer from the skin via convection and radiation and express the temperature characteristics of the ambient environment with operative temperature (t_o) (96). Note that if there is no additional source of thermal radiation present (e.g., in a laboratory chamber), then t_a ≈ t_r ≈ t_o, and the calculation of t_o is therefore not necessary.

$${\text{t}}_{\text{o}}=\frac{\left({\text{h}}_{\text{r}}{\text{t}}_{\text{r}}{\text{\hspace{0.17em}+\hspace{0.17em}h}}_{\text{c}}{\text{t}}_{\text{a}}\right)}{\left({\text{h}}_{\text{r}}{\text{\hspace{0.17em}+\hspace{0.17em}h}}_{\text{c}}\right)}\left(°\text{C}\right)$$ (7)

where h_c is the convective heat transfer coefficient and h_r is the radiative heat transfer coefficient. The value of h_c depends on numerous factors such as air velocity, the nature of the airflow, movement velocity, posture, barometric pressure, and clothing (26, 42). Thus valid estimations of h_c depend on the use of equations appropriate for the experimental conditions (see Table 2 for examples).

Table 2.

Example equations to calculate the convective heat transfer coefficient with minimal clothing

Activity	Equation	Considerations	References
Seated	hc = 3.1	vair < 0.2 m/s	(36)
Seated	hc = 8.3·$v_{\text{air}}^{0.6}$	0.2 < vair < 4.0 m/s	(36)
Treadmill walking	hc = 6.5·$v_{\text{tr}}^{0.39}$	vair < 0.2 m/s	(73)
Cycle ergometry	hc = 8.3·(0.07 + 0.0043·fped + vair)0.86		(60)
Cycle ergometry	hc = 5.5 + 1.96·$v_{\text{air}}^{0.86}$	vair < 0.2 m/s	(25, 73)

Example equations to calculate the convective heat transfer coefficient (h_c; W·m⁻²·°C⁻¹) with minimal clothing. v_air, Air velocity (m/s); v_tr, treadmill velocity (m/s); f_ped, pedaling frequency (revolutions/min). Note that at altitudes above sea level, h_c must be corrected for the reduction in barometric pressure (P_b) by a factor of (P_b/760)^0.55 (26).

In most indoor conditions, h_r may be assumed to be 4.7 W⋅m⁻²⋅K⁻¹ (3). However, a more precise value may be calculated with the standard equation:

$${\text{h}}_{\text{r}}=\text{4εσ}\frac{A_{\text{r}}}{A_{\text{D}}}{\left[\text{273.2\hspace{0.17em}+\hspace{0.17em}}\frac{{\text{t}}_{\text{sk}}{\text{+t}}_{\text{r}}}{\text{2}}\right]}^{\text{3}}\left(\text{W}\cdot {\text{m}}^{-2}\cdot \text{K}\right)$$ (8)

where ε is the nondimensional emissivity of the body surface, assumed to be 0.95 for clothed skin and 0.98 for exposed skin (34), σ is the Stefan-Boltzmann constant (5.67 × 10⁻⁸ W⋅m⁻²⋅K⁻⁴), and A_r/A_D is the fraction of the body surface participating in radiative heat transfer and determined by posture. Accepted values for A_r/A_D are 0.70 for sitting and 0.73 for standing (88, 95), with similar values reported for walking and standing and between men and women (43).

The original version of the equation for h_r above (Eq. 8) clearly states that the surface temperature of clothing (t_cl) should be used to derive h_r instead of t_sk. However, given that t_cl must be derived through an iterative procedure (75) and that under all combinations of t_a and t_r between 0 and 55°C coupled with air velocities between 0.2 and 4.0 m/s and dry clothing insulation between 0.0155 (0.1 clo) and 0.3875 (2.5 clo) m²⋅°C⋅W⁻¹ there is less than a 2 W/m² difference in estimated dry heat loss, t_cl can be more simply substituted with t_sk, which is a standard physiological measurement (see below).

The derived operative temperature is then used to estimate combined dry heat loss via convection and radiation with

$${\text{C}}_{\text{skin}}+{\text{R}}_{\text{skin}}=\frac{\left({\text{t}}_{\text{sk}}-{\text{t}}_{\text{o}}\right)}{\left({\text{R}}_{\text{cl}}\text{\hspace{0.17em}+\hspace{0.17em}}\frac{\text{1}}{\text{h}\cdot {\text{f}}_{\text{cl}}}\right)}\cdot A_{\text{D}}\left(\text{W}\right)$$ (9)

R_cl is the dry heat transfer resistance of clothing in square meters times degree Celsius per watt, values of which can be either derived from “clo” units (1 clo = 0.155 m²⋅°C⋅W⁻¹) given in tables provided by the International Organization for Standardization (ISO) 9920 standard (49), or more precisely measured directly on a thermal manikin. For a typical athletic t-shirt-shorts-socks-shoes clothing combination, an R_cl value of ~0.03 m²⋅°C⋅W⁻¹ might be expected (64). It should be emphasized that R_cl only represents the intrinsic insulation of clothing and does not include the insulative effect of the surrounding air layer. A_D is body surface area (in m²) calculated with the standard DuBois equation (22) based on an individual’s height and body mass; h is the combined convective heat transfer coefficient (in W⋅m⁻²⋅K⁻¹), which is simply calculated as h_c + h_r; f_cl is the clothing area factor, which describes the extent to which the surface area for heat exchange is increased because of clothing and can be estimated by assuming a correlation between the increase in area factor and the R_cl of a clothing ensemble with 1 + (2 × R_cl) (64). As noted above, it is important to recognize that the sum of C_skin and R_skin can be either positive or negative, indicating heat loss or gain, respectively.

The principal measurements to complete Eqs. 7–9 (and those in Table 2) are ambient temperature (t_a), mean radiant temperature (t_r), ambient air velocity (v_air), and mean skin temperature (t_sk). Although these are all standard measurements in most environmental physiology laboratories, it is important that an appropriate procedure is used and any inherent limitations understood in order to minimize the estimation error of C_skin and R_skin.

Ambient temperature should always be measured in a well-ventilated space with a sensor mounted at an appropriate height (e.g., level with participant’s chest). To prevent the effects of proximity to a warm body via radiation and convection, the sensor should be shielded, at a sufficient distance from the participant (e.g., 50 cm), and placed upstream of any airflow directed toward the participant. Standard thermistors report temperatures with an accuracy of ±0.2°C (84), whereas class 1 T-type (copper/constantan) thermocouples are reported to yield values with an accuracy of ±0.5°C. For chamber-based laboratory studies t_a values logged by chamber environmental control software should not be used for calculations, as these measurements have the potential to deviate substantially from the temperature of the air surrounding the participant.

Mean radiant temperature in most indoor laboratory environments can be assumed to be approximately equal to t_a unless there is any substantial source of thermal radiation. In the event that t_r needs to be quantified, a standard 150-mm-diameter black globe is used to measure black globe temperature (t_g). The accuracy of t_g measurements will, similarly to measurement of t_a, be dependent on the type of thermometer used; however, calibration of individual temperature sensors can improve accuracy. Values for t_r are then derived with the following equation, which also requires t_a and v_air (47):

$${\text{t}}_{\text{r}}={\left[{\left({\text{t}}_{\text{g}}\text{+273}\right)}^{\text{4}}\text{\hspace{0.17em}+\hspace{0.17em}}\frac{\text{1.1}\cdot {\text{10}}^{\text{8}}{v}_{\text{air}}^{0.6}}{\text{0.44}}\cdot \left({\text{t}}_{\text{g}}-{\text{t}}_{\text{a}}\right)\right]}^{\text{0.25}}-\text{273\hspace{0.17em}}\left(°\text{C}\right)$$ (10)

Note that black globe temperature for a given intensity of thermal radiation is altered by air velocity across the globe surface; therefore, the black globe thermometer should be positioned appropriately so that it is exposed to the same environmental airflow as the participant.

Air velocity can be measured with a hot-wire anemometer, which can yield values with an accuracy of ±0.015 m/s. However, linear air velocity measurements in free airspace can differ substantially from the often turbulent flow of air across the skin surface, particularly when airflow is augmented by fans placed in front of a participant and even more so when a particular body region is specifically targeted.

Mean skin temperature can be estimated with a weighted average of local skin temperature measurements (via thermocouples or thermistors). A recent systematic review (62) demonstrated that the accuracy of local temperature measurements is dependent on attachment type, applied pressure, and environmental conditions, but most methods yield values with an accuracy within ±1.0°C. Although the weighting factors used in the estimation of mean skin temperature are typically related to the regional distribution of body surface area, careful consideration should be given to the number of sites included in the estimation. As noted by Mitchell and Wyndham (65), the best estimation of mean skin temperature will be determined based on a large number of measurement sites, but an estimate derived from the fewest possible number of sites will be easier in practice. Since local skin temperatures show greater heterogeneity in cool conditions and, conversely, greater homogeneity in the heat (36, 65), it has been recommended that mean skin temperature estimates should include more than seven sites in the cold, four to eight sites in neutral conditions, and three or four sites in warm/hot conditions (71, 76). Commonly used mean skin temperature equations are presented in Table 3.

Table 3.

Commonly used weighting factors to estimate mean skin temperature

Measurement Site	Hardy and DuBois (35) 12 Sites	ISO 9886 (46) 8 Sites	Hardy and DuBois (35) 7 Sites	Taylor et al. (89) 6 Sites	Ramanathan (77) 4 Sites
Forehead	0.07	0.07	0.07
Shoulder		0.07			0.30
Triceps		0.07
Dorsal forearm	0.14		0.14
Dorsal hand	0.05	0.05	0.05
Chest	0.0875	0.175		0.22	0.30
Abdomen	0.0875		0.35	0.14
Scapula	0.0875	0.175		0.21
Lower back	0.0875			0.19
Anterior thigh	0.095	0.19	0.19	0.14	0.20
Posterior thigh	0.095
Shin	0.065		0.13		0.20
Calf	0.065	0.20		0.11
Dorsal foot	0.07		0.07

Estimating Heat Loss from Respiration

Respiratory heat loss (H_res) occurs via convection and evaporation. As air is inhaled, it is quickly warmed to body temperature and saturated with water vapor, so the amount of net respiratory heat loss is dependent upon the ambient temperature and humidity of inspired air. Other factors that influence H_res include the volume of air that is moved in and out of the lungs every minute (i.e., minute ventilation) and air density (13). For studies other than those performed at altitude, differences in air density are insufficient to independently result in a meaningful alteration to respiratory heat loss, and minute ventilation is adequately associated with the rate of metabolic energy expenditure (M) to use it as a proxy for the purposes of estimating H_res (59, 63, 91):

$${\text{H}}_{\text{res}}={\text{C}}_{\text{res}}+{\text{E}}_{\text{res}}\left(\text{W}\right)$$ (11)

$${\text{C}}_{\text{res}}=0.001516\cdot \text{M}\left(\text{28.56}+\text{0.641}\cdot {\text{P}}_{\text{a}}-0.885\cdot {\text{t}}_{\text{a}}\right)\left(\text{W}\right)$$ (12)

$${\text{E}}_{\text{res}}=0.00127\cdot \text{M}\left(\text{59.34}+\text{0.53}\cdot {\text{t}}_{\text{a}}-11.63\cdot {\text{P}}_{\text{a}}\right)\left(\text{W}\right)$$ (13)

where M is metabolic energy expenditure (in W); t_a is inspired air temperature (in °C); and P_a is the vapor pressure of inspired air (kPa).

Estimating Evaporative Heat Loss from the Skin Surface

The evaporation of sweat secreted onto the skin surface (H_{evap_skin}) is the primary avenue of heat loss during exposure to warm/hot environments, particularly during exercise (70). The estimation of evaporative heat loss therefore requires accurate measurements of 1) whole body sweat loss and 2) the fraction of secreted sweat that evaporates from the skin surface (i.e., sweating evaporative efficiency, or simply “sweating efficiency”).

A standard methodology for measuring whole body sweat loss through changes in body mass has been comprehensively described in a recent CORP paper (17) and is therefore not repeated here. Since the evaporation of 1 g of sweat off the skin liberates 2,426 J of latent heat energy (93), the transformation of sweat loss (in g) into evaporative heat loss (in J), if it all evaporates (i.e., sweating efficiency is 100%), can be simply calculated by multiplying each gram of sweat by 2,426. Minute-by-minute estimates of sweating and evaporative rates with the same time resolution may be performed with a Potter balance, which continuously measures body mass changes during rest or exercise with high sensitivity [±1 g (80)]. Evaporation rates based on Potter balance measurements have been previously reported in the literature (1, 68, 69, 81); however, use of this technique has declined in recent decades. A more feasible whole body sweating sample rate for most researchers is once every 15 min, and such an approach will still provide some insight into both non-steady-state and steady-state evaporative heat loss. If cumulative evaporation is required for the purpose of estimating body heat storage (see Estimating Body Heat Storage) sweat losses derived with two measurement points, the difference between preexercise and end-exercise body masses, corrected for respiratory and metabolic mass losses as well as any ingested fluids, is optimal. Importantly, all mass measurements must be performed with a precision balance (17) and without wiping sweat from the skin surface before weighing (unless wiped/dripped sweat is trapped in, for example, a towel that is subsequently weighed—preferably sealed in a plastic bag to prevent further evaporation).

When exercise is performed at a high absolute intensity, in a humid and/or still-air environment, and/or with clothing with a relatively high evaporative resistance, sweating efficiency declines. That is, a proportion of secreted sweat does not evaporate from the skin but instead remains on the skin, drips off the body altogether, and/or becomes trapped in clothing. In such circumstances, the change in body mass does not reflect evaporation, and a method to measure the quantity of dripped/trapped sweat is required. One option would be to capture dripping sweat in a tray filled with paraffin oil placed beneath a sweating subject and then determine the change in mass of the tray during the measurement period (see Ref. 1 for example). Alternatively, the rate of dripping sweat can be estimated from the literature based on anticipated sweating efficiency values (see below). Sweating efficiency is determined by the “skin wettedness” required (ω_req) for heat balance (24) or, in other words, how close the rate of evaporation required for heat balance (E_req in Eq. 15) is to the maximum evaporative rate possible in the ambient environment (E_max):

$${\text{ω}}_{\text{req}}\text{=}\frac{{\text{E}}_{\text{req}}}{{\text{E}}_{\text{max}}}\left(\text{ND}\right)$$ (14)

where ND is non-dimensional and E_req is defined by rearranging the human heat balance equation and assuming a rate of body heat storage (S) of zero:

$${\text{E}}_{\text{req}}={\text{H}}_{\text{prod}}-{\text{H}}_{\text{dry\_skin}}-{\text{H}}_{\text{res}}\left(\text{W}\right)$$ (15)

and E_max is determined by

$${\text{E}}_{\text{max}}\text{=}\frac{\left({\text{P}}_{\text{skin,sat}}-{\text{P}}_{\text{a}}\right)}{\left({\text{R}}_{\text{e,cl}}\text{+}\frac{\text{1}}{{\text{h}}_{\text{e}}\cdot {\text{f}}_{\text{cl}}}\right)}\text{\hspace{0.17em}×\hspace{0.17em}}{A}_{\text{D}}\left(\text{W}\right)$$ (16)

where P_skin,sat is the vapor pressure at the skin surface while saturated with sweat (in kPa); P_a is the partial pressure of water vapor in ambient air (in kPa); R_e,cl is the evaporative resistance of clothing (in m²⋅kPa⋅W⁻¹) (39); and h_e is the evaporative heat transfer coefficient (in W·m⁻²·kPa⁻¹) of the adjacent air layer. Values for P_skin,sat can be calculated with Antoine’s equation (74) for 100% relative humidity at the measured mean skin temperature of the participant. Ambient humidity should be measured with a precision sensor; commonly used capacitance hygrometers yield values with an accuracy of ±1% relative humidity, the equivalent of ±0.056 kPa absolute humidity at an air temperature of 35°C. Similar to the measurement of air temperature described above, values for P_a should be assessed next to the participant at an appropriate height, whereas values logged by the environmental control system for climate chamber-based studies should not be used, as they have the potential to deviate considerably from the air mass surrounding a participant. Comparable to the estimation of R_cl (in Eq. 9), values for R_e,cl can be obtained from tables provided by ISO 9920 (49) or measured with a thermal manikin that simulates skin surface sweating. A typical athletic t-shirt-shorts-socks-shoes clothing ensemble would yield a R_e,cl value of ~0.010 m²·kPa·W⁻¹ (64). Finally, h_e is calculated as the product of the convective heat transfer coefficient (h_c, see Table 2) and the Lewis relation coefficient (16.5 K/kPa), accounting for the effects of barometric pressure (P_b) (25, 58, 83):

$${\text{h}}_{\text{e}}=16\text{.}5\cdot {\text{h}}_{\text{c}}\cdot \left(760/{\text{P}}_{\text{b}}\right)\left(\text{W}\cdot {\text{m}}^{-2}\cdot {\text{kPa}}^{-1}\right)$$ (17)

Sweating efficiency (S_eff) can be estimated with (92)

$${\text{S}}_{\text{eff}}\text{\hspace{0.17em}=\hspace{0.17em}1}-\frac{{\text{ω}}_{\text{req}}^2}{\text{2}}\left(\text{ND}\right)$$ (18)

The average rate of evaporative heat loss from the skin surface (H_{evap_skin}) is then estimated with the following:

$${\text{H}}_{\text{evap}\_\text{skin}}=\text{WBSR}\cdot \text{λ}\cdot {\text{S}}_{\text{eff}}/60\left(\text{W}\right)$$ (19)

where WBSR is whole body sweat rate based on changes in body mass, accounting for the mass of sweat trapped in clothing, over time (in g/min); λ is the latent heat of vaporization of sweat (2,426 J/g); and 60 represents the conversion of minutes to seconds to obtain evaporative heat loss in watts.

It should be noted that estimations of evaporation assume a uniform distribution of sweat secretion across the skin surface, which is unlikely to be the case. Moreover, careful consideration should be given when using these equations to determine evaporative heat loss in heavily clothed individuals (see limitations of partitional calorimetry).

Estimating Body Heat Storage

Collectively, the partitional calorimetry measurements described in this CORP paper can be employed to estimate total body heat storage, that is, the cumulative change in whole body heat content over time (ΔH_b):

$${\text{ΔH}}_{\text{b}}=\underset{t\text{=0}}{\overset{t}{{\displaystyle \int }}}{\text{(H}}_{\text{prod}}{\text{\hspace{0.17em}±\hspace{0.17em}H}}_{\text{dry\_skin}}-{\text{H}}_{\text{evap\_skin}}-{\text{H}}_{\text{res}}\text{)/d}t\left(\text{kJ}\right)$$ (20)

Here, H_prod (Eqs. 3–5), H_{dry_skin} (Eqs. 6–10; Tables 2 and 3), H_{evap_skin}, (Eqs. 14–19), and H_res (Eqs. 11–13) must be multiplied by the exposure time (t) in seconds and divided by 1,000 to convert watts into kilojoules.

DETAILS OF PRACTICAL IMPORTANCE

Air Velocity

Because of the turbulent and nonuniform way in which forced air (e.g., with fans) interacts with the body surface, the accurate quantification of air velocity is problematic. Nonuniformity of airflow can be reduced if a bank of fans stacked vertically is used with the blade rotation speed of each fan matched by delivering equal electrical current to all units across a range of speeds, unrestricted by any manufacturer speed settings, with a variable autotransformer. More laminar flow can be achieved by drawing air across the body with very large-diameter fan(s) [e.g., 0.9 m in diameter (38)] placed behind the participant and inside a wind tunnel. The impact of any uncertainty surrounding air velocity on estimation of H_{dry_skin} can also be minimized by selecting an ambient air temperature that is approximately equal to mean skin temperature (i.e., 35°C) such that the skin-to-air temperature gradient is ~0°C.

Sweating Efficiency

In addition to precise measures of whole body sweat loss (17), accurate estimations of evaporative heat loss from the skin are dependent on well-defined values of sweating efficiency (Eq. 18). Sweating efficiency has been reported to decline when ω_req exceeds values as low as 0.20 (2), but the most comprehensive data available, albeit for passively heated supine participants, indicates that efficiency declines from 100% when ω_req exceeds ~0.50 (14, 15). Evaporative heat loss is therefore best estimated at low ω_req values when the experimenter can be confident that all sweat has evaporated, which is exactly the same principle as direct calorimetry (79). To ensure that a sufficiently low ω_req for this assumption of complete sweat evaporation holds true, a high air velocity, coupled with a low ambient humidity and a low evaporative resistance of clothing, should be employed. Collectively this approach serves to maximize E_max (Eq. 16), which drives down ω_req for given E_req (Eq. 15) and maximizes sweating efficiency. To assist the reader with selecting environmental conditions at which complete sweat evaporation should occur, Fig. 1 illustrates the various combinations of air temperature, air velocity, and relative humidity estimated to yield a critical ω_req of 0.50 for a lightly clothed individual with a body surface area of 1.8 m² exercising at a heat production of 200–600 W. Note that these values represent the estimated threshold limits for ω_req = 0.50; therefore, selected conditions should be cooler, drier, and/or more windy than indicated so the prevailing ω_req is actually lower.

Fig. 1.

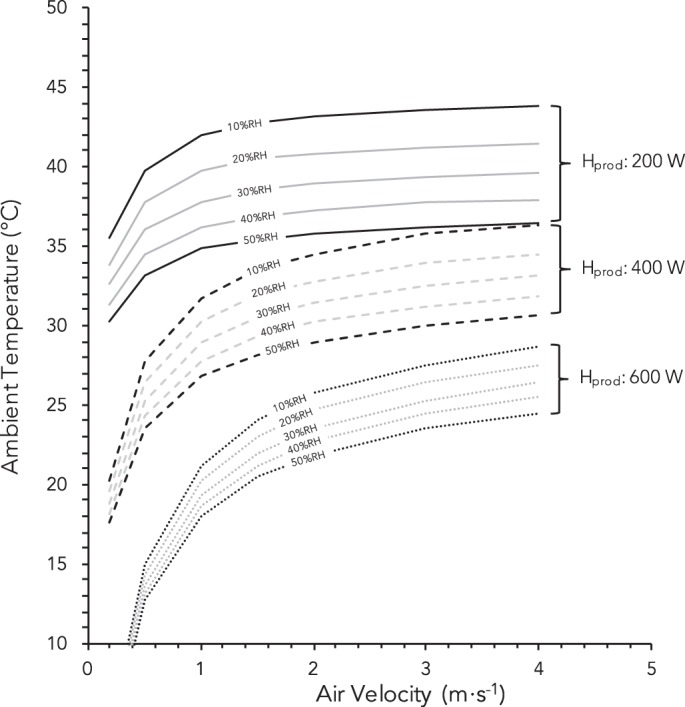
Estimated combinations of air temperature, air velocity, relative humidity (RH), and metabolic heat production (H_prod) that elicit a skin wettedness required for heat balance (ω_req) of 0.50, the critical value above which the evaporative efficiency of sweat is reported to decline from 100%. Note that selected conditions should be cooler, drier, windier, and/or with a lower heat production so that the actual ω_req is lower than 0.50. Example given for a 1.8-m² individual cycling [fraction of body surface participating in radiative heat transfer (A_r/A_D) = 0.73] with light clothing [dry heat transfer resistance of clothing (R_cl): 0.045 m²⋅°C⋅W⁻¹ (0.3 clo); evaporative resistance of clothing (R_e,cl): 0.010 m²⋅kPa⋅W⁻¹].

Reliability of Partitional Calorimetry

Few studies have directly addressed the reliability of partitional calorimetric assessments of heat balance parameters. In studies investigating clothing insulation and evaporative resistance, Havenith et al. (38) and Holmér and Elnäs (41) reported test-retest differences of ~3–4%, depending on metabolic rate.

HOW PARTITIONAL CALORIMETRY CAN BE USED

Partitional calorimetry has numerous applications in human thermoregulation research, examples of which are presented in the following sections.

Example 1: Assessing Whether an Environment Is Compensable and Predicting Sweat Losses

It is often important to ascertain whether a given combination of activity, environment, and clothing is physiologically compensable (i.e., it should be possible to attain a steady-state core temperature) before heat exposure in order to limit the risk of excessive rises in heat storage and therefore core temperature. By definition, heat stress is compensable when E_req (Eq. 15) is lower than E_max (Eq. 16). However, E_max must also be adjusted for a person’s maximum skin wettedness (ω_max; the maximum proportion of the skin surface that can be saturated with sweat), which is considered to be 1.00 for a fully heat-acclimated person (15, 78) but as low as 0.72 in an untrained, non-heat-acclimated individual (78). For example, identification of whether a heat stress condition should be compensable or not can be performed for a 75-kg man with a body surface area of 1.94 m² as follows:

• External work rate: 90 W

• Metabolic rate: V̇o₂ of 1.7 l/min with RER of 0.82 = 580 W

• Corresponding rate of metabolic heat production: 490 W

• Ambient temperatures (air, radiant): 32°C

• Relative humidity: 30%

• Air velocity: 1.0 m/s

• Clothing (minimal: only shorts, socks, and shoes): R_cl = 0.03 m²⋅°C⋅W⁻¹ and R_e,cl = 0.01 m²⋅kPa⋅W⁻¹

According to Eqs. 6–13, with an assumed t_sk of 34°C, E_req (Eq. 15) is 405 W. And with Eq. 16, E_max is theoretically 445 W, and the skin wettedness required for heat balance (ω_req; Eq. 14) is subsequently 405 W ÷ 445 W = 0.91. Given that the maximum skin wettedness is 1.00 for a fully heat-acclimated person but 0.84 for an aerobically trained but unacclimated person and 0.72 for an untrained and unacclimated person (78), steady-state core temperatures should only be attainable if the individual exposed is fully heat acclimated.

It is also important to consider whether the sweat rate required to maintain heat balance (and therefore a steady-state core temperature) is sustainable and how much rehydration may be required to prevent deleterious reductions in body fluids. To this end, whole body sweat rate (WBSR_pred) for a given person can also be estimated with

$${\text{WBSR}}_{\text{pred}}=\left({\text{E}}_{\text{req}}\cdot \mathrm{3,600}\right)/\left({\text{S}}_{\text{eff}}\cdot \text{λ}\right)\left(\text{g}/\text{h}\right)$$ (21)

where 3,600 represents the conversion of seconds to hours, S_eff is sweating efficiency (as a fraction, calculated with Eq. 18), and λ is the latent heat of vaporization of sweat (2,426 J/g).

In the example above, constant load exercise eliciting an E_req of 405 W over 1–2 h should yield a whole body sweat rate of ~1,030 g/h with an estimated S_eff of 0.58. But if exercise eliciting the same E_req were performed under conditions (e.g., with a lower humidity and/or higher air velocity) inducing a sweating efficiency of 0.90, the estimated whole body sweat rate would decline to ~655 g/h. Note that for shorter exercise durations this method will overestimate whole body sweat rate, as non-steady-state sweat rates during the earlier stages of exercise are lower.

Example 2: Identifying the Effects of a Warming or Cooling Intervention on Heat Balance

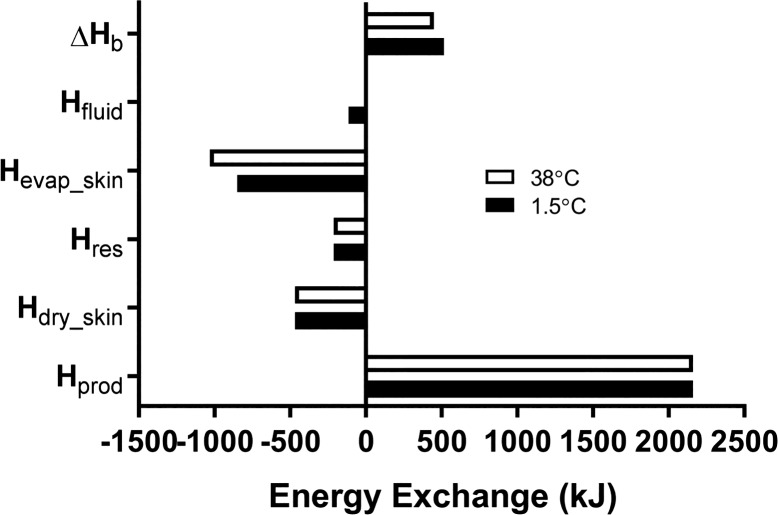
Partitional calorimetry also has the ability to assess the extent (if any) to which the alteration in one avenue of heat transfer through warming or cooling alters another, as well as the ensuing effect on heat storage. One example that has been recently investigated in studies conducted in our laboratory (4, 66, 67) is the impact of drink temperature on whole body heat balance. During exercise the ingestion of a cold fluid increases internal conductive heat loss, yet if this is compensated by proportional reductions in skin surface evaporation the benefits to reducing body heat storage are apparently lost (4, 55). The reader is asked to consider, for instance, the effect of ingesting cold water (1.5°C) or water kept close to core body temperature on heat balance during 1 h of moderate-intensity cycling (600 W of metabolic heat production) in temperate environmental conditions (25°C, 30% relative humidity) while seminude (i.e., negligible clothing insulation and vapor resistance). The results of this example are graphically depicted in Fig. 2. First, a term for conductive heat loss from the body to the ingested fluid (H_fluid) must be added to Eq. 20:

$$\Delta {\text{H}}_{\text{b}}=\underset{t\text{=0}}{\overset{t}{{\displaystyle \int }}}{\text{(H}}_{\text{prod}}{\text{\hspace{0.17em}±\hspace{0.17em}H}}_{\text{dry\_skin}}-{\text{H}}_{\text{evap\_skin}}-{\text{H}}_{\text{res}}-{\text{H}}_{\text{fluid}}\text{)/d}t\left(\text{kJ}\right)$$ (22)

where H_fluid is determined as

Fig. 2.

Example of total quantities of energy exchanged and stored with the ingestion of cold (1.5°C) or body temperature-controlled (38°C) water during exercise under neutral environmental conditions. ΔH_b, change in body heat storage; H_fluid, energy exchanged between body tissues and ingested water; H_{evap_skin}, evaporative heat loss; H_res, respiratory heat loss; H_dry__skin, dry heat loss; H_prod, metabolic heat produced. Negative values indicate heat loss (i.e., cooling). In this example, net body heat storage is slightly greater with the ingestion of cold fluid because of a corresponding attenuation in whole body evaporative heat loss.

$${\text{H}}_{\text{fluid}}=\left({\text{T}}_{\text{c}}-{\text{T}}_{\text{fluid}}\right)\cdot {\text{C}}_{\text{p}}\cdot m_{\text{fluid}}/\mathrm{1,000}\left(\text{kJ}\right)$$ (23)

Here, (T_c – T_fluid) is the core-fluid temperature gradient; C_p is the specific heat capacity of water (4.186 J·g⁻¹·°C⁻¹), m_fluid is the fluid mass in grams, and 1,000 represents the conversion from joules to kilojoules. If core temperature averages 38°C, 750 g of 1.5°C water will yield a H_fluid value of 115 kJ but ~0 kJ for ingested water kept equal to core temperature.

The cumulative metabolic heat load (H_prod) is calculated to be 2,160 kJ. For both drink temperatures, H_{dry_skin} is estimated to be 468 kJ based on a mean skin temperature of 32°C (Eqs. 6–9), while H_res is estimated to be 212 kJ (Eqs. 10–12). From Eq. 18, observed whole body sweat losses of 350 g and 425 g yield H_{evap_skin} values of 849 kJ and 1,031 kJ with 1.5°C and body temperature water, respectively. Finally, using Eq. 20, we determine that the change in whole body heat storage is 516 kJ with 1.5°C water but only 449 kJ with water maintained at a temperature close to the body core.

Example 3: Deriving Heat Exchange Properties

Another important application of partitional calorimetry is the derivation of individual heat balance parameters. One example is the determination of the total insulation or evaporative resistance associated with various clothing ensembles. Total insulation (I_tot) is the resistance to dry heat flow and includes the insulation imposed by clothing and the surrounding air. By rearranging Eq. 5, I_tot can be determined as follows (38):

$${\text{I}}_{\text{tot}}=\left({\text{t}}_{\text{sk}}-{\text{t}}_{\text{a}}\right)/{\text{H}}_{\text{dry}\_\text{skin}}\left({\text{m}}^2\cdot \text{°C}\cdot {\text{W}}^{-1}\right)$$ (24)

Given the difficulty of measuring dry heat transfer with clothing, H_{dry_skin} can be isolated based on an estimation of the remaining heat balance parameters outlined in Eq. 1:

$${\text{H}}_{\text{dry}\_\text{skin}}={\text{H}}_{\text{prod}}-{\text{H}}_{\text{res}}-{\text{H}}_{\text{evap}\_\text{skin}}-{\text{S}}_{\text{therm}}\left(\text{W}\right)$$ (25)

where S_therm is a thermometric estimate of the rate of heat storage, which is calculated based on the weighted average of the change in core and skin temperatures over time (see the following for typically used coefficients: Refs. 12, 18, 43, 51–53, 86, 87, 90). During a steady-state exposure when body temperatures are unchanging, this value will be zero. The reader is asked to consider an example in which low-intensity work (metabolic heat production of 350 W) is performed in a warm-dry (30°C, 30% relative humidity) and windy (4.0 m/s) environment while clothed, with a mean skin temperature of 34°C. With Eqs. 11–13 and 19 (accounting for sweat trapped in the clothes), steady-state H_res and H_{evap_skin} values are 30 W and 250 W, respectively. Consequently, H_dry is determined to be 70 W, and I_tot is calculated to be 4 ÷ 70 = 0.06 m²·°C·W⁻¹. A similar procedure may be applied to determine total evaporative resistance as described by Holmér and Elnäs (41).

LIMITATIONS OF PARTITIONAL CALORIMETRY

By its very nature, partitioning internal heat production and human-environmental heat transfer into individual components requires the measurement of several environmental and physiological parameters. As such, there are several sources of potential error that all must be accounted for through careful calibration and the precise use of various pieces of equipment (e.g., temperature/humidity sensors, balance scale, oxygen/carbon dioxide sensors). Any individual inaccuracy can be subsequently compounded to yield low-quality estimates of human heat balance status. Partitional calorimetry is particularly limited for estimating evaporative heat loss for individuals wearing layered clothing ensembles. Sweat trapped in clothing can ultimately evaporate, but the effective latent heat of vaporization declines dramatically (by up to ~80%) depending on the number of layers and the material properties of the clothing system worn (37). Under such circumstances, skin surface evaporation from measured sweat losses, even after accounting for sweat trapped in clothing, could be grossly overestimated. With low-vapor-permeability clothing, estimates of evaporative heat loss may be further affected by cycles of evaporation-condensation within clothing layers, which could result in a mass change of zero, despite the presence of evaporation from the skin (40). Furthermore, it should be recognized that clothing insulation and vapor resistance values may be derived under static or dynamic conditions; therefore, appropriate values should be used depending on experimental conditions used.

Although the assessment of heat balance status is used widely in many heat stress indexes (7, 9, 31, 45, 48), interpretation of heat illness risk using absolute body heat storage without reference to parallel changes in body temperatures is not advised. Indeed, heat-related illness partly evolves because of a cascade of events triggered by thermal injury to the vascular endothelium caused by high body temperatures per se (56), which presumably holds true irrespective of the absolute amount of heat stored in the body.

GRANTS

M. N. Cramer is supported by a Natural Sciences and Engineering Research Council of Canada Postdoctoral Fellowship.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.N.C. and O.J. prepared figures; M.N.C. and O.J. drafted manuscript; M.N.C. and O.J. edited and revised manuscript; M.N.C. and O.J. approved final version of manuscript.