Abstract
Excessive centrosomes often lead to multipolar spindles, and thus probably to multipolar mitosis and aneuploidy. In Caenorhabditis elegans, ∼70% of the paternal emb-27APC6 mutant embryonic cells contained more than two centrosomes and formed multipolar spindles. However, only ~30% of the cells with tripolar spindles formed two cytokinetic furrows. The rest formed one furrow, similar to normal cells. To investigate the mechanism via which cells avoid forming two cytokinetic furrows even with a tripolar spindle, we conducted live-cell imaging in emb-27APC6 mutant cells. We observed that the chromatids were aligned on only two of the three sides of the tripolar spindle, and the angle of the tripolar spindle relative to the long axis of the cell correlated with the number of cytokinetic furrows. Our numerical modeling showed that the combination of cell shape, cortical pulling forces, and heterogeneity of centrosome size determines whether cells with a tripolar spindle form one or two cytokinetic furrows.
INTRODUCTION
The centrosome is a major microtubule-organizing center in animal cells. Each centrosome contains a pair of centrioles, which duplicate only once during a cell cycle. Therefore, the number of centrosomes in a cell is strictly regulated (Nigg and Holland, 2018). Normally, dividing cells possess two centrosomes that become the two poles of the bipolar mitotic spindle to segregate the sister chromatids into two daughter cells after mitosis. Centrosomes use the microtubules elongating from them to act as a hub that aggregates forces acting on the microtubules (Mogilner et al., 2006). These forces move the centrosomes to drive translational and rotational movements of the mitotic spindle. The position and orientation of the mitotic spindle is critical for the size asymmetry and direction of cell division (Gönczy, 2008; Siller and Doe, 2009; Morin and Bellaïche, 2011).
The mechanics controlling the configuration (i.e., position and orientation) of the bipolar spindle is well studied. In contrast, the mechanisms controlling the configuration of the mitotic spindle with three or more poles (i.e., a multipolar spindle) are not well known. Multipolar spindles are formed when cells possess more than two centrosomes owing to defective regulation of their numbers (Pihan et al., 1998; Godinho and Pellman, 2014). The forces controlling configuration should be similar for both multipolar and bipolar spindles. Therefore, multipolar spindles might provide a good example to test the feasibility of the theories proposed for the regulation of bipolar spindles. In addition, the configuration of multipolar spindles might be important to understand the viability of cancer cells. Supernumerary centrosomes are frequently observed in cancer cells and are expected to induce multipolar spindles, and subsequently aneuploidy and cell death (Lingle et al., 1998; Brinkley, 2001; Boveri, 2008; Holland and Cleveland, 2009). However, cancer cells are known to proliferate efficiently, which presents a paradox (Godinho et al., 2009). One mechanism to overcome the paradox is to cluster supernumerary centrosomes into two to form a bipolar spindle (Kwon et al., 2008). However, little is known regarding spindle behavior once multipolar spindles are formed.
In this study, we investigated the configuration of tripolar spindles and consecutive cell-division pattern in the Caenorhabditis elegans embryo. The configuration of bipolar spindles is well established in the C. elegans embryo (Gönczy and Rose, 2005), and hence it is a good system to analyze the configuration of tripolar spindles. To induce reproducibly tripolar spindles in C. elegans embryos, we focused on an emb-27APC6 mutant. C. elegans emb-27 encodes a subunit of anaphase-promoting complex (APC) that is required for the initiation of chromosome segregation and other events at anaphase (Golden et al., 2000). Sperm from emb-27 mutants do not contain chromosomes, but can fertilize eggs (Sadler and Shakes, 2000). After fertilization, some embryos divide into three cells by forming two cytokinetic furrows at the first cell division, possibly by forming tripolar spindles (Sadler and Shakes, 2000). In this study, we have named the cytokinesis that forms two cytokinetic furrows and divides the cell into three daughter cells as “2-furrow cytokinesis,” whereas “1-furrow cytokinesis” refers to usual cytokinesis with one cytokinetic furrow that divides the cell into two. We have recently shown that the paternal emb-27 mutant embryo possesses three or more centrosomes (Kondo and Kimura, 2018) as expected from the previous report (Sadler and Shakes, 2000). An unexpected result was that the frequency of cells with three or more centrosomes in the mutant embryos was ∼70% (Kondo and Kimura, 2018). This high frequency is seemingly inconsistent with the defective mitosis observed only in one-third of the embryos (Sadler and Shakes, 2000). In this study, we investigated the mechanism via which some cells with three centrosomes avoid 2-furrow cytokinesis in the paternal emb-27 mutant embryo. This investigation provides insight into how centrosomes (spindle poles) behave under normal and abnormal conditions.
RESULTS
Abnormal centrosome number does not always result in excessive furrows
We have previously quantified the number of the centrosomes in paternal emb-27 mutant embryos and observed that ∼70% of the mutant embryos possessed three or more centrosomes (Kondo and Kimura, 2018). This did not agree with the number of mutant embryos with defective mitosis, which was only one-third of that reported previously (Sadler and Shakes, 2000). To investigate the relationship between the extra centrosomes and mitotic defect, we quantified the number of cell-division furrows in the paternal emb-27 mutant embryos. About 30% of the paternal emb-27 embryos at one-cell stage formed two cell-division furrows and divided into three cells (“2-furrow cytokinesis”; Figure 1). This was in agreement with the result of a previous study (Sadler and Shakes, 2000), where one-third of the cells underwent 2-furrow cytokinesis. Furthermore, ∼20% of the cells with four centrosomes still underwent 1-furrow cytokinesis. We did not observe 3-furrow cytokinesis for cells with four centrosomes during the course of this study (Figure 1). Therefore, the extra centrosomes do not always induce multipolar mitosis.
FIGURE 1:

Number of centrosomes and furrows in the paternal emb-27 mutant embryos. Frequency of the two patterns of the first cell division in control and emb-27 paternal embryos. For emb-27, frequency of total and cells with the designated number of centrosomes are shown. In the cells with one centrosome (“1cent. (n = 3)”), the cell failed cytokinesis for the initial cell cycle, but duplicated the centrosome in the next cell cycle and then divided into two daughter cells.
Only two of the three sides of the tripolar spindle are occupied by chromosomes
To understand the mechanism that determines the choice between 1-furrow and 2-furrow cytokinesis, we focused on the one-cell stage embryo with three centrosomes. Observations of centrosomes and chromosomes in these cells revealed that cells with three centrosomes always formed a tripolar spindle (n = 32; Figure 2) instead of multiple centrosomes merging to form a bipolar spindle (Ring et al., 1982; Quintyne et al., 2005). Interestingly, we noted that the chromosomes resided on only two of the three sides of the tripolar spindle in every cell (n = 32; Figure 2). Chromatids residing on two of the three sides of a tripolar spindle have been observed in other cell types (Wilson, 1925; Wheatley and Wang, 1996; Eckley et al., 1997); however, to our knowledge, this is the first report showing that such a spindle is always observed. Currently, the mechanism underlying this event is not known. Nonetheless, this feature regarding chromatid positioning may be important to understand the difference between 1-furrow and 2-furrow cytokinesis because chromatids are considered critical for the formation of cleavage furrows by positioning signaling molecules such as chromosome passenger complex and centralspindlin to the spindle midzone (Wilson, 1925; Earnshaw and Cooke, 1991; Margolis and Andreassen, 1993; Wheatley and Wang, 1996; Eckley et al., 1997; Glotzer, 2005).
FIGURE 2:
1-furrow cytokinesis and 2-furrow cytokinesis in embryos with three centrosomes. Representative time-lapse images of an embryo with three centrosomes during the first cell division. Top panels show the embryos that expressed GFP-tagged γ-tubulin (centrosome, arrows), PHPLCδ1 (cell membrane), and histone H2B (nucleus) in utero. Bottom planes show the quantified position of centrosomes (blue) and nucleus/chromatids (red). In 1-furrow cytokinesis (A), a cleavage furrow (arrowheads) was observed between separated chromatids, which are similar to normal embryos. In 2-furrow cytokinesis (B), two cleavage furrows (arrowheads) were observed. For both patterns, the chromatids are localized on only two of the three sides of the tripolar spindle. Times (hr:min:sec) are with respect to NEBD. Bars, 10 µm.
Cell geometry correlates with the furrowing patterns in embryos with three centrosomes
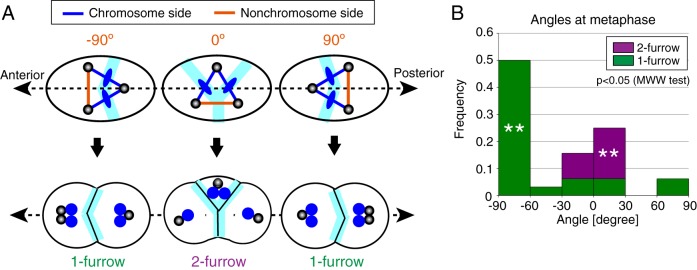
Why does the tripolar spindle induce 1-furrow cytokinesis in some case (Figure 2A) and 2-furrow ones in others (Figure 2B)? We speculated that cell geometry, together with the above-mentioned feature that two of the three sides are occupied by the chromatids, is critical for determining the number of cytokinesis furrows based on the following observations. We observed that the choice between 1-furrow or 2-furrow cytokinesis correlated with the angle relationship between the tripolar spindle and cell shape at metaphase (Figure 3). The one-cell stage of the C. elegans embryo is ellipsoidal in shape with a long axis of ∼50 μm (i.e., the anterior-posterior [AP] axis) and two short axes of ∼30 μm. We quantified the angle relationship between the tripolar spindle and the cell by focusing on the angle of the side without chromatids (“nonchromosome side”) against the long axis of a cell (Figure 3A). A cell tends to undergo 1-furrow cytokinesis when the angle of the nonchromosome side was close to −90°, whereas a cell tends to undergo 2-furrow cytokinesis when the angle was close to 0° (Figure 3B).
FIGURE 3:
Characterization of tripolar spindles in embryos with three centrosomes. (A) Definition of the angle of the side without chromatid (nonchromosome side) with respect to the anterior–posterior axis. Cleavage furrows are expected to form and complete at the light-blue area where metaphase chromosomes are positioned (top panel). If this is the case, 1-furrow or 2-furrow cytokinesis will be observed (bottom panel). For 2-furrow cytokinesis, two of the three daughter cells inherit only half the set of the chromosomes (blue), resulting in aneuploidy. (B) Frequency of 1-furrow/2-furrow cytokinesis in embryos with the designated angle of the nonchromosome side at metaphase. n = 32. **: p < 0.005, binomial test for each angle range.
The observed correlation in this study is well explained by the current knowledge on cleavage furrow formation by the mitotic spindle (Figure 3A). The cleavage furrow is induced at the midway of the two spindle poles and at the position of chromatids, which coincides in normal cells with the bipolar spindle (Rappaport, 1961; Mishima, 2016). In the C. elegans embryo, the furrow induced at the midway of the poles but without chromatids is not completed, whereas that at the position of chromatids is completed (Bringmann and Hyman, 2005). For the tripolar spindles in this study, the chromatids reside on two of the three sides (Figure 2) and thus the two furrows that potentially complete the cleavage are eventually formed. When the angle of the nonchromosome side was close to −90° or +90° (Figure 3A), the two potential furrows might be in close proximity and might merge, resulting in 1-furrow cytokinesis. In contrast, when the angle was close to 0°, the two potential furrows are distant and cannot merge. This idea is supported by our live imaging of the 1-furrow and 2-furrow cytokinesis (Figure 2).
“Open” or “closed” tripolar spindle depending on cell geometry
In the preceding section, we proposed that the 1-furrow cytokinesis is induced by the merging of two potential furrows formed at the two chromosome sides of the tripolar spindle. Our live-cell imaging revealed that the tripolar spindle “flattens” during metaphase and anaphase in a distinct manner between 1-furrow and 2-furrow cytokinesis. Taking advantage of live-cell imaging, we were able to “back-track” the centrosomes and identify which pair of centrosomes forms the chromosome side and nonchromosome side even before the centrosomes capture the chromosomes. Upon nuclear envelope breakdown (NEBD), the triangle formed by the three centrosomes is almost equilateral, that is, the lengths of the three sides are comparable (Figure 4, A and B). After the NEBD, the lengths of the chromosome sides and nonchromosome side became nonuniform, resulting in flattening of the tripolar spindle. Our quantification revealed that in the case of 1-furrow cytokinesis, the nonchromosome side became shorter than the chromosome sides (Figures 2A and 4, A(i) and B(i)), whereas in the case of 2-furrow cytokinesis, the nonchromosome side became longer than the chromosome sides (Figures 2B and 4, A(ii) and B(ii)). We called the former case “closing” of the tripolar spindle, as the angle between the two chromosome sides decreased, whereas the latter case is termed “opening” as the angle increased (Figure 4C). The closing draws the two potential furrows closer, resulting in 1-furrow cytokinesis, whereas the opening separates the two furrows further and results in 2-furrow cytokinesis. In summary, the distinct forms of the flattened tripolar spindle determine the choice between 1-furrow and 2-furrow cytokinesis.
FIGURE 4:
“Open” or “closed” tripolar spindle depending on cell geometry. (A) Length of the designated side of a tripolar spindle over time. Each line represents data from one side. n = 32. Time (T) is normalized as follows: Trelative = (T − TNEBD)/([Tfurrowingonset − TNEBD] − [Tpronuclear meeting − TNEBD]). (B) Length of the designated side of a tripolar spindle at the designated cellular event. Bars represent mean of all data shown by circles. (C) Scheme of the proposed model showing how 1-furrow and 2-furrow cytokinesis are determined depending on the angle of the tripolar spindle. The top panel is the same as that in Figure 3A, showing the angle of the tripolar spindle at NEBD to metaphase. The middle panel shows the elongation of the tripolar spindle. We assumed that only the chromosome sides (blue) elongate actively, whereas the length of the nonchromosome side (orange) depends on the movements of the two ends. The forces pulling the pole (centrosome) depend on the ellipsoidal geometry of the cell (red arrows), and the angle between the chromosome sides close (green arrows) or open (purple arrows) depending on the direction of forces. Cleavage furrows are expected to form and complete at the light blue area where metaphase chromosomes are positioned. The opening or closing induces 1-furrow or 2-furrow cytokinesis, respectively (bottom panel).
A numerical model for “open” and “closed” tripolar spindles
To examine whether existing concepts on the forces acting on the bipolar spindle account for “opening” and “closing” of the tripolar spindle, we constructed a numerical model and examined whether the tripolar spindle in the model opens or closes depending on the cell geometry (i.e., the angle of the tripolar spindle against the long axis of the cell). Our model is based on two forces.
Force 1.
At anaphase, all three poles are pulled outward because the pulling forces act on astral microtubules, as demonstrated for the usual elongation of bipolar spindles (Grill et al., 2001; Hara and Kimura, 2009), depending on the activity of heterotrimeric G proteins and their regulators (Gotta and Ahringer, 2001; Colombo et al., 2003; Srinivasan et al., 2003). The direction of the forces depends on the cell geometry—stronger along the long axis of the cell, which is likely the general property of cells known as “Hertwig’s long-axis rule” (Hertwig, 1885; Minc et al., 2011). Several mechanisms have been proposed for the generation of geometry-dependent pulling force, such as limited number of cortical force generators (Grill et al., 2003; Grill and Hyman, 2005; Hara and Kimura, 2009), cytoplasmic pulling (Hamaguchi and Hiramoto, 1986; Kimura and Onami, 2005; Minc et al., 2011), or the density of retraction fibers (in the case of adhesive cells; Théry et al., 2007). Irrespective of the mechanisms, the strength of the forces can be modeled as they are approximately proportional to the length of microtubules (Grill and Hyman, 2005; Théry et al., 2007; Hara and Kimura, 2009; Kimura and Kimura, 2011a; Minc et al., 2011; Matsumura et al., 2016). In this study, we adopted cytoplasmic pulling force as geometry-dependent force for ease of calculation (Figure 5A).
FIGURE 5:

Numerical model for “open” and “closed” tripolar spindles. (A) Our numerical 3D model to calculate the forces acting on each of the three poles that pull a pole (e.g., red circle) with a geometry-dependent force and cortical pulling forces (e.g., orange arrow, from force generators at the orange region). To calculate geometry-dependent force, we adopted cytoplasmic pulling force (e.g., blue arrow, from force generators at the light-blue region) as the underlying mechanism for ease of calculation. Other mechanisms should give similar results as long as they are approximately proportional to the length of microtubules (see main text for details). Because we focus on the angle of the tripolar spindle, we fixed the length of the chromosome sides in the model. (B) Calculation of the torque to open or close the angle between the chromosome sides depending on the angle of nonchromosome side with respect to the anterior–posterior axis (Figure 4C, middle panel).
Force 2.
Among the three sides of the tripolar spindle, two chromosome sides resist the elongation, whereas the nonchromosome side does not. While modeling the rotation of the bipolar spindles, the lengths of chromosome sides are fixed to resist the outward pulling forces (Théry et al., 2007; Minc et al., 2011). The resistance against the outward forces is considered to be generated by the cohesion of sister chromatids and the bundling of antiparallel microtubules (Mogilner et al., 2006). As the length of the chromosome side of the tripolar spindle is similar to that of the wild-type (bipolar) spindle (Figure 4, A and B), and as we were interested in the angle of the tripolar spindle, we fixed the length of the chromosome sides in our model to resist the outward pulling forces. In contrast, we did not assume any restriction on the length of the nonchromosome sides in our model, as the length of the nonchromosome side varied compared with that of the chromosome sides in our study (Figure 4, A and B).
In our three-dimensional (3D) model, these two types of forces moved the poles of the tripolar spindle. As the initial condition, we placed an equilateral triangle, which corresponds to the tripolar spindle, at the center of a prolate ellipsoid, corresponding to the cell. The three vertices of the triangle were pulled outward depending on the geometry of the cell (Figure 5A and Materials and Methods). The torque to open or close the angle between the two chromosome sides was calculated under the condition that the nonchromosome side does not resist elongation or compressive forces. The tripolar spindles with near 0° configuration tend to “open,” whereas those with near −90° or +90° configuration tend to “close,” leading to the induction of 2-furrow and 1-furrow cytokinesis, respectively (Figure 5B). Therefore, the angle of tripolar spindles against the long axis of the cell is responsible for the opening or closing of the tripolar spindle during spindle elongation, which determines the choice between 1-furrow and 2-furrow cytokinesis.
Mechanisms controlling the initial angle of tripolar spindles: Experimental observations
As proposed above, the choice between 1-furrrow and 2-furrow cytokinesis can be traced back to the angle of tripolar spindles against the long axis of a cell. Hence, we next examined how the initial angle of the spindle before elongation is determined. We first determined when this critical angle is established. As mentioned above, we back-tracked the chromosome sides and nonchromosome side before the centrosomes captured the chromosomes. The asymmetry in the length of the three sides of tripolar spindles was not evident at NEBD (Figure 4B). In contrast, the angle of the future nonchromosome side was already biased between 1-furrow and 2-furrow cytokinesis at NEBD, but not at the earlier stage of pronuclear meeting (Figure 6, A and B; 2-furrow [purple] vs. 1-furrow [green]). At pronuclear meeting, the frequency of observing 1-furrow or 2-furrow cytokinesis at each angle range was not statistically biased (p > 0.05) compared with the overall frequency of observing 1-furrow or 2-furrow cytokinesis. We propose that the angle of the triangle made by the three centrosomes at NEBD, but not earlier (i.e., meeting), is critical for the choice between 1-furrow and 2-furrow cytokinesis.
FIGURE 6:
Frequency of 1-furrow or 2-furrow cytokinesis. (A, B) Frequency of 1-furrow or 2-furrow cytokinesis in embryos with the designated angle of the nonchromosome side at NEBD (A) and pronuclear meeting (B). n = 32. **: p < 0.005, binomial test for each angle range. (C) Frequency of 1-furrow or 2-furrow cytokinesis in gpr-1/2 (RNAi) embryos with the designated angle of the nonchromosome side at NEBD. n = 15.
We also observed that the angle distribution of tripolar spindles at NEBD was not symmetric against the AP axis (Figures 3B and 5A). The −90° configuration was more favorable than the +90° configuration. In the C. elegans embryos, the centrosomes are known to be pulled by the force generators residing at the cortex via the microtubules (Grill et al., 2001). The strength of the cortical pulling force is asymmetric along the AP axis, which results in asymmetric positioning of the spindle and cell-division plane. The cortical pulling forces are dependent on gpr-1/2 gene products (Colombo et al., 2003; Srinivasan et al., 2003). If the asymmetry of the angle of tripolar spindles is regulated by the asymmetric cortical pulling force, such asymmetry should be lost by gpr-1/2 knockdown, and in fact, this was the case (Figure 6C). Therefore, the cortical pulling forces affect the angle of tripolar spindles to generate its asymmetric distribution along the AP axis.
A numerical model to predict favorable angles of tripolar spindles at NEBD
We next asked whether the 3D force calculation model constructed to calculate the opening or closing of the tripolar spindles during spindle elongation (Figure 5A) can also account for the angle distribution of the tripolar spindles before the elongation (i.e., NEBD; experimental observations: Figure 6, A and C). By using this framework, the favorable angle was predicted based on a method developed previously to calculate the orientation of bipolar spindles in mammalian cultured cells (Théry et al., 2007; Matsumura et al., 2016). When only the ellipsoidal geometry of a cell was considered, the distribution of the angle of the nonchromosome side was uniform (Figure 7A). The consequence of the model was consistent with the experimental observation using gpr-1/2 RNA interference (RNAi) embryos, which is defective for asymmetric cortical pulling force and no specific angle was favored (Figure 6C).
FIGURE 7:
Heterogeneity in centrosome size accounts for the different distributions between the angles of the chromosome and nonchromosome sides. (A) The simulated angle of the sides of the tripolar spindle before elongation. The angle of the side is 0° when the side is parallel to the long axis and +90° or −90° when perpendicular (see the orange side in Figures 3A and 4C), for both the chromosome (blue) and the nonchromosome (orange) sides. This definition is common throughout. (B, C) The experimental distribution in gpr-1/2 (RNAi) (B) and control (C) at NEBD. n = 45 for gpr-1/2 (RNAi) and n = 96 for control. *: p < 0.05; ****: p < 5 × 10−5 binomial test for each angle range. (D) The experimental heterogeneity in centrosome size at NEBD. The average volume of the two centrosomes at the ends of the nonchromosome side was divided by the volume of the centrosomes between the chromosome sides. The logarithmic ratio is shown with a box plot drawn using MATLAB software. The ratios are smaller than 1 in all conditions examined. (E, F) The simulated distribution of the angle in a model with heterogeneity in centrosome size (E), which should reflect the experimental condition of gpr-1/2 (RNAi) (B), and after adding the asymmetric cortical pulling forces (F), which should reflect the control experiment (C).
This model condition was axially symmetric with respect to the long axis of the cell, and thus did not discriminate between the chromosome and nonchromosome sides (Figure 7A). In contrast, in vivo, the distributions of the nonchromosome side and chromosome side were not equivalent even in gpr-1/2 (RNAi) embryos (Figure 7B). Close to +90° or −90°, the nonchromosome side was favored over the chromosome side, whereas the chromosome side was favored over the nonchromosome side near 0° for gpr-1/2 (RNAi) (Figure 7B). The difference in the angle distribution of nonchromosome and chromosome sides was statistically significant for control embryos (Figure 7C; p < 0.05 as per Mardia−Watson−Wheeler test). The disagreement between the model and the experiments indicated that the nonchromosome side needs to be determined nonrandomly using an uncharacterized mechanism.
Heterogeneity in centrosome size explains the angle of tripolar spindles
Our observation that chromosomes reside on two out of three sides of a tripolar spindle implies that the three poles (centrosomes) of the spindle are not equivalent. Among the three poles, only one is connected to two sides with the chromosomes, whereas the remaining two poles are connected to the chromosome and nonchromosome sides each. We call the former “chromosome poles” and the latter “nonchromosome poles.” We observed that the chromosome poles tended to be larger in size than the nonchromosome ones at NEBD (Figure 7D). In binary comparison, where a chromosome pole is compared with each of the nonchromosome poles, the chromosome poles were larger with statistically significant frequency (n = 43/64 [p < 10−7] for control, and n = 33/46 [p < 10−6] for gpr-1/2 [RNAi]). The chromosome pole was not always the largest among the three poles, but it was rarely the smallest (n = 1/32 [p < 10−4] for control, and n = 1/23 [p < 10−2] for gpr-1/2 [RNAi]). As the measured sizes of the centrosomes depend on their position relative to the focal planes of microscopy (2 μm intervals in this measurement), size measurement might involve some experimental errors. Considering the above-mentioned statistically significant tendency of the chromosome pole to be large and the possible experimental error, we concluded that one of the large poles (centrosome), possibly the largest, is selected to become the chromosome pole.
Large centrosomes have been reported to be associated with a greater number of microtubules (Greenan et al., 2010). Therefore, we modified our numerical simulation by assuming the number of microtubules growing from the chromosome pole to be larger than that growing from the other two poles. As the magnitude of the asymmetry was obscure, we searched for parameters that allowed the model to recapitulate the experimental results. This simulation reproduced the alignment of the tripolar spindle in gpr-1/2 (RNAi) experiments, in which the nonchromosome side tends to assume +90° or −90° configuration, whereas the chromosome sides tend to have 0° configuration (Figure 7, B–experiment and E–simulation). The simulation result together with the experimental observation are indicative of the heterogeneity in the size of the centrosomes, and the largest centrosome captures chromosomes on two sides, whereas the other centrosomes capture chromosomes only on one side. This heterogeneity in centrosome size accounts for the alignment of the tripolar spindle.
To reproduce the situation in control embryos, we added an asymmetry in forces pulling the centrosomes to the simulation (Kimura and Onami, 2007; 2010). The simulation reproduced the asymmetry along the AP axis of the alignment of the tripolar spindle (Figure 7, C–experiment and F–simulation). This allowed the nonchromosome side to be concentrated near −90°, but not at +90°.
The results collectively support the model, in which the arrangement (i.e., the angle with respect to the long axis) of the tripolar spindle is determined by three factors: forces that pull the spindle poles depending on the cell geometry, heterogeneity of the centrosome size, and asymmetric pulling forces. This angle of the tripolar spindle determines whether a cell undergoes 1-furrow or 2-furrow cytokinesis, which leads to the inheritance of normal chromosome number or aneuploidy, respectively. The determination of the spindle arrangement depending on the three factors should not be limited to the tripolar spindle, but can be generally applied to all types of spindles.
DISCUSSION
In this study, we investigated the patterns of cytokinesis induced after the formation of a tripolar spindle. To induce tripolar spindles in the C. elegans one-cell stage embryonic cell, we used a paternal emb-27(g48ts) mutation. This enabled the determination of the effect of multipolar spindles in a cell using the maternal, wild-type emb-27 gene product. Therefore, the phenotypes observed for the cells were determined to be the consequence of the defects in the sperm. Notably, the emb-27 sperm not only has multiple centrosomes, but is also anucleated (Sadler and Shakes, 2000). Thus, the resultant zygotes are haploid, and we cannot exclude the possibility that ploidy affected the angle of the spindle and the pattern of cytokinesis. At low frequency, we obtained emb-27 mutant sperm with multiple centrosomes but nucleated. Observation of embryos created after fertilization with such sperm might help in excluding the possibility.
As extra centrosomes were delivered into a zygote with an emb-27 sperm, the mitotic spindle formed in the one-cell stage embryonic cell was multipolar (Figure 1). In this study, we focused on the tripolar spindle, because it is the simplest form of multipolar (more than two poles) spindles. When a tripolar spindle is formed, it does not always divide into three cells, with each daughter cell possessing one centrosome (i.e., 2-furrow cytokinesis); instead, division into two cells (i.e., 1-furrow cytokinesis) was more frequent. A daughter cell contains extra centrosomes, but the chromosomes are equally segregated with 1-furrow cytokinesis (Figure 3A). Therefore, induction of 1-furrow cytokinesis in a cell with a tripolar spindle can be a mechanism for avoiding aneuploidy. The decision of adopting 1-furrow or 2-furrow cytokinesis was likely dependent on the angle of the tripolar spindle against the long axis of the ellipsoidal cell (Figure 3). Unexpectedly, in the tripolar spindle of this study, only two of three sides were occupied by chromosomes. Currently, we cannot put forward any good hypothesis to explain this observation. It is noteworthy that the paternal emb-27 mutant cell used in this study does not contain paternal chromosomes (Sadler and Shakes, 2000); hence, the chromosomes from the maternal genome are separated to two sides of the tripolar spindle. A hint may come from our observation that the two sides correlated with the position of the large centrosome (Figure 7D). As the size difference was observed at NEBD, which occurs before the centrosomes capture the chromosomes via microtubules, the large size of the centrosome is not the consequence of being connected with two chromosome sides. It should be noted that the size difference among the centrosomes is not drastic and thus may not explain the occupation of two of the three sides of the tripolar spindle in all-or-none manner. A novel mechanism might exist to regulate the occupation of chromosomes in a mitotic spindle, which requires investigation in the future.
We observed that the major determinant of the decision between 1-furrow and 2-furrow cytokinesis is the angle of the tripolar spindle at NEBD: if it is close to 0°, the cell undergoes 2-furrow cytokinesis, whereas if it is close to −90° or +90°, the cell undergoes 1-furrow cytokinesis (Figure 3). The link between the angle and the patterns of cytokinesis was explained numerically by assuming that forces pull the poles of the spindle in a geometrical manner (Figure 5). Furthermore, we succeeded in explaining the tendency in the distribution of the angle at NEBD using the same theoretical framework by adding asymmetric pulling forces and considering the heterogeneity in the size of the three centrosomes (Figure 7). In conclusion, we propose that the angle of the tripolar spindle and the patterns of cytokinesis are regulated by three factors: cell geometry-dependent forces, cell polarity-dependent pulling forces, and heterogeneity in centrosome size. These mechanisms suggest why the majority of cells with tripolar spindles avoid aneuploidy in the one-cell C. elegans embryos.
Application of this mechanism to other cells/organisms might not be straightforward. The C. elegans embryonic cell is unique in terms of its ellipsoidal shape and the feature where only two of the three sides of the tripolar spindle are occupied by chromatids. However, our results clearly indicate the possible contribution of cell geometry to the behavior of multipolar mitotic spindles, and thus might provide a new insight when considering abnormal cell division induced by extra centrosomes, such as in the case of cancer. Further, the present study characterized the forces involved in the positioning of normal bipolar spindle, which are important for symmetric and asymmetric cell divisions.
MATERIALS AND METHODS
Worm strains and maintenance
The strains used in this study are listed in Supplemental Table S1 and were generated previously for another study (Kondo and Kimura, 2018). The strains were maintained under standard conditions (Brenner, 1974). To obtain paternal emb-27 mutant embryos, temperature shift and mating were conducted as follows: 10 gravid hermaphrodites of CAL0051 were placed on a fresh 60-mm plate and allowed to lay eggs at 16°C. After 21−28 h, the adults were removed from the plate, and the plate was incubated for another 26−30 h at 16°C. Next, the plate was transferred to 25°C and incubated for another 13−18 h. Subsequently, 30 males from the plate were moved to a new 35-mm plate with 10 hermaphrodites of CAL0182 (fem-1ts), which were grown at 25°C from L1/L2 stage to prevent self-fertilization, and for 13−18 h to induce mating, and the embryos from the hermaphrodites were observed.
Live-cell imaging microscopy
For observation of embryos in utero, anesthetized adult worms were placed on 2% agar pad and gently sealed with a coverslip (Kimura and Kimura, 2012). The samples were observed using a spinning-disk confocal system (CSU-X1; Yokogawa Electric, Tokyo, Japan) mounted on a microscope (IX71; Olympus). Images were acquired every minute for the thickness of 30 µm with 2-μm z-intervals at 20 ms exposure using a UPlanSApo 60× 1.3 NA objective (Olympus) equipped with an EM-CCD camera (iXon; Andor, Belfast, UK) controlled by the Metamorph software (Molecular Devices, Sunnyvale, CA).
Image processing and analysis
For the measurement of distance L between centrosomes in Figure 4, the coordinates of each centrosome in 3D (x, y, and z) were obtained manually from the images using ImageJ and the Euclidean distance was calculated. For the computation of angle in Figures 3, 4, and 7, the coordinates of centrosomes and AP poles in 3D were measured manually from the images, and the angle against the AP axis was calculated using a custom-written code in MATLAB (MathWorks, Natick, MA). In control cells, the angle θwt was calculated using the formula θwt = abs(−[acos{dot(BI, AP)/norm(BI) × norm(AP)} × 180/π] + 90), where BI and AP are the unit vectors connecting the two poles of the bipolar spindle and the unit vector of AP axis, respectively. In the emb-27 mutant embryos with a tripolar spindle, the angle of the nonchromosomal side to the AP axis, θtri, was calculated using the formula θtri = acos{dot(TRI, AP)/norm(TRI) × norm(AP)} × 180/π, where TRI is the unit vector of the nonchromosome side. If θ ≥ 90°, the value was subtracted from 180° and replaced with the original θ.
Measurement of centrosome size using γ-tubulin::GFP fluorescence (Figure 7D) was conducted at NEBD as described in our other study (Kondo and Kimura, 2018).
Numerical simulation to calculate the torque to open or close the tripolar spindle at anaphase ( Figure 5B) or to calculate stable angles of the tripolar spindle at NEBD ( Figure 7)
We constructed a 3D simulation assuming the cell to be an ellipsoid, with one major axis of 25 μm radius and two minor axes of 15 μm radius, which is similar to the actual cell (Figure 5A and Supplemental Table S2). As we focused on the angle of the entire tripolar spindle (Figure 7) or the angle of the chromosome sides (Figure 5B), we fixed the center of the spindle at the center of the cell and only considered rotational movements around the center of the spindle (Figure 7) or the center of the chromosome sides (Figure 5B). We also assumed the tripolar spindle to be an equilateral triangle inscribed in a circle of radius 5 μm on a plane (x-y plane in Figure 5A), including the AP axis, which is similar to the situation from NEBD to metaphase in the actual cell when the rotation occurs.
Forces acting on the spindle poles.
We assumed two kinds of forces to act on the spindle pole (Kimura and Onami, 2007, 2010). First is the geometry (cell shape)-dependent force. In this study, we adopted the cytoplasmic pulling force, which pulls the astral microtubules growing from the pole outside the spindle toward the cytoplasm (Hamaguchi and Hiramoto, 1986; Kimura and Onami, 2005; Kimura and Kimura, 2011b; Wühr et al., 2010; Tanimoto et al., 2016). Other mechanisms account for the geometry-dependent force, and should give similar results as long as they are approximately proportional to the length of microtubules (see main text for details). In this study, we assumed that the astral microtubules from one pole cover the entire region of the cytoplasm opposite to the spindle (Figure 5A, light-blue region). The direction and magnitude of the cytoplasmic pulling force acting on the pole were calculated by summing up all the unit vectors heading from the pole to each of the “force generation points” evenly distributed in the cytoplasm as the tetragonal lattice points with 0.5 + N(0, 10−6) μm interval (Figure 5A, cross), where N (0, 10−6) is a random number following normal distribution with mean at 0 and SD of 0.001 μm to minimize artifacts caused by the regular interval of the lattice. This setting is consistent with the cytoplasmic pulling force proportional to the length of each microtubule (Kimura and Onami, 2005; Kimura and Kimura, 2011a; Minc et al., 2011).
The other force is the cortical pulling force, which pulls the poles from the cortex via astral microtubules (Grill et al., 2001). In this study, the direction and magnitude of the cortical pulling force acting on the pole were calculated by summing up all the unit vectors heading from the pole to each of the “force generation points” evenly distributed as the tetragonal lattice points in the cortical region (Figure 5A, crosses in the orange region, which is 2 μm thick). This setting is consistent with the cortical pulling force acting on the pole proportional to area the cortical covered by the astral microtubules (Grill et al., 2003; Grill and Hyman, 2005; Hara and Kimura, 2009; Kimura and Kimura, 2011a). In the present simulation, we set the force generated by one force generation point in the cytoplasm to be 1 arbitrary force unit (AFU), whereas that in the cortical region to be kf, and 1.5 × kf (AFU) for anterior and posterior cortexes, respectively. The kf parameter was selected from among {0.2, 0.4, 0.6, 0.8, 1, 2, 3}, and we observed kf = 2 to yield the best result resembling the experimentally obtained angle distribution (Supplemental Table S2). The asymmetry in cortical pulling force was assumed to be 1.5-fold stronger at the posterior half based on an experimental estimation (Grill et al., 2003). When we introduced asymmetry in the centrosome size, we increased the forces generated by cytoplasmic force generators pulling the large pole to be l-fold. This number was selected from among {1.05, 1.1, 1.15, 1.2, 1.25}, and we observed l = 1.1 to yield the best result resembling the experimental distribution (Supplemental Table S2).
Calculation of torque to open or close the tripolar spindle at anaphase.
For this, we calculated the torque to rotate the two chromosome sides individually by summing up all the forces acting on the two centrosomes located at the ends of the side. The torque to open the spindle (i.e., increase in the angle between the two chromosome sides) was assigned the plus sign, and that to close (decrease the angle) was assigned the minus sign. The torque calculated for each side was summed to yield the total torque in Figure 5B.
Calculation of the torque to rotate the tripolar spindle at NEBD.
We predicted the stable angle of the tripolar spindle against the long (AP) axis of the embryo by calculating the potential energy landscape as developed by Théry et al. (2007) and that used in our previous study (Matsumura et al., 2016). By summing up all the forces acting on each pole and summing up the forces acting on the three poles, we calculated the torque acting on the center of the tripolar spindle (Figure 7). The torque was always acting to rotate the spindle around the z-axis, which was reasonable considering the symmetry in the geometry of the spindle.
Calculation of energy and probability.
By summing up the torque acting against the attempt to rotate the spindle from 0° configuration (Figure 5A) to the degree of interest with 1° intervals, we calculated the potential energy landscape as described previously (Théry et al., 2007). The unit of the energy (W(θ)) is [AFU × μm]. The probability to observe a particular angle was calculated as P(θ) = Nexp(−W(θ)/d), where N is a normalization factor and d is a coefficient to convert energy to probability (Théry et al., 2007). In this study, d was chosen among {10n × π/180}, where n = {4, 4.5, 5, 5.5, 6, 6.5, 7}; we found d = 5500 (n = 5.5) to yield the best result resembling the experimental distribution (Supplemental Table S2).
Likelihood to explain the experimental results with the simulation.
To select the best set of parameters (kf, l, d) in the simulation, we calculated the log-likelihood according to the following equation: [log-likelihood] = Σi6=1 log{Cns(i)Pns(i)}+ Σi6=1 log{Ccs(i)Pcs(i)}. Here, Cns(i) and Ccs(i) are the experimental counts of observing the nonchromosome side and the chromosome side, respectively, in the ith angle distribution class. The ith angle distribution class is the angle between −90 + 30(i−1) and −90 + 30i [°]. Pns(i) and Pcs(i) are the probability in the simulation of observing the nonchromosome side and the chromosome side, respectively, in the ith angle distribution class.
Statistical analyses
To determine whether the chromosome pole is significantly larger than the nonchromosome poles (Figure 7D), we conducted the binomial test. We tested whether the probability of the chromosome pole being larger than each of the other two centrosomes is significantly larger than half. We also tested whether the probability of the chromosome pole being the smallest among the three was significantly smaller than one-third.
The statistical difference of angle distributions (Figures 3B, 6, and 7, B and C) was tested in two ways: a binomial test and the Mardia−Watson−Wheeler (MWW) test. In the binomial test, we first calculated the expected probability of observing each group to compare (i.e., 1-furrow [as group A] vs. 2-furrow [as group B], or chromosome side [group A] vs. nonchromosome side [group B]) as PA and PB ( = 1 − PA). Next, we calculated the probability of observing group A or B for nA or nB times or more within nA + nB trials at the angle range of interest (e.g., −90 to −60°, −60 to −30°) under the assumption that the probability of observing A and B is PA and PB. The calculation was conducted using Microsoft Excel software.
The MWW test is a nonparametric test to compare the angle distribution of the two groups. The calculation was performed both with “hand calculation” using Excel following the procedure described in Mardia (1967), as well as with the “wason.wheeler.test” function of R software. The results obtained from both methods were in agreement with each other. For the comparison between 1-furrow and 2-furrow in gpr-1/2 (RNAi), we did not use chi-square test, but referred to a table by Mardia (1967) as the sample size was small (n = 15).
Acknowledgments
We thank the members of our laboratory for discussion; Daiju Kitagawa, Yasushi Hiromi, Mitsuhiko Kurusu, Hiroaki Seino, Kenji Kimura, and Yohei Kikuchi for critical reading of the manuscript; and Shuji Ishihara (The University of Tokyo) and Shogo Kato (The Institute of Statistical Mathematics) for an informative lecture on angular statistics. Certain worm strains used in this work were provided by the Caenorhabditis Genetics Center, which is funded by National Institutes of Health Office of Research Infrastructure Programs (P40 OD010440). T.K. was a National Institute of Genetics postdoctoral research fellow. This work was supported by JSPS (Japan Society for the Promotion of Science) KAKENHI (Grants no. JP15H04372, no. JP15KT0083, no. JP16H00816, no. 18H05529, and no. 18H02414 to A.K.), the Naito Foundation, and the Sumitomo Foundation (141028 to A.K.).
Abbreviations used:
- AFU
arbitrary force unit
- NEBD
nuclear envelope breakdown.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E19-01-0075) on February 20, 2019.
REFERENCES
- Boveri T. (2008). Concerning the origin of malignant tumours by Theodor Boveri. Translated and annotated by Henry Harris. J Cell Sci (suppl 1), 1–84. [DOI] [PubMed] [Google Scholar]
- Brenner S. (1974). The genetics of Caenorhabditis elegans . Genetics , 71–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bringmann H, Hyman AA. (2005). A cytokinesis furrow is positioned by two consecutive signals. Nature , 731–734. [DOI] [PubMed] [Google Scholar]
- Brinkley BR. (2001). Managing the centrosome numbers game: from chaos to stability in cancer cell division. Trends Cell Biol , 18–21. [DOI] [PubMed] [Google Scholar]
- Colombo K, Grill SW, Kimple RJ, Willard FS, Siderovski DP, Gönczy P. (2003). Translation of polarity cues into asymmetric spindle positioning in Caenorhabditis elegans embryos. Science , 1957–1961. [DOI] [PubMed] [Google Scholar]
- Earnshaw WC, Cooke CA. (1991). Analysis of the distribution of the INCENPs throughout mitosis reveals the existence of a pathway of structural changes in the chromosomes during metaphase and early events in cleavage furrow formation. J Cell Sci , 443–461. [DOI] [PubMed] [Google Scholar]
- Eckley DM, Ainsztein AM, Mackay AM, Goldberg IG, Earnshaw WC. (1997). Chromosomal proteins and cytokinesis: patterns of cleavage furrow formation and inner centromere protein positioning in mitotic heterokaryons and mid-anaphase cells. J Cell Biol , 1169–1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glotzer M. (2005). The molecular requirements for cytokinesis. Science , 1735–1739. [DOI] [PubMed] [Google Scholar]
- Godinho SA, Kwon M, Pellman D. (2009). Centrosomes and cancer: how cancer cells divide with too many centrosomes. Cancer Metastasis Rev , 85–98. [DOI] [PubMed] [Google Scholar]
- Godinho SA, Pellman D. (2014). Causes and consequences of centrosome abnormalities in cancer. Philos Trans R Soc Lond B Biol Sci , 20130467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golden A, Sadler PL, Wallenfang MR, Schumacher JM, Hamill DR, Bates G, Bowerman B, Seydoux G, Shakes DC. (2000). Metaphase to anaphase (mat) transition-defective mutants in Caenorhabditis elegans . J Cell Biol , 1469–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gönczy P. (2008). Mechanisms of asymmetric cell division: flies and worms pave the way. Nat Rev Mol Cell Biol , 355–366. [DOI] [PubMed] [Google Scholar]
- Gönczy P, Rose LS. (2005). Asymmetric cell division and axis formation in the embryo (October 15, 2005). In: WormBook, ed. The C. elegans Research Community, WormBook, /10.1895/wormbook.1.30.1, www.wormbook.org. [DOI] [PMC free article] [PubMed]
- Gotta M, Ahringer J. (2001). Distinct roles for Gα and Gβγ in regulating spindle position and orientation in Caenorhabditis elegans embryos. Nat Cell Biol , 297–300. [DOI] [PubMed] [Google Scholar]
- Greenan G, Brangwynne CP, Jaensch S, Gharakhani J, Jülicher F, Hyman AA. (2010). Centrosome size sets mitotic spindle length in Caenorhabditis elegans embryos. Curr Biol , 353–358. [DOI] [PubMed] [Google Scholar]
- Grill SW, Gönczy P, Stelzer EH, Hyman AA. (2001). Polarity controls forces governing asymmetric spindle positioning in the Caenorhabditis elegans embryo. Nature , 630–633. [DOI] [PubMed] [Google Scholar]
- Grill SW, Howard J, Schäffer E, Stelzer EHK, Hyman AA. (2003). The distribution of active force generators controls mitotic spindle position. Science , 518–521. [DOI] [PubMed] [Google Scholar]
- Grill SW, Hyman AA. (2005). Spindle positioning by cortical pulling forces. Dev Cell , 461–465. [DOI] [PubMed] [Google Scholar]
- Hamaguchi MS, Hiramoto Y. (1986). Analysis of the role of astral rays in pronuclear migration in sand dollar eggs by the colcemid–UV method. Dev Growth Differ , 143–156. [DOI] [PubMed] [Google Scholar]
- Hara Y, Kimura A. (2009). Cell-size-dependent spindle elongation in the Caenorhabditis elegans early embryo. Curr Biol , 1549–1554. [DOI] [PubMed] [Google Scholar]
- Hertwig O. (1885). Das Problem der Befruchtung und der Isotropie des Eies: eine Theorie der Vererbung. Jenaische Zeitschrift für Naturwissenschaft , 276–318. [Google Scholar]
- Holland AJ, Cleveland DW. (2009). Boveri revisited: chromosomal instability, aneuploidy and tumorigenesis. Nat Rev Mol Cell Biol , 478–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura A, Onami S. (2005). Computer simulations and image processing reveal length-dependent pulling force as the primary mechanism for C. elegans male pronuclear migration. Dev Cell , 765–775. [DOI] [PubMed] [Google Scholar]
- Kimura A, Onami S. (2007). Local cortical pulling-force repression switches centrosomal centration and posterior displacement in C. elegans . J Cell Biol , 1347–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura A, Onami S. (2010). Modeling microtubule-mediated forces and centrosome positioning in Caenorhabditis elegans embryos. Methods Cell Biol , 437–453. [DOI] [PubMed] [Google Scholar]
- Kimura K, Kimura A. (2011a). A novel mechanism of microtubule length-dependent force to pull centrosomes toward the cell center. Bioarchitecture , 74–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K, Kimura A. (2011b). Intracellular organelles mediate cytoplasmic pulling force for centrosome centration in the Caenorhabditis elegans early embryo. Proc Natl Acad Sci USA , 137–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K, Kimura A. (2012). Rab6 is required for the exocytosis of cortical granules and the recruitment of separase to the granules during the oocyte-to-embryo transition in Caenorhabditis elegans . J Cell Sci , 5897–5905. [DOI] [PubMed] [Google Scholar]
- Kondo T, Kimura A. (2018). Impaired chromosome segregation results in sperms with excess centrosomes in emb-27APC6 mutant C. elegans. 449538. [Google Scholar]
- Kwon M, Godinho SA, Chandhok NS, Ganem NJ, Azioune A, Théry M, Pellman D. (2008). Mechanisms to suppress multipolar divisions in cancer cells with extra centrosomes. Genes Dev , 2189–2203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lingle WL, Lutz WH, Ingle JN, Maihle NJ, Salisbury JL. (1998). Centrosome hypertrophy in human breast tumors: implications for genomic stability and cell polarity. Proc Natl Acad Sci USA , 2950–2955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardia KV. (1967). A non-parametric test for the bivariate two-sample location problem. J R Stat Soc Series B Stat Methodol , 320–342. [Google Scholar]
- Margolis RL, Andreassen PR. (1993). The telophase disc: its possible role in mammalian cell cleavage. Bioessays , 201–207. [DOI] [PubMed] [Google Scholar]
- Matsumura S, Kojidani T, Kamioka Y, Uchida S, Haraguchi T, Kimura A, Toyoshima F. (2016). Interphase adhesion geometry is transmitted to an internal regulator for spindle orientation via caveolin-1. Nat Commun , 11858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minc N, Burgess D, Chang F. (2011). Influence of cell geometry on division-plane positioning. Cell , 414–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishima M. (2016). Centralspindlin in Rappaport’s cleavage signaling. Semin Cell Dev Biol , 45–56. [DOI] [PubMed] [Google Scholar]
- Mogilner A, Wollman R, Civelekoglu-Scholey G, Scholey J. (2006). Modeling mitosis. Trends Cell Biol , 88–96. [DOI] [PubMed] [Google Scholar]
- Morin X, Bellaïche Y. (2011). Mitotic spindle orientation in asymmetric and symmetric cell divisions during animal development. Dev Cell , 102–119. [DOI] [PubMed] [Google Scholar]
- Nigg EA, Holland AJ. (2018). Once and only once: mechanisms of centriole duplication and their deregulation in disease. Nat Rev Mol Cell Biol , 663–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pihan GA, Purohit A, Wallace J, Knecht H, Woda B, Quesenberry P, Doxsey SJ. (1998). Centrosome defects and genetic instability in malignant tumors. Cancer Res , 3974–3985. [PubMed] [Google Scholar]
- Quintyne NJ, Reing JE, Hoffelder DR, Gollin SM, Saunders WS. (2005). Spindle multipolarity is prevented by centrosomal clustering. Science , 127–129. [DOI] [PubMed] [Google Scholar]
- Rappaport R. (1961). Experiments concerning the cleavage stimulus in sand dollar eggs. J Exp Zool , 81–89. [DOI] [PubMed] [Google Scholar]
- Ring D, Hubble R, Kirschner M. (1982). Mitosis in a cell with multiple centrioles. J Cell Biol , 549–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadler PL, Shakes DC. (2000). Anucleate Caenorhabditis elegans sperm can crawl, fertilize oocytes and direct anterior-posterior polarization of the 1-cell embryo. Development , 355–366. [DOI] [PubMed] [Google Scholar]
- Siller KH, Doe CQ. (2009). Spindle orientation during asymmetric cell division. Nat Cell Biol , 365–374. [DOI] [PubMed] [Google Scholar]
- Srinivasan DG, Fisk RM, Xu H, van den Heuvel S. (2003). A complex of LIN-5 and GPR proteins regulates G protein signaling and spindle function in C. elegans . Genes Dev , 1225–1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanimoto H, Kimura A, Minc N. (2016). Shape-motion relationships of centering microtubule asters. J Cell Biol , 777–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Théry M, Jiménez-Dalmaroni A, Racine V, Bornens M, Jülicher F. (2007). Experimental and theoretical study of mitotic spindle orientation. Nature , 493–496. [DOI] [PubMed] [Google Scholar]
- Wheatley SP, Wang Y-L. (1996). Midzone microtubule bundles are continuously required for cytokinesis in cultured epithelial cells. J Cell Biol , 981–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson EB. (1925). The Cell in Development and Heredity, New York: The Macmillan Company. [Google Scholar]
- Wühr M, Tan ES, Parker SK, Detrich HW, Mitchison TJ. (2010). A model for cleavage plane determination in early amphibian and fish embryos. Curr Biol , 2040–2045. [DOI] [PMC free article] [PubMed] [Google Scholar]