A sexually transmitted infection model with long-term partnerships in homogeneous and heterogenous populations

Abstract

Population models for sexually transmitted infections frequently use a transmission model that assumes an inherent partnership length of zero. However, in a population with long-term partnerships, the infection status of the partners, the length of the partnership, and the exclusivity of the partnership significantly affect the rate of infection. We develop an autonomous population model that can account for the possibilities of an infection from either a casual sexual partner or a longtime partner who was either infected at the start of the partnership or was newly infected. The impact of the long-term partnerships on the rate of infection is captured by calculating the expected values of the rate of infection from these extended contacts. We present a new method to evaluate partner acquisition rates for casual or long-term partnerships which produces in a more realistic number of lifetime sexual partners. Results include a SI model with different infectiousness levels for the transmission of HIV and HSV-2 with acute and chronic/latent infection stages for homogeneous (MSM) and heterogeneous (WSM-MSW) groups. The accompanying reproduction number and sensitivity studies highlight the impact of both casual and long-term partnerships on infection spread. We construct an autonomous set of equations that handle issues usually ignored by autonomous equations and handled only through simulations or in a non-autonomous form. The autonomous formulation of the model allows for simple numerical computations while incorporating a combination of random instantaneous contacts between individuals and prolonged contacts between specific individuals.

1. Introduction

The impact of long-term partnerships and concurrent partnerships has been the focus of many mathematical studies ranging from Monte Carlo simulations (Kretzschmar & Morris, 1996), stochastic simulations (Doherty, Shiboski, Ellen, Adimora, & Padian, 2006; Morris & Kretzschmar, 1997), stochastic and discrete simulations (Chick, Adams, & Koopman, 2000), network simulations (Admiraal & Handcock, 2016; Eames & Keeling, 2004; Keeling & Eames, 2005; Miller & Slim, 2017; Morris et al., 2009, 2010; Onaga, Gleeson, & Masuda, 2017; Volz & Meyers, 2007) and analytic network models (Miller & Slim, 2017). Other combination of statistical and population models have been developed to capture concurrency effects using a partnership-based concurrency index (Leung et al., 2012, 2017) and nested pair formation models (Leng & Keeling, 2018). Pair formation models and pair approximation models (see a review by Kretzschmar and Heijne (Kretzschmar & Heijne, 2017)), include long-term partnerships, but have difficulty representing infection from overlapping partnerships. In addition, for each population class, the model must contain subpopulations of each single or pair combination. This quickly increases the computational and analytical complexity of the model. Despite the continued growing power of computers to run more complex numerical simulations, there is still a need for analytic models where it is easy to understand the effect of heterogeneity on parameter estimation, to develop and validate approximation schemes for epidemics, to strengthen the link between modeling and epidemiologically relevant data, and to design intervention strategies. These are strengths of population models and thus it is important that we continue to evolve these models alongside data driven simulations.

In 1992 Watts and May (Watts & May, 1992) developed a model for including the transmission of HIV from a long-term partner as well as casual encounters with a SEIR (Susceptible-Exposed-Infected-Removed) population model. This model has not been exploited by mathematical epidemiologists. The Watts and May model has a few issues inhibiting its wide use. This first issue is the model is a non-autonomous system of differential equations, that is, a system that depends explicitly on time, which makes rendering typical mathematical epidemiological measures, such as reproduction numbers, difficult. Second, the model was developed for a single susceptible population, and it is not immediately clear how to generalize to a heterogeneous population. For example, a homogeneous group would be MSM (men who have sex with men) model and a heterogeneous group would be WSM-MSW (women who have sex with men and men who have sex with women). Third, as the model was attempting to capture concurrency effects, it was assumed that long-term partners initially chosen when infectious should be included in the rate of transmission by casual sexual encounter term. Fourth, it overestimates the effect of infection due to long-term partners by assuming all long-term partners could eventually become infected (Altmann, 1998). This last assumption is not true for exclusive partnerships. In addition, it is this assumption that mandates the use of the exposed class to avoid a singularity in the model.

One of the benefits of developing an autonomous system of ordinary differential equations for a population model with long-term partnerships is that we will be able to calculate a reproduction number for the system, ${\mathcal{R}}_0$, which represents the number of secondary infections one infected individual can generate on average in a susceptible population. We demonstrate a benefit of having an analytical reproduction number with graphical studies and sensitivity studies showing how long-term partnerships can increase the spread of disease under certain situations and inhibit the spread in others.

In this paper we develop an alternate population model that incorporates long-term partnerships, including multiple partnerships that are either serially monogamous or concurrent, in an autonomous SI population model. The effect of the long-term partnerships on the rate of infection is captured by calculating the expected values of these extended contacts. In short, the rate of infection due to long-term partners equals the expected value of product of the transmission rate times the fraction of infected contacts weighted by an exponential survival distribution of long-term partnerships. The model contains a few simplifying assumptions to make the system memoryless, that is, to avoid needing previous infection status at all times. While this model is intended for sexually transmitted infections, it could be expanded to any disease that has short “zero-length” contacts (a sneeze in a crowd) and extended length contacts (repeated exposure in a hospital stay, school-setting, or family unit). The rate of infection due to repeated exposure would equal the expected value of the transmission rate times the fraction of infected contacts weighted with a distribution of contact length. However, the details of the model simplifications will differ.

In order to make the model easy to understand and replicate, we keep the heterogeneity of the populations to a minimum, however this simple method may be expanded to large systems that capture the heterogeneity of real life. In addition to the analytic population model with the inclusion of long-term partnerships, we present a new treatment for the rates that individuals have casual or long-term partnerships which will result in a more realistic number of lifetime partners. First we will present the model for a homogeneous group; second we expand the model for a small heterogeneous group. The steps employed to expand the model can be easily duplicated to include a model with a large number of differential equations.

The model and results of this paper will be presented as follows. We begin in Section 2 with a new treatment of partner acquisition rates that will be incorporated into our model. Section 3 will contain the basics of the model, including simplifying assumptions. In Section 4 we calculate the rate of infection and reproduction number for the homogeneous system and in Section 5 for the heterogeneous system. In Section 6, we apply our models to HIV and HSV-2 data to see how much adding long-term partnerships, and possible concurrency, to the model changes the prediction of the spread of HIV and HSV-2. The results are presented graphically. Next, in Section 7, we perform sensitivity analysis on the reproduction numbers for the MSM and WSM-MSW models for HIV and HSV-2. Then in Section 8 we state our conclusions and present future avenues of inquiry. The appendix contains the calculations used to obtain some of the parameter values.

2. Partner acquisition rates

We distinguish between two types of sexual partnerships: long-term partnerships and casual partnerships (defined as a single instance of a sexual encounter), the latter being mathematically speaking, partnerships of inherent length zero. We model transmission by dividing the partner acquisition rates into these two partnership categories.

The standard model for partner acquisition, taking the average number of partners per time, works well for highly active individuals (interpreted here as a large number of partners over a lifetime), but overestimates the number of lifetime partners for more typical individuals. To explain why, we will use the data from the 2011 sexual partner survey (Chandra, Mosher, Copen, & Sionean, 2013, pp. 1–74). The survey lists a median 6 lifetime partners for women between ages 14 and 44 and a median of 8 lifetime partners for men between ages 14 and 44. Since the ages span 30 years, this gives a mean of 15 years of sexual activity.

Next we suppose we have a data value for the rate of acquiring sexual partners, c. If all of the sexual encounters were only casual encounters, then after a mean of fifteen years of sexual activity, the number of lifetime partners would be $15c$. So a data value of an average annual number of sexual partners of 1.3 would result in a lifetime number, $N_{lifetime}=15\cdot c\approx$ 19 partners, far above the median of the number of lifetime partners for men and women. Hence, we need a new treatment for the rates that individuals have casual or long-term partnerships per year to reflect the average population. We divide that rate into two parts, z and $p/\tau$, where p represents the average of the total number of long-term partners, τ represents the average long-term partnership duration, and z represents the average rate of casual encounters per year. For the average number of yearly long-term partnerships, $p=0$ represents no long-term partnership and $p>1$ could represent either serial monogamy or concurrent partnerships. If an average long-term partnership lasts τ years, then $p/\tau$ represents the rate of acquiring long-term partners. Then assuming a mean of 15 years of sexual activity (to match survey data (Chandra et al., 2013, pp. 1–74)), $N_{lifetime}$, will be $15\left(z+p/\tau \right)$. If the average duration of long-term partnerships is $\tau =4.3$ years, the average number of long-term partners in a year is $p=1.2$ and there are an average of yearly casual encounters of $z=0.14$, then the number of lifetime partners over 15 years is approximately 6. This is a much lower lifetime number than if we used the traditional partner acquisition rate (for example (Hyman, Li, & Stanley, 1999)) which does not distinguish between long-term and casual partners.

3. The basic model

We will make a few simplifying assumptions to our model to ease the discussion of the model derivation. We also recognize that there are limitations to our model's accuracy.

3.1. Simplifying assumptions and limitations

• •No death due to disease or removal from the sexually active population due to disease.
• •The total number of sexually active individuals is constant, $N\left(t\right)=N_0$.
• •All individuals mix randomly with constant casual and long-term partner acquisition rates.
• •The risk factors are fixed across time.
• •High risk behavior and all partnerships are not clustered in time or within social constraints.
• •While not all individuals in long-term partnerships know their HIV or HSV-2 status, we assume that, on average, infected individuals in long-term partnerships are likely to try to prevent transmission to their long-term partner. To keep the model simple, we have not included compartments for viral suppression through medication. To compensate for this omission, we model infection transmission prevention through 85% condom usage at the measured condom effectiveness for a particular infection. Including a separate viral suppression compartment in the infected population would allow for a more realistic and much lower condom usage percentage, but would complicate the derivation of this model.
• •Long-term partnerships are chosen at a time κ which is before the current time t when we measure infection. Setting the long-term partnership formation time in this manner does not modify casual encounters during the long-term partnership.
• •The survival of long-term partnerships can be expressed as an exponential distribution.
• •The time scale of the long-term partnership is removed from the model by computing the impact of long-term partnerships on the rate of infection as an expected value calculation.
• •The model does not distinguish whether multiple partnerships are serially monogamous or concurrent.
• •The heterogeneous model presented in this paper is limited to a distinction of gender and specific disease parameter values for each gender.
• •In the expected value calculation the fraction the of infected and susceptible populations at the time κ, when the long-term partnership began, is approximated by a difference formulation based on the differential equations.
• •There may be an upper limit on allowable concurrency probability, ξ, in order for the model to be applicable. A discussion about this upper limit may be found in Sections 4.4, 5.3. In the use of this model with HIV and HSV-2 infection parameters, there is no need to impose an upper limit.

Several of these assumptions are made only for ease of explanation. For example, disease death and a non-constant population, could be included in this model, but the derivation is more complicated. In addition, as a simplification, we limit the partnership heterogeneity of the populations to gender. By the term partnership heterogeneity we refer to partnerships with a difference in gender: females with male sex partners and males with female partners (WSM-MSW). However, this simple method may be expanded to large systems that capture the heterogeneity of real life. With this simplification of the model as our goal, we have also made the assumptions for random mixing, constant risks, and constant partner acquisition rates.

3.2. Description of the basic model

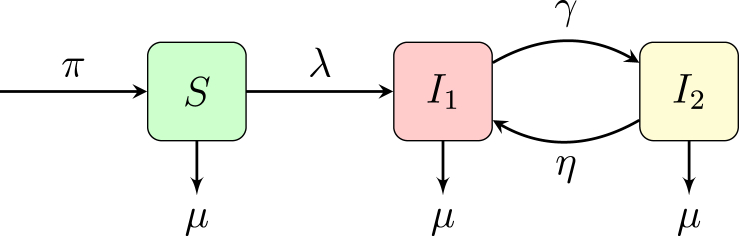
In our base SI model with infection stages with different infectiousness levels, i.e. differential infectivity, see Fig. 1, people enter the population S, the susceptible individuals, at a rate π, which represents the rate of joining the sexually active population. People move from S to $I_1$, the first infectiousness group at a rate of λ, which represents the rate of infection. Individuals move from $I_1$ to $I_2$ at a rate of γ where $1/\gamma$ represents the average length of time an individual is in the acute phase of infection. Individuals move from $I_2$ to $I_1$ at a rate of η where $1/\eta$ represents the average length of time an individual is in the chronic or latent phase of infection. In the case of HIV or HSV-2, $I_1$ would represent an acute phase which is significantly more infectious than stage $I_2$. For HIV, the acute phase is seven to ten times more infectious than chronic stage. In the case of HSV-2, individuals could return from the latent $I_2$ phase to $I_1$ during an active breakout. Each population can be exited by natural death μ.

Fig. 1.

$S{I}_1{I}_2$ model, where S is the susceptible population, $I_1$ is the acutely infected population, $I_2$ is the chronic or latent population.

The base model is described by the system of equations given below.

$$\begin{array}{ll}\frac{dS}{dt}& =\mu N_0-\lambda S-\mu S,\\ \frac{d{I}_1}{dt}& =\lambda S+\eta I_2-\left(\gamma +\mu \right)I_1,\\ \frac{d{I}_2}{dt}& =\gamma I_1-\left(\eta +\mu \right)I_2.\end{array}$$ (1)

The parameter descriptions are given in Table 1 with values for HIV and HSV-2 for the MSM population. Note that the values for z and p are calculated in the Appendix. While these numbers appear low, they are calculated from survey data (Glick et al., 2012; Van Tieu et al., 2014) where the MSM group had an average of 45 lifetime partners.

Table 1.

MSM Model: Parameter descriptions and values for HIV and HSV-2 $S{I}_1{I}_2$ simulations. Explanations for calculated values are in the appendix.

Param.	STI	Value	Description	Ref.
μ	Both	1/61 (1/years)	Natural death rate	CDC FAST STATS (2014)
τ	Both	0.53 years	Long-term Partnership Duration	Calculated in Appendix
z	Both	1.94 (1/years)	Average Number of Casual Partners/year	Calculated in Appendix
p	Both	0.56	Average Number of Long-term Partners	Calculated in Appendix
ξ	Both	24.6%	Ave. probability of Extra- partnership Sexual Act	Glick et al. (2012)
γ	HIV	365/90 (1/years)	Rate of transition from $I_1$ to $I_2$	(Fiebig et al., 2003; Robb & Ananworanich, 2016)
η	HIV	0	Rate of transition from $I_2$ to $I_1$	Estimated
${\beta }_2$	HIV	0.0149	Transmission probability for $I_2$	(Moghadas, Gumel, McLeod, & Gordon, 2003; Patel, Borkowf, Lasry, Lansky, & Mermin, 2014)
${\beta }_1$	HIV	$10.8\cdot {\beta }_1$	Transmission probability for $I_1$	(Hollingsworth, Anderson, & Fraser, 2008; Hughes et al., 2012; Pilcher et al., 2004, 2007)
$c_{eff}$	HIV	87%	Condom effectiveness	Moghadas et al. (2003)
$c_F$	HIV	$\left(1-c_{eff}\right)\cdot 85\text{\%}$	Transmission factor due to condom use	Estimated
γ	HSV-2	365/13 (1/years)	Rate of transition from $I_1$ to $I_2$	(Abu-Raddad et al., 2008; Wang, Yu, Tessmer, Kuniya, & Omori, 2017)
η	HSV-2	365/78.5 (1/years)	Rate of transition from $I_2$ to $I_1$	Abu-Raddad et al. (2008)
${\beta }_1$	HSV-2	.202	Transmission probability for $I_1$	Calculated in Appendix
${\beta }_2$	HSV-2	0	Transmission probability for $I_2$	Abu-Raddad et al. (2008)
$c_{eff}$	HSV-2	65%	Condom effectiveness	Magaret et al. (2016)
$c_F$	HSV	$\left(1-c_{eff}\right)\cdot 85\text{\%}$	Transmission factor due to condom use	Estimated

3.3. Total rate of infection: λ

Next we focus our discussion on the rate of infection, the term λ. Now that we have divided the yearly rate of acquiring sexual partners, c, into two categories, we recognize that the rate of infection should be divided into two categories as well since people can be infected by either their long-term or casual partners.

$$\lambda =\underset{\text{Infection}\text{rate}\text{from}\text{casual}\text{partners}}{\underbrace{{\lambda }_z}}+\underset{\text{Infection}\text{rate}\text{from}\text{long}-\text{term}\text{partners}}{\underbrace{{\lambda }_p^I+{\lambda }_p^S}}$$ (2)

The infection rate from casual partners, ${\lambda }_z$, will use the traditional mathematical model with a zero inherent length infection contact.

The infection rate from the long-term partners is further subdivided. Note that the infection rate is in terms of the proportion of infected individuals, $I_1/N$ and $I_2/N$. However, in the language of relationships we speak of partnerships between individuals. Throughout this paper we will discuss the infection by individuals and then make the adjustment to the fraction of the population by dividing by the total population. In the first part, ${\lambda }_p^I$, represents the rate of infection on a susceptible individual who forms a long-term partnership with an infected individual in $I_1$ or $I_2$. In the second part, ${\lambda }_p^S$, represents the rate of infection on a susceptible individual who forms a long-term partnership with an initially susceptible partner who later becomes infected by a sexual encounter outside of this partnership. We will distill the effect of the long-term partnership into expected values for the rates of infection ${\lambda }_p^I$ and ${\lambda }_p^S$. The bulk of this paper is devoted to the derivation of ${\lambda }_p^I$ and ${\lambda }_p^S$.

We begin with focus on the infections from casual partners. Then we model the contribution to the rate of infection from long-term partnerships in a homogeneous group, as did Watts and May (Watts & May, 1992), in Section 4 and expand the model to a heterogeneous group in Section 5.

3.4. Rate of infections from casual sexual encounters, ${\lambda }_z$

Let us assume that the transmission rate from an infected individual in population $I_1$ is $z{\beta }_1$ and the transmission rate from an infected individual in population $I_2$ is $z{\beta }_2$ where ${\beta }_1$ is the transmission probability per sexual encounter with an infected individual in $I_1$, ${\beta }_2$ is the transmission probability per sexual encounter with an infected individual in $I_2$, and z is the rate of casual sexual encounters. Then the total rate of infection from casual encounters is

$${\lambda }_z=\frac{z{\beta }_1{I}_1+z{\beta }_2{I}_2}{N_0}.$$ (3)

4. Rate of infection from long-term partners: homogeneous group

To give context for the derivation of the rate of infection term from long-term partnerships, ${\lambda }_p$, we revisit the population model of Watts and May (Watts & May, 1992). Starting with their model we will be able to alter the zero partnership length model of sexually transmitted infections to include long-term partnerships. Again, the idea is to include partnerships just as is accomplished by the powerful network and data driven simulation models, but to include these partnerships in a continuous ODE model to complement simulations. One weakness of the model of Watts and May is the fact that the model is non-autonomous.

A second weakness is the assumption that all susceptible partners can become infected by a partner who was initially chosen while susceptible but later became infectious. By including a non-exclusivity parameter, ξ, we remove this restriction and allow for the removal of the exposed stage. In the Watts and May model (see pg 97 of (Watts & May, 1992)) there is point with the removal of the exposed class where all susceptibles become infected which creates a “singular perturbation” (emphasis by (Watts & May, 1992)). Their incorporation of an exposed class into the model enables a time delay to avoid this problem. By recognizing that only initially susceptible long-term partners may become infected through a non-exclusive partnership, including the term ξ, provides a similar method to avoid this “singular perturbation.” Still, to be completely cautious we have mentioned in the assumption list in section 3.1, that there may be an upper limit on allowable concurrency probability, ξ, in order for the model to be applicable. A discussion about this upper limit may be found in Sections 4.4, 5.3. In the use of this model with HIV and HSV-2 infection parameters, there is no need to impose an upper limit.

A third weakness is that the model assumes if a long-term partner is infected when the partnership was formed, the infection is immediately transmitted with the same probability of a casual encounter. To allow for non-immediate infection we break the rate of infection within a long-term partnership, ${\lambda }_p$ into two parts, ${\lambda }_p^I$ and ${\lambda }_p^S$. In the first part, ${\lambda }_p^I$, a susceptible individual forms a long-term partnership with an infected individual who is in $I_1$ or $I_2$. In the second part, ${\lambda }_p^S$, a susceptible individual forms a long-term partnership with a partner who is initially susceptible, but later becomes infected by a sexual encounter outside of this partnership.

4.1. Rate of infection from long-term partners acquired when infectious ${\lambda }_p^I$

We assume that the rate of transmission of infection within a long-term partnership with an infected individual in $I_1$ is ${\chi }_1$. Similarly ${\chi }_2$ is the rate of transmission from a long-term partner in $I_2$. Both ${\chi }_1$ and ${\chi }_2$ will be fully described later in this section. We also assume that the infected partner has not transmitted the infection before time t. In essence, the rate of infection for the continuous ODE model by the fraction of infected long-term partners out of the total population is ${\lambda }_p^I$ is

$${\lambda }_p^I=E\left[\frac{{\chi }_1{I}_1+{\chi }_2{I}_2}{N}\right],$$ (4)

where $E[\left({\chi }_1{I}_1+{\chi }_2{I}_2\right)/N]$ represents the expected value of the rate of infection due to partners initially chosen while infectious. To be perfectly accurate, we will need to keep track of the number of infected individuals and total population for all time prior to the instant t at which we are measuring the populations. This is impractical, so we choose to lose some accuracy for a memory-free model. Thus, we will define ${\lambda }_p^I$ to be a linear approximation to $E[\left({\chi }_1{I}_1+{\chi }_2{I}_2\right)/N]$.

We begin the first stage of calculating this expected value by deriving the probability that an infected partner who is acquired at time κ transmits the infection at a later time t is given by the product of the following probabilities.

• 1.The probability that a partner acquired at time κ was infected at time κ: $P(X\left(\kappa \right)\in I_1\cup I_2)=(I_1\left(\kappa \right)+I_2\left(\kappa \right))/N_0=f\left(\kappa \right)$.
• 2.The probability that a partner acquired at time κ will still be a partner at time t: $P(X\left(t\right)\in Partner)$.

We begin by addressing step 2. Long-term partnerships form at the rate f and dissolve at the rate b. In addition, a death, at rate μ of either partner breaks the long-term partnership. Hence, the mean duration of a partnership is then

$$\tau =\frac{1}{b+2\mu }.$$ (5)

We assume that the length of a long-term partnership can be described by a distribution function that is a decaying exponential scaled by the length of an average long-term partnership.

$$P(X\left(t\right)\in Partner)=e^{\left(-\left(t-\kappa \right)/\tau \right)}$$ (6)

Then the expected value of the function f for a continuous random variable y, is defined as

$$E\left[f\right]={{\int }^{}}_0^{\infty }f\left(y\right)\frac{1}{\tau }{e}^{-y/\tau }d\left(y\right).$$ (7)

We change variables from y to κ, the time at which a long-term partner is chosen, by defining $y=\left(t-\kappa \right)$. Then the expected value of the function f is

$$E\left[f\right]={{\int }^{}}_{-\infty }^{t}f\left(\kappa \right)\frac{1}{\tau }{e}^{-\left(t-\kappa \right)/\tau }d\kappa .$$ (8)

Therefore we define

$$E\left[\frac{{\chi }_1{I}_1+{\chi }_2{I}_2}{N_0}\right]={{\int }^{}}_{-\infty }^t\left(\frac{{\chi }_1{I}_1\left(\kappa \right)+{\chi }_2{I}_2\left(\kappa \right)}{\tau N_0}\right)e^{\left(-\left(t-\kappa \right)/\tau \right)}d\kappa .$$ (9)

For (9) to be perfectly accurate, we need to keep track of the number of infected individuals and total population for all time prior to the instant t at which we are measuring the populations. For practical reasons, we choose to use a linear approximation to the expected value. In other words as we define the continuous function $f\left(x\right)={\chi }_1{I}_1\left(x\right)+{\chi }_2{I}_2\left(x\right)$, we need to incorporate $f\left(\kappa \right)$ in our expected value calculation using the linear approximation $f\left(\kappa \right)\approx f\left(t\right)+f^{\prime }\left(t\right)\left(\kappa -t\right)$.

$$\begin{array}{l}{\chi }_1{I}_1\left(\kappa \right)+{\chi }_2{I}_2\left(\kappa \right)\approx {\chi }_1{I}_1\left(t\right)\left[1+\left(\mu +\gamma \left(\frac{{\chi }_1-{\chi }_2}{{\chi }_1}\right)\right)\left(t-\kappa \right)\right]+{\chi }_2{I}_2\left(t\right)\left[1+\left(\mu -\eta \left(\frac{{\chi }_1-{\chi }_2}{{\chi }_2}\right)\right)\left(t-\kappa \right)\right]-{\chi }_1\lambda S\left(t\right)\left(t-\kappa \right).\end{array}$$ (10)

In other words, we are approximating the fraction of infectious individuals at time κ as the fraction of infected at time t plus the fraction of infected who died and subtracting off the fraction of individuals who became infected between times κ and t.

Then we can describe the rate of infection from the infected long-term partners as ${\lambda }_p^I$.

$${\lambda }_p^I\equiv \frac{{\chi }_1{I}_1\left(t\right){\text{Φ}}_1+{\chi }_2{I}_2\left(t\right){\text{Φ}}_2-\tau {\chi }_1\lambda S\left(t\right)}{N_0}\approx E\left[\frac{{\chi }_1{I}_1+{\chi }_2{I}_2}{N_0}\right],$$

where

$${\text{Φ}}_1=1+\tau \left(\mu +\gamma \left(\frac{{\chi }_1-{\chi }_2}{{\chi }_1}\right)\right),{\text{Φ}}_2=1+\tau \left(\mu -\eta \left(\frac{{\chi }_1-{\chi }_2}{{\chi }_2}\right)\right).$$ (11)

We follow the description of (Hyman, Li, & Stanley, 2001) to describe the transmission rates ${\chi }_1$ and ${\chi }_2$. The term ${\chi }_i$ is the transmission rate by a partner in the infected class $I_i$ with $i=1$ or 2. Just as with the casual sexual partnership infection term, the $I_i$ partner can possibly infect the susceptible partner in a single sexual act at a probability of ${\beta }_i$. However, since the partner is chosen while infectious, we assume that the partner mitigates the infection risk with condoms. We are not assuming all partners know their infection status, just that the average partner knows. We introduce the transmission factor term due to condom use, $c_F$. The term $c_F{\beta }_i$ is the transmission per sexual act, that represents the reduction from condom effectiveness and usage. The probability of not being infected in a single act is then $\left(1-c_F{\beta }_i\right)$. So the probability of not being infected after $n_i$ sexual acts with the $I_i$ partner is ${\left(1-c_F{\beta }_i\right)}^{n_i}$. Then the rate that the susceptible long-term partner will be infected from the $I_i$ long-term partner is

$${\chi }_i=\left(p/\tau \right)\left(1-{\left(1-c_F{\beta }_i\right)}^{n_i}\right),$$ (12)

where the term $p/\tau$ is the number of long-term partners per year, i.e. the rate of acquiring long-term partners. The exponent $n_i$ reflects the number of exposures over the duration of the partnership. The assumption is the standard conservative estimate of two sexual interactions per week for a year. Since an individual is in the infected class $I_1$ for only a portion of the long-term partnership, $1/\gamma$ (years), the exponent $n_1$ reflects this shortened time. For an individual in $I_2$, the exposure is for the entire duration of the partnership, τ (years).

$$n_1=104/\gamma \text{and}{n}_2=104\cdot \tau .$$ (13)

4.2. Rate of infection from long-term partners acquired when susceptible ${\lambda }_P^S$

Next we derive the rate of infection from long-term partners who were susceptible at the start of the partnership, ${\lambda }_p^S$. We assume the infection will be while the infected partner is in infection class $I_1$ since the new infection is most likely unknown to both partners. In addition, we do not assume that the long-term pair use condoms to prevent infection. Therefore

$${\lambda }_p^S=E\left[\frac{\psi I^{new}}{N}\right],$$ (14)

where $E\left[\psi I^{new}/N\right]$ represents the expected value of the fraction of newly infected (previously susceptible) partners per total population still in a partnership at time t and

$$\psi =\left(p/\tau \right){\beta }_1.$$ (15)

Again, to keep the model memory free we will define ${\lambda }_p^S$ to be a linear approximation to the expected value.

Next we derive the rate of infection from long-term partners who were susceptible at the start of the partnership, ${\lambda }_p^S$. We begin by modeling ${\lambda }_p^S$ by calculating the probability that a susceptible partner who is acquired at time κ, becomes infectious at time t and transmits is given by the product of the following probabilities. The full discussion of these probabilities and involved terms follows after the list of probabilities.

• 1.The probability that a partner acquired at time κ was susceptible at time κ: $P(X\left(\kappa \right)\in S)=S\left(\kappa \right)/N_0$.
• 2.The probability that a partner is still susceptible at time t given they were susceptible at time κ: $P\left((X\left(t\right)\in S)\right|(X\left(\kappa \right)\in S))$.
• 3.The probability distribution function that a partner acquired at time κ will still be a partner at time t: $P(X\left(t\right)\in Partner)=1/\tau \exp [-(t-\kappa )/\tau ]$.
• 4.The probability that the partner becomes infected at time t, $\lambda \left(t-\kappa \right)\xi$, where λ is the rate of infection, $t-\kappa$ the partnership length, and ξ is the probability that a partner is in engaged in an external (i.e. outside this long-term partnership) sexual partnership.

We begin with step 2, recognizing that

$$P\left((X\left(t\right)\in S)\right|(X\left(\kappa \right)\in S))=\frac{P((X\left(t\right)\in S)\cap (X\left(\kappa \right)\in S))}{P(X\left(\kappa \right)\in S)}.$$ (16)

The numerator of the conditional probability is the probability of choosing a partner that is susceptible at time κ and t, chosen from a pool of available partners at time κ. We approximate this numerator by

$$P((X\left(t\right)\in S)\cap (X\left(\kappa \right)\in S))=\min \left[\frac{S\left(t\right)}{N_0},\frac{S\left(\kappa \right)}{N_0}\right].$$ (17)

We note that to make an accurate approximation of these probabilities, $S\left(\kappa \right)/N_0$ and $S\left(t\right)/N_0$, we will need to use the flow out of the susceptible state, $dS/dt$. To make this derivation cleaner, the discussion about this flow appears after (22). So keeping with this temporary terminology, our conditional probability is then

$$\begin{array}{l}P\left((X\left(t\right)\in S)\right|(X\left(\kappa \right)\in S))=\text{min}[\frac{S\left(t\right)}{N_0},\frac{S\left(\kappa \right)}{N_0}]\cdot \frac{N_0}{S\left(\kappa \right)},=\text{min}[\frac{S\left(t\right)}{S\left(\kappa \right)},1].\end{array}$$ (18)

Our product of probabilities times the transmission rate is then

$$\begin{array}{l}[P(X\left(\kappa \right)\in S)\cdot P\left((X\left(t\right)\in S)\right|(X\left(\kappa \right)\in S))\cdot P(X\left(t\right)\in Partner)\cdot \\ \lambda \left(t-\kappa \right)\xi \cdot \psi ]=\frac{S\left(\kappa \right)}{N_0}\cdot \text{min}\left[\frac{S\left(t\right)}{S\left(\kappa \right)},1\right]\cdot \frac{1}{\tau }{e}^{\left(-\left(t-\kappa \right)/\tau \right)}\cdot \lambda \left(t-\kappa \right)\xi \cdot \psi .\end{array}$$ (19)

The expected value is

$$E\left[\frac{\psi I^{new}}{N}\right]=\frac{\xi \psi \lambda }{\tau N_0}{{\int }^{}}_{-\infty }^t\min \left[S\left(t\right),S\left(\kappa \right)\right]\left(t-\kappa \right)e^{\left(-\left(t-\kappa \right)/\tau \right)}d\kappa$$ (20)

Again, using (1) to compute a linear approximation to $S\left(\kappa \right)$ we have

$$S\left(\kappa \right)\approx S\left(t\right)[1+\lambda \left(t-\kappa \right)]-\mu \left(I_1\left(t\right)+I_2\left(t\right)\right)\left(t-\kappa \right)$$ (21)

and

$$\begin{array}{l}{{\int }^{}}_{-\infty }^t\min \left[S\left(t\right),S\left(\kappa \right)\right]\left(t-\kappa \right)e^{\left(-\left(t-\kappa \right)/\tau \right)}d\kappa =\tau S\left(t\right)\min \left[\mathrm{1,1}+\tau \left(\lambda -\mu \left(\frac{I_1\left(t\right)+I_2\left(t\right)}{S\left(t\right)}\right)\right)\right].\end{array}$$ (22)

In our simplification of this term we consider the following. If the rate of infection is increasing, then the minimum term equals 1. If the number of infected individuals is decreasing, then $\lambda \tau <\mu \tau \left(I_1\left(t\right)+I_2\left(t\right)\right)/S\left(t\right)$. The term $\mu \tau$ is a ratio of an average partnership duration over the average length of sexual activity, the latter being 61 years. The values for τ are calculated in section 6 for the WSM-MSW (women who have sex with men and men who have sex with women) populations from a survey of individuals of 14–44 years of age, with a result of $\tau =2.72$ for WSM-MSW couples. A second survey is used for the MSM (men who have sex with men) population with a computed $\tau =0.53$ years. These results are listed in Table 1, Table 2. Hence $\mu \tau \ll 1$. For medium to low rates of infection $\left(I_1\left(t\right)+I_2\left(t\right)\right)/S\left(t\right)<1$ . We can then make our simplification to the model that $\min \left[\mathrm{1,1}+\lambda \tau -\mu \tau \left(\frac{I_1\left(t\right)+I_2\left(t\right)}{S\left(t\right)}\right)\right]\approx 1$. Note that we get an equivalent result to Watts and May's definition that $P(X\left(\kappa \right)\in S)\cdot P\left((X\left(t\right)\in S)\right|(X\left(\kappa \right)\in S))\cdot P(X\left(t\right)\in Partner)\equiv S\left(t\right)/N\left(\kappa \right)$.

Table 2.

WSM-MSW Model: Parameter values for HIV and HSV-2 $S{I}_1{I}_2$ simulations. Explanations for calculated values are in the appendix.

Param.	STI	Value	Description	Ref.
${\tau }_{WM}$	Both	2.72 years	Long-term Partnership Duration	Calculated in Appendix
$z_M$	Both	0.19 (1/year)	Average Number of Casual Partners/year	Calculated in Appendix
$z_W$	Both	0.13 (1/year)	Average Number of Casual Partners/year	Calculated in Appendix
$p_M$	Both	0.81	Average Number of Long-term Partners	Calculated in Appendix
$p_W$	Both	0.87	Average Number of Long-term Partners	Calculated in Appendix
${\xi }_{WM}$	Both	11.8%	probability of Extra- partnership Sexual Act	Harper, Dittus, Leichliter, and Aral (2017)
${\beta }_{2M}$	HIV	0.004	Transmission probability for $I_{2M}$	Patel et al. (2014)
${\beta }_{2W}$	HIV	0.0008	Transmission probability for $I_{2W}$	Patel et al. (2014)
${\beta }_{1M}$	HIV	$10.8\cdot {\beta }_{1M}$	Transmission probability for $I_{1M}$	(Hollingsworth et al., 2008; Hughes et al., 2012; Pilcher et al., 2004, 2007)
${\beta }_{1W}$	HIV	$7\cdot {\beta }_{1W}$	Transmission probability for $I_{1W}$	(Hollingsworth et al., 2008; Hughes et al., 2012; Pilcher et al., 2004, 2007)
$c_{eff}$$c_{FW}$	HIV HIV	87% $\left(1-c_{eff}\right)\cdot 85\text{\%}$	Condom effectiveness Transmission factor	(Moghadas et al., 2003) (Magaret et al., 2016)
$=c_{FM}$			due to condom use
${\beta }_{1M}$	HSV-2	0.011	Transmission probability for $I_{1M}$	Calculated in Appendix
${\beta }_{1W}$	HSV-2	0.186	Transmission probability for $I_{1W}$	Calculated in Appendix
${\beta }_{2M}$$={\beta }_{2W}$	HSV-2	0	Transmission probability for $I_{2M}$ and $I_{2W}$	Abu-Raddad et al. (2008)
$c_{eff}^M$	HSV-2	96%	Condom effectiveness Men to Women	Magaret et al. (2016)
$c_{FM}$	HSV-2	$\left(1-c_{eff}^M\right)\cdot 85\text{\%}$	Transmission factor due to condom use	Estimated
$c_{eff}^W$	HSV-2	65%	Condom effectiveness Women to Men	Magaret et al. (2016)
$c_{FW}$	HSV-2	$\left(1-c_{eff}^W\right)\cdot 85\text{\%}$	Transmission factor due to condom use	Estimated

Our expected value and rate of infection due to partners chosen while susceptible is then

$${\lambda }_p^S\equiv \frac{\xi \psi \lambda \tau S\left(t\right)}{N_0}\approx E\left[\frac{\psi I^{new}}{N}\right].$$ (23)

4.3. Total rate of infection $\lambda ={\lambda }_z+{\lambda }_p^I+{\lambda }_p^S$

Combining the rate of infection from casual encounters and long-term partnerships, we can write the total rate of infection, λ, as

$$\begin{array}{ll}\lambda & ={\lambda }_z+{\lambda }_p^I+{\lambda }_p^S,\\ \lambda & =\frac{I_1\left(t\right)}{N_0}\left[z{\beta }_1+{\chi }_1{\text{Φ}}_1\right]+\frac{I_2\left(t\right)}{N_0}\left[z{\beta }_2+{\chi }_2{\text{Φ}}_2\right]-\lambda \frac{\tau S\left(t\right)}{N_0}\left[{\chi }_1-\psi \xi \right],\end{array}$$ (24)

where

$$\begin{array}{l}{\text{Φ}}_1=1+\tau \left(\mu +\gamma \left(\frac{{\chi }_1-{\chi }_2}{{\chi }_1}\right)\right),{\text{and}\text{Φ}}_2=1+\tau \left(\mu -\eta \left(\frac{{\chi }_1-{\chi }_2}{{\chi }_2}\right)\right).\end{array}$$ (25)

We note that (24) is an implicit equation for λ. Making the expression explicit for λ we have

$$\lambda =\frac{I_1\left(t\right)[z{\beta }_1+{\chi }_1{\text{Φ}}_1]+I_2\left(t\right)[z{\beta }_2+{\chi }_2{\text{Φ}}_2]}{N_0+\tau S\left(t\right)[{\chi }_1-\xi \psi ]}.$$ (26)

For the homogeneous group shown in Fig. 1, the $S{I}_1{I}_2$ model is described by the following system of equations.

$$\begin{array}{ll}\frac{dS}{dt}& =\pi -\left(\frac{I_1\left(t\right)[z{\beta }_1+{\chi }_1{\text{Φ}}_1]+I_2\left(t\right)[z{\beta }_2+{\chi }_2{\text{Φ}}_2]}{N_0+\tau S\left(t\right)[{\chi }_1-\xi \psi ]}\right)S-\mu S,\frac{d{I}_1}{dt}=\left(\frac{I_1\left(t\right)[z{\beta }_1+{\chi }_1{\text{Φ}}_1]+I_2\left(t\right)[z{\beta }_2+{\chi }_2{\text{Φ}}_2]}{N_0+\tau S\left(t\right)[{\chi }_1-\xi \psi ]}\right)S+\eta I_2-\left(\gamma +\mu \right)I_1,\\ \frac{d{I}_2}{dt}& =\gamma I_1-\left(\eta +\mu \right)I_2.\end{array}$$ (27)

Using the next generation method (Castillo-Chávez, Feng, & Huang, 2002), we calculate the reproduction number for the system, ${\mathcal{R}}_0$, as follows.

$${\mathcal{R}}_0=\frac{\left(\eta +\mu \right)[z{\beta }_1+{\chi }_1{\text{Φ}}_1]+\gamma [z{\beta }_2+{\chi }_2{\text{Φ}}_2]}{\mu \left(\eta +\gamma +\mu \right)[1+\tau \left({\chi }_1-\xi \psi \right)]}.$$ (28)

When infection due to long-term partnerships is ignored, this is equivalent to setting ${\chi }_1$, ${\chi }_2$, and ψ = 0. In this instance we return to the reproduction number of the casual encounter only system,

$${\mathcal{R}}_0^C=\frac{\left(\eta +\mu +\nu \right)z{\beta }_1+\gamma z{\beta }_2}{\mu \left(\eta +\gamma +\mu \right)}.$$ (29)

4.4. Discussion on upper limit restriction for concurrency probability: MSM

We note that the denominator term in the rate of infection and the reproduction number has a term that may be zero. We also note that keeping the denominator term in the reproduction number positive is more restrictive than keeping the denominator term positive in the rate of infection λ. To avoid the case where the term is nonpositive our initial requirement, $\xi <\min \left[\mathrm{1,1}/\left(p{\beta }_1\right)\right]$ for nonzero p, may be necessary to implement. Note if p is zero, the denominator term is always positive. To show why our assumption is necessary, we note that ${\chi }_1\tau \approx p{\beta }_1{n}_1{c}_F$ and $\psi \tau =p{\beta }_1$. So our condition for ${\mathcal{R}}_0>0$ requires

$$\frac{1}{p{\beta }_1}+n_1{c}_F>\xi ,$$ (30)

where $n_1$ represents the total number of sexual acts in the time period $1/\gamma$. When $c_F=0$, condom use and condom effectiveness is 100% and when $c_F=1$, condom use or condom effectiveness is zero. So in the ideal case of perfect condom use and effectiveness, we find the necessary condition $\xi <1/\left(p{\beta }_1\right)$.

So how does this affect our model for HIV and HSV-2? We have the following conditions:

$$\begin{array}{cc}\text{HIV}& \frac{1}{0.149p}+2.83>\xi ,\end{array}$$ (31)

$$\begin{array}{cc}\text{HSV}-2\text{:}& \frac{1}{0.202p}+5.01>\xi .\end{array}$$ (32)

Therefore, we see that there is no need to impose an upper limit on ξ.

5. Rate of infection with casual and long-term partners: heterogeneous group

5.1. Rate of infection due to partnership heterogeneity

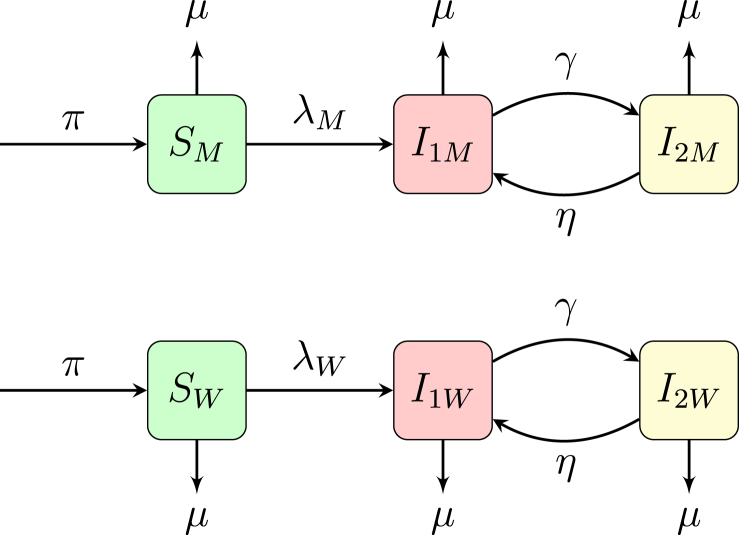
Suppose we can distinguish our sexually active population into two categories. For example, we move from modeling a homogeneous group such as MSM to a heterogeneous group as WSM and MSW. Then the number of populations doubles as shown in Fig. 2. For the sake of simplicity in this example we assume that the men and women move from category to category with the same rates, with the exception of rate of infection, but in actuality each parameter, including τ, the average duration of a long-term partnership, differs for men and women. The equations for this system are given as

$$\begin{array}{ll}\frac{d{S}_W}{dt}& =\mu N_W-{\lambda }_W{S}_W-\mu S_W,\\ \frac{d{I}_{1W}}{dt}& ={\lambda }_W{S}_W+\eta I_{2W}-\left(\gamma +\mu \right)I_{1W},\\ \frac{d{I}_{2W}}{dt}& =\gamma I_{1W}-\left(\eta +\mu \right)I_{2W},\\ \frac{d{S}_M}{dt}& =\mu N_M-{\lambda }_M{S}_M-\mu S_M,\\ \frac{d{I}_{1M}}{dt}& ={\lambda }_M{S}_M+\eta I_{2M}-\left(\gamma +\mu \right)I_{1M},\\ \frac{d{I}_{2M}}{dt}& =\gamma I_{1M}-\left(\eta +\mu \right)I_{2M}.\end{array}$$ (33)

Fig. 2.

Heterogeneous $S{I}_1{I}_2$ model with populations divided into two categories, W and M.

The parameter descriptions are given in Table 2 with values for HIV and HSV-2 for the WSM-MSW populations. Most of the previous model transfers from our previous example, however, the infection from the female long-term partner to the male long-term partner (and vice-versa) is akin to the host-vector problem of malaria. That is, in malaria, a susceptible mosquito gets infected by a human and then an infected mosquito infects a susceptible human. Because the transmission rates from mosquito-to-human and human-to-mosquito are not equivalent, the rates of the infection are not equivalent. In the context of HIV, the transmission rate from women to men is lower than the transmission rate from men to women (for HSV-2 the situation is reversed) and thus we have different rates of infection, ${\lambda }_W$ and ${\lambda }_M$.

If we look back at the model for the homogeneous group, we see we can divide λ into two parts. The first part is the infection from a casual partner or the previously infected partner, i.e. those terms with $I_1\left(t\right)$ and $I_2\left(t\right)$. The second part is the infection from a susceptible partner who has just become infected, i.e. those terms with $\lambda S\left(t\right)$.

$$\begin{array}{ll}\lambda & =\underset{\text{Infection}\text{rate}\text{from}\text{casual}\text{partners}\text{and}\text{previously}\text{infected}\text{long}-\text{term}\text{partners}\equiv T}{\underbrace{{\lambda }_z+{\lambda }_p^I}}+\underset{\text{Infection}\text{rate}\text{from}\text{newly}\text{infected}\text{long}-\text{term}\text{partners}\equiv -\lambda \theta }{\underbrace{{\lambda }_p^S}},\\ & =T-\lambda \theta .\end{array}$$ (34)

To translate this for our WSM-MSW populations, ${\lambda }_W$ has direct infection terms with $I_{1M}\left(t\right)$ and $I_{2M}\left(t\right)$ in addition to terms with ${\lambda }_M{S}_M\left(t\right)$. Hence, the rate of sexually transmitted infections within the populations M and W assuming women only interact sexually with men and men only with women, corresponding to (4.3) is

$${\lambda }_W=T_M-{\lambda }_M{\theta }_M,$$ (35)

$${\lambda }_M=T_W-{\lambda }_W{\theta }_W,$$ (36)

where

$$\begin{array}{l}{T}_M=\frac{I_{1M}\left(t\right)[z_M{\beta }_{1M}+{\chi }_{1M}{\text{Φ}}_{1M}]+I_{2M}\left(t\right)[z_M{\beta }_{2_M}+{\chi }_{2M}{\text{Φ}}_{2M}]}{N_M},\\ T_W=\frac{I_{1W}\left(t\right)[z_W{\beta }_{1W}+{\chi }_{1W}{\text{Φ}}_{1W}]+I_{2W}\left(t\right)[z_W{\beta }_{2_W}+{\chi }_{2W}{\text{Φ}}_{2W}]}{N_W},\\ {\theta }_M=\frac{\tau S_M\left(t\right)[{\chi }_{1M}-{\psi }_M\xi ]}{N_M},\\ {\theta }_W=\frac{\tau S_W\left(t\right)[{\chi }_{1W}-{\psi }_W\xi ]}{N_W},\\ {\text{Φ}}_{1M}=1+\tau \left(\mu +\gamma \left(\frac{{\chi }_{1M}-{\chi }_{2M}}{{\chi }_{1M}}\right)\right),\\ {\text{Φ}}_{2M}=1+\tau \left(\mu -\eta \left(\frac{{\chi }_{1M}-{\chi }_{2M}}{{\chi }_{2M}}\right)\right),\\ {\text{Φ}}_{1W}=1+\tau \left(\mu +\gamma \left(\frac{{\chi }_{1W}-{\chi }_{2W}}{{\chi }_{1W}}\right)\right),\\ {\text{and}\text{Φ}}_{2W}=1+\tau \left(\mu -\eta \left(\frac{{\chi }_{1W}-{\chi }_{2W}}{{\chi }_{2W}}\right)\right).\end{array}$$ (37)

Next, substituting (36) into (35) using the simplifying notation $T_M$, $T_W$, ${\theta }_M$ and ${\theta }_W$ we have

$${\lambda }_W=T_M-T_W{\theta }_M+{\lambda }_W{\theta }_M{\theta }_W.$$ (38)

Again, noticing ${\lambda }_W$ appears on both sides and solving for ${\lambda }_W$,

$${\lambda }_W=\frac{T_M-T_W{\theta }_M}{1-{\theta }_M{\theta }_W}.$$ (39)

and equivalently

$${\lambda }_M=\frac{T_W-T_M{\theta }_W}{1-{\theta }_M{\theta }_W}.$$ (40)

5.2. Reproduction number for heterogeneous group

Using the next generation method (Castillo-Chávez et al., 2002), for the heterogeneous group we find the reproduction number to be

$${\mathcal{R}}_0=\frac{-B\tau +\sqrt{B^2{\tau }^2+4A_M{A}_W[1-\left({\chi }_{1M}-{\psi }_M\xi \right)\left({\chi }_{1W}-{\psi }_W\xi \right){\tau }^2]}}{2\mu \left(\eta +\gamma +\mu \right)[1-\left({\chi }_{1M}-{\psi }_M\xi \right)\left({\chi }_{1W}-{\psi }_W\xi \right){\tau }^2]},$$ (41)

where

$$\begin{array}{ll}{A}_M& =\left({\beta }_{1M}{z}_M+{\chi }_{1M}{\text{Φ}}_{1M}\right)\left(\eta +\mu \right)+\left({\beta }_{2M}{z}_M+{\chi }_{2M}{\text{Φ}}_{2M}\right)\gamma ,\\ A_W& =\left({\beta }_{1W}{z}_W+{\chi }_{1W}{\text{Φ}}_{1W}\right)\left(\eta +\mu \right)+\left({\beta }_{2W}{z}_W+{\chi }_{2W}{\text{Φ}}_{2W}\right)\gamma ,\\ B& =[\left({\beta }_{1W}{z}_W+{\chi }_{1W}{\text{Φ}}_{1W}\right)\left(\eta +\mu \right)+\left({\beta }_{2W}{z}_W+{\chi }_{2W}{\text{Φ}}_{2W}\right)\gamma ]\left({\chi }_{1M}-{\psi }_M\xi \right)\\ & +[\left({\beta }_{1M}{z}_M+{\chi }_{1M}{\text{Φ}}_{1M}\right)\left(\eta +\mu \right)+\left({\beta }_{2M}{z}_M+{\chi }_{2M}{\text{Φ}}_{2M}\right)\gamma ]\left({\chi }_{1W}-{\psi }_W\xi \right).\end{array}$$ (42)

We see that ${\mathcal{R}}_0$ reduces to ${\mathcal{R}}_0^C$ when ${\chi }_{ik}$ and ${\psi }_k$ are set to zero for $i=\mathrm{1,2}$ and $k=M,W$.

$${\mathcal{R}}_0^C=\frac{\sqrt{z_M{z}_W\left(\gamma {\beta }_{2M}+\left(\eta +\mu \right){\beta }_{1M}\right)\left(\gamma {\beta }_{2W}+\left(\eta +\mu \right){\beta }_{1W}\right)}}{\mu \left(\eta +\gamma +\mu \right)}.$$ (43)

5.3. Discussion on upper limit restriction for concurrency probability: WSM-MSW

For ${\mathcal{R}}_0>0$ for the WSM-MSW population, we need the term

$$\frac{1}{p_M{p}_W{\beta }_{1W}{\beta }_{1M}}>\left(n_1{c}_{FM}-\xi \right)\left(n_1{c}_{FW}-\xi \right).$$ (44)

With the HIV and HSV-2 parameters we have the following conditions:

$$\text{HIV:}\frac{4133.6}{p_M{p}_W}>{\left(2.8-\xi \right)}^2,$$ (45)

$$\text{HSV}-2\text{:}\frac{488.8}{p_M{p}_W}>\left(0.1-1.2\xi +{\xi }^2\right)$$ (46)

Let us assume $p_M=p_W$. Then the equation with the HIV data will be satisfied for any ξ as long there are less than 64 long-term partners. With the HSV-2 data, as long there are less than 22 long-term partners then ξ does not need to be limited. In the “perfect storm” case of perfect condom use and effectiveness, high numbers of long-term partners and high infection transmission probabilities, then the condition will need to be imposed. In the implementation of our model with HIV and HSV-2 parameter values, no limitation on the upper limit of ξ is required.

$$\xi <\text{min}\left[1,\sqrt{\frac{1}{p_M{p}_W{\beta }_{1W}{\beta }_{1M}}}\right]$$ (47)

6. Comparison of reproduction numbers for MSM and WSM-MSW using parameter values from HIV and HSV-2

To illustrate the increase in sexually transmitted infections spread by including infection due to long-term partners in the model we provide numerical results with HIV and HSV-2 data for the homogeneous (MSM) and heterogeneous (WSM-MSW) population groups. The parameter values used for the MSM calculations are given in Table 1. Parameter values specific to WSM and MSW are given in Table 2.

The calculations for the parameter values for the MSM population with mean partnership duration τ, rates of acquiring casual partners z, and number of long-term partners p are given in the appendix. The equivalent parameter value calculations for the WSM-MSW populations are also included in the appendix.

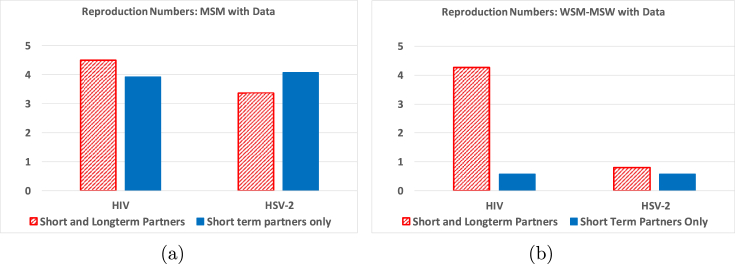
In Fig. 3 we present the values for the reproduction number, ${\mathcal{R}}_0$, for HIV and HSV-2 with and without long-term partnerships included in the model using the parameter values from Table 1, Table 2. In the calculation without long-term partners, the rate of acquiring casual partners is set to maintain the same average number of partners per year, $N^{average}=z\cdot \left(1\text{year}\right)+p$, between the models. That is, the values used were $z_{nolong-term}=z+p/\left(1year\right)$ and $p_{nolong-term}=0$. Fixing $N^{average}$ allows a comparison with the same number of partners per year between the two methods.

Fig. 3.

Test of the effect of the including long-term partnership information into the model on the reproduction numbers. All parameters are evaluated at the baseline HIV and HSV-2 values shown in Table 1, Table 2. Figure (a) represents MSM data and Figure (b) WSM-MSW data.

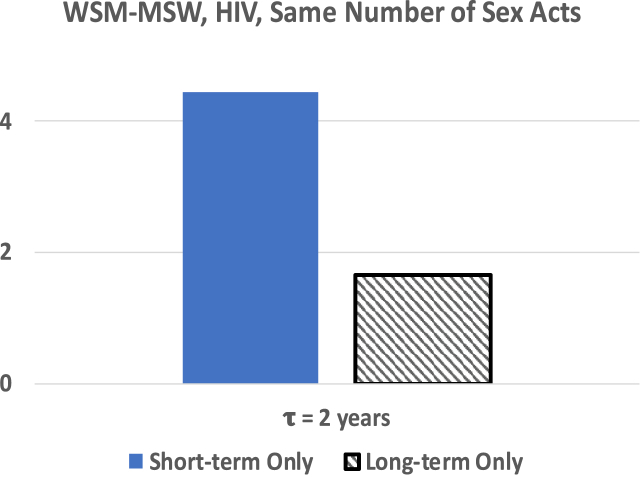
Fig. 4(a) shows that in the MSM community, including long-term partnerships that have an average length of approximately 1/2 year, in the model significantly increases the reproduction number for HIV. On the other hand, the WSM-MSW populations have an average partnership length of 2.72 years, with an increased probability of being in a long-term partnership. Fig. 4(b) shows that continued exposure to infected partners increases the reproduction number significantly for HIV. While this may initially seem contrary to what is expected, this result is to be expected due a higher rate of transmission from an infected long-term partner through repeated sex acts while each casual partner only shares one sex act. In Fig. 5 we keep the total number of sex acts constant regardless of whether only casual or long-term partnerships are involved. In this situation we see that long-term partnerships are protective for the same number of sex acts with causal partners. For a straight comparison of the equivalent number of sexual acts we assumed both the casual and long-term partnerships used the same level of transmission protection with condoms.

Fig. 4.

Test of the effect of the long-term partnership duration and the rate of acquiring long-term and casual partners on the reproduction numbers evaluated at baseline HIV parameter values shown in Table 1, Table 2 with the exception of τ and ξ. Both figures use $\xi =10\text{\%}$. The p and z values were chosen to keep the average number of partners over one year to be $4/3$. The vertical scale is different for (a) and (b) to best illustrate the effect of different p, z, and τ values for the different population groups. Figure (a) represents MSM results and (b) WSM-MSW results.

Fig. 5.

Reproduction number for WSM-MSW where the total number of sex acts per year is held constant.

Note that these models include only acute and chronic infection. If the model contained virally suppressed individuals, this increase in the reproduction number due to long-term partners should be less significant, although still present. In this instance the transmission rate by long-term partnerships may be less than through casual partnerships. This is a supposition that should be verified in a later paper.

For HSV-2, the reproduction number for the MSM population has a slight increase when long-term partnerships are included in the model. The reproduction number for HSV-2 shows a bigger increase for WSM-MSW. For HSV-2, we may suppose the long latency period provides a protective effect in a long-term partnership, but this is not clear since the number and duration of long-term partnerships and number of casual encounters is different between the MSM and WSM-MSW populations.

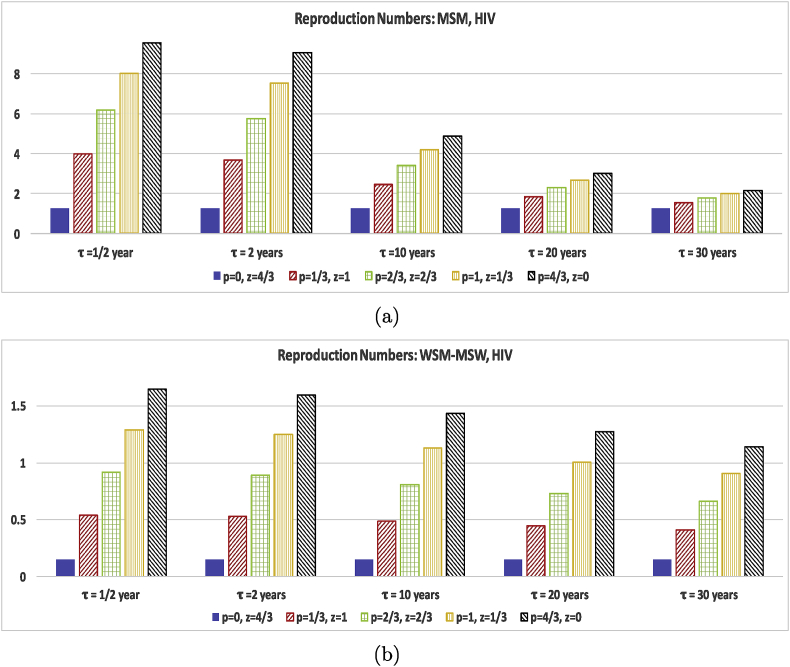
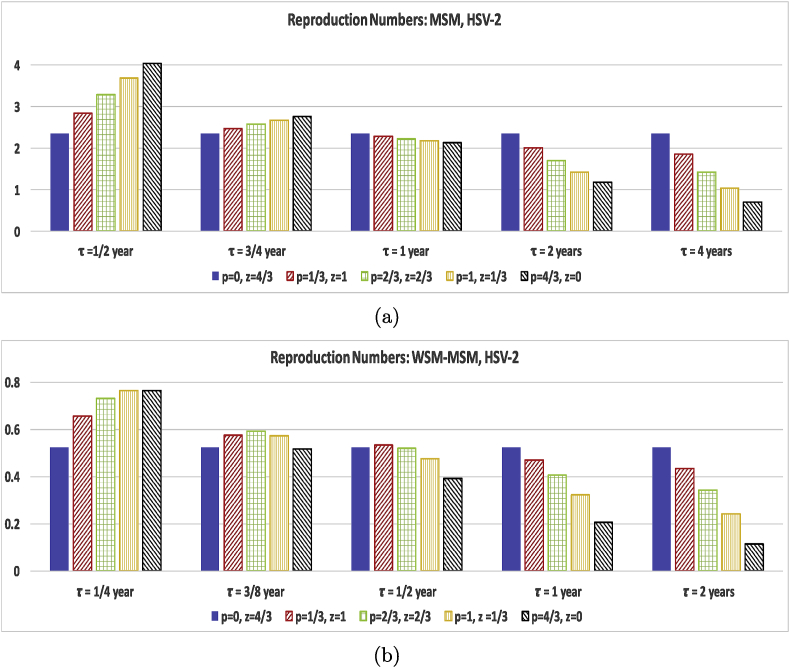
Thus to tease out the effects of long-term partnerships for homogeneous versus heterogeneous groups and infection for different length infection stages and different levels of infectivity we need to include a study comparing p, z, and τ on equal footing. So in Fig. 4, Fig. 6 we compare the effect of changing only the short and long-term partner acquisition rates for several partnership durations for the population for HIV and HSV-2 parameter values. We choose values for p and z so that the average number of partners, $N^{average}$, over one year is 4/3. For this test we fix the concurrency (non-exclusivity) probability to be $\xi =10\text{\%}$. We purposely choose low values of ξ and $N^{average}$ to capture the effect of choosing long or short term partners for individuals with only a few partners per year. We vary p and z while keeping all the other MSM data values for the homogeneous population and keeping all the other WSM-MSW data values for the heterogeneous populations. We then complete the calculations for several values of an average long-term partnership duration, τ since the long-term partnership duration is also a key factor.

Fig. 6.

Test of the effect of the long-term partnership duration and the rate of acquiring long-term and casual partners on the reproduction numbers evaluated at baseline HSV-2 parameter values shown in Table 1, Table 2 with the exception of τ and ξ. All figures use $\xi =10\text{\%}$. The $p=p_M=p_W$ and $z=z_M=z_W$ values were chosen to keep the average number of partners over one year to be $4/3$. The vertical scale is different for (a) and (b) to best illustrate the effect of different p, z, and τ values for the different population groups. Figure (a) represents MSM results and (b) WSM-MSW results.

Fig. 4, which represents HIV data parameters, shows that choosing long-term partners rather than casual partners for both MSM and WSM-MSW significantly increases the reproduction number for HIV. While the reproduction number for the WSM-MSW populations is less than one in the model capturing only casual partnerships, a few long-term partnerships tip the reproduction number over 1. The reproduction number for the MSM population does not show a significant reduction in the reproduction number as the long-term partnership duration increases from 1/2 year to 2 years. However, an increase to durations of 10, 20, and 30 years show that partnership duration length does make a significant impact on the reproduction number. The WSM-MSW reproduction number does not show the same strong dependence on the duration of the long-term partnership. The results affirm that HIV positive individuals in long-term partnerships should aim to be virally suppressed (lower transmission probability per act) in order to protect the susceptible long-term partner and to inhibit the spread of HIV in the general population.

While HIV is infectious in both the $I_1$ and $I_2$ stages, HSV-2 is only infectious in the short lived $I_1$ stage. As expected, incorporating HSV-2 data parameters into the reproduction number paints a very different story in Fig. 6. In the MSM population, including long-term partners into the model increases the reproduction number for long-term partnerships with duration of 1/2 years. As the duration τ increases even just to 3/4 year, Fig. 6(a) shows that the increase due to long-term partners is faltering. When the τ is increased to 1 year and beyond, the long-term partnership serves as a protective element in decreasing the infection spread. With all partnerships of an average duration of 4 years, the reproduction number drops below 1. For the WSM-MSW populations with only a few partners per year, the reproduction number remains below 1 for Fig. 6(b) regardless of whether short or long-term partners are chosen or the duration of partnership. Again as with MSM, short lived partnerships increase the infection spread, but once the average duration is 1/2 year, the long-term partnership acts an infection spread inhibitor. Note that we only modeled infectiousness reduction due to condom use, not including HSV-2 suppression treatment. Also, the condom reduction value used for the MSM calculation is only estimated from the well studied WSM-MSW values (Abu-Raddad et al., 2008; Schiffer, Mayer, Fong, Swan, & Wald, 2014; Wang et al., 2017), but studies (Turner et al., 2003) suggest that the reduction to be low. Thus the long-term partnerships do not significantly increase the reproduction number for MSM for durations of less than 4 years past the tipping point, ${\mathcal{R}}_0<1$. The story is more positive with the WSM-MSW population. Consistent condom usage does reduce transmission from men to women for HSV-2 by 96%, while women to men transmission is only reduced by 65%. Thus for the WSM-MSW populations we see a reduction in the reproduction number for long-term partners for a shorter duration average partnership length of 1/2 year, while the MSM population takes until durations of 1 year before reductions are seen.

7. Normalized forward sensitivity of ${\mathcal{R}}_0$

In this section we test the sensitivity of ${\mathcal{R}}_0$ to its parameters. We compute the normalized forward sensitivity index (Chitnis, Hyman, & Cushing, 2008) to determine changing which parameter values can impact the value of ${\mathcal{R}}_0$ for the two distinct populations: MSM and WSM-MSW. The sensitivity index with the reproduction number indicates the impact of the parameter on the disease free equilibrium. The forward sensitivity indices for these parameters are represented by

$${\mathcal{F}}_x=\left(\frac{\partial {\mathcal{R}}_0}{\partial x}\right)\cdot \left(\frac{x}{{\mathcal{R}}_0}\right),$$ (48)

where x represents the parameter. These forward sensitivity indices were evaluated using the baseline parameters given in Table 1, Table 2, with the results displayed in Table 3.

Table 3.

Forward sensitivity indices of ${\mathcal{R}}_0$ for $S{I}_1{I}_2$ models MSM or WSM-MSW populations evaluated at baseline HIV and HSV-2 parameter values shown in Table 1, Table 2.

Forward Sensitivity	Param.	MSM HIV	WSM-MSW HIV	MSM HSV-2	WSM-MSW HSV-2
${\mathcal{F}}_z$	z	+0.238	–	+0.630	–
${\mathcal{F}}_{z_W}$	$z_W$	–	+0.007	–	+0.099
${\mathcal{F}}_{z_M}$	$z_M$	–	+0.010	–	+0.387
${\mathcal{F}}_p$	p	+0.607	–	+0.290	–
${\mathcal{F}}_{p_W}$	$p_W$	–	+0.476	–	+0.393
${\mathcal{F}}_{p_M}$	$p_M$	–	+0.473	–	+0.138
${\mathcal{F}}_{\xi }$	ξ	+0.019	+0.002	+0.026	+0.005
${\mathcal{F}}_{\tau }$	τ	−0.045	−0.038	−0.349	−0.372

To get a measure of the importance of each parameter at the baseline value of the parameter, we look at the normalized forward sensitivity index of the basic reproduction number given in Equation (28) for the MSM model and Equation (41) for the WSM-MSW model. We calculate the sensitivity indices for the reproduction number with respect to the rate of acquiring casual partners, $z_i$, the number of long-term sexual partners, $p_i$, the probability that a partner is in engaged in an external sexual partnership, ξ, and the average duration of the long-term partnership, τ.

In order to understand how interpret these forward sensitivity indices, consider the forward sensitivity index of the reproduction number with respect to the rate of acquiring casual sexual partners, ${\mathcal{F}}_z$ in the MSM population. Looking at the corresponding forward sensitivity entry for ${\mathcal{F}}_z$ in Table 3 for the MSM group, a 10% increase (decrease) in the rate of acquiring casual sexual partners creates a 2.38% increase (decrease) in the basic reproduction number for HIV and 6.30% increase (decrease) for HSV-2. So the reproduction number for MSM with HIV data would increase from ${\mathcal{R}}_0=6.51$ to ${\mathcal{R}}_0=6.67$ when z rises from 1.94 partners per year to 2.13 partners per year. Note that the forward sensitivity index includes a measure of the size of the parameter. For example, z in the MSM model is 1.94 partners per year while $z_W=0.13$ and $z_M=0.19$ in the WSM-MSW model. So increasing the value of z by 10% from 1.94 to 2.13 represents a much larger rate of acquiring casual partners compared to increasing $z_W$ by 10% from 0.13 to 0.143.

From Table 3 it is clear that the reproduction number for the MSM model is most sensitive to changes in the parameter, p, the rate of acquiring sexual partners for HIV and to changes in the parameter, z for HSV-2. This is reflected in Fig. 4, Fig. 6. The changeover in Fig. 6 from $p=4/3$ increasing ${\mathcal{R}}_0$ for $\tau =1/2$ year to $p=4/3$ decreasing ${\mathcal{R}}_0$ for $\tau =1$ year and beyond can be explained by a comparison of the forward sensitivity numbers ${\mathcal{F}}_p=+0.290$ and ${\mathcal{F}}_{\tau }=-0.349$. Increasing p may make the reproduction number grow initially but as $\left|{\mathcal{F}}_{\tau }\right|>\left|{\mathcal{F}}_p\right|$, as τ increases, then even with an increased p value, the reproduction number decreases. The reproduction number for the MSM model with HIV data is less sensitive to the average duration of the long-term partnership, τ. As $\left|{\mathcal{F}}_p\right|\gg \left|{\mathcal{F}}_{\tau }\right|$, an increase in τ will not stop an increase in p from raising the reproduction number.

For the WSM-MSW populations, the reproduction number is most sensitive to increases in the number of long-term partners, $p_W$ and $p_M$. As with the MSM population, increasing the duration of the long-term partnership does not reverse the growth in the reproduction number caused by increasing $p_W$ and $p_M$. The insensitivity of the WSM-MSW model to $z_M$ and $z_W$ reflects why one must use unrealistically high partnership acquisition rates in a WSM-MSW HIV simulation without long-term partnerships, while it is clear HIV is spreading in the real world among heterosexuals with only few partners by comparing survey data of partnership information and CDC HIV statistics (Centers for Disease Control and Prevention, 2017).

For HSV-2, the sensitivity tests highlight the disparity between the sexes in the effectiveness of reducing transmission through condom usage. The reproduction number will grow 3.87% for each 10% increase in $p_W$ while only growing by 1.38% for a 10% increase in $p_M$. This reflects the 96% reduction in effectiveness of HSV-2 transmission from men to women and only a 65% from women to men. The flip in the behavior for $z_M$ and $z_W$, as we assume casual partners are less likely to use condoms, also reflects this effect.

The reproduction numbers for MSM or WSM-MSW show a weak sensitivity to an increase in the probability of non-exclusivity during long-term partnerships, ${\xi }_i$, for either HIV or HSV-2. In both, the forward sensitivity shows that the long-term partnership duration is more significant to the reproduction number than exclusivity. This raises the question, does this effect continue when an infected but virally suppressed population is introduced? This could lessen the chances of infection from a long-term partner selected when infectious enough to make exclusivity a more significant factor in comparison.

8. Discussion

In this paper we have developed a population model for sexually transmitted infections that includes the effect of infection spread through long-term partnerships. We partitioned our rate of infection into a term from casual partnerships and into a term from long-term partners. The extra timescale of the partnership is reduced to an expected value calculation. The manner in which we have included long-term partnerships allows for multiple long-term partnerships, although whether the partnerships are serially monogamous or concurrent is not captured. We also split the treatment of the partner acquisition rates, to achieve a more realistic number of lifetime sexual partners.

So why should one persist with a continuous population model over a discrete individual or network model? They both have their uses. A network model can incorporate more statistical data than a typical population model, but this comes at the price of huge computational complexity and lack of analytic results. As with any mathematical model of a physical system, we have made a few approximations to a true solution. These assumptions and approximations are stated in this paper along with the conditions under which these assumptions and approximations apply. With this newly developed population model we have developed a system of autonomous ordinary differential equations that can be used to perform quick numerical simulations over a short time interval or to equilibrium, and to compute analytical results such as the reproduction number.

Since we have an analytic expression for the reproduction number we are able to conduct sensitivity tests using the normalized forward sensitivity number to show how the spread of infection depends on the number of casual and long-term partners, long-term partnership exclusivity, and partnership duration. We found that the effects were infection dependent, that is the behavior of the reproduction number varied for HIV and HSV-2 infection parameters in each of the tests. We also showed that the reproduction number for a constant number of partners is highly sensitive to the duration of long-term partnerships for HSV-2, but not HIV. If the total number of sexual acts is held constant rather than the number of sex partners, then the reproduction number for HIV demonstrates that long-term partnerships provide a protective effect compared to the equivalent number of casual encounters.

We demonstrated how to develop the rate of infection for homogeneous or heterogeneous populations. Clearly any real world problem has populations with more than two types of subgroups, and this paper illustrates how to account for just two subgroups. However, the technique can be repeated for any number of subgroups. A long-term and casual sexual partnership model was successfully used in a SI model with multiple infection stages having different infectiousness levels, plus four sexual behaviors and three race/ethnicities for a total of 48 differential equations to describe HIV spread in the US (Gurski & Hoffman, 2016). A future research direction is to alter the model for other communicable diseases that have different time length exposure risks.

Handling Editor: J. Koopman

Appendix.

HSV-2 Calculations

With the length of the acute phase for HSV-2 at about 13 days (Abu-Raddad et al., 2008) and the length of the latent phase about 78.5 days (Abu-Raddad et al., 2008), there are about 4 acute phase cycles a year. The transmissions for HSV-2 for the MSM population is measured at 31 per 1000 sex acts (Turner et al., 2003) with no differentiation between acts in latent or acute phases. We define 1 cycle to be an acute phase + latent phase, which together averages 91.5 days. So we approximate ${\beta }_1$ to be

$${\beta }_1=\frac{31\text{transmissions}}{1000\text{acts}}\cdot \frac{104\text{acts}}{365\text{days}}\cdot \frac{91.5\text{days}}{1\text{cycle}}\cdot \frac{1\text{cycle}}{4\text{infectious}\text{acts}}=0.202.$$ (49)

Similarly we calculate ${\beta }_{1W}$ using 1.7 per 1000 acts (Schiffer et al., 2014) and ${\beta }_{1M}$ using 28.5 per 1000 acts (Schiffer et al., 2014).

Table 4.

Calculated parameter values for long-term partnerships.

Parameter	Value	Description	Ref.
$\ell$	30 years	Average length of sexual activity for lifetime survey respondent	Glick et al. (2012)
$N_{MSM}^{lifetime}$	45	Number of sexual partners over a lifetime, MSM	(Glick et al., 2012; Van Tieu et al., 2014)
$N_M^{lifetime}$	8	Number of sexual partners over a lifetime, MSW	Glick et al. (2012)
$N_W^{lifetime}$	6	Number of sexual partners over a lifetime, WSM	Glick et al. (2012)
$N_{MSM}^{Average}$	2	Average number of sexual partners over a year, MSM	(Glick et al., 2012; Van Tieu et al., 2014)
$N_M^{Average}$	1	Average number of sexual partners over a year, MSW	Glick et al. (2012)
$N_W^{Average}$	1	Average number of sexual partners over a year, WSM	Glick et al. (2012)
$F_{MSM}^{Partnered}$	39.4%	Percent in partnership, MSM	Van Tieu et al. (2014)
$F_{MW}^{Partnered}$	58%	Percent in partnership, MSW-WSM	Center (2017)
$f_{MSM}$	2.45/year	Formation rate for partnerships, MSM	Calculated
$f_M$	0.63/year	Formation rate for partnerships, M	Calculated
$f_W$	0.48/year	Formation rate for partnerships, W	Calculated
$b_{MSM}$	3.78/year	Breakup rate for partnerships, MSM	Calculated
$b_M$	0.39/year	Breakup rate for partnerships, M	Calculated
$b_W$	0.28/year	Breakup rate for partnerships, W	Calculated

We calculate values for the mean partnership duration τ, rates of acquiring casual partners z, and rates of acquiring long-term partners p from values in Table 1 and 4 for the MSM population. Similarly ${\tau }_{WM}$, $z_M$, $z_W$, $p_M$, and $p_W$ are calculated from values in Tables 2 and 4 for the WSM-MSW populations.

The mean long-term partner duration τ (representing both τ for MSM and ${\tau }_{WM}$ in this discussion), defined in Equation (5), is a function of the rate of partnership breakup and natural death.

To find the values for long-term partnership formation rate $f_i$ and breakup rate $b_i$, reported in Table 4, we used the mean number of lifetime partners and the expected fraction of people in a partnership. In this instance and further instances i represents $MSM$, M or W. From a study on changes in the distribution of opposite-sex partners in the U.S. (Glick et al., 2012), the mean number of lifetime partners is 6 for women and 8 for men. In the study the participants had approximately an average of 15 years of sexual activity. The number of lifetime number of partners (Kretzschmar & Heijne, 2017) is

$$N_i^{lifetime}=\frac{f_i\left(b_i+2\mu \right)}{\ell \left(f_i+b_i+2\mu \right)},$$ (50)

where $\ell$ represents the average length of time an individual is sexually active. We used the average age of respondents minus the average age of beginning sexual activity from (Glick et al., 2012) for the value for $\ell$, thereby setting $\ell =15$. Additionally we used the expected fraction of heterosexual people in a partnership, $F^{partnered}$ = 58/100 (Center, 2017). From (Van Tieu et al., 2014) the expected fraction for a MSM partnership is 394/1000. The equation for $F_i^{partnered}$ is

$$F_i^{partnered}=\frac{f_i}{f_i+b_i+2\mu }.$$ (51)

The average number of partners per year, $N_i^{average}$, was calculated from (Johnson et al., 2001) which measured that women average 2.4 male partners over 5 years and men average 3.8 female partners over 5 years. The rates of acquiring partners: $z_M$, $z_W$, $p_M$, and $p_W$ are calculated from $N_i^{average}$ and $N_i^{lifetime}$ given below.

$$N_i^{average}=\left(z_i\cdot \left(1\text{year}\right)+p_i\right)$$ (52)

$$N_i^{lifetime}=\ell \left(z_i+p_i/\tau \right)$$ (53)

The average percentage of concurrency is 14.6% for men and 9.0% for women (Johnson et al., 2001), so we define ${\xi }_{WM}$ to be the average value.

Appendix B. Supplementary data

The following is the Supplementary data to this article: