Elastographic Tomosynthesis From X-Ray Strain Imaging of Breast Cancer

Abstract

Noncancerous breast tissue and cancerous breast tissue have different elastic properties. In particular, cancerous breast tumors are stiff when compared to the noncancerous surrounding tissue. This difference in elasticity can be used as a means for detection through the method of elastographic tomosynthesis by means of physical modulation. This paper deals with a method to visualize elasticity of soft tissues, particularly breast tissues, via x-ray tomosynthesis. X-ray tomosynthesis is now used to visualize breast tissues with better resolution than the conventional single-shot mammography. The advantage of X-ray tomosynthesis over X-ray CT is that fewer projections are needed than CT to perform the reconstruction, thus radiation exposure and cost are both reduced. Two phantoms were used for the testing of this method, a physical phantom and an in silico phantom. The standard root mean square error in the tomosynthesis for the physical phantom was 2.093 and the error in the in silico phantom was negligible. The elastographs were created through the use of displacement and strain graphing. A Gaussian Mixture Model with an expectation–maximization clustering algorithm was applied in three dimensions with an error of 16.667%. The results of this paper have been substantial when using phantom data. There are no equivalent comparisons yet in 3D x-ray elastographic tomosynthesis. Tomosynthesis with and without physical modulation in the 3D elastograph can identify feature groupings used for biopsy. The studies have potential to be applied to human test data used as a guide for biopsy to improve accuracy of diagnosis results. Further research on this topic could prove to yield new techniques for human patient diagnosis purposes.

This paper tests a method to visualize elasticity of soft tissues, particularly breast tissues, via x-ray tomosynthesis. Testing with a physical phantom and an in silico phantom found the standard root mean square error in the tomosynthesis for the physical phantom was 2.093 and the error in the in silico phantom was negligible. Tomosynthesis with and without physical modulation in the 3D elastograph can identify feature groupings used for biopsy. These studies show the potential of human test data to be used as a guide for biopsy to improve accuracy of diagnosis.

I. Introduction

Elastography is an imaging technique that is now introduced to detect the tumors in the breast in addition to mammograms, which are the standard of care. Cancer tissues have different stiffness and elastic properties than that of normal breast tissue. It is due to this difference that elastography can be a powerful tool for detecting breast cancer. Elastography is particularly advantageous in 3D mammography because it is performed routinely as part of breast cancer screening. Further, breast tumors are often heterogeneous and a biopsy can easily miss sampling the diseased tissue, which results in a misdiagnosis [1].

Previous methods to acquire elastography can be categorized into several imaging platforms: Ultrasonography (US) [1]–[4], and others such as Magnetic Resonance Imaging (MRI) [9], Tactile Imaging [8], and Optical Coherence Elastography [10]. We summarize these methods for comparison in Table 1 and Table 2. Table 1 shows existing elastography methods using ultrasonography. First, Strain Imaging [1] is a technique in which compression from outside the body is applied to the tissue. An ultrasound is used to take images of the tissue before and after the compression happens. The stiffness of the materials can be determined by how much the compression deforms the tissue. The least deformed are the stiffest. There are limitations to this technique, due to the fact that the objects can move out of range of focus when the compression is applied. It also cannot be used on organs that are not close to the surface.

TABLE 1. Existing Elastography Methods Using Ultrasonography (US).

Method	Procedure	Limitation
Strain Imaging [1], [5], [6]	•an external compression applied to tissue •images before and after the compression are compared	•assumptions must be made about the nature of the soft tissue •image can move due to compression
Acoustic Radiation Force Impulse [4]	•creates 2D map of tissue stiffness •pulse of acoustic energy moves tissue •amount tissue is moved shows the tissue thickness	•only shows qualitative stiffness value along the axis of the beam
Supersonic Shear Imaging [2], [3]	•creates a source of shear waves which is moved through the medium at supersonic speed	•long acquisition time and expensive equipment

TABLE 2. Existing Elastography Using Other Types of Imaging.

Method	Procedure	Limitation
Magnetic Resonance Elastography [9]	•uses magnetic imaging to create a 3-D map of the tissue stiffness	•non clear contrast in resulting image
Tactile Imaging [8]	•translates the sense of touch into a digital image	•requires large vibration sensors that have long acquisition time
Optical Coherence Elastography [10]	•images are formed by mapping a mechanical property of the tissue	•low quality image due to speckle tracking
Phase Contrast Imaging [12], [13]	•images are formed by refraction of x-ray beams off of tissue structures	•lower contrast than external manipulation of tissue

Second, Acoustic Radiation Force Impulse Imagining (ARFI) [4] is a technique in ultrasound used to create a 2-D map of stiffness of material. Unlike the previous Strain Imaging, ARFI uses an internal ‘push’ inside the tissue in order to measure the stiffness of the material. The more that the tissue is pushed, the less stiff the tissue.

Third, Supersonic Shear Imaging [2], [3] is a type of ultrasonic imaging that can provide the user with a 2-D, real time map of tissue stiffness. This is done by creating a source of shear waves from inside the tissue of interest. This allows the viewer to see full time as the wave propagates through the tissue.

Table 2 shows existing elastography using other types of imaging. Magnetic Resonance Elastography (MRE) is performed by applying a mechanical vibrator to the surface of the patient’s body. The vibrations create shear waves that propagate down through the tissue. An image acquisition sequence measures the velocity of the waves before and after the wave bounces off tissue. This allows a computer to generate a full 3-D of the target area [9]. Tactile Imaging is a technique that translates the sense of touch into a viewable digital image. A probe with a pressure sensor array mounted on its face is used to deform soft tissue. The probe measures changes in the pressure pattern to create the image [8]. In Optical Coherence Elastography, images are made by mapping a mechanical property of the target tissue. The elastogram is formed on the microscale, showing the intermediate between that of cells and whole organs [10]. Phase Contrast Imaging (PCI) uses the refraction of x-ray beams off of tissue structures to determine the stiffness of different tissues [12], [13].

3-dimensional mammogram (3D-MMG), also called tomosynthesis, started developing in the last 5 years as a common screening procedure [14]. Elastography, however, has not been used for 3D-MMG. The resolution of 3D-MMG is much higher than traditional x-ray computed tomography (CT) and US, and the cost is less than MRI [30]. We hypothesize that 3D-MMG has a possibility to distinguish cancer types by utilizing the density/elasticity model and identification of specific Region of Interests (RoI) in 3D-MMG images. Elastography of breast tumors is underexplored and has the potential to provide novel biomarkers that can help to diagnose breast tumors. The idea of using elastic property difference to differentiate the cancerous tissue from normal breast tissue is quite innovative. If implemented successfully, the proposed technology can offer an effective way to diagnose breast cancer and help guide biopsy in the clinic.

In this paper, we propose X-ray Elastography to support a Computer-Aided Diagnosis (CAD) of a breast tumor or microcalcification. Unusual appearances of diagnostic mammography are found to be benign. As a golden standard, the biopsy procedure will be used to obtain actual tissue from the site for the pathologist, who will examine the sample microscopically to determine the precise cause of the abnormality. There are currently no comprehensive studies to analyze the cancer heterogeneity by comparison of radiology and pathology. Two image departments (radiology and pathology) provide complemental cancer features. Based on microcalcifications of diagnostic mammogram setting by comparison of microscopy, we can generate specific cancerous features such as density, stiffness, and elasticity.

The rest of the paper is organized as follows: Section II covers the relevant methods, Section III describes the proposed method in detail, Section IV discusses experimental results of the proposed method, and Section V concludes this paper.

II. Relevant Methods

There exists fundamental physics for X-ray Elastography, and tomosynthesis (3D-MMG). In this Section, we describe these two relevant studies for the proposed elastographic Tomosynthesis.

A. X-Ray Elastography

Fig. 1 illustrates the key modules of elasticity modeling [13]. X-ray mammography is the main imaging modality that is clinically used for the screening of micro calcifications. Elasticity imaging is used to measure the response of tissue as it reacts to a force or ‘push’ applied to the RoI, where two most prevalent methods, either a physical normal force, such as compression, or ultrasonic waves cause such a force through the tissue. The force is generated from directly inside the organ. The resulting displacement between resting and deformed is captured and is used to see the elasticity of different tissues [13]. This method is useful for identifying irregular growths, as the growth will generally have a differing elasticity from the surrounding tissue as shown in Fig. 1. The below equation models how a mechanical body moves in Cartesian coordinates:

where 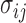are components of the stress tensor, 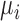are components of displacement vector, is the body force per unit volume in the 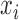direction, is the density in the media, and is time [16].

FIGURE 1.

X-ray elastography method using an ultrasonic wave to create the force on the region of interest. This diagram shows how an elastogram is captured for viewing.

B. Tomosynthesis (3D-MMG)

Fig. 2 illustrates the recent techniques on 3D-MMG [14], [15]. Digital x-ray tomosynthesis is a technique that uses slice images from basic x-ray to create a 3D picture. This method is prevalent in 3D-MMG and is used in a normal clinical setting. The slices are taken by having the x-ray tube rotate around the RoI and capture several slices. The slices are then digitally combined to produce a 3D model of the RoI.

FIGURE 2.

Concept of Tomosynthesis:. The tube rotates around to capture slices in a circle at a desired angle. The elements shown above can be seen in (2) and (3). Image receptors and X-ray Tube can vary in size and number.

The equation for x-ray attenuation of the overlying tissue is shown in (2).

where and are the diameter and attenuation coefficient of the nodule. 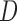and are the approximate thickness and attenuation coefficient of the overlaying tissue. is the original intensity and is the intensity exiting the tissue. The slice of 3D structure must be processed in order to compile all images from reduced view angles in tomosynthesis [14], [15].

The slices from tomosynthesis are digitally combined using iterative reconstruction techniques [14]. Iterative reconstruction is a means to create a 3D object from the 2D images. Eq. (3) below shows how to combine the 2D images.

where is the projection line integral through all voxels in the object along a given ray. is the density of structures in the 3D object, is the tomographic angle and 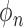is the azimuthal angle of the -th projection. l, m, n are used to represent the dimensions in a 3D space. The number of images taken must be 2K+1 [14].

III. Proposed Method: Elastographic Tomosynthesis

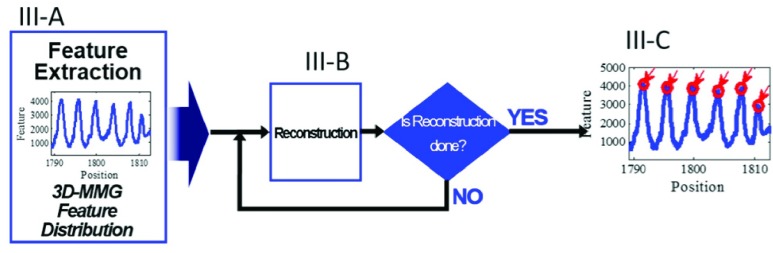
The proposed X-ray elastography of tomosynthesis consists of the following three modules: Section III-A Tomosynthesis of RoI, III-B Strain Map Extraction from 3D MGG, and III-C Cancer Feature Modeling. The overall processes are shown in Fig. 3.

FIGURE 3.

Overall processes of the proposed method and relationship among III-A, III-B, and III-C.

A. Tomosynthesis of RoI

The ability of tomosynthesis to create a 3D image of the RoI, coupled with the elastography, will allow the user to see the deformation in 3D. The multiple angles of tomosynthesis also reduces the superimposition of breast lesions by overlaying tissues [21]. After the individual X-ray slices have been captured, the slices must be reconstructed to produce the image. Reconstruction is the main aspect of digital tomosynthesis, and is what allows a 3D model to be produced from the mammography. A popular and effective reconstruction technique is Algebraic Reconstruction Technique (ART) [24]. Example of tomosynthesis is provided in Fig. 4.

FIGURE 4.

Images of the XCAT Phantom generated with the spherical tumor placed in the left breast. The tumor has a diameter of 10mm. (a) Shows the sagittal view while (b) shows the transverse view. The tumor is in red color.

The equation for the relationship between the 3D object and the 2D projections for the case of circular tomographic motion has been shown in Eq. (3) of Section II-B. The below equation is used to compute the raysums, assuming that the densities of the object can be estimated:

where is the raysum. is the density of structures in the 3D object, is the Tomographic angle and is the azimuthal angle of the 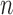-th projection. l, m, n are used to represent the dimensions in a 3D space. and refer to the q-th iteration and the -th projection image respectively [17]. A representation of many of these variables can be found in Fig. 2.

The error in each iteration is calculated as follows:

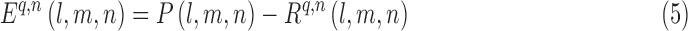where P(l, m, n) is calculated from Eq. (3) and is calculated from Eq. (4). is the error of an iteration. The voxel density is updated with each iteration using the following equation:

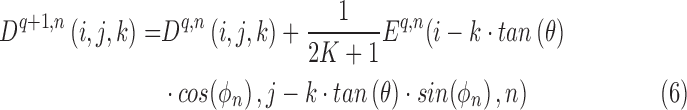The above algorithm uses the errors in Eq. (5) to be back projected along each ray. The next projection image is included, and its errors are back projected as well. This process continues until all slices have been used and have had their errors back projected. This is a single iteration, and the process will continue iterating until the error drops below a threshold as shown in Eq. (7). The threshold is set by the user in an empirical manner [36], and will produce a more accurate image the lower the threshold, named UDT.

where < means inequity where UDT should keep lowest. It is through ART that a true and clear model can be obtained, due to the fact that each iteration uses the back projected error to refine the voxel value [25]. Fig. 5 illustrates the steps in one iteration of the ART procedure.

FIGURE 5.

Flowchart of simple ART procedure. All variables shown are for all voxels in a RoI and can be calculated fully using Eqs. (3), (4), (5) and (6). The iterations will cease when is below some user defined variable UDT, as shown in Eq. (7).

B. Strain Map Extraction From 3D-MMG

The first step in the proposed method is to extract the key feature of the RoI. This key feature is the strain on the tissue under compression, which is consistent with the mechanical properties of a tissue’s elasticity. This feature is extracted by constructing a comparative strain graph. The strain calculation used to construct the graph is dependent on the deformation of an elastic tissue when exposed to some force or ‘push’ [19]. Strain can be calculated using the displacement of tissue in a respective dimension. The equation used is shown:

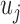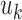where, , and are the displacement component in the 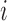-th, -th and -th directions. and are the spatial axes. is the strain in 2D. The equation given is just an example and the strain is calculated in 3D through a gradient system.

Strain on a tissue is directly related to the stress on a tissue when under force. The coefficient used to define the linear relationship between stress and strain is the elastic property of a material. This is shown below:

where is the Young’s modulus, is the force exerted on an object under tension, is the actual cross-sectional area through which the force is applied, is the amount by which the length of the object changes, and is the original length of the object. While there are other moduli of elasticity that can be used to describe an elastic material, the standard use is the Young’s modulus due to its straightforward equation and definition. Most other modulus can be calculated using Poisson’s ratio and Young’s modulus [20]. The shear modulus of elasticity is roughly equal to a third of Young’s modulus in soft tissue [18].

Stress on a tissue is calculated as a relation between the strain on the area and the material’s modulus of elasticity. The strain is how much a material moves when it is under force, and the elastic coefficient describes how much a material should be deformed under a force. The relationship is described in the equation shown:

where 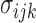is the stress in 3D, is the Young’s modulus that is constant for a homogeneous material, and is the strain in 3D. Both the stress and Young’s modulus are in units of Pascals and strain is a dimensionless unit [18].

It is not simple to calculate the Young’s modulus in a heterogeneous body, which is what the objective of this proposal is pertaining to. Due to this fact, the Young’s modulus and therefore stress are never calculated. It is possible however, to show strains on different areas of the RoI with pixel tracking. This is done through the use of a fast Fourier transform algorithm [28]. In the Fourier domain, the normalized cross-correlation is given to find displacement, shown:

where is the number of pixels in the template or interrogate block, (i, j, k) is the interrogate image block, (i, j, k) is the template image, and and are their Fourier transforms respectively.

In order to compute the displacement in subpixel resolution in a given direction, the center gravity method is used [27]. For an example, the x-direction is used, shown:

where 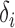is the x-directional subpixel increment from the 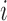-th pixel of maximum correlation. The other directions can be calculated in the same manner finding 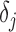and .

Table 3 shows the key features to be extracted in order to calculate the strain map. The formulas show how the features are related to one another.

TABLE 3. Key Features to be Extracted.

Name	Formula
Strain
Young’s Modulus
Stress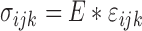
Displacement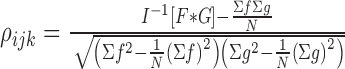
Displacement in a given direction

When the tissue is compressed, tissues with a higher Young’s modulus will be displaced a different amount than that of the tissue with a lower Young’s modulus. This displacement, which is calculated using Eq. (11) and then subsequently Eq. (12), can be used to create a comparative strain map. The comparative strain map is created in order to show how the different tissues reacted to the force. It is from this difference in displacement or strain that we can see which tissues have different elastic properties from each other. The mapping of the displacement and strain is done by taking the gradient of the subpixel resolution displacement vector.

These functions are used to derive Matlab code. This code’s objective is to produce a comparative strain graph, which is used in place of an absolute strain graph. Through the use of normalized cross correlation and sub-pixel tracking, the displacement is calculated. Using Eq. (12), we are able to fi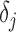nd , and 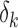, the separated displacement in each direction. These correlated values are stored in a 3xM matrix “d_vector”, where M is the number of displacement data points in a given direction. Eq. (12) is then applied to find the strain in all directions. This is done through a gradient system based on the displacement in a direction over all directions.

C. Cancer Feature Modeling

The general appearance of lesions is categorized in one of five images with elasticity scores 1, 2, 3, 4, and 5 [22], as shown in Fig. 6. Score 1 shows negative findings. Scores 2 and 3 show benign findings in oval areas surrounded by normal tissues. Score 4 shows suspicious abnormality for malignancy within the oval areas. Score 5 is highly suggestive of malignancy.

FIGURE 6.

The general appearance of lesions. The images represent the different elasticity scores from 1–5 with increasing chances of malignancy.

As the malignant cells begin to increase in number, they aggregate into 3D clusters [23]. This type of pattern motivates us to visualize the malignant cells with elastic feature. We can model these malignant cells by clustering the extracted elastic feature. The elastic feature can be positioned in 2D space. After computing the similarities between the feature data points, the similarity matrix can be sparsified only with feature data. In order to unite the elastic features which have strong correlation between each other and remove the noise generated from the elastic feature, we calculate the total strength of links coming out of the point. If two points have each other in the most nearest neighbors list, it constructs the unweighted shared nearest neighbor (SNN) graph with links between two points.

Other possible modeling techniques can be used. A popular and widely used modeling technique is the Gaussian mixture modeling with Expectation Maximization (EM) approach [23].

Eq. (13) above shows the maximizing of the log likelihood as respect to theta, or distance.

In order to better classify the difference in the key features of the mechanical features of IDC and DCIS, a finite mixture model (FMM) is used. A FMM is useful for categorizing a data set as belonging to a previously identified category (in this case type of cancer). The advantage is that a FFM is able to categorize data within a probability.

The FMM is able to provide a representation of heterogeneity in a finite number of latent classes. It is able to be used to model a statistical distribution by a mixture of other distributions.

IV. Experimental Results

A. Data

1). Physical Phantom

Data for a physical phantom was provided to us by a university in Korea. The physical phantom was generated with a cube of dimensions mm in a rigid cylinder of 10 mm length by 8 mm diameter placed in the center, which mimics breast cancer. The cube was imaged by methods of CT scanning under different amounts of pressure. A slice of the phantom is shown below in Fig. 7 (b). It can be seen that the rigid cylinder is visible in the center [27].

FIGURE 7.

(a) Shows a diagram of the dimensions of the coronal view of the phantom and shows the method by which the phantom was compressed [27]. (b) Shows a slice of the coronal view of the physical phantom through the use of Computational Tomography.

2). Phantom in Silico

We used 4D extended Cardiac-Torso (XCAT) phantom to validate the proposed method. The 4D XCAT phantom offers a realistic model of the human torso with control over cardiac and respiratory motion, which has been used in simulation of many studies [21]. Fig. 8 shows one of 16 frames of the generated phantom model. Its size is voxels.

FIGURE 8.

The difference in breathing through pixel level subtraction. The difference in the tumors is boxed in red and is zoomed in.

To get the 3D-MMG images of the phantom, Tomobox Matlab toolkit was used [26]. The size of the created 4D images was pixels for each scan. The full scan was created by using 360° rotations. 720 projections were created with 0.5° angle increments. Breathing phases were altered to provide the movement to make an elastography.

Fig. 9 shows both phantom in the transverse, coronal, and sagittal view as samples. Table 4 shows the comparison between physical phantom and phantom in silico in several parameters for the experimental data.

FIGURE 9.

The 3D Tomosynthesis of both the physical phantom and the phantom in silico. The top row shows the middle slice of 3D physical phantom, where (a) is the transverse view, (b) is the coronal view, and (c) is the sagittal view. The bottom row shows the middle slice of 3D phantom in silico, where (d) is the transverse view, (e) is the coronal view, and (f) is the sagittal view.

TABLE 4. Experimental Data.

	Physical Phantom	Phantom in silico
# of datasets	4	10
Size (voxels/dataset)
Single Gantry rotation (°)	360	360
Angular step size (°)	0.5	12
Detector panel size (pixels)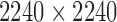
Distance between source and detector (mm)	524	1500
Distance bw source and object (mm)	167	1100
# of projections	720	30

B. Tomosynthesis of RoI Calculation

After the two phantoms are reconstructed, it is possible to calculate the error in our reconstruction methods using pixel value difference between the ideal version and our reconstructed version. The error is calculated by using the standard root mean square error (RMSE), as shown by Eq. (14).

where 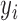is the pixel value of the original dataset, is the pixel value of the reconstruction on a by image slice.

The error taken using Eq. (14) above was also divided by the number of pixels per slice in order to calculate the average error on a pixel by pixel basis. Even though the physical phantom has far more pixels, the error in them far outstrips the in silico phantom. This suggests that with a larger the data set, in regard to the total number of pixels, a higher average error can be expected. Another way that error was explored was by changing the total number of x-ray projections used for the reconstruction process. In order to map the change in total error vs the number of projections used, Eq. (14) was used to find the error in each slice and then the average of all errors across all slices was taken. This process was repeated several times while varying the number of projections available for reconstruction.

The error results for the physical phantom can be viewed in Fig. 10 below. Fig.10 is useful for examining how error changes throughout the reconstruction process in response to relevant parameters. Fig. 10 (a) shows how error generally increases as the slice count increases. Fig. 10 (b) shows how the total error of the reconstruction decreases as the number of projections available for reconstruction increases. Increasing the number of projections used could potentially be useful for reducing the RMSE of reconstruction. Other potential sources of error for reconstruction are the breast slice thickness and projection angle used. These findings around the parameters of the study could be used to reduce error at reconstruction for future studies [31], [32].

FIGURE 10.

Reconstruction error for the physical phantom. (a) shows the Average RMSE per slice when the phantom is reconstructed using 30 projections. (b) shows the overall average RMSE of all slices when the number of projections used is varied.

Table 5 shows the difference between the average RMSE between the physical and in silico phantoms when a similar reconstruction technique is used. The table shows the massive difference in the resolution and the resulting RMSE between the two phantoms. The error in the in silico phantom is negligible, which is why a figure similar to Fig. 10 is not shown for the in silico phantom. The reason that the error for the in silico phantom is significantly lower is that the in silico phantom is of much lower resolution.

TABLE 5. Experimental Data.

	Physical Phantom	Phantom in Silico
Resolution of any given slice of Reconstruction (pixels x pixels)
Average RMSE at 30 projection reconstruction	2.093	1.67e-4

It can be seen that the difference in error is quite large between the in silico phantom and the physical phantom, even though the same method was used to calculate the error. This is most likely due to the fact that the physical phantom was of much higher resolution and more difficult to reconstruct accurately. The same goes for the human data, as the data involved slightly higher resolution.

C. Strain Map Extraction

For an effective strain map to be created, the phantom must undergo some force or ‘push’ to the tissue. This force is what causes the tissue to be mapped by stiffness coefficient.

The forces that are used on the two phantoms are shown above in Fig. 11. The force used on (a), the physical phantom, is provided through compression of the gelatinous material. The in silico phantom, shown in (b), due to the limitations of the simulation software was unable to have an outside force act upon it. By having the in silico phantom breath a small breath, a force is simulated and a strain map can be created.

FIGURE 11.

A vector map of the displacement in both the physical phantom as compression is applied and the in silico phantom as breathing occurs. (a) the vector map is placed over a slice of the coronal view of the uncompressed phantom. (b) the vector map is placed on the exhaled phantom.

The force is dispersed in 3D in the both of the phantoms due to their three-dimensional natures. For the physical phantom, the force is largely in the same direction as the compression, which is the k-direction referenced in Eqs. (8), (11) and (12). The component of displacement directly in parallel with the direction is more prominent in the areas that are close to the point of compression, i.e. the largest value of and the higher values of the transverse slice shown in Fig. 12. The displacements near to the lowest values are shown to move out toward the and directions, as the material pushes out due to compression and the bulk modulus of elasticity. This all can be seen in the four layers of displacement vector in Fig. 12.

FIGURE 12.

The displacement vector map in three dimensions for the physical phantom. This data is similar to the data in Fig. 11 (a) with an added dimension. Referring to the standard directions of orientation as used in Eqs. (8), (11) and (12), the coronal axis corresponds to the 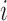direction, the sagittal axis corresponds to the direction, and the transverse axis corresponds to the direction.

Fig. 13 is an elastograph and is a plot of strain values at all location of the physical phantom near the RoI. It can be seen in the figure that the RoI is distinguished from the surrounding tissue. The RoI is made of a ridged plastic that does not have, or has low, elastic properties. The surrounding tissue, however, has a high elastic property and moves when the phantom is compressed. This is why the areas around the plastic insertion has a much higher strain value than that of the plastic insertion itself.

FIGURE 13.

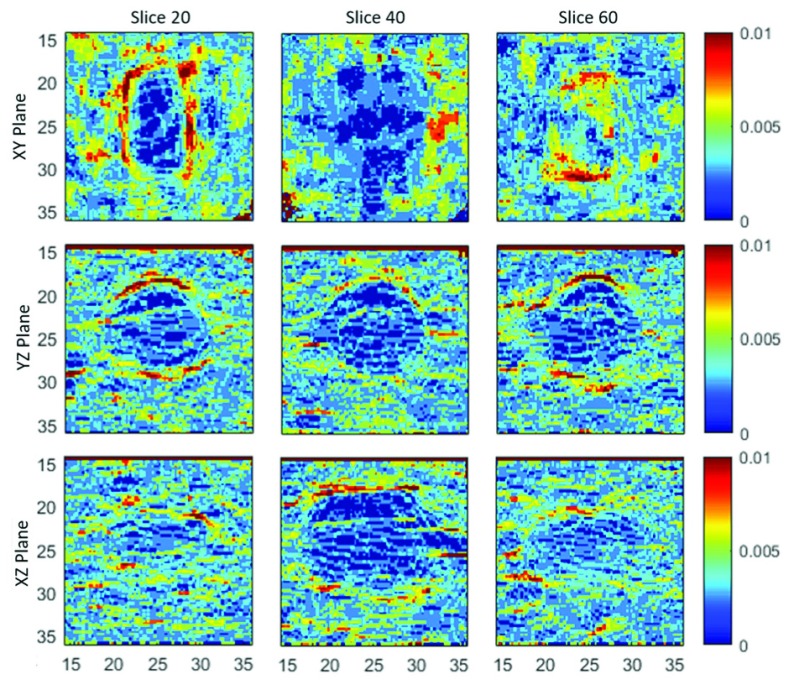
Absolute Strain Value Images in the xy plane (top), yz plane (middle), and xz (bottom) of the physical phantom from displacement in the i, j, and k direction. All images are of the middle most slice of the physical phantom.

Fig. 14 is similar to Fig. 13 in that it is an elastograph of the physical phantom. The figure shows instead the strain images at different slices of the phantom. It can be seen from the figure that the plastic insert can be more or less easily identified based on the strain direction and the slice of the plane that is viewed. The in silico phantom has a much more basic and linear displacement vector map than that of the physical phantom. As can be seen in Fig. 15, the chest of the phantom expands as the phantom inhales. This motion simulates compression or manipulation of the tumor. There is no displacement in the direction of the in silico phantom, as the chest expands freely. The direction in this case runs normal to the transverse plane in an anatomical model. The displacement of the phantoms is used to create our strain maps. The strain maps are computed using the methods from section above.

FIGURE 14.

Absolute Strain Value Images in the xy plane (top), yz plane (middle), and xz (bottom) of the physical phantom from displacement in the k direction. The first column is slice z (top) = x (middle) = y (bottom) = 20. The second column is slice z (top) = x (middle) = y (bottom) = 40. The third column is slice z (top) = x (middle) = y (bottom) = 60.

FIGURE 15.

The displacement vector map in 3D for the in silico phantom.

The pixel level subtraction shown in Fig. 16 shows that there is a definite change in position of the RoI. While this is not a true elastography and is not a suitable replacement for one, it does serve as a rough representation of how an elastograph is created. The combination of the movement vectors and the pixel level subtraction allows us to create an image that is representative of the elastic properties of the tissues. The phantoms both exhibit the same patterns when the pixel subtractions are viewed. The RoI is outlined in black, specifically in the area on the opposite side of the RoI that force was applied. This is due to the fact that the RoI is ridged and would not change in structure nearly as much as the surrounding tissue. Conversely, the soft tissue directly touching the RoI on the side opposite of the applied force is lightly colored. This points to the fact that the surrounding tissue is of a lower stiffness, and would change more than the RoI.

FIGURE 16.

A pixel subtraction of the physical phantom and in silico phantom after tomosynthesis of the uncompressed and compressed data sets of the physical phantom. The view shown is the coronal view (a) and transverse view (b). The RoI is boxed in red.

D. Elastic Feature Clustering

Fig. 17 identifies scattered feature points rather than the main cancer region. This shows that SNN is not appropriate choice for feature clustering for this slide of physical phantom elastography. When EM is applied rather than SNN, there is much better detection of the cancer region as shown in Fig. 18.

FIGURE 17.

The 2D phantom Elastography that was used in the feature clustering. This particular plot is the absolute strain in the z direction as viewed from the coronal plane. The elasticity feature extracted in red with the SNN clustering algorithm applied.

FIGURE 18.

The Gaussian mixture model with EM technique when applied to the data in Fig. 17. The maximum allowed groups of data was 5, but only three were found. The cancer can be seen as the red cluster.

Fig. 19 is the data from Fig. 18 overlaid on top of physical phantom shows the accuracy of EM clustering. The cluster group 1 detects the cancer and represented by the color red.

FIGURE 19.

The Gaussian mixture model with EM technique when applied to the data in Fig. 18. The maximum allowed groups of data was 5, but only three were found. The cancer can be seen as the red cluster. This shows the same clustering, but overlaid onto the Elastograph.

Fig. 20 shows 3D clustering features in the 5 group regions, and Fig. 21 shows the clusters imposed on top of each other. Each color represents each feature group. We conducted quantitative analysis of the feature group by iterating the log likelihood in the variable of group k. The region numbers this experiment used for EM went from 2 to 10 as shown in Fig. 22. The group with the best log likelihood was found to be k = 7. The log-likelihood graph shows that maximum region number can be relatively small. Different maximum region numbers were evaluated using clustering criteria as shown in Table 6. The three representative criteria of Cralinski-Harabasz, Davies-Bouldin, and Silhouette are used to evaluate the optimal number.

FIGURE 20.

The clustering of the elastic property in three dimensions with a max of 5 group regions.

FIGURE 21.

The clustering of the elastic property in three dimensions with a max of 5 group regions.

FIGURE 22.

The log likelihood at each iteration in the variable of group k. k ranges from 2-10.

TABLE 6. Experimental Data.

Algorithm	SNN		Gaussian Mixture with EM
Criterion	Value	Optimal K	Value	Optimal K
Calinski-Harabasz	656.34	7	712.92	7
Davies-Bouldin	0.79	5	0.759	4
Silhouette	0.485	4	0.604	2

Cralinski-Harabasz test results are higher for a more optimal , while Davies-Bouldin, and Silhouette test results are lower.

The maximum region number is selected as six, as at this region number clustering most accurately groups the cancer insert. Fig. 23 shows 3D clustering features in the 6 region number. The cancer insert is identifiable by the large, cylindrical shape in the middle of the insert. The different clusters, including the one corresponding to the cancer insert, can be easily identified in Fig. 24.

FIGURE 23.

All cluster regions overlaid on top of each other.

FIGURE 24.

The groupings of 3D clustering features in the physical phantom extracted of 6 region. The cancer insert is identified in the large cylindrical cluster #3.

There are few studies in 3D x-ray elastographic tomosynthesis, and this study is the first to perform all relevant methods on the same dataset. Comparisons to existing studies have been included in Table 7. Kim et al. [27] uses the same physical phantom as this study and strain displacement maps for comparison may be found there. The method in this study shows a 21.5% decrease in running time per slice from the previous study using the same dataset.

TABLE 7. Comparison to Existing Study.

	Others	This Study
Reconstruction Error of In Silico Phantom	.043(RMSE) [34]	.1.67e-4(RMSE)
Reconstruction Error of Physical Phantom	23.57 EE/N [35]	2.093(RMSE)
Running Time	325(s/slice) [27]	255(s/slice)
Clustering Error	15%[33]	16.667%

Ertas et al. [34] uses the ART reconstruction technique this study uses on an in silico breast phantom. [35] uses the FBP reconstruction technique on a physical phantom. The study reports EE/N(Edge enhancement over noise ration), and as a comparison the raw projection images they took from the physical phantom had an EE/N of 7.64. For this error we report the average RMSE at 30 projections. Sahiner et al. [33] shows the sensitivity error (features falsely identified as part of the cancer cluster) of feature clustering on a phantom created from real patient data. Ravi et al. [37] using a neural network based cluster-detection technique after ART reconstruction, also obtained a 15% sensitivity error for comparison to our error of 16.667%.

V. Conclusion

In this study, we proposed the use of 3D x-ray elastographic tomosynthesis with physical modulation guided biopsy as a means for more accurate detection of breast cancer. Our approach has three main steps: tomosynthesis with and without physical modulation, calculation of the 3D elastograph, and identification of feature groupings that are to be flagged for biopsy. The data used in this study was created through the in silico phantom creation software X-CAT and a physical phantom. The tomosynthesis and elastographic portion were as to be expected in the physical phantom with a clear elastograph created. The clustering algorithm was a success with the ridged plastic insert was detected using a 3D EM clustering algorithm. This yielded an error of 16.667%. The finding of this paper could be better supported with the inclusion of human breast cancer data. The ultimate goal of this method is to detect not only breast cancer in general, but to also detect the presence of heterogeneous tumors with both malignant IDC and benign DCIS.

Funding Statement

This work was supported in part by the Presidential Research Quest Fund Award at Virginia Commonwealth University, the National Science Foundation under Grant ECCS#1054333, the National Institute of Heath under Grant R01CA160688, and Susan G. Komen under Grant IIR12222224.