Disentangling the life-spans of hepatitis C virus infected cells and intracellular vRNA replication-complexes during direct acting antiviral therapy

Abstract

The decay rate of hepatitis C virus (HCV) infected cells during therapy has been used to determine the duration of treatment needed to attain a sustained virologic response, but with direct acting antivirals (DAA) this rate has been difficult to estimate. Here we show that it is possible to estimate it, by simultaneously analyzing the viral load and alanine aminotransferase (ALT) kinetics during combination DAA therapy.We modeled the HCV RNA and ALT serum kinetics in 26 patients with chronic HCV genotype 1b infection, under four different sofosbuvir based combination treatments. In all patients, ALT decayed exponentially to a set-point in the normal range by 1–3 weeks after initiation of therapy. The model indicates that the ALT decay rate during the first few weeks after initiation of therapy reflects the death rate of infected cells, with an estimated median half-life of 2.5 days in this patient population. This information allows independent estimation of the rate of loss of intracellular replication complexes during therapy. Our model also predicts that the final ALT set-point is not related to the release of ALT by dying HCV infected cells. Using ALT data, one can separately obtain information about the rate of “cure” of HCV infected cells versus their rate of death, something not possible when analyzing only HCV RNA data. This information can be used to compare the effects of different DAA combinations, and to rationally evaluate their antiviral effects.

Introduction

Currently, combination DAA therapies for HCV infection are given for 12 or 8 weeks (1–3). However, shorter duration therapies may also be possible. For instance, in the SODAPI study, a response guided proof of concept study in Chinese patients infected with genotype 1b HCV without cirrhosis given combination DAA therapy for 3 weeks, 100% sustained virological response (SVR) was achieved in patients who reached a viral load less than 500 IU/ml after 2 days of therapy (4). Mathematical analysis of the HCV RNA kinetics observed in these patients, using a multiscale model of infection, showed that there was a very rapid and profound first phase decline followed by one or two subsequent slower phases (4). Because the viral load became undetectable very rapidly, it was hard to quantify the dynamics of these later phases and assess the biological mechanisms involved. Here we analyze the dynamics of HCV RNA and serum alanine aminotransferase (ALT) levels in these patients and show that by simultaneously analyzing the viral and ALT kinetics additional information is gained about the later phases of decay, in particular the lifespan of infected cells and the loss rate of intracellular HCV RNA.

ALT is an enzyme that leaks from damaged hepatocytes during liver injury (5) and thus plays a role in detecting and monitoring viral hepatitis (6). In the context of interferon-treated HCV, Ribeiro et al. (7) showed that there is a relationship between ALT and HCV RNA kinetics. We hypothesized that the same should be true in the context of DAA therapies, where a more detailed multiscale model of HCV infection (8–10) is required to describe the viral dynamics.

We fitted our new model simultaneously to the plasma viral load and ALT data obtained from the SODAPI study (4). We found that this new approach provides information about the mechanisms that underlie ALT decay, the relationship between ALT and HCV RNA dynamics and it can be used to estimate both the infected cell death rate and the loss rate of intracellular HCV replication complexes. This information is useful to understand HCV pathogenesis, the effects of DAAs, and potentially the duration of therapy needed to eliminate all infected cells.

Materials and Methods

Data

We used the ALT and viral load data obtained from the 26 subjects with chronic HCV genotype 1b infection without cirrhosis under treatment with a combination of DAAs in the SODAPI study (4). These 26 subjects were randomized into three treatment arms: sofosbuvir (SOF) + ledipasvir (LDV) + asunaprevir (ASV) (n=12), SOF + daclatasvir (DCV) + simprevir (SMV) (n = 6) and SOF + DCV + ASV (n = 8). Subjects with a viral load <500 IU/ml by day 2 (n = 18) were treated for 3 weeks. Subjects who failed to achieve plasma HCV RNA < 500 IU/mL by day 2 were switched at day 3 from triple DAAs to SOF and LDV for a total duration of 8 or 12 weeks. Based on the plasma level by day 2, we consider four treatment groups in the present analyses. The patients in the first three groups achieved plasma HCV-RNA<500 IU/mL by day 2. The groups were defined by the DAA combination, as follows: group 1, subjects on SOF+LDV+ASV (n=6); group 2, subjects on SOF+DCV+SMV (n= 6); group 3, subjects on SOF+DCV+ASV (n=6). The fourth group (group 4) is composed of all subjects who failed to achieve plasma HCV RNA < 500 IU/mL by day 2 and thus switched at day 3 from triple DAAs to SOF and LDV (n = 8).

Model of HCV and ALT dynamics

We used a published multiscale model of HCV with-in host dynamics (8–10) to analyze the viral load decay data. The details of the model are presented in supplementary material and in Figure 1, with the symbols described in Table 1. To understand the dynamics of ALT and how it is related to the HCV RNA kinetics, we assumed that even though infected cells can be lost by death or by loss/degradation of intracellular HCV RNA and replication complexes, only the former results in ALT release. We added an equation to our model to describe this process, similar to the approach used by Ribeiro et al. (7) (Figure 1). The details of the new model including HCV and ALT dynamics are in the supplementary material.

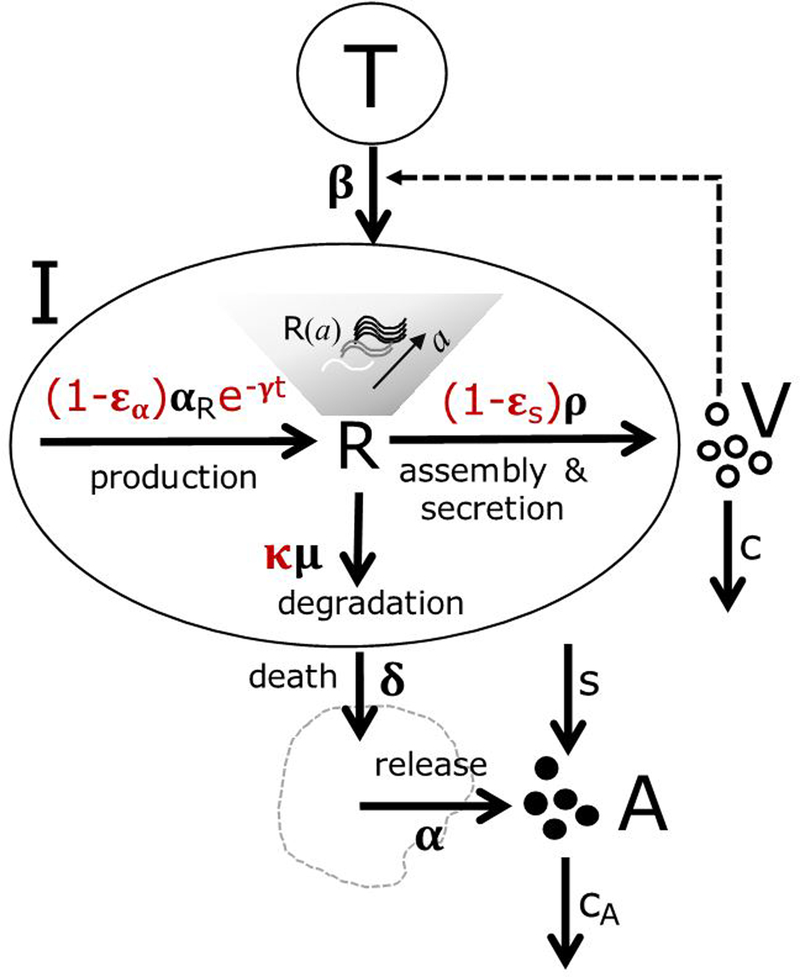
Figure 1. Schematic of the multiscale model of HCV infection and ALT release.

The model accounts for target and infected cells T and I, respectively. V and A represent virus and ALT concentration, respectively. This model accounts for the amount of intracellular vRNA, R, at time t after the initiation of therapy in cells that have been infected for time a. Intracellular vRNA is produced at maximum rate, α_R, from replication complexes (not explicitly modeled), is degraded at rate $\mu$ and is assembled into virions and exported at rate $\rho$. Virus is cleared at rate c per virion. Under DAA therapy, functional replication complexes (or equivalently negative strand HCV RNA) degrade by a first order process at rate γ (here represented by slowing down of production of vRNA), intracellular viral production is blocked with efficacy ε_α, virion assembly and secretion is blocked with efficacy ε_s, and vRNA degradation is increased by a factor $\kappa$. ALT is released with background rate s and is cleared from the circulation at rate c_A. Infected cells die at rate δ, and ALT is released from dying cells at rate αδ.

Table 1.

Description and values of the symbols used in Figure 1.

Symbols	Description	Value	Units	References
A	ALT concentration	Calculated from Eqn. (S4)	IU/L
V	Plasma HCV RNA	Calculated from Eqn. (S2)	Copies/ml
R	Intracellular HCV RNA	See Eqn. (S1)	Copies/ml
I	Infected cells	See Eqn. (S1)	Cells/ml
T	Target cells	See Eqn. (S1)	Cells/ml
V0	Initial viral load before treatment	Fitted	Copies/ml
${\mathit{\alpha }}_{\mathit{R}}$	Rate constant for HCV RNA production	40	1/day	(8, 24)
ρ	Export rate of HCV RNA	8.18	1/day	(8)
μ	Degradation rate of intracellular HCV RNA	1	1/day	(8)
κ	Effectiveness of DAAs in enhancing the vRNA degradation rate	Fitted	-
γ	vRNA replication template decay rate in the present of DAAs	Fitted	1/day
c	Viral clearance rate	Fitted	1/day
δ	Death rate of infected cells	Fitted	1/day
τv	Pharmacological delay	Fitted	Days
${\mathit{\epsilon }}_{\mathit{\alpha }}$	Inhibition of HCV RNA synthesis	Fitted	-
${\mathit{\epsilon }}_{\mathit{s}}$	Inhibition of HCV RNA export	Fitted	-
AN	ALT level in the absence of HCV infection	Fitted	IU/L/day
cA	ALT clearance rate	2	1/day
s	Rate of ALT release in the absence of HCV infection.	Calculated	IU/L	s=AN/cA
α	Amount of ALT released per dying infected cell	Calculated	IU×1000	α=cA(A0-AN)/I0

Fitting procedure

We fit simultaneously the logarithm of viral load (log V(t)) and ALT (log A(t)) derived from solution of our model (Eqs. (S2) and (S4) in Supplementary Material) to the logarithm of the corresponding data from the 26 patients during the first three weeks of therapy using nonlinear mixed-effect modeling (11). We further analyzed whether the parameters of the model were different by treatment group.

To compare model fits, we estimate the log-likelihood (log L) and compute the Bayesian Information Criteria (BIC=−2log L+mlog n, where m is the number of parameters estimated and n the number of data points (12)). We compute ΔBIC, the difference in BIC between the best model and other models analyzed. We assumed models had similar support if their ΔBIC≤2 (12). Results were also compared using the log-likelihood ratio test, Spearman’s rank correlation and the Mann-Whitney test. We assume P-values are significant when they are <0.05 (see supplementary material section 1.5 for more details).

Results

We analyzed 26 HCV-infected individuals treated with different combinations of DAAs. ALT decayed exponentially in all patients reaching values within the normal range by three weeks (Fig. 2). The ALT decay occurred concomitantly with the viral load decline but at a slower rate (see supplementary material) as would be expected if ALT release only occurred when an infected cell dies, whereas viral load decays due to infected cell death and decreases in intracellular viral RNA.

Figure 2. Individual fits (lines) of the multiscale viral kinetic and ALT models, given by Eqs. (S2) and (S4) to the plasma ALT data (circles).

Dashed horizontal line represents the normal ALT level predicted by the model (A_N=s/c_A). Parameter estimates for each individual are presented in Table S6. The first 3 rows represent the patients in treatment groups 1, 2 and 3, respectively, treated for 3 weeks, The 4^th and 5^th rows depict the patients in group 4 treated for 2 days with 3 DAAs but who did not attain a viral load < 500 IU/ml and then switched to SOF plus LDV.

To characterize the joint decline of viral load and ALT, we first fitted empirical exponential decay models simultaneously to all the data, with biphasic or triphasic decays for the viral load, and single or double exponential decays for ALT (details in supplementary material sections 1.1–1.2 and 2.1). The fits showed that only one phase of decay is observed for ALT, after a delay that lasted longer than the pharmacological delay for the viral load decline (Table S1). These fits also confirmed that the viral load decay has three distinct phases (Table S2) as predicted by the multiscale model (Eq. S2) and indicated before (4). All phases of the viral load decay are faster than the ALT rate of decay (p<6×10⁻⁴, Mann-Whitney test, Fig. S1). Furthermore, we found that the third phase of decay of viral load is significantly faster for the group of patients on SOF+LDV+ASV than for the other therapy groups (p<5×10⁻⁴, Wald test, Table S5). Nonetheless, the rate of decline of ALT was not significantly different among treatment groups (p=0.64, Kruskal-Wallis test, Table S4), consistent with the idea that ALT decay reflects cell death, whereas HCV RNA decay reflects both infected cell death and the loss of intracellular viral RNA (vRNA).

These empirical models are simpler and easier to fit (less parameters) than the mechanistic model and indicate the number of observable phases of decay. However, to understand the mechanism underlying the kinetics of ALT decay and how it relates to HCV RNA dynamics, we use the multiscale model of HCV infection and ALT dynamics Eqs. (S2, S4). In this new model, the dynamics of virus and ALT are coupled and each provides information on the other when fitted simultaneously to all the data.

The rate of ALT clearance from the plasma is so fast that it is difficult to estimate it from the data and, therefore, we performed fits by fixing the clearance rate constant, c_A, at different values (see supplementary material for detail). We found the best fit with c_A = 2 day⁻¹, but obtained similar support for other values of c_A (ΔBIC<2, Table S6), showing that this parameter cannot be accurately estimated from the available data. The value of c_A=2 day⁻¹ is similar to the value of 1.7 day⁻¹ estimated by Ribeiro et al. (7) for Caucasian HCV-infected patients and was used for the rest of our analyses. Importantly, these results also showed that the specific value of c_A used in the fits has minimal impact on the estimates for the other parameters, in particular the per capita rate of infected cell death, δ. From this analysis, we conclude that the ALT decline reflects the decay rate of infected cells, δ, which can be estimated consistently regardless of the value of c_A(see supplemental material).

Since ALT data provides extra information for our fitting, we proceeded to analyze in more detail the predictions of the mechanistic model. We could estimate both the death rate of infected cells (δ=0.29/day, Table 2) and the loss rate of replication complexes (or equivalently negative strand HCV RNA, γ). Unexpectedly, we found that γ is larger in the first treatment group (subjects on SOF+LDV+ASV with HCV-RNA<500 IU/mL by day 2) compared to the other three (p<2×10⁻⁴, Wald test, see Table 2). These results are consistent with the finding from the empirical fits that the third phase of decline is faster in group 1, because in the model this decline corresponds to the sum of δ and γ. They are also consistent with the empirical observation that the HCV RNA in group 1 subjects go undetectable sooner than in the other treatment groups (4). We also found that the rate of intracellular HCV RNA decay under treatment, κμ, was much larger than the rate of decay of replication templates, γ for all treatment groups (Table 2).

Table 2. Estimated population parameter values from the best fit of the multiscale model to the data.

Parameters where RSE is indicated as (−) where fixed in the fits and the value indicated. P-values computed using Wald-test.

			Value	R.S.E. (%)
Population estimates	τv		0.03 days	23
	εα		0.966	1
	εs		0.997	0
	AN		15.3 IU/L	6
	γ	G1: SOF+LDV+ASV	0.8 day−1	53
		Other groups	0.07 day−1 (p=0.0005)	28
	c		28.4 day−1	11
	δ		0.29 day−1	8
	κμ		3.4 day−1	21
	cA		2 day−1	-
	A0	G2: SOF+DCV+SMV	25.1 IU/L (p=0.0006)	29
		Other groups	53.7 IU/L	3
	log10(V0)	G4: SOF+LDV+ASV or SOF+DCV+ASV, then SOF+LDV	7.2 log10 cp/mL (p=3×10−6)	29
		Other groups	5.9 log10 cp/mL	3
Standard deviation random effects	τv		0.8 days	26
	εα		0.9	33
	εs		0.9	23
	AN		0.3 IU/L	15
	γ		0.9 day−1	33
	c		0.5 day−1	18
	δ		0.2 day−1	29
	κμ		0 day−1	-
	cA		0 day−1	-
	log10(A0)		0.2	15
	log10(V0)		0.8	14
Stats	-2LL		-95.8
	BIC		-17.7

Individual patient fits to the ALT and HCV RNA data are shown in Figs. 2 and 3, using the best-fit parameter estimates presented in Table S10. Our model predicts that, after a shoulder phase with a duration proportional to 1/c_A, ALT decays with rate δ during DAA treatment (t_1/2 ~ 2.4 days) until it reaches the normal level A_N=s/c_A (~15 IU/L), given by the ratio of the background ALT secretion rate, s, and the clearance rate of ALT, c_A (Figs. 4A-B, Table 2). Next, we analyzed if the decay in ALT was different between patients with different genotypes of IL28b, since in this cohort 17/9 participants had CC/CT alleles, respectively. We did not find any differences in the model parameters between these two groups.

Figure 3. Individual fits (lines) of the multiscale viral kinetic and ALT models, given by Eqs. (S2) and (S4), to the plasma HCV RNA data (circles).

Dashed horizontal line represents the limit of detection of the assay. Parameter estimates for each individual are presented in Table S6. The first 3 rows represent the patients in treatment groups 1, 2 and 3, respectively, treated for 3 weeks, The 4^th and 5^th rows depict the patients in group 4 treated for 2 days with 3 DAAs but who did not attain a viral load < 500 IU/ml and then switched to SOF plus LDV.

Figure 4. Illustrative example of the model predictions.

A. Individual fits of the model to the serum ALT concentration of patient 2326. Red circles represent ALT measurements. Solid black lines represent best fits of the model to the data. After a shoulder phase, serum ALT decline during the first few weeks of therapy reflects the death rate of infected cells δ. Then, ALT levels reach normal levels A_N= s/c_A. B. The death rate of infected cells, δ is positively correlated to the serum ALT decay rate, λ_A, obtained from the empirical single exponential model (see Supp Material). C. The model best-fit (solid line) to the viral load data (symbols) for patient 2326 predicts that the serum HCV RNA follows a three-phasic decay. The third phase reflects the death rate of infected cells and the decay rate of replication templates (δ+γ) (9, 10). The death rate of infected cells may not be identifiable from viral load data alone, but can be estimated from ALT kinetics. D. The death rate of infected cells is inversely correlated to the baseline level of ALT, prior to DAA therapy.

As a further test of our model, we analyzed its prediction that the baseline ALT level in HCV-infected patients prior to treatment, A₀, should be inversely correlated with the death rate of infected cells (see supplementary material section 2.3). In Figure 4D, we show that indeed this inverse correlation is observed and significant (r=−0.48, p=0.01).

Discussion

Alanine aminotransferase (ALT) is an enzyme that leaks from dying and damaged hepatocytes (5) as well as from other sources, such as damaged muscle cells (5). Its leakage from non-infected cells and its rate of clearance determine its normal level. Its elevation above the normal level is commonly used as a marker of the severity of liver damage. During treatment with DAAs, ALT levels decrease (13–15). Here our goal was to determine if longitudinal ALT measurements could provide quantitative information about HCV-infected cells and the mechanisms involved in HCV decay under therapy. Previous work by Ribeiro et al. modeling ALT decrease during treatment with daily dosing of standard interferon-α2b showed that there was an association between ALT and HCV RNA kinetics (7). Here we generalize that analysis to the case of treatment with DAAs. With DAAs, SVR can be obtained much more rapidly than with interferon-based treatment. In fact, for the genotype 1b patients studied here SVR was achieved with 3 weeks of therapy in those patients who reached a viral load below 500 IU/ml by day 2.

As in previous analyses of HCV decline under DAA treatment using multiscale modeling (4, 8–10), we predict a three-phase decline in viral load during combination DAA therapy: i) the first phase is driven by clearance of free virus, ii) the second phase reflects mainly the loss of intracellular HCV RNA and iii) the third phase corresponds to the progressive elimination of infected cells at rate δ, plus the decay of vRNA replication templates that occurs with rate γ during therapy (Fig. 4C). Therefore, the death rate of infected cells, δ, cannot be directly estimated from viral load measurements, because it is confounded with γ. Nevertheless, our analysis shows that by simultaneously fitting both the measured serum HCV RNA and ALT levels after initiation of treatment, both δ and γ can be estimated. This is because according to the model the decay of ALT mainly reflects the loss of infected cells, δ, while the final phase of viral load decay reflects δ+γ. For the data analyzed in this study, the death rate of infected cells has a population median value of 0.29 day⁻¹ (t_1/2= 2.4 days) and the loss rate of replication templates has a median value of 0.8 day⁻¹ (t_1/2=0.9 day) in the SOF+LDV+ASV treatment group and a median value of 0.07 day⁻¹ (t_1/2=10 days) in the other treatment groups (Table 2). We also found that a simple exponential decay model approximates the ALT decline well and the individual estimated decay rates λ_A (Table S3) differ on average by about 20% from the estimates of δ in the full viral-ALT dynamics model that considers both ALT production and clearance (Table S10). Thus, declines of ALT can give a rough estimate of the death rate of infected cells, while a full analysis of both ALT and viral load declines will give a more reliable estimate.

The death rate of infected cells estimated here, 0.29 day⁻¹, is twice as large as the infected cell death rate estimated from viral load decay kinetics observed during interferon-based therapies (16–18). This could be due to a difference in the patient populations studied or an effect of the drugs used, such as increased CD8+ T cell responses induced by DAA therapy. Chronic HCV infection is characterized by impaired HCV-specific T cell responses, with a concomitant increase in the number of exhausted T cells (19–21). Possibly due to the rapid decline in viral antigens, T cell function has been observed to be restored after DAA therapy (22) with a decline in T cell exhaustion markers (23). The increased value of the infected cell death rate, δ, estimated here is consistent with a restoration of CD8 T cell function.

According to our model, ALT decays with rate δ and then reaches a normal level that is independent of δ. This suggests that by the time of ALT normalization the majority of HCV-infected hepatocytes are cleared. All participants in our study normalized ALT by the end of the third week of therapy, suggesting that the remaining number of infected cells dying and releasing ALT was extremely small. Rong et al. (9, 10) showed, under the assumption of no new infections after DAA therapy initiation, that the number of HCV-infected cells decays due to death according to $I\left(t\right)=\frac{c{V}_0}{N\delta }{e}^{-\delta t}$ , with N being the viral burst size as defined in the supplemental material. Using this equation and our estimate of δ, the model predicts (see Fig. S6) that infected cells decrease a median of 10^2.7-fold during the first three weeks of therapy (see Fig. S7A). This is equivalent to a decrease of 99.7% from the initial infected cell number (see Fig. S7B). This drastic decline would explain why after three weeks of therapy the ALT release from the remaining infected cells would not be significant enough to elevate ALT beyond its normal level.

Our analysis using empirical exponential-decay models showed that the second phase decay rate of the viral load was correlated with the decay rate of ALT (r=0.47, p=0.015. See Fig. S1). To further understand the relation between viral and serum ALT levels, we asked if the baseline observed ALT and HCV-RNA levels were correlated with the individual estimates of the parameter δ. We found that baseline HCV-RNA levels are not correlated with δ (r=−0.3, p=0.19). However, the baseline ALT levels are negatively correlated with the death rate of infected cells, δ (r=−0.48, p=0.01) (Figure 4D). This is predicted by our model (supplementary material, section 2.3) and can be understood, because a higher death rate of infected cells leads to fewer infected cells at the baseline steady state, and thus lower ALT levels. That is, baseline ALT levels are positively correlated with the number of infected cells, but these are inversely correlated with the death rate, δ. Thus, these results suggest a strong association between viral load and ALT kinetics.

Recently, a study analyzing ALT kinetics from adults with genotype-1a or 1b infection and cirrhosis receiving at least one DAA with or without IFN concluded that there is no association between viral and ALT kinetics, including no correlation between viral load rates of decay and the ALT rate of decay (15). However, this study was quite different from ours. First, the patients were a mixture of HCV genotype 1a and 1b with cirrhosis, whereas in our study the patients were all genotype 1b and mostly in metavir fibrosis stage F0-F1. Second, the DAAs used were different with only one three drug combination (paritaprevir, ombitasvir and dasabuvir,) and three two drug combinations (daclatasvir and asunaprevir, daclatasvir and sofosbuvir, sofosbuvir and simeprevir), whereas in our study all patients were treated with a three-drug regime containing an NS5A inhibitor, a protease inhibitor and a polymerase inhibitor. Further, ALT and HCV RNA kinetics were analyzed separately, with the HCV RNA kinetics being modeled with the standard biphasic decay model. In our study we simultaneously fit the ALT and HCV RNA kinetics and used a multiscale model that has three decay phases to fit the viral load data. If we separately analyzed the ALT data using an exponential model, we found the ALT decayed exponentially at rate 0.26/day (SI Table 1), in agreement with the rate found by Cento et al. (15) of 0.27/day for the patients treated with an NS5A containing regime.

The rapid loss of ALT seen in the SODAPI study implies that with triple combination DAA therapy there was a rapid loss of HCV-infected cells. Assuming HCV is not directly cytopathic, the loss of infected cells could either be due to immune-mediated destruction or to the intracellular loss of HCV RNA without infected cell death or both. In our model both occur, but δ only reflects cell death with the concomitant release of ALT. If the rapid viral load decline restored the functionality of the cell-mediated immune response, e.g. fully reversed CD8+ T-cell exhaustion, then one might have expected to observe an ALT flare. Here ALT flares were not observed. Thus, it seems likely that therapy also induced a rapid loss of intracellular RNA and that many infected cells were cured rather than killed. This is consistent with the parameter estimates we obtained by fitting the data that suggested the loss rate of intracellular RNA, κμ, was at least 10-fold larger than the death rate of infected cells, δ (Table 2).

The model also predicts that the rate at which replication complexes decay (γ) is greater than zero in the presence of any of the DAA combinations studied. γ represents a type of “cure” rate in the sense that it measures the loss of functional replication complexes within infected cells. This is similar to κμ, which measures the loss rate of positive strand vRNA. Interestingly, in patients receiving SOF+LDV+ASV, γ has a particularly high median value of 0.8 day⁻¹ and it is significantly higher (~10-fold) than with the other treatments (p=0.0005. See Table 2). However, this result needs to be taken with caution as there were only 6 individuals treated with this drug regime and thus larger studies will be needed to confirm this finding. In addition, we do not know of any study that would explain why this combination leads to faster decay of replication complexes than the other DAA combinations in this study.

Overall, our results show that analyzing the dynamics of ALT and virus together can help define the mechanisms of decay of HCV RNA and separate the death rate of infected cells from the loss rate of functional replications complexes, something that was not possible studying the viral load data alone. Knowing these rates provides fundamental new information that may help in evaluating the effects of different DAA combinations.

Of clinical interest, the very rapid declines in HCV RNA seen in the SODAPI study, where all of the patients treated for three weeks with triple combination DAAs had undetectable HCV RNA by day 21 strongly suggests that the vast majority of HCV infected cells were either cured, i.e., lost their intracellular HCV RNA, or were killed by immune responses with subsequent release of ALT. Different combination therapies can result in a different balance of cure versus death of infected cells. Our results provide a means of distinguishing rates of infected cell death from the rate of loss of intracellular HCV RNA and replicative intermediates (replication complexes). For example, we point out that in this small study the combination SOF+LDV+ASV led to a significantly more rapid decline in replicative intermediates than the other two DAA combinations studied SOF+DCV+SIM and SOF+DCV+ASV. Further, the rate of decline of the replicative intermediates was significantly faster than the rate of infected cell death, suggesting that this combination might induce less immunopathology than other combinations, a speculation that should be evaluated in larger studies. Nonetheless, the modeling approach presented here provides a means of evaluating different DAA combinations based on the amount of infected cell death and hence immunopathology that they may cause versus infected cell cure based on the loss on intracellular HCV RNA.