Deep Learning Convolutional Neural Networks for the Estimation of Liver Fibrosis Severity from Ultrasound Texture

Abstract

Diagnosis and staging of liver fibrosis is a vital prognostic marker in chronic liver diseases. Due to the inaccuracies and risk of complications associated with liver core needle biopsy, the current standard for diagnosis, other less invasive methods are sought for diagnosis. One such method that has been shown to correlate well with liver fibrosis is shear wave velocity measured by ultrasound (US) shear wave elastography; however, this technique requires specific software, hardware, and training. A current perspective in the radiology community is that the texture pattern from an US image may be predictive of the stage of liver fibrosis. We propose the use of convolutional neural networks (CNNs), a framework shown to be well suited for real world image interpretation, to test whether the texture pattern in gray scale elastography images (B-mode US with fixed, subject-agnostic acquisition settings) is predictive of the shear wave velocity (SWV). In this study, gray scale elastography images from over 300 patients including 3,500 images with corresponding SWV measurements were preprocessed and used as input to 100 different CNN architectures that were trained to regress shear wave velocity. In this study, even the best performing CNN explained only negligible variation in the shear wave velocity measures. These extensive test results suggest that the gray scale elastography image texture provides little predictive information about shear wave velocity and liver fibrosis.

1. INTRODUCTION

In 2016 an estimated 4.9 million adults in the United States were diagnosed with liver disease, resulting in a premature death of over 40,000 people¹. Liver disease typically progresses through multiple stages. Ongoing, untreated inflammation and attempted healing of the liver leads to progressive deposition of collagen and other macromolecules (scar tissue), eventually leading to liver cirrhosis. The extent of this deposition in the liver is named fibrosis. Treatment varies based on the stage of liver fibrosis and its underlying cause. Effective patient management, including monitoring treatment efficacy, requires estimating the fibrosis stage, ideally in a non-invasive manner. The current standard of care to determine a patient’s liver fibrosis stage is to sample the patient’s liver via core needle biopsy². Not only can this procedure lead to severe complications such as internal bleeding³, but due to the limited amount of liver volume sampled, liver biopsy suffers from sample bias⁴. A newer diagnostic approach uses shear wave elastography (SWE) to measure the tissue’s intrinsic shear wave velocity (SWV). This technique involves mechanically stimulating the liver at a targeted location with a high-amplitude “push pulse”, also called an acoustic radiation force impulse (ARFI), and measuring the speed (m/s) of the resultant lateral shear waves. In liver fibrosis, an increasing amount of interstitial collagen deposition stiffens the liver and increases the SWV, which is highly correlated with the severity of liver fibrosis at biopsy². SWV is now an accepted surrogate biomarker for liver fibrosis in clinical practice². Standard US devices produce gray scale images whose pixel intensity value is based on the backscatter signal amplitude (B-mode). Although many premium systems may be loaded with the necessary software, many are not equipped with the elastography mode. Therefore, an approach that predicts the SWV and hence fibrosis from the liver texture from the B-mode image would be of high practical and clinical significance by providing a readily available measurement for physicians to make informed diagnostic decisions. Preliminary work suggests that B-mode US image texture can be used for diagnosis and fibrosis estimation. However, the authors of that work state that their model’s performance depends highly on the human expert that selects the multiple regions of interest (ROIs), and that future work should eliminate or reduce the expert’s role. The purpose of this work is to address the question of whether or not the texture in gray scale elastography images whose acquisition parameters are not tailored to the subject is predictive of shear wave velocity, using the current state of the art in image interpretation, the convolutional neural network (CNN).

2. MATERIALS AND METHODS

2.1. Study Design and Subjects

This retrospective observational study performed between 02/2016 and 02/2017 included 326 patients at risk for chronic liver disease who underwent SWE ultrasound exams for noninvasive evaluation of liver fibrosis. The patients’ ages ranged from 20 to 78 and consisted of 164 males and 162 females. Our Institutional Review Board approved this study and waived the need for informed consent. The study was conducted in compliance with Health Information and Primary Accountability Act (HIPAA).

2.2. Ultrasound Image Acquisition and ROI Definition

This study utilized gray scale elastography images of the liver for which the ground truth SWV estimate in m/s for each individual US image was also available. Gray scale elastography images are B-mode US images with fixed acquisition settings, in contrast to clinical B-mode images whose parameters are subjectively optimized for the patient by the sonographer taking into account their degree of obesity and severity of fibrosis, and thus dependent on the sonographer’s level of experience and skill. Each grayscale image was obtained using an EPIQ7G (Philips Healthcare, Bothell WA) clinical ultrasonography system with elastography capabilities. A sonographer merely needed to choose a SWE ROI (white box, Fig 1) in the center of the liver, away from the liver’s boundaries and major blood vessels to minimize confounding influence of these structures on stiffness measurements. This selection is readily performed. The SWV was measured within this ROI. The gray-scale image acquisition and SWV measurements were repeated 10 times for each patient per institutional protocol. Across the patient cohort, the SWV ranged from 0.2 to 9.3 m/s with an average of 1.60 m/s.

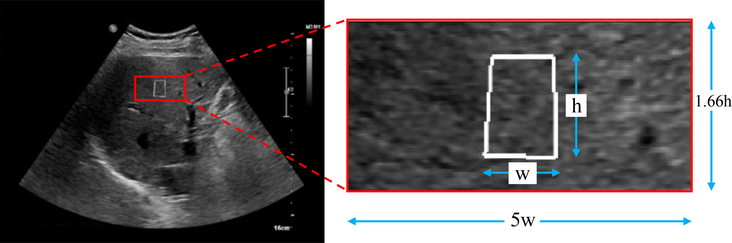
Figure 1:

An gray scale elastography image (left) and the image region used for CNN prediction (red box on right). The white box in both panels shows the ROI positioned by the technologist as the target for SWE to measure the SWV. The image region for prediction (right) has dimensions that are 5x the width (w) and 1.66x the height (h) of the elastography targeting white box.

2.3. Deep Convolutional Neural Network Architecture

This study applied CNNs to regress the SWV directly from the US texture image. The CNN framework was chosen because it automatically learns a hierarchy of filters that are optimal to make a prediction from the training images. CNNs have formed the winning approach for image object recognition, including the ImageNet challenge, since 2012. Since 2015, they have attained human-level, single-task image interpretation performance^6,7. Therefore, the CNN holds one of the best chances of finding an association between texture patterns and SWV if one exists. The CNN is a deep neural network with a feedforward architecture. Image inputs are passed into a succession of convolutional layers, that transform the inputs into a form that makes the prediction easier. The convolutional layers consist of convolutional filters and the filter kernel weights from these layers are the hierarchy of features learned for the supervised regression task in our experiments. The transformed input from the last convolutional layer is passed into a succession of fully connected layers, the last of which, the output layer, consists of a single unit that combines the learned features to output a continuous valued SWV estimate. The texture filters applied by the network are optimized through end-to-end learning via backpropagation⁸.

2.4. Image Preprocessing

The images are preprocessed for three purposes: (1) to crop the image to a large texture ROI that includes just liver pixels, (2) to spatially normalize the pixel sizes, and (3) to normalize the pixel intensities across subjects. Advanced fibrosis tends to make the liver more nodular due to bridging fibrosis within the interlobular space, with intervening nodular hepatocyte regeneration, which could result in a gray-scale image appearance with coarse echotexture. Based on the Nyquist sampling theorem, we observe that in order to sample the lowest expected spatial frequencies in the texture image, a larger ROI is needed than the elastography ARFI targeting box (Fig. 1, small white box). The texture ROI (Fig. 1, red box) that was used is the largest sized rectangle that still includes only liver pixels across our cohort. It is centered on the white target ROI but is 5x its width and 1.66x its height. The targeting ROI is 7mm wide x 12mm in height, hence our texture ROI is also of consistent dimensions across subjects. The texture ROI is resampled to the same pixel dimensions across all subjects. The intensity values of each texture ROI were normalized to have zero mean and unit standard deviation.

2.5. Network Architecture Optimization

To ensure thorough coverage of possibly relevant CNN architectures, a randomized search of 100 architectures was conducted. The architectures included an input layer followed by 1 or more convolutional layers, and finally a number of fully connected layers. The hyperparameters were randomly chosen from ranges with a step size of one, for each of the following network architecture parameters:

1. Number of convolutional layers: [1,…,10]

2. Number of filters in each convolutional layer: [2,…,64]

3. 2D filter kernel size (height and width): [2,…,11]

4. Number of fully connected layers: [2,…,5]

5. Number of units per fully connected layer: [3,…,256]

Across all the architectures tested, batch normalization was inserted with 50% probability after each convolutional layer. After the convolutional layers, a max pooling layer with a size of 2×2 was also inserted with 50% probability. After each fully connected layer, there was a 50% chance of inserting a dropout layer with a rate of 0.5. Dropout can help suppress overfitting. The loss function was mean squared error (MSE) which was minimized with ADAM optimization⁹ using β₁ = 0.7, β₂ = 0.999, and ϵ = 1×10⁻⁸. PReLU activation was used for each activation and weights were initialized to small random weights around zero using the He normal initialization, which has been shown to be optimal for PEeLU⁷. A maximum of 200 epochs was used along with early stopping. The early stopping used a minimum delta of 0 and a patience of 30 epochs.

The texture images were grouped by patient and randomly partitioned into 85% for training and 15% held out for testing. The training data was then split via 5-fold cross validation. All partitions were stratified so that the same distribution of SWV in the overall dataset appeared in the training and validation folds and in the test partition. Images from a patient were grouped so that a patient’s images appeared only in one partition (training, validation or test). The architectures were then trained with Tensorflow running on an Nvidia P100 GPU. Two networks illustrating the range of architectural complexity tested are shown in Table 1A and Table 1B.

Table 1:

Sample of the network architectures tested in the random search. The abbreviation “Conv, 10×10, 343×156, 30”,describes the size of convolutional filter, feature maps, and # filters. “Dense, 102” describes # of units in a fully connected layer. A. One of the largest networks tested. B. One of the smallest networks tested. C. The network with the lowest median MSE across the 5 folds.

Table 1A	Table 1B	Table 1C
343×156 input image	343×156 input image	343×156 input image
Conv, 10×10, 343×156, 30	Conv1, 343×156, 3×3, 8	Conv, 6×6, 343×156, 41
Batch Normalization	Flatten	Batch Normalization
Max Pooling stride 1	Batch Normalization	Max Pooling stride 1
Conv, 2×2, 171×78, 31	Dense, 51	Conv, 8×8, 171×78, 30
Batch Normalization	Dense output, 1	Batch Normalization
Conv, 6×6, 171×78, 24		Conv, 7×7, 171×78, 9
Batch Normalization		Batch Normalization
Conv, 9×9, 171×78, 7		Max Pooling stride 1
Batch Normalization		Conv, 2×2, 85×39, 26
Max Pooling stride 1		Batch Normalization
Conv, 4×4, 85×39, 12		Max Pooling stride 1
Batch Normalization		Conv, 4×4, 42×19, 57
Conv, 3×3, 85×39, 46		Batch Normalization
Batch Normalization		Conv, 8×8,42×19, 11
Max Pooling stride 1		Batch Normalization
Conv, 9×9, 42×19, 18		Max Pooling stride 1
Batch Normalization		Conv, 8×8, 21×9, 31
Max Pooling stride 1		Batch Normalization
Conv, 2×2, 21×9, 29		Max Pooling stride 1
Batch Normalization		Conv, 10×10, 10×4, 47
Max Pooling stride 1		Batch Normalization
Conv, 4×4, 10×4, 48		Conv, 4×4, 10×4, 3
Batch Normalization		Batch Normalization
Max Pooling stride 1		Flatten
Conv, 2×2, 5×2, 51		Batch Normalization
Batch Normalization		Dense, 95
Flatten		Dense, 163
Batch Normalization		Dense, 185
Dense, 14		Dropout, rate=0.5
Dense, 141		Dense output, 1
Dense, 35
Dense, 25
Dense output, 1

2.6. Model Selection

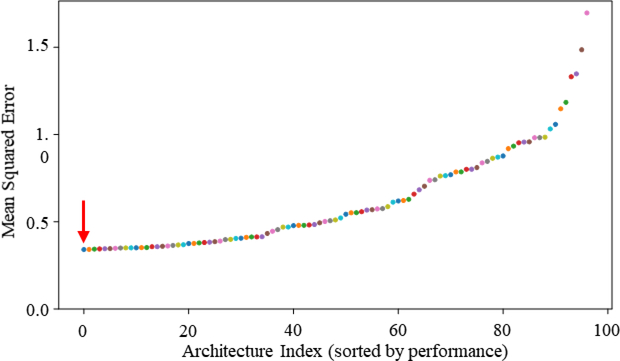
As shown in Fig. 2, the median performance of each network over the cross-validation folds was computed and the networks were sorted in increasing order of MSE. The architecture with smallest median MSE across folds was chosen as the winning architecture. The architecture of the top performing network is shown in Table 1C.

Figure 2:

The minimum median MSE for the validation data on each network across epochs, ranked from lowest to highest. The first architecture (Table 1C) indicated with the red arrow was used later to evaluate performance on the on the test data.

2.7. Quantification of Human Expert Performance

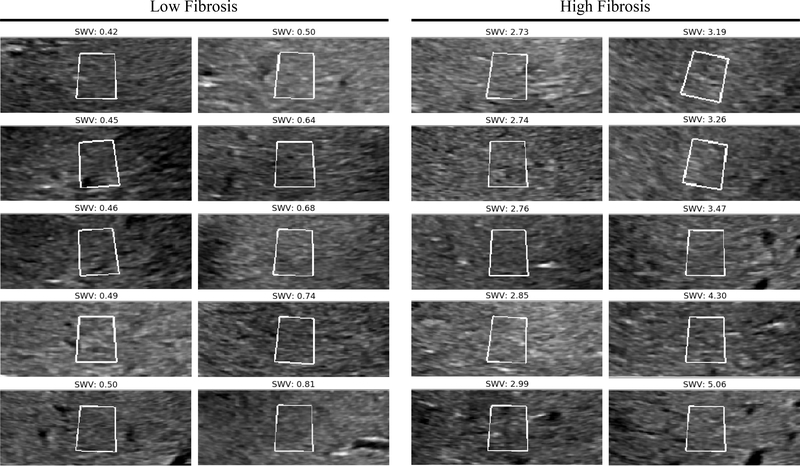
To provide a point of comparison for our automated approach, we conducted an investigation into the performance of human experts (radiologists) in classifying the level of fibrosity (high versus low fibrosity). In this investigation we selected 10 subjects with very low fibrosity (group mean SWV of 0.57 m/s +/− .13 m/s) and 10 subjects with very high fibrosity (group mean SWV of 3.34 m/s +/− .73 m/s). One representative image from each subject was chosen and the ROIs from these 20 images, are shown in Fig. 3. We blinded the experts to the true fibrosity level and asked them to classify the 20 images as low or high fibrosity.

Figure 3:

Gray scale elastography ROIs for 10 high and 10 low subjects. Shown on the left are 10 ROIs from subjects with no or little fibrosis and who have the lowest SWV. Shown on the right are 10 ROIs with the highest SWV and high fibrosis. These images were used to quantify human expert accuracy.

3. RESULTS

3.1. Performance of The Deep Neural Network on predicating SWV

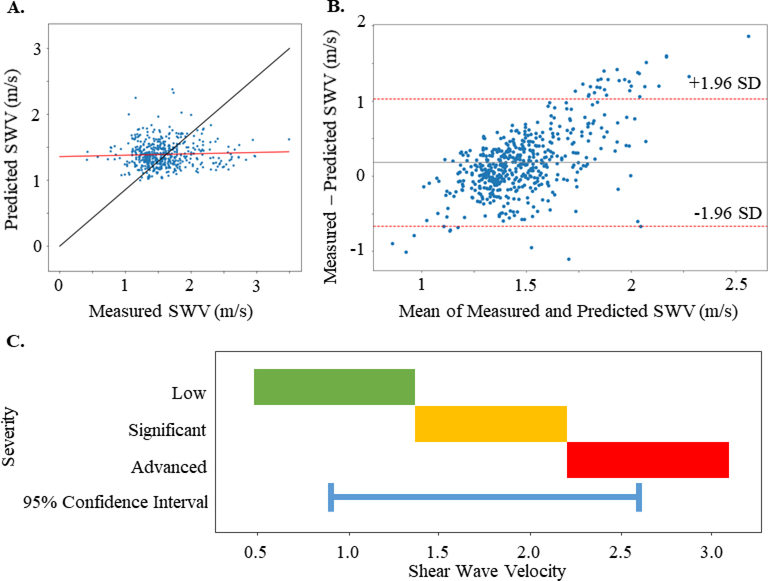
As shown in Fig. 2, the top performing network achieved the smallest median MSE across folds of 0.34 on the validation data. This network was trained on the combined training and validation data and then used to make SWV predictions on the held out test gray scale elastography images. It achieved an MSE of 0.22 on the test data. Fig 4A. shows a scatter plot of the model’s predicted SWV vs the elastography measured SWV. Fitting a line to the predictions (Fig 4A, predictions shown as blue dots, fitted line in red) yielded a slope of 0.062492 with large residuals (r²= 0.009612). This indicates that the textural pattern in gray scale elastography images was only slightly associated with SWV. The Bland-Altman plot (Fig 4B) further confirms this result and suggests that the model’s predictions could be substantially different from the SWV measured via elastography. Prior literature has defined the low fibrosis stage to have a SWV of below 1.37 m/s, significant fibrosis stage to be 1.37 to 2.2 m/s, and advanced fibrosis and/or cirrhosis to be >2.2 m/s (when using the Philips pSWE as in this study)². In this study the model’s 95% confidence interval is +/− 0.848 m/s (Fig. 4B), which can span all 3 fibrosis stages (Fig 4C) indicating that it does not reach clinical significance. Therefore, we suggest that the texture in gray scale elastography images is not predictive of the SWV from elastography.

Figure 4:

A. Comparison of predicted SWV (m/s) versus actual elastography measured SWV (m/s). The ideal predicted=measured line is shown in black, while the actual linear fit line, shown in red, demonstrates only weak correlation between the measured and predicted values. B. The Bland-Altman plot showing average of the measured and predicted SWV values versus the difference: measured - predicted. The red lines show a 95% confidence interval which are +/− 0.848 m/s from the mean. C. The range of SWV for fibrosis stages: low fibrosis (green), significant fibrosis (yellow), and advanced fibrosis (red) as described in a pSWE study². The blue line shows the 95% confidence interval of the best performing model can span all three stages.

3.2. Comparison Between Expert Human Performance and The Top Performing Deep Learning Model

When quantifying human expert (radiologist) performance (section 2.7) using the gray scale elastography images, we found that the experts performed only slightly better than chance, in agreement with our predictive model’s performance. Specifically, the mean accuracy of the experts classifying high versus low fibrosity was 58.3% with a standard deviation of 7.6%. This suggests that even for an expert in ultrasound interpretation, the gray scale elastography image contains insufficient information to differentiate fibrosity levels. This corroborates our finding that machine learning also finds the gray scale elastography image to be only slightly associated with fibrosity. We acknowledge that the expert radiologists rely on clinical B-mode images, not necessarily gray scale elastography images, and typically take into account many other patient measures other than ultrasound image texture when making a clinical diagnosis of fibrosity. However, we note that clinical B-mode images are acquired by optimizing imaging settings on per-patient basis by the sonographer and thus subject to sonographer skill, potentially introducing a confound into image analysis.

4. NOVELTY

Our tests add an extensive body of evidence from over 300 patients to help address the hypothesis whether the gray scale elastography image texture is predictive of liver shear wave velocity, an established surrogate for fibrosis level. The results of our extensive tests on 100 CNN architectures suggest that there is not a significant association between gray scale elastography image texture and SWV.

5. CONCLUSION

The computer vision community has abundant evidence that CNNs are well suited for object and texture recognition in images. Therefore, if there were an association between gray scale elastography image texture and SWV, there should be CNN architectures that reveals this association. This work demonstrates that, at least for the 326 patients from our hospital, and the 100 CNN architectures tested from a wide range of architectures, there is not a substantive association between gray scale elastography image texture and SWV. When there is no strong association, a network can memorize training data but will not generalize well to held out test data. This is what we observed. To make an informed diagnosis, radiologists use a range of information, of which image texture is a small part, however when constrained to use only gray scale elastography image texture these CNN results concur with the slightly above chance performance by the radiologists to estimate liver fibrosity categories. Possible limitations of this work include: 1) only one gray scale elastography image from each liver is taken into account while information indicative of the liver fibrosis stage could be in surrounding liver tissue, 2) newer, possibly more precise 2D shear wave elastography has since become available that were not available for this study. Also, in order to be least dependent on sonographer expertise, this study focused on the gray scale elastography images taken while the SWV is being measured. While this has the advantage of using fixed acquisition settings across all subjects, it is possible that clinical B-mode US images with settings such as gain, dynamic range, focus, transmit frequency and speckle reduction optimized for each subject could provide more informative texture.