The Child as Hacker

Abstract

The scope of human learning and development poses a radical challenge for cognitive science. We propose that developmental theories can address this challenge by adopting perspectives from computer science. Many of our best models treat learning as analogous to computer programming because symbolic programs provide the most compelling account of sophisticated mental representations. We specifically propose that children’s learning is similar to a particular style of programming called hacking—making code better along many dimensions through an open-ended set of goals and activities. In contrast to existing theories which depend primarily on local search and simple metrics, this view highlights the many features of good mental representations and the multiple complementary processes children use to create them.

Hacking as a metaphor for learning in cognitive development

Human cognitive development is qualitatively unique. Though humans are born unusually helpless, they amass an unparalleled cognitive repertoire including: intuitive theories for domains like physics and biology, formal theories in mathematics and science, language comprehension and production, and complex perceptual and motor skills. Children also learn to learn, producing higher-order knowledge that enriches existing concepts and enhances future learning. Human-like performance in any one of these domains seems substantially beyond current efforts in artificial intelligence. Yet, human children essentially acquire these abilities simultaneously and universally. They may even discover new ideas that radically alter humanity’s understanding of the world. The foundational fields of cognitive science—including philosophy, psychology, neuroscience, and computer science—face a radical challenge in explaining the richness of human development.

To help address this challenge, we introduce the child as hacker (see Glossary) as a hypothesis about the representations, processes, and objectives of distinctively human-like learning. Like the child as scientist view [1–5], the child as hacker is both a fertile metaphor and a source of concrete hypotheses about cognitive development. It also suggests a roadmap to what could be a unifying formal account of major phenomena in development. A key part of the child as hacker is the idea of learning as programming, which holds that symbolic programs—i.e. code—provide the best formal knowledge representation we have. Learning therefore becomes a process of creating new mental programs. We review support for learning as programming and argue that while on increasingly solid ground as a computational-level theory [6], it remains underspecified. We extend the idea of learning as programming by drawing inspiration from hacking, an internally-driven approach to programming emphasizing the diverse goals and means humans use to make code better. Our core claim is that the specific representations, motivations, values, and techniques of hacking form a rich set of largely untested hypotheses about learning.

Knowledge as code & learning as programming

A critical mass of work throughout cognitive science has converged on the hypothesis that human learning operates over structured, probabilistic, program-like representations [7–20, cf. 21] (Box 1), a modern formulation of Fodor’s Language of Thought (LOT) [22] as something like a programming language. Learning in the LOT consists of forming expressions to encode knowledge—for instance, composing primitives like CAUSE, GO, and UP to form LIFT [23]. This work argues that a compositional mental language is needed to explain systematicity, productivity, and compositionality in thought [9, 22, 24]; a probabilistic language capable of maintaining distributions over structures is needed to explain variation and gradation in thinking [10, 11, 25, 26]; and an expressive language—capable of essentially any computation—is needed to explain the scope of thought [27, 28]. Despite comparative and cross-cultural work seeking semantic primitives for mental languages [29], other work suggests that learners add and remove primitives, effectively building entirely new languages [2, 3, 30, 31].

Box 1: Programs and the challenge of humans’ broad algorithmic knowledge.

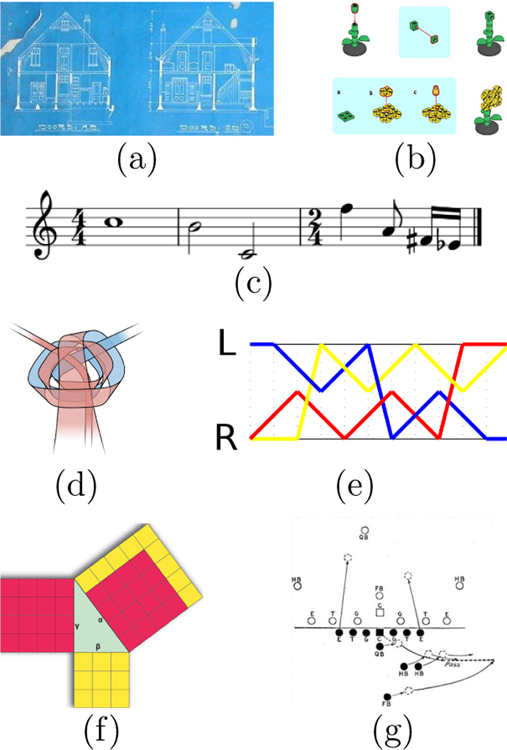
Humans possess broad algorithmic knowledge, manipulating complex data in structured ways across many domains (Table I). Symbolic programs—i.e. computer code—form a universal formal representation for algorithmic knowledge [27, 28], and may be the best model of mental representations currently available. Programs can be communicated in many forms, including not only formal programming languages but a wide variety of forms familiar in all cultures, including natural language and symbolic images (Figure I). While there have been many other proposals for modeling conceptual representations, only programs arguably capture the full breadth and depth of people’s algorithmic abilities [11]. The rapid rise of programs as tools for manipulating information—from obviously symbolic domains like mathematics and logic to seemingly non-symbolic domains like video, audio, and neural processing—further identifies programs as a capable knowledge representation [e.g. 32].

Code is expressed according to a formal syntax, and its semantics specifies computations, typically as instructions to some machine (e.g. x86 processor, Turing machine). It can model both declarative (Box 2) and procedural information (“Hacking early arithmetic”) and allow them to interact seamlessly. Code operates at multiple levels, including: individual symbols, expressions, statements, data structures & functions, libraries, and even entire programming languages. Each level can interact with the others: libraries can embed one language inside another, statements can define data structures, and higher-order functions can take functions as arguments and return functions as outputs. This leads to one of the fundamental insights that makes code so successful. By writing computations as code, they become data that can be formally manipulated and analyzed [33]. Programming languages thus become programs which take code as input and return code as output. Because all programming languages are programs, any knowledge that can be expressed in any program can be integrated into a single formal knowledge representation.

Modeling knowledge as code and learning as programming has worked well for many individual domains (“Knowledge as code & learning as programming”). We need, however, a general formalization of mental representations and how they develop. The child as hacker suggests such an account, emphasizing how information can be encoded, assessed, and manipulated as code regardless of domain, with the intention of developing formal tools applicable to broad classes of human learning phenomena.

Figure I:

Several classes of programs expressed as symbolic images: (a) blueprints; (b) assembly instructions; (c) musical notation; (d) knotting diagrams (e) juggling patterns; (f) graphical proofs; and (g) football plays.

Table I:

A sampling of domains requiring algorithmic knowledge formalizable as programs, with motivating examples.

logic	first-order, modal, deontic logic
mathematics	number systems, geometry, calculus
natural language	morphology, syntax, number grammars
sense data	audio, images, video, haptics
computer languages	C, Lisp, Haskell, Prolog, LATEX
scientific theories	relativity, game theory, natural selection
operating procedures	Robert’s Rules, bylaws, checklists
games & sports	Go, football, 8 queens, juggling, Lego
norms & mores	class systems, social cliques, taboos
legal codes	constitutions, contracts, tax law
religious systems	monastic orders, vows, rites & rituals
kinship	genealogies, clans/moieties, family trees
mundane chores	knotting ties, making beds, mowing lawns
intuitive theories	physics, biology, theory of mind
domain theories	cooking, lockpicking, architecture
art	music, dance, origami, color spaces

Learning is then program induction: discovering programs that explain how observed data were generated [34–36]. The theory thus draws on inductive programming literature stretching back to the birth of cognitive science [37, 38], and includes subsequent developments in recursive program synthesis [39], structure & heuristic discovery [40, 41], meta-programming [42, 43], genetic programming [44, 45] and inductive logic programming [36, 46]. The approach also makes use of insights from other formalizations of learning, e.g. deep learning [47], connectionism [48], reinforcement learning [49], probabilistic graphical models [50], and production systems [51]. These can be viewed as exploring specific subclasses of programs or possible implementation theories. The learning as programming approach, however, is importantly different in providing learners the full expressive power of symbolic programs both theoretically (i.e. Turing completeness) and practically (i.e. freedom to adopt any formal syntax).

This approach applies broadly to developmental phenomena—including counting [52], concept learning [13, 53], function words [54], kinship [55], theory learning [56, 57], lexical acquisition [23], question answering [15], semantics & pragmatics [25, 58, 59], recursive reasoning [60], sequence transformation [61], sequence prediction [18, 62], structure learning [63], action concepts [64], perceptual understanding [14, 65], and causality [66]. These applications build on a tradition of studying agents who understand the world by inferring computational processes that could have generated observed data, which is optimal in a certain sense [67, 68], and aligns with rational constructivist models of development [69–72].

While these ideas appear to be on increasingly solid empirical and theoretical ground, much work remains to formalize them into robust and precise descriptions of children’s learning. Most recent LOT work has argued that learners seek short (simple) programs explaining observed data, a version of Occam’s Razor. A bias for simplicity favors generalization over memorization, while a bias for fit favors representations that match the world. Mathematically, these two can be balanced in a principled way using Bayes’ theorem or minimum description length formalisms to favor simple, explanatory programs [13, 73], a principled approach [28, 74] that fits human data well [13, 53, 73, 75, 76]. Bayesian LOT models have often hypothesized that learners stochastically propose candidates by sampling from a posterior distribution over programs, a process that empirically resembles children’s apparently piecemeal, stop-start development [57].

From programming to hacking

Though these ideas have been important in formalizing LOT-based learning, views based entirely on simplicity, fit, and stochastic search are likely to be incomplete. Most real-world problems requiring program-like solutions are complex enough that there is no single metric of utility nor unified process of development (Figure 1a). Even so, modern computational approaches to learning—whether standard learning algorithms or more recent LOT models—use far fewer techniques and values than human programmers. For any task of significance, software engineering means iteratively accumulating many changes to code using many techniques across many scales (See Online Supplemental Information Figure S1).

Figure 1:

Overview of the child as hacker hypothesis. a: Code can be changed using many techniques (x-axis) and assessed according to many values (y-axis). Standard learning models in machine learning and psychology (green region) tend to focus solely on tuning the parameters of statistical models to improve accuracy. Recent LOT models (red region) expand this scope, writing functions in program-like representations and evaluating them for conciseness and sometimes efficiency. Yet, the set of values and techniques used by actual hackers (and by hypothesis, children; blue region) remains much larger. b: A comparison of three families of developmental metaphors discussed in this paper—the child as scientist, the workshop and evolutionary metaphors, and the child as hacker—along three dimensions: the kinds of knowledge learners acquire, the primary objectives of learning, and the mechanisms used in learning.

In what follows, we enrich learning as programming with a distinctly human style of programming called hacking. Today, the term “hacking” has many connotations: nefarious, incompetent, positive, ethical, and cultural. Rather than directly importing these modern connotations, we draw on earlier ideas about hacking from the origins of modern computing culture [77]. Hacking, as used here, is about exploring the limits of a complex system, starting with whatever is at hand and iteratively pushing the system far beyond what initially seemed possible. We thus begin with a notion of hacking as making code better. But the essence of hacking goes deeper. It lies in all the values that count as “better,” all the techniques people use to improve code, and a profound sense of internal motivation.

The many values of hacking

There are many dimensions along which a hacker might seek to improve her code, making it not only more accurate, but perhaps faster, clearer, more modular, more memory-efficient, more reusable, cleverer, and so on (Table 1). The simplest program is unlikely to be the most general; the fastest is usually not the easiest to write; the most elegant typically is not the most easily extensible. Importantly, real world systems do not focus exclusively on the metrics that have come to the forefront of current LOT-learning paradigms. They often maintain multiple solutions to the same problem, tuned for different sets of values. Moreover, effective systems in the real world care more about managing complexity than about being short, simple, or terse—though these are sometimes useful tools for managing complexity. Indeed, many foundational ideas in computer science are less about computation per se and more about managing the inevitable complexity that arises when putting computation to use [33, 78].

Table 1:

Learners and hackers share similar values. Hackers want to make their code better, and listed here are some features of good code. They are also features of useful conceptual systems.

Accurate	demonstrates mastery of the problem; inaccurate solutions hardly count as solutions at all
Concise	reduces the chance of implementation errors and the cost to discover and store a solution
Easy	optimizes the effort of producing a solution, enabling the hacker to solve more problems
Fast	produces results quickly, allowing more problems to be solved per unit time
Efficient	respects limits in time, computation, storage space, and programmer energy
Novel	solves a problem unlike previously solved problems, introducing new abilites to the codebase
Useful	solves a problem of high utility
Modular	decomposes a system at its semantic joints; parts can be optimized and reused independently
General	solves many problems with one solution, eliminating the cost of storing distinct solutions
Robust	degrades gracefully, recovers from errors, and accepts many input formats
Minimal	reduces available resources to better understand some limit of the problem space
Elegant	emphasizes symmetry and minimalism common among mature solutions
Portable	avoids idiosyncrasies of the machine on which it was implemented and can be easily shared
Clear	reveals code’s core structure to suggest further improvements; is easier to learn and explain
Clever	solves a problem in an unexpected way
Fun	optimizes for the pleasure of producing a solution

The many activities of hacking

To pursue these diverse objectives, hackers have developed many process-level mechanisms for improving their representations [78], including adding new functions and data structures, debugging faulty code, refactoring code, and even inventing new languages (Table 2). Hackers understand dozens or even hundreds of these mechanisms and their potential impacts on various values. Some make small, systematic, and predictable changes, while others are dramatic and transformative; most are specially tailored to specific kinds of problems. For instance, a hacker might care about speed and so cache the output of subcomputations in an algorithm. She might seek modularity and so define data structures that encapsulate information and make it accessible only through specific interfaces. Or, she might seek reusable parts and so abstract common computations into named functions. This diversity of techniques makes hacking different from both common learning algorithms and recent LOT models. Typically, these other models explore a small set of techniques for improving programs, based on relatively simple (even dumb) local methods like gradient descent, random sampling, or exhaustive enumeration.

Table 2:

Learners and hackers share similar techniques. Hackers have many techniques for changing and improving code; some are listed here. The child as hacker suggests that the techniques of hackers are a rich source of hypotheses for understanding the epistemic practices of learners.

Tune parameters	adjust constants in code to optimize an objective function.
Add functions	write new procedures for the codebase, increasing its overall abilities by making new computations available for reuse.
Extract functions	move existing code into its own named procedure to centrally define an already common computation.
Test & Debug	execute code to verify that it behaves as expected and fix problems that arise. Accumulating tests over time increases code’s trustworthiness.
Handle errors	recognize and recover from errors rather than failing before completion, thereby increasing robustness.
Profile	observe a program’s resource use as it runs to identify inefficiencies for further scrutiny.
Refactor	restructure code without changing the semantics of the computations performed (e.g. remove dead code, reorder statements).
Add Types	add code explicitly describing a program’s semantics, so syntax better reflects semantics and supports automated reasoning about behavior.
Write libraries	create a collection of related representations and procedures which serve as a toolkit for solving a entire family of problems.
Invent languages	create new languages tuned to particular domains (e.g. HTML, SQL, LATEX) or approaches to problem solving (e.g. Prolog, C, Scheme).

The intrinsic motivation of hacking

Hacking is intrinsically motivated. Though a hacker may often be motivated in part by an extrinsic goal, she always generates her own goals—choosing specific dimensions she wants to improve—and pursues them at least as much for the intrinsic reward of better code as for any instrumental purpose. Sometimes, her goal is difficult to assess objectively and so unlikely to arise extrinsically. Other times, her goal can be measured objectively, but she chooses it regardless of—perhaps in opposition to—external goals (e.g. making code faster, even though outstanding extrinsic requests explicitly target higher accuracy). Whatever their origins, her choice of goals often appears spontaneous, even stochastic. Her specific goals and values may change nearly as often as the code itself—constantly updated in light of recent changes. She is deeply interested in achieving each goal, but she frequently adopts new goals before reaching her current goal for any number of reasons: getting bored, deciding her progress is “good enough”, getting stuck, or pursuing other projects. Rather than randomly walking from goal to goal, however, she learns to maintain a network of goals: abandoning bad goals, identifying subgoals, narrowing, broadening, and setting goals aside to revisit later. Even if she eventually achieves her initial goal, the path she follows may not be the most direct available. Her goals are thus primarily a means to improve her code rather than ends in themselves.

The fundamental role of intrinsic motivation and active goal management in hacking suggests deep connections with curiosity and play [79–82], which have also been posited to play central roles in children’s active learning. We do not speculate on those connections here except to say that in thinking about intrinsic motivation in hacking, we’ve been inspired by Chu and Schulz’s work exploring the role of goals and problem-solving in play [83]. Further understanding of this aspect of both learning and hacking could be informed by our search for better accounts of play and curiosity.

In short, the components of hacking—diverse values, a toolkit of techniques for changing code, and deep intrinsic motivation—combine to make hacking both a highly successful and emotionally engaging approach to programming. The ability to select appropriate values, goals, and changes to code transforms seemingly stochastic behavior into reliably better code. The combination of internal motivation, uncertain outcomes, and iterative improvement makes hacking a creative and rewarding experience.

Hacking early arithmetic

It is helpful to look through the hacker’s lens at a concrete example of algorithmic revision from cognitive development: how preschoolers and early grade-schoolers learn to solve simple addition problems like 2 + 3. In this section, we demonstrate how the child as hacker can be used to explain key findings in arithmetic learning as natural consequences of changing code-like representations according to hacker-like values and techniques.

We focus on the well-known sum to min transition [84–89], in which children spontaneously move from counting out each addend separately and then recounting the entire set (sum strategy) to counting out the smaller addend starting from the larger addend (min strategy). Small number addition has been modeled many times [88, 90–94], but even as this case is well known, its significance for understanding learning generally [95] is not appreciated. This domain is notable because children learn procedures and, in doing so, display many hallmarks of hackers.

Throughout this transition and beyond, children do not discard previous strategies when acquiring new ones but instead maintain multiple strategies [96–99]. The work of Siegler and colleagues, in particular, explicitly grapples with the complexity of both the many values which learners might adopt and the need to select among many strategies for solving the same problem. They have shown that children appropriately choose different strategies trial-by-trial based on features like speed, memory demands, and robustness to error [88, 95].

Table 3 implements several early addition strategies as code. For the sake of space, we highlight five strategies [cf. 92, 100]. Children acquire the sum strategy through informal interactions with parents or at the onset of formal education [88, 101, 102] (sum; Table 3). sum appears optimized for instruction and learning. It is simple, uses familiar count routines, requires little rote memorization, and respects children’s limited working memory. It also computes any sum in the child’s count list, making sum an accurate and concise strategy for addition. Most recent LOT models would consider the problem well-solved. sum is slow and repetitive, however, counting every object twice.

Table 3:

Small number addition algorithms. Each entry lists: code (Algorithm Pseudocode); what a child might do and say (Trace); the number of operations (Operations); how many fingers (or other objects) are needed (Fingers); and how many numbers the child must remember simultaneously (Memory). raise(N, hand) holds up N fingers on hand by counting from 1. Y = count(hand, X) counts fingers held up on hand starting from X to return Y. Y = raiseCount(N, hand, X) combines raise and count, counting from X while holding up N fingers on hand. Resource counts for retrieval assume a previously seen problem; the values otherwise grow to accommodate a call to add, a generic adding algorithm which selects a specific addition algorithm appropriate to the addends. a₁ and a₂ denote the first and second addend, respectively.

Algorithm Pseudocode	Trace (2+5)	Resources
		Operations	Fingers	Memory
def sum(a1,a2):   raise(a1, LeftHand)   raise(a2, RightHand)   y = count(LeftHand, θ)   sum = count(RightHand, y)   return sum		2(a1 + a2) + 1	a1 + a2	1
def shortcutSum(a1, a2):  y = raiseCount(a1, LeftHand, θ)  sum = raiseCount(a2, RightHand, y)  return sum		a1 + a2 + 1	a1 + a2	1
def countFromFirst(a1, a2):  sum = raiseCount(a2, LeftHand, a1)  return sum		a2 + 1	a2	2
def min(a1, a2):  if a1 > a2:   return countFromFirst(a2, a1)  else   return countFromFirst(a1, a2)		min(a1, a2) + 1	min(a1, a2)	2
def retrieval(a1,a2):  if (a1, a2) not in seen:   seen[(a1, a2)] = add(a1, a2)  return seen[(a1, a2)]		2	0	[0, ∞)

Restructuring sum to simultaneously track both counts, updating the sum while creating each addend, counts each object only once and explicitly represents a strong generalization: here, that the two counts are not coincidental but used for closely connected purposes. The result is shortcutSum (Table 3): count out each addend, reciting the total count rather than the current addend count. shortcutSum tracks both counts using a newly implemented function, raiseCount. Maintaining simultaneous counts increases working memory load and the potential for error and is, unsurprisingly, a late-developing counting skill sum [103, cf. 104]. Addition strategies incorporating simultaneous counts naturally appear during early grade-school [103] but can be discovered earlier given practice [88].

Many techniques for improving code are sensitive to execution traces recording a program’s step-by-step behavior. In shortcutSum, for example, the first call to raiseCount is redundant: it counts out a1, the first addend, to produce y, meaning y is equal to a1. Removing the first count and replacing y with a1 produces countFromFirst (Table 3). It is on average twice as fast as shortcutSum while reducing finger and working memory demands. These changes, however, are not based on code alone; they require sensitivity to the behavior of code via something like an execution trace. While reported in children and common in theoretical accounts [93, 94, 105], there is debate about how frequently countFromFirst appears in practice [88, 91].

Changes in a hacker’s basic understanding of a problem provide another source of revisions. New understanding often comes from playing with code in the manner of “bricolage” [106] rather than formal instruction. For example, she might notice that addition is commutative—changing the addend order never affects the final sum. shortcutSum helps explain why: every raised finger increments the sum exactly once. The principle of commutativity is formally introduced as early as first grade [107], but can be independently discovered earlier [102]. Commutative strategies are also common before children understand that addition is commutative, suggesting an incomplete or incorrect understanding of addition [102, 104].

These discoveries justify swapping addend order when the first addend is smaller than the second. This gives the well-studied min strategy: count out the smaller addend from the larger addend (min; Table 3). min is perhaps the best attested small number addition strategy, common from first-grade through adulthood [84–87, 89, 108] but spontaneously developed earlier given extensive practice [88]. On average, min removes half the counting necessary for countFromFirst and further reduces finger and working memory demand. min, however, requires the ability to rapidly compare numbers—the hacking approach naturally draws on libraries of interacting, and often simultaneously developing, cognitive abilities.

Finally, a hacker given certain addition problems multiple times might realize that she could save time by memorizing and retrieving answers after computing them the first time (retrieval; Table 3), as in dynamic programming algorithms [109]. Indeed, as children age they rely decreasingly on strategies requiring external cues (e.g. fingers, verbal counting), and increasingly on memorization [88], a transition humans formally teach [107] and also discover independently [110, 111].

Much of we know about the development of small number addition is thus well-aligned with the child as hacker, which naturally accommodates and unifies many seemingly disparate phenomena. The child as hacker also suggests several next steps for work on addition and related domains. First, we need models of learning that formalize knowledge as code modified using hacker-like values, goals, and techniques. Explicitly situating arithmetic learning within the context of the child as hacker will likely suggest useful and novel hypotheses (e.g. specific hacking techniques [78] might explain specific chains of strategy introduction; differences in values might explain differences in performance [88]). Second, mathematical learning extends far beyond small number addition, including both early sensitivities to number and the development of counting, and the later development of compositional grammars for large numbers, a concept of infinity, more complex arithmetic, and so on. The child as hacker suggests ways to integrate these phenomena into a general account of mathematical development. Third, the child as hacker should also provide paths to algorithmic theories for qualitatively different kinds of knowledge acquisition (e.g. intuitive theories of the physical and social world, Box 2).

Box 2: Hacking theories of biology: intuitive and scientific accounts of kinship and inheritance.

While the small number addition example examines procedural learning in mathematics, the child as hacker equally applies to other domains and kinds of knowledge. Kinship systems (Figure I.a) can be seen as logical and declarative intuitive theories of social relatedness, and Mendelian inheritance (Figure II.a) as a probabilistic and causal formal theory of biological relatedness. A hacker might implement both by compressing a set of observations into more reusable, generalizable, and modular code. In both cases, she iteratively improves her program—adding, deleting, and revising code—and occasionally adds entirely new structures simply by defining and using them. Some changes help, others are rejected, and she eventually produces compact theories of both domains.

In learning kinship, one can frame the task as refactoring a long list of relations about individuals (Figure I.b) into rules for high-level kinship terms (Figure I.c) and a small set of basic facts (Figure I.d) from which all relations can be easily derived. Our hacker writes her theory in a logic programming language called Prolog, drawing inferences using deductive proof to learn, e.g. who her uncles are.

In learning Mendelian inheritance, one can frame the task as refactoring a long list of phenotypes and parentage records (Figure II.b) into a causal theory of biological inheritance relating phenotypes to genotypes via the three laws of inheritance (Figure II.c). Because patterns of inheritance are not strictly logical but require distributional reasoning, and because she is looking for a causal explanation, our hacker implements her theory as a generative model in a probabilistic programming language called Church [26]. She queries her theory using Church’s built-in tools for conditional inference to learn, e.g. likely genotypes for a1 and a2.

Figure I:

Mapping kinship to code: (a) a family tree labeled by three kinship systems (circle = female, colors are different terms, child generation ignores gender); (b–d) Kinship in Prolog. Prolog expresses computations as Horn clauses called rules, Head :- Body.. Head is true if each term in Body is true (empty bodies are also true); (b) initial kinship data; (c) rules for inferring kinship relations, including new primitives parent, spouse, male, and female; and (d) a small set of rules such that (c) & (d) implies all of (b).

Figure II:

Mapping Mendelian inheritance to code: (a) an overview of Mendelian inheritance; (b–c) Mendelian inheritance in Church. Church expresses computations as parenthesis-delimited trees. (b) a list of individuals (a1, a2, b1, …), their parents, and phenotypes (YW = Yellow; GN = Green; SM = Smooth; WR = Wrinkly); (c) a list of traits (dominant followed by recessive) and part of a generative theory using Mendel’s laws and a uniform prior over unknown parents (i.e. random-gene draws a pair of alleles uniformly at random).

Hacking and other metaphors

The child as hacker builds on several other key developmental metaphors. All these views are valuable and have significantly improved our understanding of learning. Here, we explain how the child as hacker extends these accounts, highlighting its potential contributions. See Figure 1b for a summary of the major claims of the views discussed in this paper.

The child as scientist

The child as scientist metaphor is one of the strongest influences on the child as hacker. With roots in the work of Piaget [1] and since extensively developed [2–5, 112], this view emphasizes how children structure their foundational knowledge in terms of intuitive theories analogous in important ways to scientific theories [113–116], and build knowledge via epistemic values and practices [5, 70–72, 117] similar to the ways scientists collect and analyze evidence and modify theories in response to evidence. construct theories which are accurate, general, and simple. The related view of rational constructivism [69] emphasizes the sophisticated mechanisms children use in theory-building—Bayesian statistical inference, constructive thinking processes such as analogy, mental simulation, and other forms of “learning by thinking” [118]), and active, curiosity driven exploration—and the importance of formalizing these mechanisms in rational computational models.

The child as scientist and the child as hacker are best seen not as competitors but as natural companions, with overlapping but complementary notions of knowledge representation, epistemic values and practices, and constraints on learning, which together paint a more complete picture of cognitive development. The child as scientist emphasizes children’s learning as centrally focused on building causal models of the world and the conceptual systems (intuitive theories) supporting these models. It asks questions about how theories are represented, what makes for good theories, and what mechanisms support theory learning, drawing inspiration from how scientists have approached these questions and implementing its proposals computationally as approximations to Bayesian inference over spaces of causal networks, probabilistic first-order logic, and probabilistic programs [11, 56, 57, 63, 66, 70, 72, 117].

The child as hacker extends these ideas with its broader view of what kinds of representations are worth learning, what values set goals for learning, and what practices are useful for accomplishing these goals: programs may go beyond the purely causal, there are many values for good programs beyond those traditionally used to assess scientific theories (accuracy, generality, simplicity), and learning draws on many algorithmic-level processes across multiple timescales, not just the stochastic sampling or search mechanisms that have traditionally been used in Bayesian models of theory learning. This view could enrich both the computational and algorithmic-level claims of child as scientist models in many specific ways. For example, intuitive theories could benefit from being formalized as domain-specific libraries or languages for writing generative probabilistic programs (e.g. Box 2), and the construction of more radically new kinds of concepts could be captured as the construction of new function and data types, not just new functions or data structures of existing types. The many values of good code in Table 1 could also have analogs in the goals that guide children in constructing their intuitive theories, and the processes of improving code in Table 2 could all have analogs in how children build their intuitive theories; perhaps these could help formalize some of the mechanisms of analogy, bootstrapping, explanation-driven and goal-driven search proposed in the child-as-scientist and rational constructivism views [3, 5, 69, 118] which have not been fully captured by previous algorithmic-level learning models.

It is perhaps fitting that scientists recognize highly familiar scientific practices and values in development, but in addition to an evocative metaphor, the child as scientist is a fruitful hypothesis. It has sparked numerous Child-As-X theories in cognitive psychology positing specific modes of scientific thinking as key throughout development. Children can be seen as: linguists determining the structure of language [119–121]; anthropologists systematically studying behavior [122]; statisticians inferring latent world structure [123, 124]; econometricians discovering preferences [125]; and philosophers refining understanding through reflection and analysis [126, 127]. We hope the child-as-hacker view will further grow this productive tradition. Efforts to formalize the child-as-scientist metaphor have also played key roles in its fruitfulness [70–72, 117, 128]. Indeed, many of the LOT models discussed earlier were explicitly developed to formalize aspects of theory learning and the broader scientific process. Formalizing the child as hacker may seem like a daunting challenge, but this process took decades of sustained interdisciplinary effort for the child as scientist. A similar long-term investment in computational models for the child as hacker could prove similarly fruitful.

Resource rationality & novelty search

The idea of resource rationality [129–131] argues that theories must account for cognition as realized in finite computational devices. Time, memory, and energy are limited. Learners can thus more quickly find practical hypotheses by evaluating resource use alongside simplicity and fit. Stanley and colleagues have developed the idea of novelty search [132, 133] around the observation that many learning problems require navigating large hypothesis spaces in finite time. Comparing trivially different hypotheses is unlikely to be helpful. They demonstrate for many classes of problems that agents sensitive to novelty learn more effectively than agents using other objectives.

Both resource rationality and novelty search are important ways of thinking about objectives in learning. The child as hacker embraces these insights, but makes claims about learners’ objectives beyond either view. First, it encourages considering both efficiency and novelty, rather than arguing for either alone. Second, it argues for a radically larger set of possible influences on the objective function, including engineering and aesthetic concerns and perhaps more (Table 1). Third, it suggests that learners’ objectives constantly change in complex and as-yet poorly understood ways, identifying a key area for future research. Rather than searching for the right human-like objective function, the child as hacker suggests that cognitive scientists seek to understand an entire space of possible objectives and the ways that learners move between them.

Workshop and evolutionary metaphors

The child as hacker is also closely related to a pair of metaphors from Siegler and colleagues emphasizing the dynamics of learning: the workshop metaphor [88] and the evolutionary metaphor [95]. The workshop metaphor emphasizes the diversity of knowledge (raw materials) and learning processes (tools) available to children when producing mental representations (products) to meet the demands of daily life (work orders), and the importance of selecting appropriate materials and tools for a given product. The evolutionary metaphor recasts these ideas in light of biological evolution, highlighting the essential role of variability, selection, and adaptation in learning. These metaphors work together to tell a broader story about learning. Both argue that we maintain multiple strategies for solving any given problem and adaptively choose among them, learning about their context-specific usefulness over time. In contrast to “staircase” theories suggesting long periods of relatively uniform thinking punctuated by brief and dramatic transitions, they suggest that children navigate “overlapping waves” as new strategies appear and others fade.

The child as hacker shares much with these metaphors. They all emphasize the importance of bringing a diverse collection of mental representations to bear during learning, as well as selecting representations, values, and learning strategies most relevant to the specific task at hand. Each view also highlights the way knowledge is iteratively revised; the outcomes of learning are themselves frequently the raw inputs for future learning. Each makes variability, selection, and adaptation central features of learning.

The mind, however, operates on representations which bear a closer resemblance to software than hardware, looking more like programs than tables or chairs. We could think of the child as hacker as updating the workshop metaphor for the software era and focusing on the tools needed to build a rich computational model of a richly computational mind: all the ways we have come to represent knowledge with programs and programming constructs, and all the values and activities of hacking for making programs better, which seem more directly tied to the goals and mechanisms of learning and more amenable to computational formalization than those of carpentry or metalwork.

The child as hacker may also be better aligned with children’s goal-orientedness during learning. Evolution is an intentionless process whose primary change mechanisms act at random. In the workshop and evolutionary metaphors, goal schemas can constrain this random search process [91] but that is different from directly and deeply guiding it. As with other forms of stochastic search or reinforcement learning, learning under an evolutionary mechanism would thus require tremendous amounts of computation and time [28]. Children’s learning, by contrast, is remarkably efficient [134], in part because it is strongly goal-directed [5]. Children’s behavior may sometimes look random, but there is almost always an underlying goal driving that behavior. Where the apparent randomness comes from, the evolutionary character, is perhaps a dynamically changing set of goals: initially X, then Y, then Z, then back to X until it is achieved. This dynamic is more consistent with the intrinsic nature of goals in hacking, where children’s goals might then address different values such that each improves representations in different ways. Externally, without access to those goals or their internal logic, both learning and hacking may look random, piecemeal, and non-monotonic—sometimes progressing, sometimes regressing. Internally, however, each is intensely goal-driven, resulting in profound, long-term growth.

In sum, the child as hacker helps to refine and advance the workshop and evolutionary views, by giving a less metaphorical take on the workshop metaphor and a better fit for the goal-driven behavior of children than the intentionless randomness of evolution. Moreover, the child as hacker makes specific suggestions beyond either metaphor, including a strong emphasis on program-like representations and the specific values and processes that guide how programs get better (Tables 1 and 2), which we hope can serve as the basis for a new generation of modeling in cognitive development.

Prospects for a computational account of learning

Hacking represents a collection of epistemic values and practices adapted to organizing knowledge using programs, and there is growing evidence that programs are a good model of mental representations. The child as hacker combines these ideas into a roadmap toward a computational account of learning and cognitive development. It makes testable claims about a general class of inductive biases humans ought to have—namely those related to synthesizing, executing, and analyzing information as programs. It also concretely identifies the representations, objectives, and processes supporting learning with those of human hackers. Finally, it makes a unifying claim about how these three might be implemented as code, procedures for assessing code, and procedures for revising code, respectively.

To explain learning in light of these claims, we must systematically use code as a lens on learning. Doing so produces testable hypotheses that differ from common alternatives. For instance, the child as hacker predicts that children frequently change beliefs in the absence of external data. It predicts that children might learn representations which are less accurate or more complex than alternatives so long as they win on, e.g. modularity or cleverness. It also predicts that, while dramatic, global changes are possible, changes to mental representations typically occur through the accumulation of simple, structured changes, similar to the way code tends to be refactored.

Both machine learning and psychology would benefit from a united effort to pursue this roadmap in developing a computational account of human learning. Machine learning would benefit greatly from the growth of empirical programs in psychology to understand how children hack their own representations (see Outstanding Questions), how real hackers assess and improve their code in practice, and how children adopt and pursue goals. Effectively searching large hypothesis spaces is a fundamental problem in machine learning, so one crucial question for this second program is how humans effectively search the space of Turing-complete computations. Psychologists and cognitive scientists would benefit greatly from a sophisticated framework for program induction. Such a framework would bring together existing knowledge about theoretical computer science, programming languages, compilers, program synthesis, and software engineering to provide tools capturing human-like approaches to solving problems in these domains.

Outstanding Questions.

• How might traditional accounts of cognitive development be usefully reinterpreted through the lens of hacking? How can core knowledge be mapped to an initial codebase? How can domain-specific knowledge be modeled as code libraries? What chains of revisions develop these libraries? How do libraries interact with each other? Which hacking techniques are attested in children, and when do they appear? Which values? How can individual learning episodes be interpreted as improving code?

• What are children’s algorithmic abilities? How do they learn in the absence of new data? What aspects of learning are data-insensitive? How do they extract information from richly structured data? What kinds of non-local transformations do we see? Do children ever find more complex theories before finding simpler ones? How do children move around the immense space of computationally expressive hypotheses?

• How do humans program? What techniques do they use? What do they value in good code? How do they search the space of programs? Does the use of many techniques make search more effective?

• How can the discoveries of computer science best inform models of human cognition? For example, what remains to be learned about human cognition from the study of compilers, type systems, or databases? How can we use the vocabulary of programming and programming languages to more precisely characterize the representational resources supporting human cognition? Are things like variable binding, symbolic pattern matching, or continuations cognitively primitive? If so, are they generally available or used only for specific domains? How does the mind integrate symbolic/discrete and statistical/continuous information during learning?

• What kinds of goals do children have in learning? What improvements do they inspire? How do they move around the space of goals? What data structures does this movement suggest for goal management?

Concluding Remarks

Our goal in introducing the child as hacker has been to offer a path toward answering central challenges of human learning and cognitive development that both reframes classic questions and helps us ask new questions. Recent work in cognitive science on constructive thinking [118], the neuroscience of programming [135], and modeling the development of core domains such as intuitive physics using game engines [136, 137] represents promising complementary steps. Recent developments in program induction and program synthesis techniques from computer science are also beginning to operationalize aspects of specific hacking techniques, including work on backward chaining of goals and subgoals [138–140], neurally-guided synthesis [141, 142], iterative refactoring [143–146], incremental programming [147–149], and learning generative probabilistic models [150, 151]. These efforts have the potential to move the child as hacker beyond just another metaphor, or just a hypothesis, to a working and testable computational account of cognitive development. But they are just first steps. We look forward to all the work that remains to be done to understand how it is that children hack their own mental representations to build yet-unparalleled tools for thinking.

Highlights.

• Programs provide our best general-purpose representations for human knowledge, inference, and planning; human learning is thus increasingly modeled as program induction—learning programs from data.

• Many formal models of learning as program induction reduce to a stochastic search for concise descriptions of data. Actual human programmers and learners are significantly more complex— using many processes to optimize a complex objective.

• The goals and activities of hacking—making code better along many dimensions through an open-ended set of goals and activities—are helping to inspire better models of human learning and cognitive development.

Glossary

Child as hacker

an algorithmic-level view of cognitive development extending the idea of learning as programming by drawing inspiration from hacking such that the specific medium, values, techniques, and practices of hacking form a rich set of hypotheses about learning, particularly in children

Hacking

making code better along many dimensions through an open-ended set of goals and activities

Learning as programming

a computational-level view of learning claiming that that the human conceptual repertoire can be understood as a mental programming language and learning as a kind of programming

Program/Code

a particular expression of a particular computation in some programming language

Program Induction

learning programs to explain how observed data were generated

Programming Language

languages with a formal syntax whose semantics express computations, typically in terms of instructions that program the behavior of some machine (e.g. the x86 processor, Turing machines)