Optimal age- and sex-based management of the queue to ventilators during the Covid-19 crisis

Abstract

Triage protocols for intensive care units are based on priorities assigned to presents, but ignore patients about to arrive, so a priority newcomer may not find a ventilator and its associated nursing staff available because they are occupied by a lower-priority patient who however was present at the moment of assignment. Conversely, waiting too long leads to losing elderly patients who could have been saved by ventilators. As age and sex are major determinants of mortality by Covid-19 and have the merit, in contrast to other priority criteria, of being immediately available to health professionals, the criterion is the minimization of the mean mortality rate weighted by age- and sex-specific life expectancies. The dynamics is a queuing process involving mortality and return home flows and competition between ages. The result is the determination of an optimal threshold age that can guide triage.

1. Introduction

The influx of patients during the Covid-19 crisis in hospitals with a limited number of ventilators and their associated nursing staff, beyond the tragedy, can lead, at the height of the crisis, to an excess of demand (by patients) over supply (in ventilators and their associated nursing staff). Economic calculation is challenged when it comes to maximizing the benefits produced by scarce resources, in the demand for a fair allocation. Indeed, the rationing of ventilators leads health professionals to make difficult choices about who to admit to a ventilator and who to put on hold. This choice is necessary in a pandemic period and should not be left to the discretion of clinicians in the heat of the moment (Emanuel et al., 2020).

This is the project of this article: to provide assistance in the management of the queue of Covid-19 patients in demand for ventilators in a situation of shortage. That is why I will reason with measures that are immediately available and accepted by health professionals, such as life expectancy, instead of the statistical value of life or Sepsis-related Organ Failure Assessment (SOFA) scores or Quality Adjusted Life Years (QALYs), which require medical tests and are not used in French hospitals. Alvarez et al. (2020), referring to Hall et al. (2020), used the “value of statistical life”, measured as a multiple of the annual GDP per head, for a theoretical discussion but without application to empirical data. These “values of statistical life” are not used in French hospitals and my wish in this article is to propose a procedure that can easily be used in hospitals. Quality Adjusted Life Years (QALYs) are a possible criterion for the selection of patients to ventilators, except that this is not practiced in French hospitals either. In addition, candidates to ventilators for Covid-19 are in such poor health that QALYs are not effective in assessing the survivability of Covid-19 patients (Langley, 2020).

Hospital queue management economists also propose priority measures based on what medical staff say: The Quick SOFA score (Angus et al., 2016) is devised to identify patients at high risk of dying from infection. I only address here those patients with Covid-19 who require a ventilator, and who are therefore all at high risk of dying from infection. This fact, as well as the fact that SOFA scores are not available in the Covid-19 statistics published by the French regional health agency, means that SOFA scores are not operational in this particular Covid-19 situation. Kim et al. (2015) pointed out the lack of systematic admission criteria in intensive care units, arguing that the identification of the most unstable patients is difficult and depends too much on the training and subjectivity of the physicians in charge. These authors propose a criterion based on the regression of the patients’ final outcomes according to whether or not they were admitted to intensive care units, their clinical severity factors, their characteristics, and seasonal factors. However, this regression is true for the 15 selected hospitals (their geographical locations are not specified) and has no reason to be standardized to other hospitals. The regression reflects what was done in these hospitals, including the subjectivity of the physicians, and is therefore not a fair criterion.

The criterion of life expectancy by age and sex that I use has the merit of being easily calculable, of avoiding speculation on the behavior of Covid-19 patients under ventilator, and of being familiar to healthcare professionals. For example, Bruno Mégarbane, head of intensive care units at Lariboisière Hospital, France, insisted that what counts is “saving lives” (French radio France info, November 3, 2020), which I interpret as “saving years of life”. However, the procedure I propose can be adapted to other priority measures, if they are available for each patient in a timely manner at the time of admission to the hospital.

In the case of Covid-19, age and sex indeed have played an eminent role in mortality risk and in practice have served as a sorting criterion, even if not in the optimal way like the one I propose here. For example, on 28 April 2020, in France, according to an estimate provided by the French Information System for Monitoring Victims of Attacks and Exceptional Health Situations (SIVIC1 ), the average age of patients in intensive care was 62.1 years, compared with 84.6 for those in conventional hospitalization, 85.1 in follow-up care and rehabilitation facilities and services (Établissements et services de soins de suite et de réadaptation), 70.7 for the deceased, and 75.8 for those returning home. Patients on ventilation were therefore considerably younger, although the flow of patients on ventilators aged 80 years and over was not zero. In a press article dated 30 July 2020, Hecketsweiler and Royer (2020), on the basis of data from a French parliamentary commission of inquiry, accused that old people were removed from hospitals at the peak of the influx of Covid-19 patients.

Biological age (Demongeot, 2009) is based on biomarkers such as serum analytes, epigenetic markers, and deficit or frailty indices. In addition to the ethical issues raised by selection among persons of same civil age, it requires a long and costly procedure, not very compatible with emergency situations. In addition, biological age may accelerate or slow down in the future, so that its value at one point in time does not preclude the probability of survival in the future. In any case, the method I propose requires period life tables and, to my knowledge, there is no life table by biological age for France yet.

“Reserving” ventilators for patients who have not yet arrived amounts to setting a threshold age above which patients are excluded from ventilators, and below which patients who are present are assigned to ventilators. There would therefore be an optimal threshold age that takes into account laws of probability of arrival at the various ages, mortality rates with or without a ventilator, rates of assignment to ventilators, and rates of return home, out from the intensive care unit or from the waiting room.

The objective I propose is to maximize the total number of expected years left to live for the population of patients eligible for ventilation, which, in relation to the population entering the hospital system, amounts to minimize the mean (over time) mortality rate weighted by life expectancies. The result is the identification of an optimal threshold age, which allows for managing the queue in the best way possible for the present patients and the patients about to arrive.

My theoretical contribution is therefore to articulate competing queues with a finite or an infinite number of servers, age and sex competition, and to combine in an original way queue theory with age- and sex-based utility theory. I also estimate instantaneous rates of transition (to death, return home, or assignment to ventilators) from the data available. The possibility of implementing it practically is adapted to the case of intensive care units in Covid-19 time. The result is that I provide a threshold age based on arrivals, mortality, and returns home. The rates of all these movements are estimated based on early findings and are therefore specific to the epidemic and the means allocated. The threshold age, as called for by Emanuel et al. (2020) for example, is no longer based on intuition and not only avoids the first-come, first-served rule, lottery, or questionable criteria such as priority to those who can attest to good deeds in the past or to priority given to patients claiming social utility, but also provides a normative framework for decision-makers.

Ethical considerations.

The first-come, first-served rule and the lottery are not efficient: Heuristically, if ventilators are allocated only to those present, by the effect of chance arrivals, “older” people “take the place” of “younger” people; conversely, if the health service waits too long for the arrival of “young” people, it unnecessarily endangers “old” people while ventilators remain idle. That is why I will use queue theory.

As a reviewer of this article objects, leaving a ventilator at rest while waiting for a patient may be felt as “repugnant”. The advantage of the first-come, first-served rule or of the lottery is that the years of life sacrificed by those who are about to arrive but will not find a ventilator available is that it is less “visible” in the hospital, as no ventilator is idle. Is not this ethically objectionable? In an emergency situation, the rule should be to save the most remaining years to live, not the present.

In this article, I provide a way to fuel the ethical debate on who to assign to ventilators by providing the solution in terms of remaining years to live. This ethical issue has much to do with the trolley problem pioneered by Thomson (1985): A runaway trolley will kill five people if it continues on its way; or save them if it is diverted, but at the cost of the life of another person who would not have been killed if the trolley had continued on its way. Here, the ventilator in first-come, first-served or in lottery modes will save the lives of patients present, but at the cost of more years to live sacrificed by people about to arrive. I do not venture any further into this deep ethical problem of the trolley, although the technical solution I propose could be used to feed it.

Healthcare professionals however are already aware that older patients may occupy ventilators to the detriment of younger patients who may arrive. They may intuitively build in an upper age limit for patient access to ventilators. What I propose here is a systematic calculation as a decision aid, based on quantified processes of arrivals, length of stay, and exits. Of course, healthcare professionals make the final decision. If this age is set a priori, too high a value leads to depriving elderly patients of ventilation, and it is inefficient to deny ventilators to elderly people if ventilators are available. Indeed, in April 2020, 3.3% of the total number of patients undergoing ventilation in the French Île-de-France region were aged 80 and over (Assistance publique des hôpitaux de Paris, 2020, p. 43). This maximum age should therefore not be set a priori or intuitively, but result from the optimal compromise between arrivals and availability of ventilators.

In Section 2, I present queue theory and ventilators; in Section 3 the objective and the queuing process (3.1), which has the originality of combining two standard queuing models, death in the waiting room for ventilators, with an infinite total number of “servers”, and the transfer to the intensive care unit, with a finite total number of servers (the ventilators (associated with their nursing staff)). In the permanent regime, I express the probability of the expected total number of patients in the system (Section 3.2), waiting for ventilators or on ventilators, and I determine the optimal threshold age allowed by the total number of ventilators. In Sections 4.1, 4.2, I present the data, estimate the instantaneous mortality and return home rates in each compartment on the basis of French longitudinal data collected at the peak of the epidemic (Sections 4.3, 4.4, 4.5). This makes it possible to represent the minimum mean mortality rate weighted by life expectancies as a function of the threshold age and the total number of ventilators (Section 4.6). The sensitivity analysis in Section 4.7 reveals the effect of each parameter on the mean mortality rate weighted by life expectancies. In particular, I evaluate the cost of a saved year of life based on the cost of a ventilator, as well as the cost of an additional patient. In this way, the economic calculation I perform (based on the life expectancies by age and sex, a piece of information that healthcare professionals can accept) translates into a practical measure for hospitals.

2. Queue theory and ventilators

Ventilators.

What are ventilators? Anesthesia ventilators ensure prolonged ventilation in intensive care unit patients under highly regulated conditions (Société française d’anesthésie et de réanimation, 2020). A ventilator can only ventilate one person at a time. Coronavirus lung infection may require up to 15 days on a ventilator.2 The French data do not give details of those that are assessed as being in insufficient condition to be removed from the ventilators and therefore disconnected in order to assign the ventilators to someone else. These cases are counted as deaths because patients who are totally dependent on ventilation cannot be removed from it or they die within minutes (Truog et al., 2020). Moreover, we cannot imagine, as in the theory of priority class queues – but these are teletraffic processes that can be suspended and then resumed – having patients going back and forth to intensive care unit because priority patients have just arrived.

Here, “ventilator” refers not only to the breathing machine, but also to the associated nursing staff, which is normally one staff for one patient on ventilator, although this rule can be adjusted in case of staff shortages.3 Ventilators without caregivers to operate them is tantamount to rendering them unusable. The risk of shortage in March 2020 concerned respiratory equipment, and as the virus was circulating in only a few French regions, it was possible to transfer anesthesiologists and specialized nurses. By February 2021, when the virus had spread everywhere, the risk of shortage had shifted to these specialized and time-consumingly trained personnel.4

The shortage of ventilators during the covid-19 crisis of spring 2020.

The shortage of ventilators and the accompanying triage were the subject of articles in the specialist press as well as in newspapers. Rosenbaum (2020) described the Italian situation in the spring of 2020 when hospitals, due to lack of resources, had to refuse many elderly patients with co-morbidities. Videos also showed the tragedy of the shortage in waiting rooms5 or in intensive care units.6 In Italy, about 10 to 25% of hospitalized patients required ventilation, in some cases for several weeks.7 For Great Britain, Lambert (2020) in the 20–26 March edition of a magazine, alerted of a serious forthcoming shortage of ventilators. Pagel et al. (2020) raised the question of how UK’s National Health Service would manage access to intensive care when resources become insufficient to treat everyone. In France, on 25 March 2020, the media reported hospitals to be in shortage of ventilators.8 Truog et al. (2020), in spring 2020, pointed out that if the shortage also concerned hand sanitizers, N-95 masks, and intensive care unit beds, it was mainly mechanical ventilators that were most in short supply.

Triage guidelines.

It is difficult to think that everyone will not have the same opportunity to access intensive care. However, all triage protocols, by definition, are based on the principle of excluding patients from intensive care (Pagel et al., 2020). Arya et al. (2020) explained that the Covid-19 outbreak and the current inability to offer intensive care to everyone in need has led their hospital to follow guidelines for selecting those who are most likely to survive and recover. Lidall et al. (2013) reviewed triage methods adopted in Scandinavian hospitals and emergency medical services for prioritizing patients for care and concluded for a lack of knowledge about potential effects of triage systems. In the Michigan (2012) protocol, frontline health workers are prioritized, with the risk that no ventilator remains available for other patients. In the 2015 New York State Task Force on Ventilator Allocation, after excluding certain patients, ventilators are assigned to those with the best chance of survival (Zucker et al., 2015). These chances are quantified by the Sequential Organ Failure Assessment score (Ventilator allocation guidelines, 2015). Patients on ventilators are routinely screened, and if the prognosis is unfavorable, ventilators are removed and assigned to other patients. Rosa Ramos et al. (2016) constructed an algorithm to treat a database of expertise capable of assigning priorities to patients after collecting useful information on them. Christian et al., 2006, Christian et al., 2014 described a collaborative process based on best evidence, expert panels, stakeholder consultations, and ethical principles to develop a triage protocol for prioritizing access to intensive care. In their recommendations, these authors suggested excluding patients with a life expectancy of less than one year (why one?) and patients with a 90% predicted mortality rate. However, these measures taken on extreme figures do not solve the shortage of ventilators for sure; it depends on in- and outflows of intensive care units. Christian et al. (2014), Zhang et al. (2020), and Pagel et al. (2020) mentioned home care and isolation to relieve the demand for ventilators.

To handle multiple categories of priorities depending on different ethical values object of contested debates, White et al. (2009) established a priority point system to provide a single score. The solution proposed by Pathak et al. (2020) to accommodate different ethical categories is by reserving a quota of ventilators to each category. In the case of Covid-19, categories may include age, sex, and comorbidities.

Queue theory in the management of intensive care units.

Mayhew and Smith (2008) used queue theory to take into account arrival flows. They distinguished between long and short treatments for injured patients arriving at hospital, but they ignored mortality and did not compete between patients on any priority criterion other than the severity of injuries (requiring long treatment if severe, short if not). In this article, the “treatment” for which patients are queuing is ventilation. Meisami et al. (2019) also used queue theory to assign patients to intensive or intermediate care units. Their optimization criterion is the average subjective measure of the lowest possible mortality risk of patients in intensive or intermediate care units. The “mortality risk metric” they used to select patients to intensive care units is not only subjective at least with respect to Covid-19, but does not provide information on the behavior of patients on ventilators. For example, regarding the excess mortality of Covid-19 patients due to thrombosis, Nicolas Gendron, a physician in the hematology department of the Georges–Pompidou hospital in Paris, pointed out that people with Covid-19 and in whom thrombosis occurs are not always those who are most at risk of thrombosis in normal circumstances.9 Moreover, Meisami et al.’s control variable is to assign patients to or remove them from intensive care units each day based on their mortality risk measures of the day, with units reserved for patients with the highest measures. This is not possible with Covid-19 because, as I mentioned, patients removed from ventilators die within minutes (Truog et al., 2020). Here, I consider that patients with Covid-19 candidates for ventilator use have the same need for ventilators. Therefore, an additional criterion other than a measure of mortality risk is needed to prioritize them once and for all and this criterion can only be dependent on input and output flows, not from subjective mortality risk measures.

3. Model

Queue theory is used when making business decisions about the resources needed to provide a service, in this case ventilators. A queuing process consists of patients arriving, waiting, being treated by servers and then leaving. Its modeling is based on the specifications of probability distributions for the arrival and behavior of servers. It is often a matter of predicting queue lengths and waiting times. Here, “leaving” means die, be put on a ventilator, or return home; the servers are death or ventilators; the criterion to be optimized is constructed from queue lengths and waiting times (which are random variables).

3.1. Objective and process

The manager’s problem is to maximize a social welfare function involving some hierarchizing criterion $e_i$ characterizing the patient $i$:

$$\underset{{\left(e_i\right)}_i}{max}E\left(U\left({\left(e_i\right)}_i\right)\right).$$ (1)

As I have advocated in the introduction, the criterion of life expectancies at current age has the advantage of being objective, so that the optimization problem becomes the minimization of the mean Covid-19-specific mortality rate weighted by age- and sex-specific life expectancies:

$$\begin{array}{ccc}\hfill \underset{\overline{a}}{min}E(-U\left(a\right))& \hfill =\hfill & \underset{\overline{a}}{min}\sum _a\sum _{n_a\ge 0}(\frac{{\mu }_1\left(a\right)}{{\mu }_1\left(a\right)+g_1\left(a\right)+\nu \left(a\right)}{W}_{n_a}\hfill \\ \hfill & \hfill \hfill & +\frac{\nu \left(a\right)}{{\mu }_1\left(a\right)+g_1\left(a\right)+\nu \left(a\right)}\frac{{\mu }_2\left(a\right)}{{\mu }_2\left(a\right)+g_2\left(a\right)}(D_{n_a}-W_{n_a}))\hfill \\ \hfill & \hfill \hfill & \times e_{a}P(N_a=n_a)\hfill \end{array}$$ (2)

where $-U\left(a\right)$ is the disutility of patients aged $a$ in years, $e_a$ the period life expectancy at age $a$, $N_a$ the random variable of the total number of patients aged $a$, $P(N_a=n_a)$ the probability that $n_a$ individuals of age $a$ are in the care system (waiting for ventilation or on it), $W_{n_a}$ the waiting time of patients of age $a$ to ventilators, death, or return home, $D_{n_a}$ the delay elapsed between entering and exiting the system. The threshold age $\overline{a}$ is involved in the value of the transfer rate $\nu \left(a\right)$ and in $W_{n_a}$ and $D_{n_a}$, as I explain below.

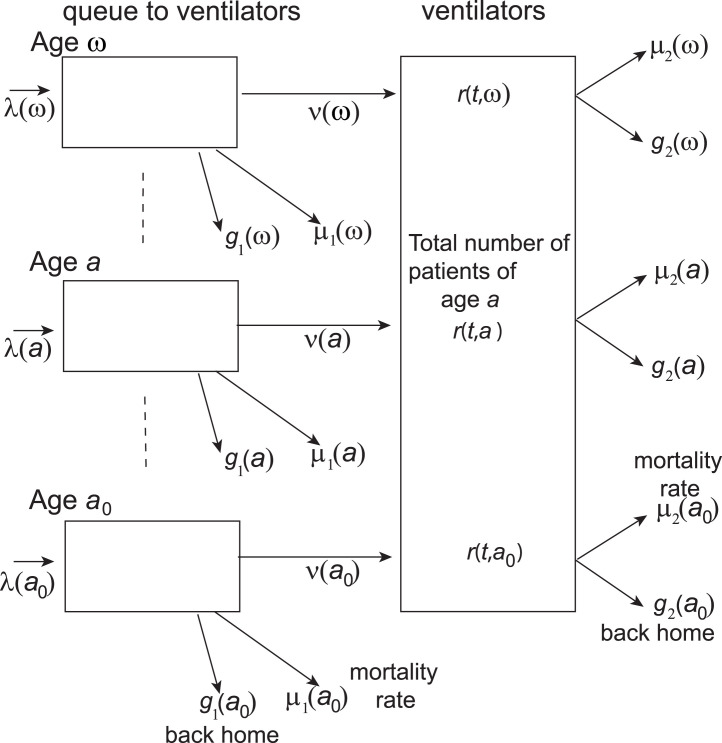
Fig. 1 shows the process: At time $t$, patients of age $a$ in demand of ventilation arrive at hospital where they either die from Covid-19 at instantaneous rate ${\mu }_1\left(a\right)$, return home at instantaneous rate $g_1\left(a\right)$, are assigned to ventilators at instantaneous rate $\nu \left(a\right)$, or remain in the waiting queue. In the intensive care unit, that is on ventilation, they die at instantaneous rate ${\mu }_2\left(a\right)$ from Covid-19 or return home at instantaneous rate $g_2\left(a\right)$. The time of the process is short enough and, concomitantly, the mortality for Covid-19 and the flow of return home are high enough to neglect mortality from other causes. Fig. 1 represents a continuous-time Markov chain $X\left(t\right)$ at time $t$ for which the state is the total number of patients $N\left(t\right)$ in the system.

Fig. 1.

Compartments in the queue at hospital of patients in demand of ventilators.

3.2. Expression of $P(N=n)$: combining M/M/c and M/M/$\infty$ queues

In queuing theory, Kendall (1953) denotes the arrival process, service distribution, and the total number of servers in the form:

“arrival process/service distribution/number of servers”.

The letter “M” means that the process is Markovian, that is, Poisson for the arrival process or exponential for the service time distribution required by each patient.

3.2.1. Case of a single age $a$

First consider a single age $a$. The process combines a M/M/$\infty$ queue of instantaneous rates ${\mu }_1\left(a\right)$ for death and $g_1\left(a\right)$ for return home and a M/M/c queue of instantaneous rate $\nu \left(a\right)$ for assignment to a total number $c\in \mathbb{N}$ of ventilators.

The arrival process is Poisson at instantaneous rate ${\lambda }_a$. The service time of each of the $c$ ventilators is exponentially distributed with instantaneous rate ${\mu }_2\left(a\right)+g_2\left(a\right)$, so that, as departures from the intensive care unit are Poisson, $c({\mu }_2\left(a\right)+g_2\left(a\right))$ ventilators are expected to become available between times $t$ and $t+dt$. The service times are assumed to be independent and independent of the inflow process. I assume the stability condition ${\lambda }_a\ge c\nu \left(a\right)$. Transitions can only occur upwards by one or downwards by one and remain exponentially long in each state. This is therefore equivalent to a birth-and-death process. The transition probability function $P_{ij}\left(t\right)$ is the probability that the process is in state $j$ at time $t>0$, knowing that it was in state $i$ at time $0$ (Zukerman, 2012):

$$P_{ij}\left(t\right)=P(X\left(t\right)=j\mid X\left(0\right)=i).$$ (3)

The continuous-time version of Chapman–Kolmogorov equations is:

$$P_{ij}(t+\tau )=\sum _{n=0}^{\infty }{P}_{in}\left(t\right)P_{nj}\left(\tau \right)\text{ for all}t\ge 0,\tau \ge 0.$$ (4)

At the limit:

$$\underset{\Delta t\to 0}{lim}\frac{P_{ij}(t+\Delta t)-P_{ij}\left(t\right)}{\Delta t},$$ (5)

which yields Kolmogorov’s backward equation:

$$P_{ij}^{\prime }\left(t\right)=\sum _{n\ne i}{\delta }_i{P}_{in}\left(t\right)P_{nj}\left(t\right)-{\delta }_i{P}_{ij}\left(t\right)\text{ for all }i,j,\mathrm{and}t\ge 0,$$ (6)

where, here, ${\delta }_i={\lambda }_a+{\mu }_1\left(a\right)+g_1\left(a\right)+\nu \left(a\right)$. As it is a birth-and-death process, this expression simplifies into

$$\begin{array}{ccc}\hfill P_{0j}^{\prime }\left(t\right)& \hfill =\hfill & {\lambda }_a(P_{1j}\left(t\right)-P_{0j}\left(t\right))\hfill \\ \hfill P_{ij}^{\prime }\left(t\right)& \hfill =\hfill & -({\lambda }_a+{\mu }_1\left(a\right)+g_1\left(a\right)+\nu \left(a\right))P_{ij}\left(t\right)+\hfill \\ \hfill & \hfill \hfill & {\lambda }_a{P}_{i+1,j}\left(t\right)+({\mu }_1\left(a\right)+g_1\left(a\right)+\nu \left(a\right))P_{i-1,j}\left(t\right)\hfill \\ \hfill & \hfill \hfill & \text{ for all }i>0.\hfill \end{array}$$ (7)

As the continuous-time Markov chain is irreducible, aperiodic, and stable (Zukerman, 2012), the limit of $P_{ij}(t$) exists for $t\to \infty$, and the permanent-regime probabilities, which are invariant measure probabilities,

$${\pi }_j=\underset{t\to \infty }{lim}{P}_{ij}\left(t\right)$$ (8)

exist. Its infinitesimal generator $Q={\left(Q_{ij}\right)}_{ij}$ is a matrix of one-step infinitesimal rates:

$$\begin{array}{ccc}\hfill Q_{i,i+1}& \hfill =\hfill & {\lambda }_a\mathrm{for}i=0,1,2,\dots \hfill \\ \hfill Q_{i,i-1}& \hfill =\hfill & i({\mu }_1\left(a\right)+g_1\left(a\right))+min(c,i)\nu \left(a\right)\mathrm{for}i=1,2,\dots \hfill \\ \hfill Q_{0,0}& \hfill =\hfill & -{\lambda }_a\hfill \\ \hfill Q_{i,i}& \hfill =\hfill & -{\lambda }_a-i({\mu }_1\left(a\right)+g_1\left(a\right))+min(c,i)\nu \left(a\right)\hfill \\ \hfill & \hfill \hfill & \mathrm{for}i=1,2,\dots \hfill \\ \hfill Q_{ij}& \hfill =\hfill & 0\mathrm{for}\mid i-j\mid >1.\hfill \end{array}$$ (9)

The permanent-regime probabilities ${\pi }_j$ are solutions to

$$\begin{array}{ccc}\hfill \sum _i{\pi }_i{Q}_{ij}& \hfill =\hfill & 0\text{ for all}j,\hfill \\ \hfill \sum _i{\pi }_i& \hfill =\hfill & 1.\hfill \end{array}$$ (10)

By successive substitutions, this amounts to

$${\pi }_i{Q}_{i,i+1}={\pi }_{i+1}{Q}_{i+1,i},i=0,1,2\cdots ,$$ (11)

yielding

$$\begin{array}{ccc}\hfill {\pi }_1& \hfill =\hfill & A{\pi }_0\hfill \\ \hfill {\pi }_2& \hfill =\hfill & \frac{A}{2}{\pi }_1=\frac{A^2}{2}{\pi }_0\hfill \\ \hfill & \hfill \cdots \hfill & \hfill \\ \hfill {\pi }_c& \hfill =\hfill & \frac{A^c}{c!}{\pi }_0\hfill \\ \hfill & \hfill \cdots \hfill & \hfill \\ \hfill {\pi }_{c+j}& \hfill =\hfill & \frac{A^{c+j}}{c!(c+B)\cdots (c+jB)}{\pi }_0\mathrm{for}j=1,2,3\cdots \hfill \end{array}$$ (12)

with

$$\begin{array}{ccc}\hfill A& \hfill ≔\hfill & \frac{{\lambda }_a}{{\mu }_1\left(a\right)+g_1\left(a\right)+\nu \left(a\right)}\hfill \\ \hfill B:& \hfill =\hfill & \frac{{\mu }_1\left(a\right)+g_1\left(a\right)}{{\mu }_1\left(a\right)+g_1\left(a\right)+\nu \left(a\right)}.\hfill \end{array}$$ (13)

As ${\sum }_{i\ge 0}{\pi }_i=1$,

$$\begin{array}{ccc}\hfill {\pi }_0& \hfill =\hfill & {\left(\sum _{n=0}^c\frac{A^n}{n!}+\sum _{j=1}^{\infty }\frac{A^{c+j}}{c!(c+B)\cdots (c+jB)}\right)}^{-1}.\hfill \end{array}$$ (14)

For ${\mu }_1\left(a\right)+g_1\left(a\right)=0$ and $\nu \left(a\right)>0$, ${\pi }_{c+j}$ is the expression of a M/M/c (Zukerman, 2012), and for ${\mu }_1+g_1>0$ and $\nu \left(a\right)=0$, the expression of a M/M/$\infty$ (that is, a Poisson).

3.2.2. Competition between ages for access to ventilator

Ventilators are released according to a Poisson law of parameter ${\sum }_{a=a_0}^{\overline{a}}r(t,a)({\mu }_2\left(a\right)+g_2\left(a\right))$, with ${\sum }_{a=a_0}^{\overline{a}}r(t,a)\le c$, where $r(t,a)$ is the total number of ventilators occupied at time $t$ by patients of age $a$. Because $e_a$ decreases with age $a$ greater than say 20 years, which is realistic in the case of Covid-19, the disutility $E(-U)$ in Eq. (2) is minimal when filling from the youngest to the oldest. In the framework of a triage protocol based on age, the numbers $n_a$ for $a<\overline{a}$ follow Poisson laws. It follows that

$$\begin{array}{ccc}\hfill \nu \left(a\right)& \hfill =\hfill & 1-{\mu }_1\left(a\right)-g_1\left(a\right)\mathrm{for}a\le \overline{a},\hfill \\ \hfill \nu \left(a\right)& \hfill =\hfill & 0\mathrm{for}a>\overline{a},\hfill \end{array}$$ (15)

which results in $A={\lambda }_a$ and $B={\mu }_1\left(a\right)+g_1\left(a\right)$ in Eq. (12) for $a\le \overline{a}$ and $A={\lambda }_a∕({\mu }_1\left(a\right)+g_1\left(a\right))$ and $B=1$ for $a>\overline{a}$.

The optimal age $a^{\ast }$ is the first age at which the expected total number of ventilators is saturated, which, by taking expectations, defines $a^{\ast }$:

$$\sum _{a=a_0}^{a^{\ast }-1}(1-{\mu }_1\left(a\right)-g_1\left(a\right)){\lambda }_a<\sum _{a=a_0}^{a^{\ast }}r(t,a)({\mu }_2\left(a\right)+g_2\left(a\right))\le \sum _{a=a_0}^{a^{\ast }}(1-{\mu }_1\left(a\right)-g_1\left(a\right)){\lambda }_a.$$ (16)

The assignment rate for patients of age $a^{\ast }$ is still $1-{\mu }_1\left(a\right)-g_1\left(a\right)$ (if there were enough ventilators, all patients of age $a^{\ast }$ would be affected) except that there may not be enough and only part of $n_{a\ast }$ may be assigned to ventilators.

The distribution of $n_a$ for $a\le a^{\ast }$ is conditioned to

$$q_a≔\sum _{b=a_0}^{a-1}{n}_b$$ (17)

and the conditional Poisson probability ${\pi }_n^{(a\mid q_a)}$ of $n_a$ knowing $q_a$, for $a\le a^{\ast }$ and $q_a<c$, is

$$\begin{array}{ccc}\hfill {\pi }_1^{(a\mid q_a)}& \hfill =\hfill & {\lambda }_a{\pi }_0^{(a\mid q_a)}\hfill \\ \hfill & \hfill \cdots \hfill & \hfill \\ \hfill {\pi }_n^{(a\mid q_a)}& \hfill =\hfill & \frac{{\lambda }_a^n}{n!}{\pi }_0^{(a\mid q_a)}\mathrm{for}n\le c-q_a\hfill \\ \hfill & \hfill \cdots \hfill & \hfill \\ \hfill {\pi }_{c-q_a+j}^{(a\mid q_a)}& \hfill =\hfill & \frac{{\lambda }_a^{c-q_a+j}}{(c-q_a)!(c-q_a+B)\cdots (c-q_a+jB)}{\pi }_0^{(a\mid q_a)}\mathrm{for}j=1,2,3\cdots ,\hfill \end{array}$$ (18)

with $B={\mu }_1\left(a\right)+g_1\left(a\right)$ and ${\pi }_0^{(a\mid q_a)}$ obtained as in Eq. (14). As for a simple sum of Poisson distributions, the $a-1$ processes combine to yield the distribution of $q_a$ as a M/M/c queue:

$$\begin{array}{ccc}\hfill {\pi }_{q_a}& \hfill =\hfill & \frac{A^{q_a}}{q_a!}{\pi }_0\mathrm{for}{q}_a\le c\hfill \\ \hfill {\pi }_{q_a}& \hfill =\hfill & \frac{A^{q_a}}{c!(c+B)\cdots (c+(q_a-c)B)}{\pi }_0\mathrm{for}{q}_a>c,\hfill \end{array}$$ (19)

which leads to the distribution

$${\pi }_n^{\left(a\right)}={\pi }_1^{(a\mid q_a)}{\pi }_{q_a}.$$ (20)

For $q_a\ge c$, $\nu \left(a\right)=0$, $A={\lambda }_a∕({\mu }_1\left(a\right)+g_1\left(a\right))$, and $B=1$, no one of age $a$ has access to ventilators:

$${\pi }_n^{(a\mid q_a)}=\frac{A^n}{n!}{e}^{-A}\mathrm{for}n=1,\dots .$$ (21)

The expected total number $E\left(N_{Q_a\mid q_a}\right)$ of patients of age $a$ queuing to ventilators knowing $q_a$ is

$$E\left(N_{Q_a\mid q_a}\right)=\sum _{n_a=c-q_a}^{\infty }(n_a-c-q_a){\pi }_n^{(a\mid q_a)}$$ (22)

and, by Little’s (1961) formula (Stidham, 1972, Stidham, 1974), the expected waiting time is

$$E\left(W_{Q_a\mid q_a}\right)=\frac{E\left(N_{Q_a\mid q_a}\right)}{{\lambda }_a}.$$ (23)

The expected time $E(S_a\mid q_a)$ spent on a ventilator for a patient admitted to intensive care is:

$$\begin{array}{ccc}\hfill E(S_a\mid q_a)& \hfill =\hfill & \frac{1}{{\mu }_2+g_2}\mathrm{for}{q}_a<c,\hfill \\ \hfill & \hfill =\hfill & 0\mathrm{otherwise}.\hfill \end{array}$$ (24)

Eqs. (18), (19), and (20) for computing the probabilities and Eqs. (22), (23), and (24) for computing the expected time spent in the waiting room or on ventilators allow for calculating the minimum expected mean mortality rate weighted by life expectancies in Eq. (2).

4. Application

4.1. The data

The objective is still to show how the optimal age $a^{\ast }$ and the total number of deaths vary with the total number $c$ of ventilators under empirical conditions of mortality, transfer to ventilators, and return home. I estimate these rates on the basis of available data. While queue management deals with the population in the different states at any time, estimating transition forces requires longitudinal follow-up of patients over time.

I use follow-up data collected by the French Information System for Monitoring Victims of Attacks and Exceptional Health Situations (SIVIC, compiled by the Assistance publique des hôpitaux de Paris on 28 April 2020)10 at peak dates of inflow for Covid-19 in hospitals.

4.2. Life expectancies $e_a$ by age $a$

In its weekly epidemiological update of 7 May 2020, Santé publique France reports that 73% of patients were men. That is why I calculate $e_a$ as the sum of 73% of male life expectancy and 27% of female life expectancy, from Insee data 2016–2018.11

4.3. Mean instantaneous rates in intensive care units: mortality ${\mu }_2$ on ventilator and return home $g_2$

From Table 1 which presents the follow-up of patients at D $+$ 10 since their admission to ventilation at day D $+$ 0 $=$ 18 April 2020, I derive the proportion of patients still on ventilation, using basic calculus of mortality analysis (Bonneuil, 1997). It corresponds to

$$e^{-10({\mu }_2+g_2)}=\frac{575}{947}=0.607,$$ (25)

where ${\mu }_2$ and $g_2$ are the mean instantaneous rates over ages of those on ventilation.

Table 1.

Follow-up at D$+$10 by age group of 947 patients on ventilators as of April 18.

On ventilators	575	Conventional hospitalization	138
Deceased	101	Facility & Aftercare &
Return home	112	Rehabilitation Services	21

Assistance publique des hôpitaux de Paris, 2020.

From Table 1, I also draw the proportion $\frac{112}{947}$ of patients returned home, which corresponds to

$${\int }_0^{10}{g}_2{e}^{-({\mu }_2+g_2)t}dt=\frac{g_2}{{\mu }_2+g_2}(1-e^{-10({\mu }_2+g_2)})=\frac{112}{947}=0.118.$$ (26)

From Eqs. (25), (26),

$${\hat{\mu }}_2=0.0349\text{ per day}\mathrm{and}{\hat{g}}_2=0.0150\text{ per day}.$$ (27)

4.4. Mean instantaneous mortality rate ${\mu }_1$ and return home rate $g_1$ of patients waiting for a ventilator

To estimate the mean instantaneous mortality rate ${\mu }_1$ and return home rate $g_1$, I use the statistics presented in Table 2 from the follow-up at Day 41 of patients aged 60 to 80 years who entered hospital on March 18, 2020. The total numbers of observations before 60 and after 80 are too low, so I will either take these rates equal to the mean values estimated for the 60–80 age group or extrapolate them from these average rates by augmenting them with an exponential growth factor in age.

Table 2.

Follow-up at D$+$41 of 240 patients of age 60–80 in hospital on 18 March 2020.

On ventilators	16	Conventional hospitalization	29
Deceased	51	Facility & Aftercare
Return home	137	& Rehabilitation Services	7

Assistance publique des hôpitaux de Paris.

Table 2 a priori groups together hospitalized patients requiring ventilation (at instantaneous risks ${\mu }_1$ of mortality, $g_1$ of return home, and $\nu$ of transfer to ventilators) with those not requiring ventilation (subject to instantaneous risks ${\mu }_1^0$ of mortality and $g_1^0$ of return home). Let $p$ be the proportion at Day 0 of patients requiring ventilation in Table 2. Patients may not immediately be assigned on ventilation; it may take a time $t_0$ before the risk of being assigned on a ventilator is effective, which includes the delay taken in hospitals to identify the specific presence of Covid-19 (Charmelot, 2020). The rate of transfer to ventilators is $\nu =0$ for $t<t_0$, $\nu$ taken constant for $t\ge t_0$. The total number of patients on ventilators at time $t$ is:

$$\begin{array}{ccc}\hfill R\left(t\right)& \hfill =\hfill & p\nu {\int }_{t_0}^t{e}^{-({\mu }_1+g_1)t_0}{e}^{-(\nu +{\mu }_1+g_1)(\tau -t_0)}{e}^{-({\mu }_2+g_2)(t-\tau )}d\tau \hfill \\ \hfill & \hfill =\hfill & \frac{\nu e^{-(g_2+{\mu }_2)t}}{\nu +g_1+{\mu }_1-g_2-{\mu }_2}(e^{(-g_1-{\mu }_1+{\mu }_2+g_2)t_0}\hfill \\ \hfill & \hfill \hfill & -e^{-\nu (t-t_0)-({\mu }_1+g_1-{\mu }_2-g_2)t}).\hfill \end{array}$$ (28)

The total number of patients returned home at time $t$ is:

$$\begin{array}{ccc}\hfill H\left(t\right)& \hfill =\hfill & p(g_1{\int }_0^{t_0}{e}^{-({\mu }_1+g_1)\tau }d\tau +g_1{\int }_{t_0}^t{e}^{-({\mu }_1+g_1+\nu )\tau }d\tau \hfill \\ \hfill & \hfill \hfill & +g_2\nu {\int }_{t_0}^t{\int }_{\tau }^t{e}^{-({\mu }_1+g_1)t_0}\hfill \\ \hfill & \hfill \hfill & \times e^{-({\mu }_1+g_1+\nu )({\tau }^{\prime }-t_0)}{e}^{-({\mu }_2+g_2)(\tau -{\tau }^{\prime })}d{\tau }^{\prime }d\tau )\hfill \\ \hfill & \hfill \hfill & +(1-p)g_1^0{\int }_0^t{e}^{-({\mu }_1^0+g_1^0)\tau }d\tau \hfill \\ \hfill & \hfill =\hfill & p\left(\nu \frac{g_2}{\nu +g_1+{\mu }_1-g_2-{\mu }_2}\right(\frac{e^{-({\mu }_1+g_1)t+\nu (t_0-t)}(1-e^{-({\mu }_2+g_2)(t_0-t)})}{{\mu }_2+g_2}\hfill \\ \hfill & \hfill \hfill & +\frac{e^{-({\mu }_1+g_1)t_0}-e^{\nu (t_0-t)-({\mu }_1+g_1)t}}{\nu +g_1+{\mu }_1})+\frac{g_1}{g_1+{\mu }_1}(1-e^{-(g_1+{\mu }_1)t_0})\hfill \\ \hfill & \hfill \hfill & +\frac{g_1}{\nu +g_1+{\mu }_1}(e^{-(\nu +g_1+{\mu }_1)t_0}-e^{-(\nu +g_1+{\mu }_1)t}))\hfill \\ \hfill & \hfill \hfill & +(1-p)\frac{g_1^0}{{\mu }_1^0+g_1^0}(1-e^{-({\mu }_1^0+g_1^0)t}).\hfill \end{array}$$ (29)

The total number of patients remaining in hospital without a ventilator at time $t$ is:

$$\begin{array}{ccc}\hfill S\left(t\right)& \hfill =\hfill & p{e}^{-({\mu }_1+g_1)t-\nu (t-t_0)}+(1-p)e^{-({\mu }_1^0+g_1^0)t}.\hfill \end{array}$$ (30)

The total number of deaths at time $t$ is:

$$\begin{array}{ccc}\hfill D\left(t\right)& \hfill =\hfill & p({\mu }_1{\int }_0^{t_0}{e}^{-({\mu }_1+g_1)\tau }d\tau +{\mu }_1{\int }_{t_0}^t{e}^{-({\mu }_1+g_1+\nu )\tau }d\tau \hfill \\ \hfill & \hfill \hfill & +{\mu }_2\nu {\int }_{t_0}^t{\int }_{\tau }^t{e}^{-({\mu }_1+g_1)t_0}{e}^{-({\mu }_1+g_1+\nu )({\tau }^{\prime }-t_0)}\hfill \\ \hfill & \hfill \hfill & \times e^{-({\mu }_2+g_2)(\tau -{\tau }^{\prime })}d{\tau }^{\prime }d\tau )\hfill \\ \hfill & \hfill \hfill & +(1-p){\mu }_1^0{\int }_0^t{e}^{-({\mu }_1^0+g_1^0)\tau }d\tau \hfill \\ \hfill & \hfill =\hfill & p(\frac{\nu {\mu }_2}{\nu +g_1+{\mu }_1-g_2-{\mu }_2}\hfill \\ \hfill & \hfill \hfill & \times (\frac{e^{-(g_1+{\mu }_1)t+\nu (-t+t_0)}-e^{-(g_1+{\mu }_1)t+(\nu -g_2-{\mu }_2)(-t+t_0)}}{{\mu }_2+g_2}\hfill \\ \hfill & \hfill \hfill & +\frac{e^{-(g_1+{\mu }_1)t_0}-e^{-\nu (t-t_0)-(g_1+{\mu }_1)t}}{{\mu }_1+g_1})+\frac{{\mu }_1}{{\mu }_1+g_1}(1-e^{-({\mu }_1+g_1)t_0})\hfill \\ \hfill & \hfill \hfill & +\frac{{\mu }_1}{\nu +{\mu }_1+g_1}(e^{-(\nu +{\mu }_1+g_1)t_0}-e^{-(\nu +{\mu }_1+g_1)t}))\hfill \\ \hfill & \hfill \hfill & +(1-p)\frac{{\mu }_1^0}{{\mu }_1^0+g_1^0}(1-e^{-({\mu }_1^0+g_1^0)t}).\hfill \end{array}$$ (31)

Minimizing the distance of expressions in Eqs. (28), (29), (30), and (31) to their empirical values:

$$\underset{{\mu }_1,g_1,\nu ,t_0,{\mu }_1^0,g_1^0,p}{min}{(D\left(41\right)-\hat{D}\left(41\right))}^2+{(R\left(41\right)-\hat{R}\left(41\right))}^2+{(S\left(41\right)-\hat{S}\left(41\right))}^2+{(H\left(41\right)-\hat{H}\left(41\right))}^2,$$ (32)

where $\hat{D}\left(41\right)$, $\hat{R}\left(41\right)$, $\hat{S}\left(41\right)$, and $\hat{H}\left(41\right)$ are the empirical values in Table 2, provides (rates per day):

$$\begin{array}{c}{\hat{\mu }}_1^0=0.0042,{\hat{g}}_1^0=0.0334,\hfill \\ {\hat{\mu }}_1=0.0357,{\hat{g}}_1=0.0075,\hfill \\ {\hat{t}}_0=10\mathrm{days},\hat{\nu }=0.1493,\hat{p}=0.3693.\hfill \end{array}$$ (33)

The instantaneous mortality rate ${\hat{\mu }}_1$ in the waiting room is almost equal to the instantaneous mortality rate ${\hat{\mu }}_2$ on ventilator. The difference in treatment is reflected in the instantaneous rate ${\hat{g}}_2$ of return home, which is double the rate ${\hat{g}}_1$ of those in the waiting room. If there was no transfer to ventilation, the probabilities of dying after a time $t$ would be:

$${\hat{\mu }}_1{e}^{-{\int }_0^t({\hat{\mu }}_1+{\hat{g}}_1)d\tau }>{\hat{\mu }}_2{e}^{-{\int }_0^t({\hat{\mu }}_2+{\hat{g}}_2)d\tau }$$ (34)

due to ${\hat{\mu }}_2\approx {\hat{\mu }}_1$ and ${\hat{g}}_2>{\hat{g}}_1$.

The value obtained for ${\hat{t}}_0$ of 10 days from the data in Table 2 is consistent with the 8-day estimate of the median duration on ventilation (interquartile interval: 6–11 days, on the basis of 3,403 patients) provided by Santé publique France in its weekly epidemiological update of 7 May 2020, situation on 5 May 2020.

4.5. Inflow instantaneous rate ${\lambda }_a$

Estimating the inflow ${\lambda }_a$ is not immediate because patient statistics mix patients in demand for ventilators with others. At best, to my knowledge, hospital statistics give daily numbers $S(t,[a,a+9])$ of patients at day $t$ by age class $[a,a+9]$, $R(t,[a,a+9])$ on ventilation, $H(t,[a,a+9])$ return home, and $D(t,[a,a+9])$ dead. As patients in total number $S(t,[a,a+9])$ and patients in number $R(t,[a,a+9])$ on ventilation are found the following day $t+1$ either in hospital, on ventilators, dead, or return home:

$$\begin{array}{ccc}\hfill S(t,[a,a+9])+R(t,[a,a+9])& \hfill =\hfill & R(t+1,[a,a+9])\hfill \\ \hfill & \hfill \hfill & +D(t+1,[a,a+9])\hfill \\ \hfill & \hfill \hfill & +H(t+1,[a,a+9])\hfill \\ \hfill & \hfill \hfill & +S_1(t+1,[a,a+9]),\hfill \end{array}$$ (35)

where $S_1(t,[a,a+9])$ is the sum of patients at $t$ who remained in hospital and those on ventilation at $t$ who returned to hospital at $t+1$. The total number of patients at $t+1$ is then:

$$S(t+1,[a,a+9])=S_1(t+1,[a,a+9])+{\lambda }_{[a,a+9]},$$ (36)

where ${\lambda }_{[a,a+9]}$ is the total rate of inflow over the considered age class $[a,a+9]$. From Eqs. (35), (36), I deduce ${\lambda }_{[a,a+9]}$ by age class.

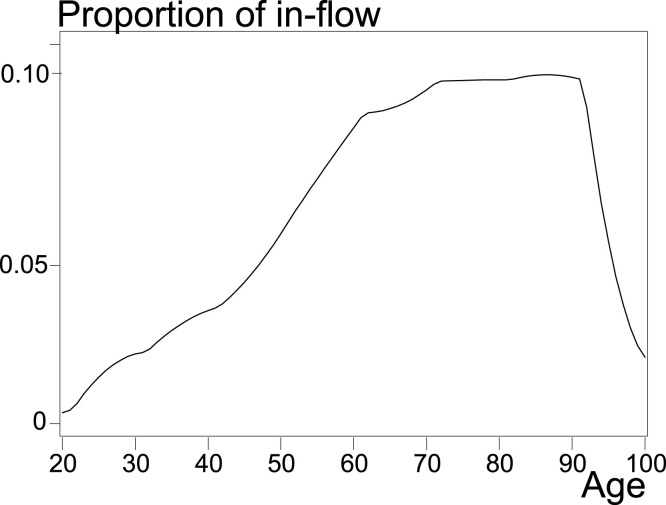
With French data from March 18 to May 1, 2020, I estimate ${\lambda }_a$ on the basis of Table 3. The figures start at 20 years instead of 0 for the reason that the flows before 20 years are very low.

Table 3.

Average daily inflows (in total numbers of patients) in hospitals by age class: France as a whole from 18 March to 1 May 2020. Standard deviations in parentheses.

Age class
20–29	30–39	40–49	50–59	60–69	70–79	80–89	90$+$
57.8	109.8	175.3	290.8	359.5	384.2	388.2	173.0
(103.7)	(238.6)	(392.5)	(663.0)	(801.5)	(797.5)	(778.1)	(360.6)

Fig. 2 presents the normalized ${\hat{\lambda }}_a∕{\sum }_{a=20}^{100+}{\hat{\lambda }}_a$ by annual age obtained from Table 3 by cubic spline.

Fig. 2.

Estimated distribution of hospital inflows ${\hat{\lambda }}_a∕{\sum }_{a=20}^{100+}{\hat{\lambda }}_a$ by age for the whole of France from 18 March to 1 May 2020.

Santé publique France, data.gouv.fr.

4.6. The optimum age for assigning ventilators

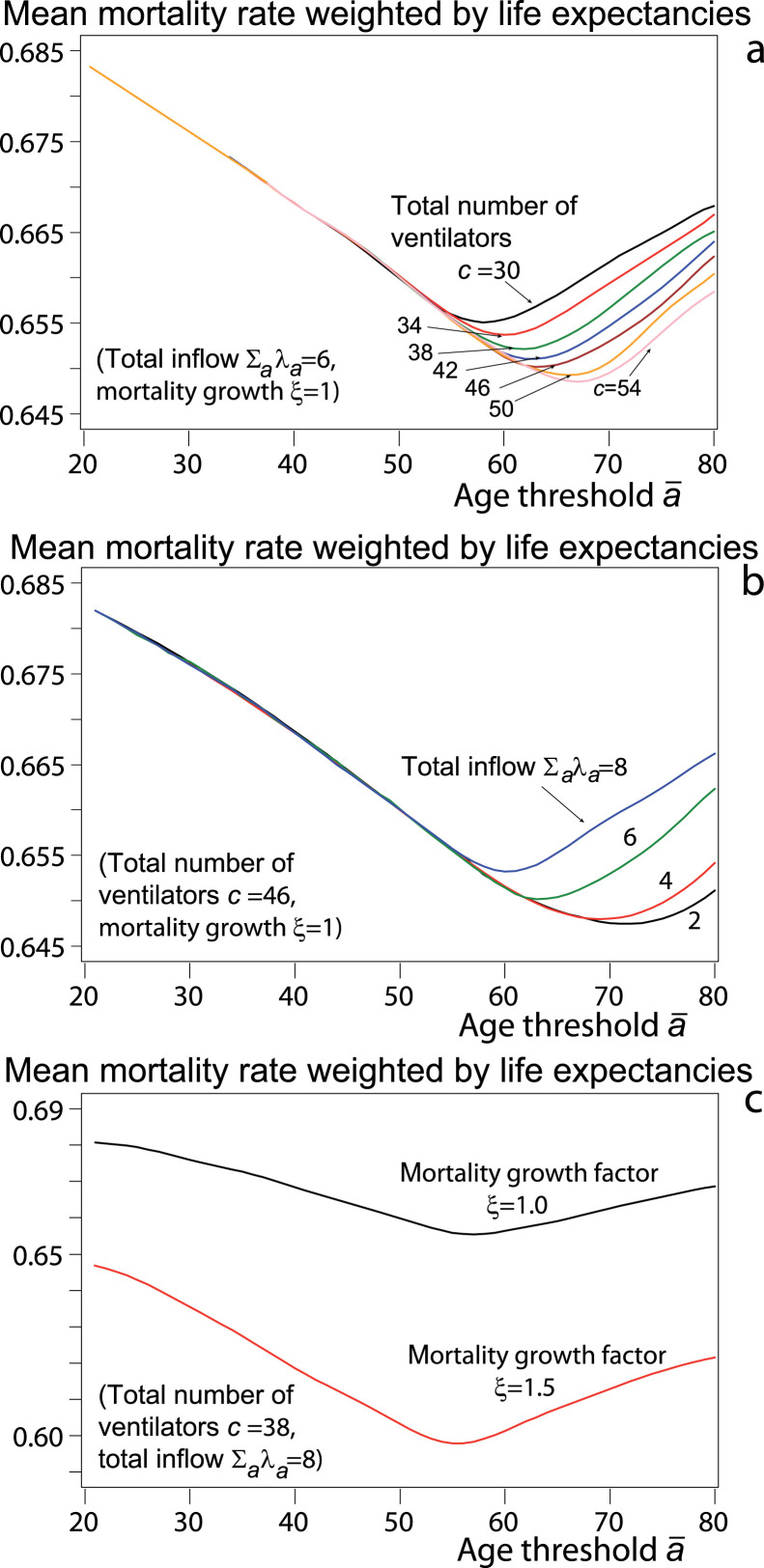
With the distribution of instantaneous rates ${\hat{\lambda }}_a∕{\sum }_{a=20}^{100+}{\hat{\lambda }}_a$ and with ${\mu }_1$, $g_1$, ${\mu }_2$, and $g_2$ constant in age and equal to their estimated values ${\hat{\mu }}_1$, ${\hat{g}}_1$, ${\hat{\mu }}_2$, and ${\hat{g}}_2$, the variation in Figs. 3 of the mean mortality rate weighted by life expectancies highlights the optimal age. Fig. 3a shows that the mean mortality rate decreases with the stock $c$ of ventilators. For example, for $c$ $=$ 54 ventilators, the minimum age is 67 years, at which the mean mortality rate is 4.7% less than if the threshold age is $\overline{a}=20$ years and 1.5% if $\overline{a}=80$ years. Fig. 3b also shows that the larger the total inflow of patients, the higher the weighted mean mortality rate, because these patients do not access all to ventilators.

Fig. 3.

Mean mortality rate weighted by life expectancies, for ${\hat{\mu }}_1$, ${\hat{g}}_1$, ${\hat{\mu }}_2$, ${\hat{g}}_2$, and comparison of the cases $\xi =1$ (mortality and return home rates constant in age) and $\xi =1.5$ taken as example for ${\mu }_i\left(a\right)={\hat{\mu }}_i{\xi }^{(a-70)∕30}$ and $g_i\left(a\right)={\hat{g}}_i{\xi }^{-(a-70)∕30}$, age $a$ in years.

Fig. 3c compares the case where the instantaneous rates ${\mu }_i\left(a\right)={\hat{\mu }}_i$ and $g_i\left(a\right)={\hat{g}}_i$, $i=1,2$ are constant in age ($\xi =1$) and the case ${\mu }_i\left(a\right)={\hat{\mu }}_i{\xi }^{(a-70)∕30}$, and $g_i\left(a\right)={\hat{g}}_i{\xi }^{(a-70)∕30}$, $i=1,2$ for $\xi =1.5$. The mean mortality rate weighted by life expectancies decreases when $\xi$ increases, because younger patients, whose mortality rates are lower, correspond to more saved years left to live than patients over 70 lose such years. Also, the higher $\xi$, the faster the mortality rate ${\mu }_1$ decreases before minimum age, because increasing $\overline{a}$ saves more years to live.

4.7. Sensitivity analysis

The expression of $a_{min}$ is given in Eq. (16). 100 runs of the curve of $\overline{a}$ (each having 60 values of threshold age $\overline{a}$, between 21 and 80 in abscissa) allow expressing the first-order dependence of the mean mortality rate $E(-U)$ weighted by life expectancies as a function of $c$ and ${\sum }_{a=20}^{100+}{\lambda }_a$ both describing $[2,30]$ and for values of

$$\begin{array}{ccc}\hfill {\mu }_i& \hfill =\hfill & \overline{{\mu }_i}{\xi }^{\frac{a-70}{30}},\hfill \\ \hfill g_i& \hfill =\hfill & {\overline{g}}_i{\xi }^{-\frac{a-70}{30}},i=1,2,\hfill \end{array}$$ (37)

with values of ${\overline{\mu }}_1$ drawn uniformly in $[0.5{\hat{\mu }}_1,1.5{\hat{\mu }}_1]$, ${\overline{\mu }}_2$ in $[0.5{\overline{\mu }}_1,0.95{\overline{\mu }}_1]$, ${\overline{g}}_1$ in $[0.5{\hat{g}}_1,1.5{\hat{g}}_1]$, ${\overline{g}}_2$ in $[0.5{\hat{g}}_2,1.5{\hat{g}}_2]$, and $\xi$ in $[1.0,1.5]$. The distribution of ${\lambda }_a∕{\sum }_{a=20}^{100+}{\hat{\lambda }}_a$ is represented in Fig. 2.

The influence of each parameter is quantified by the regression:

$$\begin{array}{ccc}\hfill -U\left(a\right)& \hfill =\hfill & \underset{(0.008)}{0.245}-{\underset{(0.0001)}{0.0026}}^{\ast }{a}_{min}+\left(-{\underset{(0.007)}{0.278}}^{\ast }+{\underset{(0.013)}{0.159}}^{\ast }\frac{a-a_{min}}{100}\right)\hfill \\ \hfill & \hfill \hfill & \left(\frac{a-a_{min}}{100}\right){\mathbb{1}}_{a\le a_{min}}\hfill \\ \hfill & \hfill \hfill & +\left({\underset{(0.024)}{0.436}}^{\ast }-{\underset{(0.121)}{1.228}}^{\ast }\frac{a-a_{min}}{100}\right)\left(\frac{a-a_{min}}{100}\right){\mathbb{1}}_{a>a_{min}}\hfill \\ \hfill & \hfill \hfill & -{\underset{(0.00005)}{0.00025}}^{\ast }c\hfill \\ \hfill & \hfill \hfill & +{\underset{(0.0004)}{0.0021}}^{\ast }\sum _{a=20}^{100+}{\lambda }_a-{\underset{(0.002)}{0.103}}^{\ast }\xi +{\underset{(0.047)}{12.756}}^{\ast }{\overline{\mu }}_1\hfill \\ \hfill & \hfill \hfill & +{\underset{(0.058)}{5.400}}^{\ast }{\overline{\mu }}_2-{\underset{(0.153)}{0.669}}^{\ast }{\overline{g}}_1\hfill \\ \hfill & \hfill \hfill & -{\underset{(0.073)}{1.160}}^{\ast }{\overline{g}}_2,\hfill \\ \hfill a_{min}& \hfill =\hfill & {\underset{(0.33)}{57.21}}^{\ast }-{\underset{(0.16)}{0.40}}^{\ast }\xi -{\underset{(0.01)}{3.09}}^{\ast }\sum _{a=20}^{100+}{\lambda }_a+{\underset{(0.003)}{0.353}}^{\ast }c\hfill \\ \hfill & \hfill \hfill & +{\underset{(3.36)}{143.07}}^{\ast }{\overline{\mu }}_1\hfill \\ \hfill & \hfill \hfill & +{\underset{(4.35)}{82.89}}^{\ast }{\overline{\mu }}_2+{\underset{(11.70)}{113.54}}^{\ast }{\overline{g}}_1+{\underset{(5.37)}{169.68}}^{\ast }{\overline{g}}_2\hfill \\ \hfill & \hfill \hfill & N=6000,R^2=0.98,\mathrm{correlation}=0.00.\hfill \end{array}$$ (38)

When $a_{min}$ increases, more people have access to ventilators, which decreases the rate $-U$. The curve of $-U$ versus $\overline{a}$ is close to a decreasing left branch of a parabola for $\overline{a}\le a_{min}$ and an increasing left branch of another parabola for $a>a_{min}$ because, in both cases, the increase of $\overline{a}$ gives access to patients with decreasing life expectancy (the increase of $\overline{a}$ has decreasing returns). An additional ventilator decreases the weighted mean mortality rate by 0.00025 per day directly, after controlling for other variables, and by $0.353\times 0.0026$ through the increase of $a_{min}$. The total effect is that an additional ventilator decreases the weighted mortality rate by $0.00025+0.353\times 0.0026=0.0012$, that is, saves 1.2 years of life per 1000 patients per day (36 years of life per month).

The price of a ventilator before the pandemic was between $35,000 and $45,000 in New York City at the end of March 2020.12 Since then, the effort to manufacture low-cost ventilators has been considerable and low-cost ventilators are being produced on an industrial scale, so that the price at the beginning of 2021 should be between $1000 and $5000,13 depending on the market. The cost of a year of life depends on the duration of the pandemic. As an example, the first wave in France lasted from 23 March to 8 June 2020 (Santé publique France, 2020), or 76 days. Then, one year of life cost $p∕(76\times 0.0012)$, where $p$ is the price of a ventilator. This cost is halved in case the second wave lasts that long.

An additional incoming patient (distributed over ages) increases the rate $-U\left(a\right)$ by 0.010 per day (0.0022 directly and $-0.0026\times -3.09$ through $a_{min}$). Patients aged between the former $a_{min}$ (before increase of ${\sum }_{a=20}^{100+}{\lambda }_a$) and the new $a_{min}$ (after increase of ${\sum }_{a=20}^{100+}{\lambda }_a$) have their mortality rate increase from ${\mu }_2$ to ${\mu }_1$. Moreover, additional patients older than the new $a_{min}$ are subject to ${\mu }_1$. The fact that the effect per day of an additional ventilator and the effect of an additional patient are almost equal in absolute value must not hide the fact that the ventilator is there to continue saving lives while the patient is destined to eventually leave the hospital.

As in Fig. 3b, increasing ${\sum }_{a=20}^{100+}{\lambda }_a$ after controlling for the total number of ventilators leaves more people in the waiting room, and increases the weighted mean mortality rate. As in Fig. 3c, increasing $\xi$, controlling for ${\mu }_1$ and ${\mu }_2$, decreases mortality at ages below 70 and increases it at ages above 70. The coefficient of ${\overline{\mu }}_1$ is double that of ${\overline{\mu }}_2$ for the reason that not all patients have access to ventilators and therefore ${\mu }_1$ affects more patients, especially older patients. Likewise, not surprisingly, the higher the return home rates $g_1$ and $g_2$, the lower the mean mortality rate weighted by life expectancies.

Fisher tests show that the coefficients of $(a-a_{min})$ for $a\le a_{min}$ and $a>a_{min}$ are statistically different at the 1% level, as are the coefficients of ${(a-a_{min})}^2$: the curve of $-U$ versus $\overline{a}$ is not symmetrical, and there is no reason for it to be, as gains or losses are measured in life expectancies $e_a$, which decrease with age. The coefficients of ${\overline{\mu }}_1$ and ${\overline{\mu }}_2$ and those of ${\overline{g}}_1$ and ${\overline{g}}_2$ are also statistically different, which is consistent with the fact that the patient population in the intensive care unit is selected.

5. Conclusion

Age has played a prominent role in the allocation of ventilators in this time of shortage. If the criterion is to maximize the total number of years of life saved, which, in relation to the population of patients in demand for ventilators, is the mean rate of mortality weighted by age- and sex-specific life expectancies, if not by co-morbidities, then considering only those present leads to lose years of life that could have been saved. Choosing a threshold age makes it possible to systematize a possible practice. In this case, I have shown that there is an optimal cut-off age, depending on the flow rates and the total number of available ventilators.

Making this process operational requires estimating the rates of inflow, mortality, and return home, which can be done on the basis of a Kalman filter, but this procedure is classical and beyond the scope of this article. Replacing life expectancies to measures resulting from biological age or SOFA scores is feasible if these measures are readily available.

However, having a strict threshold age is likely to be not accepted by the population (Hecketsweiler and Royer, 2020). Reserving a quota for age groups above the optimal age is a possibility to mitigate the hardness of the triage under a pre-set age. In any case, determining this optimal age is necessary for a triage protocol that would at best save the expected number of years to live.

Manuscript handled by Editor Aditya Goenka