Virial Based Berendsen Barostat on GPUs using AMOEBA in Tinker-OpenMM

Abstract

The Tinker-OpenMM package for AMOEBA molecular dynamics on GPU has long been limited to the Monte Carlo barostat due to the lack of virial calculation. In this paper, we report the calculation of the internal virial for the AMOEBA forcefield. This constitutes the first GPU implementation of a polarizable internal virial. This is followed by the implementation of the Berendsen barostat into Tinker-OpenMM as a demonstration of the capability of Tinker-OpenMM to calculate the virial with sufficient accuracy to enable pressure control. These additions enable the further improvement of Tinker-OpenMM to include a wide range of virial-based barostat algorithms.

Introduction:

Proper pressure control is essential for molecular dynamics (MD) that requires simulation of pressure effects[1]. For example, molecular dynamics has proven invaluable in the prediction of the structure of compounds such as glasses[2], nanomaterials[3], and metals[4]^,[5] under extreme pressures as high as 1,000,000 Atmospheres. Many of the common spectroscopic techniques are ineffective under high pressures. For example, even pioneering NMR studies are limited to around 2000–3000 Atmospheres[6]. Since NMR is the main technique to gain dynamics information about molecular systems, MD simulations act as a valuable complement to the limited experimental tools available at higher pressures. As another, biological example, proteins have evolved to maintain structure and function at the pressure experienced by an organism. For most organisms, this pressure is near 1 Atm. However, there has been increasing interest in the dynamics of proteins from piezophiles that live under extreme pressures as high at 1100 Atms[7], pressures that would denature most proteins. Molecular dynamics studies of the pressure stability of these enzymes have revealed that protein dynamics of pressure tolerant enzymes (at least in Dihydrofolate Reductase) are altered to enable increased flexibility at high pressures[8], thus enabling substrate exchange. A better understanding of these adaptations may allow for biosynthetic applications or mutagenesis of proteins for high pressure industrial applications[9]. Material science and biochemical studies such as these require robust pressure control that allows for simulation in not only ambient pressures, but also at extreme pressures. This pressure control is implemented via a simulation component known as a barostat.

Most barostat implementations require the calculation of a system property known as the virial[10]. The virial is defined as the change in energy with respect to volume (i.e. dU/dV). The virial is the sum of two components, an internal, potential interaction derived component, and a kinetic energy term. For most systems, the internal virial has a tendency to push system volume inwards, while the kinetic term pulls system volume outwards. For simple pairwise forces, the internal virial expression is also equivalent to the dot product of force and distance. However, for some forces, internal virial calculations derived from dU/dV are required (such as during the calculation of the virial due to multipole forces using Ewald summation[11]). The virial can then be converted into an instantaneous pressure using the equation $P_{inst}=\frac{1}{3*V}*(2*KE-W),$ with KE being kinetic energy, and W being the average of the diagonal components of the internal virial tensor for the case of an isotropic barostat. This instantaneous pressure is then used to scale box dimensions and coordinates in order to bring the instantaneous pressure closer to the target external pressure. There are a wide range of virial-requiring barostats, including the Nose Hoover barostat[12–14], the Berendsen barostat[1], and the Langevin piston method[15].

Tinker-OpenMM[16] is a modified version of OpenMM[17, 18] designed for GPU computation containing many features not present in the main release of OpenMM. These additions include the latest modifications of the AMOEBA polarizable forcefield[19, 20] and the ability to perform free energy perturbation calculations. However, Tinker-OpenMM is lacking in pressure control methodologies. Since Tinker-OpenMM currently doesn′t compute the AMOEBA virial (unlike the base Tinker package[21, 22] for CPU computation), Tinker GPU pressure scaling can only be accomplished via a Monte Carlo Barostat[23]. The Monte Carlo barostat uses the target pressure, and system energy to probabilistically select increases or decreases in system box size. The Monte Carlo barostat results in the correct equilibrium system density and volume ensemble. However, the Monte Carlo barostat is less effective than virial-based barostats in the equilibration of molecular systems that are far from equilibrium density. Therefore, it is desirable for Tinker-OpenMM to contain virial-based barostats.

When making an initial choice of barostats, we wanted to implement a barostat that was already present in Tinker CPU so as to enable comparisons of these already well-validated platforms with the GPU results. Tinker CPU currently supports the Nose-Hoover barostat and the Berendsen barostat. The Nose-Hoover barostat was initially considered, however, the Tinker implementation of the Nose-Hoover barostat contains a thermostat coupled to a barostat. This coupling introduces complications in analysis, leaving the possibility that any error is due to the thermostat, not just the barostat. By implementing the Berendsen barostat, temperature control can be handled by the already implemented Bussi thermostat[24] .One disadvantage of the Berendsen barostat is that correct volume ensembles are not achieved.[23] This makes the Berendsen barostat inappropriate for production simulations, and limits effective use cases to initial equilibration. However, implementation of the Berendsen barostat can act as an effective initial test of if a GPU based virial can enable consistent pressure control. This is especially important since forces (and thus the virial, which uses many force intermediate terms in its calculation) needs to be calculate at a lesser, 32-bit precision (as opposed to the 64-bit computation utilized by Tinker CPU). This lack of precision could result in a drift in equilibrium densities in the GPU when compared to the CPU. Indeed, significant total energy drifts are observed when integrating positions at 32-bit precision, indicating that calculation of system properties using 32bit precision can cause significant difference in system behavior[17]. Since the AMOEBA internal virial (or indeed, any polarizable virial) has not been implemented in CUDA for GPU-MD, it is unclear if a GPU based implementation of the AMOEBA virial would enable sufficient precision for robust pressure control. In this paper, we show implementation of the AMOEBA virial on GPUs within Tinker-OpenMM and use the Berendsen Barostat as a test of the utilization of this virial for pressure control schemes.

Methods:

Derivation of virial:

Given unit cell vectors, a_α = [a_α1, a_α2, a_α3]^T, α = 1, 2, 3, which form the edges of the cell, the cell matrix is defined as

$$\mathit{A}=\left[{\underset{\_}{a}}_1,{\underset{\_}{a}}_2,{\underset{\_}{a}}_3\right]=\left[\begin{array}{lll}{a}_{11}\hfill & a_{21}\hfill & a_{31}\hfill \\ a_{12}\hfill & a_{22}\hfill & a_{32}\hfill \\ a_{13}\hfill & a_{23}\hfill & a_{33}\hfill \end{array}\right]$$ (1)

The instantaneous pressure is given by [25]

$$p_{\alpha \beta }=\frac{1}{V}\left({\sum }_{i}m{v}_{i\alpha }{v}_{i\beta }-W_{\alpha \beta }\right)$$ (2)

The first term on the RHS corresponds to the kinetic energy contribution while the second term is the internal virial:

$$W_{\alpha \beta }=-{\sum }_{i,j>i}{r}_{ij,\alpha }{f}_{ij,\beta }$$

The average of three diagonal components of pressure tensor give the usual scalar pressure in an isotropic system.

The virial tensor can also be evaluated from derivatives of potential energy [26]

$$\frac{\partial U}{\partial a_{\alpha \beta }}={\sum }_{\gamma =1}^3{W}_{\alpha \gamma }{a}_{\beta \gamma }^{-1}$$

which can be conveniently applied to obtain virial for a system handled by Ewald sum

$$W_{\alpha \beta }={\sum }_{\gamma =1}^3\frac{\partial U_{EWald}}{\partial a_{\alpha \gamma }}{a}_{\gamma \beta }$$ (4)

Note the partial derivative is with respect fixed s, fractional coordinate (refer to SI for further details).

The Ewald energy for multipoles is

$$U_{Ewald}=U_{real}+U_{recip}+U_{self}$$ (5)

The self-energy term is independent of cell dimension a and makes no contribution to pressure. The real space component of pressure tensor intuitively takes the form [27]

$$W_{\alpha \beta }^{real}=-{\sum }_{i,j>1}{r}_{ij,\alpha }{f}_{ij,\beta }^{real}$$

where $f_{ij,\beta }^{real}$ is the force between site i and j computed in the Ewald real space, and the summation is over all pairs of sites. The remaining reciprocal component is to be derived using above eq (4) and is presented in the supplementary materials.

The virial due to torque( for the x,x component) is calculated as ΔX_x * Fx_x + ΔX_y * Fx_y + ΔX_z * Fx_z. Subscripts denote the X, Y, and Z frame defining atoms. All other terms are calculated analogously. This dot product definition of the virial can be used because this torque is not volume dependent[28]. The forces used in this calculation ignore the self-torque component.

Virial Implementation:

Calculation of the diagonal and off diagonal components of the virial tensor were added to the end of the appropriate GPU force kernels (contained in Tinker-Openmm/plugins/amoeba/platform/cuda/src/kernels) via adaptation of the vir() array modifications present in the Tinker CPU codebase. Modifications were made to the Multipole, van der Waals, angle, angle-torsion, bond, out of plane bend, pi-torsion, stretch-bend, stretch-torsion, torsion-torsion, and torsion forces. For all forces except the more complicated multipole force (along with polarization), all changes were made at the end of the kernel, guarded by an if USES_VIRIAL preprocessor directive. The multipole virial is contained throughout multipole.cu, multipolePme.cu, and pmeMultipoleElectrostatics.cu, with all virial components either utilizing the USES_VIRIAL directive or are contained within routines that are executed only if the virial is required for a given simulation. The flagging of virial-requiring terms with the USES_VIRIAL directive enables virial-dependent calculations only in simulations in which the virial is required, removing computational expenses in simulations that do not use the virial. GPU virial computation can be turned on in the interface by a call to OpenMM_System_setUsesVirial (omm->system, (OpenMM_Boolean) true). The GPU virial was split into fast, bonded (available by calling CudaContext.getFastVirial()) and slow, nonbonded (available by calling CudaContext.getSlowVirial()) components. This separation allows for the implementation of multistep algorithms (such as r-RESPA[29]) that require averaging of fast components by the number of inner steps.

Berendsen Barostat Implementation:

The Berendsen barostat was coded for use with the RESPA integrator present in Tinker-OpenMM. Briefly, a routine scaleBox() was added into the CustomStepKernel implementation present in platforms/cuda/src/CudaKernels.cpp. The scaleBox routine performs pressure scaling identical to that present in the Tinker interface, based on the barostat scheme presented in[1] Briefly, after each step, the kinetic energy and virial potential were used to determine the box length scaling constant according to the equation Lengthscale $=({(1+\mathrm{\Delta }t*\frac{\beta }{\tau }*\left(P_{\text{inst}}-P_{\text{target}}\right))}^{1/3}.$The compressibility (ϐ ) was chosen as that of water (0.000046), with τ equaling the default Tinker CPU value of 2.0. The instantaneous pressure was calculated using the equation $P_{inst}=\frac{k}{3*V}*(2*KE-W),$ with k being a conversion factor between kJ/mol/ų to Atmospheres (equal to 16.39). In order to increase system stability, the fast virial was averaged across all inner steps. The actual scaling of atomic coordinates is accomplished using the GPU kernel scaleCoordinates() inside platforms/cuda/src/kernel/monteCarloBarostat.cu, which scales the positions of molecular centers(as opposed to scaling each individual atom independently). The command addscalebox () was placed at the end of the RESPA definition in the Tinker ommstuff.cpp interface, after the BUSSI scaling routine, causing the scaleBox() routine to be called at the end of each r-RESPA step.

Virial Value Confirmation:

The virial build of Tinker-OpenMM was modified to print both the fast, bonded virial, and the slow, non-bonded virial at each r-RESPA inner step. 1000 steps of MD were then performed using a 1.0 fs timestep, with output of a structural archive files every step. The total virial for each GPU generated frame was then calculated using the Tinker “analyze” routine. The average and percent difference were then calculated on a per-component basis using only the diagonal component of the virial. The first 500 frames were ignored, in order to compare near-equilibrium frames

MD Procedures:

All Molecular Dynamics calculations were performed using a 2.0fs timestep, and the RESPA integrator, with structural output every 1ps. All calculations were performed at 1Atm pressure using the Berendsen barostat, and 298K temperature using the BUSSI thermostat[24], unless otherwise noted. Simulations utilized an Ewald cutoff of 7.0 Å, and a van der Waals(vdW) cutoff of 12.0 Å.

Molecular Systems:

All small molecule systems consisted of pure liquids available in the example/ folder of the tinker release and utilized the amoeba09 parameters. The water system utilized consisted of a cubic box of 2,210 water molecules run using the AMOEBAwater14 forcefield. The protein system utilized was the bench7.xyz solvated Dihydrofolate Reductase (DHFR) test system of 23,558 atoms. Bench7 is included in the bench/ folder of the Tinker CPU distribution, and uses the amoebabio09 parameters. The RNA system utilized was a solvated double stranded RNA molecule consisting of the sequence 5′-AAGCUGCCAG-3’, 3′-UCGACGGU-5′, using the amoebanuc17 parameter file, and contained 40, 303 atoms.

Results:

Virial CPU vs GPU Comparison

Since the virial for each force often contains mathematical intermediates of the force (or even the calculated force itself), a computationally efficient internal virial must be calculated at 32-bit precision. This potentially limits internal virial accuracy when compared to the 64-bit precision utilized by Tinker CPU. Initial tests of the internal virial consisted of calculating the difference in the diagonal internal virial components calculated using the Tinker-OpenMM GPU and Tinker CPU platforms. Since only the diagonal components contribute to isotropic pressure, the off-diagonal internal virial tensor components were ignored. This comparison was accomplished by performing 1000 steps of MD on a minimized starting structure, using a build of Tinker-OpenMM modified to print out the slow and fast virials every r-RESPA inner step. The first 500 structures of this simulation were not included in internal virial analysis in order to test near-equilibrium values. The internal virial tensor for these final 500 frames were then calculated using Tinker′s “analyze” routine. The Dihydrofolate Reductase (DHFR) protein system showed an average diagonal internal virial component difference of 9.0±6.0 kcal/mol/ų, with a percent difference of 0.08±0.06% (Table 1). The RNA system displayed slightly greater raw divergence, at 14.3±9.6 kcal/mol/ų due to larger system size. For the RNA system, the percent difference was identical to that of the protein system, with a percent difference of 0.08±0.05%. It was unclear if this degree of accuracy was sufficient to enable virial-based pressure control. Most of the divergence in CPU and GPU calculated internal virial was identified as being a result of the particle mesh Ewald virial, which cannot be improved upon without increasing to 64-bit precision. Calculation at this increased precision would result in an unacceptable approximately 30-fold reduction in performance[17]. At this speed reduction, the performance advantage of the GPU platform is essentially negated. It was thus decided to proceed with Berendsen pressure control testing with this virial divergence.

Table 1:

Average and absolute virial divergence between simulation frames generated using Berendsen barostat Molecular Dynamics (MD) on GPU and the CPU analysis of these frames. GPU MD was run for 1000 steps of MD using a 1fs timestep, and per-component average divergence was calculated for frames 500 to 1000.

	Protein	RNA
Absolute Difference(kcal/mol/Å3)	9.0±6.0	14.3±9.6
Percent Difference	0.08±0.06%	0.08±0.05%

Equilibration of Small Molecule Systems:

Since it was uncertain if the internal virial accuracy was sufficient to enable pressure control, it was necessary to test the capabilities of the GPU platform on a wide range of small molecules. In addition to water, pure liquids of formamide, benzene, and methanol were chosen to represent a diverse set of molecular properties. This series of compounds was simulated at 1 Atmosphere pressure using Tinker CPU for 1ns to generate equilibrium structures and velocities using a well validated computational platform. These simulation starting points were then run using the Berendsen barostat for 30ns at 1A tm to confirm that this equilibrium is maintained. All of the tested small molecules maintained the same density as in the CPU simulation (Table 2), an indication that the Tinker-OpenMM system is able to maintain stable simulations for a wide range of chemical moieties.

Table 2.

Comparison of equilibrium density of CPU and GPU Berendsen barostat simulations, and GPU Monte Carlo. GPU results are taken over 30ns, and CPU results are taken over 1ns. Both results ignore the first 200ps.

Compound	GPU Density	CPU Density	Monte Carlo
Benzene	0.878±0.007	0.877±0.007	0.880±0.009
Formamide	1.124±0.004	1.124±0.004	1.124±0.006
Methanol	0.781±0.002	0.783 ±0.002	0.782±0.004
Water	0.994±0.003	1.002±0.003	0.998±0.005

Equilibration of Water at High Pressures

It is essential that any barostat be able to equilibrate systems that are at an initial none-quilibrium density. The previous series of tests started the simulated systems at equilibrium, and did not determine the ability of the Tinker-OpenMM platform to simulate systems at pressures other than 1 atm. In order to test both capabilities, a series of simulations of water were conducted at 1, 1000, 2000, and 4000 atmospheres. Critically, all 4 series of simulations were started with structures and velocities of a 1 Atmosphere water system generated using CPU. Therefore, reaching the correct equilibrium requires that the higher-pressure systems increase in density, demonstrating the capability of the GPU Berendsen barostat to equilibrate to different pressures. This series of Berendsen simulations reached near-equilibrium densities within 20ps and displayed equilibrium densities essentially identical to those observed in the 1ns CPU simulation (Figure 1) that were started at 1 Atm pressure. The minor shift observed in equilibrium densities is likely due to integration and velocity precision differences. The percent virial divergence is small enough so as this consistent shift is not easily explained by virial divergence. The previous test (with all compounds at 1 Atm) could have been passed by a barostat with little to no box size evolution. The change of box size to reach equilibrium densities occurs relatively rapidly, while still maintaining an appropriate long-term equilibrium. This is a strong indication that the Tinker-OpenMM Berendsen barostat can perform pressure equilibration to densities identical to that of the CPU Berendsen platform, despite the less accurate virial.

Figure 1:

Average density for Berendsen GPU and Berendsen CPU MD simulations on water at various pressures. Values are reported as average ± standard deviation. First 200ps of simulation time was ignored in calculation. CPU simulations were conducted for 1ns, and GPU simulations were simulated for 30ns.

Comparison of Berendsen and Monte Carlo Barostats on GPU

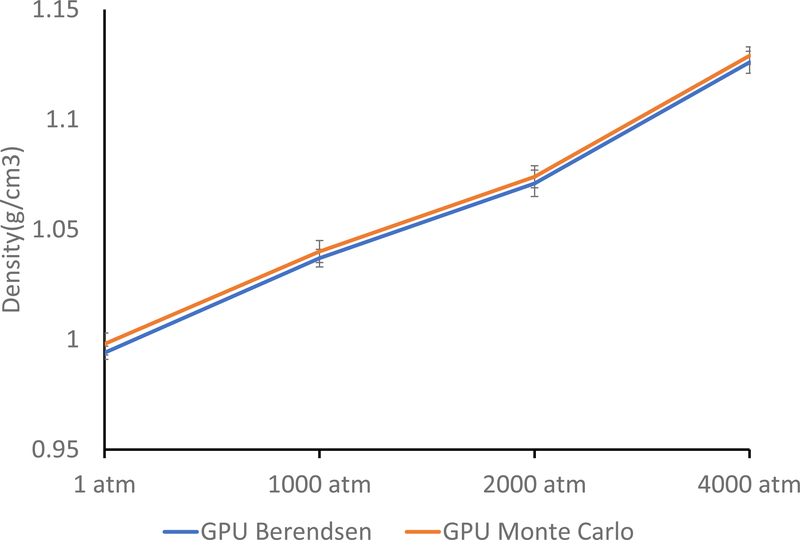
The only previous pressure equilibration platform present in Tinker-OpenMM was the Monte Carlo Barostat. Unlike the Berendsen barostat, the Monte Carlo barostat displayed ensemble pressure and velocity fluctuations, and thus is more suitable for production simulation. The weakness of the Monte Carlo barostat, however, is the equilibration of structures far from equilibrium. Therefore, a likely pipeline would consist of an initial equilibration with the Berendsen barostat, followed by production simulations using Monte Carlo, or another (to be developed) virial based barostat such as Nose-Hoover. In order for this pipeline to work effectively, the equilibrium densities of the Monte Carlo and Berendsen barostat should be in agreement. To test this agreement, the water density tests at 1, 1000, 2000, and 4000 Atmospheres, as well as the other liquids at 1 Atmosphere, were repeated using the Monte Carlo barostat in Tinker-OpenMM on GPUs. The Monte Carlo barostat showed comparable densities to the GPU Berendsen barostat for both water (Figure 2) and organic liquids (Table 2). This close agreement enables a smooth transition between the Monte Carlo and Berendsen barostats. This agreement is even closer than that observed between the GPU and CPU Berendsen barostats. This is an indication that the small divergence observed between the two platforms may be due to precision issues related to the velocity and components of the platform rather than the barostat.

Figure 2:

Average density for Berendsen GPU and Monte Carlo GPU simulations on water at various pressures. Values are reported as average ±standard deviation. First 200ps of simulation time was ignored in calculation. Both series of simulations were simulated for 30ns.

Conclusions:

Over time, Tinker-OpenMM is nearing the molecular dynamics capabilities of the Tinker-CPU platform. One of the biggest limitations of the Tinker-OpenMM platform has previously been the lack of virial-based pressure control methods. These virial-based methods are often more stable during initial equilibration than the Monte Carlo barostat. While the Berendsen barostat lacks the proper ensemble volume averages, it is an important steppingstone in virial-based pressure control on GPU. Prior to this study, it was unclear if the lesser accuracy of OpenMM force (and thus virial) calculation would be accurate enough to enable robust pressure control. The results of this study indicate that this inaccuracy is unlikely to be an issue in the implementation of pressure control schemes. In the near future, we aim to add a wide range of the diversity of barostats that require the virial, such as Nose-Hoover or the Langevin Piston.