Abstract
The present study evaluates the water quality status of 6-km-long Kali River stretch that passes through the Aligarh district in Uttar Pradesh, India, by utilizing high-resolution IRS P6 LISS IV imagery. In situ river water samples collected at 40 random locations were analyzed for seven physicochemical and four heavy metal concentrations, and the water quality index (WQI) was computed for each sampling location. A set of 11 spectral reflectance band combinations were formulated to identify the most significant band combination that is related to the observed WQI at each sampling location. Three approaches, namely multiple linear regression (MLR), backpropagation neural network (BPNN) and gene expression programming (GEP), were employed to relate WQI as a function of most significant band combination. Comparative assessment among the three utilized approaches was performed via quantitative indicators such as R2, RMSE and MAE. Results revealed that WQI estimates ranged between 203.7 and 262.33 and rated as “very poor” status. Results further indicated that GEP performed better than BPNN and MLR approaches and predicted WQI estimates with high R2 values (i.e., 0.94 for calibration and 0.91 for validation data), low RMSE and MAE values (i.e., 2.49 and 2.16 for calibration and 4.45 and 3.53 for validation data). Moreover, both GEP and BPNN depicted superiority over MLR approach that yielded WQI with R2 ~ 0.81 and 0.67 for calibration and validation data, respectively. WQI maps generated from the three approaches corroborate the existing pollution levels along the river stretch. In order to examine the significant differences among WQI estimates from the three approaches, one-way ANOVA test was performed, and the results in terms of F-statistic (F = 0.01) and p-value (p = 0.994 > 0.05) revealed WQI estimates as “not significant,” reasoned to the small water sample size (i.e., N = 40). The study therefore recommends GEP as more rational and a better alternative for precise water quality monitoring of surface water bodies by producing simplified mathematical expressions.
Keywords: Kali River, WQI, Spectral reflectance, MLR, ANN, GEP
Introduction
İn recent years, water quality of major rivers, lakes and ponds in India has alarmingly deteriorated due to significant population increase leading to rapid urban development and industrialization. Increased anthropogenic activities including direct discharge of untreated industrial effluents, domestic sewage and agricultural waste have severely degraded the quality of surface water bodies. In India, the management strategies for cleaning up of rivers are often not optimally prioritized and therefore, spatiotemporal monitoring of pollution levels becomes essential to devise effective measures for reclamation of the degraded urban water bodies (Farhad et al., 2013; Abba et al., 2015). In situ measurement and monitoring of water quality at point locations is exhaustive and time taking (Song et al., 2012). Mathematical models integrated with geospatial techniques form a reliable time-saving solution towards controlling and sustainably managing the surface water resources (Mondal and Satpaty, 2020). Geospatial techniques offer uninterrupted scaled monitoring of several water quality parameters (WQPs) over large water bodies at spatiotemporal scales (Fulazzaky et al., 2010; Prabu et al., 2011).
In the last two decades, water quality monitoring of the urban water bodies has been the focus of research for researchers across the globe. The qualitative assessment of river water quality is carried out in terms of its physical, chemical and biological parameters and involves the analysis of complicated data matrix with large number of water quality attributes. Many studies concentrated on evaluating pollution levels in terms of individual WQPs, namely electrical conductivity (EC), turbidity, dissolved oxygen (DO), total dissolved solids (TDS), biochemical oxygen demand (BOD), chemical oxygen demand (COD), alkalinity, total suspended sediment (TSS), chlorophyll-a (Chl-a), and heavy metals such as Iron (Fe), magnesium (Mg), chromium (Cr) and lead (Pb) by utilizing remote sensing data in geographical information system (GIS) framework (Milanović Pešić et al., 2020; Nas et al., 2010; Sharma et al., 2018; Waxter, 2014; Yao et al., 2020). To reduce the number of WQPs in the analysis, a lot of consideration has been given to the development of single numerical indicators to ascertain the overall water quality trends with respect to the threshold limits. The water quality index (WQI) is a numeric indicator of the degree of severity in the quality of water for practical usage within the prescribed range and is computed by considering several significant quality parameters (Bordalo et al., 2006; Dunca, 2018; Markogianni et al., 2014; Mohamed et al., 2019; Said & Hussain, 2019; Sharaf, 2017; Sharma et al., 2018; Syahreza et al., 2012; Zhu, 2013). To classify the degree of severity, WQI is grouped into broad classes, i.e., excellent, good, moderate, poor, etc. For assessing the quality of any water body, numerous water quality indices have been proposed. Most commonly utilized WQIs are weighted arithmetic index method (Brown et al., 1970), national sanitation foundation water quality index (NSFWQI) (Hoseinzadeh et al., 2014), overall index of pollution (OIP) (Sargaonkar & Deshpande, 2003), etc. The OIP furnishes an in-depth understanding of the water quality status of the surface water sources, especially under Indian conditions (Sargaonkar & Deshpande, 2003). Remote sensing of water quality involves visible and infrared portion of the electromagnetic spectrum to explore the sensitivity of spectral band combinations by utilizing advanced computing techniques. Several data-driven approaches have been implemented to quantify the relationship between actual and modeled WQPs for qualitative modeling of water quality and requires input data, model parameters, and other relevant information (Bordalo et al., 2006). Many studies employed statistical approaches to explore linear correlations, such as MLR, logarithmic relation and exponential relation, while others concentrated on more efficient, nonlinear analytical methods, viz. artificial neural network (ANN), genetic programming (GP), group method of data handling (GMDH), GEP, etc., in conjunction with geospatial techniques (Akbal et al., 2011; Avdan et al., 2019; Boyacioglu, 2010; Chapagain et al., 2010; Hussain et al., 2008; Lotfinasabasl et al., 2018).
In recent years, ANN modeling has been widely utilized to quantify the severity of water quality issues due to its fast training process and ability to solve linear and nonlinear complex problems (Bonansea et al., 2015; Nasri, 2010; Nathan et al., 2017). Many studies utilized the BPNN and radial basis function (RBF) neural network for evaluating water quality and provided favorable outcomes through modeling complex nonlinear response functions, such as spectral reflectance values and WQP estimates (Ekercin, 2007; Gürsoy & Atun, 2019; Marquez et al., 2018; Zhang et al., 2003; Zhao et al., 2014). In river management programs, ANNs have effectively been used to evaluate the WQI levels to simulate wetland processes (Reynolds & Maberly, 2002; Kuo et al., 2007; Li et al., 2009; Song et al., 2012; Wang et al., 2012). Chu et al. (2013) developed ANN model that could effectively predict the quality of the surface water bodies and introduced the factor analysis technique to identify significant water quality parameters. In another study conducted by Hafeez et al. (2018), four machine learning approaches, namely artificial neural network (ANN), random forest (RF), cubist regression (CB) and support vector regression (SVR), were compared for retrieval of water quality indicators (i.e., Chl-a, SS and turbidity) over the coastal waters of Hong Kong by employing water reflectance values acquired from hand-held spectroradiometer and satellite data. Results revealed ANN as the best performer than other three approaches. More recent studies conducted by Wang et al. (2019, 2020) inferred deep learning process as a promising tool for formulating environmental property prediction models for screening of green solvents. Several studies successfully applied GEP, along with GP, to a variety of water resources issues (Azamathulla & Ghani, 2011; Ghavidel & Montaseri, 2014; Liu & Wang, 2019; Zakaria et al., 2010). Furthermore, these techniques have been considered as substantial tools in solving complex environmental and river engineering problems (Aras et al., 2007; Chen et al., 2008; Mohammadpour et al., 2015). Ni et al. (2012) effectively evaluated the water fluctuations in the wetlands by utilizing the GP approach. Xu and Qin (2013) measured the agricultural water quality through the combined application of GA and fuzzy simulation. In a significant study by Martí et al. (2013), comparison of three approaches, namely ANN, GEP and MLR for estimation of outlet dissolved oxygen in micro-irrigation, was carried out, and the outcomes revealed GEP as the most effective approach. In a recent study carried out by Li and Wang (2019), a reliable turbidity model was developed to predict reservoir turbidity based on Landsat-8 satellite imagery by utilizing an MLR and GEP approach. Results revealed GEP to be more rational and accurate for turbidity simulation. Quantification of pollution levels in water bodies during the lockdown period worldwide forms a crucial aspect for researchers to interpret the short and long-term effect of the coronavirus disease 2019 (COVID-19) on the river dynamics. It has been reported in few recent studies that the pollution level has exceedingly reduced and most water bodies have completely been restored (Clifford, 2020; Häder et al., 2020; Stone, 2020).
Kali River, a major source of irrigation in western Uttar Pradesh, India, has completely deteriorated due to ever increasing disposal of municipal and industrial waste from adjoining cities. Some earlier studies suggested the river water quality as safe for irrigation purposes, whereas later studies revealed river water to be severely polluted with heavy metal concentrations exceeding far beyond the permissible limits (Mishra et al., 2015; Maurya & Malik, 2016). The Kali River has been identified as the most critically contaminated after Markanda River (in Haryana State) in terms of BOD levels (CPCB, 2012). Spatial monitoring of the water quality of Kali River by employing reliable data-driven approaches is a prerequisite to conserve and manage the river restoration process. Therefore, the main objective of the study is to evaluate and map WQI estimates along a 6-km-long stretch of the Kali River passing through the Aligarh district in Uttar Pradesh, India, by utilizing high-resolution IRS P6 LISS IV imagery. Eleven spectral reflectance band combinations were formulated to identify the most significant band combination associated with the observed WQI at the sampling locations. Three approaches, namely MLR, BPNN and GEP, were employed to relate WQI as a function of most significant band combination. The performance of three approaches was assessed by via quantitative indicators such as coefficient of determination (R2), root mean square error (RMSE) and mean absolute error (MAE). A one-way ANOVA (analysis of variance) test was also performed to assess significant differences among WQI estimates from the three approaches at a confidence level of 0.05. Maps depicting spatial variation of WQI levels in the river stretch were generated in GIS framework. The present study configures the basis for policy makers and environmentalists to devise effective and sustainable strategies and policies to reclaim the completely degraded river ecosystems.
Materials and methods
Study area
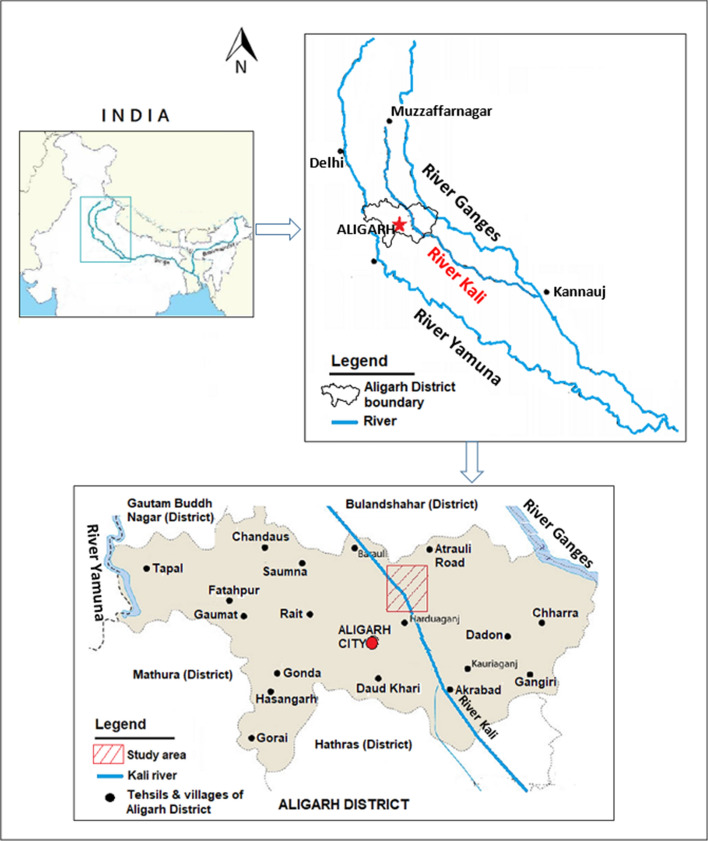
The study area, illustrated in Fig. 1, covers 6-km-long stretch of Kali River (meaning “black” in the local language) that passes through the Aligarh district in Uttar Pradesh, India. Study area is confined within latitude 28.11°N to 28.15°N and longitude 78.14°E to 78.18°E at an elevation of 213 m above the mean sea level. The river had been a major source of water for domestic as well as irrigation requirements in the past two decades. The Kali River originates from the village of Antwada, in the Muzaffarnagar district, Uttar Pradesh, passes through many important cities and joins the Ganges River at the city of Kannauj in the Farrukhabad district. The river covers a total span of almost 300 km. Large cities, including Meerut, Hapur and Bulandshahr, accommodate numerous small- and large-scale industries along the river banks, such as sugar mills, paper mills, textile industries, slaughterhouses and distilleries. The current status of the river justifies its name, owing to the excessive discharge of domestic sewage and untreated industrial effluents into the river thus, conveying more than 60 per cent of the pollution load (CPCB, 2012). Over the years, the river has completely transformed into a highly toxic flow of chemicals, harmful for human consumption, and offers a restricted use for irrigation or any other purpose. Toxic water from the Kali River is widely consumed for fulfilling the irrigation requirements of surrounding areas. The present condition of the river is pity and demands immediate attention for its reclamation.
Fig. 1.
Location map of the study area (map not to scale)
Data collection and analysis
River water samples were collected from the midstream at a depth of 0.5 m on April 27, 2018, concurrent to the date of satellite overpass. Grab sampling procedure was adopted for the analysis of various WQPs as recommended by the standard methods of analysis (APHA, 1998). Water samples from the Kali River were analyzed in the laboratory of Environmental Engineering, Civil Engineering Department, AMU, Aligarh, and the WQI for each sampling location was estimated from 11 physicochemical parameters and heavy metals, namely pH, EC, DO, TDS, BOD, COD, alkalinity, Fe, Mn, Cr and Pb. The heavy metal concentration was measured by adopting American Society for Testing and Materials (ASTM, 2000) procedure involving the digestion of water samples with concentrated HNO3 and employing an atomic absorption spectrophotometer (AAS).
WQI values for 40 water samples were computed by following a three-step procedure (Water programme, 2007). The first step assigns weight (wi) to all the WQPs ranging from 1 to 5 in accordance with their relative significance towards the overall quality grading of the water for irrigation purposes. The relative significance among WQPs was decided on the basis of collective expert opinions taken from different published studies (Ramakrishnaiah et al., 2009; Nabizadeh et al., 2013; Suneetha et al., 2015). The highest weight value, i.e., 5, was assigned to two heavy metals, i.e., Pb and Cr, on account of their prominence towards rendering severity to the water quality. Lower rank of 1 was assigned to pH, and 2 was assigned to COD and BOD. Ranks 3 and 4 were appropriately assigned to alkalinity, TDS, DO, EC, Fe and Mn on the basis of their relative severity (Srinivasamoorthy et al., 2008). The second step computes the relative weight (Wi) as per the equation below.
| 1 |
where Wi is the relative weight, wi is the individual parameter weight, and n is the number of parameters. In the third step, a quality rating scale (qi) for each parameter was evaluated by dividing its concentration levels for every water sample by its corresponding standard concentration, as per the Bureau of Indian Standards (BIS, 1986).
| 2 |
where qi is the quality rating in percent, Ci is the concentration of each chemical parameter in each water sample in mg/L, and Si is the irrigation water quality standard for each chemical parameter in mg/L. Finally, the WQI for each sampling location was computed as per Brown et al. (1970) expressed as Eq. 3, where SLi is the product of Wi and qi.
| 3 |
The WQI values corresponding to the sampling locations were evaluated by following the above procedure and scaled for quality rating in accordance with BIS (1986) specifications, provided in Table 1.
Table 1.
WQI and corresponding water quality rating as per the BIS (1986) specifications
| S no | WQI | Status | Possible usages |
|---|---|---|---|
| 1 | 0–50 | Excellent | Drinking, irrigation and industrial |
| 2 | 50–100 | Good | Domestic, irrigation and industrial |
| 3 | 100–200 | Poor | Irrigation |
| 4 | 200–300 | Very poor | Restricted use for all purposes |
| 5 | > 300 | Severe | Proper treatment required before use |
Remote sensing data used
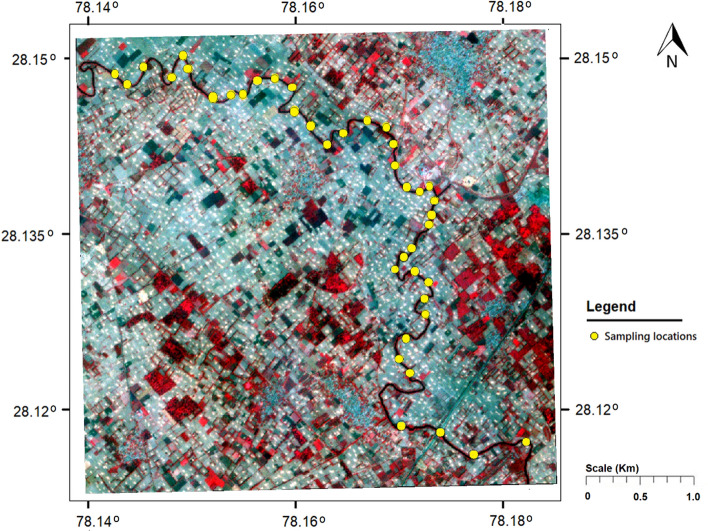
Image from IRS P6 Resourcesat-2 LISS IV sensor of April 27, 2018, was utilized in the present study for evaluating and mapping the water quality of Kali River in terms of WQI measures. The study area was delineated, and a subset image was created using the Erdas Imagine software, shown in Fig. 2. IRS LISS IV sensor produces a high-resolution multispectral image in three bands (i.e., green, red and near Infrared) with 5.8 m spatial resolution in the multispectral mode at nadir. Corresponding to the sampling locations, pixel values with reference to digital numbers (DN) from three spectral bands were extracted and converted into physical quantities (e.g., radiance) and then into spectral reflectance. The process takes into account the terrain and atmospheric corrections. The conversion involved the utilization of the radiometric “gain and offset” extracted from the image metadata and employed Eqs. 4 and 5 for radiance and reflectance, respectively, proposed by Chander and Markham (2003)
| 4 |
where λ is the specific spectral band of the image; Lλ is the spectral radiance for band λ at the sensor’s aperture (mW/cm2/µm/str); gainλ is the radiometric calibration gain (mW/cm2/µm/str/DN) for band λ from product metadata (gain values for three bands were considered: G = 52, R = 47 and NIR = 31); DNλ is digital number value for band λ of the image; and offsetλ is the radiometric calibration (mW/cm2/µm/str) for band λ from product metadata, which is zero for the three bands
| 5 |
where ρP is the dimensionless planetary reflectance, d is the Earth–Sun distance (astronomical units, 1 − (0.01674 cos (0.9856 (JD-4)))2, where JD is Julian Day), ESUNλ is the average solar exo-atmospheric spectral irradiances (mW/cm2/µm) at 1 astronomical unit (AU) distance between the Earth and Sun, θs is the Sun’s zenith angle (~ 67.337461° from product metadata), and Lλ is the spectral radiance for band λ at the sensor’s aperture (mW/cm2/µm/str).
Fig. 2.
Subset image of study area with sampling locations along the river stretch
Modeling approaches
Multiple linear regression (MLR)
MLR analysis predicts the unknown variable from two or more known variables that are termed as the predictors. In other words, a multiple regression analysis aids in predicting the Y value for given X1, X2, …, Xk values. The multiple regression equation of Y with known X1, X2, …, Xk is given by
| 6 |
where b0 is the intercept and b1, b2, b3, …, bk are the regression coefficients that correspond to the slope in a linear regression equation. An MLR was employed to examine the most appropriate formulated spectral reflectance band combination, producing WQI estimates with high R2 values and low RMSE and MAE values.
Artificial neural network (ANN)
The feed forward backpropagation neural network (FF-BPNN) algorithm looks for the least error function in weight space by employing the gradient descent method. The learning process resolves the complexity of the problem through randomly assigning weights that produce the least error function. The entire process is executed in two phases. In the first phase, assigned weights to the network architecture are initialized randomly to propagate forward, along with input data, to compute the target value. In the second phase, the error between the actual and estimated targets is compared and the error value that is higher than the threshold value is rolled backward through the network. The weight values are recalculated, and the process is continued until the minimum error is attained. During the training process, the errors for both training and testing data decrease with number of iterations until a constant minimum error value is attained. Training is stopped at a point when, the least difference between training and testing data errors is observed so as to avoid overtraining of the network (Said et al., 2008). The most general neural network architecture consists of three layers, i.e., input, hidden and output layers, as illustrated in Fig. 3.
Fig. 3.
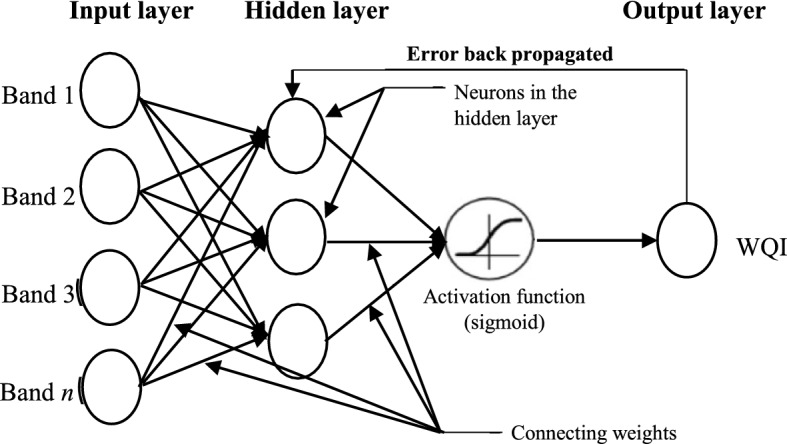
Neural network architecture with input variables as bands/band combinations and WQI as target variable
Every unit in a layer is connected with units in the adjoining layer with a unique weight value. Variables in the input layer, along with connected weights, propagate to every unit of the next hidden layer. The end product of every unit forming an output is compounded with weights of preceding connecting units and is advanced to the successive layer before finally being subjected to the sigmoid activation function. The output value from the jth unit of layer m is represented as
| 7 |
where S is the sigmoid activation function, as proposed by Rumelhart et al. (1986), and
| 8 |
The function f(x) acquires values from zero to unity for the entire range of inputs; x is the input value, viz. obtained for of layer m, as
| 9 |
where is the threshold value of the jth unit of layer m. and are the outputs of the ith unit of layer m − 1 and the weight of the connection between ith and jth units of layers m − 1 and m, respectively. The error function is expressed as
| 10 |
where Tk is the desired target value and Ok is the corresponding output value determined for k training samples.
Gene expression programming (GEP)
GEP, proposed by Ferreira (2001), is an evolutionary technique that has the advantage of solving complex nonlinear problems based on the GP approach developed by Koza (1999). GEP is an improved version of GA and GP that overcomes premature convergence and a 100 times higher evolution rate. GEP undergoes a continuous evolution process with the random propagation of an initial population comprising of individual chromosomes of predefined length containing one, or more than one, gene. The structure of genes comprises a head and a tail. The head consists of both functions and terminals, whereas the tail holds only terminals. For reaching an optimal solution to the defined problem, the head length h is selected; further, the tail length t is related to h, and the function is evaluated by using Eq. 11 below:
| 11 |
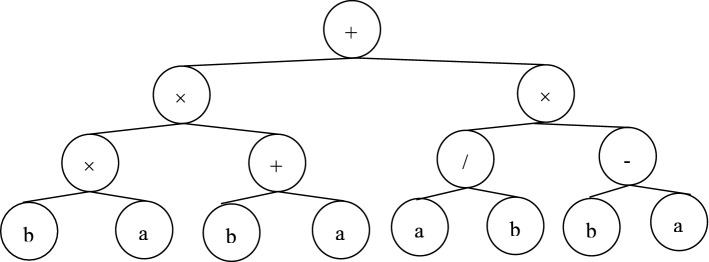
where n is the number of arguments of the function. Ferreira (2001) represented the encoded genetic information in the gene in the form of an expression tree (ET). With the help of the unequivocal Karva language, the gene composition of a given ET can be generalized on the basis of simple rules of top–down and right–left (Li and Wang, 2019). An example of a gene is shown in the form of an ET in Fig. 4, for which an equivalent mathematical expression is encoded as [(b × a) × (b + a)] + [(a/b) × (b − a)].
Fig. 4.
An example of gene ET
The fitness of every chromosome i in the initial population is computed by utilizing the fitness function fi expressed as Eq. 12, proposed by Ferreira (2001).
| 12 |
where M is the selection range, Ci,j is the value recalled by the ith chromosome for the jth fitness case, and Tj is the target value for the jth fitness case. It is to be noted that, for a perfect fit, Ci,j = Tj and fi = fmax = Ct × M. Fitness function resolves the selection of the optimal chromosomes for the next generation level through modifications achieved by genetic operators such as mutation, inversion, transposition and recombination.
Mutation is the most effective genetic operator that represents the probability of a function or a variable (symbol) to get mutated in each generation. Any symbol in the gene heads can be replaced by a terminal function; however, in the gene tails, terminals can be replaced by variables only, since there is no function in the tail. Inversion chooses a random starting as well as ending symbol in a gene, which is then reversed in order. Transposition involves actuating a sequence of symbols from one position to another within a gene or from one gene to another gene in the same chromosome. In a recombination stage, two new chromosomes are developed by the exchange of genetic information through random selection. The process is analogous to the breeding of two biological species that produces a new offspring sharing genetic material from both parents. Figure 5 illustrates the generalized process of GEP model building in the form of a flowchart.
Fig. 5.
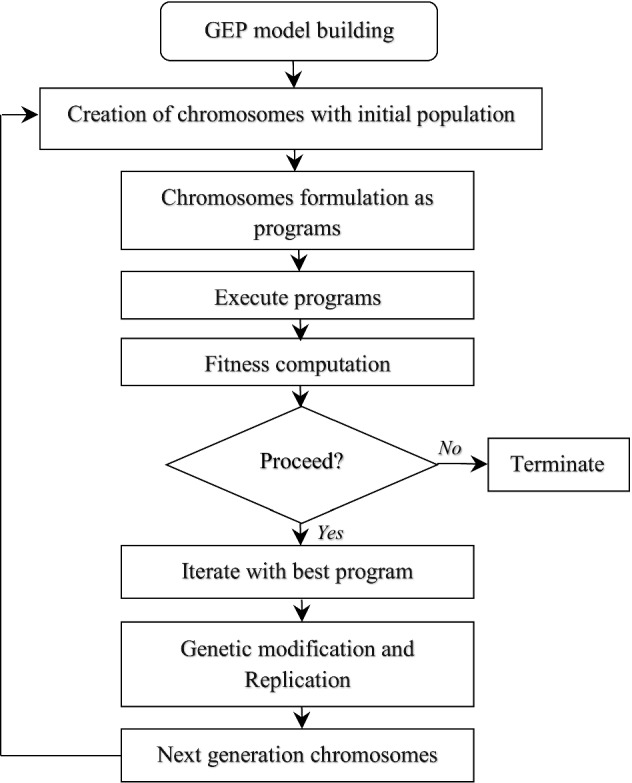
Flowchart illustrating the process of GEP model building
Table 2 depicts 11 spectral reflectance bands/band combinations (including three inherent single bands, i.e., green, red and infrared) formulated to explore the most significant band combination related to the observed WQI estimates. As described in the preceding sections, WQI estimates as a function of most sensitive spectral band combination were examined via three approaches and the performance were compared using R2, RMSE and MAE (quantitative indicators). Out of 40 data samples in total, 80% were used for training and testing or calibration and the remaining (20%) were used for validation. Neural network architectures were developed in accordance with the band combinations, i.e., 2, 3, 4, 5 and 6 spectral bands/combinations as input variables. The same band combinations were analyzed for MLR and GEP approaches, keeping WQI as target variable. For BPNN and GEP analysis, the entire data set was normalized to lie within 0 to 1 range by using Eq. 13 below (Rajurkar et al., 2004), to ensure that data are logically structured and proportionally scaled.
| 13 |
where is the normalized, unitless variable; Xi is the observed variable; and Xmax is the maximum value in the data range. The optimal count of neurons in the hidden layer was ascertained by a hit-and-trial procedure. The learning rate for BPNN was gradually varied within the defined range of 0.01 to 0.5. The final values of the learning rate and the optimum count of neurons in the hidden layer obtained by the trial process are provided in Table 2.
Table 2.
Formulated band combinations with details of BPNN architectures
| Band combination cases | Input/independent variables | Target variable | Network architecture I–H–Oa | Learning rate | |
|---|---|---|---|---|---|
| No | Description | ||||
| 1 | 2 | G, R | WQI | 2–2-1 | 0.058 |
| 2 | 2 | G, NIR | 2–2-1 | 0.072 | |
| 3 | 2 | R, NIR | 2–3-1 | 0.069 | |
| 4 | 3 | G, R, NIR | 3–4-1 | 0.087 | |
| 5 | 4 | G, R, NIR, G/R | 4–5-1 | 0.055 | |
| 6 | 4 | G, R, NIR, G/NIR | 4–3-1 | 0.047 | |
| 7 | 4 | G, R, NIR, R/NIR | 4–6-1 | 0.025 | |
| 8 | 5 | G, R, NIR, G/R, G/NIR | 5–4-1 | 0.065 | |
| 9 | 5 | G, R, NIR, G/R, R/NIR | 5–6-1 | 0.046 | |
| 10 | 5 | G, R, NIR, G/NIR, R/NIR | 5–7-1 | 0.095 | |
| 11 | 6 | G, R, NIR, G/R, G/NIR, R/NIR | 6–8-1 | 0.075 | |
aI–H–O: input–hidden layer neurons–output
Further, for building the optimal GEP model, the number of chromosomes or population size after many trials was selected as 50, the gene head length was selected as 14, and the number of genes per chromosome was selected as 8. Seven necessary function operators, i.e., + , − , × , ÷ , 1/a, − a, a2, were adopted for building the simplified GEP model with a reduced iteration process as well as nonconvergence occurrences. Furthermore, subgene ETs were linked by an addition function. The parameters adopted for the optimal GEP model for precise evaluation of WQI levels are illustrated in Table 3.
Table 3.
Parameters adopted for the optimal GEP model
| Parameter | Value |
|---|---|
| Population size | 50 |
| Genes per chromosomes | 8 |
| Gene head length | 14 |
| Maximum generations | 5000 |
| Fitness function | R2 |
| Precision (hit tolerance) | 0.01 |
| Mutation rate | 0.054 |
| Inversion rate | 0.1 |
| Computational functions |
+ , − , × ,/,1/a,a2, − a Addition, subtraction, multiplication, division, inverse, square, negation |
| Linking function | addition |
| IS transposition rate | 0.1 |
| RIS transposition rate | 0.1 |
| Gene transposition rate | 0.1 |
| Recombination one-point rate | 0.3 |
| Recombination two-point rate | 0.3 |
Results
In situ water samples collected were analyzed for 11 WQPs in the laboratory, and the basic descriptive statistics of the samples are summarized in Table 4. The physicochemical and heavy metal concentrations ranged far beyond the permissible limits prescribed under BIS specifications, although there were no traces of Cr and Mn in all the measured samples. The WQI values computed from nine WQPs (excluding Cr and Mn) for 40 water samples collected along the Kali River stretch ranged between 203.7 and 262.33, and rated under “very poor” category on the basis of BIS criteria provided in Table 1. The WQI range indicates restricted use of river water almost for all purposes including irrigation. The results of the WQI estimates from the three employed approaches, i.e., MLR, BPNN and GEP, are illustrated in Table 5.
Table 4.
Descriptive statistics of the measured WQPs
| S. no | Water quality parameters (mg/l) | Range min–max | Mean | Standard deviation ( σ) | Population variance (s2) | Sample variance ( σ2) | SEMa | BIS standard (BIS, 1986) |
|---|---|---|---|---|---|---|---|---|
| 1 | pH | 6.93–7.56 | 7.33 | 0.12 | 0.0147 | 0.0141 | 0.0242 | 6.5–8.5 |
| 2 | EC (μs/cm) | 1083–1852 | 1644 | 190.61 | 36,334 | 34,881 | 38.12 | 300 |
| 3 | TDS | 754–851 | 800.32 | 20.06 | 402.56 | 386.53 | 4.013 | 500 |
| 4 | Alkalinity | 540–680 | 616.68 | 40.39 | 1631.56 | 1566.3 | 8.078 | 200 |
| 5 | COD | 72.15–91.20 | 81.55 | 6.10 | 57.38 | 49.32 | 1.515 | 250 |
| 6 | DO | 2.08–6.74 | 5.85 | 1.04 | 1.089 | 0.882 | 0.211 | 5 |
| 7 | BOD | 23.20–38.50 | 29.61 | 4.02 | 16.124 | 15.48 | 0.803 | 5 |
| 8 | Cr | 0 | 0 | 0 | 0 | 0 | 0 | 0.05 |
| 9 | Pb | 0.19–0.24 | 0.21 | 2.21 | 1.4 × 10–4 | 1.1 × 10–4 | 0.002 | 0.1 |
| 10 | Fe | 0.01–0.03 | 0.02 | 0.01 | 8.7 × 10–5 | 8.4 × 10–5 | 0.0018 | 0.3 |
| 11 | Mn | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 |
aSEM standard error of means
Table 5.
Coefficient of determination (R2), RMSE and MAE between the observed and estimated WQIs from three approaches
| Band combination cases | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Inputs/variables | Xa | 2 | 2 | 2 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 6 | |
| Iterations | Ib | 35,234 | 28,731 | 32,186 | 33,174 | 36,871 | 44,528 | 47,351 | 51,277 | 49,545 | 55,285 | 57,368 | |
| MLR | Cal (80%) | R2 | 0.46 | 0.66 | 0.65 | 0.72 | 0.81 | 0.77 | 0.56 | 0.59 | 0.51 | 0.32 | 0.27 |
| RMSE | 18.51 | 15.67 | 9.45 | 6.85 | 4.36 | 7.31 | 10.52 | 12.35 | 11.68 | 17.77 | 21.45 | ||
| MAE | 16.77 | 15.21 | 8.63 | 5.37 | 3.00 | 6.82 | 8.86 | 10.73 | 11.24 | 15.52 | 18.96 | ||
| Val (20%) | R2 | 0.34 | 0.52 | 0.47 | 0.51 | 0.60 | 0.55 | 0.57 | 0.49 | 0.43 | 0.15 | 0.09 | |
| RMSE | 16.52 | 8.96 | 13.76 | 9.63 | 6.30 | 7.55 | 7.37 | 11.52 | 13.93 | 28.79 | 36.21 | ||
| MAE | 15.23 | 8.44 | 10.73 | 8.68 | 4.64 | 7.15 | 6.97 | 9.38 | 12.51 | 23.48 | 31.92 | ||
| BPNN | Cal Tr Tec | R2 | 0.84 | 0.88 | 0.85 | 0.95 | 0.92 | 0.89 | 0.92 | 0.87 | 0.79 | 0.87 | 0.93 |
| RMSE | 3.78 | 3.64 | 3.32 | 2.36 | 2.58 | 3.38 | 3.76 | 4.81 | 5.24 | 4.95 | 3.17 | ||
| MAE | 3.34 | 3.46 | 2.98 | 2.15 | 2.42 | 3.15 | 3.28 | 4.47 | 4.89 | 4.33 | 2.87 | ||
| Val (20%) | R2 | 0.76 | 0.79 | 0.84 | 0.87 | 0.85 | 0.81 | 0.83 | 0.69 | 0.73 | 0.79 | 0.83 | |
| RMSE | 5.21 | 6.87 | 5.91 | 4.48 | 5.85 | 6.76 | 6.62 | 7.23 | 7.17 | 6.95 | 6.34 | ||
| MAE | 4.85 | 5.54 | 5.73 | 3.61 | 4.97 | 6.16 | 5.65 | 7.12 | 6.78 | 6.23 | 5.92 | ||
| GEP | Cal (80%) | R2 | 0.78 | 0.84 | 0.91 | 0.88 | 0.94 | 0.92 | 0.89 | 0.83 | 0.91 | 0.79 | 0.82 |
| RMSE | 6.89 | 6.34 | 5.21 | 5.96 | 2.49 | 3.16 | 3.67 | 7.78 | 3.41 | 7.39 | 6.57 | ||
| MAE | 5.74 | 5.22 | 4.78 | 5.17 | 2.16 | 2.87 | 2.83 | 6.41 | 2.75 | 5.53 | 5.27 | ||
| Val (20%) | R2 | 0.63 | 0.79 | 0.82 | 0.86 | 0.91 | 0.87 | 0.81 | 0.76 | 0.82 | 0.71 | 0.79 | |
| RMSE | 8.87 | 7.21 | 6.87 | 6.34 | 4.45 | 5.92 | 6.54 | 7.11 | 7.08 | 7.87 | 8.29 | ||
| MAE | 7.34 | 6.88 | 6.12 | 5.43 | 3.53 | 4.58 | 5.71 | 6.51 | 5.24 | 6.19 | 7.33 | ||
aX no. of input/independent variables, bI total no. of iterations for BPNN, cTr training data (60%), Te testing data (20%), Cal calibration, Val validation
‘Bold’ indicates the optimal WQI model achieved
Results from the MLR analysis indicate that, out of 11 band combination cases analyzed, a combination of 4 bands, i.e., G, R, NIR and G/R (band combination case no. 5), exhibited strong correlation with the observed WQI yielding R2 ~ 0.81 and low RMSE and MAE values (i.e., 4.36 and 4.64, respectively) for calibration data. However, the same band combination yielded WQI estimates with R2 ~ 0.6, and relatively high RMSE and MAE values (i.e., 6.3 and 4.64) for validation data. Regression coefficients for the most significant band combination are provided in Table 6, and the formulated regression equation is expressed as Eq. 14. Scatter plot between the observed and estimated WQI for calibration and validation data is illustrated in Fig. 7(a), depicting estimated values of the WQI within ± 20% error lines. The regression equation formulated for the most significant band combination was utilized in the generation of spatially distributed WQI map of the river segment.
| 14 |
Table 6.
MLR coefficients for calibration data for the most appropriate band combination
| Multiple regression equation where Y = WQI | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| BCa case Nn | Xb | Parameter distribution | Regression coefficients | R2 (Calc) | RMSE | MAE | R2 (Vald) | RMSE | MAE |
| 5 | 04: G, R, NIR, G/R |
X1 = G X2 = R X3 = NIR X4 = G/R |
b0 = − 183.98 | 0.81 | 4.36 | 3.0 | 0.60 | 6.3 | 4.64 |
| b1 = 2309.74 | |||||||||
| b2 = 297.18 | |||||||||
| b3 = 200.93 | |||||||||
| b4 = 35.84 | |||||||||
aBC band combination,bX no. of input/independent variables, cCal calibration, dVal validation
Fig. 7.
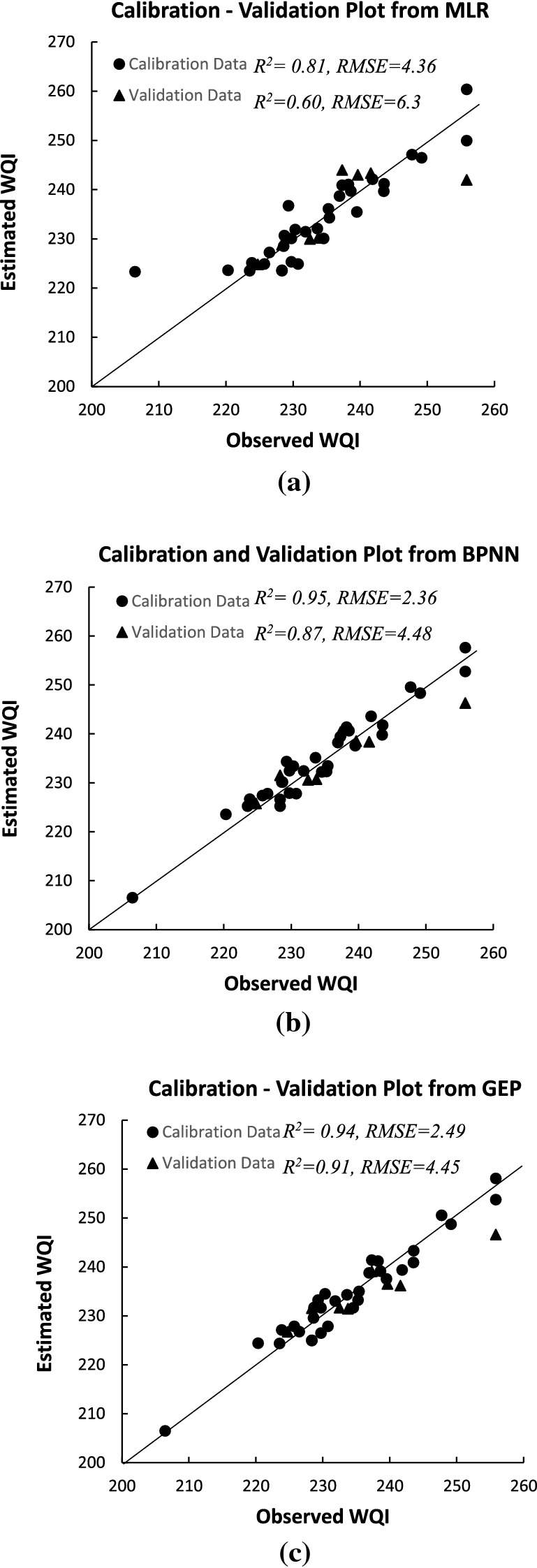
Scatter plots between observed and estimated WQIs from a MLR approach for band combination 5; 4 inputs, b BPNN approach for band combination 4; 3 inputs and c GEP approach for band combination 5; 4 inputs
Neural network architectures for all band combinations were trained using the TRAINGD function and FF-BPNN algorithm. Optimal architectures were obtained during the training process by adopting the number of neurons in the hidden layer from 2 to 10 and varying the learning rate in the defined range of 0.001 to 0.5. It was observed that neural network architectures trained with 3, 4 and 6 neurons in the hidden layer yielded much better WQI estimates in terms of R2, RMSE and MAE values (Table 6).
Results further reveal that neural network architecture trained with 3 input bands, i.e., G, R and NIR, and 4 neurons in the hidden layer (i.e., 3-4-1) produced WQI estimates with highest accuracy than the rest of combinations, yielding R2 ~ 0.95 and 0.87, RMSE as 2.36 and 4.48, and MAE as 2.15 and 3.61 for calibration and validation data, respectively. Scatter plot between the observed and estimated WQIs as shown in Fig. 7b depicted WQI estimates within ± 10% error lines. It was also observed that almost all neural network architectures with different band combinations conceded WQI estimates with considerable accuracies for calibration data, i.e., R2 ranging from 0.92 to 0.79, respectively. Table 7 illustrates the final weight matrix for the most optimal neural network architecture (i.e., 3-4-1) producing highest WQI retrieval accuracies.
Table 7.
Final weight matrix of the trained BPNN model with 3 input variables
| Predictor variables | BPNN prediction model (hidden layer) | |||
|---|---|---|---|---|
| Connecting weights of 4 neurons | ||||
| Input layer | N1 | N2 | N3 | N4 |
| G | − 0.234 | 0.046 | 0.824 | 0.147 |
| R | − 0.463 | − 0.042 | 0.568 | − 0.221 |
| NIR | 0.173 | − 0.386 | − 0.034 | − 0.579 |
| Bias | 0.251 | − 0.366 | − 0.721 | 0.632 |
| Target variable (WQI) output layer | 0.437 | − 0.254 | − 0.022 | 0.771 |
N1 neuron 1, N2 neuron 2, N3 neuron 3, N4 neuron 4
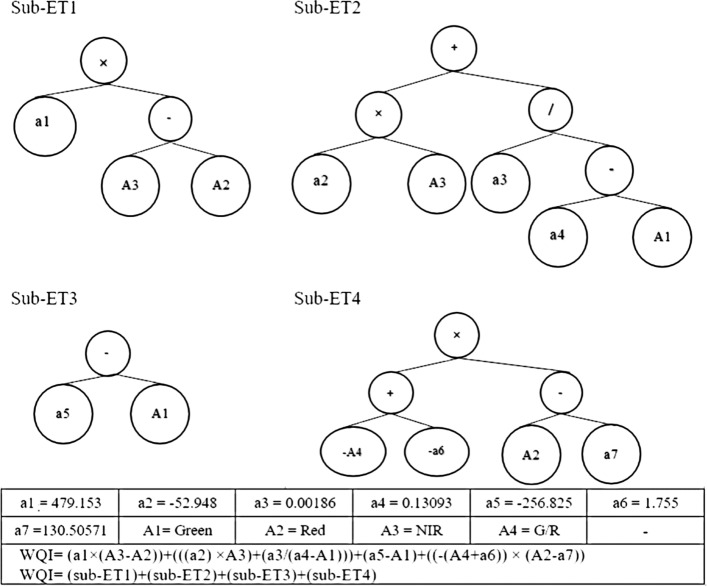
The optimal GEP model was achieved through many trials (Table 6), comprising a chromosomal architecture with 50 chromosomes, head length at 14 and number of genes at 8, and 4 spectral bands as input, viz. G, R, NIR and G/R (band combination case no. 5). The optimized GEP model produced WQI estimates with considerably high accuracies, yielding R2 ~ 0.94 and 0.91, RMSE as 2.49 and 4.45, and MAE as 2.16 and 3.53 for calibration and validation data, respectively. As observed from the results, GEP model performs substantially well with validation data as compared with BPNN and MLR models, thus indicating significant rationality in the optimized GEP model. The optimal GEP model constitutes four subordinate expression trees (i.e., sub-ET1, sub-ET2, sub-ET3 and sub-ET4), developed in accordance with the selection of the number of input variables and function operators during model-building process. Sub-ETs were linked together by an addition function to finally form the mathematical expression that was further simplified to obtain more generalized form for estimating the WQI, expressed as Eq. 15. The developed subgene ETs are shown as in Fig. 6, and a scatter plot between the observed and estimated WQI is shown in Fig. 7c, depicting estimated WQI values within ± 10% error lines.
| 15 |
Fig. 6.
Expression trees for the optimal GEP model with 4 spectral bands
Discussion
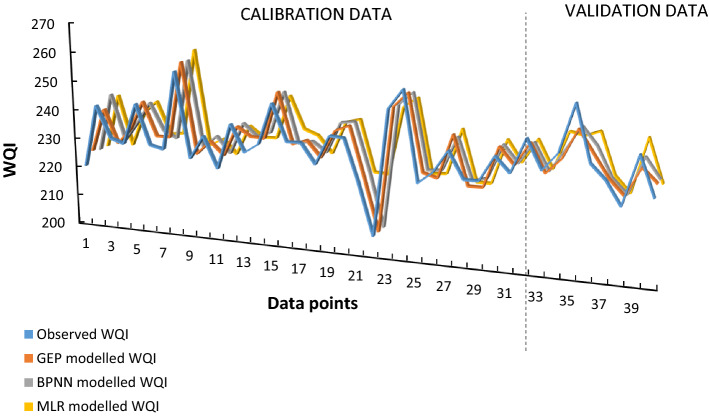
The severe contamination of River Kali stretch assessed through the laboratory analysis of 11 physicochemical parameters and heavy metals as well as WQI estimates is mainly attributed to the unrestricted toxic waste disposal from numerous small- and large-scale industries. Although several studies on Kali River water quality have predicted the similar outcomes (CPCB, 2012; Mishra et al., 2015; Singh et al., 2020; Sirohi et al., 2014), a comprehensive monitoring of WQI levels by formulating spectral band combinations has been lacking. Results from the three approaches further reveal that GEP outperforms the other two approaches in terms of WQI estimates for validation data (i.e., R2 ~ 0.91, 0.87 and 0.60; RMSE ~ 4.45, 4.48 and 6.30 for GEP, ANN and MLR, respectively), suggesting a higher measure of explanatory power possessed by this approach. Moreover, the GEP approach is simple and produces reliable WQI measures and reduces substantial time and effort by optimizing the computations to generate simplified prediction expressions. This technique is highly recommended by many researchers (Hashmi et al., 2011; Mohammadpour et al., 2016; Liu & Wang, 2019) for the water quality evaluation of wetlands and other surface water bodies. In addition, the ANN approach is relatively time-consuming and does not furnish any governing equations of the optimized models, which is considered as one of its major disadvantages. The WQI estimates predicted by MLR model were of insufficient accuracy when tested with validation data, since this approach utilizes the method of least squares and is linear in nature. However, MLR is still practicable for its fast predicting ability. Figure 8 depicts comparative line plots of WQI estimates for calibration and validation data, along with the observed WQI measures.
Fig. 8.
Comparative line plot of observed WQI and estimated WQI from the three employed approaches
The contamination levels throughout the Kali River stretch exhibited consistency which lead to similar spectral distribution of remotely-sensed signal above the water surface. Therefore, WQI maps created in the GIS framework (Fig. 9) from the three approaches corroborate to the actual severity in WQI levels, exhibited by the darker spectral tones covering the entire length of the river segment. This severe contamination in the river is majorly attributed to the addition of industrial effluents, agricultural runoff, natural matter and nutrients in the water body (Jindal & Sharma, 2011).
Fig. 9.
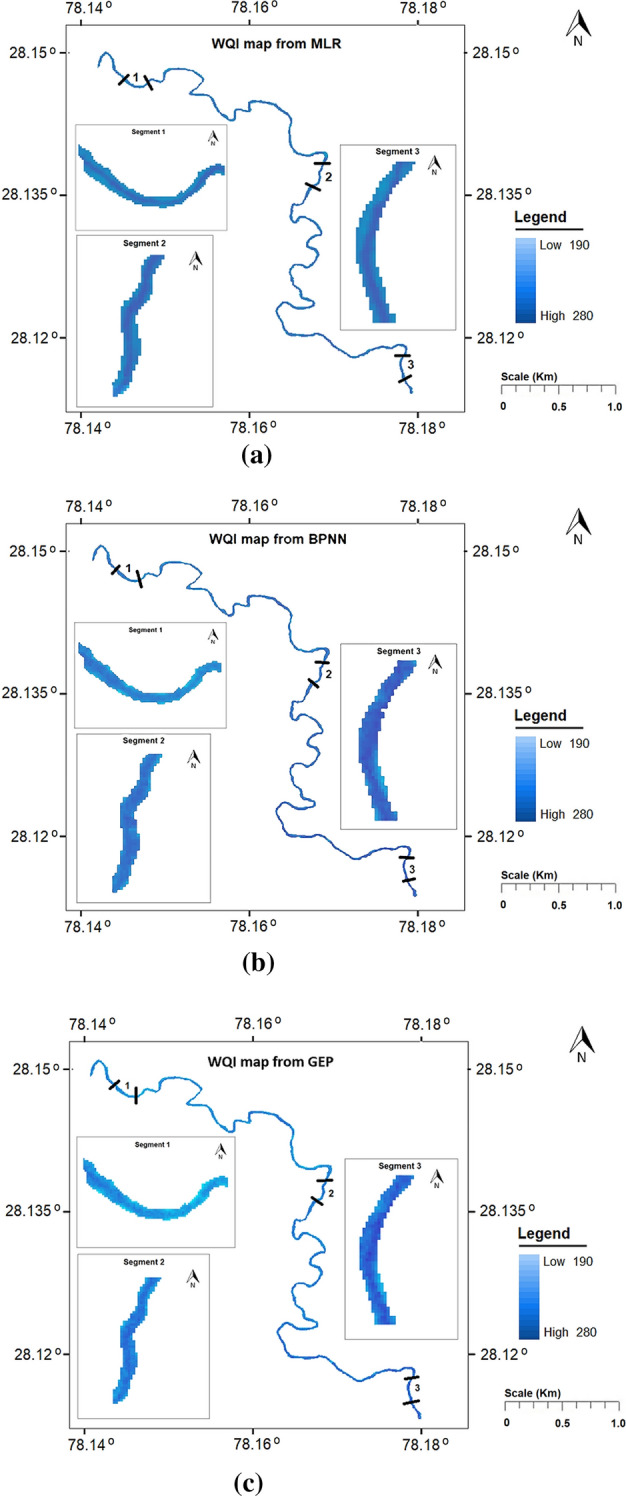
WQI maps of the river stretch generated from a MLR, b BPNN and c GEP analysis
A one-way ANOVA test for means and variance was applied to further ascertain the spatial variability of WQI estimates from the three approaches. The null hypothesis “H0” stated “no significant difference between means of WQI estimates from the three approaches,” whereas alternate hypothesis “Ha” stated “significant difference between means of WQI estimates from three approaches.” The test results unveiled F-statistic (i.e., F = 0.01 and p-value, i.e., p = 0.994) as exceedingly higher than the significance level α = 0.05 (Table 8), implying that there were no critical differences in the mean values and variances of WQI estimates. The ANOVA test results therefore fail to reject the null hypothesis inferring that the WQI estimates from the three approaches are statistically “not significant.” The data set may, however, be consistent with the differences of practical importance. Moreover, failing to reject the null hypothesis does not necessarily imply that no potential difference in the data set exists, rather; an increased sample size could bring out the difference. Thus, larger sample sizes allow hypothesis tests to detect effects that are statistically significant. Further, to visually summarize and compare the results, box plot of WQI estimates shown in Fig. 10, were analyzed. İt was observed that, the respective medians of each box plot laid at the same level (i.e., 233.23 for GEP, 232.94 for ANN and 231.96 for MLR) suggesting no likely difference between the three estimated WQI groups. The median line of the three box plots further indicates symmetric data representation with no right or left skewness within each of the three WQI groups. Upon comparing the interquartile ranges, the relatively longer box corresponding to MLR revealed slight dispersion in WQI estimates.
Table 8.
One-way ANOVA test for WQI estimates from the three employed approaches
| Square summation | Degree of freedom | Mean of square | F | P-value | F crit | |
|---|---|---|---|---|---|---|
| Between groups | 0.9329 | 2 | 0.4665 | 0.01 | 0.994 | 3.08 |
| Within groups | 9830.53 | 117 | 84.021 | |||
| Total | 9831.47 | 119 |
As the P-value is more than 0.05, it is not significant at 2.5% level
Fig. 10.
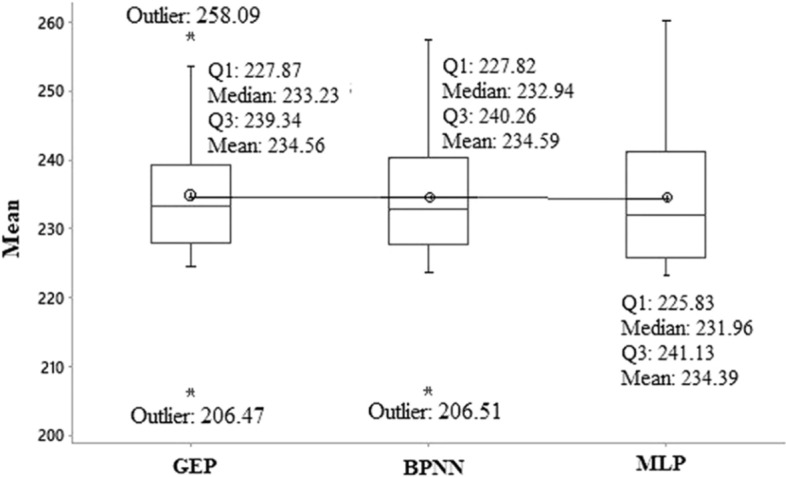
Boxplot of WQI estimates from the three employed approaches
Overall comparison of the results indicate that GEP is much superior to MLR and ANN approaches. Furthermore, despite the restrictive spectral resolution of IRS P6 LISS IV sensor (i.e., comprising three bands), a combination of 4 bands (i.e., G, R, NIR, G/R) is identified as the most effective for modeling WQI levels through GEP approach. The methodology adopted and the WQI maps generated can be of immense help in the decision making to impose corrective conservation measures for improvement in the Kali River water quality so that the river may regain its historical importance. Moreover, the methodology can be implemented to other contaminated surface water bodies to generalize the GEP model prediction ability.
Conclusions
The present study evaluates WQI levels along 6-km-long Kali River segment from three approaches, namely MLR, BPNN and GEP, by utilizing spectral reflectance values from high-resolution IRS P6 LISS IV image. The water samples were collected from 40 random locations along the river stretch and analyzed for seven physicochemical and four heavy metal concentrations (i.e., 11 WQPs in total). All measured WQP concentrations ranged beyond the permissible limits as per BIS specifications, except for Cr and Mn, that were found to be absent in the water samples. Further, the WQI values computed from nine WQPs were found to range between 203.7 and 262.33, thus, designating the river condition as unfit for all purposes. Eleven spectral reflectance band combinations (including three inherent single bands) were considered to explore the sensitivity of the most significant band/band combination with the observed WQI. The analyses of the results revealed that GEP approach outperformed both BPNN and MLR approaches with considerably high WQI retrieval accuracies, yielding R2 ~ 0.94 and 0.91, RMSE as 2.49 and 4.45 and MAE as 2.16 and 3.53 for calibration and validation data, respectively. Results further revealed that both GEP and MLR approaches identified the combination of 4 spectral bands (i.e., G, R, NIR, G/R) as the most significant band combination for estimating WQI levels, whereas BPNN recognized 3 band combination (i.e., G, R, NIR) as the most significant. The results are also suggestive of the fact that machine learning approaches, viz. ANN and GEP, yield promising potential for water quality monitoring by utilizing spectral band combinations, wherein GEP proved to be superior. The ANOVA test revealed statistically insignificant difference among WQI estimates from the three approaches at a confidence level of 0.05, attributed to small river water sample size. The spatial distribution maps of WQI levels exhibited uniform spectral tones in the entire river stretch, signifying the severity of pollution concentrations in the river water. The study showcases the river condition as extremely critical, requiring immediate attention of the decision makers involved in the task of its reclamation. Future research can be focused on using hyperspectral satellite data along with integrated approaches such as fuzzy optimal model, GP, support vector machine (SVM) and RBF along with an increased water sample size.
Acknowledgements
Authors acknowledge anonymous reviewers for their constructive comments and suggestions that have substantially improved the quality of the manuscript.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Saif Said, Email: saif_said@rediffmail.com.
Shadab Ali Khan, Email: shadab7856gc@gmail.com.
References
- Abba SI, Said YS, Bashir A. Assessment of water quality changes at two location of Yamuna River using the National Sanitation Foundation of water quality. Journal of Civil Engineering and Environmental Technology. 2015;2(8):730–733. [Google Scholar]
- Akbal F, Gürel L, Bahadır T, Güler İ, Bakan G, Büyükgüngör H. Multivariate statistical techniques for the assessment of surface water quality at the mid-Black Sea coast of Turkey. Water Air Soil Pollution. 2011;216:21–37. [Google Scholar]
- APHA . Standard methods for the examination of water and waste water. 20. American Public Health Association; 1998. p. 1998. [Google Scholar]
- Aras E, Togan V, Berkun M. River water quality management model using genetic algorithm. Environmental Fluid Mechanics. 2007;7:439–450. [Google Scholar]
- ASTM . American society for testing and materials. Published by United States Environmental Protection Agency; 2000. p. 20402. [Google Scholar]
- Avdan ZY, Kaplan G, Goncu S, Avdan U. Monitoring the water quality of small water bodies using high-resolution remote sensing data. International Journal of Geo-Information (MDPI) 2019;8:553. [Google Scholar]
- Azamathulla HM, Ghani AA. Genetic programming for predicting longitudinal dispersion coefficients in streams. Water Resources Management. 2011;25:1537–1544. [Google Scholar]
- BIS. (1986). Indian standard specification for irrigation water. IS: 11624. Indian Standard Institute, India.
- Bonansea M, María CR, Lucio P, Susana F. Using multi-temporal landsat imagery and linear mixed models for assessing water quality parameters in Río Tercero Reservoir (Argentina) Remote Sensing of Environment. 2015;158:28–41. [Google Scholar]
- Bordalo AA, Teixeira R, Wiebe WJ. A water quality index applied to an international shared river basin: The case of the Douro River. Environmental Management. 2006;38:910–920. doi: 10.1007/s00267-004-0037-6. [DOI] [PubMed] [Google Scholar]
- Boyacioglu H. Utilization of the water quality index methods: A classification tool. Environmental Monitoring and Assessment. 2010;167:115–124. doi: 10.1007/s10661-009-1035-1. [DOI] [PubMed] [Google Scholar]
- Brown RM, McClelland NI, Deininder RA, Tozer RG. A water quality index- do we dare? Water Sewage Works. 1970;117(10):339–343. [Google Scholar]
- Chander G, Markham B. Revised Landsat-5 TM radiometric calibration procedures and post calibration dynamic ranges. IEEE Transactions on Geoscience and Remote Sensing. 2003;41:2674–2677. [Google Scholar]
- Chapagain SK, Pandey VP, Shrestha S, Nakamura T, Kazama F. Assessment of deep groundwater quality in Kathmandu valley using multivariate statistical techniques. Water Air Soil Pollution. 2010;210:277–288. [Google Scholar]
- Chen L, Tan CH, Kao SJ, Wang TS. Improvement of remote monitoring on water quality in a subtropical reservoir by incorporating grammatical evolution with parallel genetic algorithms into satellite imagery. Water Resources. 2008;42:296–306. doi: 10.1016/j.watres.2007.07.014. [DOI] [PubMed] [Google Scholar]
- Chu HB, Lu WX, Zhang L. Application of artificial neural network in environmental water quality assessment. Journal of Agriculture Science and Technology. 2013;15(2):343–356. [Google Scholar]
- Clifford, C. (2020). The Water in Venice, Italy's Canals Is Running Clear amid the COVID-19Lockdown—Take a Look. Retrieved 17 April 2020 from https://www.cnbc.com/2020/03/18/photos-water-in-venice-italys-canals-clear-amid-covid-19lockdown.html.
- CPCB . Reconnaissance survey of pollution load of River Kali. Central Pollution Control Board; 2012. [Google Scholar]
- Dunca, A. M. (2018). Water pollution and water quality assessment of major transboundary rivers from Banat (Romania). Journal of Chemistry (Article ID 9073763).
- Ekercin S. Water quality retrievals from high resolution IKONOS multispectral imagery: A case study in Istanbul, Turkey. Water Air Soil Pollution. 2007;183:239–251. [Google Scholar]
- Farhad Yousefabadi, L.O., Shariati, F., & Mardookhpour, A. (2013). A Comparison of water quality indices for Haraz River. Department of Environmental Engineering Lahijan Branch, Islamic, 3(3), 30–36.
- Ferreira C. Gene expression programming: a new adaptive algorithm for solving problems. Complex Systems. 2001;13(2):87–129. [Google Scholar]
- Fulazzaky MA, Seong TW, Masirin MIM. Assessment of water quality status for the Selangor River in Malaysia. Water Air Soil Pollution. 2010;205:63–77. [Google Scholar]
- Ghavidel ZZS, Montaseri M. Application of different data-driven methods for the prediction of total dissolved solids in the Zarinehroud basin. Stochastic Environmental Research and Risk Assessment. 2014;28:2101–2118. [Google Scholar]
- Gürsoy Ö, Atun R. Investigating surface water pollution by integrated remotely sensed and field spectral measurement data: A case study. Polish Journal of Environmental Studies. 2019;28:2139–2144. [Google Scholar]
- Häder DP, Banaszak AT, Villafañe VE, Narvarte MA, González RA, Helbling EW. Anthropogenic pollution of aquatic ecosystems: Emerging problems with global implications. Science of Total Environment. 2020;713:136586. doi: 10.1016/j.scitotenv.2020.136586. [DOI] [PubMed] [Google Scholar]
- Hafeez S, Wong MS, Ho HC, Nazeer M, Nichol J, et al. Comparison of machine learning algorithms for retrieval of water quality indicators in case-II waters: A case study of Hong Kong. Remote Sensing. 2018;11(684):1–26. [Google Scholar]
- Hashmi MZ, Shamseldin AY, Melville BW. Statistical downscaling of watershed precipitation using gene expression programming (GEP) Environmental Modelling and Software. 2011;26:1639–1646. [Google Scholar]
- Hoseinzadeh E, Khorsandi H, Wei C, Alipour M. Evaluation of aydughmush river water quality using the national sanitation foundation water quality index (NSFWQI), river pollution index (RPI), and forestry water quality index (FWQI) Desalination and Water Treatment. 2014;54:2994–3002. [Google Scholar]
- Hussain M, Ahmed SM, Abderrahman W. Cluster analysis and quality assessment of logged water at an irrigation project, eastern Saudi Arabia. Journal of Environment Mangement. 2008;86(1):297–307. doi: 10.1016/j.jenvman.2006.12.007. [DOI] [PubMed] [Google Scholar]
- Jindal R, Sharma C. Studies on water quality of Sutlej River around Ludhiana with reference to physicochemical parameters. Environmental Monitoring and Assessment. 2011;174(1–4):417–425. doi: 10.1007/s10661-010-1466-8. [DOI] [PubMed] [Google Scholar]
- Koza JR. Genetic programming: On the programming of computers by means of natural selection. The MIT Press; 1999. [Google Scholar]
- Kuo J, Hsieh M, Lung W, She N. Using artificial neural network for reservoir eutrophication prediction. Ecological Modelling. 2007;200:171–177. [Google Scholar]
- Li H, Liu CG, Fan J, et al. Application of back-propagation neural network for predicting chlorophyll-A concentration in rivers. China Water and Waste Water. 2009;25(5):75–79. [Google Scholar]
- Liu LW, Wang YM. Modelling reservoir turbidity using Landsat 8 satellite imagery by gene expression programming. Water (MDPI) 2019;11:1479. doi: 10.3390/w11071479. [DOI] [Google Scholar]
- Lotfinasabasl S, Gunale VR, Khosroshahı M. Applying geographic information systems and remote sensing for water quality assessment of mangrove forest. ActaEcologicaSinica. 2018;38:135. [Google Scholar]
- Markogianni V, Dimitriou E, Karaouzas I. Water quality monitoring and assessment of an urban Mediterranean lake facilitated by remote sensing applications. Environmental Monitoring and Assessment. 2014;186(8):5009–5026. doi: 10.1007/s10661-014-3755-0. [DOI] [PubMed] [Google Scholar]
- Marquez LCG, Bejarano FMT, Espınoza ACT, Rodríguez IRH. Use of LANDSAT 8 images for depth and water quality assessment of El Guájaro reservoir, Colombia. Journal of South American Earth Sciences. 2018;82:231. [Google Scholar]
- Martí P, Shiri J, Duran-Ros M, Arbat G, De Cartagena FR, Puig-Bargués J. Artificial neural networks vs. gene expression programming for estimating outlet dissolved oxygen in micro-irrigation sand filters fed with effluents. Computers and Electronics in Agriculture. 2013;99:176–185. [Google Scholar]
- Maurya PK, Malik DS. Distribution of heavy metals in water, sediments and fish tissue (Heteropneustisfossilis) in Kali River of western UP India. International Journal of Fisheries and Aquatic Studies. 2016;4(2):208–215. [Google Scholar]
- MilanovićPešić A, Brankov J, MilijaševićJoksimović D. Water quality assessment and populations’ perceptions in the National park Djerdap (Serbia): Key factors affecting the environment. Environment Development and Sustainability. 2020;22:2365–2383. doi: 10.1007/s10668-018-0295-8. [DOI] [Google Scholar]
- Mishra S, Kumar A, Yadav S, Singhal MK. Assessment of heavy metal contamination in Kali river, Uttar Pradesh, India. Journal of Applied and Natural Science. 2015;7(2):1016–1020. [Google Scholar]
- Mohamed E, Ioannis G, Anas O, Jarbou B, Petros G. Assessment of water quality parameters using temporal remote sensing spectral reflectance in arid environments Saudi Arabia. Water. 2019;11(3):556. [Google Scholar]
- Mohammadpour R, Shaharuddin S, Chang C, Zakaria N, Ghani AA, Chan N. Prediction of water quality index in constructed wetlands using support vector machine. Environmental Science and Pollution Research. 2015;22:6208–6219. doi: 10.1007/s11356-014-3806-7. [DOI] [PubMed] [Google Scholar]
- Mohammadpour R, Shaharuddin S, Zakaria NA, Ghani AA, Vakili M, Chan NW. Prediction of water quality index in free surface constructed wetlands. Environmental Earth Sciences. 2016;75:139. doi: 10.1007/s12665-015-4905-6. [DOI] [Google Scholar]
- Mondal M, Satpati L. Human intervention on river system: a control system—A case study in Ichamati River, India. Environment Development and Sustainability. 2020;22:5245–5271. doi: 10.1007/s10668-019-00423-3. [DOI] [Google Scholar]
- Nabizadeh R, Amin MV, Alimohammadi M, Naddafi K, Mahvi AH, Yousefzadeh S. Development of innovative computer software to facilitate the setup and computation of water quality index. Journal of Environmental Health Science and Engineering. 2013;11:1. doi: 10.1186/2052-336X-11-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nas B, Ekercin S, Karabork H, Berktay A, Mulla DJ. An application of Landsat-5TM image data for water quality mapping in lake Beysehir, Turkey. Water Air Soil Pollution. 2010;212:183–197. [Google Scholar]
- Nasri M. Application of Artificial Neural Networks (ANNs) in prediction models in risk management. World Applied Science Journal. 2010;10(12):1493–1500. [Google Scholar]
- Nathan NS, Saravanane R, Sundararajan T. Application of ANN and MLR models on groundwater quality using CWQI at Lawspet, Puducherry in India. Journal of Geoscience and Environment Protection. 2017;5:99–124. doi: 10.4236/gep.2017.53008. [DOI] [Google Scholar]
- Ni Q, Wang L, Zheng B, Sivakumar M. Evolutionary algorithm for water storage forecasting response to climate change with small data sets: The Wolonghu Wetland, China. Environmental Engineering and Science. 2012;29:814–820. [Google Scholar]
- Prabu PC, Wondimu L, Tesso M. Assessment of water quality of Huluka and Alaltu Rivers of Ambo, Ethiopia. Journal of Agricultural Science and Technology. 2011;13(1):131–138. [Google Scholar]
- Rajurkar MP, Kothyari UC, Chaube UC. Modelling of Daily Rainfall runoff relationship with artificial neural network. Journal of Hydrology. 2004;285:96–113. [Google Scholar]
- Ramakrıshnaıah CR, Sadashıvaıah C, Ranganna G. Assessment of water quality index for the groundwater in Tumkur Taluk, Karnataka State, India. E-Journal of Chemistry. 2009;6(2):523–530. [Google Scholar]
- Reynolds CS, Maberly SC. A simple method for approximating the supportive capacities and metabolic constraints in lakes and reservoirs. Freshwater Biology. 2002;47(6):1183–1188. [Google Scholar]
- Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back propagating errors. Nature. 1986;323:533–536. [Google Scholar]
- Said S, Hussain A. Pollution mapping of Yamuna river segment passing through Delhi using high resolution GeoEye-2 imagery. Applied Water Science. 2019;9:46. doi: 10.1007/s13201-019-0923-y. [DOI] [Google Scholar]
- Said S, Kothyari UC, Arora MK. ANN-based soil moisture retrieval over bare and vegetated areas using ERS-2 SAR data. Journal of Hydrologic Engineering. 2008;13(6):461–475. [Google Scholar]
- Sargaonkar A, Deshpande V. Development of an overall index of pollution for surface water based on a general classification scheme in Indian context. Environmental Monitoring and Assessment. 2003;89:43–67. doi: 10.1023/a:1025886025137. [DOI] [PubMed] [Google Scholar]
- Sharaf EIDE, Zhang Y, Suliman A. Mapping concentrations of surface water quality parameters using a novel remote sensing and artificial intelligence framework. International Journal of Remote Sensing. 2017;38(4):1023–1042. [Google Scholar]
- Sharma G, Said S, Hussain A. Water quality mapping of Yamuna River stretch passing through Delhi sate using high resolution GeoEye-2 imagery. International Journal of Applied Geospatial Research. 2018;9(4):23–35. [Google Scholar]
- Singh G, Patel N, Jindal T, Srivastava P, Bhowmik A. Assessment of spatial and temporal variations in water quality by the application of multivariate statistical methods in the Kali River, Uttar Pradesh, India. Environmental Monitoring and Assessment. 2020;192:394. doi: 10.1007/s10661-020-08307-0. [DOI] [PubMed] [Google Scholar]
- Sirohi S, Sirohi SPS, Tyagi PK. Impact of industrial effluents on water quality of Kali River in different locations of Meerut, India. Journal of Engineering Technology and Research. 2014;6:4347. [Google Scholar]
- Song KS, Li L, Li S, Tedesco L, Hall B, Li LH. Hyperspectral remote sensing of total phosphorus (TP) in three central Indiana water supply reservoirs. Water Air Soil and Pollution. 2012;223:1481–1502. [Google Scholar]
- Srinivasamoorthy K, Chidambaram M, Prasanna MV, Vasanthavigar M, John Peter A, Anandhan P. Identification of major sources controlling Groundwater Chemistry from a hard rock terrain—A case study from Mettur taluk, Salem district, Tamilnadu. India. Journal of Earth System Sciences. 2008;117(1):49–58. [Google Scholar]
- Stone, M. (2020). Carbon emissions are falling sharply due to coronavirus. But not for long. Retrieved 17 April 2020 from https://www.nationalgeographic.com/science/2020/04/co-ronavirus-causing-carbon-emissions-to-fall-but-not-for-long/.
- Suneetha M, SyamaSundar B, Ravindhranath K. Calculation of water quality index (WQI) to assess the suitability of groundwater quality for drinking purposes in Vinukonda Mandal, Guntur District, Andhra Pradesh, India. Journal of Chemical and Pharmaceutical Research. 2015;7(9):538–545. [Google Scholar]
- Syahreza, S., MatJafri, M. Z., & Lim, H. S. (2012). Water quality assessment in Kelantan delta using remote sensing technique. Proceedings of SPIE 8542, Electro-Optical Remote Sensing, Photonic Technologies and Applications VI, 85420X.https://doi.org/10.1117/12.978931
- Wang L, Li X, Cui W. Fuzzy neural networks enhanced evaluation of wetland surface water quality. International Journal of Computation and Applied Technology. 2012;44:235–240. [Google Scholar]
- Wang Z, Su Y, Jin S, Shen W, Ren J, Zhang X, Clark JH. A novel unambiguous strategy of molecular feature extraction in machine learning assisted predictive models for environmental properties. Green Chemistry. 2020;22:3867–3876. [Google Scholar]
- Wang Z, Su Y, Shen W, Jin S, Clark JH, Ren J, Zhang X. Predictive deep learning models for environmental properties: the direct calculation of octanol–water partition coefficients from molecular graphs. Green Chemistry. 2019;21:4555–4565. [Google Scholar]
- Water Programme. (2007). Global drinking water quality index development and sensitivity analysis. In Report of United Nations Environment Programme and Global Environment Monitoring System. (GEMS)/Water Programme.
- Waxter, M. T. (2014). Analysis of Landsat satellite data to monitor water quality parameters in Tenmile Lake, Oregon. MSc. Thesis, Portland State University.
- Xu TY, Qin XS. Solving water quality management problem through combined genetic algorithm and fuzzy simulation. Journal of Environmental Information. 2013;22:39–48. [Google Scholar]
- Yao H, Ni T, Zhang T. Estimation of phosphorus flux into the sea through one reversing river using continuous turbidities and water quality modeling. Environment Development and Sustainability. 2020;22:4251–4265. doi: 10.1007/s10668-019-00382-9. [DOI] [Google Scholar]
- Zakaria NA, Azamathulla HM, Chang CK, Ghani AA. Gene expression programming for total bed material load estimation—A case study. Science of the Total Environment. 2010;408:5078–5085. doi: 10.1016/j.scitotenv.2010.07.048. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Pulliainen JT, Koponen SS, Hallikainen MT. Water quality retrievals from combined Landsat TM Data and ERS-2 SAR data in the Gulf of Finland. IEEE Transactions on Geoscience and Remote Sensing. 2003;41:622–629. [Google Scholar]
- Zhao F, Zhu FQ, Feng ZK. Study on water body information extraction method based on ZY-3 Imagery. Bulletin of Surveying and Mapping. 2014;3:007. [Google Scholar]
- Zhu L. Water quality analysis and evaluation of current situation in the riparian of west lake Taihu in Yixing. Nanjing Forestry University; 2013. [Google Scholar]