Compliant 3D frameworks instrumented with strain sensors for characterization of millimeter-scale engineered muscle tissues

Significance

Tissue-on-chip systems offer important capabilities in engineering of living tissues for diverse biomedical applications in disease model studies, drug screening, and regenerative medicine. Conventional approaches use two-dimensional layouts that cannot suppport interfaces to geometrically complex three-dimensional (3D) tissue constructs in a deterministic fashion. Here, we present concepts in engineering systems that allow intimate contact with and stable mechanical coupling to 3D tissues for high-precision measurements of tissue contractility, as demonstrated in 3D, millimeter-scale engineered skeletal muscle tissues. These compliant, 3D frameworks instrumented with advanced sensors and other functional electronics, may significantly enhance the capabilities of tissue-on-chip systems.

Abstract

Tissue-on-chip systems represent promising platforms for monitoring and controlling tissue functions in vitro for various purposes in biomedical research. The two-dimensional (2D) layouts of these constructs constrain the types of interactions that can be studied and limit their relevance to three-dimensional (3D) tissues. The development of 3D electronic scaffolds and microphysiological devices with geometries and functions tailored to realistic 3D tissues has the potential to create important possibilities in advanced sensing and control. This study presents classes of compliant 3D frameworks that incorporate microscale strain sensors for high-sensitivity measurements of contractile forces of engineered optogenetic muscle tissue rings, supported by quantitative simulations. Compared with traditional approaches based on optical microscopy, these 3D mechanical frameworks and sensing systems can measure not only motions but also contractile forces with high accuracy and high temporal resolution. Results of active tension force measurements of engineered muscle rings under different stimulation conditions in long-term monitoring settings for over 5 wk and in response to various chemical and drug doses demonstrate the utility of such platforms in sensing and modulation of muscle and other tissues. Possibilities for applications range from drug screening and disease modeling to biohybrid robotic engineering.

Tissue-on-chip (TOC) technologies, also known as organ-on-chip or microphysiological systems, can recapitulate native tissue environments in vitro. These engineered platforms can be used for research in drug discovery, disease development, and regenerative medicine as alternatives to animal and traditional cell culture models (1). Recent reports describe TOC platforms that capture certain essential features of the lung, heart, liver, and brain (2–7). A frontier is in the development of architectures that mimic the three-dimensional (3D) layouts of native tissues, with the ability to monitor and control natural biological and physiological processes across a broad range of electrical, biochemical, and mechanical cues (8, 9). Three-dimensional engineered tissues can reproduce essential structural and functional features of natural biological systems with much greater relevance to living organisms than traditional two-dimensional (2D) cell cultures. Most existing TOC platforms adopt simple planar geometries, due partly to the limited ability to build functional 3D architectures as scaffolds and functional interfaces. While advances in flexible electronics allow for devices in the form of patches (4, 10) or meshes (11–13) that can roll or fold to interface with surfaces of engineered tissues, challenges remain in creating deterministic 3D electronic scaffolds as interfaces to engineered thick tissues in a controlled, 3D spatiotemporal manner. Specific challenges are in precisely defining the 3D locations and/or spatial arrangements of functional electronics for accurate monitoring and regulation of tissue functions. Recent efforts toward these goals include the development of 3D multifunctional electronic scaffolds formed by mechanically guided assembly, as demonstrated in the recording of extracellular potentials of small dorsal root ganglion neuron networks and cardiac cell cultures formed on 3D scaffolds (14, 15) and in electrical stimulation and drug release (15).

These technologies offer promising avenues for biological research, but they are not, however, designed for interfaces to grown 3D tissues, nor do they provide mechanical support or sensing of forces or displacements of relevance to smooth, skeletal, or cardiac muscle constructs. Skeletal muscle, in particular, is an interesting target as the most abundant tissue in the human body, comprising ∼40% of the total mass (16). Skeletal muscle-on-chip platforms are important in the study of Duchenne muscular dystrophy disease, and they offer potential for drug screening in this and other contexts (17–19). In addition, 3D engineered skeletal muscles under electrical and optical control can serve as biohybrid actuators in soft robotics for walking, swimming, or pumping functions (20–22). Characterization of skeletal muscle tissue contractility typically relies on image-based methods to monitor motions against soft structures such as elastomeric pillars or hydrogel skeletons (6, 17, 18, 20, 23–26). Mechanical models based on classic beam theories connect these motions to forces. Uncertainties in the constitutive properties of the materials and the geometries of the structures, together with limits in imaging resolution, video frame rate, and imaging processing techniques, contribute to inaccuracies in the measurements.

Here, we introduce a class of microfabricated 3D frameworks that can be created in precisely engineered shapes and geometries as mechanical interfaces to 3D skeletal muscle tissues for precise measurements of the spatial and temporal contractile forces associated with optical stimulation under a wide range of conditions. These systems exploit recent advances in mechanically guided assembly techniques to form compliant, 3D frameworks instrumented with strain sensors that connect to external control electronics. A key feature of the engineering approach is that it is compatible with well-developed planar electronic, optoelectronic, photonic, and microelectromechanical systems. The shape-matched 3D geometries and mechanically compliant layouts of these frameworks enable intimate contact and stable mechanical coupling to the tissues of various 3D geometries. Measurements of the contractile forces generated by 3D optogenetically active muscle rings and comparisons with results of conventional optical microscopy demonstrate the utility of these technologies in 3D tissue engineering.

Results

Design, Fabrication, and Characterization of 3D Frameworks Instrumented with Strain Sensors.

The design and fabrication approaches exploit recent advances in mechanically guided assembly methods that enable geometric transformation of functional materials from planar layouts into 3D architectures with well-defined layouts and wide-ranging options in designs (27–29). The process starts with formation of a 2D precursor structure that includes a polymer substrate (polyimide [PI], 12.5 µm in thickness), a thin lithographically patterned film of metal (chromium/gold, 10/100 nm in thickness), and a top encapsulation layer (parylene C, 5 µm in thickness) (a basic design appears in Fig. 1A). The metal pattern defines a collection of resistive strain sensors and a set of electrical interconnects. Specifically, narrow (5 µm in width) serpentine traces form sensing elements of strain sensors arranged in two groups located on the two sides of the symmetric 2D precursor. Each group forms an independent sensing unit that consists of four strain sensors (R₁ through R₄) with two on each side of a mesoscale “post” structure that rises out of the plane. A laser ablation step defines the shape of this structure and other lateral features of the 2D precursor. Deposition of a bilayer of Ti/SiO₂ on the backside of the precursor through a shadow mask forms sites for bonding to a prestrained elastomer substrate (polydimethylsiloxane [PDMS]). Releasing the prestrain initiates a buckling process that transforms the 2D precursor into a 3D configuration that consists of two buckled posts each surrounded by four strain sensors. The designs of these posts facilitate integration with 3D engineered muscle tissues, as described subsequently. Details of the fabrication and assembly processes appear in SI Appendix, Fig. S1 and Materials and Methods. SI Appendix, Fig. S2 shows the layout of the 2D precursor. This overall scheme provides access to a wide range of complex 3D architectures that embed various functional components. Fig. 1B shows a complex, spider-like 3D configuration (2D precursor layout shown in SI Appendix, Fig. S3) with sensing functionality similar to that of the basic design in Fig. 1A, highlighting the design versatility. SI Appendix, Fig. S4 and Movie S1 illustrate the process of 2D to 3D shape transformation simulated by finite element analysis (FEA) (Materials and Methods). The overall similarity of experimental and computational shapes and the good agreement between key dimensional parameters (SI Appendix, Fig. S5) validate the use of FEA as a tool to guide the structure design.

Fig. 1.

Design, sensing mechanism, and characterization of compliant 3D frameworks instrumented with strain sensors. (A) Optical image of a 2D precursor used for assembly of this 3D system, consisting of three layers (parylene, Cr/Au, and PI, Right Inset) with embedded strain sensors (Bottom Inset) in the metal layer. (B) FEA results and experimental images shown in perspective view (Top) and side view (Bottom) for a complex 3D framework designed to highlight the versatility of the assembly approach. (C) Optical image highlighting the strain sensors near the base of a post. (D) Computed change in strain in response to an indentation displacement of 10 µm from one side of a post, featuring two strain sensors (resistors R₃ and R₄) on opposite sides. (E) Schematic illustration of a Wheatstone bridge circuit consisting of four strain sensors. (F) Relative change in the resistance of a parylene/gold/PI strain sensor upon cyclic stretching (Inset: experimental setup of the tensile test) to 0.4% uniaxial strain. The results define the gauge factor. (G) Computed and experimental results for the indentation force and the corresponding change in output voltage as functions of the indentation displacement. (Scale bars: 2 mm in A [50 µm in Inset], 5 mm [Top] and 2 mm [Bottom] in B, 1 mm in C.)

The locations of the four resistive strain sensors that surround the buckled 3D posts serve critical roles in the sensing process. Fig. 1C highlights two strain sensors strategically located on one side of the 3D post. Roughly half of each strain sensor resides within the corresponding bonding site, stably adhered to the substrate by covalent bonds, while the other half delaminates upon buckling as a result of the comparatively weak van der Waals interactions. The result defines a curved profile that supports a flat, roof-like region. All of the strain sensors are in a state of compressive strain (absolute value $-{\epsilon }_{l,0}$; SI Appendix, Fig. S6A) along their longitudinal directions because the metal layer lies above the neutral mechanical plane and the local curvature is negative (concave). The maximum equivalent strain (SI Appendix, Fig. S6B) in the gold layer that arises from the buckling process is within its fracture limit (30, 31). The peak strain in the gold appears close to the boundary of bonded/delaminated regions. While this peak value may slightly exceed the elastic threshold of gold thin films (32), a low level of plastic deformation in these local regions has negligible influence on the ability to measure contractile forces accurately. Detailed discussion of this issue appears in SI Appendix, Note S1.

In this 3D geometry, the strain sensors are sensitive to small forces applied horizontally to the buckled posts due to their small bending stiffness. Fig. 1D shows the computed change in the strain of the metal layer ($\mathrm{\Delta }\epsilon ={\epsilon }_l-{\epsilon }_{l,0}$, ∼0.01%) induced by a horizontal force (0.18 mN) applied from the left side of the post. This force results in a slight bending of the post toward the right, causing a decrease in the absolute values of the compressive strains of R₁ and R₃, and an increase in the absolute values of the compressive strains of R₂ and R₄ (Fig. 1D). A full Wheatstone bridge circuit converts the changes in the resistances of R₁ through R₄ into a voltage V_o (Fig. 1E) according to $V_{\mathrm{o}}=\left(\frac{R_3}{R_3+R_4}-\frac{R_2}{R_1+R_2}\right)V_e$, where V_e is the excitation voltage.

Establishing quantitative correlation between V_o/V_e and the force applied to the posts involves measurement of the gauge factors of the strain sensors (SI Appendix, Note S2) through tensile tests on planar devices (parylene/metal/PI) fabricated using the methods described above (Fig. 1F). For uniaxial tensile strains between 0.1 and 0.5%, these sensors exhibit linear responses to strain, as expected for gold thin films under strains less than 1% (33), with gauge factors of 2.68 ± 0.04 (SI Appendix, Fig. S7). Use of this gauge factor in mechanical models yields a relationship between structural deformations and the electrical readouts. Indentation tests on 3D frameworks instrumented with strain sensors provide direct comparisons of the results of FEA computations and experiments. The measurements involve force-displacement curves from the indenter and synchronized readout of voltage responses from the strain sensors (SI Appendix, Fig. S8). The data show a linear dependence between both the force and the change in output voltage with indentation displacement across a range of 30 µm (Fig. 1G). The measurements match the results of FEA.

Integration of Skeletal Muscle Rings with Compliant, Instrumented 3D Frameworks.

The instrumented 3D frameworks described above adopt features tailored for interaction with millimeter-scale ring structures formed using mouse skeletal muscle tissues according to procedures described elsewhere (24, 34). The steps for preparing such rings and integrating them onto the 3D frameworks appear schematically in Fig. 2A. The process starts with delivery of optogenetic myoblasts seeded in an extracellular material solution into a soft mold of PDMS (SI Appendix, Fig. S9). Transfection of blue light–sensitive ion channel Channelrhodopsin-2 (ChR2), namely, ChR2 (H134R), to C2C12 murine myoblasts follows lentiviral transduction protocols for optogenetically active skeletal muscle tissues (24, 34). The seeded cell/gel solution solidifies through a thrombus reaction to form a muscle ring inside the mold. After differentiation of the myoblasts into myotubes for 5 d, manual transfer of the muscle ring onto the 3D framework completes the integration. The muscle ring wraps around the two posts (2.85 mm in spacing) in contact with the sidewalls (Fig. 2 B and C). The compliance of the 3D framework is engineered to provide stable mechanical coupling to the muscle ring in order to maintain stable muscle ring location and orientation for measurement and modeling purposes, while allowing deformations of the 3D posts. The top surfaces of the posts include two pairs of microscale “flaps” (480 µm in length, 450 µm in width) designed to retain the muscle ring during periods of spontaneous contractions. Additional images and FEA results appear in SI Appendix, Fig. S10.

Fig. 2.

Integration of an engineered skeletal muscle ring onto a compliant 3D framework instrumented with strain sensors. (A) Schematic illustration of the process for forming an optogenetic skeletal muscle ring by molding of Ch2 C2C12 myoblasts and for integrating the resulting ring onto a 3D framework for sensing. (B) Optical images (side view) showing the 3D framework before (Top) and after (Bottom) integration with a muscle ring. (C) Optical image of the integration of a skeletal muscle ring with the 3D framework. (D) Confocal image of an optogenetic muscle ring integrated with the 3D framework. The results highlight alignment of the myotubes (Inset), visualized with an antibody against nuclei (DAPI; blue), mature myosin (MF-20; green), and α-actinin protein (red). (E) Perspective view bright field (BF) (Left) and fluorescence images (Middle and Right) after staining to highlight the integration of an optogenetic muscle ring with a 3D framework at a location near one end of a post. (Scale bars: 2 mm in B and C, 1 mm in D [50 µm in Inset], 500 µm in E.)

The posts provide a uniaxial constraint to facilitate cell alignment during compaction of the muscle ring. In this way, the myotubes mature in a macroenvironment that leads to native organization of functional skeletal muscle. Confocal images of the muscle ring integrated with the 3D framework highlight the longitudinal alignment of the myotubes with the muscle ring wrapped around the posts, visualized with an antibody against α-actinin protein (red), nuclei (4′,6-diamidino-2-phenylindole [DAPI]; blue) and mature myosin (MF-20; green) in Fig. 2D and SI Appendix, Fig. S11. Scanning electron microscopy (SEM) images of a dehydrated muscle ring on this same platform also show a high degree of myofiber alignment (SI Appendix, Fig. S12). Bright field and fluorescent images in 3D perspective view highlight the integration (Fig. 2E and SI Appendix, Fig. S13).

Optical Stimulation of Optogenetic Muscle Rings Integrated onto 3D Frameworks.

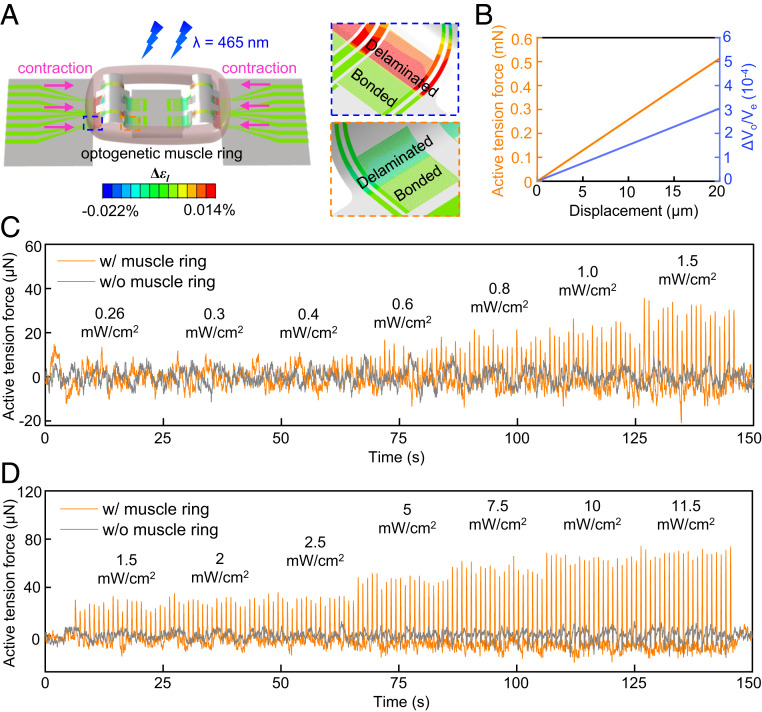
Muscle rings formed in this manner contract in response to optical (λ = 465 nm) stimulation to generate active contractions. The alignment of the myotubes gives rise to anisotropic muscle ring contraction in response to optical stimulation with contraction mainly in the tangential direction of the ring, as described in SI Appendix, Note S3 and Fig. S14. FEA models validated by the indentation tests can yield accurate relationships between the contractile force, the contractile displacement, and the electrical readout of the sensors. A passive tension force develops in the muscle ring upon integration of the muscle ring onto the sensor due to expected effects of mechanical coupling. Optical stimulation induces additional, dynamic active tension forces as a result of the muscle responsivity to optical stimulation. These responses represent the primary focus of studies reported here. FEA calculations of the active and passive components of the forces appear in SI Appendix, Note S4 and Fig. S15. Fig. 3A shows the change in the strain of the metal sensing layer induced by muscle contraction with a contractile displacement of 10 µm on each side of the posts toward the center. The computed active tension forces and electrical readout both exhibit linear relationships with the contractile displacement (Fig. 3B) within distances of up to 20 µm. These results enable quantitative conversion of sensor responses to contractile displacements and active tension forces.

Fig. 3.

Measurements of active tension forces produced by an optogenetic muscle ring in response to optical stimulation. (A) Computed change in strain of the 3D framework in response to optical stimulation (contractile displacement: 10 µm), featuring two strain sensors on opposite sides of a post (inside dashed lines). (B) Computed active tension forces of the muscle ring and the corresponding relative output voltage of the strain sensor as functions of the contractile displacement. (C) Active tension forces with and without integration with an optogenetic skeletal muscle ring, in response to optical stimulation at intensities of 0.26, 0.3, 0.4, 0.6, 0.8, 1.0, and 1.5 mW·cm⁻² with 1 Hz pulse frequency and 50 ms pulse width. (D) Active tension forces with and without integration with an optogenetic skeletal muscle ring, in response to optical stimulation at intensities of 1.5, 2, 2.5, 5, 7.5, 10, and 11.5 mW·cm⁻² with 1 Hz pulse frequency and 50 ms pulse width.

A custom experimental setup inside a temperature-controlled (37 °C) chamber supports optical stimulation with controlled intensities and time dependencies via an optical fiber (SI Appendix, Fig. S16). An inverted microscope allows for optical imaging through the transparent PDMS substrate that supports the device. A comparison of the measured active tension forces with and without a muscle ring integrated onto a representative 3D framework appears in Fig. 3 C and D. The sensor readout V_o for this study, after digitally filtering out (5 Hz low-pass filter) high-frequency noise appears in SI Appendix, Fig. S17. Applying an additional high-pass filter (0.1 Hz) eliminates baseline drift caused by fluctuations of the external voltage supply for purposes of determining the peak amplitudes as measurements of the active tension forces induced by muscle contractions. The computed amplitudes of peaks from the sensor without the muscle ring remain within 10 µN, largely invariant with increasing optical intensity. By contrast, sensors in 3D frameworks with muscle rings show increasing active tension forces with 1 Hz peaks synchronized to the stimulation frequency. The active tension forces increase with strength of muscle contraction and corresponding increases in the optical intensity. The data indicate that noise from photothermal and ambient effects is negligible. A resistive temperature sensor integrated into a planar region of the 3D framework captures changes in temperature adjacent to (∼1.8 mm distance) the strain sensors (temperature calibration method appears in SI Appendix, Note S5). The results provide estimates of photothermal effects that could arise during optical stimulation, as discussed in SI Appendix, Fig. S18 and Note S5.

A comparison of results obtained in the manner described above with those captured by optical microscopy highlights the key differences. Here, electrical sensor readout occurs simultaneously with video recording through an inverted microscope. FEA of the mechanics of the 3D frameworks (Fig. 3B) converts measured contractile displacements to active tension forces. The trends in forces and motions correlate with optical intensity from 1.5 to 11.5 mW/cm², with similar peak amplitudes (Fig. 4A and Movie S2). A direct comparison involves contractile displacements computed based on the readout of the instrumented 3D framework and measured by optical microscopy. The results are consistent for this range of optical intensities (SI Appendix, Fig. S19), thereby establishing the validity of the approaches in 3D mechanical sensing introduced here. Close inspection of the measured active tension forces in Fig. 4B highlight important distinctions between these two schemes: The instrumented 3D framework records continuous and consistent peaks in the active tension forces due to high sampling rates (100 kS/s); by contrast, optical microscopy yields inconsistent results due to comparatively low frame rates (14.9 frames per second [fps]) of the standard video recording setups used here. The 100 kS/s sampling rate of the 3D framework corresponds to an equivalent video recording frame rate of 10⁵ fps, which can be difficult to achieve even for advanced high-speed optical imaging systems.

Fig. 4.

Comparison of active tension force measurements by instrumented 3D frameworks and by optical microscopy. (A) Comparison of the active tension forces of an optogenetic skeletal muscle ring measured by an instrumented 3D framework and by optical microscopy, in response to optical stimulation at intensities of 1.5, 2, 2.5, 5, 7.5, 10, and 11.5 mW·cm⁻² with 1 Hz pulse frequency and 50 ms pulse width. (B) Selected time frames of the active tension forces measured in A. (C) Amplitudes of all the active tension peaks measured by an instrumented 3D framework and optical microscopy under optical stimulation with frequencies of 0.5, 1, 2, 4, and 6 Hz. (D) Comparison of the measured peak frequency from the 3D framework and optical microscopy as a function of the optical stimulation frequency. (E) Comparison of measured amplitudes of active tension forces from the 3D framework and optical microscopy as a function of the optical stimulation frequency. Error bars correspond to the calculated SD from the peaks of the activen tension forces shown in C. (F) Active tension forces measured by the 3D framework and optical microscopy at a stimulation frequency of 6 Hz showing the advantages of the 3D framework in measurement accuracy as compared with optical microscopy. (G) Comparison of active tension forces of an optogenetic skeletal muscle ring measured by a 3D framework and optical microscopy, in response to optical stimulation with pulse widths of 1, 2, 3, 5, 10, 20, 30, and 50 ms.

These advantages in measurement speed are particularly important for monitoring high-frequency muscle contractions. Fig. 4C shows the amplitudes of active tension forces of an optogenetic muscle ring (1 d after integration) measured by an instrumented 3D framework and by optical microscopy (Movie S3) for optical stimulation at frequencies from 0.5 Hz to 6 Hz with a fixed optical intensity (11.5 mW·cm⁻²) and pulse width (50 ms). At stimulation frequencies of 0.5 Hz and 1 Hz, both sensor readout and optical microscopy capture all of the peaks and show similar amplitudes. Discrepancies may result from slight deviations in the shapes and contact areas of the muscle ring and in uncertainties in imaging and postimage processing. Large errors in the amplitudes (measurement period 20 s) start to appear in optical microscopy at and above frequencies of 2 Hz. The peak frequencies also begin to deviate from the stimulation frequencies for values above 4 Hz. These issues do not appear in data from the sensor (Fig. 4D). Forces measured by both methods decrease as the stimulation frequency increases (Fig. 4E), consistent with incomplete muscle relaxation between adjacent stimuli (34). Measurements obtained with the 3D framework are consistently larger than those with optical microscopy, again due mainly to the limited frame rate. Fig. 4F and SI Appendix, Fig. S20 show magnified waveforms of the active tension forces measured by the two methods, clearly demonstrating advantages in electronic sensing.

The duration of optical stimulation also influences the level of muscle contraction. Fig. 4G presents the active tension forces of an optogenetic muscle ring (1 d after integration) as a function of pulse width for fixed intensity (11.5 mW·cm⁻²) and frequency (1 Hz) measured by the 3D framework and optical microscopy (Movie S4). The forces increase significantly with increased pulse width from t_w = 1 to 20 ms before reaching a plateau. This behavior suggests that the time threshold for activating full muscle contraction is roughly 20 ms, consistent with previous reports on optogenetic stimulation of skeletal muscles from transgenic mice expressing the ChR2 (35). Detailed comparisons appear in SI Appendix, Fig. S21.

Long-Term Studies.

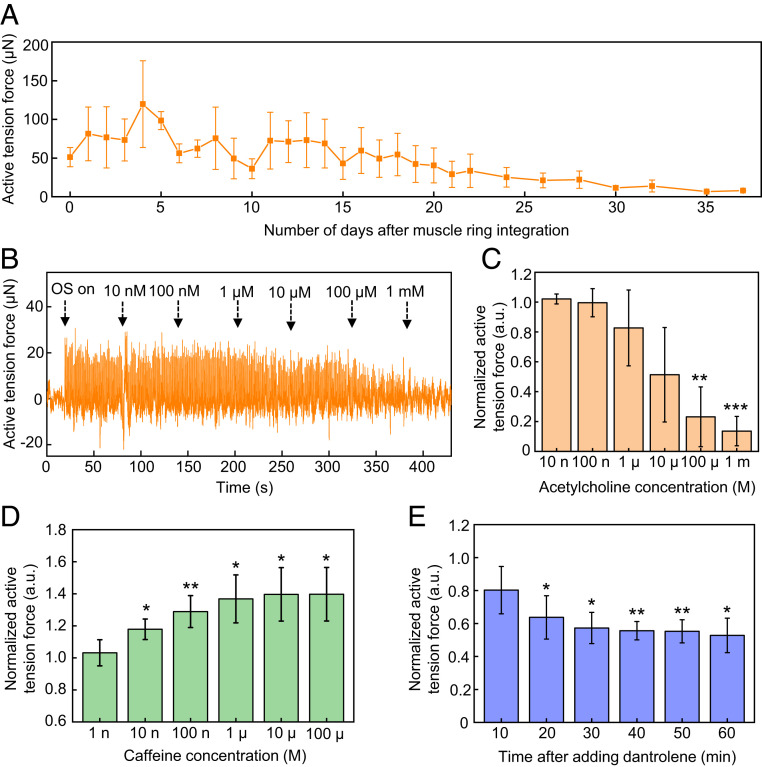
Three-dimensional frameworks are well suited for long-term monitoring. Fig. 5A presents results recorded over 37 d after muscle ring integration. Upon integration, the active tension force increases to an average peak value of ∼120 µN within 4 d (on day 9 after differentiation) as a result of maturation for myotubes during differentiation. Subsequently, the magnitude gradually decays over a period of ∼4 wk caused by the steady degradation of 3D tissues due to proteases secreted by the cells (36, 37). SI Appendix, Fig. S22 shows a series of optical images before integration, after selected days of integration, and after removal of the muscle ring. After removal, the posts return to their original shapes. The distances between the posts before integration and after removal are 2.86 mm and 2.81 mm, respectively, consistent with an elastic, reversible response. Optical stimulation of a new muscle ring on a 3D framework after the long-term studies shows similar active tension forces to those at the beginning of the long-term studies (SI Appendix, Fig. S23), verifying the stability of the 3D frameworks. Tests of viability of the muscle ring on the instrumented 3D framework, determined by an assay using 3-(4,5-dimethylthiazol-2-yl)-5-(3-carboxymethoxyphenyl)-2-(4-sulfophenyl)-2H-tetrazolium (MTS), show results identical to those for a ring cultured in a PDMS mold, for durations up to 5 wk after integration onto the 3D framework (SI Appendix, Note S6 and Fig. S24).

Fig. 5.

Development of active tension forces over time and responses to introduction of drugs. (A) Development of the active tension forces under optical stimulation measured by optogenetic muscle rings integrated with compliant 3D frameworks instrumented with strain sensors over a period of 37 d after integration. Error bars correspond to the calculated SD from three measurements. (B) Active tension forces measured by a representative optogenetic muscle ring in response to optical stimulation with simultaneous addition of acetylcholine at different working concentrations. (C) Normalized active tension forces of optogenetic muscle rings in response to optical stimulation with simultaneous addition of acetylcholine at different working concentrations. Error bars correspond to the calculated SD from four measurements. (D) Normalized active tension forces from optogenetic muscle rings in response to optical stimulation with simultaneous addition of caffeine at different working concentrations. Error bars correspond to the calculated SD from four measurements. (E) Change of normalized active tension forces of optogenetic muscle rings in response to optical stimulation with addition of 100 µM working concentration of dantrolene. Error bars correspond to the calculated SD from three measurements. Statistical significance: *P < 0.05, **P < 0.01, ***P < 0.001.

Drug Studies.

The open architectures of these 3D frameworks create additional opportunities such as those in dose–response studies of drugs that influence muscle contractile strength. Experiments with acetylcholine, caffeine, and dantrolene demonstrate some possibilities. Acetylcholine is a representative neurotransmitter, and caffeine is a chemical agent. Both interact with skeletal muscle (38). Dantrolene is a commercial drug that prevents malignant hyperthermia as a skeletal muscle relaxant by binding to the RYR1 receptor and inhibiting Ca²⁺ release from the sarcoplasmic reticulum (39).

Fig. 5B shows the active tension forces of an optogenetic muscle ring under 1 Hz pulsed optical stimulation (11.5 mW·cm⁻² intensity and 50 ms pulse width) during addition of acetylcholine at 100 nM to 1 mM working concentrations. Fig. 5C presents the normalized active tension force, defined as the ratio of the active tension force after adding acetylcholine with each concentration to the initial active tension force before adding acetylcholine. The results indicate that acetylcholine with concentration higher than 1 μM causes larger decreases in active tension forces. Statistical significances appear in active tension forces after addition of 100 μM and 1 mM with 0.0045 and 0.0004 for P values, respectively, compared with those before adding acetylcholine. A conclusion from these studies is that ∼10 to 100 µM is likely the threshold acetylcholine concentration for effectively preventing muscle relaxation, corresponding to inhibition of periodic muscle contractions caused by optical stimulation. Acetylcholine is a neurotransmitter secreted by motor neurons through the neuromuscular junction to cause skeletal muscle contraction. After muscle contraction, excess acetylcholine that remains at the neuromuscular junction can be hydrolyzed by the acetylcholinesterase enzyme to relax the muscle. High-concentration acetylcholine overwhelming the capacity to hydrolyze the neurotransmitter by acetylcholinesterase in this system leads to the accumulation of acetylcholine in the skeletal muscle, thereby paralyzing muscle contraction.

Caffeine triggers the release of calcium ions from sarcoplasmic reticulum to increase skeletal muscle contraction and overcome muscle fatigue (38, 40). As Fig. 5D shows, the normalized active tension force in optogenetic muscle rings stimulated by pulsed light increases with additions of caffeine, while it saturates in 100 µM to ∼40% of increase compared with that before addition of caffeine. Statistical significance appears in the active tension force after additions of higher than 10 nM of caffeine with P values below 0.05. The saturation behavior may be explained by overdoses of caffeine, which is known to cause rhabdomyolysis due to an excessive concentration of intracellular calcium; 400 to 500 µM (80 to 100 µg/mL) of caffeine in vivo is considered lethal (41, 42).

Experiments with dantrolene involve a modification of the measurement procedure to accommodate the poor solubility of dantrolene in water and the slow rates of diffusion. Here, recordings of muscle responses at different times occur after changing the cell media with 100 µM of dantrolene. Fig. 5E indicates that the normalized active tension force decreases after the addition of 100 µM dantrolene before it saturates after 30 min. Statistical significance in the active tension force with P values lower than 0.05 appears longer than 20 min after the addition of the drug. SI Appendix, Fig. S25 shows that 10 µM of dantrolene causes significant decrease in the normalized active tension force 30 min after addition. While the average normalized active tension forces in 100 µM are lower than those in 10 µM, no statistical significance appears between the two concentrations. These results indicate that it may take 20 to 30 min for the dantrolene to cause significant decrease in the active tension force, likely due to the poor solubility and slow diffusion rates of dantrolene in water-based media. These drug studies show potential utility of the system for sensitive measurements of responses of skeletal muscle tissues to various drugs, of relevance in screening, disease model studies, and medical countermeasures.

Discussion

The 3D frameworks reported here exploit mechanically guided assembly processes to form systems that provide millimeter-scale mechanical supports with integrated microscale strain sensors for measurements of tissue contractility in 3D engineered skeletal muscle tissues. These compliant 3D architectures enable intimate contact and robust device–tissue coupling for precise electronic sensing of mechanical responses under optical and chemical stimulation, with key advantages over traditional microscopy methods. Further improvement in the sensitivity is achievable via the use of strain sensing materials with larger gauge factors such as monocrystalline silicon (29). High-sensitivity measurements of engineered muscle tissue contraction are potentially useful for muscular disease studies or biohybrid robotic systems. The design and fabrication schemes presented in this study have additional potential in multifunctional sensing modalities for measurements of electrical potential, temperature, electrochemistry with distributed collections of electronic, piezoelectric, optical, and optoelectronic components for advanced modulation of tissue functions in a wide range of applications in studies of other 3D tissue constructs based on cardiomyocytes, neurons, and others (8, 9). In a complementary set of possibilities, these constructs may represent interesting architectures for actuation and control of biohybrid robots (21, 34, 36). The ideas presented here also scale naturally to arrayed configurations for high-throughput sensing in tissue engineering for drug screening and disease model studies.

Materials and Methods

Fabrication of the 3D Frameworks Instrumented with Strain Sensors.

Fabrication of the instrumented 3D frameworks began with spin coating (3,000 rpm for 50 s) a layer of PDMS (10:1 mixing ratio) on a glass slide. Partial curing (90 °C for 60 s) of the PDMS, followed by lamination of a film of PI (12.5 µm in thickness) on top and complete curing (110 °C for 3 min) allowed further processing. A lift-off process defined a patterned metal layer (Cr/Au, 10 nm/100 nm in thickness) on the surface of the PI. Deposition of a layer of parylene C (5 µm) and subsequent patterning using oxygen plasma etching (March RIE) formed a top encapsulation layer. Laser ablation (LPKF ProtoLaser R) defined the outline of the 2D precursor, followed by transfer of the 2D precursor from the PDMS-coated glass to a water-soluble tape (polyvinyl alcohol [PVA]). Deposition of Ti/SiO₂ (10 nm/50 nm in thickness) on the back side of the 2D precursor through a shadow mask defined the bonding sites. A sheet of PDMS (45:1 mixing ratio) served as the platform for mechanically guided assembly. Ultraviolet (UV) ozone treatment of the 2D precursor and of the PDMS created hydroxyl groups on the surfaces to allow covalent surface reactions between the SiO₂ and the PDMS. Prestretching the PDMS to a uniaxial strain of 40%, laminating the 2D precursor/PVA tape on top and heating the system (70 °C for 10 min) led to strong adhesion at the bonding sites. Dissolving the PVA tape with water and releasing the prestretch transformed the 2D precursor into a 3D framework by controlled buckling.

Data Acquisition and Signal Processing.

Anisotropic conductive film connected the leads of the instrumented 3D frameworks to a printed circuit board for electrical measurements. A PowerLab computer interface (ADInstruments, Model 8/35) recorded the voltage output signal at a sampling rate of 100 kS/s from the Wheatstone bridge at an applied excitation voltage V_e = 0.5 V. For 1 Hz optical stimulation, a digital bandpass filter of 0.1 to 5 Hz eliminated high-frequency noise and smoothed the signal. Studies with different stimulation frequencies used a digital bandpass filter of 0.1 to 20 Hz for similar purposes. A custom MATLAB (MathWorks) code calculated the peak amplitudes from the data.

Gauge Factor Measurement.

A planar strain sensor fabricated using procedures similar to those used to form the 2D precursors served as a structure for determining the calibration factor, with the 12.5 µm PI film replaced by a thicker (127 µm in thickness) PI substrate to minimize spontaneous curling and bowing of the film. A PowerLab computer interface recorded the change in resistance of the strain sensor (a digital low-pass filter of 5 Hz eliminated high-frequency noise) upon application of a triangular cyclic tensile strain measured (10 S/s sampling rate) by a dynamic mechanical analyzer (DMA; TA Instruments RSA-G2).

Indentation Test.

An indenter system (Bruker Hysitron BioSoft Indenter) with a vertical indenter (400 µm in diameter) provided force-displacement recordings on an instrumented 3D framework rotated by 90°. During approach of the indenter, a force threshold of 20 µN defined the point of contact between the indenter and the sidewall of a post. Repeating an approach (1 µm/s for 5 s)-hold (5 s) step before reaching a maximum indentation displacement of 50 µm followed by repeated retraction (1 µm/s for 5 s) hold (5 s) yielded force-displacement curves at a sampling rate of 60 Hz. Synchronized recording (400 S/s sampling rate with 0.5 Hz low-pass digital filtering; excitation voltage: 3 V) of the 3D framework signal via a PowerLab computer interface correlated the mechanical deformation of the 3D framework to electrical readout.

Optogenetic Muscle Ring Fabrication.

Optogenetic C2C12 myoblasts were cultured in the growth media. Fig. 2A illustrates the formation of an extracellular matrix-embedded muscle ring by thrombus reaction with thrombin and fibrinogen. Seeding occurred in a PDMS mold (5 mm/6.6 mm for inner/outer diameters) after mixing with 30% Matrigel (Thermo Fisher), thrombin (Sigma-Aldrich), and fibrinogen (Sigma-Aldrich) (24). The computer-aided design and an image of the mold appear in SI Appendix, Fig. S9 A and B. The growth media with 1 mg/mL⁻¹ aminocaproic acid added to the ring mold 90 min after seeding prevented proteolytic degradation (37). Three days after seeding, the media was switched to the differentiation media. On day 5 after differentiation, the muscle rings were transferred from the mold and integrated onto the 3D frameworks manually using tweezers. The muscle rings were incubated at 37 °C, and the media were changed every other day before integration and every day after integration. Further details of the fabrication can be found in SI Appendix, Note S7.

Immunofluorescence Imaging.

The muscle ring was rinsed in phosphate-buffered saline (PBS), fixed in 4% paraformaldehyde (Electron Microscopy Sciences) for 30 min, permeabilized with 0.25% (v v⁻¹) Triton X-100 (Sigma-Aldrich) for 20 min, and incubated overnight in blocking solution with 1% (w v⁻¹) bovine serum albumin (Sigma-Aldrich) in PBS at 4 °C. The primary antibodies, mouse anti-myosin heavy chain (MF-20) and rabbit anti α-actinin, were used to stain for myosin and the sarcomere, respectively, with 1:500 and 1:200 dilution ratios, followed by incubation overnight at 4 °C. The secondary antibodies, AlexaFluor-488 anti-rabbit and AlexaFour-564 anti-mouse (ThermoFisher), were used to stain α-actinin and MF-20 antibodies, respectively, followed by incubation overnight with DAPI to stain the nucleus at 4 °C. The muscle ring on the 3D framework was mounted with Vectashield antifade mounting media (Vector Laboratories). Between each step, the sample was washed with PBS three times for 5 min. The Multiphoton Confocal Microscope Zeiss 710 and Zeiss Stereo Discovery V20 Microscope were used for fluorescence imaging. The Zeiss Stereo Discovery V20 Microscope provides a larger depth of focus for 3D perspective views (Fig. 2E) with a higher fluorescence background, compared with the Multiphoton Confocal Microscope Zeiss 710.

SEM Imaging.

Samples were rinsed in PBS, fixed in 4% paraformaldehyde, and dehydrated using a series of ethanol solution with concentrations of 33, 67, 95, and 100% (three times) for 10 min. Gold/palladium was deposited on the dried sample for 70 s with a sputter coater. FEI Quanta FEG 450 environmental SEM was used to acquire images.

FEA.

Simulations for the compressive buckling of 3D frameworks were performed using the commercial software ABAQUS. Four-node finite strain shell elements (S4) were adopted, with refined mesh (∼100,000 elements) smaller than the width of the metal trace to ensure accuracy. The indentation was modeled by applying a concentrated force on the buckled 3D framework at the contact position with the indenter. The muscle ring tension was modeled by applying a uniform pressure on the 3D framework in the area where muscle ring attaches to the framework. All materials are linear elastic, except that a double linear plasticity model is adopted for Au in SI Appendix, Note S1. The Young’s moduli of PI, parylene, Au, and Cr are $E_{\text{PI}}$=2.5 GPa, $E_{\text{Parylene}}$= 2.76 GPa, $E_{\text{Au}}$= 78 Gpa, and $E_{\text{Cr}}$= 279 GPa, respectively; the Poisson ratios are ${\nu }_{\text{PI}}$= 0.34, ${\nu }_{\text{Parylene}}$= 0.40, ${\nu }_{\text{Au}}$= 0.44, and ${\nu }_{\text{Cr}}$= 0.21, respectively.

Optical Stimulation and Tracking.

Stimulation used an optical fiber and a 465 nm LED module driver. The driver and Doric Studio software were used to control the frequency, light intensity, and pulse width. Electrical measurements and optical stimulation were performed in an environmental chamber at 37 °C, as in SI Appendix, Fig. S16. Simultaneous measurements from 3D frameworks and optical microscopy were synchronized at the beginning of the measurements. Movements of muscle rings due to optical stimulation were tracked and recorded using an Olympus IX81 inverted microscope (Olympus) at a frame rate of 14.9 fps and processed using the software Tracker (https://physlets.org/tracker). For frequency studies, 0.5, 1, 2, 4, and 6 Hz pulses with 11.5 mW∙cm⁻², 50 ms of pulse width were applied for 20 s for each frequency value. For intensity studies, 0.26, 0.3, 0.4, 0.6, 0.8, 1.0, 1.5, 2, 2.5, 5, 7.5, 10, and 11.5 mW∙cm⁻² for 1 Hz pulses with 50 ms widths were applied for 20 s for each intensity value. For pulse width studies, 1, 2, 3, 5, 10, 20, 30, and 50 ms of pulses with 1 Hz and 11.5 mW∙cm⁻² were applied for 20 s for each pulse width value. The light intensity was measured with an optical power meter (Thorlabs).

Long-Term Studies.

Experiments involved measurements during optical stimulation (with pulses at 11.5 mW∙cm⁻², 1 Hz, and 50 ms) every day until day 22 after muscle ring integration, followed by measurements every 2 d until day 32, then on day 35 and day 37. The samples were fed with the differentiation media every day.

Drug Studies.

Acetylcholine chloride (Sigma-Aldrich), caffeine (Sigma-Aldrich), and dantrolene sodium (Sigma-Aldrich) were used for drug studies. Acetylcholine chloride and caffeine were dissolved in PBS and diluted for a series of different concentrations. A total of 5 µL solution was added to the 1 mL of media that contained the muscle ring on the 3D framework, increasing the drug concentration every minute from low to high concentrations in the optical stimulation with 1 Hz, 11.5 mW∙cm⁻², and 50 ms of light pulses. The working concentrations of acetylcholine and caffeine were diluted by ∼200 times of the Bolus concentrations as shown in the SI Appendix, Table S1. Dantrolene sodium was initially dissolved in 20 mM dimethyl sulfoxide (Sigma-Aldrich) and diluted in PBS due to its poor solubility in water (39). Light pulses with 1 Hz, 11.5 mW∙cm⁻², and 50 ms were applied for 1 min and measured electrically before adding the dantrolene solution and in 5, 10, 20, 30, 40, 50, and 60 min after adding it. Paired t tests are used to calculate P values for active tension forces between before and after the addition of chemicals. Unpaired t tests are used to calculate P values for active tension forces between the addition of 10 and 100 µM of dantrolene.

Data Availability

All study data are included in the paper and supporting information.