Assessing school-based policy actions for COVID-19: An agent-based analysis of incremental infection risk

Abstract

Many schools and universities have seen a significant increase in the spread of COVID-19. As such, a number of non-pharmaceutical interventions have been proposed including distancing requirements, surveillance testing, and updating ventilation systems. Unfortunately, there is limited guidance for which policy or set of policies are most effective for a specific school system. We develop a novel approach to model the spread of SARS-CoV-2 quanta in a closed classroom environment that extends traditional transmission models that assume uniform mixing through air recirculation by including the local spread of quanta from a contagious source. In addition, the behavior of students with respect to guideline compliance was modeled through an agent-based simulation.

Estimated infection rates were on average lower using traditional transmission models compared to our approach. Further, we found that although ventilation changes were effective at reducing mean transmission risk, it had much less impact than distancing practices. Duration of the class was an important factor in determining the transmission risk. For the same total number of semester hours for a class, delivering lectures more frequently for shorter durations was preferable to less frequently with longer durations. Finally, as expected, as the contact tracing level increased, more infectious students were identified and removed from the environment and the spread slowed, though there were diminishing returns.

These findings can help provide guidance as to which school-based policies would be most effective at reducing risk and can be used in a cost/comparative effectiveness estimation study given local costs and constraints.

1. Introduction

Since March 2020, when The World Health Organization [1] declared the outbreak of Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) a pandemic, public health organizations have been challenged to devise proper guidelines, practical interventions, and effective policy actions to slow the spread of the disease. Despite ongoing vaccination programs against COVID-19, new cases have remained relatively high [2]. Governments and public health systems should be prepared for the possibility that COVID-19 continues to exist and becomes a recurrent seasonal disease. Achieving herd immunity is still a challenge considering individuals who are either not eligible to receive the vaccine or decline to be immunized [3], and is unlikely to be achieved in some countries such as the US [4]. Furthermore, recent changes in the strain of SARS-CoV-2 in the United Kingdom, South Africa, and India, as well as its increasing propagation across the globe, have posed new challenges for countries – even ones with high rates of vaccination – to return to normal [5,6]. Therefore, providing impactful non-pharmaceutical interventions and guidelines is, and will remain, of importance. There are a number of impactful non-pharmaceutical interventions that help to contain the outbreak including practicing social distancing, providing high quality air filtration and ventilation, and performing surveillance testing and contact tracing. However, since differences in individual behavior and risk of infection vary by location, interventions need to be tailored accordingly [7].

Schools and universities have had higher than average infection rates and require particular attention. For instance, US cities with universities have higher death rates than average [8], and vaccinations are still not a mandate for many schools and universities [9]. In order to assess public health actions, it is important to gain an understanding of the spread of COVID-19 in closed environments as well as behavioral aspects of susceptible individuals. Significant literature exists on simulating the spread of COVID-19 through compartment models or social-network analysis [[10], [11], [12]]. Agent-based models (ABMs) have also been widely used to incorporate the propagation of COVID-19 at the interpersonal level based on individual actions [13].

Given the airborne nature of SARS-CoV-2 [14,[15], [16]], there is considerable potential for exposure when inhaling microscopic aerosols and respiratory droplets at short to medium distances in closed environments. A commonly used model for estimating the risk of airborne transmission of viruses was developed by Riley and colleagues based on an epidemiological study of a measles outbreak [17]. This model has widely been used for quantitative assessment of infection risk associated with airborne diseases, including analyzing ventilation strategies in clinical and other closed environments [[18], [19]]. However, the assumption of homogenous transmission in this model is limiting and a more precise analysis at the particle level will better estimate transmission risk. Although modeling non-homogenous transmission is difficult, computational techniques such as Monte-Carlo simulation are an effective approach for estimation [20].

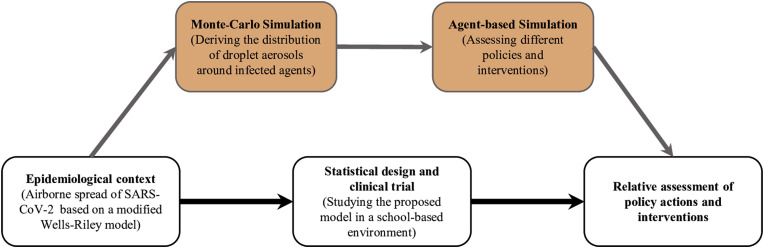
We present a two-stage approach, at the particle and interpersonal levels, to estimate incremental risk of infection with SARS-CoV-2 in closed environments. We further estimated the epidemiological aspects through an agent-based simulation. The benefit of conducting a modeling and simulation approach is that it can assess the impact of policy actions which are currently not implemented for a specific population and can provide guidance for future clinical trial designs [[21], [22]]. As demonstrated in Fig. 1 , we estimated the impact of multiple policy actions on the spread of COVID-19 among students in schools and universities and performed scenario-based analyses in order to compare the level of effectiveness associated with those interventions. These interventions included classroom distance requirements, air recirculation levels, contact tracing, class scheduling, and length of class periods for a fixed total number of class hours

Fig. 1.

A schematic diagram of the role for agent-based simulations on clinical and experimental trial design and policy assessment.

2. Materials and methods

2.1. Particle level: traditional vs novel estimation of quanta emission

In a recent study, Buonanno et al. [23,24] estimated the quanta emission rate of an infectious subject using a forward emission approach. Based on the Wells-Riley emission rate formula, they calculated the quanta emission rate of SARS-CoV-2 as a function of respiratory parameters for varying droplet concentrations produced during expiratory activities such as whispering, speaking, and breathing, ranging from 0.80 μm to 5.5 μm particles [25]. The quanta emission rate (ER_q, quanta h⁻¹) is defined by:

$$E{R}_q=c_v.c_i.V_{br}.N_{br}.\underset{0}{\overset{10\mu m}{\int }}{N}_b\left(D\right).d{V}_d\left(D\right)$$ eq −1

where c_v is the viral load in the sputum (RNA copies mL⁻¹), c_i is the ratio between one infectious quantum and the infectious dose expressed in viral RNA copies, V_br is the volume of air exhaled per breath (cm3), N_br is the rate of breathing (breath h⁻¹), N_b(d) is the concentration of droplets (part cm−3) as a function of droplet diameter (D), and V_d(D) is the volume of a single droplet (mL) as a function D.

The quanta concentration in an indoor environment at the time t is defined as:

$$n\left(t\right)=\frac{ERq\cdot I}{IVRR.V}+\left(n_0+\frac{E{R}_q\cdot I}{IVRR}\right)\cdot \frac{{\text{e}}^{-IVRR.t}}{V}\left(quanta{m}^{-3}\right)$$ eq −2

where n₀ represents the initial number of quanta in the space, I is the number of infectious agents present in the indoor environment, V is the volume of indoor environment under study, and ER_q is the quanta emission rate (quanta h⁻¹) mentioned previously. IVRR (Infectious Virus Removal Rate) is the sum of the air exchange rate via ventilation, the particle deposition on surfaces (e.g., due to gravity or surface absorptive characteristics), and viral inactivation [26].

Transmission risk is a function of the exposure time (t) of susceptible agents and the cumulative quanta concentration over time:

$$R=\left(1-{\text{e}}^{-IR\underset{0}{\overset{T}{\int }}n\left(t\right)\text{d}t}\right)(\%)$$ eq −3

where IR is the inhalation rate (h⁻¹) of the agent in exposure (affected by their type of respiratory activity), and T is the total time of exposure (h).

One shortcoming of the Wells-Riley based models for estimating the airborne transmission risk of viruses is that they assume homogeneous mixing of air in indoor environments. In other words, the number of infectious agents present in an indoor environment and the volume of the environment are the determining factors to calculate transmission risk. Although this assumption makes it easier to perform computational analysis, it ignores that the closer a susceptible agent is to an infectious source the higher the risk of transmission will be for that agent.

We modified this traditional approach by taking into account the quanta emitted directly to a subject in the vicinity of an infectious agent, as well as the additional quanta level spread through ventilation. We discretized the indoor space into cells in which at most one agent is present. For instance, if 4 subjects are seated 2 m apart in an enclosed space of volume that is 6 × 6 × 3 m³, each subject is surrounded by a 3 × 3 × 3 m³ cell. We assumed that each person inhales particles present in their cell, while their exhaled particles cross to other cells [27]. This leads to the airborne spread of viral load from the infectious agent to susceptible individuals. Further, the particles are then spread homogenously through the indoor space through the ventilation system.

2.1.1. Direct transmission of the viral load - Monte Carlo simulation

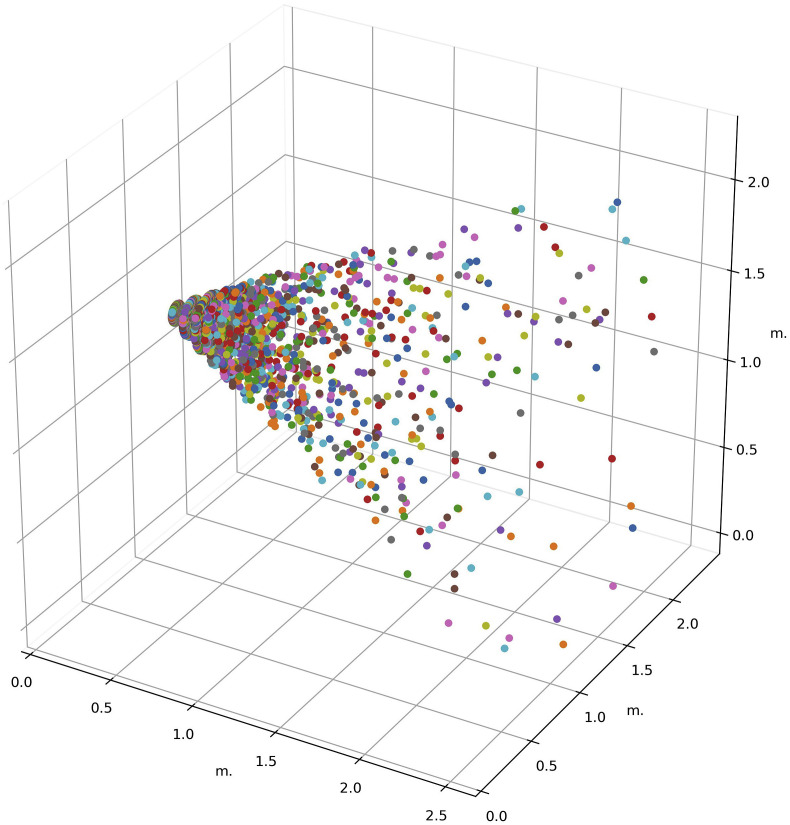
In order to estimate the quanta directly emitted by an infectious individual, we assumed that agents produce quanta through respiratory activities like breathing or coughing. In a recent study, Guo et al. [28] developed an approach to obtain the spatial distribution for the probability of infection using fluid mechanics approaches combined with the Wells-Riley model with the aim of optimizing of built environments and determining the optimal distribution of people or facilities in the confined space. In another recent study, Zhanga, et al. [27]. Modeled the distribution of droplet aerosols in an air-conditioned room based on the airflow velocity of coughing and breathing. Although different respiratory activities produce droplet aerosols with different diameters (varying from 1 μm to 100 μm) and different transmission distances (based on the type of activity, for example coughing), airborne pathogens can spread up to 6 m away from the mouth opening. We focused our study on infection prevention policies for a closed environment (i.e., classroom) and model droplet aerosol spread as a cone-shaped blend of particles coming out of the mouth and nose. The distribution of particles in the quanta-cone is assumed to follow a quadratic decay, meaning that the average number of quanta over each slice of equal thickness of the cone along its height is constant. Fig. 2 illustrates the quanta-cone.

Fig. 2.

A schematic view of sample quanta-cone with the height of 2.5 m and diameter of 1.2 m, derived using Monte Carlo simulation.

The second step for estimating the direct quanta emission rate is to determine how many infectious particles directly enter the surrounding cells of other agents in the vicinity of an infectious one. We used Monte Carlo simulation to produce the quanta cone where any infectious agent is located. The height, radius, and density of the quanta-cone are chosen based on the characteristics of SARS-CoV-2 and the type of respiratory activities we target.

2.1.2. Indirect transmission of the viral load

Droplet aerosols produced by an infectious person will eventually rise and enter the air ventilation system or fall and remain on the ground [14]. Therefore, not only do droplets directly infect agents close enough to the source, but they also homogenously return to the indoor space through the ventilation system. We assumed that all infectious airborne pathogens eventually get recirculated but allow different filtration rates to be set as a parameter in the model. Therefore, circulated air contains a fraction of quanta that is far away from the infectious source.

In order to determine the indirect quanta emitted by each individual, considering the assumption of homogeneity of ventilated particles in the air, we counted the number of particles inside the virtual cell surrounding each person. By adding up the direct and recirculated quanta emitted to non-infected agents within their specific cell, we obtained the total quanta and calculated the transmission risk of COVID-19 for each individual.

2.2. Interpersonal level: an agent-based simulation

We developed an agent-based simulation of a classroom with students seated randomly throughout the class based on distancing requirements and a teacher located in front of the class, in order to track the propagation of SARS-CoV-2 among students over the course of the semester. The agent-based model tracks specific agent locations and captures student behavior with regards to their adherence to guidelines as an important factor in the spread of the disease.

2.2.1. Properties of autonomous agents and the environment scope

We assumed that the likelihood of whether a student attends class while experiencing mild symptoms is based on their level of stress and resilience. An agent can either be healthy (susceptible), exposed but not infectious, asymptomatic, pre-symptomatic, mildly symptomatic, severely symptomatic, immune, or deceased in any stage of the simulation. They transferred from one state to another based on the probability determined from the transmission risk model. There is limited literature on how long a recovered person is immune to reinfection and so we conservatively assumed that the recovered student remained immune throughout the semester.

Several factors such as demographic characteristics of the students, the degree to which they trust science, and their perceived risk of COVID-19, influence how well they comply with regulations [29]. More importantly, stress level and resilience heavily affects a student's mental well-being [30] and therefore how well they can decide whether or not they show up to class when experiencing mild, indistinguishable symptoms. Sex is also considered to affect the level of adherence to Covid19 guidelines [31]. Note that the symptoms of COVID-19 are largely indistinguishable from those caused by other types of respiratory virus infections [32]. The higher a student's stress level, the more likely they are to not show up while having mild symptoms such as coughs or low-grade fever. The higher their resilience, the less likely they experience severe disease symptoms and the more likely they attend the class while being infectious.

We used a decision-making algorithm to estimate the probability of attending class. Students were randomly assigned a stress level of high/low and a resilience level of high/low, as well as a level of adherence to rules based on their sex. For high stress level, the probability of showing up was (1 – level of adherence to rules) × (1 – stress level impact × resilience level impact). This implies, for example, that high resilience level can reduce the impact of high stress and together increase the probability of showing up. In other words, students decide to attend the class while having mild symptoms with a probability of (1 – level adherence to the rules) unless they have a high stress level. High stress level increases their anxiety and perhaps their need to contact healthcare providers rather than neglecting symptoms. The impact of stress level was balanced by the level of resilience; low resilience amplifies the impact of high stress while high resilience reduces the impact of high stress.

Classroom size and layout are parameters that allow the model to be run with any number of students in any desired classroom setting. In order to capture the incremental effect of school policies on the spread of the disease, we do not consider the case where students get infected outside of the classroom. Fig. 3 shows an example of a 49-seat classroom filled with 40 students and one teacher with different initial health states.

Fig. 3.

The classroom scheme and the estimated risk map for a 49-seat classroom. Students sitting in front of infectious agents have higher risk of infection. The risk of infection is assumed to be zero for already infected agents and empty cells.

2.2.2. Model parameters and assumptions

Parameters, rates, and factors used in the model are presented in Table 1 . Some of the model parameters, such as incubation period, follow a distribution based on the uncertainty in the characteristics of diseases. We assumed at least one infected student was present in the classroom on the first day in order to address the patient zero problem [33]. As a result, all simulations would contain a form of disease propagation. Moreover, we held the assumption that an average student wears a two-layer cloth mask, which provides on average of 70% protection against droplets [34].

Table 1.

Model parameters summary.

	Parameter	Value/Range	Reference	Description
Propagation ratios	Prevalence rate	0.017	[35]	Latest prevalence rate of COVID-19
	Asymptomatic ratio	0.40	[36]	Among all the infected population
	Pre symptomatic ratio	0.60	[36]	Among all the infected population
	Mildly symptomatic ratio	0.81	[37]	Among all the pre-symptomatic population
	Severely symptomatic ratio	0.19	[37]	Among all the pre-symptomatic population
	Fertility rate	0.023	[37]	–
Behavioral factors	Adherence to rules factor	0.88 (female), 0.83 (male)	[[38], [39]]	Different among males and females
	Stress level impact	0.6	Assumed, [40]	Stress and increase adherence to rules by 60%
	Resilience impact	0.46	[41]	Resilience can reduce stress by 46%
Disease characteristics	Incubation period	Normal (μ = 5.75, σ = 5.75/3)* (days) *99.5% of the distribution is within (0, 11.5)	[37]	The period between exposure and the onset of symptoms
	Latent period	Normal (μ = 2, σ = 2/3)* *68% of the distribution is within (1.33, 2.67)	[37]	The period between exposure and the onset of the period of communicability
	Recovery period	14 (days)	[37]	The period between symptoms onset and recovery (end of preciousness and isolation)
Transmission model parameters	D	1.83 (m)	Assumed	Distance between agents
	ERq	120*0.30 (quanta h−1)	[23,24] [34]	Quanta emission rate with two-layer cotton mask
	IVRR	0.87–2.2 (h−1)	[23,24]	Infectious virus removal rate
	IR	0.9 (h−1)	[23,24]	Inhalation rate
	Class duration	150, 75, 75*, 50 (mins)	Assumed	* Two types of schedule
	Number of sessions per week	1, 2, 2*, 3	Assumed	* Two types of schedule
Testing parameters	Surveillance testing sample size	0.10	Assumed [2],	Sample size varies by University, from 1% to 100% of the population
	Test accuracy	90%	[42]	Test accuracy ranges from 84.0% to 97.6% depending on the type of test.
	Test results delay	2 (days)	Assumed	–
	Contact tracing level	0.00, 0.25, 0.50, 0.75, 1.00	Assumed	The percentage of all contacts that can be traced

The model was coded in Python via Jupyter Notebook Version 2.0.0., in an object-oriented programming framework. The source code and other related information can be found at http://GitHub.com/Rey-Zafarnejad/Agent-Based-Analysis-of-Incremental-Infection-Risk-Associated-with-SARS-CoV-2.

2.3. Policy level: school policy actions and interventions

We considered a range of policy options for schools and universities and estimated the incremental impact on COVID-19. Each are detailed below.

2.3.1. Class schedule and duration

Both the duration of exposure and number of times a student enters a classroom with at least one other infected student plays a critical role in the risk of infection. Most universities use a 16-week schedule per semester, and for 3 credit-hour course, require 2400 min of in-class time. It is important to understand the trade-off between class duration and number of sessions per week for a fixed number of semester class minutes. For example, is there greater risk meeting three times per week for 50 min each class or two times per week for 75 min each class?

It is also possible to consider different schedules for classes with two sessions per week. One possible schedule is two days a week, with 2 days and 5 days in between the sessions, respectively (e.g., Tuesdays and Thursdays); while another possible schedule splits the week into 3 days and 4 days between the sessions, respectively (e.g., Mondays and Fridays). The overlap of class schedules and delays could affect the results. Therefore, we considered all variations of schedules.

2.3.2. Social distancing

Many schools and universities practice social distancing based on CDC prevention guidelines (CDC, 2020e) to help reduce the spread of coronavirus infections. An important issue is to understand how the spread of COVID-19 changes with differing distance requirements in closed classroom environments.

2.3.3. Ventilation and air filtration

One of the parameters used in calculating infection risk is the infectious virus removal rate (IVRR), which consists of three parts: i) air exchange rate via ventilation, ii) particle deposition on surfaces (e.g., due to gravity or other surface absorptive characteristics), and iii) viral inactivation [26]. Air filtration and ventilation helps remove infectious particles from the air and mix in fresh air thereby slowing down the spread. We focus on the level of quanta removal rate rather than how quanta are being removed by different mechanisms. If the filtration rate was 100% effective, only fresh air with no quanta would be recirculated. Environmental factors such as temperature, relative humidity, particle velocity, and other indoor air characteristics can also affect the active viral load in the air and the resulting transmission risk [27,43].

2.3.4. Surveillance testing and contact tracing

According to CDC Pandemic Planning Scenarios [37], asymptomatic and pre-symptomatic individuals who have not yet developed symptoms have the greatest infectivity and therefore identifying them as early as possible is important. Although the efficiency and effectiveness of available tests are crucial to accurately identify infected individuals, the procedure of conducting the test including who to test, how frequently to perform testing, and which type of test (viral test or antibody test) to carry out, are important decisions.

A supplementary way to control the spread of coronavirus disease is through monitoring and testing a particular sample of the population by tracing their close contacts, and testing those in contact with infectious sources [44]. However, there can be inaccuracies in this approach since it primarily relies on self-reported data [45]. Further, there may be insufficient testing and privacy issues [42]. We assumed that the school is capable of tracing a certain percentage (specified in as a model parameter) of contacts when an infectious agent is severely symptomatic (thus automatically confirmed) or is tested positive. Successfully identified individuals with close contact will be tested afterwards.

3. Results

3.1. Comparison between the classic and novel transmission models

A limitation of traditional models of airborne transmission risk is that they do not consider the location of a susceptible agents with respect to a contagious one. In order to study this effect, we ran the agent-based model for a class of 40 students (with female to male proportion of 72%) and a teacher in a classroom with seats of 7 rows and 7 columns (composed of 49 cells of 6 × 6 × 8 ft³). Each student was randomly located in a cell and the teacher could freely move within a set of 7 cells at the front of the classroom. We assumed that the teacher is not contagious in the initial state. There were 9 randomly selected empty seats in the classroom and at least one initial infectious student present in the classroom (either asymptomatic or pre-symptomatic) which initiated the spread. We ran the simulation for one session of a 3-h class to demonstrate the difference between the traditional and novel calculation of the transmission risk.

As demonstrated in Fig. 4 , there are several possible cumulative risk curves that depend on how the students were seated in the class. The orange curve shows the traditional Wells-Riley based transmission risk as a function of time, which was equal for all the susceptible agents (student or teacher) present in the classroom. The longer the students were present in the classroom the higher the risk of transmission became. However, considering the importance of location, there were several possible cumulative risks for present agents shown by the purple curves. For example, if an agent was placed right in front of an infectious agent (which means they were located inside a quanta-cone) the probability of infection was significantly higher than when an agent was seated far away from an infectious individual and the only infection risk came from recirculated particles. Therefore, the highest transmission risk is associated with the time there were one or more individuals in the vicinity of an infectious agent, and the lowest (positive) transmission risk is related to when only indirectly infecting particles were effective. As a result, the traditional transmission risk, and the lowest positive novel transmission risk overlap; traditional Wells-Riley based transmission risk is a lower bound for the risk of airborne transmission of diseases.

Fig. 4.

Transmission risk among students – traditional and novel risk models: the orange curve shows the traditional transmission risk as a function of time. The purple curves show different possible transmission risks based on a class with randomly seated students. The closer a susceptible agent is to an infectious one, the higher the risk of transmission.

3.2. Assessing different policy interventions on the estimated risk of transmission

3.2.1. Class schedule and duration, surveillance testing and contact tracing

In this section we discuss the results of performing agent-based simulation over the course of a semester and assess the impact of different interventions and policy actions on the transmission risk of SARS-CoV-2. As mentioned previously, course schedule and class duration, surveillance testing and contact tracing, social distancing and ventilation were the primary policies considered. For the sake of simplicity, we assumed that students are seated 6 ft apart and the IVRR is 1.87 (h⁻¹). Moreover, we considered four different course schedules and corresponding class durations (three-times a week Mon/Wed/Fri – 50 min each, twice a week Tue/Thu – 75 min each, twice a week Mon/Fri – 75 min each, once a week – 150 min). Other model characteristics remained the same (as described in Section 3-1).

In order to model surveillance testing with contact tracing, we assumed that testing was performed on a weekly basis for a random sample of ten percent of the students. After one to two days test results were released and students who tested positive were quarantined and tested every week in order to ensure the safety of other students. Quarantined students were not allowed to return to class until they tested negative. Whenever an individual tested positive or was severely symptomatic (assuming those showing severe symptoms were identified and quarantined already), a contact tracing procedure would begin. During the contact tracing process, a number of students would be chosen and tested immediately based on the contact tracing level that indicates the sample size. If a student tested positive in this procedure, they were quarantined and tested again every week until they were COVID-19 free or received a negative result. Since being in a closed environment was one of the fundamental assumptions of the model, we only traced individuals in contact with the infected agent within the classroom.

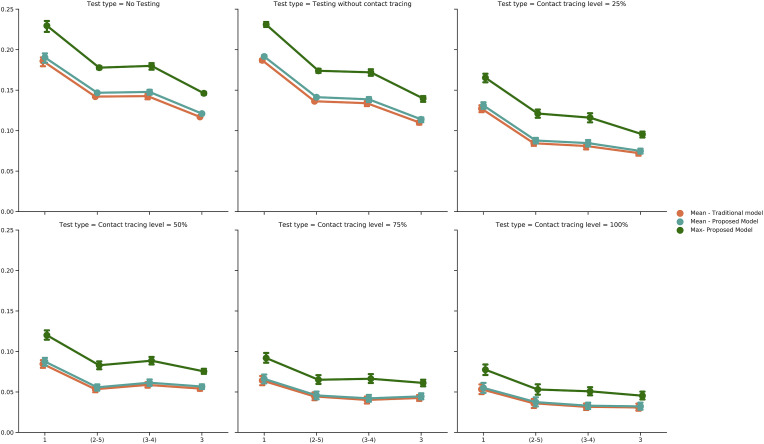
As shown in Fig. 5 , class duration was an important factor for transmission risk. Longer class times led to higher rate of spread. The difference between twice a week schedules was not significant in different scenarios (Table 3 in Appendix 1). On the other hand, 150-min classes had higher infection risk than 50-min classes in all scenarios, although the difference in transmission risk between the two types was decreased as the level of contact tracing increased (Table 3 in Appendix 1) since more infectious students were identified and removed from the environment.

Fig. 5.

Transmission risks under different number of sessions per week; (2–5) and (3–4) indicate two days a week schedule with 2,5/3,4 days in between sessions.

3.2.2. Ventilation and social distancing

Intuitively, the more distant the agents are located from one another and the higher the rate of air filtration, the lower the risk of transmission should be. Nonetheless, there are essential limitations such as classroom space and air filtration ability that determines how well social distancing and ventilation can work. Social distancing requires larger classrooms or fewer students, both of which may not necessarily be feasible. On the other hand, enhancing the air filtration can be costly and, in most cases, difficult to achieve in a timely manner. However, in this section we discuss the impact of different distances and ventilation rates on the estimated transmission risk, assuming that it was possible to do so. The simulation was run for the same settings, with a class schedule of three days a week and no testing.

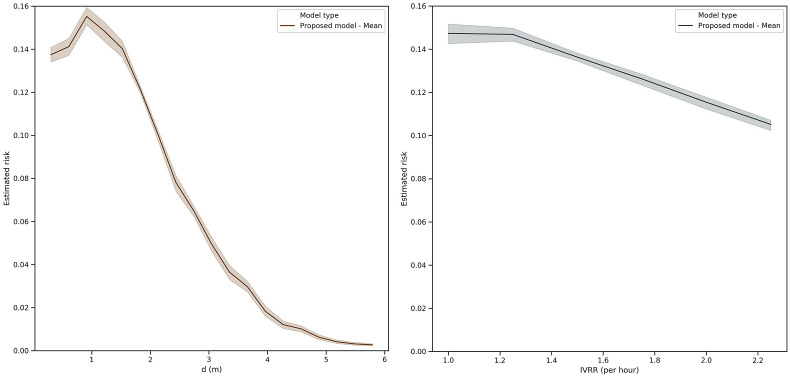
Fig. 6 demonstrates the impact of distance and ventilation on the estimated transmission risk. Although initially there was an increase in the mean transmission risk when students were less than 1 m away, as students became more distant from one another, the estimated risk of infection decreased rapidly until the risk was almost zero. On the other hand, assuming a fixed distance between agents (~1.8 m), we saw that the infectious virus removal rate (IVRR) had a linear decay effect on the estimated transmission risk.

Fig. 6.

The impact of distance and ventilation on the mean transmission risk in a 3- days a week class with no testing or contact tracing within 100 replications of the model.

3.3. Assessing different policy interventions on the size of the epidemic

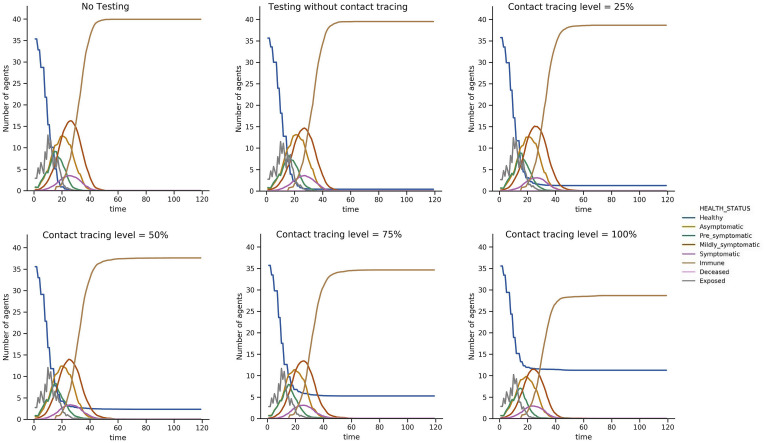
We tracked the real time health status associated with each individual agent through the simulation. We assumed that when a susceptible agent was in the vicinity of an infectious individual, their health status became exposed and after a few days, infected. Depending on the severity of the symptoms and demographical characteristics of the agent, they would end up either as immune or deceased. Fig. 7 illustrates the state of the system at the end of each day, in a 120-day-long simulation (100 replications) for 3 days a week class schedule. There was an obvious improvement in the system as testing and then contact tracing were added to the model. Since the testing process was assumed to be entirely based on a random selection of students, and if a student was not severely symptomatic or was not tested at all while infectious, most of the students eventually experienced the disease throughout the semester. Nonetheless, higher levels of contact tracing could clearly reduce the mean number of infected students over the course of the semester, with a reduction of more than 30% in the mean total number of infected agents when contact tracing is conducted at the highest level when an initially infected agent is present in the system.

Fig. 7.

Epidemic size: the average number of agents experiencing each possible health status per day, for 100 replications. As more controlling policies are put into action, the epidemic size reduces.

4. Discussion

We quantified the impact of a variety of school-based policies for reducing COVID-19 infections in classroom settings using a two-stage approach. The proposed approach extends traditional transmission models in three ways. First, we relaxed the assumption of uniform mixing through air recirculation in a closed environment by including the local spread of quanta from a contagious source. Second, we modeled the behavior of students with respect to guideline compliance through an autonomous agent-based simulation. Finally, we performed a scenario-based analysis to study the impact of proposed model in the long run. The potential significance of risk reduction through the policies assessed in our work is important for school administrators. Even though the focus of this work was for classroom settings in schools and universities, the findings can be applied to any closed environment with distancing and ventilation facilities such as business conference rooms, theaters and concert halls, and places of worship.

The main contribution of this paper is the novel approach of estimating the incremental risk of infection associated with transmission of viral load in closed environments. The results imply that the assumption of homogenous transmission proposed by Wells and Riley underestimate the risk of infection for individuals in the vicinity of the infectious patient (for a 90-min period of presence in a closed environment, the relative risk of infection can be as higher as 1.3 times). We also found that the risk of infection for agents far from the source of infection are close to what traditional Wells-Riley model estimates.

As for the policy analyses, Table 2 summarizes the key findings and associated implications. We found that distancing requirements had the most dramatic impact, decreasing infection risk by over 65% when distancing increased from 1.5 m to 3 m. Several implications arise from these results. In order for school administrators to promote social distancing, there needs to be plenty of campus facilities, classrooms and laboratories as well as human resources, staff and faculty members. However, distance learning tools, virtual classes and hybrid teaching that are advised to reduce in-person gatherings have been a reasonable remedy for practicing social distancing when facing lack of sufficiently large classrooms [46,47]. Therefore, we confirm that the easiest to implement and most effective method to reduce the risk of transmission is practicing social distancing. Alongside this intervention, adjusting class schedules is also an effective policy to reduce the infection risk among students. We find that when holding in-person classes, shorter yet more frequent sessions are preferable since they reduce the risk of infection by more than 40%. Compared to longer less frequent sessions A combination of social distancing and reducing class duration can be considered as an immediate action by school administrators at the time of similar epidemics.

Table 2.

Key findings and associated implications regarding policy assessment – only significant changes are reported here.

Policy	Range of Effectiveness (reduction in the relative mean transmission risk %)	Requirements for Implementation	Speed of Implementation	Source(s)
Social Distancing	~ 65% (M = 64.68, SD = 12.65) Comparing 1.5 m vs 3 m distance between seats	Campus facilities including larger classrooms and labs - human resources and faculty members - virtual tools for distance learning	Rapid	[46] [47]
Class schedule and duration	> 40% (M = 40.30, SD = 8.03) Comparing once-a-week vs three-times-a-week schedule	Similar to social distancing	Rapid	Assumption
Ventilation and air filtration	> 28% (M = 28.44, SD = 11.27) Comparing IVRR = 1 vs 2.2	Financial resources, safety challenges	Slow	[43]
Surveillance testing and contact tracing	> 70% (M = 71.25, SD = 16.58) Comparing no contact tracing vs max contact tracing level	Ethical, legal, security and privacy requirements	Slow	[44]

Another set of interventions that were studied in this work were ventilation and air filtration, as well as surveillance testing and contact tracing. We found that ventilation changes were effective at reducing mean transmission risk by 25%, while higher levels of contact tracing were associated with higher reduction in the transmission risk (for the highest level of contact tracing, there was 70% reduction of the transmission risk compared to no contact tracing). These policy actions are still promising, however, providing resources for implementing them is not possible for all schools, or at least not feasible in a timely manner. Using digital contact tracing methods such as mobile apps and surveys appear to be relatively easy methods to trace contacts among students; however, in practice there are security and privacy issues and more importantly an inability to identify asymptomatic individuals either by surveillance testing or contact tracing [44]. Providing air cleaning methods such as air filtration and ultraviolet germicidal irradiation (UVGI), ventilation and advanced air distribution methods are expensive and time consuming [43] and at the same time, not as effective as the previously described policies as they reduce transmission by roughly 28%.

It is important to mention that there are several limitations to this study. First and foremost, the data for parameter estimation is still somewhat limited. Although it is easy to perform sensitivity analysis over a range of values, we decided to rely on current information and focused on assessing different policies against the spread of COVID-19 in a comparative manner. In addition, we assumed randomized seating in a classroom and did not study the impact of entrance/exit/movement of the agents. This could be extended by developing a hybrid model using network and phase transition analysis. Finally, we did not explicitly consider the cost of interventions in our model which can be a topic of study using methods such as cost-benefit analysis.

5. Conclusion

The information provided in this work could provide school and university administrators with information that will allow them to tradeoff the benefit of infection risk reduction with the cost of implementation and hence identify the best portfolio of interventions for their specific setting. In addition, the proposed model has applicability in other settings including policies to reduce the spread of tuberculosis in clinics in resource constrained countries that do not have the resources to effectively isolate infected patients, and the spread of other infectious disease outbreaks in closed settings such as measles.

Appendix.

Table 3.

Pairwise statistical significance, mean estimated risk for different testing types and class schedules (E.g. (2–5) indicates twice a week class, with 2 days and 5 days in between sessions each week.)

Test type	Comparison between	Decrease in relative estimated risk (%)	P-Value
No Testing	1 & (2–5)	−22.92859307	7.78E-34
No Testing	1 & (3–4)	−22.38583209	5.07E-28
No Testing	1 & 3	−36.43440135	3.18E-59
No Testing	(2–5) & (3–4)	0.704231305	0.57267465
No Testing	(2–5) & 3	−17.52375987	3.40E-61
No Testing	(3–4) & 3	−18.10052164	2.19E-33
Testing without contact tracing	1 & (2–5)	−26.21191343	4.85E-95
Testing without contact tracing	1 & (3–4)	−27.60694191	9.15E-69
Testing without contact tracing	1 & 3	−40.50588898	4.00E-105
Testing without contact tracing	(2–5) & (3–4)	−1.890587684	0.150827744
Testing without contact tracing	(2–5) & 3	−19.3716577	1.11E-39
Testing without contact tracing	(3–4) & 3	−17.81793367	4.85E-23
Contact tracing level = 25%	1 & (2–5)	−33.04294744	1.36E-35
Contact tracing level = 25%	1 & (3–4)	−35.47258901	1.69E-35
Contact tracing level = 25%	1 & 3	−42.88151741	3.36E-51
Contact tracing level = 25%	(2–5) & (3–4)	−3.628656699	0.232224364
Contact tracing level = 25%	(2–5) & 3	−14.69385165	6.97E-08
Contact tracing level = 25%	(3–4) & 3	−11.48183119	1.95E-04
Contact tracing level = 50%	1 & (2–5)	−36.33525192	1.05E-19
Contact tracing level = 50%	1 & (3–4)	−29.83105901	1.16E-14
Contact tracing level = 50%	1 & 3	−35.21480929	1.79E-21
Contact tracing level = 50%	(2–5) & (3–4)	10.21631767	0.040307504
Contact tracing level = 50%	(2–5) & 3	1.759910564	0.691255565
Contact tracing level = 50%	(3–4) & 3	−7.672554559	0.055895315
Contact tracing level = 75%	1 & (2–5)	−30.85989953	2.62914E-07
Contact tracing level = 75%	1 & (3–4)	−36.36859778	3.7326E-10
Contact tracing level = 75%	1 & 3	−32.63912962	3.76965E-09
Contact tracing level = 75%	(2–5) & (3–4)	−7.967443237	0.266966906
Contact tracing level = 75%	(2–5) & 3	−2.573369264	0.70534712
Contact tracing level = 75%	(3–4) & 3	5.861049787	0.392950847
Contact tracing level = 100%	1 & (2–5)	−31.9272862	7.30E-05
Contact tracing level = 100%	1 & (3–4)	−39.96963412	3.62E-08
Contact tracing level = 100%	1 & 3	−41.44829553	2.81227E-08
Contact tracing level = 100%	(2–5) & (3–4)	−11.81434892	0.217198567
Contact tracing level = 100%	(2–5) & 3	−13.98652823	0.157257011
Contact tracing level = 100%	(3–4) & 3	−2.463189057	0.792342997