Semi-Automatic Planning and Three-dimensional Electrospinning of Patient-Specific Grafts for Fontan Surgery

Abstract

This paper proposes a semi-automatic Fontan surgery planning method for designing and manufacturing hemodynamically optimized patient-specific grafts. Fontan surgery is a palliative procedure for patients with a single ventricle heart defect by creating a new path using a vascular graft for the deoxygenated blood to be directed to the lungs, bypassing the heart. However, designing patient-specific grafts with optimized hemodynamic performance is a complex task due to the variety of patient-specific anatomies, confined surgical planning space, and the requirement of simultaneously considering multiple design criteria for vascular graft optimization. To address these challenges, we used parameterized Fontan pathways to explore patient-specific vascular graft design spaces and search for optimal solutions by formulating a nonlinear constrained optimization problem, which minimizes indexed power loss (iPL) of the Fontan model by constraining hepatic flow distribution (HFD), percentage of abnormal wall shear stress (%WSS) and geometric interference between Fontan pathways and the heart models (InDep) within clinically acceptable thresholds. Gaussian process regression was employed to build surrogate models of the hemodynamic parameters as well as InDep and N_v (conduit model smoothness indicator) for optimization by pattern search. We tested the proposed method on two patient-specific models (n=2). The results showed the automatically optimized (AutoOpt) Fontan models hemodynamically outperformed or at least are comparable to manually optimized Fontan models with significantly reduced surgical planning time (15 hours versus over 2 weeks). We also demonstrated feasibility of manufacturing the AutoOpt Fontan conduits by using electrospun nanofibers.

I. Introduction

Single ventricle heart disease (SVHD) causes oxygenated blood and deoxygenated blood to mix in circulation. Untreated SVHD is associated with a 70% mortality rate during the first year of life [1]. The surgical treatment of SVHD involves three staged surgical procedures [2]. Palliative shunt surgery is performed to introduce aortic flow into the pulmonary arteries and maintain oxygenation. The Glenn procedure disconnects the superior vena cava (SVC) from the right atrium and attaches the SVC to the pulmonary arteries (PA), which enables the upper body’s deoxygenated blood to directly go to the lungs. In the final stage, as illustrated in Fig. 1, the Fontan procedure disconnects inferior vena cava (IVC) from the right ventricle and attaches to the PA by using a synthetic extracardiac conduit [3] or via an intra-atrial tunnel [4]. This directs the lower body blood flow to the lungs, bypassing the heart. Although 20-year survival rates after the Fontan procedure are 74% ~ 82% [5], [6], [7], patients may suffer long-term complications including pulmonary arteriovenous malformations (PAVMs) [8], [9], decreased exercise capacity [10], and protein losing enteropathy [11], etc.

Fig. 1.

Illustration of a single ventricle heart and a Fontan pathway. The Fontan conduit connects the PA and the inferior vena cava (IVC). Deoxygenated blood from the superior vena cava (SVC) and IVC is directed to the lungs.

Clinical evidence shows the correlation between hemodynamics in the Fontan pathway and the cause or exacerbation of the complications [10], [12]. Patients can have long-term benefits for health and quality of life by receiving an ideally reconstructed Fontan pathway with a balanced hepatic flow distribution (HFD) [13] and minimum energy loss [14]. However, patient-specific Fontan grafts are still under clinical investigation for the approval by the U.S. Food and Drug Administration (FDA). In addition, the commerically available FDA approved grafts [15], [16] are manufactured with synthetic materials, which do not grow with the child and could require revision or replacement in the long term [17].

3D-printable tissue engineered vascular grafts (TEVG) offer a promising strategy to create patient-specific, hemodynamically optimized Fontan conduit [18]. Manufactured by FDA-approved biodegradable scaffolds, TEVG allow the patient’s own cells to proliferate and provide physiologic functionality and growth over time. Our pre-clinical trial of TEVG in sheep models showed neotissue formation with mechanical properties comparable to those of the native tissue [19]. To improve Fontan pathway hemodynamics, we adopted iterations of computer-aided-design (CAD) followed by computational fluid dynamic (CFD) simulation [20], and investigated the surgeon’s intuition in Fontan pathway construction by using clay modeling [21]. Besides using general-purpose CAD software to design Fontan conduits, specialized modeling tools such as SURGEM [22] can simplify the surgical planning process. Despite these advances, significant engineering efforts and frequent communication with surgeons for feedback are still required, which may take weeks to design a Fontan pathway for a single patient, and still result in sub-optimal hemodynamics [23]. There is a need to speed up the design process and reduce human efforts for identifying globally optimized Fontan pathways, which can be achieved by automating the design and optimization process.

Design optimization of Fontan pathways involves solving a nonlinear constrained optimization problem that has been extensively studied for structural optimization of aircraft since late 1950s [24]. Gradient-based and gradient-free optimization methods were developed and utilized in various design optimization tasks. The adjoint approach as one of the most efficient gradient-based optimization methods [25] features that the computation cost of derivatives of objective functions is independent of the design space dimensions. However, the solution may converge to local optima which are significantly worse than the global optimum. In contrast, gradient-free optimization can apply global search strategies on surrogate functions of computationally expensive simulations to find near-globally optimal solutions [26]. Surrogate-based optimization suffers the curse of dimensionality with the design space dimension practically being limited to 10~20 [27]. Thus, the application of optimization methods is task dependent. For cardiovascular optimization problems [28], research has been focused on idealized vessel models for problem simplification. The gradient-based optimization methods were used to optimize design parameters of 2-dimensional (2D) idealized coronary artery bypass grafts [29], [30], [31]. Prior studies employed gradient-free surrogate-based optimization methods to design bifurcated Y-grafts with unequal branch diameters on 3-dimensional (3D) idealized Fontan models analyzing their influence on HFD [32]. Another study demonstrated the usage of the surrogate-based optimization method for designing an idealized Y-graft geometry to minimize power loss by using a wall shear stress (WSS) constraint [33]. The thrombosis risk in the Fontan links to abnormally low WSS. Reducing regions of abnormal WSS in Fontan pathway may potentially prevent thrombus formation [34]. Despite these research achievements, designing patient-specific Fontan TEVG with optimized hemodynamic performance is still a complex task due to the variety of patient-specific anatomies, confined surgical planning space, and the requirement of simultaneously considering multiple criteria for graft design optimization.

Aiming to fill this gap, we aim to contribute a semi-automatic Fontan pathway planning method to significantly reduce human effort and turnaround time for designing hemodynamically optimized patient-specific grafts. The realization of this work involves solving two key problems. The first problem is how to parameterize Fontan pathways and explore patient-specific design space by considering potential interference with other anatomies. We introduced a 10-dimensional design space for enabling pathway adjustments based on anastomosis locations, orientations, conduit sizes and shape deformation. The feasibility of a Fontan pathway is measured by interference depth with other anatomies, which is computed by an interference detection algorithm developed in this work. The second problem is how to find feasible solutions in the design space that can optimize hemodynamic performance of Fontan models. We performed nonlinear constraint optimization on iPL with WSS, HFD and geometric interference as constraints. Surrogate models of hemodynamic parameters and geometric interference were built by using Gaussian process regression. Multi-start pattern search optimization was applied on the surrogate model of iPL to find a near-globally optimal set of design parameters. To automate the Fontan pathway planning and optimization work flow, we developed a computation framework based on our prior work [35] to seamlessly integrate mesh manipulation, hemodynamic simulation, training data collection and surrogate optimization. To evaluate the performance of the our proposed method, we setup hemodynamics performance comparison study among the Fontan models designed by surgeon’s unconstrained modeling method [21], engineer’s manual optimization method [20], and the automatic optimization method, as well as patients’ native Fontan models that require surgical revision. We also investigated how graft implantation errors, uncertainty of boundary conditions (BC) and exercise conditions affect the hemodynamic performance of optimized grafts. In addition, we also demonstrated the feasibility of combining our Fontan conduit optimization technique with the manufacturing of patient-specific TEVG by using electrospun biodegradable nanofibers.

II. Anticipated Workflow of Fontan Surgery

We propose a workflow for designing and manufacturing patient-specific hemodynamically optimized conduit for Fontan surgery, which consists of five consecutive steps as shown in Fig. 2: 1) obtaining magnetic resonance angiography (MRA) data for the patient’s heart and vascular geometry, and phase-contrast MRI (pC-MRI) data for the determination of blood flow data for CFD simulation; 2) image segmentation to reconstruct the 3D models of SVC, IVC, PA, aorta and heart; 3) Fontan pathway planning and optimization; 4) manufacturing of patient-specific grafts; and 5) graft implantation in the patient. This work focuses on automatically optimizing the Fontan pathways and manufacturing them into patient-specific TEVG. The automatic graft optimization involves Fontan pathway parameterization, high-fidelity simulations to collect training data, and building surrogate functions of iPL, WSS, HFD, InDep and N_v for design parameter optimization. To manufacture the Fontan conduits, mandrels are 3D-printed according to the geometries of optimized Fontan pathways. Electrospun nanofibers, such as poly(L-lactic acid) (PLLA) and poly(ϵ-caprolactone) (PCL), are collected on the mandrels to form the patient-specific TEVG.

Fig. 2.

Schematic workflow diagram of the semi-automatic Fontan surgical planning, patient-specific graft manufacturing, and implantation. Starting with three-dimensional (3D) contrast-enhanced magnetic resonance angiography (MRA) data, 3D models of the superior vena cava (SVC), the pulmonary arteries (PA), the inferior vena cava (IVC), the aorta and the heart are reconstructed by image segmentation. Fontan surgical planning is initialized by the 3D models and the blood flow data and includes conduit parameterization, development of surrogate models, and constrained optimization. A patient-specific optimized graft is manufactured by electrospun nanofibers before implantation.

In the first two steps of the anticipated workflow, cardiovascular MRA data were collected in DICOM format from two anonymized patients who had received Fontan surgery and need surgical revision. Image segmentation of MRA data was conducted by using commercially available software Mimics (Materialise, Leuven, Belgium) for reconstructing 3D Fontan models that include the proximal cavae and branch pulmonary arteries, as illustrated in Fig. 3A. Clean cuts and extensions were made to the smoothed models at inlets and outlets (IVC, SVC, LPA RPA) for partially developing velocity profiles and avoiding spurious influence of the BC respectively, as shown in Fig. 3B-C. From 4D MRI data, time-averaged flow rates at IVC and SVC (Q_IVC, Q_SVC) as well as LPA/RPA flow split ratio can be obtained. The outlet flow conditions at LPA and RPA (Q_LPA, Q_RPA) were prescribed by the measured LPA/RPA flow split ratio of total inlet flow rate to maintain conservation of mass. Table I presents the body surface areas (BSAs) and the inlet/outlet flow rates. To prepare the models for Fontan pathway planning and graft optimization, the existing, non-optimized conduits were removed from Fontan models to mimic the patients’ vessel structures before receiving the Fontan surgery. Fig. 3D shows a patient-specific model to use for testing our semi-automatic Fontan pathway planning method.

Fig. 3.

Illustration of model preparation for automatic Fontan pathway planning. (A) 3D reconstruction of the Fontan model for revision with the heart model by applying image segmentation on the patient’s MRI data. (B)-(C) Preparing Fontan revision model for hemodynamic simulation by making clean cuts and extensions at inlets and outlets for prescribing the BC. (D) Completed preparation of a superior cavopulmonary connection (SCPC) model by removing the native Fontan pathway.

TABLE I.

Patient-specific Data. BSA-body surface area; Q_IVC, Q_SVC, Q_LPA, Q_RPA-time-averaged flow rates at IVC, SVC, LPA, RPA.

Patient ID	Case 1	Case 2
BSA [m2]	1.593	1.625
QIVC [m3 s−1]	4.03e-5	3.29e-5
QSVC [m3 s−1]	2.30e-5	1.62e-5
QLPA [m3 s−1]	2.76e-5	2.37e-5
QRPA [m3 s−1]	3.57e-5	2.54e-5

III. Fontan Pathway Generation

A. Fontan Pathway Parameterization

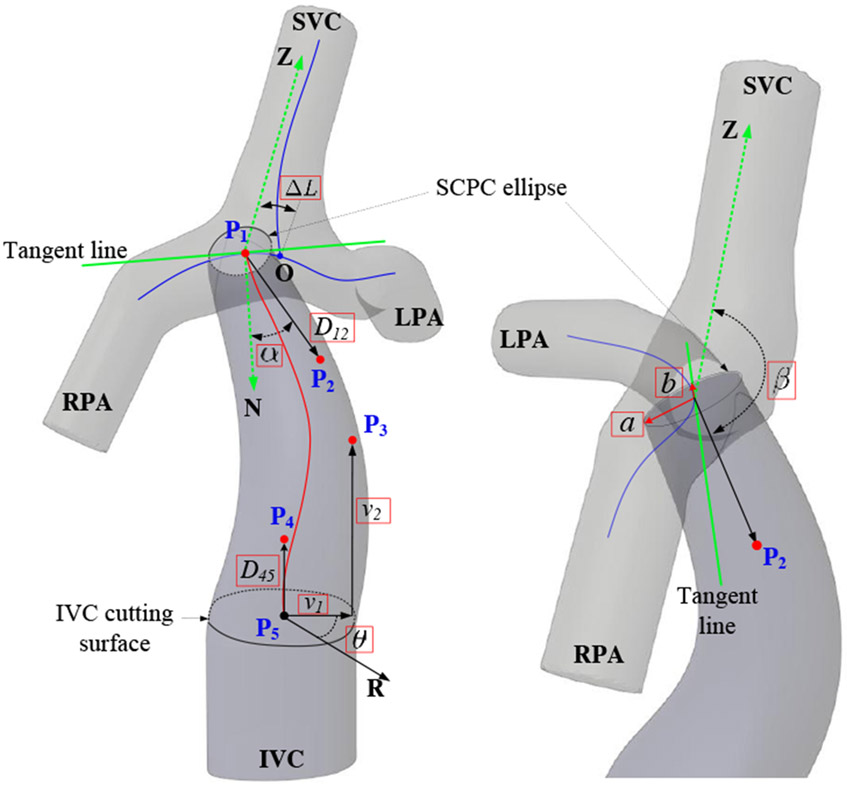
We focus on designing conduit-shaped grafts instead of bifurcated Y-grafts. From a practical perspective, limitation in available space restricts limb sizes of Y-grafts and imposes significant anastomosis challenges, although Y-grafts show promising results on improving HFD [36], [37]. Research studies demonstrate that power loss and WSS of a Fontan pathway correlate to the conduit’s diameter [38]. As shown in Fig. 4, the IVC cutting surface curve is unchanged during the pathway planning, we parameterize the conduit’s diameter by using the superior cavopulmonary connection (SCPC) ellipse radii a and b. HFD correlates to the conduit’s caval offset and connection angle [39] which represent the anatomosis location and orientation of the conduit on the SCPC model. To explore these variations, we employ parameters ΔL for representing the caval offset on the centerline between the LPA and the RPA (curve length of OP₁) and α, β for connection angle of the conduit. To enable the conduit to have sufficient flexibility for avoiding interference with other anatomies, we parameterize the conduit’s trajectory by using a fourth-order Bézier curve [40]. Thus, the conduit’s trajectory (red line) can be explored by varying the locations of P₁ ~ P₅. P₁ is the function of ΔL. P₂ is the function ΔL, α, β and D₁₂. P₃ is the function of v₁, v₂ and θ, where v₁ is the Euclidean distance from P₃ to $\overrightarrow{{\mathbf{P}}_5{\mathbf{P}}_4}$, v₂ is the distance from P₃ to the IVC cutting surface, θ is the azimuth angle between the reference direction R and the direction of v₁. P₄ is the function of D₄₅. P₅ is a fixed point locating at the center of the IVC cutting surface. In summary, we propose a 10-dimensional design space $\mathbf{x}=\{a,b,\alpha ,\beta ,\Delta L,D_{12},v_1,v_2,\theta ,D_{45}\}\in {\mathcal{R}}^{10}$, which are highlighted in red rectangular boxes in Fig. 4.

Fig. 4.

Fontan conduit parameterization. The conduit starts from the inferior vena cava (IVC) cutting surface, ends at the superior cavopulmonary connection (SCPC) ellipse which moves along the centerline between the left pulmonary artery (LPA) and the right pulmonary artery (RPA). The design parameters in the red boxes explore the geometry of a Fontan pathway.

The conduit’s trajectory C(t) is formulated in (1) by using P₁ ~ P₅.

$$\mathbf{C}(t)=\sum _{i=0}^{n=4}\left(\begin{array}{c}\hfill n\hfill \\ \hfill i\hfill \end{array}\right)(1-t{)}^{n-i}\cdot t^i\cdot {\mathbf{P}}_{5-i}t\in [0,1]$$ (1)

The conduit’s attaching point P₁ moves along the LPA-RPA centerline (the horizontal blue line in Fig. 4). Its location is defined by an offset parameter ΔL, which represents the curve length of OP₁. Note that the tangent line of the LPA-RPA centerline at P₁ conincides with the radius b. The location of P₂ is defined by four parameters: ΔL, α, β and D₁₂. α denotes the included angle between $\overrightarrow{{\mathbf{P}}_1{\mathbf{P}}_2}$ and $\overrightarrow{\mathbf{N}}$ which is perpendicular to the SCPC ellipse surface. β represents the included angle between $\overrightarrow{{\mathbf{P}}_1{\mathbf{P}}_2}$ and $\overrightarrow{\mathbf{Z}}$ which is paralleled to the centerline along SVC. D₁₂ represents the distance between P₁ and P₂. $\overrightarrow{{\mathbf{P}}_5{\mathbf{P}}_4}$ is perpendicular to the IVC cutting surface. D₄₅ is the distance between P₄ and P₅. The upper and lower bounds of a and b are determined by the maximal and minimal inscribed sphere diameters along the LPA-RPA centerline, which are computed by using the Vascular Modelling Toolkit (VMTK) [41]. α and β are in the range of [−45°, 45°] and [135°, 180°] respectively. θ is in the range of [0°, 360°]. The bounds of the other design parameters depend on patient-specific models.

B. Fontan Conduit 3D Modeling

Hemodynamics simulation of Fontan models requires combining the SCPC model, each conduit model and the IVC model into a full Fontan model. To guarantee a smooth Fontan pathway, we quantify the geometric quality of conduits by comparing the radius of curvature of the conduit centerline ${\widehat{\mathbf{r}}}_i$ and the conduit’s radius vector r_i at pathway points W_i. r_i has the smallest included angle with ${\widehat{\mathbf{r}}}_i$ on the i^th conduit mesh layer, as illustrated in Fig. 5B. A parameter N_v is designed for indicating number of bad mesh layers with $\Vert {\mathbf{r}}_i\Vert >\Vert {\widehat{\mathbf{r}}}_i\Vert$ (shown in Fig. 5C) that results in self-intersecting mesh on the conduit’s surface.

Fig. 5.

Fontan conduit modeling and evaluation of conduit model quality. (A) Construction of the conduit’s surface points based on a set of design parameters. (B) Conduit quality evaluation by comparing the conduit’s centerline curvature radii ${\widehat{\mathbf{r}}}_i$ and the conduit’s radii r_i. (C) Case illustration of $\Vert {\mathbf{r}}_i\Vert >\Vert {\widehat{\mathbf{r}}}_i\Vert$.

Algorithm 1 describes the method of Fontan conduit 3D modeling. The algorithm’s inputs include the sampled design parameters x_s, the SCPC model for extracting the centerlines, and the IVC model for specifying the surgical cutting surface. The output of the algorithm provides the conduit’s mesh model and the model quality indicator N_v. As shown in Fig. 5A, the Fontan pathway trajectory C(t) is first discretized and represented as W_i = C(i/N), where N denotes the total way-point number and 1 ≤ i ≤ N. The SCPC ellipse curve and the IVC cutting curve are also discretized and saved to model point arrays ${\mathbf{MP}}_N\in {\mathcal{R}}^{M\times 3}$ and ${\mathbf{MP}}_1\in {\mathcal{R}}^{M\times 3}$ respectively in the global coordinate system. To construct the conduit surface points around each W_i, local coordinate systems are defined by using unit vectors ${\mathbf{e}}_1^i$, ${\mathbf{e}}_2^i$, ${\mathbf{e}}_3^i$. Rotational matrix ${\mathbf{R}}_i=[{\mathbf{e}}_1^i,{\mathbf{e}}_2^i,{\mathbf{e}}_3^i{]}^T$ converts MP_i to local coordinates ${\mathbf{MP}}_i^L$. The local coordinates of the conduit model points ${\mathbf{MP}}_i^L$ around W_i can be computed by blending ${\mathbf{MP}}_1^L$ and ${\mathbf{MP}}_N^L$ with $f({\mathbf{MP}}_1^L,{\mathbf{MP}}_N^L,i)$, where f is a blending function. The line 12 of Algorithm 1 shows the equation for calculating the global coordinates of the conduit model points MP_i. By computing the radius of the curvature ${\widehat{\mathbf{r}}}_i$ and the conduit’s radius vector r_i, the lengths of ${\widehat{\mathbf{r}}}_i$ and r_i are compared to determine if N_v will be increased. In Section VI, we develop a surrogate function for N_v(x) and use it as a nonlinear constraint to optimize the design parameters x.

Algorithm 1 Conduit Modeling Algorithm

$$\begin{gathered} \begin{array}{cc}\hfill & \mathrm{Input}:\mathrm{A}\text{set of sampled design parameters}{\mathbf{x}}_s\in \mathbf{x},\text{SCPC}\hfill \\ \hfill & \text{model, IVC model}\hfill \\ \hfill & \mathrm{Output}:\text{Conduit model, Number of bad layers}{\mathrm{N}}_{\mathrm{v}}\hfill \\ \hfill & \\ 1:\mathbf{Initialization}{\mathrm{N}}_{\mathrm{v}}=0\hfill \\ \hfill & \\ 2:\text{Compute}N\text{conduit way-points}\mathbf{W}\in {\mathcal{R}}^{N\times 3}\text{by (1)}\hfill \\ \hfill & \\ 3:\text{Compute}M\text{discretized}\text{points}\text{of}\text{the}\text{SCPC}\text{ellipse}\hfill \\ \hfill & {\mathbf{MP}}_N\in {\mathcal{R}}^{M\times 3}\hfill \\ \hfill & \\ 4:\text{Compute}M\text{discretized points of the IVC cutting curve}\hfill \\ \hfill & {\mathbf{MP}}_1\in {\mathcal{R}}^{M\times 3}\hfill \\ \hfill & \\ 5:\mathbf{while}i\le N\mathbf{do}\hfill \\ \hfill & \\ 6:\text{Compute}{\mathbf{e}}_1^i,{\mathbf{e}}_2^i,{\mathbf{e}}_3^i\in {\mathcal{R}}^{3\times 1}\mid \{\text{Unit vectors of axes of}\hfill \\ \hfill & \text{local coordinate systems with the origin at}{\mathbf{W}}_i.\}\hfill \\ \hfill & \\ 7:{\mathbf{R}}_i=[{\mathbf{e}}_1^i,{\mathbf{e}}_2^i,{\mathbf{e}}_3^i{]}^T\hfill \\ \hfill & \\ 8:i=i+1\hfill \\ \hfill & \\ 9:\mathbf{end}\mathbf{while}\hfill \\ \hfill & 10:{\mathbf{MP}}_1^L={\mathbf{R}}_1\cdot {\mathbf{MP}}_1,{\mathbf{MP}}_N^L={\mathbf{R}}_N\cdot {\mathbf{MP}}_N\hfill \\ \hfill & 11:\mathbf{while}i\le N\mathbf{do}\hfill \\ \hfill & 12:{\mathbf{MP}}_i={\mathbf{R}}_i^T\cdot f({\mathbf{MP}}_1^L,{\mathbf{MP}}_N^L,i)+{\mathbf{W}}_i\hfill \\ \hfill & 13:\text{Compute}{\widehat{\mathbf{r}}}_i,{\mathbf{r}}_i\hfill \\ \hfill & 14:\mathbf{if}\Vert {\widehat{\mathbf{r}}}_i\Vert \le \Vert {\mathbf{r}}_i\Vert \mathbf{then}\hfill \\ \hfill & 15:{\mathrm{N}}_{\mathrm{v}}={\mathrm{N}}_{\mathrm{v}}+1\hfill \\ \hfill & 16:\mathbf{end}\mathbf{if}\hfill \\ \hfill & 17:i=i+1\hfill \\ \hfill & 18:\mathbf{end}\mathbf{while}\hfill \end{array} \end{gathered}$$

IV. Computation of Fontan Hemodynamics

A. Fontan Hemodynamics

For computing Fontan hemodynamics, 3D meshes of Fontan models need to be generated with defined mesh regions to apply the BC. Fig. 6 demonstrates the process of mesh generation for Fontan models with a virtually planned pathway. Fig. 6A shows the SCPC model and IVC model, and a planned conduit model as separate models. Fig. 6B shows merging of the models into a single watertight stereolithograhpy (STL) model with no internal mesh. The model merging is conducted by three steps: 1) converting the three separate STL models into solid models; 2) Boolean union the solid models into a single solid model; and 3) converting the single solid model into an STL file. This model merging process is automated by using FreeCAD application programming interfaces [42].

Fig. 6.

Mesh preparation for Fontan hemodynamic simulation. (A) Illustration of the SCPC model, the inferior vena cava (IVC) model, and the conduit model as individual surface meshes. (B) Merging of the surface meshes from different models into an integrated Fontan surface mesh. (C) Generating mesh for computational fluid dynamics (CFD) simulation and specifying boundary areas and %WSS measurement areas.

We employed OpenFOAM [43], which is an open source software package for CFD simulation, to compute Fontan hemodynamics.Validation of using openFoAM to compute hemodynamics has been demonstrated in [44]. The snappyHexMesh mesh generator in OpenFOAM was used to generate mesh for Fontan models. The mesh size is controlled in the range of 0.35 mm~0.7 mm according to our previous mesh convergence study [45]. Three boundary layers with 0.35 mm surface mesh size were applied to each model mesh for computing WSS. To define boundary regions of the mesh model, four bounding boxes are specified in Fig. 6C to indicate the locations of SVC, IVC, LPA and RPA. Since the SCPC model and the IVC model were unchanged during the surgical planning for the same patient, the bounding boxes can be initialized at the beginning. We used the topoSet utility in openFoAM to select mesh surfaces within the bounding boxes, and applied createPatch utility to define the boundary faces. Previous research study demonstrated good agreement between using time-averaged and pulsatile BC in simulating Fontan hemodynamics [12]. Thus, in this study we prescribed time-averaged mass flow rates at the inlets and outlets as BC according to the volumetric flow rates in Table I and the blood density.

A few assumptions were made for ensuring reasonable computation time of hemodynamic simulations while still obtaining meaningful hemodynamic parameters. The blood was modeled as incompressible, Newtonian fluid [46] with a density of 1060 kg m⁻³ and a dynamic viscosity of 3.5 × 10⁻³ Pa s. Considering the low Reynolds number of the two cases (Re < 1000), the blood flow was modeled as laminar. For large vessels such as PA and venae cavae, it is acceptable to model the vessel walls as rigid structure [36].

Hemodynamic performance of Fontan models are evaluated by using three parameters: iPL, %WSS of the parameterized Fontan pathway and HFD. The calculation of these parameters involves solving 3D steady-state Navier-Stokes (NS) equations in the domain of a Fontan model. We employed the SimpleFoam solver and set the convergence values of pressure and velocity residuals as 10⁻⁴.

iPL is a dimensionless resistive index that correlates with exercise capacity [10], which is formulated as

$$\text{iPL}=\frac{{\text{BSA}}^2}{\rho Q_s^2}\left[\sum _{\text{SVC,IVC}}Q(\overline{p}+\frac{1}{2}\rho {\overline{u}}^2)-\sum _{\text{LPA,RPA}}Q(\overline{p}+\frac{1}{2}\rho {\overline{u}}^2)\right]$$ (2)

where Q is flow rate, Q_s = Q_IVC + Q_SVC is the systemic venous flow rate, $\overline{p}$ is static pressure, ρ is the blood density, $\overline{u}$ is flow velocity, BSA is the patient’s body surface area.

The normal physiologic range of WSS for venous flow is 1 ~ 10 dynes/cm² (0.1 ~ 1 Pa) [47]. We quantify %WSS as

$$\%\text{WSS}=\frac{{\text{Area}}_{\text{lowWSS}}}{{\text{Area}}_{\text{Conduit}}}$$ (3)

where Area_lowWSS is the luminal surface areas in the Fontan conduit with WSS<1 dynes/cm² (0.1 Pa), Area_Conduit represents the total surface area of the conduit, which can be automatically selected by setting a %WSS measurement region as shown in Fig. 6C.

Algorithm 2 Intersection Depth of Conduit and Heart Models

$$\begin{gathered} \begin{array}{cc}\hfill & \mathrm{Input}:\mathrm{A}\text{set}\text{of}\text{sampled design parameters}{\mathbf{x}}_s\in \mathbf{x},\text{SCPC}\hfill \\ \hfill & \text{model, IVC model, Heart model}(M_H)\hfill \\ \hfill & \mathrm{Output}:\text{Maximum intersection depth (InDep)}\hfill \\ \hfill & \\ 1:\text{Run Algorithm 1, obtain the conduit model}{M}_C\hfill \\ \hfill & \\ 2:\text{Compute intersection model}{M}_I=M_C\cap M_H\hfill \\ \hfill & \\ 3:\text{Construct zero matrix}{\mathbf{M}}_{\mathbf{InDep}}\in {\mathcal{R}}^{N\times M}\hfill \\ \hfill & \\ 4:\mathbf{while}i\le N\mathbf{do}\hfill \\ \hfill & \\ 5:\mathbf{while}j\le M\mathbf{do}\hfill \\ \hfill & \\ 6:\text{Generate a ray}{\gamma }_{i,j}\text{from}{\mathbf{W}}_i\text{passing by}{\mathbf{MP}}_{i,j}\hfill \\ \hfill & \\ 7:\text{Compute intersections}L(M_I,{\gamma }_{i,j})=[{\mathbf{p}}_1,\dots ,{\mathbf{p}}_K]\hfill \\ \hfill & \\ 8:\mathbf{if}K=1\mathbf{then}\hfill \\ \hfill & \\ 9:\text{Reverse}{\gamma }_{i,j}\to {\widehat{\gamma }}_{i,j},\text{compute}{\mathbf{p}}_1^{\prime }=L(M_I,{\widehat{\gamma }}_{i,j})\hfill \\ \hfill & 10:{\mathbf{M}}_{\text{InDep}}(i,j)=\Vert {\mathbf{p}}_1-{\mathbf{p}}_1^{\prime }\Vert \hfill \\ \hfill & 11:\mathbf{end}\mathbf{if}\hfill \\ \hfill & 12:\mathbf{if}K=2\mathbf{then}\hfill \\ \hfill & 13:{\mathbf{M}}_{\text{InDep}}(i,j)=\Vert {\mathbf{p}}_1-{\mathbf{p}}_2\Vert \hfill \\ \hfill & 14:\mathbf{end}\mathbf{if}\hfill \\ \hfill & 15:j=j+1\hfill \\ \hfill & 16:\mathbf{end}\mathbf{while}\hfill \\ \hfill & 17:i=i+1\hfill \\ \hfill & 18:\mathbf{end}\mathbf{while}\hfill \\ \hfill & 19:\text{InDep}=\max ({\mathbf{M}}_{\mathbf{InDep}})\hfill \end{array} \end{gathered}$$

HFD is defined as the ratio of blood from the IVC to the LPA and the RPA, respectively. The HFD was evaluated by applying the one-way coupling Lagrangian particle tracking method on the steady-state flow that is the final solution of the NS equations. A total of 2000 massless infinitesimal particles were randomly distributed at the IVC, and passively carried by the fluid flow. According to the number of particles received at the LPA (N_LPA) and the RPA (N_RPA), the HFD was calculated by

$$\text{HFD}=\frac{{\text{HFD}}_{\text{RPA}}}{{\text{HFD}}_{\text{LPA}}},{\text{HFD}}_{\text{LPA}}=\frac{{\mathrm{N}}_{\text{LPA}}}{{\mathrm{N}}_{\text{TOT}}},{\text{HFD}}_{\text{RPA}}=\frac{{\mathrm{N}}_{\text{RPA}}}{{\mathrm{N}}_{\text{TOT}}}$$ (4)

where N_TOT represents the total particle number.

V. Computation of Conduit-Heart Intersection in Automatic Fontan Surgical Planning

The virtually generated Fontan pathways from the conduit’s design space may interfere with other portions of the anatomy such as the heart. As shown in Fig. 7A, three Fontan pathways are automatically generated, but one of them is an infeasible pathway because of its intersection with the heart. in order to eliminate the infeasible pathways during the automatic planning of Fontan conduits, we define the geometric interference between the heart model and a conduit model by using the maximum intersection depth (InDep). For the heart model, its volume periodically changes during blood pumping cycles. To make conservative intersection estimation, the peak volume of the heart model at the start of systole should be used.

Fig. 7.

Computation of geometric interference between a Fontan conduit and the heart model. (A) Illustration of feasible and infeasible Fontan pathways in Fontan surgical planning. (B) 3D Illustration of the geometric interference with the highlighted intersection volume. (C) Illustration of computing intersection depth (InDep) based on the intersection volume.

Algorithm 2 describes the InDep computation method for each conduit design (M_C). Except the heart model (M_H), all the other inputs are identical to the inputs of Algorithm 1. Given M_C and M_H, an intersection model M_I can be computed by operating a Boolean intersection M_C ∩ M_H, as illustrated in Fig. 7B. A zero matrix M_InDep with dimensions of N × M is initialized for containing intersection depths at different locations of M_C, where N is number of way-points W_i (1 ≤ i ≤ N), M is the number of surface points ${\mathbf{MP}}_i\in {\mathcal{R}}^{M\times 3}$ on the i^th layer of M_C. At each W_i (the red dots in Fig. 7C), M rays γ_i,j are generated pointing to the conduit surface points MP_i,j (1 ≤ j ≤ M). We adopt a ray tracing algorithm [48] to compute a list of intersection points L(M_I, γ_i,j) for M_I and γ_i,j. There are three different cases: no intersection (K = 0), one intersecting point p₁ (K = 1) and two intersecting points p₁, p₂ (K = 2). As shown in Fig. 7C, K = 1 happens when W_i locates inside M_I. In this case, a ray with reversed direction ${\widehat{\gamma }}_{i,j}$ is used to find the opposite intersecting point ${\mathbf{p}}_1^{\prime }$. The value of $\Vert {\mathbf{p}}_1-{\mathbf{p}}_1^{\prime }\Vert$ is saved to M_InDep(i, j). K = 2 may happen when W_i locates outside M_I. In this case, M_InDep(i, j) = ∥p₁ − p₂∥. After the ray tracing process, the maximum element in M_InDep(i, j) is returned as InDep.

VI. Surrogate-Based Optimization

The design performance of Fontan conduits is measured by five parameters iPL, HFD, %WSS, N_v, InDep. To find a set of conduit design parameters x_o ∈ x that optimizes the hemodynamics of the Fontan pathway, we conducted constrained optimization based on surrogate models f_iPL (x), f_HFD (x), f_%WSS (x), f_Nv (x) and f_InDep (x), where x is the design space.

A. Building Surrogate Models

Gaussian process regression (GPR) was used to build surrogate models based on training datasets that were collected from high-fidelity simulations. The lower bounds (LB) and upper bounds (UB) of the design space for the two patient-specific cases are illustrated in Table II. Note that we used the range of RPA-LPA centerline point index ΔL_ind to define the upper bound and the lower bound for design space sampling. ΔL can be calculated by accumulating the adjacent point distances between P₁ and O, as shown in Fig. 4.

TABLE II.

Bounds of Design Space x for Case 1 and Case 2. LB–Lower Bound, UB–Uppper Bound.

x	a (mm)		b (mm)		α (°)		β (°)		ΔLind		D12 (mm)		v1 (mm)		v2 (mm)		θ (°)		D45 (mm)
	LB	UB	LB	UB	LB	UB	LB	UB	LB	UB	LB	UB	LB	UB	LB	UB	LB	UB	LB	UB
Case 1	5	14	5	11	−45	45	135	180	60	120	3	30	0	50	0	40	0	360	3	30
Case 2	5	12.5	5	12.5	−45	45	135	180	190	300	3	30	0	50	0	40	0	360	3	30

To generate N_s sets of design parameters for representing the design space, Latin hypercube sampling (LHS) method was employed. High-fidelity hemodynamic simulations are computationally expensive. For reducing the computation time, we deployed our codes on a high-performance computation cluster (HPCC).

Let f_e (x) represent a surrogate model

$$f_e(\mathbf{x})={\widehat{\zeta }}_e+{\mathbf{c}}_e^T(\mathbf{x}){\mathbf{C}}_e^{-1}({\widehat{\mathbf{f}}}_e-{\widehat{\zeta }}_e\mathbf{f}),$$ (5)

where e = {iPL, HFD, %WSS, N_v, InDep}, C_e represents the covariance matrix with its elemental kernel function modeled as

$$C_e({\mathbf{x}}^i,{\mathbf{x}}^j)=\text{exp}\left(-\sum _{s=1}^{N_s}{\Theta }_s\Vert {\mathbf{x}}^i-{\mathbf{x}}^j{\Vert }^2\right).$$ (6)

c_e(x) is the covariance vector

$${\mathbf{c}}_e(\mathbf{x})=[C_e(\mathbf{x},{\mathbf{x}}^1),\dots ,C_e(\mathbf{x},{\mathbf{x}}^{N_s})].$$ (7)

Θ_s denotes the correlation length, which is optimized by maximum likelihood estimation. ${\widehat{\mathbf{f}}}_e$ represents the vector of N_s observed high-fidelity parameters. f is a unity vector with dimensions of 1 × N_s. ${\widehat{\zeta }}_e$ is calculated by using generalized least squares in (8).

$${\widehat{\zeta }}_e=({\mathbf{f}}^T{\mathbf{C}}_e^{-1}\mathbf{f}{)}^{-1}{\mathbf{f}}^T{\mathbf{C}}_e^{-1}{\widehat{\mathbf{f}}}_e.$$ (8)

We implemented GPR to build surrogate models by using the Surfpack software library [49].

The accuracy of surrogate models depends on the number and location of samples in the design space. We applied 10-fold cross-validation to test surrogate models with different numbers of training samples, and used mean absolute error (MAE) to quantify the surrogate model accuracy (Supplementary Materials, S1). We found surrogate models trained by 2000 samples provide good balance between prediction accuracy and computation time.

B. Constrained Nonlinear Optimization

We aim to find a set of design parameter x_o for minimizing iPL while constraining HFD, %WSS, InDep, N_v in acceptable ranges. For HFD, there is no clinical cutoff to prevent pulmonary arteriovenous malformations. Haggerty et al. [12] show that the mean LPA split is 44% with interquartile range 31% to 57%. Thus we aimed to have the acceptable HFD range to match this cohort as 40%/60% ~ 60%/40%. According to our prior study [21], we set %WSS below 10% for reducing the thrombosis risk. A maximum of 2 mm intersection depth between a conduit model and the heart model is deemed clinically acceptable. We also need to impose N_v ≤ 2 for filtering out bad conduit meshes. The constrained nonlinear optimization problem can thus be formulated in (9).

$$\begin{gathered} \underset{{\mathbf{x}}_o\in \mathbf{x}}{\text{min}}{f}_{\text{iPL}}({\mathbf{x}}_o) \\ \text{s.t.}0.67\le f_{\text{HFD}}({\mathbf{x}}_o)\le 1.5 \\ {f}_{\%\text{WSS}}({\mathbf{x}}_o)<10\% \\ {f}_{\text{InDep}}({\mathbf{x}}_o)<2\text{mm} \\ {f}_{{\mathrm{N}}_{\mathrm{v}}}({\mathbf{x}}_o)\le 2 \end{gathered}$$ (9)

It is desired to find the globally optimal solution to (9). However, unless f_iPL(x) has certain properties [50], there is no mathematical guarantee to find global optima. Instead, we sampled multiple start points (different sets of design parameters) to search for near-globally optimal solution in the design space (Supplementary Materials, S2). To minimize f_iPL(x), we employed the asynchronous parallel pattern search (APPS) method [51] that does not require gradient information of the objective function.

VII. Performance Evaluation

A. Comparison of Various Fontan Pathway Planning Methods

To evaluate the performance of our proposed method, we provide a side-by-side hemodynamics comparison among the Fontan models designed by surgeon’s unconstrained modeling (SUM) method [21], engineer’s manual optimization (ManuOpt) method [20], and the automatic optimization (AutoOpt) method, as well as patients’ native Fontan models for Case 1 and Case 2.

The procedures of model preparation for both SUM and ManuOpt are similar to those for AutoOpt as described in Section II. The post-surgical Fontan pathway was removed from the models to create SCPC models as shown in Fig. 3D. For SUM, the SCPC models and the heart models were 3D printed and mounted on fixtures to allow an experienced cardiac surgeon to handcraft his ideal Fontan pathways by using modeling clay. The SUM Fontan models were then 3D scanned to STL files for further analysis. For ManuOpt, Fontan pathways were created over several CAD-CFD iterations by using tube-shaped conduits or bifurcated conduits. The final ManuOpt models were selected with lowest iPL and normal range of HFD and %WSS.

In Fig. 8, the first columns of Case 1 and Case 2 show iPL of the Fontan models with native, SUM, ManuOpt and AutoOpt pathways. The heart and vessel models are also shown to demonstrate the Fontan pathways are anatomically feasible. The second and third columns of Case 1 and Case 2 show %WSS and HFD respectively. Hemodynamics of the Fontan models were computed by using the method in Section IV-A. Any abnormal hemodynamic parameters are highlighted in red considering the design criteria: iPL<0.03, %WSS<10%, 0.67<HFD<1.5.

Fig. 8.

Hemodynamic performance comparison of Fontan pathway designs of Case 1 and Case 2 among native models, the surgeon’s unconstrained modeling (SUM), the models from engineer’s manual optimization (ManuOpt) and automatic optimization. The values highlighted in red are outside their normal ranges or constraints (iPL<0.03, %WSS<10%, 0.67≤HFD≤1.5). The red rectangles indicate the areas for computing %WSS.

In Case 1, only the native model has abnormally high iPL (0.0424). The SUM model has the lowest iPL (0.0228). The iPL of the AutoOpt model (0.0266) is slightly lower than that of the ManuOpt model (0.0274). %WSS of all the cases falls in the defined threshold range. The SUM model’s %WSS is significantly higher than that of the other models due to its larger conduit diameter. WSS values are plotted on the Fontan models in the range of 0.1 Pa~1 Pa and the red rectangles indicate the areas for %WSS calculation. The ManuOpt and AutoOpt models both have HFD within the HFD thresholds. The AutoOpt model’s hemodynamic performance outperforms that of the ManuOpt model in iPL, %WSS and HFD.

In Case 2, iPL of all the models are within the normal range. Although the native model and the SUM model have significantly lower iPL than that of the ManuOpt and AutoOpt models, their %WSS and HFD are all outside the design thresholds. In this case, the ManuOpt model performs slightly better than the AutoOpt model in iPL and %WSS, but the AutoOpt model’s HFD performs slightly better than that of the ManuOpt model.

The ManuOpt models were selected from three consecutive design iterations. Followed by preparation of the patient’s models (SCPC, IVC, heart), each iteration includes generating a cohort of graft designs based on multiple design parameters, computing all the generated Fontan models on a HPCC for parallel CFD computation, post-processing the results and selecting the best set of parameter to generate the cohort of graft designs for the next iteration. Each iteration took about one week with most of the time spent on CFD computation and post-processing. The turnaround time (including human effort and computational effort) of designing a ManuOpt model for each patient is about three weeks [21]. In contrast, the design of an AutoOpt model only requires human effort for model preparation and spent most of the time on the training data collection for the surrogate models. We employed a HPCC by using 40 CPU cores and 4 Gigabyte random-access memory (RAM) per core to run 2,000 high-fidelity models, which took approximately 15 hours for each patient. The time spent on building surrogate models and multi-start optimization was negligible (within a few minutes).

B. Sensitivity Analysis

To evaluate the robustness of the proposed automatic Fontan graft optimization method, we performed three different types of sensitivity analysis to investigate (1) how imperfect graft implantation affects the hemodynamic performance of AutoOpt grafts; (2) how uncertainty of LPA/RPA flow split affects the hemodynamic performance of AutoOpt grafts; and (3) how uncertainty of LPA/RPA flow splits affects the training data for building surrogate models of the hemodynamic parameters and subsequently affects the shapes and hemodynamic performance of AutoOpt grafts.

1). Sensitivity Analysis of Graft Implantation

In Fig. 9, we demonstrated two types of graft implantation errors for both of the patient cases. The first row of the plots show how the anastomosis angle offsets ±10° affect iPL, HFD and %WSS. The means (μ) and standard deviations (σ) of iPL, HFD, %WSS of each patient are represented as μ ± σ. For the patient case 1, we have 0.0271 ± 0.0005 for iPL, 1.0779 ± 0.2811 for HFD, and 0.0029 ± 0.0009 for %WSS. For the patient case 2, we have 0.0179 ± 0.0003 for iPL, 1.0169 ± 0.0955 for HFD, and 0.1057 ± 0.0086 for %WSS.

Fig. 9.

Sensitivity analysis of AutoOpt graft implantation. The top row and the bottom row demonstrate how the graft connection angle offsets and the graft connection displacements affect the hemodynamic performance respectively.

Multiple regression analysis and two sample t-tests (2-tailed, 95% confidence interval) were performed between the hemodynamic parameters and the anastomosis errors. The value of hemodynamic parameters from each patient case were normalized. Our results show that there were significant correlations between HFD and angle offset (r = 0.924, p = 8.4E–10), between %WSS and angle offset (r = 0.847, p = 6.5E–7), between iPL and connection displacement (r = 0.849, p = 5.9E–7), between HFD and connection displacement (r = 0.97, p = 9.2E–14), where r is the Pearson’s correlation coefficient, p represents p-value with significance level of 0.05. Our results agree with the findings in [52].

2). Sensitivity Analysis of BC in Hemodynamic Performance of AutoOpt Grafts

For testing how uncertainty of LPA/RPA flow splits affects the hemodynamic performance AutoOpt grafts, we introduced ±20% perturbation to the original Q_LPA and adjusted Q_RPA to conserve the systemic venous flow rate Q_IVC+Q_SVC. The updated BC ${\widehat{Q}}_{{}_{\text{LPA}}}$, ${\widehat{Q}}_{{}_{\text{RPA}}}$, ${\widehat{Q}}_{{}_{\text{IVC}}}$ and ${\widehat{Q}}_{{}_{\text{SVC}}}$ are illustrated in Table III in the top 6 rows.

TABLE III.

BC for sensitivity analysis by introducing ±20% perturbation to Q_LPA, and BC of different exercise levels. The values of original BC are from Table I.

Conditions	BC of Case 1				BC of Case 2
	${\widehat{Q}}_{{}_{\text{LPA}}}[{\mathrm{m}}^3∕\mathrm{s}]$	${\widehat{Q}}_{{}_{\text{RPA}}}[{\mathrm{m}}^3∕\mathrm{s}]$	${\widehat{Q}}_{{}_{\text{IVC}}}[{\mathrm{m}}^3∕\mathrm{s}]$	${\widehat{Q}}_{{}_{\text{SVC}}}[{\mathrm{m}}^3∕\mathrm{s}]$	${\widehat{Q}}_{{}_{\text{LPA}}}[{\mathrm{m}}^3∕\mathrm{s}]$	${\widehat{Q}}_{{}_{\text{RPA}}}[{\mathrm{m}}^3∕\mathrm{s}]$	${\widehat{Q}}_{{}_{\text{IVC}}}[{\mathrm{m}}^3∕\mathrm{s}]$	${\widehat{Q}}_{{}_{\text{SVC}}}[{\mathrm{m}}^3∕\mathrm{s}]$
+20% QLPA	3.31e-5	3.02e-5	4.03e-5	2.30e-5	2.84e-5	2.07e-5	3.29e-5	1.62e-5
+10% QLPA	3.04e-5	3.29e-5	4.03e-5	2.30e-5	2.61e-5	2.30e-5	3.29e-5	1.62e-5
+5% QLPA	2.90e-5	3.43e-5	4.03e-5	2.30e-5	2.49e-5	2.42e-5	3.29e-5	1.62e-5
−5% QLPA	2.62e-5	3.71e-5	4.03e-5	2.30e-5	2.25e-5	2.66e-5	3.29e-5	1.62e-5
−10% QLPA	2.48e-5	3.85e-5	4.03e-5	2.30e-5	2.13e-5	2.78e-5	3.29e-5	1.62e-5
−20% QLPA	2.21e-5	4.12e-5	4.03e-5	2.30e-5	1.89e-5	3.02e-5	3.29e-5	1.62e-5
2×QIVC	4.52e-5	5.84e-5	8.06e-5	2.30e-5	4.01e-5	4.29e-5	6.68e-5	1.62e-5
3×QIVC	6.27e-5	8.12e-5	1.209e-4	2.30e-5	5.55e-5	5.94e-5	9.87e-5	1.62e-5

Fig. 10 shows the iPL, HFD and %WSS of the AutoOpt grafts (computed based on the original BC in Table I) under the updated BC. The x-axis represents the BC in Table III. The means and standard deviations for iPL, HFD and %WSS are 0.0268 ± 0.0008 (Case 1) and 0.0181 ± 0.0005 (Case 2), 1.0610 ± 0.2207 (Case 1) and 0.9642 ± 0.2512 (Case 2), and 0.0028 ± 0.0007 (Case 1) and 0.1058 ± 0.0068 (Case 2), respectively. The results show only the normalized HFD results significantly correlates with and the uncertainty of flow splits (r = 0.989, p = 2.9E–11).

Fig. 10.

Hemodynamic performance of AutoOpt grafts under uncertain BC.

3). Sensitivity Analysis of Surrogate-based Optimization

In the analysis, we firstly evaluated how the uncertainty of LPA/RPA flow splits affects the geometrical shape of AutoOpt grafts (via influencing the training data of surrogate models). We used the optimized design parameters (Supplementary Materials, S2) as the initial guesses for the constrained optimization with the updated surrogate models. To quantify the geometrical shape changes (comparing with the AutoOpt grafts by using the training data collected from the original BC) of the optimized grafts, we introduced a bidirectional root mean square error of Hausdorff distances [53] in (10) to measure their similarly, where p and p′ represent 3D surface points of the two graft models M_C1 and M_C2 respectively as shown in Fig. 11A.

Fig. 11.

Geometry changes of AutoOpt grafts by introducing uncertain LPA/RPA flow splits, and their resulted hemodynamic performance.

$$\mathbf{S}=\sqrt{\frac{1}{N}\left\{\sum _{\mathbf{p}\in {\mathrm{M}}_{\mathrm{C}1}}{\left(\underset{{\mathbf{p}}^{\prime }\in {\mathrm{M}}_{\mathrm{C}2}}{\text{min}}\Vert \mathbf{p}-{\mathbf{p}}^{\prime }\Vert \right)}^2+\sum _{{\mathbf{p}}^{\prime }\in {\mathrm{M}}_{\mathrm{C}2}}{\left(\underset{\mathbf{p}\in {\mathrm{M}}_{\mathrm{C}1}}{\text{min}}\Vert \mathbf{p}-{\mathbf{p}}^{\prime }\Vert \right)}^2\right\}}$$ (10)

Fig. 11B shows the results of graft shape similarity. The categories along the x-axis represent graft shape comparing groups. For example, $G_{+20\%}^{Org}$ represents comparing the shapes of the AutoOpt grafts, which were learned and computed from the original training dataset and a modified training dataset with the BC indicated in the row of +20% Q_LPA in Table III. The means and standard deviations of S for the two patient cases are 2.165 ±0.1796 mm and 0.4459 ±0.0527 mm respectively. The normalized S are not significantly correlated to the uncertainty of the BC in the training datasets (p > 0.05).

Fig. 11C shows the hemodynamic performance of the AutoOpt grafts that were computed from the training data with modified BC. These BC are labeled in the x-axis and detailed in row 1 to row 6 in Table III. The means and standard deviations of iPL, HFD and %WSS are 0.0303±0.0007 (Case 1) and 0.0190 ± 0.0003 (Case 2), 1.0848 ± 0.1081 (Case 1) and 0.8773 ± 0.0423 (Case 2), 0.0015 ± 0.0007 (Case 1) and 0.1013 ± 0.0025 (Case 2), respectively. The statistic analysis indicated none of the hemodynamic parameters are significantly correlated to the uncertainty of BC in the training datasets (p > 0.05).

C. Influence of Exercise Conditions on AutoOpt Grafts

Fig. 12 shows the hemodynamic performance of the AutoOpt grafts (computed from the training datasets with original BC) by doubling and tripling the averaged flow rates at IVC to mimic different levels of exercise conditions. The flow rates at SVC were kept as original values [54], and the flow rates at LPA and RPA were calculated based on original flow splits and new systemic venous flow rates at each exercise level. The exercise BC are in the last two rows of Table III.

Fig. 12.

Hemodynamic performance of AutoOpt grafts under exercise conditions. Original indicates the BC in Table I. The BC of 2×Q_IVC and 3×Q_IVC are indicated in the last two rows of Table III.

The result indicates that as the exercise intensity increases, iPL rapidly increases (0.114 under 2×Q_IVC condition, 0.311 under 3×Q_IVC), and %WSS rapidly decreases. The result aligns with the prior research [10], which shows the correlation between the patient’s exercise capacity and total cavopulmonary connection (TCPC) power loss. The HFD values of the both cases are generally within the threshold. One patient (Case 2) has more steady HFD than the other (Case 1) under the exercise conditions.

D. Patient-Specific TEVG Manufacturing

To demonstrate the feasibility of manufacturing the patient-specific AutoOpt grafts shown in the last row of Fig. 8 for the two patients, we employed electrospinning technique to 3D-print the grafts. The electrospinning process applied high electric field on a polymer solution, which mixed polyglycolide (PGA) and poly(l-lactide-co-ϵ-caprolactone) (PLCL). By increasing the electric field, the strand of polymer solution squirted out of the spinneret and was collected by grounded spinning mandrels, as conceptually shown in Fig. 2D. The mandrels with the AutoOpt graft geometries were 3D-printed by using acrylonitrile butadiene styrene (ABS) polymers and wrapped by aluminum foil for electroconductivity. In clinical application, the mandrels will be 3D-printed by stainless steel for easy sterilization. Fig. 13 shows the aluminum foil wrapped mandrels and the grafts made by the nanofiber. The 3D-printed TEVG has a uniform wall thickness of 657 ±36 μm.

Fig. 13.

3D printed mandrels and AutoOpt TEVG for Case 1 and Case 2.

The burst pressure and compliance of the TEVG were evaluated in a sheep model for 6 months in our prior study [19]. The burst pressures of preoperative TEVG, 6-month TEVG and native IVC are 6167 ±5627 mm Hg, 11,685±11,506 mm Hg, 13,062±6847 mm Hg respectively. There was no significant difference among the groups (p > 0.05). The compliance of preoperative TEVG was significantly greater than that of native IVC, but there was no significant difference between 6-month TEVG and native IVC.

VIII. Discussion

To the best of our knowledge, this is the first effort to automatically design patient-specific hemodynamically optimized Fontan grafts. We are aware of that any engineered graft designs, even when fully optimized, lack the surgeon’s full confidence in direct implementation. In our prior work, we have developed a patient-specific graft design user interface [55], which is able take the surgeon’s intuitive Fontan pathway planning as the initial design parameters for the automatic optimization method. Our technique can bridge the gap between machine intelligence and clinical medicine, allowing the surgeon to directly incorporate their unique understanding of surgical field into the design of Fontan grafts, as well as directly receiving optimized surgical planning based on the surgeon’s preferred Fontan pathways. In addition, although our automatic Fontan graft optimization method doesn’t consider the fenestration attachment of the grafts to the right atrium, clinical study has demonstrated no compression from outside of non-ring enforced grafts for all the patients [56]. In our future work, we will expand this technique to include other grafts such as bifurcated grafts.

We introduced %WSS as a design constraint to prevent oversizing Fontan conduits that can lead to flow stagnation and thrombosis. This measurement is based on our prior study [21] and has not been clinically validated. The threshold %WSS<10% was an arbitrary cutoff. However, it is convenient to alter this measurement in our technique according to other physiologic standards. In addition to %WSS, we used InDep to measure the interference between Fontan pathway and the heart model. Clinically, the conduit’s physical interaction is more tolerable with the heart than with other vessels. Although we did not directly consider conduit-vessel interaction in this article, it is straightforward to apply an additional f_InDep in (9) with stricter thresholds.

The sensitivity analysis performed in this paper indicates that HFD is the most sensitive parameter among the hemodynamic parameters for Fontan surgical planning. The HFD of an optimized graft can be significantly affected by anastomosis displacement/offset during surgical implantation and uncertainty of post-operative BC. In this work, we predict the post-operative BC by using pre-operative BC, following the work of [57]. Although a clinical study indicates there are no significant differences in pre- to post-operative changes in flow rates [52], the differences may still affect the accuracy of surgical planning. Further improvement of the prediction of post-operative BC could be approached by using a lumped parameter network [58] that can dynamically adjust flow and pressure at the boundaries to accommodate changes in post-surgical Fontan anatomies. Alternatively, instead of pursuing accurate prediction of post-operative BC and surgical implantation for maximizing the performance of an optimal graft design, applying robust design optimization techniques [59] in the semi-automatic Fontan surgical planning workflow could be a practical solution to better tolerate the uncertainty and keep HFD within the thresholds by statistically modeling the uncertainty of BC and anastomosis errors and integrating the uncertainty models in the graft design optimization process. One other limitation of this study is the expressiveness of the design space representation. Manual designs, including the engineer’s CAD deigns and the surgeon’s clay modeling, allow subtle tuning of the conduit’s geometry especially at the conduit-SCPC anastomosis area. A thorough design space study will be conducted to improve this aspect.

IX. Conclusion

We proposed a semi-automatic extracardiac Fontan pathway planning method for designing patient-specific hemodynamically optimized Fontan conduits. We tested the proposed method in two patient-specific models (n=2), and compared hemodynamic performance between ManuOpt Fontan models and AutoOpt Fontan models. The results demonstrated that the AutoOpt model hemodynamically outperformed the ManuOpt model in one case. In the other case, AutoOpt and ManuOpt models have comparable hemodynamic performance. It is worth noting that the average AutoOpt design time was about 15 hours, while the average ManuOpt design time was over two weeks. Our study showed HFD of an optimized Fontan pathway was significantly affected by anastomosis errors and uncertainty of BC. Accurate prediction of BC and accurate graft implantation are important to maintain optimal postoperative hemodynamic performance. We also showed the feasibility to 3D-print the AutoOpt conduits as TEVG by using biodegradable materials.

Nomenclature

%WSS

Percentage of abnormal wall shear stress

AutoOpt

Automatic optimization

BC

Boundary conditions

CAD

Computer aided design

CFD

Computational fluid dynamics

HFD

Hepatic flow distribution

HPCC

High-performance computing cluster

InDep

The maximum intersection depth between Fontan pathway and other anatomies

iPL

Indexed power loss

IVC

Inferior vena cava

LPA

Left pulmonary artery

ManuOpt

Manual optimization

PA

Pulmonary arteries

RPA

Right pulmonary artery

SCPC

Superior cavopulmonary connection

SUM

Surgeon’s unconstrained modeling

SVC

Superior vena cava

TEVG

Tissue engineered vascular grafts

WSS

Wall shear stress