Intelligent Computing with Levenberg–Marquardt Backpropagation Neural Networks for Third-Grade Nanofluid Over a Stretched Sheet with Convective Conditions

Abstract

This article discussed the influence of activation energy on MHD flow of third-grade nanofluid model (MHD-TGNFM) along with the convective conditions and used the technique of backpropagation in artificial neural network using Levenberg–Marquardt technique (BANN-LMT). The PDEs representing (MHD-TGNFM) transformed into the system of ODEs. The dataset for BANN-LMT is computed for the six scenarios by using the Adam numerical method by varying the local Hartman number (Ha), Prandtl number (Pr), local chemical reaction parameter (σ), Schmidt number (Sc), concentration Biot number (γ₂) and thermal Biot number (γ₁). By testing, validation and training process of (BANN-LMT), the estimated solutions are interpreted for (MHD-TGNFM). The validation of the performance of (BANN-LMT) is done through the MSE, error histogram and regression analysis. The concentration profile increases when there is an increase in Biot number and the local Hartmann number; meanwhile, it decreases for the higher values of Schmidt number and the local chemical reaction parameter.

Introduction

The liquid that carries the nanometer-sized solid particle dispersion is called nanofluid. There are two main categories: first one is single-phase modeling and second is two-phase modeling. In the single-phase modeling, both the nanoparticles and the liquid examine as a monophasic mixture, whereas in the two-phase modeling nanoparticles are considered explicitly from the base liquid and its properties.

Choi and Eastman [1] concluded that the cooling potential of typical liquids can be improved by the inclusion of nanoparticles into basic liquids. There are some applications in which nanofluids are very useful like grinding machine and air-conditioners. The random movement of small particles in a fluid is called Brownian motion (BM). The importance of BM in enhanced thermal conductivity of nanofluids was addressed by Jang and Choi [2]. Shukla and Dhir [3] investigated the influence of BM on the nanofluid’s thermal efficiency.

Viscosity of nanofluids was experimentally reviewed by Bashirnezhad [4]. The transport properties of nanoliquids were discussed by Michaelides [5]. Slip flow over a nanofluids and the radiative heat transmission were examined by Souayeh et al. [6]. With thermal radiation, the magnetic flow of viscous liquid was analyzed by Makinde et al. [7]. Sheremet et al. [8] examined the magnetic flow of nanoliquid (unsteady) in a cavity. Makinde and Aziz [9] concluded that the concentration of nanoparticles upgrades for the greater Biot number.

Buongiorno [10] studied the Brownian diffusion and convective transport of nanofluids. The flow of nanofluids via nanochannel was addressed by Ghahremanian et al. [11]. Magnetohydrodynamic (MHD) studies represent the motion of electroconductive fluid in a magnetic field. Magnetohydrodynamic flow of nanofluids (non-Newtonian) along with the activation energy was studied by Ahmad et al. [12].

Through a stretched surface, the thermodiffusion effects on nanofluids (magnetic) were addressed by Awad et al. [13]. The fluid’s viscosity takes energy by the movement of the liquid and changes it in the internal energy. This procedure is irreversible (partially) and known as viscous dissipation. The impact of viscous dissipation through a stretched surface on unsteady magnetohydrodynamic flow was studied by Reddy et al. [14]. He also addressed the impact of heat source over a stretching sheet on magnetohydrodynamic flow (unsteady). Through a porous stretched sheet, Tak and Lodha [15] studied the impact of viscous dissipation and transverse magnetic field on flow. Zami et al. [16] demonstrated the heat transfer and the boundary layer flow of a nanoliquid through a nonlinearly porous stretchable/non-stretchable sheet.

Ramzan et al. [17] incorporated the impact of bio-convection on three-dimensional tangential hyperbolic partially ionized nanofluid system. Mahanthesh [18] demonstrated the significance of viscous and Joule heating effects on heat transport of hybrid nanoliquid. The Brinkman–Forchheimer flow of single-walled and multi-walled carbon nanotube fluid in a microchannel was investigated by Shashikumar [19]. Under uniform mass and heat flux conditions, the statistical and exact computations of radiated flow of Casson and nanofluid were studied by Mackolil [20]. With thermophoresis and BM effects, the dynamics of third-grade non-Newtonian liquid were analyzed by Mahanthesh [21]. Mackolil [22] carried out a sensitivity analysis of MHD Marangoni convection of nanofluid.

Mahanthesh [23] studied the influence of thermal radiation on the steady 3D flow of nanoliquid over a stretched surface. Impacts of aluminum nanoparticles are observed through experimental study by Lade et al. [24]. The 2-phase MHD flow of a fluid through a dust suspension was demonstrated by Mahanthesh [25]. The exact and statistical investigation of magnetohydrodynamic flow due to hybrid nanosized particles dispersed in hybrid base liquid was carried out by Mahanthesh [26]. In magnetic field along with boundary conditions, the heat transfer features of nanofluid through a rotating plate were discussed by Mahanthesh [27]. The hybrid nanofluid flow in an annulus with quadratic thermal radiation was examined by Thriveni [28].

In a non-Darcian permeable surface, the unsteady magnetohydrodynamic flow of a nanofluid was demonstrated by Rahman and Gamal [29]. With Newtonian heating, the unsteady MHD flow in a permeable medium was studied by Hussanan et al. [30]. Reactants need an amount of energy to activate a chemical reaction which is known as activation energy. Effect of binary chemical reaction and activation energy in MHD flow over a vertical sheet for a nanofluid was demonstrated by Mustafa et al. [31].

Khanafer and Vafai studied the dynamic viscosity and the thermal conductivity effects in the presence of convective heat transfer [32]. In a permeable medium, the laminar flow of viscous fluid with nanoparticles was examined by Hamad et al. [33]. The flow of nanofluid effected by the viscous heating and convection was analyzed by Pal and Mandal [34].

Exponentially stretched sheet and the rotating flow of nanofluid were numerically analyzed by Mushtaq et al. [35]. Magyari and Keller [36] examined the heat transfer properties. Cortell [37] analyzed the thermal boundary layer. Over a stretching surface, the MHD flow of nanofluid with Navier slip conditions was studied by Seth and Meshra [38].

W Jamshed utilized the Maxwell nanoliquid in his research problem based on thermal examination in solar collector [39]. Al Hossainy [40] discussed in his paper the heat transport phenomenon of magnetohydrodynamic radiative Carreau hybrid nanoliquid. Jamshed [41] discussed a solar thermal application by utilizing hybrid nanoliquid in his research model. Over a porous stretched surface, the flow of incompressible micropolar Prandtl liquid was investigated by Sajid [42]. He [43] also studied the heat transfer characteristics of Reiner–Philippoff hybrid nanoliquid in solar aircraft wings. The analysis of heat transfer of magnetohydrodynamic rotating flow of nanofluid over a stretched sheet was carried out by Shahzad [44]. Over an inclined plate, the flow of third-grade nanoliquid along with the lubrication impacts was discussed by Nazeer [45]. With the Joule heating impacts, the flow of nth-order reactive fluid over an elongated surface was examined by Shamshuddin [46].

This model involves the third-grade nanofluid, and there are many research articles that involve the applications of third-grade nanofluid. Sajid [47] examined the third-grade nanofluid flow over an infinite permeable sheet. Similarly, the same problem of the flow of third-grade nanofluid past an infinite porous sheet is studied by Rajagopal et al. [48]. Cortell [49] computed the mathematical solution for this problem by applying the Runge–Kutta method. Mekheimer [50] used third-grade nanofluid in his research as an application of cancer therapy. Hatami et al. [51] and Hamzehnezhad et al. [52] also used third-grade non-Newtonian fluid in their research problem.

In the presented research article, the authors have considered the backpropagation in artificial neural network (ANN) using Levenberg–Marquardt technique (BANN-LMT) has been developed to analyze the MHD flow of third-grade nanofluid model (MHD-TGNFM) along with the convective conditions. Xu [53] applied artificial neural networks to solve the issues related to solid waste. S Mangini [54] studied the quantum computing models for the ANNs and there are many other research articles based on the applications of ANN [55–58].

There are different numerical methods to investigate the flow of third-grade nanofluid over a stretched sheet, but the stochastic numerical method is used for the flow problem due to their effectiveness and worth. Recently, many researchers implemented the stochastic numerical technique for fluid flow systems [59–61]. Some artificial intelligence-based techniques are used by the research workers [62–65]. MATLAB and Mathematica infrastructures are utilized for these numerical computations. The solution of the mathematical expression for MHD-TGNFM is calculated viably by using the technique of backpropagation in artificial neural network using the Levenberg–Marquardt technique (BANN-LMT). The value and worth of the suggested BANN-LMT were established by comparing the results of the proposed BANN-LMT to the results of Adams numerical technique for various scenarios of MHD-TGNFM mathematical model. Multiple implementations of BANN-LMT in terms of MSE-based indices have demonstrated the performance’s authenticity and verification through statistical analyses. Aside from the MHD-TGNFM mathematical model's accurate and precise results, the ease of comprehending the ideas, consistency, smooth operation and extendibility is also noteworthy advantages.

In the presented study, a novel application of the integrated stochastic computational intelligent solver BANN-LMT is presented with the following salient features:

• The solution of the mathematical expression for MHD-TGNFM is calculated viably by using the technique of backpropagation in artificial neural network using the Levenberg–Marquardt technique (BANN-LMT).

• The worth and the value of the suggested BANN-LMT were established by comparing the results of BANN-LMT to the results of Adams methods for various scenarios of MHD-TGNFM mathematical model.

• Multiple implementations of BANN-LMT in terms of MSE-based indices have proven the verification and authenticity of the performance through statistical assessment investigations.

• Beside the accurate and precise results for the MHD-TGNFM and easy to understand the concepts, smooth operation, exhaustive applicability, consistency and extendibility are another valuable perks.

Mathematical Modeling

This paper discusses the 2D (MHD-TGNFM) along with the convective mass and heat conditions. Due to a stretched sheet, the flow is generated. The exertion of magnetic field (B₀) to the surface is in the perpendicular direction. The fluid phases and the nanoparticles are supposed to be in the thermal equilibrium state. Taking the small value of Reynolds number (magnetic) can ignore the impact of electric field and Hall current. Here, the model is examined in Cartesian coordinate system in which y-axis is in the perpendicular direction to the sheet and the stretched sheet is along the x-axis. The sheet is stretched at the x-axis where y = 0. And the velocity is u_w(x) = ax^m, where m and a are assumed as constants. By using the heat convection, the temperature at the sheet was controlled. h1 and h2 are the heat and mass transfer coefficients. Bruce [66] and Joseph [67] experimentally showed that there are materials that are

1. Weekly shear thinning but exhibit strong normal stresses. (first order)

2. Equal shear thinning and normal stress effects. (second order)

3. Strongly shear thinning but exhibit weak normal stresses. (third order)

In this study, third-grade fluid is examined. The main aim of this investigation is to give the numerical solution of MHD-TGNFM. There are some equations that govern the flow in (MHD-TGNFM). For third-order fluid, the Cauchy stressed tensor is:

$${\tau }^{\ast }=pI+\tilde{\mu }{\widehat{A}}_1^{\ast }+{\alpha }_1{\widehat{A}}_2^{\ast }+{\alpha }_2{\widehat{A}}_2^{\ast 2}+{\beta }_1{\widehat{A}}_3^{\ast }+{\beta }_2\left({\widehat{A}}_2^{\ast }{\widehat{A}}_1^{\ast }+{\widehat{A}}_1^{\ast }{\widehat{A}}_2^{\ast }\right)+{\beta }_3\left(\text{Tr}{\widehat{A}}_1^{\ast 2}\right){\widehat{A}}_1^{\ast }$$ 1

where $\tilde{\mu }$ is the dynamic velocity, p is the pressure, ${\alpha }_{1,}{\alpha }_2,{\beta }_1,{\beta }_2$ and ${\beta }_3$ are the material constants. Now the Rivlin–Ericksen tensor $\left({\widehat{A}}_1^{\ast },{\widehat{A}}_j^{\ast }\right)$ is:

$${\widehat{A}}_1^{\ast }=\mathrm{\nabla }\stackrel{⌣}{V}+{(\mathrm{\nabla }\stackrel{⌣}{V})}^{\overline{\text{T}}},$$ 2

$${\widehat{A}}_j^{\ast }=\frac{\text{d}{\widehat{A}}_{j-1}^{\ast }}{\text{d}t}+{\widehat{A}}_{j-1}^{\ast }L+L^{{}^{\overline{\text{T}}}}{\widehat{A}}_{j-1}^{\ast },(j>1),$$ 3

where $\frac{\text{d}}{\text{d}t}$ = material derivative, $\stackrel{⌣}{V}$ = velocity of fluid.

The constraints drive from Clausius–Duhem inequality are the following:

$$\tilde{\mu }\ge 0,\left|{\alpha }_1+{\alpha }_2\right|\le \sqrt{24\tilde{\mu }{\beta }_3},{\alpha }_1\ge 0,{\beta }_3\ge 0,{\beta }_1=0={\beta }_2,$$ 4

Equation (1) implies

$${\tau }^{\ast }=-pI+\tilde{\mu }{\widehat{A}}_1^{\ast }+{\alpha }_1^{\ast }{\widehat{A}}_1^{\ast }+{\alpha }_2^{\ast }{\widehat{A}}_2^{\ast 2}+{\beta }_3^{\ast }\left(\text{Tr}{\widehat{A}}_1^{\ast 2}\right){\widehat{A}}_1^{\ast },$$ 5

where Tr shows the trace.

The governing equations for (MHD-TGNFM) can be shown as follows [68]:

$$\frac{\partial u}{\partial x}+\frac{\partial \upsilon }{\partial y}=0,$$ 6

$$u\frac{\partial u}{\partial x}+\upsilon \frac{\partial u}{\partial y}=\nu \frac{{\partial }^{2}u}{\partial y^2}+\frac{{\alpha }_1}{\rho }\left(\begin{array}{c}u\frac{{\partial }^{3}u}{\partial x\partial y^2}+3\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial x\partial y}\\ +\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}+\upsilon \frac{{\partial }^{3}u}{\partial y^3}\\ \end{array}\right)+2\frac{{\alpha }_2}{\rho }\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial x\partial y}+6\frac{\beta }{\rho }\left({\left(\frac{\partial u}{\partial y}\right)}^2\frac{{\partial }^{2}u}{\partial y^2}\right)-{\sigma }^{\ast }\frac{B_0^2}{\rho f}u,$$ 7

$$u\frac{\partial T}{\partial x}+\upsilon \frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\frac{{\left(\rho C\right)}_{\text{p}}}{{\left(\rho C\right)}_{\text{f}}}\left(D_{\text{B}}\left(\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}\right)+\frac{D_{\text{T}}}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right),$$ 8

$$u\frac{\partial C}{\partial x}+\upsilon \frac{\partial C}{\partial y}=D_{\text{B}}\left(\frac{{\partial }^{2}C}{\partial y^2}\right)+\frac{D_{\text{T}}}{T_{\infty }}\left(\frac{{\partial }^{2}T}{\partial y^2}\right)-K_{\text{r}}^2(C-C_{\infty })exp\left(\frac{-E_{\text{a}}}{\kappa T}\right){\left(\frac{T}{T_{\infty }}\right)}^n,$$ 9

where the activation energy is $E_a$, the Boltzmann constant is $\kappa$ = 8.61 × ${10}^{-5}$ eV/K, reaction rate is $K_r^2$, fitted rate constant is n, where the range of n is − 1 < n < 1.

$K_{\text{r}}^2(C-C_{\infty })exp\left(\frac{-E_{\text{a}}}{\kappa T}\right){\left(\frac{T}{T_{\infty }}\right)}^n$ is the modified Arrhenius equation.

Boundary conditions are the following,

$$\begin{array}{c}u=u_{\text{w}}(x)=a{x}^{\text{m}},\upsilon =0,\\ -k\frac{\partial T}{\partial y}=h_1(T_f-T),\\ -D_{\text{B}}\frac{\partial C}{\partial y}=h_2\left(C_{\text{f}}-C\right)\text{at}y=0\\ \end{array}$$ 10

$$u\to 0,T\to T_{\infty },C\to C_{\infty }\text{as}y\to \infty$$ 11

where u and $\upsilon$ are the velocity components on the (x, y) co-ordinates, respectively, dynamic viscosity is µ, kinematic viscosity is represented by $\upsilon =\frac{\mu }{\rho f}$, ρf represents the density of ordinary liquid, ${\alpha }_1$, ${\alpha }_2$ and $\beta$ are representing the material parameters, temperature is T, electric conductivity is ${\sigma }^{\ast }$, k is the thermal conductivity, fluid’s thermal diffusivity is α, where $\alpha =\frac{k}{{(\rho C)}_{\text{f}}}$, the fluid’s heat capacity is ${(\rho C)}_{\text{f}}$,effective heat potential of nanoparticles is represented by ${(\rho C)}_{\text{p}}$, thermophoresis and Brownian diffusion coefficients are represented by $D_{\text{T}}$ and $D_{\text{B}}$, concentration is represented by C, the temperature far away from sheet is represented by $T_{\infty }$, $C_{\infty }$ stands for ambient temperature, reaction rate is represented by $K_r$, fitted rate constant is n, variable heat transfer coefficient is $h_1$ and variable mass transfer coefficient is $h_2$, where $h_1=h_{\text{t}}{x}^{\frac{m-1}{2}}$ and $h_2=h_{\text{m}}{x}^{\frac{m-1}{2}}$, now set:

$$\begin{array}{c}u=a{x}^m{f}^{\prime }(\chi ),\upsilon =-{\left(\frac{av(m+1)}{2}\right)}^{\frac{1}{2}}{x}^{\frac{m-1}{2}}\left(f(\chi )+\chi \frac{m-1}{m+1}{f}^{\prime }(\chi )\right),\\ \varphi (\chi )=\frac{C-C_{\infty }}{C_{\text{f}}-C_{\infty }},\theta (\chi )=\frac{T-T_{\infty }}{T_{\text{f}}-T_{\infty }},\chi =x^{\frac{m-1}{2}}{\left(\frac{a(m+1)}{2v}\right)}^{\frac{1}{2}}y,\\ \end{array}$$ 12

Now from Eqs. (7)–(11), take the following forms [68]

$$\begin{array}{c}{f}^{″\prime }+f{f}^{″}-\frac{2m}{m+1}{\left(f^{\prime }\right)}^2+{\in }_1\left((3m-1)f^{\prime }{f}^{″\prime }+2(m-1)\chi \right)f^{″}{f}^{″\prime }-\left(\frac{m+1}{2}\right)f{f}^{(iv)}+\frac{3(3m-1)}{2}{\left(f^{″}\right)}^2\\ +{\in }_2\left((3m-1){\left(f^{″}\right)}^2+(m-1)f^{″}{f}^{″\prime }\chi \right)+6{\in }_3{\text{Re}}_x\left(\frac{m+1}{2}\right){\left(f^{″}\right)}^2{f}^{″\prime }-\left(\frac{2}{m+1}\right)f^{\prime }{\text{Ha}}^2=0,\\ \end{array}$$ 13

$${\theta }^{″}+Pr\left(f{\theta }^{\prime }+\text{Nt}{\theta }^{\prime 2}+\text{Nb}{\theta }^{\prime }{\varphi }^{\prime }\right)=0,$$ 14

$${\varphi }^{″}+\text{Scf}{\varphi }^{\prime }+\left(\frac{\text{Nt}}{\text{Nb}}\right){\theta }^{″}-\left(\frac{2}{m+1}\right)\text{Sc}\mathrm{\sigma }{(1+\theta \delta )}^{n}exp\left(\frac{-E}{1+\theta \delta }\right)\varphi =0,$$ 15

$$\begin{array}{c}f(0)=0,f^{\prime }(0)=1,\\ {\theta }^{\prime }(0)=-{\gamma }_1(1-\theta (0)),\\ {\varphi }^{\prime }(0)=-{\gamma }_2(1-\varphi (0)),\\ \end{array}$$ 16

$$f^{\prime }(\infty )\to 0,\theta (\infty )\to 0,\varphi (\infty )\to 0,$$ 17

where the material parameters of nanofluid (third grade) are represented by $\chi$, ${\in }_1$, ${\in }_2$ and ${\in }_3$, ${\text{Re}}_x$ and Ha represent the local Reynolds number and the local Hartmann number, the Prandtl number is Pr, Brownian and thermophoresis parameters are represented by Nb and Nt, dimensionless activation energy is E, Schmidt number is Sc, local chemical reaction number is represented by σ, temperature difference parameter is represented by δ, thermal and concentration Biot number is represented by ${\gamma }_1$ and ${\gamma }_2$.These parameters are as follows:

$$\begin{array}{c}{\in }_1=\frac{{\alpha }_{1}a{x}^{m-1}}{\mu },{\in }_2=\frac{{\alpha }_{2}a{x}^{m-1}}{\mu },{\in }_3=\frac{\beta a^2{x}^{2(m-1)}}{\mu },{\text{Re}}_x=\frac{a{x}^{m+1}}{v},H{a}^2=\frac{{\sigma }^{\ast }{B}_0^2}{a\rho f{x}^{m-1}},\\ Pr=\frac{v}{\alpha },\text{Nb}=\frac{{(\rho C)}_{\text{p}}{D}_{\text{B}}\left(C_{\text{f}}-C_{\infty }\right)}{{(\rho C)}_{\text{f}}v},\text{Nt}=\frac{{(\rho C)}_{\text{p}}{D}_{\text{T}}\left(T_{\text{f}}-T_{\infty }\right)}{{(\rho C)}_{\text{f}}v{T}_{\infty }},E=\frac{E_{\text{a}}}{\kappa T_{\infty }},\text{Sc}=\frac{v}{D_{\text{B}}},\\ {\gamma }_1=\frac{h_t}{k}\sqrt{\frac{2v}{a(m+1)}},{\gamma }_2=\frac{h_{\text{m}}}{D_{\text{B}}}\sqrt{\frac{2v}{a(m+1)}},\delta =\frac{\left(T_{\text{f}}-T_{\infty }\right)}{T_{\infty }},\sigma =\frac{K_{\text{r}}^2}{a{x}^{m-1}},\\ \end{array}$$ 18

Solution Methodology

The MATLAB command ‘nftool’ is used to execute the technique of backpropagation in artificial neural network using the Levenberg–Marquardt technique (BANN-LMT). The following figure shows the neural network for (BANN-LMT).

There are six variations for MHD-TGNFM. This article discusses the variation of local Hartman number (Ha), Prandtl number (Pr), local chemical reaction parameter (σ), Schmidt number (Sc), thermal Biot number (γ₁) and concentration Biot number (γ₂). Every scenario has further four cases. There are 10 physical quantities that have the fixed values for every scenario. By the variation of six physical quantities, the impact on velocity, concentration and temperature distribution is examined in this study. Now the values of the other parameters are given in Table 1.

Table 1.

Values of constant parameters

${\in }_1$	${\in }_2$	${\in }_3$	${\text{Re}}_x$	Nb	Nt	$\delta$	m	E	n
0.0	0.2	0.2	0.1	0.3	0.1	0.3	1.5	0.5	0.5

The inputs for the dataset are between 0 and 6, and the time interval is 0.06 with hiding 10 neurons. Utilizing the technique of Adam numerical method with the help of ‘NDSolve’ in Wolfram Mathematica with the variations of local Hartman number, Prandtl number, local chemical reaction parameter, Schmidt number, thermal Biot number and concentration Biot number in MHD-TGNFM. These variations are listed in Table 2, whereas Table 1 shows the value of the parameters which have the constant values. And these parameters are material parameter, Brownian movement parameter, thermophoresis parameter, temperature difference parameter, fitted rate constant, activation energy and Reynolds number.

Table 2.

Scenarios for MHD-TGNFM

Scenarios	Cases	Physical quantities
		${\gamma }_2$	${\gamma }_1$	Ha	Pr	Sc	$\sigma$
01	1	0.1	0.4	0.1	1.0	1.0	0.3
	2	0.3	0.4	0.1	1.0	1.0	0.3
	3	0.6	0.4	0.1	1.0	1.0	0.3
	4	0.9	0.4	0.1	1.0	1.0	0.3
02	1	0.4	0.5	0.1	1.0	1.0	0.3
	2	0.4	0.7	0.1	1.0	1.0	0.3
	3	0.4	0.9	0.1	1.0	1.0	0.3
	4	0.4	1.1	0.1	1.0	1.0	0.3
03	1	0.4	0.4	0.0	1.0	1.0	0.3
	2	0.4	0.4	0.45	1.0	1.0	0.3
	3	0.4	0.4	0.7	1.0	1.0	0.3
	4	0.4	0.4	0.9	1.0	1.0	0.3
04	1	0.4	0.4	0.1	0.8	1.0	0.3
	2	0.4	0.4	0.1	1.0	1.0	0.3
	3	0.4	0.4	0.1	1.2	1.0	0.3
	4	0.4	0.4	0.1	1.4	1.0	0.3
05	1	0.4	0.4	0.1	1.0	1.2	0.3
	2	0.4	0.4	0.1	1.0	1.4	0.3
	3	0.4	0.4	0.1	1.0	1.6	0.3
	4	0.4	0.4	0.1	1.0	1.8	0.3
06	1	0.4	0.4	0.1	1.0	1.0	0.4
	2	0.4	0.4	0.1	1.0	1.0	0.6
	3	0.4	0.4	0.1	1.0	1.0	0.8
	4	0.4	0.4	0.1	1.0	1.0	1.0

Analyzation and Discussion of Result

To compute the dataset for BANN-LMT, the six different scenarios are discussed and that variations are for local Hartman number (Ha), Schmidt number (Sc), thermal Biot number (γ₁), Prandtl number (Pr), local chemical reaction parameter (σ) and concentration Biot number (γ₂). Here the Prandtl number shows the ratio between momentum diffusivity and thermal diffusivity, where the Schmidt number is the ratio between the momentum diffusivity and the mass diffusivity. The ratio is between the heat transfer resistances in a body and at the surface of the body.

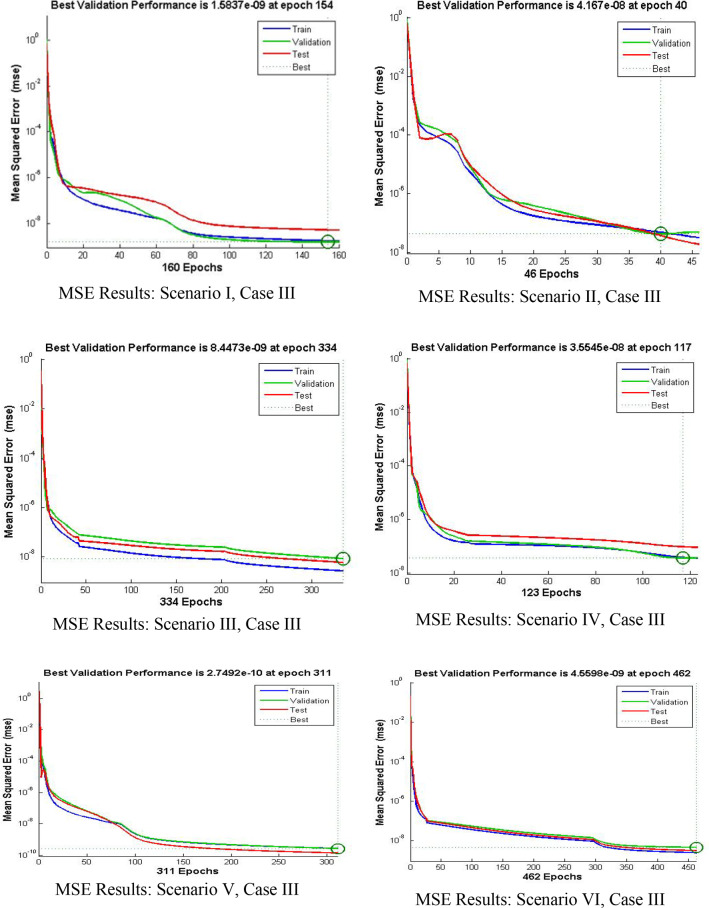
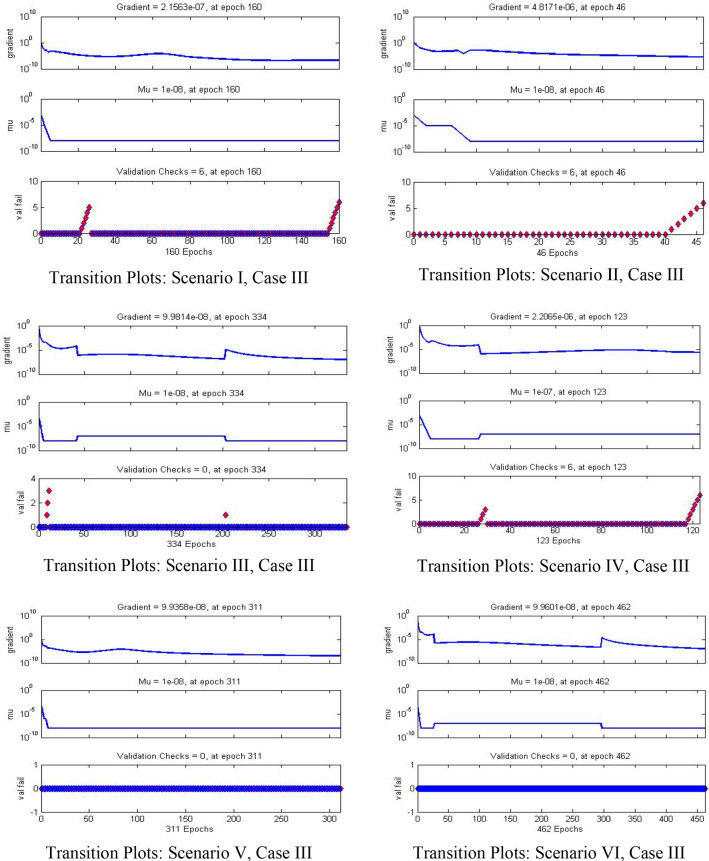
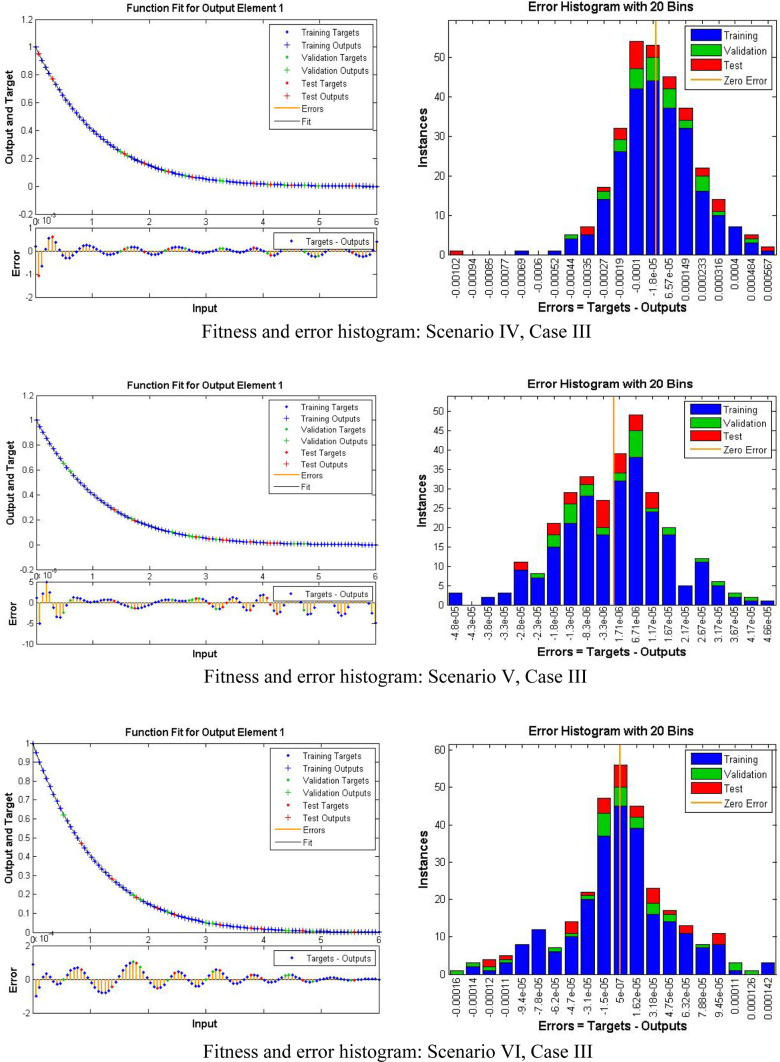
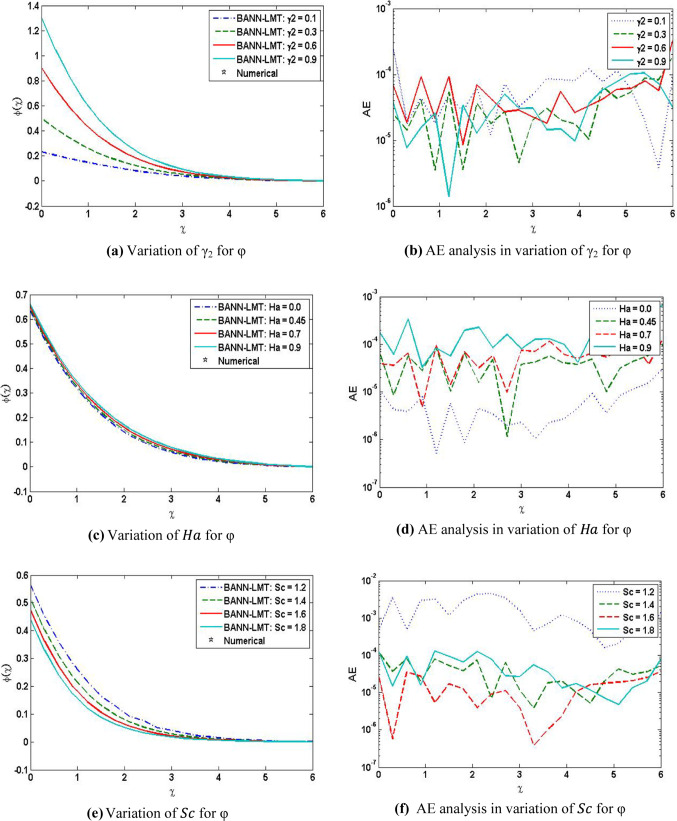
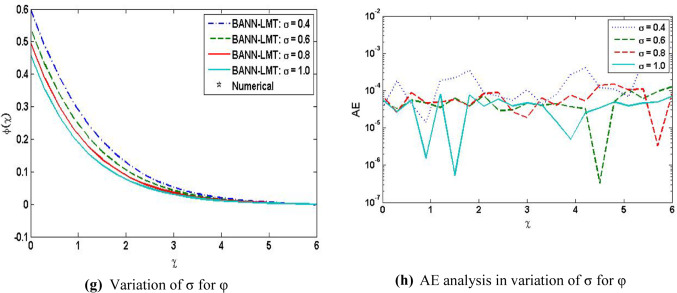
These variations are for the four cases of MHD-TGNFM over a stretching sheet. Adam numerical method is used to compute the dataset for $f^{\prime }\left(\chi \right)$, $\theta \left(\chi \right)$ and $\varphi$($\chi$). The input is between 0 and 6 with 0.06 step size for the four cases of the scenarios of BANN-LMT of MHD-TGNFM. MATLAB built command ‘nftool’ is used to determine the solution for the third-grade nanofluid model (MHD-TGNFM). The dataset for $f^{\prime }\left(\chi \right)$, $\theta \left(\chi \right)$ and $\varphi$($\chi$) is computed for 101 points, from which 10% points are used for testing, 10% for validation and 80% for training as shown in Fig. 1. And Fig. 2 shows the flowchart. Figure 3 depicts the performance of each third instance in all BANN-LMT scenarios. And the training state is shown in Fig. 4. The fitness and the error histogram are represented in Fig. 5, and Fig. 6 shows the regression graphs for every third instance of all the scenarios. Table 3 represents the data for training, validation, testing, epochs, performance, Mu and time taken.

Fig. 6.

Regression plots of BANN-LMT for third instance of all events of MHD-TGNFM

Fig. 1.

The design of neural network for (MHD-TGNFM)

Fig. 2.

Flowchart of MHD-TGNFM

Fig. 3.

The performance plots of BANN-LMT for third instance of all events of MHD-TGNFM

Fig. 4.

Transition plots of BANN-LMT for third instance of all events of MHD-TGNFM

Fig. 5.

Fitness and error histogram plots of BANN-LMT for third instance of all events of MHD-TGNFM

Table 3.

Outcomes of BANN-LMT of MHD-TGNFM

Scenario	Instances	MSE data			Performance	Gradient	Mu	Final epoch	Time (s)
		Training	Validation	Testing
1	1	2.44E − 09	1.34E − 07	2.71E − 09	2.44E − 09	8.90E − 09	1.00E − 08	185	4
	2	1.20E − 09	2.66E − 09	1.62E − 09	1.20E − 09	9.91E − 08	1.00E − 08	173	3
	3	1.75E − 09	1.58E − 09	5.26E − 09	1.69E − 09	2.16E − 07	1.00E − 08	160	2
	4	8.08E − 10	1.31E − 09	9.78E − 10	8.08E − 10	9.96E − 08	1.00E − 08	268	5
2	1	8.30E − 10	4.27E − 09	1.08E − 09	8.30E − 10	9.97E − 08	1.00E − 08	534	9
	2	5.47E − 10	3.43E − 11	9.11E − 10	5.47E − 10	9.95E − 08	1.00E − 08	292	5
	3	4.73E − 08	4.17E − 08	3.68E − 08	3.08E − 08	4.82E − 06	1.00E − 08	46	< 1
	4	2.87E − 08	2.58E − 08	1.18E − 07	2.05E − 08	1.01E − 05	1.01E − 05	45	< 1
3	1	7.35E − 11	1.36E − 10	9.29E − 11	7.35E − 11	9.95E − 08	1.00E − 09	417	7 s
	2	1.66E − 09	7.30E − 09	7.64E − 09	1.66E − 09	9.46E − 08	1.00E − 08	186	3
	3	2.66E − 09	8.44E − 09	5.86E − 09	2.66E − 09	9.98E − 08	1.00E − 08	334	5
	4	3.57E − 08	4.84E − 08	3.11E − 08	2.90E − 08	7.07E − 07	1.00E − 07	50	< 1
4	1	2.27E − 09	3.35E − 09	4.57E − 09	2.27E − 09	9.97E − 08	1.00E − 08	571	10
	2	1.61E − 10	8.62E − 09	3.26E − 10	1.61E − 10	9.92E − 08	1.00E − 09	592	10
	3	3.75E − 08	3.55E − 08	9.38E − 08	3.46E − 08	2.21E − 06	1.00E − 07	123	2
	4	1.35E − 09	2.57E − 09	3.60E − 09	1.35E − 09	9.99E − 08	1.00E − 08	179	3
5	1	1.91E − 05	1.25E − 05	5.31E − 05	9.49E − 07	0.000127	1.00E − 08	14	< 1
	2	1.40E − 09	8.66E − 10	8.81E − 10	1.40E − 09	9.98E − 08	1.00E − 08	309	5
	3	2.81E − 10	2.75E − 10	1.43E − 10	2.81E − 10	9.94E − 08	1.00E − 08	311	5 s
	4	4.25E − 09	2.56E − 09	3.88E − 10	3.96E − 09	1.03E − 06	1.00E − 09	225	3
6	1	8.71E − 08	8.26E − 08	3.05E − 07	5.97E − 08	2.36E − 05	1.00E − 08	32	< 1
	2	1.54E − 09	2.53E − 09	1.23E − 09	1.54E − 09	9.93E − 08	1.00E − 08	290	5
	3	2.46E − 09	4.56E − 09	3.14E − 09	2.46E − 09	9.96E − 08	1.00E − 08	462	9
	4	1.17E − 09	1.18E − 09	9.23E − 10	1.17E − 09	9.91E − 08	1.00E − 08	195	3

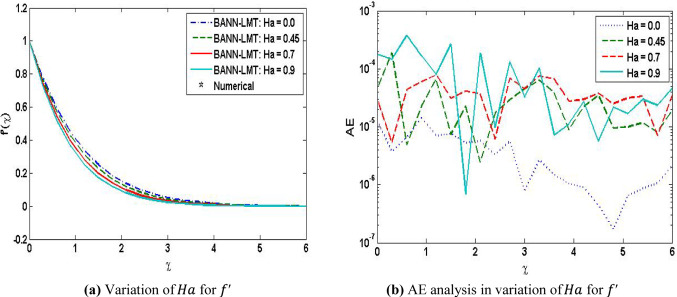
Velocity profile decreases for the increasing values of local Hartman number. The temperature profile increases when there is an increase in thermal Biot number and the local Hartmann number, whereas the increase in the values of Prandtl number causes the drop in temperature profile. The concentration profile increases with the increase in concentration Biot number and the local Hartmann number. And it decreases with the increase in Schmidt number and the local chemical reaction parameter. Figure 7a shows the impact of the variation of Ha on f′(χ) and 7b shows the absolute error about ${10}^{-3}$ to ${10}^{-7}$. Figure 8a, c and e depicts the variation of thermal Biot number, local Hartman number and Prandtl number on the temperature profile. Figure 8b, d and f shows the absolute error about ${10}^{-3}$ to ${10}^{-7}$. Figure 9a, c, e and g shows the variation of concentration Biot number (γ₂), local Hartman number (Ha), Schmidt number (Sc) and local chemical reaction parameter (σ) on the concentration profile. Figure 9b, d, f and h shows the absolute error about ${10}^{-3}$ to ${10}^{-6},{10}^{-3}$ to ${10}^{-7},{10}^{-2}$ to ${10}^{-7}\text{and}{10}^{-2}$ to ${10}^{-7}$.

Fig. 7.

Assessment of BANN-LMT for $f^{\prime }$ with reference dataset of MHD-TGNFM

Fig. 8.

Assessment of BANN-LMT for $\theta$ with reference dataset of MHD-TGNFM

Fig. 9.

Assessment of BANN-LMT for φ with reference dataset of MHD-TGNFM

In the literature above mentioned in introduction, the researchers used NDSolve and many other techniques to compute the solution, but this paper examined MHD-TGNFM by utilizing BANN-LMT, where the Levenberg–Marquardt technique is a supervised learning technique in which the input and output are given. The performance, regression, fitness, error histogram and training state plots can easily be computed with this technique and give a close approximated solution plots and the absolute error plots.

Artificial intelligence-based neural networks are frequently used to solve different flow problems due to their effectiveness and worth. It has many applications in different research models. Some recent models using the AI-based neural techniques are COVID 19 model [69], medicines [70], urological diseases model [71], Emden–Fowler model [72], dust density model [73], pathology [74], and dentistry [75].

Impact on Velocity Profile ${\mathit{f}}^{\mathbf{\prime }}\left(\mathit{\chi }\right)$

MATLAB is used to analyze the results of BANN-LMT for the investigation of the impact of variation of local Hartman number (Ha) on the velocity profile $f^{\prime }\left(\chi \right)$. Figure 7a shows the impact of the variation of Ha on $f^{\prime }\left(\chi \right)$ and 7b shows the absolute error about ${10}^{-3}$ to ${10}^{-7}$. It can be easily seen that the velocity distribution shows a decrease with the increase in local Hartman number.

Impact on Temperature Profile $\mathit{\theta }\left(\mathit{\chi }\right)$

MATLAB analyzed the results of BANN-LMT to determine the effect of variation of local Hartman number (Ha), Prandtl number (Pr) and thermal Biot number (γ₁) on the temperature profile. Figure 8a, c and e depicts the variation of thermal Biot number, local Hartman number and Prandtl number on the temperature profile. Figure 8b, d and f shows the absolute error about ${10}^{-3}$ to ${10}^{-7}$. The temperature profile shows an increasing behavior when there is an increase in thermal Biot number and the local Hartmann number, whereas the increase in Prandtl number causes the decrease in temperature profile.

Impact on Concentration Profile φ(χ)

MATLAB analyzed the results of BANN-LMT to determine the effect of variation of local Hartman number (Ha), local chemical reaction parameter (σ), Schmidt number (Sc), and concentration Biot number (γ₂) on the concentration profile. Figure 9a, c, e and g shows the variation of concentration Biot number (γ₂), local Hartman number (Ha), Schmidt number (Sc) and local chemical reaction parameter (σ) on the concentration profile. Figure 9b, d, f and h shows the absolute error about ${10}^{-3}$ to ${10}^{-6},{10}^{-3}$ to ${10}^{-7},{10}^{-2}$ to ${10}^{-7}\text{and}{10}^{-2}$ to ${10}^{-7}$. The concentration profile rises with the upsurge in concentration Biot number and the local Hartmann number. And it drops with the rise in Schmidt number and the local chemical reaction parameter.

Conclusion

The analysis of BANN-LMT to determine the results of magnetohydrodynamic flow of third-grade nanofluid model (MHD-TGNFM) by varying the Prandtl number (Pr), local chemical reaction parameter (σ), Schmidt number (Sc), local Hartmann number (Ha), thermal Biot number (γ₁) and concentration Biot number (γ₂). The PDEs of the third-grade nanofluid model are changed into a system of ODEs. Adam numerical solver generated the dataset of MHD-TGNFM. Eighty percentage of the reference data are used for the training, 10% for the testing and 10% for the validation of BANN-LMT. MSE plots, regression, performance and the other graphs justify the technique used for MHD-TGNFM. The temperature distribution rises with the increase in thermal Biot number and the local Hartmann number, whereas the increase in Prandtl number causes the reduction in temperature profile.

In the future research, the presented BANN-LMT can be used as an effective/accurate stochastic technique for second-grade fluidic system [76], Casson nanofluid flow model [77], Jeffrey fluid model [78], dusty Casson fluid flow model [79], Darcy–Forchheimer flow model [80], MHD hybrid fluid flow model [81] and 2D Sutterby fluid flow model [82].

Abbreviations

MHD

Magnetohydrodynamic

σ

Local chemical reaction parameter

Pr

Prandtl number

γ₂

Concentration Biot number

${\in }_1$

Material parameter

${\in }_3$

Material parameter

$\text{Nt}$

Thermophoresis parameter

ζ

Material parameter

E

Activation energy

BANN-LMT

Backpropagation in artificial neural network using Levenberg–Marquardt technique

p

Pressure

$\tilde{\mu }$

Dynamic viscosity

$\stackrel{⌣}{V}$

Fluid velocity

J/mol

Joule per mole (unit of $E_a$)

$\upsilon$

Kinematic viscosity

ρf

Density of fluid

T

Temperature

${\sigma }^{\ast }$

Electric conductivity

k

Thermal conductivity

α

Thermal diffusivity

${(\rho C)}_f$

Heat capacity

$D_{\text{T}}$

Thermophoresis coefficient

C

Concentration

$T_{\infty }$

Temperature far away from sheet

MSE

Mean square error

Ha

Local Hartman number

γ₁

Thermal Biot number

Sc

Schmidt number

${\in }_2$

Material parameter

$\text{Nb}$

Brownian movement parameter

$\delta$

Temperature difference parameter

n

Fitted rate constant

${\text{Re}}_x$

Reynolds number

MHD-TGNFM

Magnetohydrodynamic flow of third-grade nanofluid model

Pa

Pascal (unit of pressure)

Pa s

Pascal second (unit of dynamic viscosity)

$E_{\text{a}}$

Activation energy

$K_r$

Reaction rate

St

Stokes (unit of $\upsilon$)

Kg/m³

Unity of density

K

Kelvin

S/m

Siemens per meter (unit of ${\sigma }^{\ast }$)

W/m-K

Watt per meter-Kelvin (unit of k)

m²/s

Square meter per second (unit of α)

J/K

Joule per kelvin (unit of ${(\rho C)}_f$)

$D_{\text{B}}$

Brownian diffusion coefficient

M

Molarity (unit of C)

$C_{\infty }$

Ambient temperature

Funding

None.

Declarations

Conflict of interest

The authors declare that they have no competing interests.