Gradient boosted trees with individual explanations: An alternative to logistic regression for viability prediction in the first trimester of pregnancy

Highlights

• •Interpretable machine learning models efficiently predict miscarriages.
• •Gradient boosted trees algorithm offers serious assets for clinical modeling.
• •Clinical predictive models’ interpretation can be improved with decision paths.
• •Post-hoc interpretably provides straightforward explanations for physicians.

Abstract

Background

Clinical models to predict first trimester viability are traditionally based on multivariable logistic regression (LR) which is not directly interpretable for non-statistical experts like physicians. Furthermore, LR requires complete datasets and pre-established variables specifications. In this study, we leveraged the internal non-linearity, feature selection and missing values handling mechanisms of machine learning algorithms, along with a post-hoc interpretability strategy, as potential advantages over LR for clinical modeling.

Methods

The dataset included 1154 patients with 2377 individual scans and was obtained from a prospective observational cohort study conducted at a hospital in London, UK, from March 2014 to May 2019. The data were split into a training (70%) and a test set (30%). Parsimonious and complete multivariable models were developed from two algorithms to predict first trimester viability at 11–14 weeks gestational age (GA): LR and light gradient boosted machine (LGBM). Missing values were handled by multiple imputation where appropriate. The SHapley Additive exPlanations (SHAP) framework was applied to derive individual explanations of the models.

Results

The parsimonious LGBM model had similar discriminative and calibration performance as the parsimonious LR (AUC 0.885 vs 0.860; calibration slope: 1.19 vs 1.18). The complete models did not outperform the parsimonious models. LGBM was robust to the presence of missing values and did not require multiple imputation unlike LR. Decision path plots and feature importance analysis revealed different algorithm behaviors despite similar predictive performance. The main driving variable from the LR model was the pre-specified interaction between fetal heart presence and mean sac diameter. The crown-rump length variable and a proxy variable reflecting the difference in GA between expected and observed GA were the two most important variables of LGBM. Finally, while variable interactions must be specified upfront with LR, several interactions were ranked by the SHAP framework among the most important features learned automatically by the LGBM algorithm.

Conclusions

Gradient boosted algorithms performed similarly to carefully crafted LR models in terms of discrimination and calibration for first trimester viability prediction. By handling multi-collinearity, missing values, feature selection and variable interactions internally, the gradient boosted trees algorithm, combined with SHAP, offers a serious alternative to traditional LR models.

List of abbreviations

AUC

area under the curve

CI

confidence Interval

CRL

crown –rump length

FH

fetal heart

GA

gestational age (in days)

LGBM

light Gradient Boosted Machine

LMP

last menstruation period

LR

logistic regression

MSD

mean sac diameter

MYSD

mean yolk sac diameter

PUQE score

pregnancy-unique quantification of emesis and nausea

SHAP

SHapley additive exPlanations

1. Introduction

First trimester miscarriage is the most common complication of early pregnancy. Although difficult to assess, its incidence in recognized pregnancies is estimated around 13–17% in recent studies [1], [2], [3]. These adverse events can be traumatizing and can cause psychological distress for several months following a loss [4], [5], [6]. Diagnostic uncertainty in early pregnancy is associated with increased anxiety [7], justifying the need for models that accurately predict the outcome of a pregnancy. In order to predict the risk of miscarriage, several models based on logistic regression (LR) have been developed over the years [8], [9], [10], [11], [12], [13]. Despite good discriminative performance (AUC between 0.75 and 0.95), a significant number of miscarriages remain difficult to predict using these models.

The rise of artificial intelligence and machine learning (ML) in recent decades has led to the development of more complex algorithms which have demonstrated outstanding performance in numerous settings [14], [15], [16], including diagnosis performance similar to human medical-experts [14]. In comparison to LR, more sophisticated ML models are intrinsically nonlinear, avoiding the explicit formulation of interaction terms and/or nonlinear transformation of variables. In addition, some ML algorithms can also natively handle missing values, i.e. they can be trained on incomplete datasets whereas data imputation is needed before using LR [17]. Recently, advanced machine learning algorithms have been applied to various pregnancy-related conditions. For instance, Liu et al. demonstrated that tree-based ensembles outperformed traditional regression-based methods to predict early pregnancy loss after in vitro fertilization [18], although the evaluation and hyper-parameters tuning procedures were not reported. Moreira et al. used averaged one-dependence estimators to predict the childbirth outcome of pregnancies with hypertensive disorders [19]. Bruno et al. applied Support Vector Machine to predict recurrent pregnancy losses [20]. Kuhle et al. compared logistic regression with advanced machine learning algorithms for the prediction of fetal growth abnormalities [21]. The early prediction of adverse pregnancy outcomes with efficient models offer the opportunity to prevent a range of future complications [22]. However, despite significant advantages, the use of advanced ML to develop clinical models is still relatively uncommon.

A common barrier to the adoption of more advanced ML models in clinical practice is often explained by their lack of transparency regarding predictions [23,24]. However, more recently, a model-agnostic framework based on Shapley values has emerged that explains individual predictions [25]. Methods based on Shapley values decompose each model's prediction as a collaboration of individual variables. It is therefore straightforward to perceive the contribution of each individual variable to the final prediction. This approach has a solid theoretical foundation derived from game theory to provide useful post-hoc model explanations and make ML models more interpretable.

In this study, we aimed to assess the utility of interpretable machine learning for first trimester viability prediction. We first compared the predictive and calibration performance of LR models and gradient boosted trees. We then derived meaningful explanations at the patient-level and compared the global behavior of both algorithms. Finally, we highlighted the potential benefits of machine learning with post-hoc interpretability strategy for clinical modeling.

The paper is organized as follows: in Section 2, we first introduce the data cohort and the sets of variables. We then describe the two models used to predict the first trimester viability, as well as the performance metrics and the validation strategy employed, before introducing the SHAP post-hoc interpretability framework. The Section 3 reports the results in terms of models performance and interpretability. In Section 4, we discuss the main findings of this study and we elaborate on the different levels of post-hoc interpretability and its application to clinical predictive modeling. Finally, we highlight the advantages and limitations of both predictive modeling approaches, before addressing our concluding remarks.

2. Materials and methods

2.1. Data and study design

The study was based on data derived from a prospective observational cohort study based at Queen Charlotte's & Chelsea Hospital, London, conducted between March 2014 and May 2019. The study had been approved by NHS National Research Ethics Service (NRES) Riverside Committee London (REC 14/LO/0199) and NHS North East – Newcastle and North Tyneside 2 Research Ethics Committee (17/NE/0121). All participants provided written informed consent. Details on the study design and recruitment criteria can be found in [26].

Women with intrauterine pregnancies (either a confirmed viable pregnancy or pregnancy of unknown viability) were recruited and followed up with serial ultrasound scans in the first trimester. Demographic, clinical and ultrasound scan data were collected. The main outcome was defined as the presence of viable pregnancy at 11–14 weeks of gestational age (GA). All scans when a diagnosis of miscarriage was made were excluded. Participants with unknown date of last menstrual period (LMP) were also excluded. Due to the progressive drop out of miscarriage patients from the cohort, data at more advanced GA are biased towards viable pregnancies. In the present dataset, 15.5% of samples are associated with a miscarriage before 70 days of gestational age, whereas this proportion drops to 6.3% after 70 days.

To avoid the algorithms learning that these pregnancies are at less risk of miscarriage, we focused on the first half of the first trimester: scans with GA greater than 70 days were therefore excluded.

2.2. Variables and univariates analysis

Two sets of variables were used in the models. To limit the risk of overfitting, a restricted set of predefined variables was chosen based on expert opinion and previous published studies [[8], [9], [10], [11], [12], [13],15,27]. This parsimonious features set contained: maternal age, number of previous miscarriages, worst bleeding score reported, difference in estimated GA between LMP and mean sac diameter (MSD), GA by LMP, the Pregnancy-Unique Quantification of Emesis and Nausea (PUQE) score, crown-rump length (CRL), MSD, fetal heart (FH) and MSD*FH. This last term models an interaction between MSD and the presence of FH. Since advanced ML algorithms should model such interaction without explicit formulation, this term was omitted with the gradient boosted trees algorithm.

To assess the internal feature selection mechanism of gradient boosted trees algorithm, a more complete set of variables was also used in parallel, independently of expert knowledge. This complete set includes the parsimonious set augmented by: maternal ethnicity, gravida, parity, supplementation with folic acid, smoking status, certainty of LMP, previous cesarian section, bleeding score at presentation', number of bleeding days, pain score at presentation, no of days with pain, worst pain score, mean yolk sac diameter (MYSD), presence of amnion sign, GA by MSD, GA by CRL. A detailed description of the symptom variables can be found in [26]. Univariate analysis of the cohort characteristics with regard to the main outcome were performed with the Student's t‐test for continuous variables and the chi‐square test for binary or categorical variables.

2.3. Internal validation

The initial dataset was split into a training (70%) and test set (30%), stratified according to the main outcome to preserve a similar outcome prevalence between both sets. To avoid data leakage, i.e. the contamination of the training set with information from the test set in case data are not independent, the ultrasound scans from the same patients were strictly allocated to either the training or the test set.

2.4. Predictive models

• 1.Logistic regression

Multivariable logistic regression was used as a baseline model against more advanced ML models. Logistic regression is a statistical model used to perform regression analyses on binary outcomes. More specifically, logistic regression is a generalized linear model defined as : logit(p(y = 1)) = Xβ, where p ∈ [0, 1],  y is the dependent binary variable, X is the matrix of independent predictors, also known as explanatory variables and β is the vector of parameters, or coefficients, optimized during model training. The binary dependent variable y is related to the linear model Xβ through the logit link function defined as:

$$\begin{array}{ccc}& & logit\left(p\left(y=1\right)\right)=log\left(\frac{p\left(y=1\right)}{1-p\left(y=1\right)}\right),\hfill \\ & & \text{where}p\left(y=1\right)=\frac{exp\left(X\beta \right)}{1+\exp \left(X\beta \right)}\hfill \end{array}$$

As a generalized linear model, logistic regression does not require a normal distribution of the residuals. In addition, unlike ordinary linear regression, logistic regression models do not rely on homoscedasticity. The additive constraint of multivariable regression restricts the model capacity but facilitates the understanding of the prediction process.

To account for repeated measurements (e.g. clustered data), LR was trained using the cluster robust variance-covariance matrix. Multiple imputation was used to accommodate the presence of missing values. The training set was imputed 20 times using Multiple Imputation by Chained Equations and predictive mean matching [28]. Missingness was assumed to be at random.

• 2.Light gradient boosted machine (LGBM)

We used a gradient boosted trees algorithm as the advanced ML model. Gradient boosted trees is a tree-based ensemble algorithm that produce prediction by averaging a large number of individual decision trees predictions. The individual decision trees are constructed sequentially with the goal to reduce the error of the previous model at each iteration. With gradient boosting, the structure of the next tree to add to the current ensemble is determined through the optimization of an objective function $\mathcal{L}$ via its gradient [29]. However, converting a decision tree learning algorithm into an optimization problem is not straightforward as the gradient with respect to the model's parameters is not directly computable. With special formulations of $\mathcal{L}$, it is possible to optimize the construction of a new tree such that for each node split, the best split is chosen, taking into account the model complexity. Turning the objective function into a splitting criterion avoids the intractable problem of constructing all possible trees at each iteration.

If the function f_i represents the structure of a single decision tree, each new tree is added to the previous fixed ensemble as follows:

$${\widehat{y}}_i^{\left(0\right)}=0$$

$${\widehat{y}}_i^{\left(1\right)}={\widehat{y}}_i^{\left(0\right)}+f_1\left(X_i\right)$$

$${\widehat{y}}_i^{\left(2\right)}={\widehat{y}}_i^{\left(1\right)}+f_2\left(X_i\right)$$

… where ${\widehat{\mathrm{y}}}_{\mathrm{i}}$ and X_i represent the prediction and the vector of explanatory variable for patient i, respectively.

The final predictions after adding t trees to the ensemble are given by:

$${\widehat{y}}_i^{\left(t\right)}=\sum _{k=1}^t{f}_k\left(X_i\right)={\widehat{y}}_i^{\left(t-1\right)}+f_t\left(X_i\right)$$

Tree-based ensembles have demonstrated state-of-the-art performance in various settings, frequently outperforming neural networks in tabular datasets (e.g. [30]). They are often easier to optimize than neural networks which require additional architecture specifications. Tree-based ensembles also benefit from an existing implementation for the exact calculation of Shapley values (see below) in the SHAP package [31]. LightGBM [32] was used to implement the gradient boosted trees. The number of trees was chosen with early stopping. The optimization of the other hyperparameters was performed with tree-structured parzen estimators through 5-folds cross validation of the training set [33]. The list of hyperparameters tuned is reported in Table S2, other parameters were used with their default settings. Models are referred as parsimonious or complete following the dataset on which they were trained.

2.5. Performance

The predictive performance of the models was assessed on the test set. Overall performance was assessed with the Brier score which measure the accuracy of probabilistic predictions, the lower the score, the better [34]. Discriminative performance was assessed with the area under the curve (AUC) of ROC curves. Statistical comparisons between two models AUC was performed with the DeLong method [35]. Calibration was assessed with the calibration slope and the calibration-in-the-large [34]. For the calibration slope, a significant departure from the perfect calibration slope of 1 was assessed by the Wald-test [34].

We reported those metrics in two different forms: (1) raw metric evaluated on the whole test set, not adjusted for the presence of repeated measurements from the same patients: (2) longitudinal metrics: for each GA t, the corresponding metric was computed on the subset of samples included in a time window of 20 days, centered on t. In case of repeated measurements per patient within that time window, only the closest prediction to t was included to compute the metric. All metrics are reported with a 95% confidence interval (CI).

2.6. Post-hoc interpretability

To derive explanations of the model's individual predictions, we used the SHAP framework: an additive feature attribution method [25]. These model-agnostic methods rely on explanation models to decompose each prediction as a sum of individual feature contributions. Following the notation of Lundberg and Lee [25], the explanation model g of additive feature attribution methods takes the form:

$$\mathrm{g}\left({\mathrm{z}}^{\prime }\right)={\varphi }_0+\sum _{j=1}^{\mathrm{d}}{\varphi }_{\mathrm{j}}{\mathrm{z}}_{\mathrm{j}}{}^{\prime }$$

where z′ ∈ {0, 1}^d is a simplified version of z, represented by a binary vector of dimension d, which simulates any subset of predictors from z by indicating their presence or their absence. z_j′ represents therefore the presence (=1) or absence (=0) of feature j in z. φ_j ∈ R represents the feature attribution of the j^th variable of z.

In the SHAP method, those feature attributions φ_j are represented by Shapley values, derived from the collaborative game theory where a game payout is fairly distributed among the players of a game, taking into account the possible combinations of players. In the predictive analytics context, the game payout is the prediction and the players are the variables. The computation of the Shapley values guarantees a fair decomposition of the final prediction among the set of variables values. The Shapley value of a variable value represents its contribution to the current prediction. With SHAP, this contribution is expressed as a relative contribution between the current prediction and a baseline prediction value often set to E[f(X)] Therefore, the SHAP values estimate the contribution of each variable to explain the difference between f(X) and E[f(X)], the averaged prediction of the model. As a result, the explanations provided under the SHAP frameworks are contrastive which makes them more intuitive to understand for non-expert users[36]. In addition, SHAP is the only additive attribution method that remains locally faithful to the black box model prediction.

$$y=f\left(\mathrm{x}\right)=g\left({\mathrm{x}}^{\prime }\right)={\varphi }_0+\sum _{j=1}^{\mathrm{d}}{\varphi }_{\mathrm{j}}{\mathrm{x}}_{\mathrm{j}}{}^{\prime }$$

where φ₀ corresponds to a baseline prediction, often set to E[f(X)]. A more detailed explanation with theoretical formulation can be found in [25,30].

In order to derive meaningful comparisons amongst different models, we set the common baseline value to the outcome prevalence in the training set (0.88), which estimates the overall prior probability of miscarrying in the study-population. The Shapley values can be obtained from two different methods. The interventional approach breaks the potential inter-variables dependency to compute the features SHAP values, referred in the text as independent SHAP, while the correlated approach relies on the conditional expectation, which takes into account inter-features correlations. Recent studies suggest [37,38] that the conditional expectation approach can be misleading as some variables that are not used explicitly by the model can receive credits if they correlate with some other important variables. Where appropriate, we used the training set as background dataset for feature perturbation to compute the SHAP values using the interventional approach. For tree-based ensemble models, first order interaction SHAP values [31] were also computed.

The aggregation of SHAP values from individual predictions provides global model explanations. Global feature importance was obtained as the mean of absolute SHAP value across all instances for each variable. Similarly to the longitudinal visualization for the model performances, longitudinal features importance was also computed.

2.7. Software

All analysis have been performed with Python 3.6.6.

3. Results

• 1.Study cohort

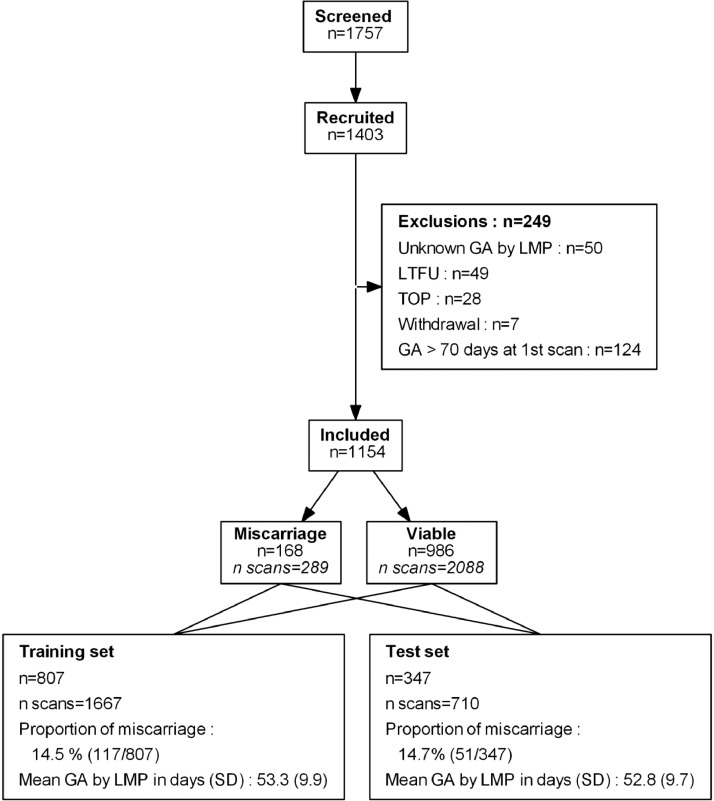
Fig. 1 displays the study flowchart. Patients who underwent termination of pregnancy (n = 28), withdrew from the study (n = 7), and who were lost to follow up (n = 40) were excluded. Additionally, patients with unknown or missing LMP (n = 50) were also excluded. A total of 1154 patients (986 viable pregnancies and 168 miscarriage) were available for the analysis. On average, each patient underwent 2.05 (± 0.83 SD) ultrasound scans (miscarriages: 1.70 (± 0.73 SD); viable pregnancies: 2.65 (± 0.83 SD)). After stratified splitting, the training set and the test set consisted in 807 and 347 patients respectively. Table S1 summarizes the descriptive statistics of the cohort at the patient and ultrasound scan levels, including the number of missing values per variable.

• 2.Model performances

Fig. 1.

Study flowchart n represents the number of unique patients and n scans the number of scans. All repeated scans of a given patient were strictly allocated to either the training or the test set. GA: gestational age; LMP: last menstruation period; LFTU: lost to follow-up, TOP: termination of pregnancy.

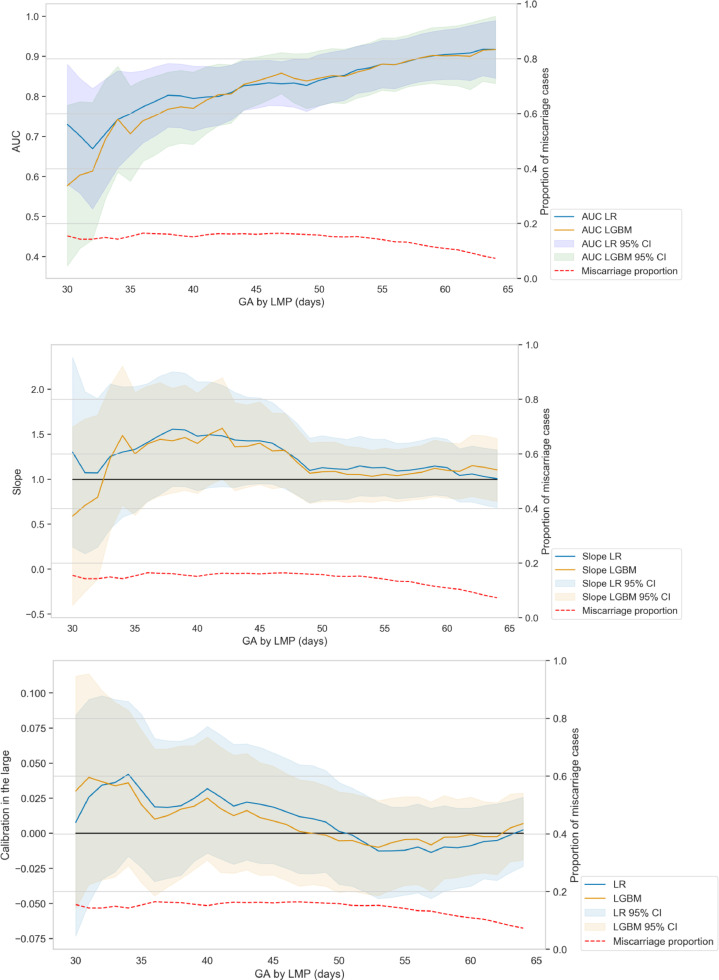
The overall performance metrics (with 95% CI) for parsimonious and complete models are reported in Table 1. Compared to the parsimonious LR, the parsimonious LGBM model had similar overall (Brier scores: 0.078 vs 0.076), discriminative (AUC 0.860 vs 0.885; p-value: 0.279) and calibration performance (calibration slope: 1.183, p-value: 1.222 vs 1.195, p-value: 0.098; calibration in the large: 0.001 vs 0.001). Furthermore, our results did not demonstrate the need to impute the training and testing data when using LGBM (Table 1). Therefore, all subsequent analysis and figures are based on LGBM without imputation. The models based on a preselected set of meaningful variables had similar discriminant performances as models based on the complete set of variables (LR models AUC: 0.886 vs 0.876, p-value: 0.348; LGBM models AUC: 0.885 vs 0.889, p-value: 0.574, Table 1). Moreover, the parsimonious LGBM had slightly better calibration performances than the complete LGBM (Slope: 1.195, p-value: 0.098 vs 1.298, p-value: 0.019, cal. in the large: 0.001 vs 0.010). Fig. 2 displays the parsimonious models performances longitudinally, based on the GA by LMP at the time of the scan. This longitudinal metrics assessment demonstrates similar behavior between LR and LGBM. Fig. S1 displays the same metrics for the complete models. Complete LGBM model demonstrated slightly worse calibration performance than complete LR model which can be explained by a greater flexibility of LGBM models. However, the discriminative performance of complete LGBM model was higher than complete LR, probably due to the built-in feature selection mechanism of LGBM.

Table 1.

Predictive performances of the models on the test set – raw metrics with 95% CI. The Brier score assesses the accuracy of probabilistic predictions, the lower the score the better. AUC evaluates the discrimination performance. The calibration in the large evaluates the mean calibration and corresponds to the difference between the averaged binary outcome and the averaged prediction. The calibration slope summarizes how the predicted risks correspond to the observed risks. An ideal calibration slope is equal to 1 and departures from 1 indicate potential model miscalibration (e.g. due to over/underfitting). Overall, LR and LGBM performed similarly in terms of calibration and discrimination. Complete LGBM models demonstrated similar discriminative performances as parsimonious models but their calibration was slightly worse, probably resulting from a too large flexibility compared to LR models.

	Parsimonious Models			Complete Models
	LR + MICE	LGBM with missing data	LGBM + MICE	LR + MICE	LGBM with missing data	LGBM + MICE
Brier score	0.078 (0.065 0.093)	0.076 (0.062 0.090)	0.078 (0.063 0.092)	0.080 (0.066 0.095)	0.076 (0.062 0.090)	0.076 (0.063 0.090
AUC	0.886 (0.852 0.919)	0.885 (0.8480.922)	0.881 (0.845 0.918)	0.876 (0.841 0.911)	0.889 (0.854 0.924)	0.892 (0.852 0.926)
Calibration in the large	0.001 (−0.022 0.019)	0.001 (−0.021 0.020)	0.002 (−0.023 0.019)	0.005 (−0.026 0.016)	0.010 (−0.031 0.010)	0.014 (−0.035 0.006)
Calibration slope	1.183 (0.950 1.415)	1.195 (0.964 1.424)	1.158 (0.934 1.380)	1.030 (0.824 1.235)	1.298 (1.048 1.547)	1.344 (1.087 1.599)

Fig. 2.

Longitudinal assessment of the performance metrics for the parsimonious models. AUC, calibration slope and calibration in the large are displayed depending on the GA by LMP at the date of scan using a time window of 30 days around the GA. Both LR and LGBM display similar profiles in terms of discrimination and calibration performance. Note that the proportion of pregnancies remaining at risk of miscarriage naturally decreases with time, which partly explains the increase of AUC for higher GA. AUC: area under the curve; GA: gestational age; LGBM: light gradient boosted machine; LMP: last menstruation period; LR: logistic regression.

In summary, LGBM models performed as good as LR approaches, without the need of missing values imputation and explicit specifications of variable interactions.

• 3.Post-hoc interpretability

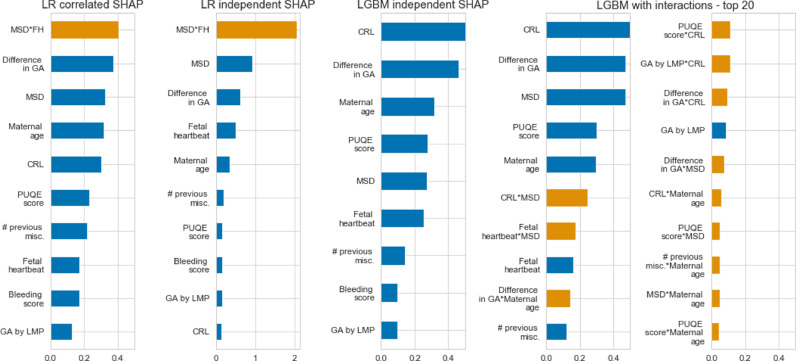
The feature importance expressed as the mean of individual absolute SHAP values per variable are displayed in Fig. 3 for the parsimonious models and in Fig. S2 for the complete models. The preselected variables were mostly associated with a high feature importance in the complete models (Fig. S2). These results also reflect the univariate analysis as reported in Table S1. A notable exception is the worst bleeding score variable. Although an important potential predictor for miscarriage, this variable was associated with poor feature importance in most of the models (Fig. 3).

Fig. 3.

Raw features importance measured with averaged absolute SHAP values per variable.

Variables that contribute significantly to the model's predictions for many patients have a high importance depicted as a large averaged absolute SHAP value. Main effects are colored in blue, interaction effects (first order variable interaction) are colored in orange. For LR models, the correlated SHAP approach (first column) takes variables collinearity into account when computing the SHAP values. The resulting feature importance is more balanced among correlated variables than the independent SHAP approach (second column) which directly reflects the LR coefficients. LGBM are reported with main effect only (third column) and with first order interactions (fourth and fifth columns, only the top 20 features). Despite similar performances, the algorithms have a different internal use of the same set of features. For example, the interaction MSD*FH is the main driving force of the LR model but appears as the 7th most important variable (second interaction term) in LGBM. CRL: crown-rump length; GA: gestational age; LGBM: light gradient boosted machine; LMP: last menstruation period; LR: logistic regression; MSD: mean sac diameter; PUQE: Pregnancy-Unique Quantification of Emesis.

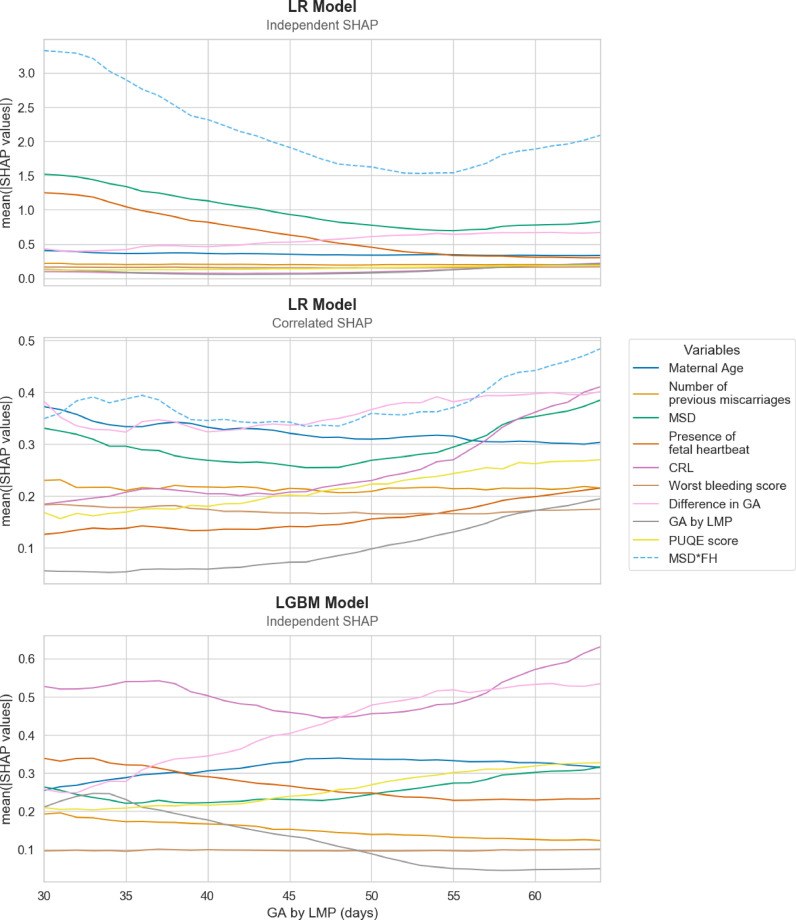
The features importance as described above was not necessarily constant through time as reported in Fig. 4. The longitudinal assessment of features importance from the LR model demonstrates that, under the independent assumption, the interaction term MSD*FH was the determining variable throughout all gestational ages, far above the other predictors, although its importance decreases in the second half of the examined period. Taking into account correlated variables, it remained the first driving variable but its importance decreased as the credit was shared among other variables. On the LGBM model, this analysis demonstrated that the CRL globally stayed the most significant variable while the importance of the MSD variable decreased with GA. In the opposite, the difference in estimated GA between LMP and ultrasound measurements became more important in the second half of the examined period.

Fig. 4.

Longitudinal features importance measured as averaged absolute SHAP values per variable. In the LR model, under the independent SHAP values computation, the interaction term MSD*FH is much more important in the beginning than in the second half of the examined period, although it remains from far the main driving variable throughout all gestational ages. Under the correlated approach, this interaction term remains the most important variable, but the credit is now shared among other correlated variables. In the LGBM model, the CRL variable stays the main variable while the importance of MSD decreases with GA. On the other hand, the difference in estimated GA becomes more important in the second half of the examined period. CRL: crown-rump length; FH: fetal heart; GA: gestational age; LGBM: light gradient boosted machine; LMP: last menstruation period; LR: logistic regression; MSD: mean sac diameter; PUQE: Pregnancy-Unique Quantification of Emesis.

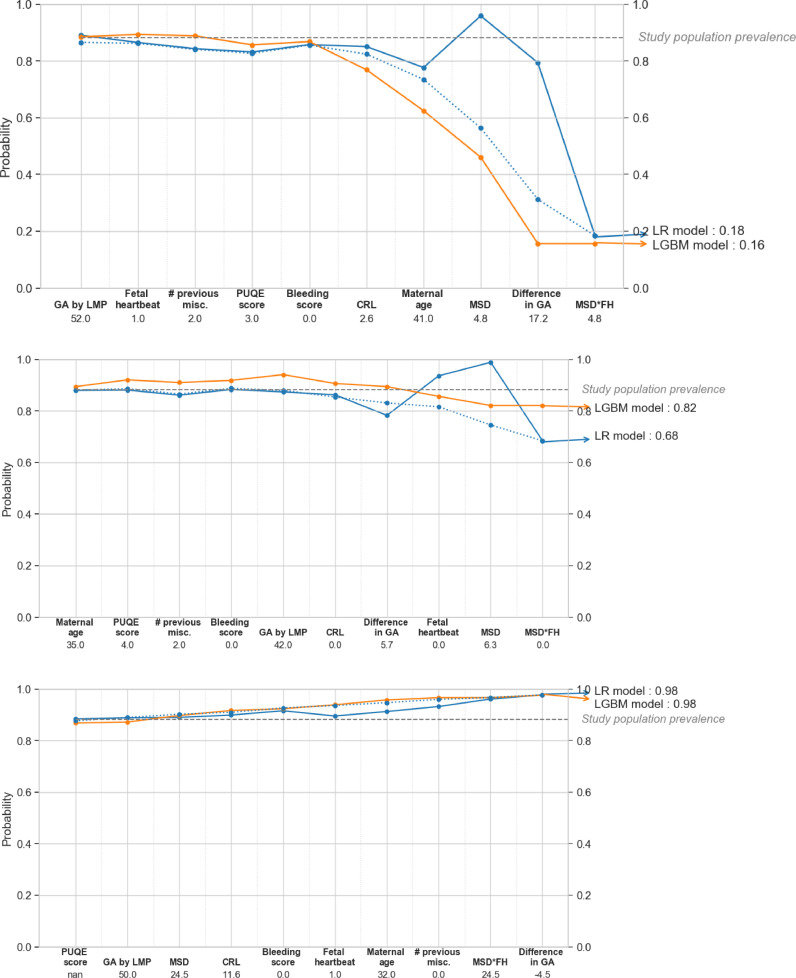
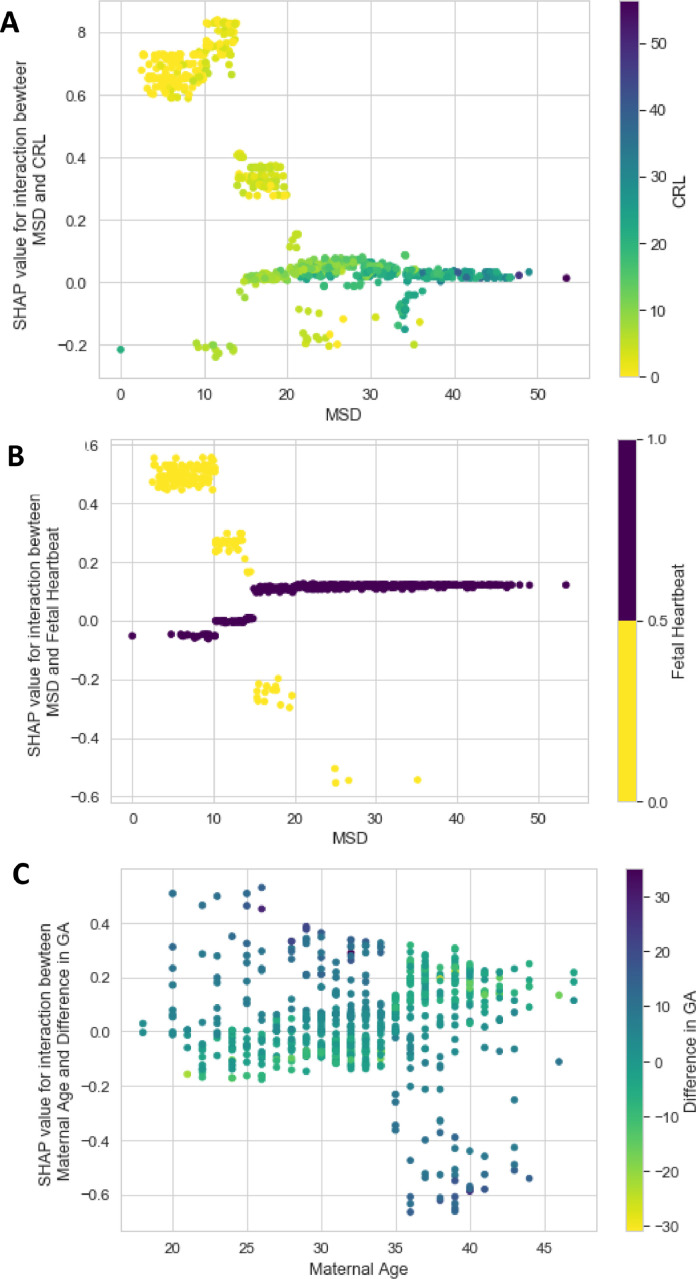
The decision paths followed by the LR and LGBM parsimonious models for three patients with different predicted risks are displayed in Fig. 5. Finally, the three main first-order interaction effects modeled by LGBM were CRL*MSD, FH*MSD and Maternal Age * Difference in GA, and are displayed in Fig. 6.

Fig. 5.

Decision path plots. Example of individual prediction explained with the SHAP values for 3 instances of the test set (dashed line = correlated SHAP, plain line = independent SHAP). The SHAP values attributed to each variable fixed at their current value (as indicated below the x-axis) are gradually summed from left to right to explain the departure of the current prediction from the study population prevalence (gray dashed line), acting as a baseline viability probability. The bigger the magnitude of the SHAP value, the larger the variable contribution to the final prediction. The variables are ordered from lower to higher importance at the prediction level. For example, in the top graph, small values of CRL (2.6 mm) and MSD (4.8 mm) in combination with an older maternal age (41 years) and a large difference in estimated GA (17.2 mm) produce a low chance of viability from both models. CRL: crown-rump length; GA: gestational age; LGBM: light gradient boosted machine; LMP: last menstruation period; LR: logistic regression; MSD: mean sac diameter; Nan: missing; PUQE: Pregnancy-Unique Quantification of Emesis.

Fig. 6.

Top three of interaction effects learned from LGBM and measured with the SHAP framework. The x-axis variable represents the first variable of the interaction. The color bar on the right indicates the value of the second variable present in the interaction. The SHAP value of the interaction is reported on the y-axis. (A). MSD*CRL, intrauterine pregnancies without visible embryo (CRL equals to zero) have a higher predicted risk of miscarriage (depicted as negative SHAP values) when MSD increases; (B). MSD*FH, pregnancies with high MSD without FH present have a higher predicted risk of miscarriage than with FH (see the negative SHAP values of yellow dots for MSD greater to 15 mm); and (C). Maternal Age * difference in GA: a large discrepancy in GA is modeled as a protective variable in young women while it becomes a risk factor in older women. CRL: crown-rump length; FH: fetal heartbeat, GA: gestational age; MSD: mean sac diameter.

4. Discussion

In this paper, we compared the predictive performance and the interpretability of an advanced ML algorithm over a carefully specified LR model. Overall, the different models demonstrated similar predictive performances. Both algorithms, although delivering different explanations, were intuitively explained by the SHAP framework at the local-level, i.e. for each individual patient prediction, and at the global or model-level. While LR models remain simple to implement and to train, gradient boosted trees algorithms demonstrated additional potential benefits for clinical modeling. A comparative on the use of LR vs LGBM for clinical modeling is reported in Table 2.

Table 2.

A comparison of logistic regression models and gradient boosted trees for clinical modeling.

	Logistic Regression	Gradient boosted trees
Predictive performance
Discrimination	Comparable if models correctly specified
Calibration	Comparable if models correctly specified
Interpretability
Raw interpretability	Based on model's coefficients. Subject to: multicollinearity, various unit scales, logit transform,… Not straightforward for physicians	Complex, possibility to extract feature importance. Not straightforward for physicians
Under the SHAP framework
Model-level	SHAP feature importance
Patient-level	Decision path plots Individual predictions explained as a sum of SHAP values
Collinearity	Handled by correlated SHAP	Less affected by collinearity
Variable interactions	Based on the pre-specified interactions	Possible with SHAP interaction values
Specificities
Missing values	Require complete datasets	Handle missing data internally
Feature selection	Possible with l1-regularization	Internal
Non-linearity (e.g. interactions)	Pre-specified	Internal
Optimization	Careful variable specifications	Require hyper-parameters tuning

4.1. Predictive performance

For the specific problem of first trimester viability, and given the dataset available, more advanced models such as gradient boosted trees did not demonstrate outstanding benefit in terms of predictive performance over a simple linear model carefully crafted with an interaction term. The raw and longitudinal performance metrics on the test set were similar for both algorithms (Table 1 and Figs. 2, S1), with the exception of the complete LGBM model's calibration slope which was worse than with the complete LR model (calibration slope of 1.298, p-value: 0.019 vs 1.030, p-value: 0.776, respectively and Fig. 1b). This corroborates previous studies which found the absence of performance gain from advanced models compared to LR in clinical modeling [21,39,40].

4.2. Interpretability

4.2.1. Model-level interpretability with SHAP feature importance

Although both algorithms displayed similar performances, parsimonious LR and LGBM demonstrated different behaviors when inspecting the models under the SHAP framework. The predictions from the LR model are mostly driven by the interaction term MSD*FH (Figs. 3,4), whereas LGBM predictions are mostly driven by CRL and the difference in estimated GA (Figs. 3,4). This phenomenon is known as the Rashomon effect [41], where multiple algorithms with similar performances can have completely different internal mechanism to derive their final predictions. The SHAP framework remains a method to derive individual explanations regarding a specific model. As a result, it should not be regarded as a way to derive absolute (causal) explanations. Model dependency should therefore be kept in mind when delivering post-hoc explanations to physicians.

4.3. Longitudinal SHAP feature importance and GA-dependence

Variables such as maternal age or the history of previous miscarriages are naturally independent of GA and display therefore a constant feature importance throughout the range of GA (Fig. 4). On the other hand, some variables demonstrate changes in their feature importance depending on the GA (Fig. 4). This phenomenon is partly explained by the specificities of the dataset and the encoding of the data. For instance, the fetal heartbeat is frequently absent (FH=0) on ultrasound scans performed at very early GA, irrespective of the future pregnancy outcome. Therefore, the interaction term MSD*FH of the LR model is encoded as zero, even if MSD is observed. As the pregnancy evolves, it becomes unlikely not to observe a fetal heartbeat. As a result, for more advanced GA, a smaller proportion of pregnancies displays a null value for the interaction term FH*MSD. Because the overall feature importance is expressed as a mean of absolute values, the highly negative SHAP values associated with MSD*FH=0 are counterbalanced by the large positive SHAP values when both MSD and FH are observed in the second half of the period (Fig. 4A). When the credit is shared among correlated variables, this phenomenon is significantly reduced (Fig. 4B). A similar phenomenon explains why the importance of the CRL variable increases with higher GA in the LGBM model (Fig. 4C). For early GA, the embryo is often not visible. Therefore, the proportion of pregnancies where the CRL variable is encoded as zero is higher for early GA compared to advanced pregnancies. The positive discrepancy in GA estimation, a strong predictor of miscarriage, increases with GA. Hence, the large positive differences in GA, associated with large negative SHAP values, are mostly observed in the second half of the period explaining the constant increase in variable importance for the discrepancy in GA (Fig. 4C).

These considerations highlight a drawback of the SHAP framework: the measure of feature importance, computed as mean(|SHAP values|), is directly dependent on the composition of the sample. The data used to compute the feature importance should be representative of the targeted population. The aggregation of individual SHAP explanations under the absolute operator might also obfuscate complex patterns of variable importance.

4.4. Interpretability under multicollinearity

Interestingly, CRL had a very low importance in the parsimonious LR model under the independent SHAP approach (Fig. 3, coefficient's p-values = 0.532 from Table S3). This is mostly explained by the collinearity with other variables (especially MSD) and highlights the limitations of LR in presence of correlated variables which disturbs the relationship between independent and dependent variables. Although this problem does not necessarily impact the prediction performance, it infringes the interpretability of LR models. Thoughtful variables selection a priori, dimensionality reduction or regularization can alleviate this phenomenon [42]. However, the correlated method for SHAP values presents an interesting alternative to display interpretable feature importance in the presence of collinearity as it shares credits among correlated variables, even if not explicitly used by the model. Under this method, the CRL variable importance drastically increased and reflected a more realistic view of this ultrasound parameter importance (Fig. 3). On the other hand, LGBM, due to its boosted nature, is more robust to the multicollinearity problem, as depicted in the feature importance analysis even under the independent SHAP approach (Fig. 3).

4.5. Interpretable individual predictions with decision path plots

At the individual prediction level, the SHAP framework decomposes each prediction into a sum of Shapley values. This sum explains the departure of the current prediction from a baseline prediction. The SHAP values attributed to each variable value can be organized into a meaningful visualization plot to derive the decision path followed by the model to reach the current prediction. Examples of such decision paths plots are reported in Fig. 5. Those plots constitute a meaningful way to translate complex algorithms decisions into interpretable predictions. As a model-agnostic explainer relying on the original variables additively, it allows for meaningful comparisons between different algorithms.

4.6. Exploring interaction effects

The SHAP values from non-linear models can be computed taking first order interactions into account [31]. The interaction plots, based on Shapley values, provide a clever alternative to partial dependence plots. In the parsimonious LGBM, the interaction effect between MSD and FH ranked 6th in terms of feature importance and constitutes the 2nd most important interaction term (out of 36 possible combinations) which corroborates its use in the LR model (and in previous study [27]). The interaction between CRL and MSD was the most important interaction effect and bears similar interpretation as the interaction between MSD and FH: intrauterine pregnancy without visible embryo is at higher risk of miscarriage when MSD increases. In the third interaction effect, a large discrepancy in GA appears to be modeled as a protective variable in young women while it becomes a risk factor in older women. Such interaction has never been reported and its clinical relevance remains uncertain as it might result from spurious findings based on the specificity of the training set.

4.7. SHAP framework for LR models

While LR models are often labeled as interpretable models, it is yet to demonstrate that every clinician fully understands the intricacy of such models, especially in the presence of non-linear terms and multicollinearity. We have demonstrated that the SHAP framework provides straightforward visualization of the feature importance and individual prediction explanations with decision path plots, irrespective of the variables’ scales and collinearity. Intuitive decision path plots are easy to understand and do not require deep knowledge of LR formulation. Therefore, we believe that, as a post-hoc explanation method, the SHAP framework can also benefit simple clinical models such as LR models in complement to traditional coefficients analysis.

4.8. Gradient boosted trees advantages

Besides models’ performance and interpretability, we also demonstrated that LGBM produced similar results on incomplete datasets compared to imputed data. The internal handling of missing values by LGBM constitutes therefore a potential advantage over LR where (multiple) imputation should be carefully performed beforehand. Furthermore, the inherent non-linearity of LGBM algorithms facilitates the development of efficient models as it does not require explicit interaction terms like LR models.

Finally, while a clever preselection of meaningful variables by expert knowledge is often recommended to prevent unnecessarily complicated models with an increased risk of overfitting [43], without prior knowledge it can be difficult to establish such pre-defined set of variables. Despite its flexibility, LGBM models maintained good discriminative performance even with a large set of variables on the complete dataset. This demonstrates the efficient internal feature selection/weighting mechanism of gradient boosted trees. The high ranking of the pre-specified variables within the complete LGBM model also reflected this feature selection mechanism.

4.9. Strengths and limitations

To the best of our knowledge, this study is one of the first to apply interpretable ML to first trimester viability prediction. The models were trained on a qualitative dataset from a well-defined prospective study using of validated symptom scores from early on in the first trimester. The models development included proper missing values imputations and hyper-parameters tuning. Unlike many previous comparative studies, this paper provides a rigorous models comparison through an extensive performances assessment beyond simple discriminative performance, including calibration and longitudinal visualizations of the performance metrics based on the GA.

One of the limitations of this study is the absence of a proper external validation set. However, we should note that the focus of this paper is not on building the ultimate predictive model but rather to demonstrate the potential of ML with post-hoc interpretability methods for early pregnancy predictive analytics. Secondly, our models use an estimation of GA by LMP, which is, however, not always available or accurate in practice [44]. Lastly, we would like to point out some practical limitations of the Shapley values approach. Because of its feature perturbation nature, the computation of Shapley values often need access to a background dataset (unless using the specific approach for tree ensembles [31]), which might impinge its use for model deployment. Moreover, depending on the dataset dimensionality, this perturbation step can be computationally expensive due to the combinatory nature of the Shapley value computation.

5. Conclusion

In this paper, we have demonstrated and assessed the use of machine learning enhanced by a post-hoc interpretability method for first trimester viability prediction. Gradient boosted algorithms performed as good as carefully crafted LR models in terms of discrimination and calibration. Furthermore, gradient boosted trees algorithms present several advantages over traditional LR models, such as the handling of missing values and the internal modeling of non-linearity, making them serious candidates for future works on first trimester prediction. Finally, we showed that the understanding of clinical models, including traditional LR models, can be improved by the use of additive feature attribution frameworks.

Declaration of Competing Interest

The authors declare that no conflict of interest exists