Modeling the effects of age and hearing loss on concurrent vowel scores

Abstract

A difference in fundamental frequency (F0) between two vowels is an important segregation cue prior to identifying concurrent vowels. To understand the effects of this cue on identification due to age and hearing loss, Chintanpalli, Ahlstrom, and Dubno [(2016). J. Acoust. Soc. Am. 140, 4142–4153] collected concurrent vowel scores across F0 differences for younger adults with normal hearing (YNH), older adults with normal hearing (ONH), and older adults with hearing loss (OHI). The current modeling study predicts these concurrent vowel scores to understand age and hearing loss effects. The YNH model cascaded the temporal responses of an auditory-nerve model from Bruce, Efrani, and Zilany [(2018). Hear. Res. 360, 40–45] with a modified F0-guided segregation algorithm from Meddis and Hewitt [(1992). J. Acoust. Soc. Am. 91, 233–245] to predict concurrent vowel scores. The ONH model included endocochlear-potential loss, while the OHI model also included hair cell damage; however, both models incorporated cochlear synaptopathy, with a larger effect for OHI. Compared with the YNH model, concurrent vowel scores were reduced across F0 differences for ONH and OHI models, with the lowest scores for OHI. These patterns successfully captured the age and hearing loss effects in the concurrent-vowel data. The predictions suggest that the inability to utilize an F0-guided segregation cue, resulting from peripheral changes, may reduce scores for ONH and OHI listeners.

I. INTRODUCTION

Younger adults with normal hearing (YNH) have a remarkable ability to segregate and understand a single speaker in the presence of multiple speakers. They utilize various cues to segregate the speech of a single person. Some of these cues are the differences in sound levels and their durations, the variations in speech spectral characteristics, and the difference in fundamental frequency (F0) between speakers (e.g., Brokx and Nooteboom, 1982; Bregman, 1990). Among these available cues, the F0 difference between speakers is widely studied. Classical concurrent vowel identification experiments are used to understand the F0 difference as a segregation cue. In such experiments, two steady-state synthetic vowels with equal levels and durations are presented concurrently to one of the ears of a listener (i.e., monaural presentation). The task of the listener is to identify the individual vowels presented in the concurrent vowel pair. The common observation is that the percent identification of both vowels improves with increasing F0 difference and then typically asymptotes for F0 differences of ∼3 Hz and greater (e.g., Assmann and Summerfield, 1990, Arehart et al., 2005; Summers and Leek, 1998).

The increase in identification of both vowels for the YNH subjects is due to an improvement in segregating two vowels using the F0 difference. At zero-F0 difference, only formant difference cues are available for identification. With increasing F0 difference, the ability to segregate vowels improves and thereby assists in identifying both vowels. There have been several attempts to develop a computational model for YNH subjects that could capture the pattern of identification scores of both vowels (Scheffers, 1983; Assmann and Summerfield, 1990; Meddis and Hewitt, 1992). These models require identifying either one or both F0s correctly for segregating two vowels prior to identification. Among these, the Meddis and Hewitt (1992) model successfully captured the gradual improvement in the identification scores of both vowels with increasing F0 difference (0 to 6 Hz) and then the scores asymptoted at 6-Hz F0 difference. The Meddis and Hewitt (1992) model suggests that the auditory-nerve-fiber temporal coding of the two F0s improves with increasing F0 difference, resulting in enhanced F0-guided segregation that contributes to correct identification. Subsequently, Chintanpalli and Heinz (2013) and Settibhaktini and Chintanpalli (2020) successfully tested the same F0-guided segregation algorithm (Meddis and Hewitt, 1992) but with more recent auditory-nerve (AN) models (Zilany and Bruce, 2007; Zilany et al., 2014) for identifying both vowels as a function of F0 difference. These AN models are physiologically realistic and successfully capture normal AN-fiber responses (e.g., cochlear nonlinearities, phase-locking) to vowels, which is essential for YNH modeling. Chintanpalli and Heinz (2013) also showed a relationship between F0-guided segregation as measured using the percent F0 segregation metric) and the identification score for both vowels. More specifically, the improvement in the score was due to enhancement in percent segregation with increasing F0 difference (consistent with Settibhaktini and Chintanpalli, 2020).

A. Effects of age and hearing loss on concurrent vowel identification

Several concurrent vowel studies have considered how the F0 difference cue affects the identification scores due to increased age and hearing loss (HL). The identification scores of both vowels across F0 differences are reduced with increasing age (Snyder and Alain, 2005; Vongpaisal and Pichora-Fuller, 2007; Arehart et al., 2011). Other studies show that identification scores across F0 differences are also reduced with HL (Arehart et al., 1997; Arehart et al., 2005; Summers and Leek, 1998). Chintanpalli et al. (2016) provides the only behavioral data in the concurrent-vowel literature that explicitly addressed the effects of age and HL on percent identification scores in a single study. Chintanpalli et al. (2016) collected concurrent-vowel data across three different listening groups: YNH, older adults with normal hearing (ONH), and older adults with hearing loss (OHI). The overall identification scores of both vowels across F0 differences were reduced for ONH subjects, compared with the YNH subjects. The scores for OHI subjects were the lowest across F0 differences. Furthermore, the percent correct of one vowel in the pair was >95% at each F0 difference for all three listening groups, suggesting that the F0 difference cue was important for identifying both vowels of the pair. The percent correct of one vowel was computed as the proportion of vowel pairs (out of 25) in which at least one vowel was correctly identified in each pair.

Possible peripheral mechanisms underlying reduced identification scores for ONH and OHI subjects are yet to be examined. Moreover, no computational model in the literature has captured the age and hearing loss effects on concurrent vowel scores across F0 differences. Thus, a computational model needs to be developed by incorporating the known anatomical and physiological changes in the periphery that can occur due to increase in age and HL.

B. Anatomical and physiological changes in peripheral system due to age and hearing loss

Several anatomical and physiological changes occur in older listeners with and without HL, where various mechanisms can be affected to varying degrees in the peripheral auditory system (Eckert et al., 2021). These factors include endocochlear-potential (EP) decline, cochlear hair-cell damage or loss, and cochlear synaptopathy (CS). These mechanisms can each affect peripheral encoding and reduce the perception of concurrent vowels for older listeners with and without HL. Hence, this section outlines the literature specific to these mechanisms, which are potential factors in the perceptual outcomes of Chintanpalli et al. (2016).

The EP is the cochlear battery applied between the scala media and scala tympani regions of the cochlea. It is essential for the normal mechanoelectrical transduction of the hair cells. The normal EP value is ∼90 mV. However, with increasing age, this value is reduced to ∼60 mV or even lower; an effect that has been observed across various animal studies (e.g., Schmiedt et al., 1996; Schmiedt et al., 2002; Mills et al., 2006). When the EP was reduced using furosemide, the neural thresholds (using the compound action potentials) of young gerbils correlated well with the thresholds of quiet-aged gerbils (e.g., Schmiedt et al., 2002; Mills et al., 2006). Dubno et al. (2013) used the audiogram profiles from animal models to successfully classify aged-human audiograms and concluded that the EP is a primary factor for human audiometric threshold shifts. In addition, the EP reduction results in significant alterations in AN-fiber tuning-curves shapes (e.g., broadened tuning resulting from larger effects at the tip, with less-reduced tail sensitivity, Sewell, 1984; Schmiedt et al., 1990). The significant effects at the tip were also seen in basilar-membrane responses following furosemide, but not the tail effects; suggesting outer-hair-cell (OHC) dysfunction was primarily responsible for the frequency-specific tip effects, while inner-hair-cell (IHC) dysfunction contributed to both tail and tip effects in a frequency-independent manner (Ruggero and Rich, 1991). These effects include reduced cochlear amplification as measured by basilar-membrane responses (Ruggero and Rich, 1991), compound action potentials (Schmiedt et al., 1996; Schmiedt et al., 2002; Mills et al., 2006; Gleich et al., 2016), and distortion-product otoacoustic emissions (Wang et al., 2019). These findings suggest that EP reduction affects the functionality of both OHCs and IHCs, since the EP is the battery for both types of hair cells. It is expected that these OHC and IHC effects may influence the tuning and temporal coding that underlie concurrent-vowel segregation and identification.

Noise-induced hearing loss (NIHL) occurs primarily because of mechanical damage to the OHCs and IHCs, both through stereocilia damage and hair-cell death (Liberman and Dodds, 1984a,b). Due to the OHC damage, the strength of cochlear nonlinearities (e.g., compression, suppression, broadened tuning and best-frequency shifts) is reduced (e.g., Rhode, 1971; Ruggero et al., 1997). There is also reduced frequency selectivity and sensitivity of AN fibers (e.g., Liberman and Dodds, 1984b; Miller et al., 1997). Due to IHC damage, AN-fiber sensitivity is reduced without affecting frequency selectivity (e.g., Liberman and Dodds, 1984b; Miller et al., 1997). Computational AN-modeling work suggests that AN-fiber tuning-curve effects following NIHL are well accounted for by roughly 2/3 OHC and 1/3 IHC damage (Bruce et al., 2003). Physiological studies have suggested that EP reduction is not a major contributor for permanent threshold shifts in NIHL animals (e.g., Wang et al., 2002; Kujawa and Liberman, 2019). Additionally, recent temporal-bone studies suggest that in older human adults, EP reduction (i.e., metabolic loss) is not a significant factor compared to hair-cell damage (i.e., sensory loss) (Wu et al., 2020a; Wu et al., 2020b). However, these anatomical studies were unable to make functional evaluations of the combined effects of EP reduction and hair-cell damage in OHI subjects, which is a difficult issue to address given that both effects contribute directly to OHC and IHC functionalities. Nonetheless, as with isolated aging, the combined effects of OHC and IHC dysfunction are expected to degrade concurrent-vowel segregation and identification.

With increasing age, there is a proportional loss of medium-spontaneous-rate (MSR) and low-spontaneous-rate (LSR) AN fibers for characteristic frequencies (CFs) ≥ 6 KHz (Schmiedt et al., 1996). For NIHL, there is a proportional loss of high-spontaneous-rate (HSR) AN fibers (e.g., Liberman and Dodds, 1984a; Heinz and Young, 2004). However, phase-locking to pure tones in quiet, which can be interpreted as characterizing the fundamental ability of AN fibers to follow fast fluctuations, does not depend strongly on spontaneous rate (SR) distributions for normal AN fibers (Johnson, 1980). Furthermore, phase-locking of AN fibers to pure tones in quiet is neither altered with increased age (Heeringa et al., 2020) nor with HL (Miller et al., 1997; Henry and Heinz, 2012). The degradations in temporal coding of synthetic single or concurrent vowels in quiet with HL (Palmer and Morjani, 1993) do not arise from changes in fundamental temporal-coding ability or SR distributions, but are more likely due to tuning changes associated with reduced cochlear nonlinearity. Nonetheless, these changes are expected to degrade concurrent-vowel segregation and identification.

Animal studies also show that both normal aging and NIHL can lead to lost synaptic connections innervating IHCs (normal aging; Stamataki et al., 2006; Sergeyenko et al., 2013; NIHL; Furman et al., 2013; Liberman and Kujawa, 2017). This CS is hidden from audiometric results and is thought to alter speech-recognition scores without changing audiometric thresholds (Grant et al., 2020; Mepani et al., 2020). Wu et al. (2019) showed that a large number of AN fibers are disconnected from their corresponding hair cells based on temporal bone analyses from normal-aging humans. It was concluded that over 60% of synaptic connections were lost, when averaged across the audiometric frequencies, for humans over 50 years of age. Johannesen et al. (2019) showed that the slope of auditory-brainstem-response wave-I amplitude with level was reduced with increasing age in humans, suggesting the presence of CS. Modeling suggests that CS can impair the temporal coding of complex sounds (Bharadwaj et al., 2014), which is expected to degrade concurrent-vowel segregation and identification for both ONH and OHI listeners.

C. Goal and hypothesis of the current study

The goal of the current study was to determine whether the peripheral changes that can occur with increased age and/or HL can account for reduced concurrent vowel scores across F0 differences for ONH and OHI subjects. The data collected by Chintanpalli et al. (2016) is used to validate the model predictions for three different listening groups (YNH, ONH, and OHI). The configuration of mean audiometric thresholds of the OHI subjects of Chintanpalli et al. (2016), see Table I, fall under the combined metabolic and sensory category of classified audiogram shapes, having acoustic overexposure (Dubno et al., 2013). This result combined with the recent anatomical studies suggests that older adults have significant hair-cell damage, in addition to EP reduction (Wu et al., 2020a; Wu et al., 2020b). Hence, it is reasonable to assume that the OHI subjects in Chintanpalli et al. (2016) had combined EP reduction and NIHL, which both affect the OHC and IHC functionalities.

TABLE I.

Mean values of the pure-tone thresholds (dB hearing level) for YNH, ONH, and OHI subjects of Chintanpalli et al. (2016).

	Frequency (Hz)
Subjects	250	500	1000	2000	3000	4000	6000	8000
YNH	7.7	8.0	2.0	3.7	4.0	1.7	6.8	5.0
ONH	9.7	9.3	7.3	10.0	12.3	15.7	18.3	32.7
OHI	13.0	17.3	18.3	26.3	38.8	48.7	59	61

We hypothesized that (1) EP reductions and CS contribute to reduced concurrent vowel scores across F0 differences in ONH subjects, (2) more significant reduction in the functionalities of OHCs and IHCs (due to combined EP drop and mechanical hair-cell damage) and CS contribute to the lowest scores across F0 differences in OHI subjects, and (3) CS is larger for OHI subjects due to the combined effects of HL and age. These hypotheses were tested by comparing predicted concurrent-vowel segregation and identification across subject groups.

II. METHODS

A. Stimuli

The current study utilized the same set of concurrent vowels used in Chintanpalli et al. (2016). Five different vowels (/i/, /u/, /ɑ/, /æ/, and /ɝ/) were generated using a matlab implementation of a cascade formant synthesizer (Klatt, 1980). The duration of each vowel was 400-ms, including 15-ms raised-cosine rise and fall ramps. The center frequencies and bandwidths of the five formant (F1–F5) filters used to generate these vowels are shown in Table II and were similar to the previous concurrent-vowel studies (e.g., Summers and Leek, 1998; Chintanpalli et al., 2013).

TABLE II.

Formants in Hz for five different vowels. Values in parenthesis of the first column correspond to bandwidth around each formant (in Hz).

Vowel	/i/	/ɑ/	/u/	/æ/	/ɝ/
F1 (90)	250	750	250	750	450
F2 (110)	2250	1050	850	1450	1150
F3 (170)	3050	2950	2250	2450	1250
F4 (250)	3350	3350	3350	3350	3350
F5 (300)	3850	3850	3850	3850	3850

A concurrent vowel was generated by summing a pair of single vowels. In each pair, one vowel's F0 was always fixed at 100 Hz, while the other vowel's F0 was either at 100, 101.5, 103, 106, 112, or 126 Hz. These conditions correspond to F0 differences of 0, 1.5, 3, 6, 12, and 26 Hz, respectively. There were 25 concurrent vowel pairs for each non-zero F0 difference condition. To maintain an equal number of vowel pairs, the 0-Hz F0 difference condition had five identical vowel pairs and ten different vowel pairs, but the latter was repeated twice. Overall, 150 concurrent vowels (25 pairs × 6 F0 differences) were presented to each of the listening models. Consistent with Chintanpalli et al. (2016), the individual vowel was presented at 65 dB sound pressure level (SPL) for YNH and ONH models, whereas 85 dB SPL was used for the OHI model to compensate for reduced audibility due to HL. However, the vowel pair level was ∼3 dB higher than the individual vowels in each model.

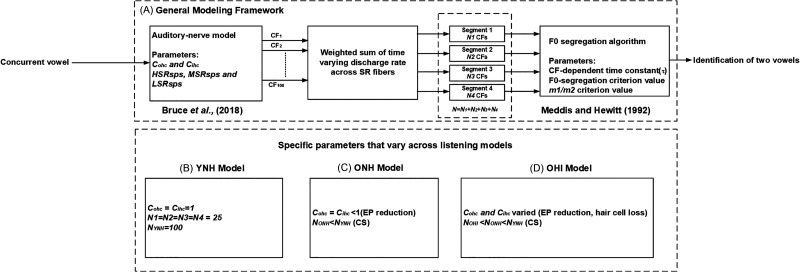
B. General modeling framework

Figure 1 shows the block diagram of the general modeling framework used across the listening models for predicting the identification of both vowels across F0 differences. In this framework, a physiologically based AN model (Bruce et al., 2018) was cascaded with a modified F0-guided segregation algorithm (Meddis and Hewitt, 1992) [Fig. 1(A)].

FIG. 1.

Block diagram illustrating the steps involved in the computational model to predict the concurrent vowel scores across F0 differences. (A) General modeling framework across three listening models. The parameters of the AN model are C_ohc, C_ihc, HSRsps, MSRsps, and LSRsps, whereas the parameters for the F0-segregation algorithm are the CF-dependent time constant (τ), and F0-segregation and m1/m2 criterion values. The AN responses are obtained for 100 CFs that ranged logarithmically between 250 and 4000 Hz. These 100 CFs are divided into four octave-spaced segments [i.e., segment 1 (250 to 500 Hz); segment 2 (500 to 1000 Hz); segment 3 (1000 to 2000 Hz); and segment 4 (2000 to 4000 Hz)] using N₁, N₂, N₃, and N₄ for the low to high CF bands, respectively]. (B) Parameters modified for YNH computational model. (C) Parameters modified for ONH computational model. (D) Parameters modified for OHI computational model. For the ONH and OHI models, the number of CFs in each segment is varied to simulate CS. For hypothesis testing, only the parameters associated with the peripheral stage were altered to predict the concurrent vowel scores for ONH and OHI models, whereas the same parameter values were used for the F0-segregation algorithm across all three peripheral models.

1. AN model

The AN model developed by Bruce et al. (2018) was used to predict the temporal responses to concurrent vowels. This model was an extension of previous models, which have been rigorously tested against neurophysiological responses from cats to both simple and complex stimuli, including pure tones, two-tone complexes, amplitude-modulated tones, forward masking and single vowels (e.g., Carney, 1993; Bruce et al., 2003; Zilany and Bruce, 2007; Zilany et al., 2014). A key feature is the ability to alter the functionalities of OHCs and IHCs, using the two distinct parameters (C_ohc and C_ihc). These values range from 1 (normal) to 0 (complete hair-cell loss). Intermediate values result in partial OHC or IHC dysfunction. Relevant to the current study, the model captures (1) the level-dependent changes in cochlear nonlinearities for normal AN fibers, (2) the reduction in cochlear nonlinearities for impaired AN fibers, (3) the level-dependent changes in temporal coding of vowel formants and F0 (e.g., Zilany and Bruce, 2007; Chintanpalli et al., 2014) for normal AN fibers, and (4) the reduction in temporal coding of higher formants (e.g., F2 and F3, due to enhanced F1 coding) for impaired AN fibers (e.g., Zilany and Bruce, 2007).

The AN model's input was a concurrent vowel and the output was a time-varying discharge rate of an AN fiber for a particular CF. These AN responses were predicted across 100 CFs, (250 to 4000 Hz). The discharge rate was obtained at each of these CFs for different SR fibers. More specifically, as per the anatomical and physiological functions (Liberman, 1978), the AN population was classified into three SR distributions: HSR (SR ≥ 18 spikes/s), MSR (0.5 ≤ SR<18 spikes/s), and LSR (SR < 0.5 spikes/s). To obtain the population of AN responses, each CF's overall discharge rate was calculated as the weighted sum of the discharge rates as per the distribution of SR fibers (61% of HSR fibers, 23% of MSR fibers, and 16% of LSR fibers; Liberman, 1978). These weighted discharge rates across CFs were presented as inputs to a modified Meddis and Hewitt (1992) F0-guided segregation algorithm to predict concurrent vowel scores across F0 differences [Fig. 1(A)].

2. F0-guided segregation algorithm

The Meddis and Hewitt (1992) model was the first to capture the effect of F0 difference on concurrent vowel identification scores for YNH subjects. More specifically, the predicted scores improved with increasing F0 differences and then asymptoted at higher F0 differences. In this model's F0-guided segregation algorithm, the auto-correlation function (ACF) of the time-varying discharge rate was computed for each CF with a time constant ( $\tau$) = 10 ms. A pooled-ACF (PACF) was computed by summing the ACFs across all CFs. The dominant F0 for each vowel pair was estimated by computing the inverse delay of the largest peak in the pitch region (4.5–12.5 ms) of the PACF. It specifies for which F0 the ACFs across CFs are primarily responding. Furthermore, the computation of dominant F0 is required for deciding whether F0-guided vowel segregation can be allowed prior to the identification of individual vowels. If the number of ACF channels that showed a peak at the dominant F0 was greater than an F0-segregation criterion value, then the model decided there was only one F0 present (i.e., no-F0 difference); otherwise, the model decided two F0s were present and proceeded with the F0-guided vowel segregation. In the latter case, all ACF channels that showed a peak at the dominant F0 were summed together to obtain a PACF of one vowel (PACF1). The residual ACF channels were summed together to obtain a PACF of the other vowel (PACF2). The inverse Euclidean distance metric was then used between the timbre region (0.1–4.5 ms) of the segregated PACF (PACF1 or PACF2) and the timbre regions of previously-stored PACF templates of single vowels. The model predicted the individual vowel that had a maximum inverse distance from each segregated PACF. If the model predicted a single F0, then the timbre regions of the total (i.e., unsegregated) PACF and five single vowels were compared using the distance metric. The model predicted a single vowel (presented twice) if the ratio of the best and second-best match was greater than the m1/m2 criterion value; otherwise, two different vowels were predicted. The parameter values of the segregation algorithm (i.e., ACF time constant, F0-segregation criterion, m1/m2 criterion) were varied such that the model's scores of both vowels across F0 differences were successful in capturing the pattern of concurrent-vowel data (Assmann and Summerfield, 1990). Instead of a constant $\tau$, the current study utilized CF-dependent time constants for computing the ACFs across CFs (Bernstein and Oxenham, 2005; Chintanpalli et al., 2014; Settibhaktini and Chintanpalli, 2020) to account for the effect of auditory filtering on pitch perception. At lower CFs, slower time constants are required due to longer impulse responses, resulting from smaller-bandwidth auditory filters. Similarly, faster time constants are required at high CFs.

C. YNH model

The C_ohc and C_ihc values across selected CFs were equal to 1 to simulate the normal functionalities of OHCs and IHCs [Fig. 1(B)]. The parameters HSRsps, MSRsps, and LSRsps (spikes/s) of Fig. 1(A) corresponds to the SR values used for HSR, MSR, and LSR fibers, respectively. These parameter values were chosen by matching the AN model's thresholds with the mean audiometric thresholds between 250 and 4000 Hz for YNH subjects. The upper limit was 4000 Hz, as all vowel formants are less than 4000 Hz (Table II). Table I shows the mean audiometric thresholds for YNH, ONH and OHI subjects of Chintanpalli et al. (2016). At each audiometric frequency, the AN model's threshold was the minimum sound level required to produce a firing rate ten spikes/s above SR, obtained using the peri-stimulus time histogram of AN population responses. If the relative pure-tone average (PTA) difference between the actual and model thresholds was less than 10%, then the thresholds were judged to match in the current study.

D. ONH model

The ONH model included the effects of EP loss and CS to predict the concurrent vowel scores across F0 differences. The parameters that were varied to simulate these effects are shown in Fig. 1(C). In the current study, the EP reduction was assumed to affect both types of hair cells to an equal extent (i.e., C_ohc = C_ihc). To simulate a reduction in the EP, the equal C_ohc and C_ihc values were varied to match the AN model's thresholds with the mean audiometric thresholds between 250 and 4000 Hz for ONH subjects (Table I). The number of logarithmically spaced CFs in each octave-spaced segment were reduced using the parameters N₁, N₂, N₃ and N₄ of Fig. 1(C) to approximate the reduced number of AN fibers sending information centrally due to CS. The number of AN fibers in each octave-spaced segment was reduced based on the Peterson and Barney (1952) study, which showed that F1 and F2 are important for vowel identification. As F1 and F2 of the five single vowels (except F2 of /i/) used in the current study were within the first three CF segments (Table II), the number of CFs were reduced primarily in these three segments (since overall-performance sensitivity was limited for the high-CF segment).

E. OHI model

The effects of hair-cell loss (and EP reduction) and CS were included in the OHI model to predict the concurrent vowel scores across F0 differences. The parameters to simulate these effects were shown in Fig. 1(D). The C_ohc and C_ihc values were reduced to fit the noise-induced hearing impaired data from cats (using the fitaudiogram2 matlab function of Zilany et al., 2009), for a desired mean audiometric thresholds between 250 and 4000 Hz for OHI subjects (Table I). Similar to the ONH model, CS was included by reducing the number of CFs primarily in the first three octave-spaced segments; however, the effect of CS was larger for the OHI model due to the combined effects of age and HL. For both the ONH and OHI models, it was assumed that CS has the same effect on all types of SR fibers, consistent with the modeling framework of Encina-Llamas et al. (2019), in which all types of SR fibers were required to be reduced in the AN model to simulate CS effects on the envelope following response in humans.

III. RESULTS

Table III shows parameter values used to successfully capture the effect of F0 difference on the concurrent vowel scores for the three listening models. To obtain the YNH model scores, the parameter values for HSRsps, MSRsps, and LSRsps were 50, 4, and 0.1 spikes/s, respectively, which resulted in a relative PTA difference = 9.4% (< 10%). Additionally, the F0-segregation and m1/m2 criterion values were 85% and 2, respectively, with the CF-dependent time constants shown in Table III. These parameter values were the same for the ONH and OHI models to evaluate how peripheral changes affect scores across F0 differences.

TABLE III.

Model parameters used across the three different listening models. SR parameters are given in spikes/s. The time constant varied across CFs ( $\tau$= 270-ms for 250 ≤ CF<440 Hz; $\tau$ = 256-ms for 440 ≤ CF<880 Hz; $\tau$ = 250-ms for 880 ≤ CF<1320 Hz; $\tau$ = 249-ms for CF ≥1320 Hz).

Models	Parameters
	AN model					CS (number of CFs in each octave segment, from low to high CFs)				Segregation algorithm
	HSRsps	MSRsps	LSRsps	Cohc	Cihc	N1	N2	N3	N4	$\tau$	F0-seg	m1/m2
YNH	50	4	0.1	1	1	25	25	25	25	same	85	2
ONH				0.85	0.85	4	3	3	20
OHI				Varied	Varied	2	1	1	16

Figure 2 shows the percent correct of both vowels and the corresponding percent segregation as a function of F0 difference for the three listening models. Consistent with other YNH modeling studies (Meddis and Hewitt, 1992; Chintanpalli and Heinz, 2013; Settibhaktini and Chintanpalli, 2020), the predicted scores (solid line) increased with F0 difference and then asymptoted at 6-Hz F0 difference [Fig. 2(A)]. This identification score pattern is similar to the Chintanpalli et al. (2016) concurrent-vowel data for YNH subjects (dashed line). The percent F0 segregation (i.e., ability to utilize F0-guided segregation prior to identification) improved with increasing F0 difference and reached the maximum at higher F0 differences [Fig. 2(E)]. The improvement in the identification of both vowels [Fig. 2(A)] can be attributed to enhancement in percent segregation with increasing F0 difference [Fig. 2(E)].

FIG. 2.

Predicted effects of F0 difference on percent concurrent vowel identification (top panels, solid lines) and percent segregation (bottom panels). Percent F0 segregation is computed as the proportion of vowel pairs (out of 25) in which the ACFs were segregated into two different sets. YNH model (A and E), ONH model with only EP reduction (B and F), ONH model (C and G), and OHI model (D and H). Note that the same F0-guided segregation parameter values are used across models. To simulate CS, only 30 CFs (i.e., 4, 3, 3, and 20 across the four segments) and 20 CFs (i.e., 2, 1, 1, and 16 across the four segments) out of 100 are used for ONH and OHI models (third and fourth columns), respectively. The percent identification scores of Chintanpalli et al. (2016) are shown in the top panels using the dashed lines, rather than the rationalized arcsine transformed scores.

To assess whether EP reduction can solely account for the reduced concurrent vowel identification scores, Figs. 2(B) and 2(F) show the ONH model scores and percent segregation across F0 differences. The C_ohc and C_ihc values of the AN model (Bruce et al., 2018) were decremented from 1 with a step-size of 0.05, and it was found that when C_ohc = C_ihc = 0.85 (Table III), the AN model's thresholds matched (relative PTA difference = 9%) the mean audiometric thresholds for ONH subjects (Table I). Thus, EP reduction was represented using equal model parameters C_ohc and C_ihc controlled by the mean audiometric thresholds of the ONH subjects. The model scores did not match with Chintanpalli et al. (2016) concurrent-vowel data for ONH subjects [solid vs dashed lines, Fig. 2(B)], but the scores were closer to YNH model instead [Fig. 2(A)]. Hence, EP reduction based on audiometric threshold-matching did not solely address the reduced concurrent vowel scores for ONH subjects. This finding suggests that the inclusion of CS might be required for better predictions for the ONH model.

Figures 2(C) and 2(G) show the ONH model percent scores for both vowels and its corresponding percent segregation as a function of F0 difference with the inclusion of the EP reduction (C_ohc and C_ihc = 0.85) and CS. For the ONH model, the functional effects of CS on vowel coding were captured by reducing the number of CFs in the four octave-spaced segments using the parameters N₁, N₂, N₃, and N₄ [Fig. 1(C)]. These parameter values were decremented manually from 25 with a step-size of 1. It was found that when the number of CFs in each segment was 4, 3, 3, and 20, respectively, the ONH model scores fit successfully with the concurrent-vowel data [Fig. 2(C)]. Thus, with the inclusion of CS (i.e., 30 CFs total), identification scores of both vowels across F0 differences [Fig. 2(C), solid line] were similar to Chintanpalli et al. (2016) concurrent-vowel data for ONH subjects [Fig. 2(C), dashed line]. Note that the smaller apparent degree of CS in the high-CF segment results from the lack of sensitivity of the N₄ parameter given this CF region is mostly above the F1 and F2 of the vowels.

Figures 2(D) and 2(H) show the OHI model percent scores for both vowels and its corresponding percent segregation as a function of F0 difference due to HL and CS. The estimated AN thresholds at audiometric frequencies, obtained after fitting, were matched (relative PTA difference = 1.45%) with the mean thresholds for OHI subjects (Table I). In this case, the C_ohc and C_ihc values were predicted to produce 2/3 OHC loss (in dB) and 1/3 IHC loss at each CF, based on the assumption that hair-cell damage is the dominant effect (Wu et al., 2020a; Wu et al., 2020b). This 2/3-OHC-loss configuration comes from estimates of human listeners with mild-to-moderate sensorineural HL (Plack et al., 2004) and NIHL AN-fiber data (Miller et al., 1997, Bruce et al., 2003). The impaired AN responses using these C_ohc and C_ihc values were obtained. Although the estimation of C_ohc and C_ihc is based on NIHL data (and thus may not appear to include EP reduction), EP reduction can in fact be considered as being included because the NIHL values of C_ohc and C_ihc were significantly less than 0.85 used in the ONH model to capture EP reduction. This approach is consistent with recent studies suggesting the functional effect of reduced EP (metabolic loss) is minimal in the presence of sensory loss due to mechanical hair-cell damage (Wu et al., 2020a; Wu et al., 2020b) and with the idea that both hair-cell damage and reduced EP affect OHC and IHC function, in different proportions.

Due to combined effects of age and HL, more CFs were removed in the OHI model than the ONH model. When the number of CFs across four segments were 2,1,1 and 16, respectively, the OHI model scores [Fig. 2(D), solid line] were fit successfully with the OHI data [Fig. 2(D), dashed line] of Chintanpalli et al. (2016). Hence, the model fitted the lower scores for OHI subjects by reducing the functionalities of OHCs and IHCs, and the total number of CFs (i.e., to 20) in the F0-guided segregation algorithm.

The percent F0 segregation was lower for the ONH model [Fig. 2(G)] and lowest for the OHI model [Fig. 2(H)] as a function of non-zero F0 difference, when compared with the YNH model [Fig. 2(E)]. This finding indicates that the lower scores for ONH and OHI models could be attributed to reduction in percent segregation with increasing F0 difference. However, for 0-Hz F0 difference, the scores for both the models were lower than the YNH model, suggesting that formant difference cues are also reduced for identification. Table IV shows the F0 benefit comparison between concurrent-vowel data (Chintanpalli et al., 2016) and the models' scores. The predicted F0 benefits were similar to Chintanpalli et al. (2016) data.

TABLE IV.

F0 benefit (in percent) comparison between concurrent vowel data (Chintanpalli et al., 2016) and the three listening models.

Listening group	Percent F0 benefit
	Data	Model
YNH	32	36
ONH	22	16
OHI	6.8	4

The scores for one vowel correct identification across vowel pairs were 100% at each F0 difference, regardless of the listening model used. These scores matched well with the Chintanpalli et al. (2016) data (result not shown). Consistent with YNH subjects (Chintanpalli and Heinz, 2013; Chintanpalli et al., 2014), these findings suggest that formant difference cues may be sufficient to perceive one vowel correctly, while the F0 difference is vital for identifying both vowels, even for ONH (Snyder and Alain, 2005) and OHI subjects.

To understand the availability of F0 difference and formant difference cues for identification across the three listening models, the vowel pair /i, æ/ was analyzed for illustration purposes. Figure 3 shows the model responses to /i (F0 = 100 Hz), æ (F0 = 106 Hz)/ presented to the YNH model. Figure 3(A) shows the individual ACF channels across 100 CFs that are logarithmically spaced between 250 and 4000 Hz. The estimated dominant F0 was correctly identified as 106 Hz [Fig. 3(D)]. The model does F0-guided segregation, as only 74% of the ACF channels showed a peak at 9.43 ms (i.e., F0 = 106 Hz), which was less than the segregation criterion value (85%). The ACF channels that had a peak at 9.43 ms were grouped together [Fig. 3(B)], whereas the remaining channels were grouped separately [Fig. 3(C)]. Two individual segregated PACFs were computed from these groups for vowel identification. The timbre region of these PACFs was compared with the previously stored templates of five single vowels. The model identified /æ/ and /i/ correctly [Figs. 3(E) and 3(F)]. The individual F0 was identified correctly for /æ/ [Fig. 3(E)] but not for /i/ [Fig. 3(F)]. The model successfully identified both vowels, as only one correct estimation of F0 is required for vowel segregation and identification (Meddis and Hewitt, 1992).

FIG. 3.

Model responses for /i (F0 = 100 Hz), æ (F0 = 106 Hz)/ presented to the YNH model. The first column corresponds to the individual ACF channels from 100 different AN fibers. These channels are added together to obtain the pooled ACF (D). The estimated dominant (F0) is 106 Hz, as indicated by an arrow (D). The second column shows only ACF channels that have a peak at 9.43 ms (B) and the remaining channels are placed in the third column (C). The model vowel responses are correct, as shown in (E) and (F). Note that the timbre regions of the templates /æ/ and /i/ (thin solid lines) are shown in (E) and (F) with an arbitrary vertical and horizontal offset for clarity. For visualization purposes, only 50% of channels are shown in the ACF plots.

Figure 4 shows the model responses for the same vowel pair/i (F0 = 100 Hz), æ (F0 = 106 Hz)/, but presented to the ONH model. The dominant F0 was identified correctly as 106 Hz [Fig. 4(D)]. Only 66.66% of 30 channels showed a peak at 9.43 ms and thus, F0-guided vowel segregation was allowed before vowel identification. In this case, the model identified both the vowels and individual F0s correctly [Figs. 4(E) and 4(F)]. Figures 3 and 4 suggest that the F0-guided vowel segregation was beneficial for this vowel pair for correct identification in both the YNH and ONH models.

FIG. 4.

Model responses for/i (F0 = 100 Hz), æ (F0 = 106 Hz)/presented to the ONH model. The first column corresponds to the individual ACF channels of the 30 selected AN fibers (4, 3, 3, and 20 across four segments) due to CS. The figure layout is similar to Fig. 3. The estimated dominant F0 is 106 Hz, as indicated by an arrow (D). The model vowel responses are correct, as shown in panels (E) and (F).

Figure 5 shows model responses for the same vowel pair /i (F0 = 100 Hz), æ (F0 = 106 Hz)/, but for the OHI model. The peak in the pitch region of the PACF occurred at 9.43 ms, corresponding to correct estimation of the dominant F0 = 106 Hz [Fig. 5(B)]. Here, the model did not segregate based on F0 difference, as the percent ACF channels that showed a peak at 9.43 ms was 90% (>85% criterion value). The model incorrectly identified /æ, æ/ based on the m1/m2 criterion value of 2 and predicted a single F0 = 106 Hz. Due to the lack of the F0-guided segregation [Fig. 2(H)], vowel identification was based on the formant difference cues only, which resulted in incorrect identification.

FIG. 5.

Model responses for/i (F0 = 100 Hz), æ (F0 = 106 Hz)/presented to the OHI model. (A) Only 20 ACF channels (2, 1, 1, and 16 across four segments) are included due to CS. (B) These channels are added together to obtain the pooled ACF, where the estimated F0 is 106 Hz (arrow). Figure layout similar to Fig. 3, but without segregated ACFs. The model predicts an incorrect vowel response /æ, æ/ for this no-F0 segregation condition.

To illustrate how the lack of the F0-guided segregation cue (i.e., with only formant difference cues) for both ONH and OHI models resulted in incorrect responses, another vowel pair /u (F0 = 100 Hz), æ (F0 = 106 Hz)/ was also analyzed (results not shown). Similar to Fig. 3, the YNH model identified both the vowels correctly based on the segregated PACFs. For the ONH and OHI models, there was a peak at 9.43 ms that corresponded to correct estimation of dominant F0 = 106 Hz. Additionally, the percent ACF channels that showed a peak at 9.43 ms was 86.66% and 90% for ONH and OHI models, respectively. Thus, the model did not segregate using the F0 difference but had to identify the vowels based on the m1/m2 criterion value of 2 (as in Fig. 5). The model incorrectly identified /æ, æ/ and predicted a single F0 = 106 Hz. Due to the lack of F0-guided segregation in both models [Figs. 2(G) and 2(H)], the vowel pair was incorrectly identified, as the identification was based only on the formant difference cues.

IV. DISCUSSION

A. Effect of F0 difference cue on concurrent vowel scores across three listening models

The predictions for the three different listening models (Fig. 2) were successful in capturing the pattern of concurrent vowel identification scores across F0 differences. Furthermore, the F0 benefits were similar between the data and the model scores (Table IV). The percent segregation was reduced with increasing age [Fig. 2(G)], suggesting that the F0-guided segregation ability was limited, which correlated well with the ONH model's reduced scores [compare Fig. 2(A) with 2(C)]. This segregation was further reduced due to HL [Fig. 2(G)], resulting in the lowest scores for the OHI model [compare Fig. 2(C) with 2(D)]. These predictions suggest that the limited vowel segregation based on F0 difference for ONH and OHI subjects might contribute to reduced concurrent vowel scores. For each listening model, the one vowel identification was 100% and matched the concurrent-vowel data (results not shown), suggesting that F0 difference is essential for identifying both vowels in the pair (consistent with Chintanpalli et al., 2016).

B. Effect of CS on predicting concurrent vowel scores

CS is an important anatomical change in the periphery due to normal aging and HL but has a negligible effect on the audiometric profile (Liberman and Kujawa, 2017). The effect of CS on perception is yet to be fully understood. Thus, the current study attempts to evaluate this effect by predicting concurrent vowel scores for ONH and OHI subjects. The predictions confirm that scores are reduced for the ONH model by including CS [compare Fig. 2(B) with 2(C)]. Furthermore, the OHI model scores [Fig. 2(D)] were lowest primarily due to CS (hearing impairment also contributed).

The current study assumed a loss of all AN-fiber SR types at each CF to simulate the CS effect for the ONH and OHI models. The rationale was to use as simple a model as possible to represent the basic loss of AN fibers with CS, without being more specific than current data justify. While CS data from rodents suggest LSR fibers are lost in greater proportion than HSR fibers (Furman et al., 2013), whether this occurs remains unknown. In fact, model simulations that capture the effect of CS on envelope following responses required loss of all SR types to account for the human data (Encina-Llamas et al., 2019). By having 25 CFs per octave in the YNH model, reducing the total number of AN fibers within each octave is a simple way to capture the main effect of fewer AN fibers conveying information to central-processing structures.

C. Sensitivity of predicted concurrent vowel scores to model parameter values

It is assumed that OHC and IHC dysfunction are equal in response to EP reduction in the ONH model. The C_ohc and C_ihc values were estimated by matching the AN-model thresholds with the mean audiometric thresholds for ONH subjects. The ONH model scores solely based on C_ohc and C_ihc = 0.85 had a minimal effect on the concurrent vowel scores, relative to YNH model [compare Fig. 2(A) with 2(B)]. We also investigated the sensitivity of ONH model scores to C_ohc and C_ihc being equal or not for representing EP reduction. It was found that when C_ohc = 0.8 and C_ihc = 0.85, there was still a good fit (relative PTA difference < 10%) between the AN-model thresholds and mean audiometric thresholds of ONH subjects. With this change the concurrent vowel scores were the same as shown in Fig. 2(B) (result not shown). These findings suggest that the ONH model scores are not particularly sensitive to exactly equal contributions of OHC and IHC for reducing the EP.

The values for the HSRsps, MSRsps, and LSRsps fibers of the AN model were 50, 4, and 0.1 spikes/s, respectively (Table III). These values were selected, such that AN-model thresholds matched well with mean audiometric thresholds for YNH subjects (Chintanpalli et al., 2016) with relative PTA difference <10%. It is possible that an alternative set of SR values could be obtained to match the mean YNH thresholds, in which the F0-guided segregation parameter values might need to be adjusted to fit the YNH data [similar to Fig. 2(A)]. However, as long as the ONH and OHI models were developed based on the approaches proposed in the current study (Fig. 1), the models' scores are expected to provide a good fit to concurrent-vowel data and thus would not alter the overall conclusions of this study.

The OHI subjects were assumed to have NIHL, with 2/3 OHC dysfunction (in dB) and 1/3 IHC dysfunction at each CF. It is possible that the OHI subjects could have a different configuration of OHC and IHC losses at each CF; however, the current modeling represents a simple approach in assuming the same proportion of OHC to IHC loss at all CFs given that it is difficult to estimate this proportion in individual subjects. Furthermore, our approach assumes that these values include both the EP-reduction metabolic effects (equal reduction in C_ohc and C_ihc) along with the sensory effects (larger reduction in C_ohc and C_ihc), consistent with suggestions from recent temporal-bone studies in humans that the functional effects of EP reduction are minimal in the presence of sensory loss (Wu et al., 2020a; Wu et al., 2020b). Recently, Eckert et al. (2021) noted that the subjects in Wu et al. (2020a) were predominantly older males with acoustic overexposure and hence their findings (i.e., larger sensory than metabolic effects) may not be applicable to the entire older adult population with HL. Moreover, there are other population-based studies suggesting that the relationship between metabolic and sensory effects may differ across OHI subjects (Dubno et al., 2013; Allen and Eddins, 2010). Thus, it is possible that OHI subjects could have different etiologies or auditory phenotype than the current assumption of NIHL effects. As techniques become available to define the specific effects of EP reduction and sensory damage on OHC and IHC dysfunction in individual subjects, impaired AN responses (obtained using the newly estimated C_ohc and C_ihc values across CFs) could be used to refine the OHI model, with other etiologies, to predict the concurrent vowel scores.

D. Physiological mechanisms underlying reduced concurrent vowel scores due to age and hearing loss

In the YNH model, concurrent vowel scores increased with improved segregation as a function of F0 difference [Figs. 2(A) and 2(E)]. Since the model is based on ACF, this result suggests that, (1) enhanced segregation ability with F0 difference can result from improved AN-fiber temporal coding for at least one F0 of the vowel pair, and (2) better segregation can improve the temporal coding of formants in each vowel to aid identification. The lower scores for the ONH and OHI models suggests that degraded AN-fiber temporal coding for F0s and formants due to age and HL can reduce concurrent vowel identification by limiting segregation ability, with greater effects for age and HL combined.

E. Conclusions and future work

To understand the effects of age and HL on the ability to utilize the F0 difference cue, the current study predicted concurrent vowel scores across F0 differences for three different listening groups. To assess age effects, EP reduction and CS were included [Figs. 1(A) and 1(C)]. The identification scores were reduced across F0 differences for the ONH model and were successful in capturing the pattern of scores of concurrent-vowel data [Fig. 2(C)]. For the OHI model, hair-cell damage, EP loss and CS (with a larger effect than for the ONH model) were incorporated [Figs. 1(A) and 1(D)], which resulted in the lowest predicted concurrent vowel scores and captured the pattern of behavioral scores [Fig. 2(D)]. The reduced vowel segregation in both the ONH and OHI models [Figs. 2(G) and 2(H)] suggests a limited use of the F0-guided segregation cue with increased age and HL. These model predictions support our hypotheses and suggest that peripheral changes due to increased age and HL can contribute to reduced concurrent vowel scores for ONH and OHI subjects (through reduced segregation and identification due to degraded temporal coding of F0 and formant cues).

The current modeling study can be extended to predict the effects of age and HL on concurrent vowel scores for short durations. Settibhaktini and Chintanpalli (2020) used a similar modeling framework, but reduced only the F0-segregation criterion value to predict the concurrent vowel scores for shorter durations in YNH subjects. The same modeling approach can be adopted to analyze age and HL effects on shorter-duration vowels. These predictions will help in designing an experimental paradigm (e.g., suitable duration and level) for aged and hearing-impaired listeners, for which behavioral data are unavailable. Furthermore, the current modeling framework can be used to predict the perceptual consequences of variations in the degree of metabolic and sensory components that likely occur across the population of older listeners with HL (Eckert et al., 2021).