Nucleation kinetics of calcium oxalate monohydrate as a function of pH, magnesium, and osteopontin concentration quantified with droplet microfluidics

Abstract

A droplet-based microfluidic platform is presented to study the nucleation kinetics of calcium oxalate monohydrate (COM), the most common constituent of kidney stones, while carefully monitoring the pseudo-polymorphic transitions. The precipitation kinetics of COM is studied as a function of supersaturation and pH as well as in the presence of inhibitors of stone formation, magnesium ions (Mg²⁺), and osteopontin (OPN). We rationalize the trends observed in the measured nucleation rates leveraging a solution chemistry model validated using isothermal solubility measurements. In equimolar calcium and oxalate ion concentrations with different buffer solutions, dramatically slower kinetics is observed at pH 6.0 compared to pHs 3.6 and 8.6. The addition of both Mg²⁺ and OPN to the solution slows down kinetics appreciably. Interestingly, complete nucleation inhibition is observed at significantly lower OPN, namely, 3.2 × 10⁻⁸ M, than Mg²⁺ concentrations, 0.875 × 10⁻⁴ M. The observed inhibition effect of OPN emphasizes the often-overlooked role of macromolecules on COM nucleation due to their low concentration presence in urine. Moreover, analysis of growth rates calculated from observed lag times suggests that inhibition in the presence of Mg²⁺ cannot be explained solely on altered supersaturation. The presented study highlights the potential of microfluidics in overcoming a major challenge in nephrolithiasis research, the overwhelming physiochemical complexity of urine.

I. INTRODUCTION

Kidney stone (renal lithiasis or nephrolithiasis) is a serious health problem worldwide with increasing incidence.^1,2 Stone formation is a physiochemical process, where crystallization of inorganic salts in the presence of biological constituents is followed by growth, aggregation, and retention within the urinary tract. Although urine consists mainly of water (95%), it also contains organic solutes such as urea; creatinine; uric acid; trace amounts of peptides, enzymes, carbohydrates, hormones, fatty acids, and pigments; and inorganic ions such as sodium, potassium chloride, magnesium, calcium, ammonium, sulfates, and phosphates.^3,4 In other words, kidney stone formation occurs in a complex solution matrix. This matrix-complexity is a major challenge in constructing a physical understanding of kidney stone formation. Remarkably, the relative amounts of these components can be affected by patient-specific conditions such as age, genetic effects, medical history, fluid intake, diet habits, fluctuation in urine pH, or environmental conditions such as temperature and climate.^5–8 The average pH of urine is 6.0, yet it can range between 4.0 and 8.0; clinical studies have shown that lower pH values cause the highest risk for forming kidney stones.^3,9 Despite a broad body of literature, a physiochemical mechanism explaining the causal relationship between kidney stone formation and patient-specific urine composition is not yet established. The overwhelming complexity of the urine matrix is a major roadblock in developing preventive treatments informed by a mechanistic understanding, particularly in the pesky case of re-emerging stones.

The analyses of kidney stones from patients reveal that they contain inorganic crystals merged with organic constituents such as proteins and dead cells.^10,11 There are three main types of crystals in kidney stones: calcium oxalate (CaOx), calcium phosphate, and uric acid. Almost 80% of stones consist predominantly of hydrate crystals of calcium oxalate.^10–15 Calcium oxalate crystals can be present as dihydrate (weddellite) or calcium oxalate monohydrate (COM, whewellite), which is the most common and the most stable form at body temperature (37 °С).^3,5,16,17 People who exhibit a high risk for kidney stone formation tend to excrete urine with higher supersaturation with respect to COM compared to non-stone formers. This condition is referred to as hypercalciuria, i.e., high Ca levels in the urine, and the amount of calcium can reach values greater than 300 mg/24 h for men and 250 mg/24 h for women.^2,5,18,19

In the human body, there are numerous organic and inorganic compounds that might either facilitate (promoters) or prevent (inhibitors) stone formation. Low urine volume and high calcium, sodium, oxalate, and urate concentrations in the urine are known to promote the formation of kidney stones.²⁰ On the other hand, stone formation is considered to be inhibited by various inorganic substances such as citrate and magnesium and organic substances such as nephrocalcin, urinary prothrombin fragment-1, and osteopontin (OPN).²¹ OPN is a single-chain protein with a molecular weight of approximately 33 kDa, present in urine in amounts higher than 100 nM.²² Reports in the literature mention that OPN inhibits crystal growth and changes the morphology of CaOx crystals.^22–24 Studies on the effect of magnesium mention that Mg²⁺ ions suppress COM formation by increasing its solubility.^18,25 Various methods have been used to study nucleation and growth kinetics of COM^26,27 and the effect of additives on the kinetics.^28,29

In studies focusing on nucleation kinetics, effective nucleation rates have been determined from induction time measurements where the emergence of the first crystal is recorded as the induction time at a fixed supersaturation.³⁰ Since nucleation is a stochastic process, a large number of identical experiments (in the order of hundred) are needed to get a statistically accurate value of the induction time distribution for a particular value of supersaturation ratio.^26,27 Using the induction time distribution, cumulative induction time probability, p(t), curves can be constructed. Fitting models such as the single exponential, Weibull function (discussed in Sec. II B 3) allows the determination of effective nucleation rates. Once effective nucleation rates at different supersaturations are experimentally extracted, analysis and interpretation in terms of the “often criticized” classical nucleation theory (CNT) allows a deeper look into the nucleation mechanics. There is a broader discussion in the literature on the possible nucleation pathways describing the evolution of structure. There are two schools of thought describing the nucleation pathway: classical and non-classical, also referred to as two-step nucleation. CNT describes the formation of an ordered nucleus as the association of monomeric units that overcome a free-energy barrier at a critical nucleus size. On the other hand, the non-classical pathway considers the formation of an intermediate amorphous dense state prior to the formation of an ordered nucleus. A broader review of the evidence for non-classical nucleation can be found in studies by Vekilov with a focus on protein crystallization³¹ as well as Gebauer and Cölfen focusing on pre-nucleation clusters as seen in inorganic systems.³² For CaOx nucleation, Hajir et al.³³ and others discuss the nucleation pathway and provide evidence for pre-nucleation clusters and hence a non-classical path.³⁴ Smeets et al. demonstrated that CNT concepts can be used to describe complex nucleation mechanisms.³⁵ Most recently, Kashchiev published an extension of the CNT to include two-step nucleation of crystals reconfirming the idea that CNT concepts can be used to study non-classical pathways.³⁶ In this study, we use CNT without making assumptions on the nucleation pathway to rationalize observed trends.

As shown by Ruiz-Agudo et al.³⁴ for nucleation of CaOx and by Gebauer et al.³⁷ and Smeets et al.³⁵ for CaCO₃ precipitation, the activities of both the free and bound anions and cations in the solution are essential in the investigation of nucleation kinetics. However, in electrolyte solutions such as the solutions used in this study and the urine solutions in the kidney, the supersaturation of the solution with respect to the aforementioned stone forming crystals is strongly dependent on the properties of the solution^38,39 such as the presence of background electrolytes, often characterized by the ionic strength,^40,41 and the pH, which influences the composition of the ions in the solution due to protonation and de-protonation reactions.^40,42 Moreover, the supersaturation can also be strongly affected by the formation of soluble ion pair complexes.⁴² Therefore, a solution chemistry model must be used to describe the speciation of the electrolyte solutions used for the nucleation experiments.⁴³ Recently, such a model has been described extensively, which gave an excellent prediction of the solubility of Ca ions in different buffered and nonbuffered calcium oxalate solutions.⁴³ This model considers the (de)-protonation reactions and the ion pair formation, often referred to as complexation reactions, in the solution and the solid formation of the different species in the electrolyte solution. The model is based on the Davies equation of the Debye–Hückel theory to describe the activities of the species in the solution. In this way, the effects of the various process conditions on both the supersaturation and the nucleation kinetics can be separated.^38,43,44

To generate a statistically significant number of data points via batch lab-scale approaches is a labor and time-intensive process.^45,46 To this end, microfluidic approaches have been proposed and successfully implemented.^47–53 With the microfluidic techniques, one can work with minute amounts of solutions at the microliter scale while conducting a significant number of identical experiments.^49,54–56 Particularly, the use of uniformly sized micro-droplets as isolated crystallization micro-reactors has been investigated in multiphase droplet microfluidics.^57–59 In a droplet microfluidic system, a dispersed phase flow is emulsified in continuous phase in the presence of surfactants.^49,52 Despite the recent surge in applications of lab on a chip technology in studies focusing on CaOx stone formation, a droplet-based microfluidic platform enabling nucleation/precipitation kinetics studies of CaOx compounds with focus on nephrolithiasis⁵ has not been reported, to the best of our knowledge.

In this work, we describe a droplet-based microfluidic platform designed and optimized for measuring the nucleation/precipitation kinetics of the calcium oxalate monohydrate. To this end, the following functions are realized in the 3D printed microfluidic platform: (i) bringing together two aqueous flows carrying prescribed concentrations of calcium chloride (CaCl₂) and sodium oxalate (NaOx) along with other additives for the induction time experiments, (ii) creation of uniform size water droplets carrying calcium and oxalate ions dispersed in a carrier oil phase, (iii) rigorously mixing droplet contents to ensure constant supersaturation immediately after the two streams are brought in contact, and (iv) trapping and stabilization of droplets within observation contraptions allowing monitoring throughout induction time measurements (up to 12 h). The advantage of the proposed microfluidic system is that the operations of bringing two reactive solutions and mixing them are rapidly conducted to avoid any biasing coming from manual handling of fluids. Using this microfluidic platform, we study COM nucleation kinetics at varying calcium and oxalate ion concentrations in ultrapure water and in buffer solutions dictating the solution pH. Moreover, we quantify the effect of magnesium (Mg²⁺) and osteopontin (OPN) on the nucleation kinetics of COM. The pseudo-polymorphic form of CaOx is monitored during induction time measurements with in situ and ex situ techniques. We interpret the measured nucleation rates in the context of the classical nucleation theory (CNT) without making assumptions whether the nucleation pathway is non-classical or classical.⁶⁰ To this end, we leverage a solution chemistry model describing the solution chemistry and the complex formation, based on the Davies extension of the Debye–Hückel theory where the details of the model can be found in the study by Ibis et al.⁴³ The previously developed solution chemistry model is validated by comparing the measured and modeled solubility of COM for all of the samples used in the nucleation induction experiments. We observe that the presence of OPN and Mg²⁺ ions inhibit apparent nucleation. The observed inhibition effect of OPN at significantly lower concentrations than Mg²⁺ ions emphasizes the often-overlooked role of macromolecules on COM nucleation due to their low concentration presence in urine.⁶¹ Moreover, analysis of growth rates calculated from observed lag times in induction time measurements suggests that the presence of Mg²⁺ ions alters the growth process and their effect cannot be explained solely on supersaturation.

II. MATERIALS AND METHODS

The overarching design objective is to create a statistically significant number (order of hundreds to thousands) of well-mixed micro-batch reactors with controlled supersaturation to acquire statistically significant nucleation induction time measurements. To this end, we describe the developed microfluidic platform designed for the following purposes: (a) to generate stable, well-mixed droplets from two reacting streams dispersed in an inert oil medium and (b) to minimize the droplet coalescence during the observation phase.

A. Microfluidic design

The microfluidic device can be divided into three different zones; droplet formation, mixing, and storage [Fig. 1(b)]. Aqueous droplets are formed in this K-junction zone in the presence of a surfactant in the droplet formation zone. The mixing zone ensures complete mixing with serpentine-shaped bends that act as passive mixers.⁶² These bends ensure complete internal mixing of the droplets before they reach the storage section [Fig. 1(b)]. The storage zone is the last section where the droplets are trapped for observation throughout an induction time experiment (up to 6 h).

FIG. 1.

Experimental setup and microfluidic platform: (a) Schematic of the experimental setup with insets showing polarized light microscopy images of droplets during induction time measurements. (b) Illustration of the droplet formation, the mixing, and the storage zones in the microfluidic platform.

1. Droplet formation and mixing

Three inlets, two for the aqueous solutions and one for the continuous phase (oil phase), are brought together in a K-shaped junction shown in Fig. 1(b) for droplet generation. To ensure the mixing of two aqueous streams carrying calcium and oxalate ions, serpentine-shaped passive mixers are utilized after the K-junction.⁶³ As the droplets move through serpentine-shaped passive mixers, an asymmetric drag force acts on the droplets and creates asymmetric flow patterns, consequently mixing the droplet contents in each bend.⁶⁴ Previously developed experimental correlations based on droplet mixing experiment channels of various geometries predict that a droplet subject to the flow rate and channel geometry used in this study is completely mixed after five bends.⁶⁴ In the design of the proposed microfluidic platform, we included 13 bends ensuring complete mixing of the contents of the droplet. Hence, we ensure that the contents of the droplets have been mixed rigorously when they enter the storage section shown in Fig. 1(b). Complete mixing is an important design requirement for the microfluidic platform as the interpretation of nucleation rates requires constant supersaturation assumption, i.e., ion concentrations inside droplets need to be uniform. Tightly regulated air pressure is utilized to avoid pressure fluctuations commonly observed in syringe pumps (pressure pump, Fluigent, MFCS-EZ). A mixture of hydrofluoroether oil (HFE3-Ethoxy-1,1,1,2,3,4,4,5,5,6,6,6-dodecafluoro-2-trifluoromethylhexane, 3M, CAS297730-93-9) and fluorinated surfactant (Sphere Fluidics, CAS240119-1) is used as the continuous phase. The surfactant is added to prevent the Polydimethylsiloxane [PDMS, (C2H6OSi)n, The DOW Chemical Company] matrix from absorbing the oil and to help in droplet formation/stabilization. The continuous phase contains 0.5% V/V surfactant in hydrofluoroether. The effect of the surfactant on COM nucleation was not investigated, as producing stable droplets without the surfactant was not possible.

2. Storage

Once the droplets are produced, they are stored in hydrodynamic traps whose sizes are 200 μm depth, 400 μm width, and 1200 μm length, as shown in Fig. 1(a). The hydrodynamic traps ensure that droplets stay in the designated positions throughout the induction time measurements. The elevated hydrodynamic resistance due to the narrow necks (180 μm) at the entrance and exit of hydrodynamic traps ensures that the droplets do not drift or coalesce due to the evaporation of continuous and dispersed phases through the PDMS or through the inlet/exit ports. Such drift and coalescence are undesired as these effects promote coalescence decreasing the number of droplets contributing to nucleation induction time measurements and alter supersaturation. Ensuring that the droplets do not drift and merge is essential to acquire statistically sound measurements.

3. Microfluidic mold preparation

The microfluidic chip is designed in SolidWorks and 3D printed (EnvisionTEC Micro Plus Hi-Res—43 × 27 mm). The printer has a resolution of 30 μm for the x and y directions and a resolution of 25 μm for the z direction.^49,50 A UV curing chamber (Photopol light-curing furnace, Dentalfarm) is used to make a fully cured mold. To peal chips off easily from the mold, the printed mold is hydrophobized with Trichloro(1H,1H,2H,2H-perfluorooctyl) silane (Sigma-Aldrich, CAS 78560-45-9). Further details on the chip can be found in Sec. 1 in the supplementary material.

4. Chip fabrication

To fabricate a chip, PDMS and curing agent at a 7:1 (w/w) ratio are prepared. The mixture is stirred until it appears to be cloudy. Upon mixing, the mixture is centrifuged (Universal 320 R, Hettich Zentrifugen) at 7400 rpm and 20 °C for 15 min to remove bubbles. The resulting transparent PDMS mixture is poured on the 3D printed mold, and the mold is placed inside a desiccator. A vacuum pump is connected to the desiccator to remove the air bubbles introduced during the pouring process. Then, the mold is placed in the oven at 65°C overnight to ensure complete curing of the PDMS. Once the chip is completely cured, holes are punched at the inlets. Subsequently, PDMS and curing agent at a 10:1 (w/w) ratio are prepared to coat the microscope slide (thickness 1 mm) with PDMS. 0.5 ml of this new PDMS solution is spin coated at 4500 rpm and semi-cured for 1 min. The pealed and cured PDMS (with a 7:1 ratio) channel top is placed on the microscope slide with the semi-cured PDMS layer (10:1) for 20 min at 65 °C. Once they stick with each other, the device is kept in the oven overnight at 65 °C to complete curing. The experiments are performed in a thermostated room at 20 °C.

5. Monitoring crystal induction with polarized light microscopy

To enhance the contrast between the crystals and the surroundings, polarized light microscopy is used with two polarizing filters, as shown in Fig. 1(a). Polarized microscopy ensures that a dark background is created while the crystals shine bright and can be easily detected. Moreover, polarized microscopy enables the identification of the pseudo-polymorphic form of the crystals.

B. Microfluidic induction time measurements

1. Solution preparation for microfluidic experiments

CaCl₂ and NaOx are dissolved separately into two beakers containing 50 ml ultrapure water or buffer. The solutions are connected to separate microfluidic device inlets. Once two droplets merge, the concentration of CaCl₂ and NaOx solutions fed into the inlets are diluted by a factor of two, and final ion concentrations inside droplets are determined. The final concentrations of CaCl₂ and NaOx in droplets for different supersaturated solutions are given in Table II. The equimolar concentrations, namely, 4.1 × 10⁻⁴ M of CaCl₂ and 4.1 × 10⁻⁴ M of NaOx, are used as a final concentration in the droplets for three different buffer solutions (see Table III). For the inhibitor experiments, the droplets contain equimolar concentrations, namely, 4.1 × 10⁻⁴ M CaCl₂ and 4.1 × 10⁻⁴ M NaOx with varying amounts of MgCl₂ (Table IV) and osteopontin (osteopontin human recombinant, Sigma-Aldrich, expressed in HEK 293 cells, ≥97%). In microfluidic induction time experiments, MgCl₂ is dissolved in an aqueous stream containing CaCl₂ and organic inhibitor; osteopontin is dissolved in an aqueous stream containing NaOx. The osteopontin stock solution (8 μg/ml) is prepared. Other OPN concentrations, 1.6 × 10⁻⁸, 3.2 × 10⁻⁸, and 4.8 × 10⁻⁸ M, are obtained by dilution. The solutions for microfluidic induction time experiments are prepared fresh for every experiment to avoid contamination.

TABLE II.

Added equimolar concentrations of CaCl₂ and NaOx in ultrapure water. The free [Ca²⁺] and [C₂O₄²⁻], the activity coefficient, γ, and the S values in the droplets were determined using the solution chemistry model and represent equilibrium values prior to possible precipitation of COM. The latter values are only accurate until the point of nucleation.

Added total [Ca2+] = [C2O42−] × 10−4 M	Free [Ca2+]  × 10−4 M	Free [C2O42−] × 10−4 M	Activity coefficient (γ)	Estimated S (in droplets)
1.35	1.09	1.09	0.89	1.18
2.05	1.55	1.55	0.87	1.64
2.75	1.97	1.97	0.85	2.05
4.10	2.72	2.71	0.83	2.74
5.50	3.42	3.41	0.81	3.36

TABLE III.

pH values and the added equimolar CaCl₂ and NaOx concentrations of the different buffer solutions for the nucleation induction experiments. Buffer solutions used to obtain the different pH values are specified in Table I. The free [Ca²⁺] and [C₂O₄²⁻] concentrations, the activity coefficient, γ, and the S values in the droplets were found using the solution chemistry model. These values are equilibrium values prior to possible precipitation of COM and are only accurate until the point of the first nucleation.

pH	Added total [Ca2+] = [C2O42−] × 10−4 M	Free [Ca2+] × 10−4 M	Free [C2O42−] × 10−4 M	Activity coefficient (γ)	Estimated S (in droplets)
3.6	4.1	3.61	0.75	0.81	1.64
6.0	4.1	2.06	3.64	0.32	1.09
8.6	4.1	2.75	2.91	0.73	2.53

TABLE IV.

Added MgCl₂, CaCl₂, and Na₂C₂O₄ concentrations in the samples, used to study the effect of Mg²⁺ ions on the nucleation induction time. The free [Ca²⁺] and [C₂O₄²⁻] concentrations, the activity coefficient γ, and the S values in the droplets were found using the solution chemistry model. These values are equilibrium values prior to possible precipitation of COM and are only accurate up to the point of the first nucleation.

Added total [Ca2+] = [C2O42−] × 10−4 M	[Mg2+] × 10−4 M	Free [Ca2+] × 10−4 M	Free [C2O42−] × 10−4 M	Activity coefficient (γ)	Estimated S (in droplets)
4.1	0.0	2.72	2.71	0.827	2.74
4.1	0.05	2.72	2.70	0.827	2.74
4.1	0.5	2.78	2.56	0.823	2.68
4.1	0.875	2.82	2.46	0.821	2.64
4.1	1.0	2.83	2.42	0.820	2.62
4.1	1.25	2.86	2.36	0.818	2.60

2. Procedure for induction time measurements

Once the droplets are produced, mixed, and stored, they are imaged with polarized light microscopy automatically with a Nikon Eclipse Ti Series Inverted Microscope. The automated microscope stage, shown in Fig. 1(a), takes a micrograph of droplets within a given field of view and moves to an adjacent field of view till the whole chip is imaged. Once the whole chip is imaged, the individual micrographs are stitched together and stored constructing a time stamp image for induction time measurements. One such image is shown in Fig. 2(a). The imaging process including the acquisition and stitching takes 2 min. Once the first image is acquired, the imaging process for the second one immediately begins. A time-lapse movie is recorded, and the time frame in which the first crystal emerges in each droplet is manually analyzed to construct cumulative induction time probability functions, p(t), shown in Figs. 4–7. The spatial resolution for detecting a crystal in a droplet is dictated by the optical resolution of the microscope lens and camera used (one pixel is ∼1.67 μm). It is noteworthy to mention that a reference image was taken at t = t₀ for each droplet in the storage section. To distinguish the crystals from artifacts such as random white pixels or dirt, the analysis was made by comparing every droplet image at t_n with the immediate previous one at t_n−1 and at t₀, thus detecting white crystals accurately. Owing to the stochastic nature of nucleation events, over 100 droplets are tested simultaneously for one measurement to obtain the cumulative induction time probability function for the nucleation induction time.

FIG. 2.

The total dissolved calcium concentration in equilibrium for different pH values (a) and for different magnesium concentrations (panel b). The solid symbols are measured values with ICP-OES, and open symbols are the predicted values via our solution chemistry model,⁴³ respectively. Calcium values represent the average of nine data points for each pH value and magnesium concentration. The regression statistics give a p-value of 0.08 for Fig. 2(b).

FIG. 4.

The cumulative induction time probability, p(t), as a function of the detection time, t, for different added Ca²⁺ concentrations in ultrapure water fitted with the exponential function with delay time [Eq. (1)]. The numbers of used droplets are 107, 112, 129, 102, and 103 for concentrations of 1.35 × 10⁻⁴, 2.05 × 10⁻⁴, 2.75 × 10⁻⁴, 4.10 × 10⁻⁴, and 5.50 × 10⁻⁴ M, respectively. The ratio of added molar concentration of Ca²⁺ and C₂O₄²⁻ ions is the same for all experiments [Ca²⁺]/[C₂O₄²⁻] = 1 for all solutions. The calculated initial free Ca²⁺ and C₂O₄²⁻ ion concentrations, their activity coefficient, and the initial supersaturation of COM in the droplets are given in Table II.

FIG. 5.

The cumulative induction time probability, p(t), curves for different pH values fitted with the single exponential with delay time [Eq. (1)]. The numbers of used droplets are 118, 105, and 124 for pH values of 3.6, 6.0, and 8.6, respectively. The composition of the buffer solutions for pH values of 3.6, 6.0, and 8.6 are shown in Table I. The added equimolar Ca²⁺ and C₂O₄²⁻ concentration of 4.1 × 10⁻⁴ M is used in all experiments. The calculated initial free Ca²⁺ and C₂O₄²⁻ ion concentrations, their activity coefficient, and the initial supersaturation of COM in the droplets are given in Table III.

FIG. 6.

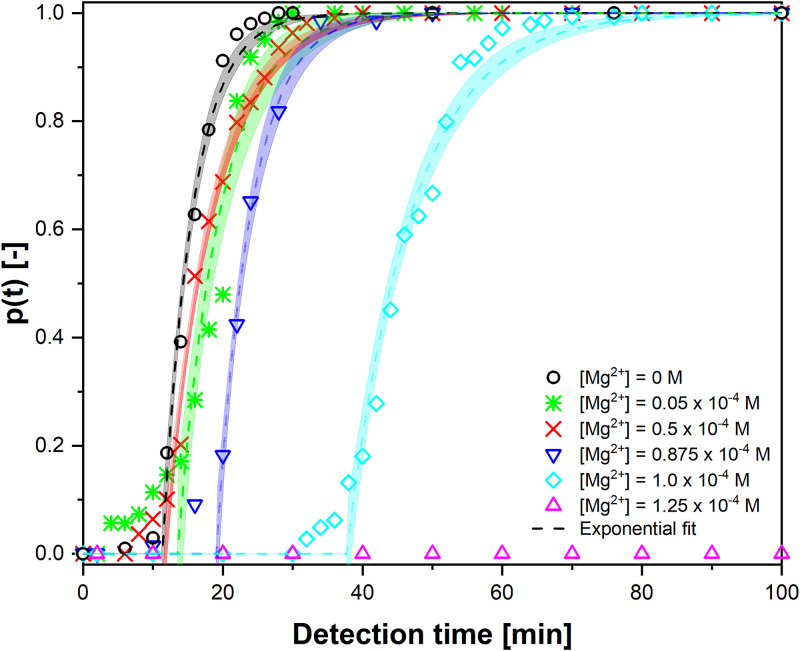
The cumulative induction time probability curves, p(t), at specific Mg²⁺ concentrations fitted with the single exponential with delay time [Eq. (1)]. The numbers of used droplets are 107, 106, 109, 113, 108, and 102 for concentrations of magnesium: 0, 0.05 × 10⁻⁴, 0.5 × 10⁻⁴, 0.875 × 10⁻⁴, 1 × 10⁻⁴, and 1.25 × 10⁻⁴ M, respectively. The varying concentrations of Mg²⁺ ions are added to equimolar calcium and oxalate concentration of [Ca²⁺] = [C₂O₄²⁻]= 4.1 × 10⁻⁴ M. The calculated initial free Ca²⁺ and C₂O₄²⁻ ion concentrations, their activity coefficient, and the initial supersaturation of COM in the droplets are given in Table IV.

FIG. 7.

The cumulative induction time probability, p(t), curves at specific osteopontin concentrations fitted with the single exponential with delay time [Eq. (1)]. The numbers of used droplets is 107, 102, 111, and 105 for concentrations of osteopontin: 0, 1.6 × 10⁻⁸, 3.2 × 10⁻⁸, and 4.8 × 10⁻⁸ M, respectively. The Ca²⁺ and C₂O₄²⁻ concentrations are kept constant at 4.1 × 10⁻⁴ M.

3. Analysis of induction time measurements

Using a statistically significant collection of induction time experiments, a cumulative induction time probability function, p(t), can be constructed as described in Sec. II B 2. The experimentally acquired p(t) are fitted by different models to calculate the effective nucleation rate, J, using models such as single exponential with delay time in Eq. (1) or Weibull function shown in Eq. (2),

$$\mathrm{p}(\mathrm{t})=1-{\mathrm{e}}^{-\mathrm{JV}(\mathrm{t}-t_G)}=1-{\mathrm{e}}^{-\left(\frac{\mathrm{t}-{\mathrm{t}}_G}{\tau }\right)},$$ (1)

where V is the volume of the liquid phase, J is the nucleation rate, t is the time, and t_G is the time it takes for a formed nucleus to grow to a crystal of a detectable size, which is dependent on the detection system; the parameter $\tau$ is defined as 1/JV.

The Weibull function is commonly used to describe the probability distribution to account for measured deviations from the exponential behavior of the p(t) plot,

$$\mathrm{p}(\mathrm{t})=1-{\mathrm{e}}^{-{\left(\frac{\mathrm{t}}{\tau }\right)}^{\mathrm{k}}}.$$ (2)

The shape parameter k is well suited to fit the sometimes-encountered s-shaped p(t) plots and informs us of the functional form of the nucleation rate. When k = 1, the Weibull model reduces to an exponential model. For k < 1, the nucleation rate is decreasing, and for k > 1, the nucleation rate is increasing with time. The physical interpretation of the increasing or decreasing nucleation rates under conditions with constant concentrations and temperature indicated by the Weibull function is, however, not straightforward.³⁰ Once the p(t) functions are fitted with these models, the estimated nucleation rates, J are calculated as shown in Table V. The combined J values along with the corresponding supersaturation values extracted from solution chemistry modeling facilitates the classical nucleation theory (CNT)^30,65 analysis of nucleation induction time experiments. Using the CNT expression given in Eq. (3), the nucleation induction time measurements with different solutions can be compared as shown in Fig. 8. The CNT expression is given as

$$\mathrm{J}(\mathrm{S})=\mathrm{AS}\exp \left(-{\displaystyle \frac{\mathrm{B}}{\mathrm{l}{\mathrm{n}}^2\mathrm{S}}}\right),$$ (3)

where A and B are called the kinetic and thermodynamic nucleation rate parameter, respectively, and S is the supersaturation ratio.

TABLE V.

The fitted parameters with 95% confidence intervals and the corresponding statistics from the single exponential model with delay time for the different experimental conditions. MSE stands for mean squared error.

	Delay time (tG) (min)		τ (min)		J (m−3 s−1)	Statistics
	Value	Standard error	Value	Standard error	Value	Reduced chi-square	MSE
[Ca] = 2.05 × 10−4	240.49	4.16	31.82	4.05	6.18 × 1011	7.23 × 10−03	0.085
[Ca] = 2.75 × 10−4	20.74	0.22	11.62	0.37	2.26 × 1011	4.34 × 10−04	0.021
[Ca] = 4.1 × 10−4	11.34	0.16	4.30	0.24	8.34 × 1010	8.90 × 10−04	0.030
pH = 3.6	35.41	0.84	30.61	1.65	6.61 × 1009	1.56 × 10−03	0.039
pH = 8.6	23.41	0.08	6.06	0.15	3.34 × 1010	1.72 × 10−04	0.013
[Mg] = 0.05 × 10−5	13.52	0.46	6.05	0.72	1.18 × 1011	5.59 × 10−03	0.075
[Mg] = 0.5 × 10−5	11.65	0.20	6.68	0.31	1.30 × 1011	1.03 × 10−03	0.032
[Mg] = 0.875 × 10−5	19.06	0.22	4.94	0.39	9.59 × 1010	1.00 × 10−03	0.032
[Mg] = 1 × 10−5	37.73	0.35	9.25	0.56	1.80 × 1011	2.25 × 10−03	0.047
[OPN] = 1.6 × 10−8	48.73	5.02	60.28	7.86	1.17 × 1012	1.27 × 10−02	0.112

FIG. 8.

Apparent nucleation rate, J, and the corresponding S value for all of the measured induction times of COM at different conditions plotted in the context of classic nucleation time, i.e., different calcium and oxalate ion concentrations in de-ionized water given in Fig. 4, different pH values given in Fig. 5, and magnesium ion concentrations given in Fig. 6. Only the induction time data for different calcium and oxalate ion concentrations (green data points) in de-ionized water are fitted to Eq. (3). The dotted line is the fit with the parameters A = 4.05 × 10⁸ m⁻³ s⁻¹ (1.83 × 10⁷ to 8.96 × 10⁹) and B = 0.47 (−0.80 to 1.73) and gray shaded area is the 95% confidence interval.

C. COM solubility, modeling, pseudo-polymorph characterization, and error propagation

1. Procedure for COM solubility measurements

We quantify COM solubility under the same conditions used in this study for the nucleation induction time experiments. In fact, the isothermal solubility experiments⁴³ represent the end points in the induction time measurements assuming that equilibrium is reached. To measure the COM solubility in ultrapure water, two aqueous solutions of 4.1 × 10⁻⁴ M calcium chloride (CaCl₂, Sigma-Aldrich, CAS10043-52-4, ≥93.0%) and 4.1 × 10⁻⁴ M sodium oxalate (Na₂C₂O₄, Sigma-Aldrich, CAS62-76-0, ≥99.5%) are mixed rigorously and allowed to crystallize. After approximately 24 h, the supernatant is isolated by filtration and analyzed with inductively coupled plasma optical emission spectroscopy (ICP-OES). To check whether 24 h equilibration time is sufficient to reach the thermodynamic equilibrium between the crystals and the dissolved calcium and oxalate ions in the solution, we measured the Ca²⁺ concentration as a function of time. The Ca²⁺ concentration remained stable after a couple of hours later.⁴³ To quantify the effect of magnesium on COM solubility, five different amounts of magnesium chloride (MgCl_2, Sigma-Aldrich, CAS7786-30-3, ≥98.0%) are mixed with an equimolar ion concentration 4.1 × 10⁻⁴ M of CaCl₂ and NaC₂O₄ in ultrapure water. Finally, isothermal solubility experiments with three different pH buffers are conducted using the equimolar concentration of CaCl₂ and NaOx in buffer solutions (see Table I) for the composition of the buffer solutions. The results of the solubility measurements, which represent the equilibrium end point of the experiments described in Sec. II B 2, are given in Fig. 2 and will be discussed in Sec. II C 2.

TABLE I.

List of reagents and their concentrations used in the preparation of buffer solutions for microfluidic induction time and isothermal solubility experiments.

pH values	Chemical name	Final concentration (M)
3.6	Glycine	5.0 × 10−2
	Hydrogen chloride	5.0 × 10−3
6.0	Sodium acetate	1.8 × 10−3
	Acetic acid	1.6 × 10−3
8.6	Glycine	5.0 × 10−2
	Sodium hydroxide	4.0 × 10−3

The procedure for isothermal solubility measurement is as follows: CaCl₂ and NaOx are dissolved separately in two beakers containing 50 ml ultrapure water (ELGA PURELAB, resistivity: 18.2 MΩ cm at 23.6 °C). Both solutions are rigorously stirred with the ultrasonicator (Branson 2510, Ultrasonic Cleaner) for 10 min at room temperature to ensure that all compounds dissolve. The solutions are mixed and allowed to crystallize in a 100 ml Easymax reactor (Mettler Toledo, Columbus, OH, USA). For experiments with magnesium, 0.05 × 10⁻⁴, 0.5 × 10⁻⁴, 0.875 × 10⁻⁴, 1.0 × 10⁻⁴, and 1.25 × 10⁻⁴ M of MgCl₂ are dissolved in an aqueous CaCl₂ solution and then mixed with NaOx in the Easymax 102 reactor. For pH experiments, CaCl₂ and NaOx are dissolved in buffer solutions and then brought together and mixed in the Easymax reactor. The stirring rate is set at 400 rpm through 24 h to ensure proper mixing. Then, the stirrer of Easymax was stopped, the crystals were allowed to sediment, and 1 ml equilibrated solution was taken with a 1 ml pipet. The equilibrated solution was filtered with a syringe and filter (Whatman, 0.22 μm pore diameter). The samples were 10× diluted into 10 ml volumes with ultrapure water or buffer solution (for the pH experiments) and kept at room temperature. 10 ml samples were needed for the analysis with ICP-OES (SPECTRO Analytical Instruments, Kleve, Germany). Each experimental condition was repeated three times. The filtrate solutions were analyzed at three calcium emission lines at 317.9, 393.4, and 396.3 nm. The measurements conducted at all three wavelengths show quantitatively the same results, yet the emission line of 317.9 nm gave the smallest standard deviation. This situation was also observed in the literature and attributed to interference from other ions present.^66,67

The chemicals used to prepare the buffer solutions and their final concentrations are listed in Table I. For the lower pH of 3.5, glycine (C₂H₅NO_2, Sigma-Aldrich, CAS-1310-73-2, ≥95%) and hydrogen chloride (HCl, Sigma-Aldrich, CAS-7647-01-0, 1 M) were used; for the intermediate pH = 6, sodium acetate (CH₃COONa, Sigma-Aldrich, CAS-127-09-3, ≥99%) and acetic acid (CH₃COOH, Sigma-Aldrich, CAS-64-19-7, 99.8%) were used; and glycine and sodium hydroxide (NaOH, Sigma-Aldrich, CAS-1310-73-2, ≥95%) were used for the higher pH, 8.6.^68,69

2. Solution chemistry model

To interpret microfluidic induction time measurements in the context of the classic nucleation theory, we evoke a previously developed solution chemistry model⁴³ taking into account the effects of the process conditions, ionic strength, and complex formation on the COM solubility. This model also considers the protonation reactions of the oxalate and the ions of the buffer solution as well as the formation of soluble complexes, i.e., stable ion pairs between positive and negative ions in the solution.^42,70 This model, which is extensively described by Ibis et al.,⁴³ uses the Davies approximation of the Debye–Hückel equation for the estimation of the activities in the solution, providing excellent predictions for the COM solubility measurements at different concentrations of calcium and different pH values.⁴³ The supersaturation ratio with respect to COM is calculated according to Eq. (4),

$$\mathrm{S}=\sqrt{{\displaystyle \frac{[\mathrm{C}{\mathrm{a}}^{2+}][{\mathrm{C}}_2{\mathrm{O}}_4^{2-}]{\gamma }^2}{{\mathrm{K}}_{\mathrm{SP},\mathrm{COM}}}}},$$ (4)

in which K_SP,COM is the solubility product of COM, which was estimated in a previous study to be 6.7 × 10⁻⁹ at 25 °C⁴³ on the basis of the solubility measurements of COM in pure water. [Ca²⁺] and [C₂O₄²⁻] are the free ion concentrations in the solutions at equilibrium in the absence or prior to precipitation of COM. To calculate the S values of the different solutions, the model calculates the free ion concentrations and their activity coefficients (γ) taking into account the protonation, de-protonation, and ion pair reactions of all present species, including the buffer species. The added initial concentration of Ca²⁺ and C₂O₄²⁻ are given in Tables II–IV for different amounts of CaCl₂ and NaOx, in different buffer solutions and different amounts of magnesium additives.

To validate the model, the isothermal solubility measurements described in detail in Sec. II C 1 were compared with the simulated values of the model. The total dissolved calcium concentration at equilibrium is measured with ICP-OES. The total dissolved calcium concentrations from ICP-OES measurements and modeling results are given for varying pH values in Fig. 2(a) and for different magnesium ion concentrations in Fig. 2(b). The measurements indicate the strong effect of the pH and the used buffer solution on the solubility of COM, represented here as the total dissolved Ca²⁺ ion concentration, which is determined by the ICP-OES method. The total dissolved [Ca²⁺] is the highest at pH 6.0 in the sodium acetate buffer and somewhat lower in the glycine buffers at pH values of 8.6 and 3.6, which are, however, still higher than 1.14 × 10⁻⁴ M found for COM in ultrapure water. It is worth nothing that the ICP-OES results for pH = 3.6 deviate from the simulation. This might be explained by the fact that around this pH, the CaOx solubility curve is steep. During the storage period (max 24 h) of the samples prior to ICP-OES measurement, a slight variation in the pH value could occur by CO₂ absorption or evaporation. The results of the model and the experiments closely agree and confirm the much higher solubility of COM at pH 6.0. Further analysis of the model results learns that the high ionic strength of the sodium acetate buffer, resulting in low values of the activity coefficients, and the formation of calcium acetate ion pairs have a strong influence on the increased solubility of COM under these conditions.

The effect of the increasing Mg²⁺ ion concentration on the total dissolved [Ca²⁺] is only small as shown in Fig. 2(b) and hardly exceeds the standard deviation of the experiments. However, the model calculates values for the total dissolved [Ca²⁺] very close to the experimental values and also shows a small but distinct increase in the solubility of COM as a function of the Mg²⁺ ion concentration mainly due to the formation of MgC₂O₄⁺ ion pairs.

As the solution chemistry model gives very good predictions of the solubility for the different conditions, we are confident that the model will provide us with a trustworthy estimation of the supersaturation of the various solutions used for the nucleation induction time experiments in Figs. 2(a) and 2(b). The differences in the total dissolved [Ca²⁺] values found at different pH values and Mg²⁺ concentrations mean that the equal concentration of Ca and oxalate ions added in the different samples will not lead to equal supersaturation levels and thus to different nucleation rates in the nucleation induction time experiments performed at the different conditions. The S values of the different samples estimated by the solution chemistry model are given in Tables II–IV. The estimated S values are also important for the analysis of the cumulative induction time probability function in terms of the CNT.

For the magnesium inhibitor experiments, part of the ultrapure water is substituted with magnesium chloride solution, according to Table IV.

3. Polymorphic characterization of crystals in droplets and the excess COM crystals in ultrapure water

To check whether the nucleated crystals are COM or other calcium oxalate hydrates, the polymorphic form of the crystals in the microfluidic induction time experiments are characterized in situ, using polarized light microscopy and Raman scattering, and ex situ, with powder x-ray diffraction (PXRD). Due to the low calcium and oxalate concentrations in the experiments, we repeated the preparation of equilibrated suspensions described in the Materials and Methods section ten times to get a sufficient amount of crystals to employ Raman and x-ray diffraction detection for the control group experiment. To characterize crystals in droplets, the microfluidic system is operated continuously to collect a sufficient volume of droplets (40 ml) in a Falcon tube. Consequently, the sample is centrifuged at 7400 rpm during 15 min to remove the oil phase around the collected droplets. The suspensions were left for 1 h to allow the crystals to sediment. Additionally, COM (CaC₂O₄⋅H₂O, Sigma-Aldrich, CAS563-72-4) is mixed with ultrapure water (ELGA PURELAB, resistivity: 18.2 MΩ cm at 23.6 °C)—referred to as COM suspended in water in Fig. 9(a). For in situ Raman measurements in Fig. 9(a), the sedimented suspension is decanted, and the concentrated suspension is analyzed with a Raman probe (Kaiser Optical Systems) immersed in the suspension. For x-ray diffraction analysis, the crystals are isolated by filtration with a 0.45 μm pore size filter (Whatman® membrane filters nylon), then washed with ultrapure water three times, and dried to avoid unwanted contaminant crystallization. The washed crystals are kept at room temperature for drying for two days prior to PXRD experiments. PXRD experiments are performed with these crystals placed on a silicon holder with a powder x-ray diffractometer (Bruker, Cu Ka1, k = 1.5406 A°) as shown in Fig. 9(b). The acquired spectra are compared to reference spectra of COM, calcium oxalate dihydrate (COD), and calcium oxalate trihydrate (COT) in the CCDC database. The plotted PXRD patterns are taken from the Mercury tool of the Cambridge Structural Database corresponding to COM (CALOXM03), COD (CAOXAL), and COT (ZZZUOQ01).

FIG. 9.

Analysis of measured growth rates of COM calculated from delay times in p(t) curves for different calcium and oxalate ion concentrations given in Fig. 4 (green dots) and magnesium ion concentrations given in Fig. 6 (red squares).

4. Error propagation

Droplets are stored in chambers in the storage part of the chip. They take an ellipsoidal shape. Droplet volumes are estimated using the images from the microfluidic chip. The average surface area of the droplets is found using three droplets via the publicly available software, Image J. The projected surface area 0.257 (±0.013) × 10⁻⁶ m² is multiplied with the channel depth (2.0 × 10⁻⁴ m) to calculate the volume of the droplets. The droplet volume is found as 5.15 × 10⁻¹¹ m³. The droplets stayed at the same position throughout the induction time measurement. Their sizes did not change significantly throughout experiments, as shown in Fig. S2 in the supplementary material.

Induction times are obtained considering the 95% confidence interval of the fitted equation. Errors are then calculated following the standard procedure for error propagation, i.e., by calculating the root of the added quadratic errors for each variable,

$$\begin{array}{rl}\mathrm{f}& =\mathrm{f}(\mathrm{x},\mathrm{y}),\mathrm{x}\pm \delta \mathrm{x},\mathrm{y}\pm \delta \mathrm{y},\\ \delta \mathrm{f}& =\sqrt{{\left({\displaystyle \frac{\mathrm{\partial }\mathrm{f}}{\mathrm{\partial }\mathrm{x}}\delta \mathrm{x}}\right)}^2+{\left({\displaystyle \frac{\mathrm{\partial }\mathrm{f}}{\mathrm{\partial }\mathrm{y}}\delta \mathrm{y}}\right)}^2},\end{array}$$ (5)

where $\mathrm{f}$ is the calculated function; in this case, $\mathrm{f}=\ln \left(\frac{\mathrm{J}}{\mathrm{S}}\right)$, where $\mathrm{J}=\frac{1}{\tau \mathrm{V}}$. δ is the uncertainty of every variable.

III. RESULT AND DISCUSSION

In a typical experiment, the microfluidic chip is loaded with over 100 droplets at identical concentrations and temperature, hence supersaturation, as shown in Fig. 3. Individual droplets are monitored as a function of time as presented in Figs. 3(b)–3(d). The emergence of the first crystal in each droplet is detected and recorded to generate a list of induction times for each droplet under the constant supersaturation assumption. From the measured induction times, the cumulative induction time probability function, p(t), is constructed. The p(t) is defined as the cumulative number of droplets containing at least one detected crystal divided by the total number of droplets at a given time, t.

FIG. 3.

Microscopy image of the microfluidic chip (a) showing droplet generation, mixing, and storage zones. Time-lapse images of individual droplets captured under polarized light microscopy [(b)–(d)]. The calcium and oxalate ion concentrations in ultrapure water are equal, [Ca²⁺] = [C₂O₄²⁻] = 4.10 × 10⁻⁴ M, which corresponds to S = 2.74 predicted by the solution chemistry model.

The effect of different values of added equimolar calcium and oxalate concentrations on the kinetics of nucleation from the solution is quantified by microfluidic nucleation induction time measurements described in detail in Sec. II B 2. The cumulative induction time probability distributions, p(t), for a set of initial calcium and oxalate concentrations are plotted against the detection time in Fig. 4. Table II provides the added concentrations of Ca²⁺ and C₂O₄²⁻ ions and corresponding initial free concentrations of Ca²⁺ and C₂O₄²⁻ ions, their activity coefficients, and the resulting initial supersaturation of COM in the droplets calculated using the aforementioned solution chemistry model. To calculate the initial values, it is assumed that equilibrium is obtained for the protonation, de-protonation, and ion pair reactions, but COM has not yet precipitated. Fitting a single exponential with delay time given in Eq. (1) to p(t) curves in Fig. 4 allows determining the initial lag time, t_G, and the average nucleation induction time, $\tau$. The initial lag time can be considered the time required for crystals to grow to an observable size, determined by the resolution of microscope optics. The nucleation rate is predominantly related to the slope of p(t) curves, hence $\tau$.³⁶ Increasing supersaturations result in smaller average induction times, corresponding to faster nucleation rates evident from steeper slopes of the p(t) curves in Fig. 4. At the lowest calcium concentration of 1.35 × 10⁻⁴ M (corresponding to supersaturation, S = 1.18 in Table II), no crystals were formed over 6 h.

Interestingly, decreasing lag times are observed for the samples with [Ca²⁺] of 2.05 × 10⁻⁴ M, 2.75 × 10⁻⁴ M, and 4.1 × 10⁻⁴ M, while at [Ca²⁺] of 5.50 × 10⁻⁴ (S = 3.36), no lag time can be identified anymore. At the higher [Ca²⁺] concentrations, crystals are already present in all droplets 2 min after the start of the experiment, the minimal detection time step in our system. Considering the observed p(t) curves in Fig. 4, an equimolar calcium and oxalate concentration of 4.1 × 10⁻⁴ M was chosen as the reference concentration to be tested at different pH values and in the presence of additives as higher concentrations cannot be studied with our experimental approach.

Figure 4 also shows the fits to Eq. (1) along with 95% confidence intervals. The numerical values of the determined $\tau$, J, and t_G values are given in Table V together with the confidence intervals and the statistical errors of the estimated values. In the calculation, a constant volume is assumed for all droplets, and the uncertainty in droplet size is considered as described in Sec. II C 4. The results of this quantitative analysis will be discussed together with the experiments in Figs. 5 and 6 in the following.

Figure 5 shows how COM nucleation kinetics is altered in a set of buffer solutions producing solutions of different pH values. Nucleation kinetics of COM is studied at fixed added equimolar calcium and oxalate concentrations of 4.1 × 10⁻⁴ M in Fig. 5. Table I gives the composition of the used buffer solutions, and Table III shows the calculated supersaturations in the droplets. At pH 6.0 in the sodium acetate/acetic acid buffer, no nucleation was observed. Even after 700 min, no crystals were detected, which can be explained by the low supersaturation of the droplets in this experiment (S = 1.09). Also, in the experiments in ultrapure water with a comparable S value (S = 1.18), no crystals were detected within the experimental time scale. At pH 8.6, the nucleation rate is comparable and at pH 3.6 somewhat lower than that in the reference concentration in ultrapure water (Fig. 4). However, if we compare the experiments at pH 3.6 with that in ultrapure water at the same supersaturation ([Ca²⁺] = [C₂O₄²⁻] = 2.05 × 10⁻⁴ M, S = 1.64), the nucleation rate is much faster and the lag time is much smaller at the low pH. It should be noted that in addition to the S value, the ratio of the free Ca²⁺ and C₂O₄²⁻ ion concentrations are different at different pH values, whereas this ion ratio is still about one at pH of 8.6. At the low pH value, the free Ca²⁺ ions concentration is almost five times higher than that of the C₂O₄²⁻ ions, due to ion pair formation and protonation of the oxalate ion (see Table III). Also, the shape of p(t) is slightly different at low pH, bending off at p(t) values around 0.9, which could give an indication of (pseudo) polymorphism.⁷¹ The possible formation of COD crystals instead of COM has been examined using XRD and Raman (see Fig. 9), but no indication of polymorphism was found within the sensitivity of the aforementioned methods. Yet, one should not completely rule out this (pseudo) polymorphism explanation as XRD and Raman cannot detect (pseudo) polymorphs if they are present below 5%–10% by weight.

To summarize the experiments at different pH values, we did not observe crystal formation within the experimental time scale at pH 6.0 but observed fast nucleation rates at acidic (pH = 3.6) and basic conditions (pH = 8.6). This result is qualitatively in line with the medical literature,^72,73 where low and high urine pH are considered to play a significant role in stone formation.^74,75

Figure 6 focuses on the influence of magnesium ions on the nucleation kinetics of COM in ultrapure water. In all the experiments given in Fig. 6, the reference equimolar calcium and oxalate concentrations of 4.1 × 10⁻⁴ M are used. The initial S values in the experiments shown in Fig. 5 depends on the added Mg concentrations and are calculated using the solution chemistry model described in Sec. II C 2 (see Table IV). The supersaturation in the droplets decreases only slightly with increasing Mg²⁺ concentrations (from 2.74 to 2.60). Figure 6 shows that also the slopes of the p(t) curves decreased only slightly with the Mg²⁺ concentration, in line with the small changes in supersaturation values given in Table IV. On the other hand, we see a strong influence of the Mg²⁺ concentrations on the lag times of the p(t) curves. This will be further analyzed in the following through a quantitative analysis of the probability curves.

Finally, the inhibitory effect of OPN on COM nucleation kinetics is reported in Fig. 7. Three different OPN concentrations, 1.6 × 10⁻⁸, 3.2 × 10⁻⁸, and 4.8 × 10⁻⁸ M, were added to the droplets carrying equimolar calcium and oxalate concentrations [Ca²⁺] = [C₂O₄²⁻] = 4.1 × 10⁻⁴ M. The experiments conducted with OPN concentrations of 3.2 × 10⁻⁸ and 4.8 × 10⁻⁸ M did not show any crystals after running the experiments for more than 3 h. A striking observation is the distinct shape p(t) curve with 1.6 × 10⁻⁸ M OPN. At this OPN concentration, p(t) has a sigmoidal shape different from curves observed in Figs. 4–6.

The sigmoidal shape and effective inhibition at significantly lower concentrations than magnesium ions might be connected to the molecular structure complexity of OPN relative to simple magnesium ions. Due to the fact that OPN is rich in dicarboxylic acids, stronger interaction of OPN with crystal faces is expected.⁷⁶ The chemical structure of OPN might promote binding to a mineral surface²² or Ca²⁺ ions might induce fixed conformation of OPN.^77,78 All of these possibilities may result in slower kinetics with an increasing amount of OPN. Moreover, the medical literature suggests that OPN is present in urine at concentrations higher than 100 nM, and it might play a critical role in kidney stone formation. Previously published reports point out that patients with urolithiasis have lower concentrations of OPN in their excretion.⁷⁹ Despite the simplicity of the solution matrix in our experiments, we find that OPN suppresses COM formation completely at the same order of magnitude concentrations as it is found in urine. Even at this level, this finding calls for more investigation on the role OPN and other macromolecules play in kidney stone formation when present in patient urine despite their minute concentration.

To summarize the results of microfluidic induction time measurements, given in Figs. 4–7, the numerical values of the fitted parameters for $\tau$, t_G, and J and the statistical fit parameters, given in Table V, will be discussed. In general, reasonably good fits of the single exponential curve were obtained for most of the experiments. Only in a few cases, [CaCl₂] = 0.205 mM in ultrapure water, at the lowest magnesium concentration, and at pH 3.6 (see Table III), the p(t) curve showed non-typical shapes sometimes with a large delay, which was difficult to fit with Eq. (1) and gave rise to large uncertainty (see Table V). Therefore, p(t) fits were also made using the Weibull function [Eq. (2)] comparing the results in terms of their goodness of fit statistics. We did not find a clear improvement in the goodness of fit using the Weibull function except in the aforementioned two cases and concluded that Eq. (1) described the cumulative probability curves adequately for our purpose. The fits to p(t) curves with the Weibull function are given and discussed in the Figs. S3–S6 and Tables S1–S4 in the supplementary material.

Hammadi et al.⁵⁹ showed longer induction times in smaller volumes with a series of solute/solvent systems where the solubility depends strongly on temperature. Despite the fact that solubility of our system does not strongly depend on the temperature, we should as well expect longer induction times in smaller droplet volumes. At this stage, we can only hypothesize about the origin of the deviations from Eq. (1) observed in some of the experiments. Our first hypothesis is that the observed variations from single exponential behavior may originate from two separate nucleation events occurring at different time scales, a fast and a slow process. As nucleation occurs at a higher rate on surfaces in contact with the solution compared to homogeneous nucleation,⁸⁰ one may suspect that droplets in contact with impurities, solid microfluidic walls, and liquid–liquid interfaces⁸¹ may trigger nucleation at different rates giving raise to observed deviation. However, this hypothesis is at odds with the finding of Duft and Leisner,⁸² who deduced that surface nucleation does not lead to the deviation of the shape of the p(t) curve but only to its steepness. Second, due to the density difference between the droplets and the surrounding oil phase, the thin oil film⁸³ between the droplets and channel walls can be squeezed out bringing the droplets in contact with PDMS walls.⁵⁵ Both these solid–liquid and liquid–liquid interfaces might trigger time dependent heterogeneous nucleation rates, which could affect the shape of the p(t) curve. Finally, earlier nucleation events can be triggered at the liquid–liquid mixing front when the two reactive streams make contact before the droplet reaches the mixing zone shown in Fig. 1(a). Another potential explanation can be the non-classical nucleation pathway supported by reports focusing on the nucleation pathway of CaOx.³⁴ One may imagine the distribution of pre-nucleation clusters triggering nucleation at different time scales resulting in p(t) deviating from a single exponential. The last potential explanation is the formation of pseudo-polymorphs below the detection limit of PXRD and Raman. It should be noted that all of these rationalizations are mere hypotheses that need further deductions.

As discussed in the Introduction and in Sec. II B 2, the CNT predicts an exponential shape of the p(t) curve and the t_G delay can be interpreted as the time for the nuclei to grow from the nanoscale into a detectable crystal size. The clear advantage of such quantitative analysis of the experimental data is that it provides a statistics-based analysis of the nucleation and growth kinetics from the presented experiments; it also gives us insight in the underlying nucleation mechanisms. Yet, using CNT analysis should not be blindly interpreted as assuming that the nucleation pathway is classic. As demonstrated by Smeets et al.³⁵ experimentally and later in a CNT extension by Kashchiev, CNT concepts can be used to gain insights into nucleation even for systems following non-classical pathways.³⁶

To rationalize the influence of the supersaturation on the nucleation rate, we turn to Eq. (3). where ln(J/S) values are plotted against 1/(ln²(S)) in Fig. 8 (complete analysis can be found in Sec. 3 in the supplementary material). The plotted experimental J values are extracted from fitting the p(t) functions in Figs. 4–6, and the estimated S values are calculated using the solution chemistry model. The dashed line in Fig. 8 represents the fit of Eq. (3) to experiments conducted in de-ionized water (presented in Fig. 4), and the shaded area corresponds to the confidence interval of the fit. The fitted A and B values and their confidence intervals are A = 4.05 × 10⁸ m⁻³ s⁻¹ (1.83 × 10⁷ to 8.96 × 10⁹) and B = 0.47 (−0.80 to 1.73), respectively. Note that only the experiments with varying initial concentrations of Ca²⁺ and C₂O₄²⁻ ions in de-ionized water are used in this fit. It is highly likely that a varying composition in the different samples resulting from the additions of the buffer solutions and/or the MgCl₂ solutions will affect the kinetic parameter A of the solution and thus making the fit of Eq. (3) to all experiments illegitimate.

According to Roelands et al.,⁸⁴ the nucleation process can be categorized through the kinetic parameter into homogeneous (A_HON ∼ 10³⁵ m⁻³ s⁻¹) or heterogeneous (A_HEN ∼ 10¹⁵–10²⁵). Thus, for the conditions tested in this work, we can conclude that COM nucleation is heterogeneous under the experimental conditions covered in Fig. 4. This is expected as the nucleation happens inside droplets dispersed in a continuous oil phase, so that the liquid–liquid interface or microfluidic device walls can provide heterogeneous surfaces promoting COM nucleation. It is noteworthy to mention that the confidence interval of the CNT fit in Fig. 8 is very large indicating a bad fit. This is due to the low number of data points available in Fig. 4 as two of the chosen S values provided J values outside measuring capabilities of the microfluidic setup. The broad confidence intervals can also be attributed to a non-classical pathway providing a broad distribution of time scales, hence a bad fit to a single exponential. Moreover, the nucleation kinetic parameter for COM crystals was estimated by Hsu et al.⁸⁵ as 2.57 × 10¹¹ m⁻³ s⁻¹. Yet, these values are not comparable since in their work, COM crystallization was performed in 250 ml stirred crystallizers using a synthetic urine medium resulting in S = 13.65, while the present work studied the crystallization of COM on droplets in ultrapure water solutions and at significantly lower supersaturations. In summary, Fig. 8 provides limited insight, yet we think attempting such analysis is relevant provided that one does not make assumptions on the classical or non-classical nature of nucleation. Despite previous reports providing evidence on the non-classical nature of COM nucleation, the CNT framework can still provide insights as demonstrated experimentally by Smeets et al.³⁵ and more recently by Kashchiev.³⁶

In the next step, we turn our attention to the analysis of the observed delay time, t_G, in p(t) curves. From the fitted values of t_G given in Table V, the experimental growth rate, G_exp, can be calculated assuming that t_G is the time required for a crystal to grow to the detection limit. The detection limit is estimated as 4 ± 1 pixel corresponding to 6.4 ± 1.7 μm based on the resolution of the microscope images used to detect the crystals in the microfluidic induction time measurements. G_exp is then calculated for each experiment presented in Figs. 4 and 5 by dividing the detection limit to t_G. The obtained G_exp values calculated from this procedure and the corresponding S values are plotted in Fig. 9. The data presented in Fig. 9 can be further analyzed to gain insight into the growth mode of COM crystals. The G_exp and S values then can be used to estimate the parameters of a simple growth rate equation; G_exp = k_G (S − 1)^p, where p is the power of the supersaturation term and S is the calculated supersaturation value in the droplets of these experiments. A p-value of 1 is attributed to diffusion limited or rough growth and a p-value of 2 or higher is expected for birth and spread or spiral growth mode.⁸⁶

The most striking observation from Fig. 9 is the distinct S dependence of G_exp of experiments conducted in with (red squares) and without Mg²⁺ ions (green circles) presented in Figs. 4 and 5, respectively. These growth rates show distinct S dependences. The growth rates with different added total Ca²⁺ concentrations in de-ionized water show a milder S dependence, whereas increasing the Mg²⁺ ion concentration shows a steeper dependence. Next, we turn our attention to the analysis of growth mode by fitting the growth rate model, G_exp = k_G (S − 1)^p to experiments conducted with and without Mg²⁺ ions. The estimated parameters k_G and p for green circles (experiments without Mg²⁺ ions presented in Fig. 4) are estimated by fitting the growth rate model as 0.23 ± 1.05 and 1.7 ± 8.8, respectively. The quality of the fit is not so high due to the low number of data points used and due to the uncertainties related to the estimation of the t_G parameter. The aforementioned atypical shape of the p(t) curves gave rise to considerable uncertainty in the estimation of t_G. This large uncertainty prevents us from reaching any conclusion on the exact nature of the growth model. The second striking deduction emerges from fitting G_exp values increasing Mg²⁺ ion concentrations to the growth rate model. Fitting of the growth rate function on the basis of these experiments would require a p-value in the order of 10, which is unrealistic. This suggests that inhibition of the growth rate by Mg²⁺ ions is not caused directly by the change in the supersaturation but that another mechanism is involved. The observed non-typical shape of the experimental p(t) curves mostly in combination with large lag times could be an indication of a different nucleation mechanism, the occurrence of the surface nucleation at the oil–water interface, preferential binding of Mg²⁺ ions to kink sites, or be caused by polymorphism.⁷¹ As has been shown by Duft and Leisner,⁸² the occurrence of surface nucleation at the liquid–air interface is not likely to give rise to a completely different shape of the p(t) curve⁸² and still an exponential behavior is expected. For the nucleation in sparingly soluble systems, such as CaCO₃ and CaC₂O₄, a non-classical nucleation mechanisms have been proposed,^35,37 due to the formation of amorphous intermediates or precursors, which would lead to other characteristics of the probability curve. Finally, the possible formation of COD crystals instead of COM has been examined using XRD and Raman in Fig. 10, but no indication of polymorphism was found. Yet, as previously mentioned in the discussion about the deviation of exponential behavior of p(t) curves, the formation of pseudo-polymorphs below the detection limit of PXRD and Raman should not be ruled out.

FIG. 10.

Characterization of the crystal structure of the formed crystals under various conditions. (a) Raman spectra of collected droplets removed from the oil phase (red); COM crystals suspended in ultrapure water (green), COM Powder from supplier (magenta), and ultrapure water (black). (b) XRD spectra of dried crystals from droplets (red), COM powder from supplier (black), COM reference (dark green), COD reference (orange), and COT reference (purple).

Finally, we explore the possibility of pseudo-polymorphs forming in microfluidic experiments by Raman [Fig. 10(a)] and PXRD [Fig. 10(b)] characterization described in detail in the Materials and Methods section. The characteristic COM Raman bands are observed in Fig. 10(a) at 504, 508 (O–C–O), 897 (C–C), 1463, 1490 (C–O), and 1629 cm⁻¹ (C–O).^87–89 These shared peaks, evident in spectra corresponding to crystals formed inside microfluidic droplets denoted “Droplets” and in the reference case of COM crystals from supplier suspended in ultrapure water denoted as “COM suspended in water,” imply that the pseudo-polymorphic form crystallized with microfluidic experiments is COM. In addition to in situ Raman measurements conducted in the solution, ex situ PXRD measurements where the excess crystals are filtered, washed, and dried before diffraction measurements are conducted. Figure 10(b) provides PXRD spectra of the precipitated crystals from canonical microfluidic experiments denoted as “Crystal from droplets” and the reference case of COM crystals denoted as “COM powder from supplier” along with reference spectra of three calcium oxalate (pseudo)polymorph/hydrate from CCDC database, namely, calcium oxalate monohydrate (COM), calcium oxalate dihydrate (COD), or calcium oxalate trihydrate (COT).⁹⁰ The PXRD peaks of COM reference share the identical peaks with the PXRD spectra of “Crystals from droplets,” and the PXRD spectra of COM crystals as purchased from supplier referred to as “COM powder from supplier.” After precipitation, no transition from COM to other CaOx hydrate forms was observed during the induction time measurements within the accuracy of Raman and PXRD techniques.

IV. CONCLUSIONS

We present a coupled experimental and modeling study focusing on the COM nucleation rate, quantified using microfluidic induction time measurements in a droplet-based microfluidics platform. Leveraging the multiplexing capability of droplet microfluidics, ours minimizes the use of materials while ensuring a statistically significant number of identical experiments. We interpret the presented nucleation induction time experiments using a previously published solution chemistry model based on the Davies extension of the Debye–Hückel theory, which was validated using isothermal solubility measurements.⁴³ The model enables the interpretation of the pronounced effects of pH, ionic strength, solution chemistry on the solubility of the COM crystals, and on the prevailing supersaturation under the studied conditions. The presented induction time measurements and p(t) curves coupled with modeling point out that the presence of Mg²⁺ ions appears to slightly alter supersaturation from 2.74 to 2.60, while its effect on the lag time is considerable. Further analysis on the growth rate in the presence of Mg²⁺ ions reveals that the inhibition mechanism cannot be explained solely by supersaturation. Furthermore, we observed that OPN suppresses COM nucleation at significantly lower concentrations compared to Mg²⁺ ions. The pronounced inhibition effect of OPN at much lower concentrations compared to Mg²⁺ ions emphasizes the often-overlooked role of macromolecules on COM nucleation due to their low concentration presence in urine. We hope that the presented study highlights the potential of microfluidics in unraveling the underlying physicochemical mechanisms behind kidney stone formation, particularly in addressing the overwhelming complexity of the urine composition phase space. With our following work, we will use this study as a stepping stone to focus on more complex artificial urine solutions essential for our overarching goal of quantitatively predicting CaOx formation in kidneys from patient urine composition.

SUPPLEMENTARY MATERIALS

The supplementary material contains figures and tables to evaluate single exponential and Weibull functions on effective nucleation rates, growth rate analysis, and interpretation in the classical nucleation theory (CNT) at different supersaturation ratios significantly.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

The manuscript was written through the contributions of all authors. All authors have read and agreed to the published version of the manuscript.

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.