Estimation of the capillary level input function for Dynamic Contrast-Enhanced MRI of the breast using a deep learning approach

Abstract

Purpose:

To develop a deep learning approach to estimate the local capillary-level input function (CIF) for pharmacokinetic model analysis of dynamic contrast enhanced (DCE)-MRI.

Methods:

A deep convolutional network was trained with numerically simulated data to estimate the CIF. The trained network was tested using simulated lesion data and used to estimate voxel-wise CIF for pharmacokinetic model analysis of breast DCE-MRI data using an abbreviated protocol from women with malignant (n=25) and benign (n=28) lesions. The estimated parameters were used to build a logistic regression model to detect the malignancy.

Result:

The pharmacokinetic parameters estimated using the network-predicted CIF from our breast DCE data showed significant differences between the malignant and benign groups for all parameters. Testing the diagnostic performance with the estimated parameters, the conventional approach with AIF showed an AUC between 0.76 and 0.87, and the proposed approach with CIF demonstrated similar performance with an AUC between 0.79 and 0.81.

Conclusion:

This study shows the feasibility of estimating voxel-wise CIF using a deep neural network. The proposed approach could eliminate the need to measure AIF manually without compromising the diagnostic performance to detect the malignancy in the clinical setting.

1. Introduction

T₁-weighted Dynamic Contrast Enhanced (DCE)-MRI has been widely used to investigate the changes in tissue microstructural environment with tumor growth and treatment (1). Intravenously injected T₁-shortening contrast agents typically extravasate into the extravascular extracellular space in a lesion with leaky tumor vessels, which results in different T₁-weighted signal changes over time depending on the extravascular extracellular space volume and vascular properties. These tissue signal dynamics can be quantified by performing pharmacokinetic model analysis. Pharmacokinetic model parameters have been used to quantitatively characterize different types of cancer, such as breast cancer (2), prostate cancer (3), and liver cancer (4, 5). However, translation of such pharmacokinetic model analysis into clinical exams still remains challenging.

One of the challenges for clinical translation of pharmacokinetic model analysis is measurement of an adequate arterial input function (AIF) that serves as the input to a model to predict tissue pharmacokinetic dynamics. Measurement of AIF from different locations often leads to a significant difference in quantification of blood flow (6). Substantial variations of the estimated parameters can still be observed even after selecting AIF from a same location, depending on the operators (7). It is also possible that the field of view of the image does not include an adequate arterial vessel for AIF measurement, or the vessels in the field of view are not the ones feeding the lesion of interest.

There have been numerous approaches to measure AIF from acquired dynamic images. Some of these previous studies employed a semi-automatic algorithm to select AIF with minimal user input. This type of approaches includes a relatively simple algorithm to select the top 5% of voxels with the highest peak (8), the k-means clustering algorithm to automatically select AIF (9), and a combination of a gamma-variate function to reduce the number of selected voxels and a clustering algorithm to detect AIF (10, 11). The clustering algorithms are not deterministic because they are generally initiated with random selection of initial clusters. In addition, these algorithms still require users to tune the parameters to obtain optimal results.

Another group of studies for AIF selection is based on blind source separation techniques, such as Principal Component Analysis (PCA) and Independent Component Analysis (ICA). These techniques assume that AIF can be separated when the data are projected in a statistical domain discovered from the data. Sanz-Requena et al. (12) used a PCA approach with prostate DCE-MRI data to automatically segregate the arterial component from the image. They used a population-averaged AIF as the reference to correlate with principal components in order to select the arterial component. This approach can be used when a major artery is present within the image, such as the external iliac arteries in prostate data. Other similar studies (13-16) have used ICA to maximize the non-Gaussianity of the sources to separate the arterial component from the dynamic images. This approach was used to segment spatial sources to identify arterial voxels and also to separate temporal components of a local region to find out the vascular component in the region, as demonstrated by Calamante et al. (14) using Dynamic Susceptibility Contrast (DSC)-MRI data. However, these approaches still require a user intervention to select the arterial components with visual inspections and/or to threshold the contribution of those components.

While measuring a global AIF at the upstream vessel poses multiple challenges briefly discussed above, several previous studies have demonstrated the efficacy of using the local AIF, or the capillary-level input function (CIF), for each individual voxel (14, 17, 18). The significance of having a voxel-wise CIF is paramount in pharmacokinetic model analysis of DCE-MRI data for two main reasons; first, for resolving the need to measure AIF, and second, for eliminating the need to model the transport of contrast agent from an arterial vessel in upstream used for AIF measurement to the capillaries in voxels at different locations. A recent study by Duan et al. (19) measured the local AIF by constructing the constrained model that adopts the parameters from fitting the AIF measured at the upstream vessel. Although this approach attempts to measure the capillary level input function neighboring the tissue voxel, it still relies on accurate measurement of AIF at the upstream. Therefore, there is an unmet need for a more reliable approach for estimating CIF that is independent of measuring AIF.

In recent years, deep learning has been emerged as a powerful tool for image segmentation (20, 21) and also to segment regions for AIF measurement in DSC-MRI (22). However, it has not been shown, to our knowledge, whether deep learning can be used to estimate the CIF for an individual voxel in DCE-MRI. Here, we assess the feasibility of using a deep learning model to estimate voxel-wise CIF in DCE-MRI. We limit the scope of the study to the case of breast DCE-MRI exams using an abbreviated scan protocol of 2.5 min with a temporal resolution of 6.5 s/frame. An abbreviated MRI could detect biologically significant cancers which enhance rapidly, while using a decreased scan time (23, 24). We aim to develop a deep learning model-based method that allows fully automatic pharmacokinetic model analysis of DCE-MRI data without using AIF.

2. Methods

2.1. Breast DCE-MRI Study

This Health Insurance Portability and Accountability Act-compliant study was performed with approval from our Institutional Review Board and written informed consent from each subject. This study recruited 84 women, who had a malignant (n=25; ages, 30-75 years; mean 50 years), a benign (n=28; ages, 25-68 years; mean, 41 years) lesion or a known family history of breast cancer (n=31; ages, 25-55; mean, 38 years) with no suspicious lesion. Malignant lesions include invasive ductal carcinomas (IDC) (n=18), invasive lobular carcinomas (ILC) (n = 5), or a mix of IDC and ILC (n=1) and ductal carcinomas in-situ (DCIS) (n=1). Benign lesions include biopsy-proven fibrocystic changes (n=14) and lesions confirmed by imaging (n=14). The lesions were manually segmented in 3D by a fellowship-trained breast imaging radiologist (LH with 5 years of experience). The women with known family history of breast cancer but no suspicious lesion were included to obtain an independent set of AIF data and generate the simulation data used for training the deep neural network models. The women with either malignant or benign lesion were used to assess the diagnostic performance of the proposed method.

All subjects had a diagnostic breast MRI exam on a whole-body 3T scanner (MAGNETOM TimTrio, Siemens Heathcare, Erlangen, Germany) with a 16-channel breast coil (In vivo, Orlando, FL). A radial stack-of-star 3D spoiled gradient echo sequence with golden-angle spoke ordering was used to acquire 288 spokes with 83 partitions for 2.5 min. The scan parameters include axial slab orientation, TE=1.8ms, TR=4.87ms, flip-angle=10 degrees, field of view = 320×320 × 212 mm³, and bandwidth = 520 Hz/pixel. The image matrix size was 320×320×192 with a spatial resolution of 1×1×1.1mm. Spectrally-selective Adiabatic Inversion Recovery (SPAIR) was used for fat suppression. Twofold readout oversampling (640 sample points/spoke) was used to minimize spurious aliasing along each spoke. All partitions in the slice direction corresponding to one radial angle were acquired sequentially before rotating to the next angle. After baseline acquisition of 60 s, a single dose of gadobutrol (Gadavist, Bayer Healthcare Pharmaceuticals) at 0.1 mM/kg body weight was injected at 2 mL/s intravenously while the scan continued for another 1 min 30 s. The total acquisition time for the abbreviated DCE-MRI scan was 2 min 30 s.

DCE images were reconstructed using the GRASP-Pro (Golden-angle Radial Sparse Parallel imaging with improved performance) approach (25) which imposes a combination of an explicit low-rank spatiotemporal subspace constraint and a temporal sparsity constraint. For the low-rank subspace constraint, the low-resolution portion of radial k-space (160 ×160) was used to generate standard low-resolution GRASP images, which were then used to estimate temporal basis functions. The first K basis components (K=6 in this study) were used as the bases to reconstruct the full-resolution images. Temporal finite differences were used as the temporal sparsity constraint for minimizing total variation. As shown previously (25), the reconstructed images with these constraints provide sharper images than the conventional GRASP-reconstructed images, with reliable temporal fidelity. The dynamic images were reconstructed with 13 spokes per frame, yielding a temporal resolution of 6.5 s/frame.

2.2. Pharmacokinetic model analysis

We performed the conventional pharmacokinetic model analysis on the breast DCE-MRI data using the extended Tofts model (eTofts), the two-compartment exchange model (TCM), and the extended vascular tree model (EVM), as depicted in Figure 1, all of which use AIF, in order to obtain the range of pharmacokinetic model parameters relevant for the breast MRI data included in this study. For clarification, the definitions of these models are provided in Supporting Information. For the EVM analysis, we evaluated with a range of 3 to 10 branches in the arterial tree to cover possible configurations, and the branch resulting in the best fit was selected, as similarly performed in the previous study (26). For the conventional pharmacokinetic model analyses using AIF, AIF was acquired by manually selecting a region of interest (ROI) in the aorta, as shown in Figure 2. The top 20% of the voxels in the ROI with the highest peak in the enhancement ratio curve were selected and averaged to yield the AIF used in the analysis. AIF selection was conducted with non-uniform Fast Fourier Transform (NUFFT) (27) images to minimize any influence from the GRASP-Pro reconstruction with spatial and temporal constraints. Since the acquired AIF was noisy, we fitted a model which consists of a Gaussian and an exponential decay, adopted from the previous study (28), to the AIF data to produce a clean case-specific AIF, as depicted in Figure 2(d). The pre-contrast T1 value was assumed to be 1.7s, adopted from a previous study (29).

Figure 1.

Pharmacokinetic models used in this study. The extended Tofts model (eTofts) with an arterial input function instantly mixes in the capillary bed (left) and Two-compartment exchange model (TCM) and the extended vascular-tree model (EVM) that models the transport and the dispersion of the arterial input function to the capillary bed (middle) and the Capillary Exchange Model (CXM) with a capillary input function predicted by the trained network as the input (right). The estimated kinetic parameters from each model are v_e, volume fraction of extracellular-extravascular space (EES); v_p, volume fraction of the blood plasma compartment; F_p, the blood flow from the artery to the capillary bed; PS, the bidirectional endothelial permeability-surface product; t₀, the time it takes for a contrast agent to pass through each branch of vessel in the arterial tree.

Figure 2.

(a)An example of a drawn ROI at the aorta for acquiring the case-specific AIF. An example of a drawn ROI for (b) a malignant lesion and for (c) a benign lesion. (d)An example of a case-specific AIF acquired from aorta and the AIF-model fitted function used in this study (top) and an example of a contrast concentration-time curve for a malignant and a benign lesion (bottom) An example of the capillary-level input function modelled with TCM and EVM calculated from the estimated kinetic parameters for (e) a malignant (top) and a benign lesion (bottom).

Each voxel in malignant or benign lesions was analyzed with the case-specific AIF using TCM, eTofts, and EVM, and then the best model that described the contrast dynamics was selected based on the Akaike information criterion (30), using the following equation:

$$\mathit{AIC}=\mathit{n}\cdot \mathbf{ln}\left(\frac{\mathit{RSS}}{\mathit{n}}\right)+2(\mathit{k}+1)+\frac{2\mathit{k}(\mathit{k}+1)}{(\mathit{n}-\mathit{k}-1)}$$ [1]

where n is the number of temporal frames in our dynamic data, k is the number of model parameters and RSS is the fitting residual sum of squares. Since the data acquisition was conducted as a part of clinical breast MRI exams, there was not enough scan time available for T₁ mapping. The pre-contrast T₁ values were assumed to be 1.45 s for all voxels in the lesion ROI, which is the average of the malignant and the benign lesion T₁ values in a previous study (2).

2.3. Convolutional Neural Network for estimating capillary input function

We frame the task of estimating capillary input function (CIF) as an inverse problem to find out the GBCA concentration time curve in the capillary network of a voxel C_p(t) from the signal enhancement ratio curve E_t(t) = S_t(t)/S_t(0) of the voxel and its neighboring voxels. Here, S_t(t) is the signal intensity time curve depending on the GBCA concentration C_t(t) and the pulse sequence used for DCE-MRI data acquisition. The forward problem is based on the capillary exchange model (CXM) depicted in Figure 1 and defined by Equation [S6] in Supporting Information:

$${\mathit{C}}_{\mathit{t}}(\mathit{t})=\left({\mathit{v}}_{\mathit{p}}\delta (\mathit{t})+{\mathit{v}}_{\mathit{e}}\mathit{R}(\mathit{t})\right)\ast {\mathit{C}}_{\mathit{p}}(\mathit{t})$$ [2]

where the residual function R(t) = (PS/v_e)exp(−t · PS/v_e), δ(t) is the Dirac delta function, and * represents convolution. We assume that the CIF remains same within a local area, such as a small patch of 3×3 voxels. This assumption is also assessed by inspecting the difference between the estimated CIF at a voxel and the CIFs of the neighboring 8 voxels within a patch. As shown in Supporting Information Figure S1, the mean Euclidean distance of CIFs within a patch shows homogeneity, confirming our assumption. The set of CIF data within a local area is defined as an M-dimensional multivariate time series, X = [X¹, X², …, X^M] with ${\mathit{X}}^{\mathit{i}}\in {\mathbb{R}}^{\mathit{T}}$ where T is the number of time points in the DCE-MRI data, M the number of voxels in the patch, and X¹ = X² = X^M (i.e., same CIF within a patch). The output of the forward model is another multivariate time series for the enhancement ratio curves of the local area that can serve as multiple measurements containing information about the common CIF in the local area; Y = [Y¹, Y², …, Y^M] with ${\mathit{Y}}^{\mathit{i}}\in {\mathbb{R}}^{\mathit{T}}$. Then, the forward problem is defined as the following:

$$\mathit{Y}=\mathit{G}\cdot \mathit{K}\cdot \mathit{X}+\eta$$ [3]

where G is the operator to convert GBCA concentration to MRI signal enhancement ratio, K is the non-linear contrast kinetic model operator based on the CXM, and η is additive noise. In this framework, the task of the deep neural network is to find X for a given Y. Note that the operator K also has unknown contrast kinetic parameters such that it is not possible to have an analytical solution for X.

For this task, we propose a convolutional neural network as shown in Figure 3. We aligned all pixels in the first dimension and laid out all temporal domains in the second dimension, yielding 2-dimensional Casorati matrix $\mathit{Y}\in {\mathbb{R}}^{\mathit{M},\mathit{T}}$. M is 9 in our present study using a patch of 3 ×3 voxels. We perform 2D-convolution on the rearranged input matrix to capture potentially unique features along the temporal domain, while maintaining the correlation among pixels within that patch. A total of twelve 2D-convolutional layers are connected in series and each convolutional layer is linked with a Rectified Linear Unit (ReLU) activation function. After two layers, skip connections are made and filters are concatenated together. This structure is inspired by the Residual Network (ResNet) (31). The number of filters is doubled at each layer for the first 5 layers and subsequently halved on the remaining layers to collapse back to a single filter at the end. Since there are more temporal points in the second dimension as compared to the number of pixels in the first dimension, we use a 3-by-5 convolution window. We concatenate the first and last time point in either side to keep the number of the temporal channel the same after convolution. For the first dimension, we concatenate the top voxel’s dynamic curve to the bottom of the patch and the bottom voxel’s dynamic curve to the top.

Figure 3.

(a) A small patch with a 3-by-3 pixel window of DCE data is re-aligned as the 2-dimensional matrix $\mathit{Y}\in {\mathbb{R}}^{\mathit{M},\mathit{T}}$, where M is 9 with a 3 × 3 patch, and T is 22 temporal frames in our study (b) Schematic diagram for the proposed deep neural network structure. Total of 12 convolutional layers are connected series with the skip connections in the middle layers. The network receives a patch of DCE data and estimates the capillary level input function for the center voxel of the patch.

The model was trained using the stochastic gradient descent method. Our loss function is designed to reduce the mean square error between the ground truth CIF of the voxel at the center of the patch, X^C, which is calculated from the equation [S2] or [S5] for TCM or EVM, respectively, and the predicted CIF from the network:

$$\mathcal{L}(\Theta )=\frac{1}{{\mathit{n}}_{\mathit{t}}}{\sum }_{\mathit{i}=1}^{{\mathit{n}}_{\mathit{t}}}\mid {\mathit{X}}^{\mathit{C}}-{\mathit{f}}^{\mathit{C}}(\mathit{Y}\mid \Theta ){\mid }^2$$ [4]

where ${\mathit{f}}^{\mathit{C}}(\mathit{Y}\mid \Theta )$ denotes the prediction of our proposed convolutional network that maps the patch of tissue dynamics Y to the CIF for the center voxel Xc, for given parameters Θ.

We trained two separate deep neural networks for EVM and TCM, respectively. To train each network, we numerically generated 2 sets of 100,000 3-by-3 patches of dynamic data for each model, in which 90,000 patches were used in training and 9,000 were used in validation. The remaining 1,000 patches were used as the test set to evaluate the performance of each trained network. Each voxel in a patch was randomly selected as either a malignant or a benign tissue and was assigned with kinetic parameters selected randomly from uniform distribution within the range acquired from the clinical data using each model, as presented in Table 1. We also included patches that partially contain the kinetic parameters of glandular tissue to simulate the boundary tumor tissues, hoping to maintain the accurate prediction for mixed tissues at the boundary. We introduced 20% variation in each selected parameter to induce some heterogeneity within a patch. DCE-MRI data were generated using either TCM or EVM. To add Rician noise in the simulated patches, Gaussian noise with a variance of 5% of the baseline signal intensity was added to both real and the imaginary channel, assuming the simulated signals only reside in the real channel. For generation of the simulation data, a set of AIFs were collected from the independent cohort of 31 cases, but not included in the study cohort with malignant and benign lesions. The selection of AIFs was conducted in the same manner as described in the previous section for pharmacokinetic model analysis. Upon generating this data, the ground truth CIF was calculated using equation [S2] and [S5] for TCM and EVM, respectively.

Table 1.

Pharmacokinetic parameters (median with inter-quartile range) estimated using the case-specific AIF and network-predicted CIF

	TCM(Ca)			EVM (Ca)			eTofts (Ca)
	Malignant	Benign	p-value	Malignant	Benign	p-value	Malignant	Benign	p-value
ve	0.17(0.16)	0.10(0.09)	0.110	0.34(0.20)	0.20(0.10)	0.002 *	0.43(0.36)	0.30(0.37)	0.003 *
vp	0.044(0.11)	0.037(0.08)	0.347	0.018(0.017)	0.01(0.006)	0.110	0.001(0.00)	0.001(0.00)	0.347
PS	0.51(0.66)	0.34(1.72)	0.529	0.24(0.44)	0.12(0.15)	0.008 *	0.22(0.22)	0.11(0.09)	0.002 *
Fp	0.43(0.51)	0.15(0.18)	0.001 *
t0				0.55(0.01)	0.55(0.01)	0.599
	AIC-selected (Ca)			CXM (Cp-TCM)			CXM (Cp-EVM)
	Malignant	Benign	p-value	Malignant	Benign	p-value	Malignant	Benign	p-value
ve	0.30(0.27)	0.20(0.13)	0.005 *	0.22(0.12)	0.16(0.07)	0.002 *	0.28(0.15)	0.17(0.07)	0.002 *
vp	0.013(0.01)	0.010(0.0)	0.032 *	0.030(0.036)	0.016(0.01)	0.018 *	0.018(0.009)	0.014(0.006)	0.032 *
PS	0.27(0.56)	0.13(0.12)	0.002 *	0.56(0.45)	0.35(0.15)	0.002 *	0.26(0.19)	0.16(0.08)	0.002 *

TCM: the two-compartment exchange model; EVM: the extended vascular-tree model; eTofts: the extended Tofts model; CXM: the Capillary Exchange Model; C_a: analysis conducted with AIF; C_p-TCM: analysis conducted with CIF from the network trained with TCM patches; C_p-EVM: analysis conducted with CIF from the network trained with EVM patches; v_e, volume fraction of extracellular-extravascular space (EES); v_p, volume fraction of the blood plasma compartment; F_p, the blood flow from the artery to the capillary bed; PS, the bidirectional endothelial permeability-surface product; t₀, the time it takes for a contrast agent to pass through each branch of vessel in the arterial tree.

With the test set, we performed pharmacokinetic model analysis in two different ways: 1) using either TCM or EVM with the same AIF (C_a) used in generating the simulation images, and 2) using CXM with the predicted CIFs from the trained networks (C_p-TCM and C_p-EVM). We assessed the pair-wise difference between the estimated parameters from each model and the ground-truth values.

2.4. Application to the clinical data

We applied a sliding window to our breast DCE data to make 3-by-3 voxel patches as inputs to the trained network that generated the capillary level input function for the center voxel of each patch. Voxel-wise pharmacokinetic model analysis was conducted using CXM with voxel-wise CIF, C_p(t), provided by each deep neural network (i.e., C_p-TCM and C_p-EVM). In addition, the pharmacokinetic model analysis with the global AIF, C_a(t), measured from the aorta was also conducted for all voxels in the lesions using TCM, eTofts, and EVM. Model selection was performed using AIC as described in equation [1]. The median value of each case was used to measure the range of each parameter for either the malignant or the benign group. Statistical significance was tested between two groups using the Wilcoxon rank sum test and the p-values were corrected for the multiple comparison using False Discovery Rate method (32).

To assess the diagnostic performance of estimated kinetic parameters for detecting the malignancy of breast cancer, we established a logistic regression model using all the acquired parameters of each model, described as:

$$\mathit{p}(\mathit{y}=1\mid \mathit{X})=1∕(1+\mathbf{exp}(-{\theta }^{\mathit{T}}\mathit{X}))$$ [5]

where p(y = 1∣X) is the probability of a lesion being malignant (y = 1) given the set of estimated pharmacokinetic parameters X, and θ is the set of weights defined as θ = [β₀, β₁, …, β_n] with n for the number of estimated pharmacokinetic parameters (n=3 for CXM and eTofts; n=4 for TCM and EVM)

We reported the area under the Receiver Operating Characteristic curve (AUC) along with the sensitivity and the specificity calculated using the cutoff value determined by maximizing the Youden index. We also performed leave-one-out analysis and assessed the performance of the logistic regression models.

3. Results

3.1. Pharmacokinetic Model Analysis with AIF

Figure 4 shows a summary of the pharmacokinetic analysis using the conventional approach of using case-specific AIF acquired at the aorta with three models, TCM, EVM, and eTofts. For each tumor, voxel-wise analysis was conducted using the three models and the best model for each voxel was selected based on the AIC. Figure 4(a) shows the fractions of the selected models for each tumor ROI in the malignant and benign groups. Malignant lesions show 0.18±0.25, 0.51±0.59, and 0.24±0.31 fractions for TCM, EVM, and eTofts, respectively, while benign lesions show 0.23±0.23, 0.47±0.44, and 0.29±0.25 fractions for TCM, EVM, and eTofts, respectively. There was no significant difference between malignant and benign lesions in terms of the model selection. Figure 4(b) shows the box-whisker plots of the estimated kinetic parameters from each model, as well as from the parameters selected based on the AIC score. The analysis using TCM revealed a statistically significant difference in F_p between the malignant and the benign groups (p < 0.05), while with the EVM, both v_e and PS significantly different (p < 0.05). When using eTofts, both v_e and PS showed significant differences between the two groups (p < 0.05). It is worth noting that the v_p estimation from the eTofts model was substantially lower than that from the TCM and the EVM, approaching zero (0.001 ± 4 × 10⁵ and 0.001±5×10⁷ for malignant and benign lesions).

Figure 4.

(a) Fraction of selected model among the extended Tofts (eTofts), the extended vascular-tree model (EVM) and the two-compartment exchange model (TCM) for each voxel in malignant (top) or benign (bottom) cases. The model selection is performed using Akaike information criterion (AIC), based on the number of parameters in each model and the fitting residue between the acquired signal and the estimated contrast dynamics. (b) Summary of the Pharmacokinetic (PK) model analysis using the case-specific AIF acquired from the aorta. The box-whisker plot displays the median values of each estimated PK parameters in each subject. Asterisks (*) indicates the significant difference between the malignant and the benign group, tested using the Wilcoxon rank sum test at the 5% significance level. v_e, volume fraction of extracellular-extravascular space (EES); v_p, volume fraction of the blood plasma compartment; F_p, the blood flow from the artery to the capillary bed; PS, the bidirectional endothelial permeability-surface product; t₀, the time it takes for a contrast agent to pass through each branch of vessel in the arterial tree.

For the best set of parameters selected based on AIC, all the parameters showed significant differences between the malignant and the benign groups (p < 0.05). With the proposed approach with the network-predicted CIF and CXM, we also found significant differences between the two groups (p < 0.05) in all parameters. The median value and the interquartile ranges of each parameter are reported in Table 1 for both malignant and benign groups using each model.

3.2. Evaluation of deep neural network from test set

Performance of the trained deep neural network is summarized in Figure 5 for both TCM and EVM models. Each test set comprises 1,000 patches generated using either TCM or EVM. Prediction of CIF was obtained from the network trained with patches generated from each model. The pharmacokinetic model analysis was conducted for the center voxel of each patch using the AIF and the network-predicted CIF. The pair-wise error was computed for estimated parameters from each model against the ground-truth parameters and shown as the boxplots in Figure 5.

Figure 5.

Summary of the pharmacokinetic model analysis on the test set of 1,000 simulated patches for the deep neural network trained with the simulated patches generated using the TCM (left) and the EVM (right). The pharmacokinetic model analysis was performed using the same AIF used for patch generation (C_a) with respective models and the network-predicted CIF (C_p) with the Capillary Exchange Model (CXM). Same set of analysis was also repeated on the test dataset after mixing a Gaussian noise with a variance of 5% of base-line signal to both real and imaginary channel. The magnitude images were used for the analysis, introducing the Rician noise to the simulated patches. The pair-wise error rate was calculated from each estimated kinetic parameter against the ground-truth parameter used for the data generation.

For the network trained with patches generated from TCM, the median errors of the estimated parameters were 35% for v_e, 50% for v_p, and 6% for PS. Even with the noise, the error remained at 38% for v_e, 77% for v_p, and 0.4% for PS. In contrast, the parameters estimated using the case-specific global AIF (C_a; same AIF used to generate test data) exhibited the median errors of 7% for v_e, 15% for v_p, 4% for F_p, and 27% for PS with noise-free patches. When the noise is added, the error increased up to 19% for v_e, 101% for v_p, 3% for F_p, and 34% for PS.

For the network trained with EVM patches, the median errors were 7% for v_e, 1% for v_p, and 1% for PS with noise-free data, and 1% for v_e, 10% for v_p, and 3% for PS when noise was added. In contrast, the kinetic parameters estimated using AIF resulted in a median error of 3% for t₀, 1% for v_e, 9% for v_p, and 2% for PS, with noise-free data, while the errors increased to 5% for t₀, 7% for v_e, 17% for v_p, and 8% for PS when the noise is introduced.

3.3. Clinical breast DCE-MRI data

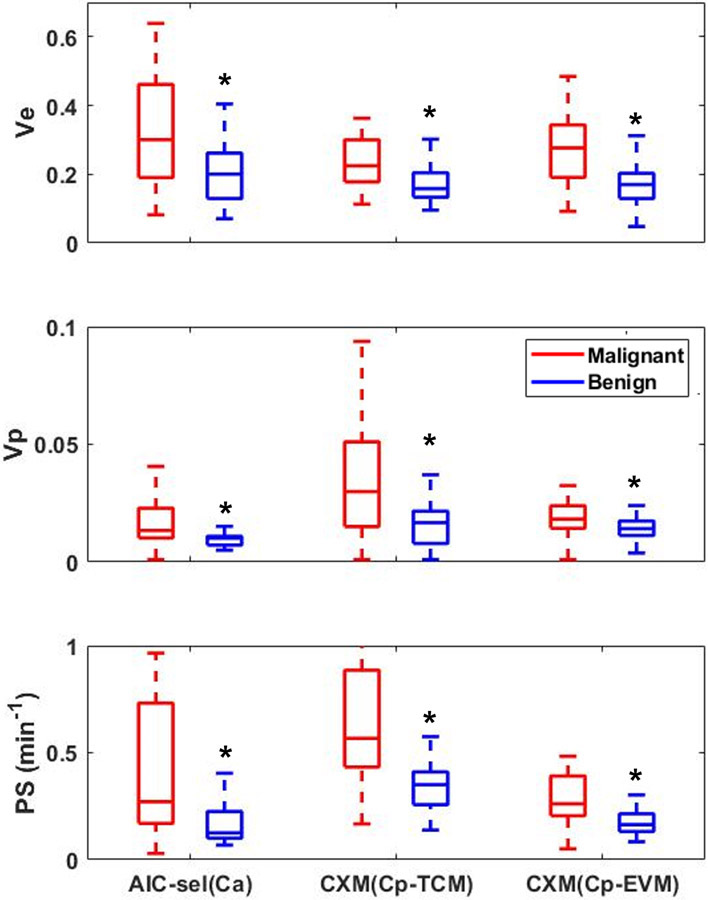
Pharmacokinetic model analysis was conducted for all 53 patients with either malignant or benign lesions, using both the AIF-based and CIF-based models described above. A representative example of one case is shown in Figure 6 for three parameters (v_e, v_p and PS) included in all models. This example shows that the v_p and PS are noticeably different between TCM(C_a) and EVM(C_a), and also between CXM results using C_p estimated using networks trained by TCM and EVM-generated data. This trend can also be observed in the results of all cases shown in Figure 7. Overall, the pharmacokinetic model parameters estimated by using CIF (C_p) using the deep learning network are close to the values estimated by the pharmacokinetic models using AIF (Ca). All three parameters of CXM are significantly different between the malignant and benign groups.

Figure 6.

Example of the estimated pharmacokinetic parameter maps using the case-specific AIF (C_a) with Two Compartment exchange Model (TCM), the extended vascular-tree model (EVM) or the extended Tofts model (eTofts). Among these three models, the model selection was performed using the Akaike information criterion (AIC). The capillary-level input function was estimated from both deep neural network trained with TCM patches (CXM (C_p-TCM)) and with the EVM patches (CXM (C_p-EVM)). Similar pharmacokinetic model analysis was conducted using the network-predicted CIF using the Capillary Exchange Model (CXM). The lesions were marked by our radiologist. Each row shows the estimated parameter maps: v_e, volume fraction of extracellular-extravascular space (EES); v_p, volume fraction of the blood plasma compartment; and PS, the bidirectional endothelial permeability-surface product.

Figure 7.

The median values of the estimated pharmacokinetic parameters, v_e, v_p, and PS. The parameters estimated with the case-specific arterial input function (AIF) using 3 models (TCM, EVM and eTofts) and model selection was performed using AIC (AIC-sel(C_a)). The capillary-level input function (CIF) was estimated using either the network trained with TCM patches (CXM (C_p-TCM)) or with EVM patches (CXM (C_p-EVM)). Asterisks (*) indicates the significant difference between the malignant and the benign group, tested using the Wilcoxon rank sum test at the 5% significance level. The estimated parameters from each model are: v_e, volume fraction of extracellular-extravascular space (EES); v_p, volume fraction of the blood plasma compartment; and PS, the bidirectional endothelial permeability-surface product.

The diagnostic performance of the pharmacokinetic parameters was assessed using the Area under the Receiver Operator Curve (AUC) of the logistic regression model using all parameters of each model (Figure 8). The parameters estimated with TCM had the highest AUC of 0.87, while EVM and eTofts had similar diagnostic performance (AUC of 0.78). With the AIC-selected parameters, the AUC was 0.76. When using the proposed CIF network, improved diagnostic performance was observed, with an AUC of 0.81 for CXM with C_p-TCM and an AUC of 0.79 for CXM with C_p-EVM.

Figure 8.

Receiver Operating Characteristic (ROC) curve for the logistic regression models using the parameters estimated with the case-specific AIF using Two Compartment exchange Model (TCM), the Extended Vascular-tree Model (EVM), the extended Tofts model (eTofts) and AIC-selected parameters among these 3 models (AIC-sel). Similar analysis was performed with the paramteres estimated with the network-predicted CIF from the network trained with either TCM patches (CXM (C_p-TCM)) or the EVM patches (CXM (Cp-EVM)). With the network-predicted CIF, the Capillary Exchange Model (CXM) was used for estimating parameters.

The leave-one-out cross-validation analysis revealed a sensitivity/specificity/AUC of 79%/81%/0.87 for TCM, 68%/75%/0.78 for EVM, and 69%/79%/0.78 for eTofts. When parameters were selected based on AIC, the sensitivity/specificity/AUC were 62%/83%/0.76. When using the network-predicted CIF (C_p), the sensitivity/specificity/AUC were 68%/96%/0.81 for CXM (C_p-TCM) and 68%/89%/0.79 for CXM (C_p-EVM). The mean and the standard deviation of ROC performance from the leave-one-out analysis is listed in Table 2.

Table 2.

Diagnostic performance measure of the logistic regression models based on the pharmacokinetic model parameters

	Sensitivity	Specificity	AUC	Cut-off
TCM(Ca)	0.79±0.05	0.81±0.04	0.87±0.01	0.39±0.08
EVM(Ca)	0.68±0.10	0.75±0.09	0.78±0.01	0.42±0.06
eTofts(Ca)	0.69±0.15	0.79±0.13	0.78±0.01	0.45±0.09
AIC(Ca)	0.62±0.07	0.83±0.06	0.76±0.01	0.46±0.04
CXM (Cp-TCM)	0.68±0.02	0.96±0.01	0.81±0.01	0.58±0.03
CXM (Cp-EVM)	0.68±0.05	0.89±0.04	0.79±0.01	0.53±0.03

4. Discussion

Reliable measurement of AIF has been one of the key challenges in pharmacokinetic model analysis of DCE-MRI data. AIF typically has the most rapid signal enhancement in a given DCE-MRI dataset and substantially higher level of peak contrast enhancement, which imposes more demanding requirements on data acquisition techniques for temporal resolution and handling the T₂* effect. A higher spatial resolution is also required to select voxels within an arterial vessel to measure AIF without partial volume effect. Even in the case of advanced studies meeting these demands for data acquisition, however, it remains nontrivial to model how the contrast agent concentration measured at the arterial level (i.e., global AIF) is related to the contrast agent concentration at the capillaries of a voxel of interest (i.e., local CIF).

In order to address these significant challenges, we implemented a deep-learning approach to estimate the voxel-wise CIF for pharmacokinetic model analysis using two vascular transport models implemented in TCM and EVM. In this proof-of-concept study, we demonstrated the feasibility of training a deep neural network to estimate CIF from the signal changes in a tissue voxel. As suggested by the analysis of the test set data, the pharmacokinetic parameters estimated using CIF were found to yield more accurate estimation in more realistic, noisy data, as compared to the estimation using the case-specific AIF. Also, we demonstrated that the CXM parameters using CIF have a diagnostic accuracy for breast cancer detection comparable to the best set of kinetic parameters using AIF. These results suggest that the pharmacokinetic model analysis of DCE-MRI data can be conducted without using AIF but using our deep learning approach to obtain voxel-wise CIF.

There have been several different approaches introduced to address the challenge of measuring AIF. One approach is to use a healthy tissue ROI as a reference to estimate AIF based on the assumption that the kinetic parameters of the reference tissue remain constant (33, 34). These approaches typically use muscle as the reference tissue with pharmacokinetic parameter values from the literature and reverse-calculate AIF. However, the assumed pharmacokinetic parameters for muscle tissue has large inter-subject variabilities (35), which would lead to errors in estimating AIF. Another common method to overcome the uncertainty from AIF selection is to use a population-based AIF (28, 36-38). Although using a population-averaged AIF seems promising, using a fixed AIF for all subjects could lead to substantial errors in parameter estimation. Ziayee et al. investigated the impact of using different selection of AIF on kinetic parameters of the prostate (39). Their study demonstrated that the parameters estimated with a case-specific AIF selected within the image exhibited differences up to 66% as compared to the parameters estimated with the population-averaged AIF. It was also found that using a population-base AIF does not improve repeatability of pharmacokinetic parameter estimation compared to image-derived AIFs from individual subjects. (40) This suggests that case-specific AIF needs to be used for pharmacokinetic model analysis if selection of AIF can be done reliably.

Several previous studies have introduced a deep neural network to aid the selection of AIF (22, 41). However, these networks were designed to spatially classify and identify the arterial voxels within an image. Therefore, the selection of AIF was limited to the voxels within a field of view, if any, and was still susceptible to challenges such as partial volume effect. Our deep neural network approaches the problem in a fundamentally different way. The network is trained with a wide range of tissue concentration-time curves generated from multiple AIFs from different subjects using the pharmacokinetic model. Therefore, the network recognizes the given signal-time curves of a small patch and predicts the CIF feeding the adjacent tissues in the patch.

Applying this novel approach to clinical breast DCE data with an abbreviated scan protocol for 2:30 min, we found that the estimated parameters with the network-predicted CIF can effectively separate malignant lesions from benign lesions. When using TCM with case-specific AIF, only F_p, the blood flow from the artery to the capillary bed, which is highly dependent on the AIF, showed a significant difference. Also, the estimation using the eTofts model with AIF showed substantial underestimation of v_p, which supports the need to model the transport of AIF and the effective use of CIF in the analysis. In contrast, our CIF approach allows an automatic and deterministic selection of the input function that can estimate kinetic parameters to predict malignancy. The diagnostic performance of the proposed method with this abbreviated exam data (AUC = 0.81 for CXM (C_p-TCM) and AUC=0.79 for CXM (C_p-EVM)) is similar to that of the conventional approach of using AIF and AIC-based model selection (AUC = 0.76) and is close to those of previous studies in which the AUC values ranged widely from 0.6 to 0.9 (2, 42, 43). However, unlike the conventional approach which requires the manual selection of AIF, which are prone to human errors, our approach allows automatic yet more deterministic selection of the input function for DCE analysis without compromising the diagnostic performance.

Limitations of our study include a small number of patients in each group, which would result in less accurate estimated parameters between the malignant and benign lesion groups. As the result, the estimated CIF using these parameters may be introduced with some biases. We try to overcome these potential biases by including the large range of PK parameters to cover inhomogeneous tissue properties of tumor, as well as the various shapes of AIF. However, we acknowledge that the initial selection of AIF for parameter estimation, model selections, or inherent uncertainty in non-linear optimization may also contribute to biases toward modelling CIF. Since it is not possible to measure the CIF directly using MRI, we strive to model CIF using different PK models. Another limitation lies with the absence of pre-contrast T1 measurement. Due to this limitation, this proof-of-concept study was conducted with the pre-contrast T1 fixed to a constant value. However, it is straightforward to replace this constant T1 value with measured T1 values in future studies. The pre-contrast T1 information would allow more accurate estimation of PK parameters, thus yielding a better modeling for CIF. Future research is needed to further refine the accurate selection of AIF and to validate the CIF estimation using other perfusion technique such as Arterial Spin Labelling, along with the proper measurement of pre-contrast T1. The present study was also limited to investigating the feasibility of using a deep neural network for CIF estimation, and as such we have not explored different types and depths of the deep neural network to find the optimal design for CIF estimation, which is beyond the scope of this study. Our clinical DCE data is an abbreviated exam with the scan duration of only 2.5 min. Regardless of the short scan time in a clinical setting, our approach was able to successfully estimate CIF to distinguish malignant lesions from benign ones. Application of this approach in clinical setting would allow fully automated pipeline for DCE analysis, which can expedite the diagnosis in the malignancy. However, pharmacokinetic model parameter estimation within a short scan time can potentially introduce uncertainties. Therefore, further study is warranted to investigate other approaches for parameter estimation, such as deep learning, to reduce parameter uncertainty inherent to relatively short scan times.

5. Conclusions

The present study has demonstrated the feasibility of using a deep neural network to estimate voxel-wise capillary level input functions that could be used for pharmacokinetic analysis in DCE-MRI. Our preliminary study results suggest that the trained network can predict CIF from DCE-MRI data of the neighboring voxels, which in turn can be used for pharmacokinetic parameter estimation for the voxels without using manually selected AIF. Future studies are warranted to further develop our deep neural network, which could enable a fully automated data analysis pipeline for DCE-MRI during clinical practice.

Supplementary Material

supinfo

Supporting Information Figure S1. An example of a correlation map between a voxel and the surrounding 8 voxels in a 3-by-3 patch. The correlation is calculated based on the mean of the Euclidean distance of the estimated capillary-level input function (CIF) to those of the neighboring voxels. The estimation of CIF was calculated based on the kinetic parameters resulted with the case-specific AIF using either the TCM (left) using equation [2] or the EVM (right) using equation [5].

Supporting Information Figure S2. (a) Fraction of selected branch estimated from the extended vascular-tree model (EVM) for either the malignant (top) or the benign (bottom) cases. (b) Mean fraction of selection for each branch ranging from 3 to 10 in malignant and benign groups.

Supporting Information Table S1. The median error rate computed from the estimated kinetic parameters against the ground-truth kinetic parameters. The pharmacokinetic model analysis was conducted using the respective models (i.e. TCM and EVM) that generated the simulated patches, and the similar analysis was conducted using the capillary-input function predicted from the network trained with respective patches with the Capillary Exchange Model (CXM). The same analysis was repeated after mixing a Gaussian noise with a variance of 5% of base-line signal in both real and imaginary channel, and the magnitude images were used for the analysis.