Cox regression is robust to inaccurate EHR-extracted event time: an application to EHR-based GWAS

Abstract

Motivation

Logistic regression models are used in genomic studies to analyze the genetic data linked to electronic health records (EHRs), and do not take full usage of the time-to-event information available in EHRs. Previous work has shown that Cox regression, which can account for left truncation and right censoring in EHRs, increased the power to detect genotype–phenotype associations compared to logistic regression. We extend this to evaluate the relative performance of Cox regression and various logistic regression models in the presence of positive errors in event time (delayed event time), relating to recorded event time accuracy.

Results

One Cox model and three logistic regression models were considered under different scenarios of delayed event time. Extensive simulations and a genomic study application were used to evaluate the impact of delayed event time. While logistic regression does not model the time-to-event directly, various logistic regression models used in the literature were more sensitive to delayed event time than Cox regression. Results highlighted the importance to identify and exclude the patients diagnosed before entry time. Cox regression had similar or modest improvement in statistical power over various logistic regression models at controlled type I error. This was supported by the empirical data, where the Cox models steadily had the highest sensitivity to detect known genotype–phenotype associations under all scenarios of delayed event time.

Availability and implementation

Access to individual-level EHR and genotype data is restricted by the IRB. Simulation code and R script for data process are at: https://github.com/QingxiaCindyChen/CoxRobustEHR.git

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Genome-wide association studies (GWAS) rose to popularity about 15 years ago and have become a powerful approach for the discovery of genetic variations associated with complex human traits and diseases (Bush and Moore, 2012). GWAS is used to determine the genetic markers, usually single-nucleotide polymorphisms (SNPs), that contribute to a particular phenotype or disease of interest within a population of unrelated individuals. A popular way to conduct GWAS is to use data from the electronic health record (EHR) to ascertain phenotypes. Phecodes are sometimes used as a simple way to define phenotypes using billing codes from the International Classification of Diseases (ICD) in the EHR (Denny et al., 2016). The use of large cohorts and the evolution of GWAS to have the ability to assess millions of SNPs in the EHR have led to the discovery of many unique significant genotype–phenotype associations.

Traditionally, case–control genomic studies have used logistic regression models to analyze the genetic data linked to EHR data, but this method does not consider the longitudinal nature of EHR observations. Cases are typically defined as individuals who experienced the event of interest at any timepoint in their record, without taking into account the time at which the event occurred. To incorporate this, in addition to logistic regression models that completely ignore the event time (Harold et al., 2009; Mullins and Bigdeli, 2019), logistic regression models that adjust for the time-to-event have been employed (Miyashita et al., 2013; Simón-Sánchez et al., 2011; van der Net et al., 2008), as well as logistic regression models that adjust for EHR length (Hughey et al., 2019). Furthermore, many papers adjust for age without specifying the time when the age was defined, hence it is not clear which logistic model is being used (Lu et al., 2020; Perrot et al., 2020; Tanigawa et al., 2020). The use of Cox regression, which can account for both the right censoring and left truncation that occurs in EHR data, has also been explored. Previous work has shown that Cox regression is advantageous over logistic regression in genomic studies using the EHR with increased power to replicate known genotype–phenotype associations (Hughey et al., 2019).

Though GWAS of SNPs often include time-to-event data, logistic regression is often used instead of Cox regression in analysis since it is less computationally expensive, despite some recent efforts to speed up the analysis for GWAS (Bi et al., 2020; Rizvi et al., 2019; Staley et al., 2017). Another resistance of using the Cox model in EHR-based analysis is the concern of recorded time accuracy. The longitudinal nature of EHR data is useful in that it provides information regarding disease development and progression due to repeated clinical visits (Pendergrass and Crawford, 2019). Individuals enter the healthcare system at various ages (left truncation) and may leave the system before they have an event (right censoring). This time-to-event information can be utilized in certain modeling techniques. However, due to the structure of EHR data, the time-to-event that is used in Cox regression may not always be accurate. Hersh et al. (2013) identifies several caveats of data quality in EHRs, including the correctness and completeness of the data. EHRs may contain inaccurate data since careful documentation on the event time is not always a priority for clinicians, as the data in EHRs are collected for clinical and billing use, not for research. In addition, EHRs do not always contain the complete information of a patient, since the patient may receive care in a different institution or be lost to follow-up.

In GWAS, an individual is considered a case if they have evidence of a phecode at some point in their record, and the time-to-event (i.e. the time of onset for the disease) is the age at which they first receive a diagnosis code. If an individual has large gaps in their record, the age at which they first show the phecode on their record could potentially be older than the age at which they actually developed the disease. We refer to the setting with positive age difference between when an individual actually develops the disease and when the phecode shows up on the record as delayed event time. It is known that the score test for a simple Cox regression model with one binary exposure is equivalent to the log-rank test, a non-parametric rank-based approach, and hence, robust to the independent delayed event time on the observed time (Therneau and Grambsch, 2000). However, it remains unclear its impact on Cox models when other covariates are included in the model and/or the error is not independent. As Cox models use the time-to-event information directly, it is of interest to compare its validity to logistic regression models in the presence of delayed event time.

Both covariate measurement error and outcome measurement error can be found in regression models. There is extensive literature addressing how to correct for bias induced by covariate measurement error. For example, Liu and Liang (1991) discuss a method to correct for non-differential misclassification in covariates with generalized linear models. Morrissey and Spiegelman (1999) compare three common methods used to correct biased odds ratio due to misclassification of a binary covariate, including the matrix method (Barron, 1977), inverse matrix method (Marshall, 1990) and maximum likelihood estimator. The Simulation and Extrapolation method (SIMEX) aims to reduce bias caused by additive measurement error in covariates (Cook and Stefanski, 1994). Despite the vast knowledge in covariate measurement error, there is less literature concerning outcome measurement error. In linear models, it is known that random outcome error does not bias regression coefficients. However, this does not hold for non-linear models, which has been explored for binary or failure time outcomes (Magder and Hughes, 1997; Meier et al., 2003; Wang et al., 2016). Recently, Oh et al. (2018) have extended the SIMEX method to reduce bias in regression coefficients in the presence of random multiplicative error in the event time. However, the error is assumed to follow $N(0,{\sigma }^2)$ (i.e. error can be either positive or negative) and is independent of the event time and covariates. Tong et al. (2020) propose a method to reduce bias in estimating associations caused by error in EHR-derived phenotypes, with, however, requirements of validated subsets.

In this article, we sought to determine the impact of delayed event time with positive error on the performance of Cox regression and logistic regression models in simulations and for identifying genotype–phenotype associations in genetic data linked to EHR data. We explore several types of error or misclassification that can introduce bias into the regression parameters, including independent or random error (non-differentiable), error that depends on covariates or confounders (conditionally non-differentiable) and error that depends on the exposure (differentiable) to the time-to-event outcome. We showed by simulation studies and a real-world GWAS application that while logistic regression does not model the time-to-event directly, Cox regression is more robust to the delayed event time scenarios than various logistic regression models used in the literature, and the logistic regression model that adjusted for EHR record length outperforms the other two logistic regression models considered in this article.

2 Motivation and methods

2.1 Modeling schemes

We first define the Cox model and three commonly used logistic regression models used in GWAS studies. The models are fit with an exposure variable, z, and two types of covariates ${\mathbf{x}}_1$ and ${\mathbf{x}}_2$, where ${\mathbf{x}}_1$ is a $p\times 1$ vector of confounders for the exposure and ${\mathbf{x}}_2$ is a $q\times 1$ vector of covariates that is associated with the outcome but not with the exposure. Both simulations with and without left truncation, T_lt, are conducted. The observed time, T_obs, is the minimum of the event time, T_e, and the right censoring time, T_c, for each observation. E is the event indicator and is defined as $E=I(T_{\mathrm{e}}<T_{\mathrm{c}})$. One Cox regression model and three logistic regression models used in the GWAS literature in the presence of right censoring are considered.

M1 Cox proportional hazards regression model (Cox):

$$h(t|z,{\mathbf{x}}_1,{\mathbf{x}}_2)=h_0(t)\hspace{0.17em}\text{exp}\hspace{0.17em}\{{\beta }_{1}z+{\mathit{\beta }}_2^{\prime }{\mathbf{x}}_1+{\mathit{\beta }}_3^{\prime }{\mathbf{x}}_2\}$$ (1)

M2 Logistic regression model (adjusting for time difference) (LRM_obs):

$$\begin{array}{c}\text{logit}[P(E=1|z,{\mathbf{x}}_1,{\mathbf{x}}_2,T_d)]\\ ={\beta }_0+{\beta }_{1}z+{\mathit{\beta }}_2^{\prime }{\mathbf{x}}_1+{\mathit{\beta }}_3^{\prime }{\mathbf{x}}_2+{\beta }_{4}f(T_d)\end{array}$$ (2)

where $T_{\mathrm{d}}=T_{\text{obs}}$.

M3 Logistic regression model (without adjusting for time) (LRM_u):

$$\text{logit}[P(E=1|z,{\mathbf{x}}_1,{\mathbf{x}}_2)]={\beta }_0+{\beta }_{1}z+{\mathit{\beta }}_2^{\prime }{\mathbf{x}}_1+{\mathit{\beta }}_3^{\prime }{\mathbf{x}}_2$$ (3)

M4 Logistic regression model (adjusting for record length) (LRM_rl):

$$\begin{array}{c}\text{logit}[P(E=1|z,{\mathbf{x}}_1,{\mathbf{x}}_2,T_{\text{rl}},T_{\mathrm{c}})]\\ ={\beta }_0+{\beta }_{1}z+{\mathit{\beta }}_2^{\prime }{\mathbf{x}}_1+{\mathit{\beta }}_3^{\prime }{\mathbf{x}}_2+{\beta }_{4}f(T_{\text{rl}})\end{array}$$ (4)

where $T_{\text{rl}}=T_{\mathrm{c}}$ is the EHR length. Note that Model 4 is usually not considered as an alternative of the Cox model as, unlike EHR-based application, T_c is not observable for E = 1 in most time-to-event applications.

With the existence of left truncation, the Cox model adapting to left truncation is readily available (Klein and Moeschberger, 2003). T_d in LRM_obs model became $T_{\mathrm{d}}=T_{\text{obs}}-T_{\text{lt}}$ and LRM_u remained the same. In LRM_rl model, $T_{\text{rl}}=T_{\mathrm{c}}-T_{\text{lt}}$, so M4 became:

$$\begin{array}{c}\text{logit}[P(E=1|z,{\mathbf{x}}_1,{\mathbf{x}}_2,T_{\text{rl}},T_{\mathrm{c}})]\\ ={\beta }_0+{\beta }_{1}z+{\mathit{\beta }}_2^{\prime }{\mathbf{x}}_1+{\mathit{\beta }}_3^{\prime }{\mathbf{x}}_2+{\beta }_4{T}_{rl}+{\beta }_{5}f(T_{\mathrm{c}})\end{array}$$ (5)

In all models, β₁, the coefficient of the exposure, is the parameter of interest, and the unknown function $f(·)$ is modeled using a cubic smoothing spline with three degrees of freedom.

2.2 Delayed event time scenarios

2.2.1. Delayed diagnosis

To better understand the motivation, consider the following example: suppose the event of interest is being diagnosed with a certain disease (phecode), and there are two individuals who develop the disease at the same time. Depending on certain characteristics of the patients, such as their financial standing or insurance status, the patients are diagnosed at different times after developing the disease. A patient who does not have insurance may likely put off going to the doctor until it is necessary and be diagnosed later, while a patient with insurance may go to the doctor right away. The time difference between when a patient develops the tumor and is diagnosed with the disease (or the phecode shows up on their record) is the delayed event time, ϵ, which is being simulated in the models. Only positive delayed event time is considered; for example, if a patient develops the disease at age 40, the delayed event time can only occur after age 40 until diagnosis. Different delayed event time scenarios are considered, and specific examples of these scenarios are given in Section 2.3.

Before the delayed event time, ϵ, is incorporated, the true event time and true censoring time are denoted as T_e and T_c, respectively. The true observed time is thus $T_{\text{obs}}=\text{min}(T_{\mathrm{e}},T_{\mathrm{c}})$ and the event indicator is $E=I(T_{\mathrm{e}}<T_{\mathrm{c}})$. In this simulation, the delayed event time is added to the event time only, and the observed time with delayed event time is the minimum of the true event time plus delayed event time and the true censoring time: ${\tilde{T}}_{\text{obs}}=\text{min}(T_{\mathrm{e}}+ϵ,T_{\mathrm{c}})$. This leads to an event indicator of $\tilde{E}=I(T_{\mathrm{e}}+ϵ<T_{\mathrm{c}})$. Due to the nature of this simulation, the delayed event time that is added to T_e can lead to three different cases that relate ${\tilde{T}}_{\text{obs}}$ with T_obs, in which $\tilde{E}$ does not always equal to E. These cases are explained in Supplementary Appendix SA, but it should be noted that the magnitude of the proportion of misclassified events will change the relative performance of the models. In addition, if left truncation is present, there are occurrences of the simulated event time being less than the simulated left truncation time. In the research to evaluate the Cox model with left truncation, these occurrences are usually removed from the simulated dataset as they are considered as not meeting the criteria or not at risk (Howards et al., 2007; Schiesterman et al., 2013). In practice, identifying these patients requires additional efforts such as manually reviewing medical notes. At the absence of such effort or when the additional information is not available, an observation in this situation will be considered as a control since they do not have the event of interest during their record. This is corresponding to the scenario that the patient was diagnosed before entering the current healthcare system. In the simulation, both practices as well as the presence and absence of left truncation will be evaluated for all four models. In EHR-based research, the simulation with truncation mimics the study based on a single-site EHR system, while the simulation without truncation corresponds to the study based on a unified EHR system.

2.2.2. Baseline shifted

Another type of delayed event time occurs when the baseline time is shifted by a fixed delayed event time, ϵ. For example, consider that we are interested in the time from cancer diagnosis to cancer mortality. If the diagnosis time is delayed such as in Section 2.2.1, both the times of cancer-related death (T_e) and the last record of the patient (T_c) from diagnosis are reduced by the same delayed event time. As the example that motivates this scenario does not have a left truncation design, only censoring without truncation is considered.

In baseline shifted, the delayed event time is subtracted from both T_e and T_c to obtain the observed time with the delayed event time: ${\overline{T}}_{\text{obs}}=\text{min}(T_{\mathrm{e}}-ϵ,T_{\mathrm{c}}-ϵ)$. This leads to an event indicator of $\overline{E}=I(T_{\mathrm{e}}-ϵ<T_{\mathrm{c}}-ϵ)$, so $\overline{E}=E$ and ${\overline{T}}_{\text{obs}}=T_{\text{obs}}-ϵ$ for every observation. Thus, the observations do not partition into different delayed event cases as described in Supplementary Appendix SA for delayed diagnosis. The baseline time shifting could, however, lead to data removal due to $T_{\mathrm{e}}-ϵ<0$ and/or $T_{\mathrm{c}}-ϵ<0$. This happens when the disease was not diagnosed before the event (i.e. death) or the censoring time (i.e. last EHR record time).

2.3 Distribution of delayed event time

Five delayed event time scenarios are examined in this study. (i) We consider when there is no delayed event time, which can occur if a patient is diagnosed with a disease as soon as it develops (or the phecode shows up on the EHR). If the phecode of interest is an acute disease requiring an emergency visit, the diagnosis time is most likely accurate. (ii) We consider delayed event time caused by factors independent of the exposure and covariates, such as a delayed clinic visit due to scheduling. (iii) In addition, we consider exposure-dependent delayed event time, which can occur if the delay is related to a particular SNP that is being studied or a drug of interest in a clinical trial. (iv) Another delayed event time scenario is confounder-dependent delayed event time. If the delayed event time is caused by a disease being easier to diagnose in one sex over the other since it is more common in that sex, and sex is a confounder of the exposure of interest, the confounding scenario occurs. (v) Last, we consider covariate-dependent delayed event time that is independent of the exposure. For example, someone with a lower income may take longer to go to the doctor and be diagnosed, but income is not associated with SNPs.

2.4 Simulation study

2.4.1. Data-generation process

We simulated data for the delayed diagnosis scenario motivated in Section 2.2.1 and the baseline-shifted scenario motivated in Section 2.2.2. Specifically, two covariates x₁ and x₂ were independently generated from Bernoulli with P = 0.3 and N $(0.5,0.4)$, respectively. The exposure, z, was simulated from a Bernoulli distribution with $P={[1+\text{exp}(1.25-x_1)]}^{-1}$, i.e. x₁ is a confounder for z.

Different distributions for the event time and censoring time were considered. We first simulated the event time from Model (1) with baseline hazard generated from either exponential $(0.001)$ or log-normal $(6.5,1)$. The former model belongs to the accelerated failure time model while the latter does not. The regression coefficients for x₁ and x₂ were log(2) and the coefficient for z was varied to examine the type I error rate and power. The censoring time was simulated from $\text{Unif}(a_1,a_2)$, where a₁ and a₂ were specified to obtain different numbers of observations in each delayed event case as explained in Supplementary Appendix SA. We also simulated censoring time from a multivariable Cox regression model with baseline hazard generated from exponential $(0.002)$, where the parametric component included x₁ and x₂ for conditionally non-informative censoring. The regression coefficients for x₁ and x₂ were log(2). Although rare in our motivating study, we additionally considered when the censoring distribution was simulated from a Cox model that depended on both the covariates and exposure for comparison. Again, the regression coefficients for x₁ and x₂ were log(2), and the coefficient for z was varied. We conducted the delayed diagnosis simulation both with and without left truncation. When left truncation was present, it was simulated from Unif(50, 150). The mean event rate varied in the simulations depending on the delayed event case, the coefficient for z and the censoring distribution.

In the simulation study, we considered sample size n = 500 and fit the four models as described in Section 2.1. To evaluate the type I error and power of these models, we conducted 5000 simulations, where the regression coefficient for z was rejected if the P-value was less than 0.05. We evaluated the type I error when the coefficient for z was simulated to be zero, and evaluated the power when the coefficient for z was simulated to be log(1.1), log(1.15), log(1.25), log(1.5) and log(2).

2.4.2. Delayed event time scenarios

We simulated five delayed event time scenarios which added delayed event time, ϵ, to T_e. When there was no delayed event time, the value of ϵ was equal to zero. Independent delayed event time was simulated from $\text{Unif}(b_1,b_2)$. When the delayed event time was associated with the exposure, z, it was simulated from $\text{Unif}(c_1,c_2)$ and $\text{Unif}(c_2,c_3)$ for subjects exposed and not exposed, respectively. The same distributions were used when the delayed event time was associated with the confounder, but for subjects with $x_1=1$ and $x_1=0$, respectively. Delayed event time that was associated with the covariate, x₂, was simulated from log-normal $(d\times x_2,1)$. The parameters b₁, b₂, c₁, c₂, c₃ and d were varied to obtain different numbers of observations in each delayed event case as explained in Supplementary Appendix SA and explore different magnitudes of delayed event time.

2.5 Genomic study application

2.5.1. Data-generation process

To determine the impact of delayed event time on Cox and logistic regression models in a real-world application, we conducted GWAS in the genetic data linked to EHR data (Denny et al., 2018). We selected ten phenotypes in which to compare the ability of Cox and logistic regression models to detect known genotype–phenotype associations in the presence of simulated delayed event time, which are listed in Supplementary Appendix SB, Supplementary Table S1. These phenotypes were chosen before the analysis was performed. Cases for each phenotype were defined as individuals who had the phecode in the EHR on two distinct dates, and controls as those who did not have the phecode in the EHR. Left truncation, T_lt, was present in the EHR and corresponded to the age at the first visit in the healthcare system. The event age, T_e, was defined as the age on the second date of receiving the phecode of interest. The right censoring age, T_c, was the age at the last visit in the record. The observed age, T_obs, was T_e and T_c for cases and controls, respectively.

Since we aimed to understand the impact of delayed event time and the robustness of the models in the empirical data, we assumed the event age in the EHR data was the ‘true’ event age for each patient who was a case (i.e. there was no delayed event time in the EHR). We simulated delayed event time, and it was added to the event time only, corresponding to Simulation 1 in which ${\tilde{T}}_{\text{obs}}=\text{min}(T_{\mathrm{e}}+ϵ,T_{\mathrm{c}})$. Due to the structure of the EHR data, since only patients who had the phecode of consideration on two distinct dates had an age for the event time, the delayed event time was only added to the cases. Thus, a case could become a control in the presence of delayed event time if $T_{\mathrm{e}}+ϵ>T_{\mathrm{c}}$, where T_c corresponded to their last ever visit. A control remained a control.

In the genomic application, we considered the four models described in Section 2.1. For all four models, the linear component included genotype and the first four components of genetic ancestry. The model either included a term for biological sex or the data were restricted to females or males only depending on the phenotype. Cox used the counting process formulation with left truncation and the observed age. LRM_obs included additional terms for the age difference (as a cubic spline with three degrees of freedom), which was the difference between the observed age and the left truncation age, $T_{\mathrm{d}}=T_{\text{obs}}-T_{\text{lt}}$. LRM_u included no additional terms concerning age. LRM_rl included additional terms for age at the last visit (as a cubic spline with three degrees of freedom) and the record length, which was the difference in age between the first ever and last ever visits.

2.5.2. Delayed event time scenarios

We considered four delayed event time scenarios to add to the event age for each phenotype. We considered delayed event time that depended on significant SNPs. For a particular phecode, all the significant SNPs at the $P\le 5\times {10}^{-8}$ significance level were selected. The number of significant SNPs ranged from 1 to 298 among the ten phecodes used. The coding for the SNP was the allele count. If a patient had at least one of the alleles, the delayed event time was simulated from $\text{Unif}(0,0.5)$. If the patient had none of the alleles, the delayed event time was simulated from $\text{Unif}(0.5,1)$. The scale of age was years, so values of delayed event time equal to 0.5 and 1 corresponded to 6 months and 1 year, respectively. We also considered delayed event time that depended on non-significant SNPs. For each phecode, the same number of SNPs that were significant were randomly sampled from the non-significant SNPs. The delayed event time was simulated in the same way as for the significant SNPs. We considered delayed event time that depended on sex, which was only used in phecodes that were associated with both females and males. In this case, it was simulated from $\text{Unif}(0,0.5)$ for females and $\text{Unif}(0.5,1)$ for males. Last, we simulated independent delayed event time from Unif(0, 1) for all patients.

3 Results

3.1 Simulation results

We used a series of simulations to compare the Cox regression and logistic regression models under different delayed event time scenarios to mimic the application in the EHR data. Since the effect sizes of the two methods are not equivalent (i.e. hazard ratios and odds ratios), the performance of the four models was compared in terms of type I error and power in the presence of delayed event time. We also evaluated the bias of the estimation for exposure for the Cox model only.

3.1.1. Simulation 1—delayed diagnosis

Figures 1–3 plot the type I error and power for Simulation 1 (with left truncation) when the event time is simulated from a Cox model with baseline hazard from an exponential distribution and the censoring time is simulated from a uniform distribution. Table 1 shows the corresponding biases of the β₁ estimate from Cox. Additional results for other simulations are included in Supplementary Appendix SC. In Figures 1 and 2, observations with event time before entry time were removed from the data analyzed by all four models (denoted as removal-practice), and in Figure 3, those observations were included and considered as censored or control (denoted as censor-practice).

Fig. 1.

Results from Simulation 1 when the event time was generated from a Cox model with baseline hazard from an exponential distribution, the censoring time was generated from a uniform distribution with left truncation, and the observations with simulated event times before truncation were removed from the analysis (removal-practice). The parameters led to a small number of observations with a misclassified event status (detailed in Supplementary Appendix SA). *Type I error evaluated at log(1). Power evaluated at log(1.1), log(1.15), log(1.25), log(1.5), log(2)

Table 1.

Bias of β coefficient for z from Model 1 (Cox) that corresponds to the simulations shown in Figures 1–3

	True value for β1
	log(1)	log(1.1)	log(1.15)	log(1.25)	log(1.5)	log(2)
Figure 1. Simulation 1, left truncation, random censoring, removal-practice, small misclassification
No error	–0.015	–0.012	–0.011	–0.007	–0.001	–0.007
Independent error	–0.014	–0.012	–0.012	–0.009	–0.007	–0.006
Exposure-dependent error	–0.010	–0.008	–0.007	–0.006	–0.001	0.005
Confounder-dependent error	–0.012	–0.009	–0.006	–0.006	–0.002	0.002
Covariate-dependent error	–0.011	–0.012	–0.014	–0.017	–0.025	–0.040
Figure 2. Simulation 1, left truncation, random censoring, removal-practice, large misclassification
No error	–0.002	–0.000	0.000	0.001	0.002	0.004
Independent error	–0.007	–0.025	–0.035	–0.053	–0.097	–0.183
Exposure-dependent error	2.217	2.219	2.220	2.222	2.228	2.241
Confounder-dependent error	–0.000	0.001	0.002	0.002	0.003	0.004
Covariate-dependent error	–0.003	–0.011	–0.015	–0.025	–0.048	–0.096
Figure 3. Simulation 1, left truncation, random censoring, censor-practice, small misclassification
No error	–0.001	–0.039	–0.059	–0.100	–0.201	–0.410
Independent error	–0.007	–0.026	–0.036	–0.055	–0.103	–0.193
Exposure-dependent error	2.130	2.119	2.114	2.103	2.071	1.997
Confounder-dependent error	–0.000	–0.015	–0.022	–0.038	–0.082	–0.179
Covariate-dependent error	–0.003	–0.024	–0.035	–0.058	–0.116	–0.236

Note: Bias is presented for log(1) for log(1.1), log(1.15), log(1.25), log(1.5), log(2).

Fig. 2.

Results from Simulation 1 when the event time was generated from a Cox model with baseline hazard from an exponential distribution, the censoring time was generated from a uniform distribution with left truncation, and the observations with simulated event times before truncation were removed from the analysis (removal-practice). The parameters led to a large number of observations with a misclassified event status (detailed in Supplementary Appendix SA). *Type I error evaluated at log(1). Power evaluated at log(1.1), log(1.15), log(1.25), log(1.5), log(2)

Fig. 3.

Results from Simulation 1 when the event time was generated from a Cox model with baseline hazard from an exponential distribution, the censoring time was generated from a uniform distribution with left truncation, and the observations with simulated event times before truncation were considered censored (censor-practice). The parameters led to a large number of observations with a misclassified event status (detailed in Supplementary Appendix SA). *Type I error evaluated at log(1). Power evaluated at log(1.1), log(1.15), log(1.25), log(1.5), log(2)

We first consider removal-practice. In all of the delayed event time scenarios, except for exposure-dependent delayed error (differential error), Figures 1 and 2 show that Cox performs either the same or better than two of the logistic regression models with controlled type I error rate and improved power for increasing effect size. Models LRM_u and LRM_rl perform well and similarly. However, LRM_obs, performs substantially worse in terms of power than the other three models. This is because in LRM_obs, the effect of z leaks through T_d when it has a non-null effect. The difference between Figures 1 and 2 is due to the censoring rate and misclassification rate at the presence of delayed event time. The misclassification occurs when the delayed event time causes an observation who is originally a case to become a control. In Figure 1, the event rate of the no delayed event time scenario is about 20% and the misclassification rate is 3.5–13% of remaining samples. In Figure 2, the event rate is about 50% and the misclassification rate is 34–39%. As shown in Table 1, the bias is negligible in all scenarios when the misclassification rate is low, and increases with increasing misclassification rate when the effect is not null as in Figure 2. When delayed error depends on z, none of the models have an acceptable performance. This scenario is almost impossible in a GWAS study, but it is likely for other EHR-based applications, such as drug repurposing (Wu et al., 2019).

To evaluate the impact of censor-practice, we compare Figure 2 to Figure 3 under the same simulation settings, except Figure 2 uses removal-practice and Figure 3 uses censor-practice. When there is no delayed event time, about 21–30% of observations have their simulated event time before entry time and are hence removed in Figure 2 but classified as censored or control in Figure 3. The latter leads to biased estimate in Cox even under the no delayed event time scenario (see Fig. 3 in Table 1), because the riskier observations with shorter event times are more likely to be misclassified as censored. This truncation-related misclassification is different from the previous delayed event time related misclassification. With the presence of delayed event time, the observed event time is less likely to occur before entry time and, hence, reduces the likelihood of being misclassified as censored. Combining the truncated-related misclassification and delayed event time related misclassification, the Cox model, under all but the exposure-dependent delayed event time scenario, has smaller bias than in the no delayed event time scenario, which also leads to increased power in Figure 3.

For the rest of Simulation 1, only the results for large delayed event time scenario are presented in Supplementary document due to limited space. When the event time is generated from a Cox model with baseline hazard from a log-normal distribution, the results are consistent to those described for the exponential baseline hazard (results not shown). When the censoring is conditionally non-informative, Cox always performs the best in terms of power, followed by LRM_rl (Supplementary Appendix SC, Supplementary Fig. S1 for removal-practice and Supplementary Fig. S2 for censor-practice, corresponding bias of Cox in Supplementary Table S2). The difference in power between these two models is larger than when the censoring distribution is independent of the covariates. Again, when there is exposure-dependent delayed error and a high proportion of subjects with misclassified events, all four models are invalid. When the censoring distribution depends on both the covariates and exposure, inflated type I error is associated with LRM_obs and LRM_u (Supplementary Appendix SC, Supplementary Fig. S3 for removal-practice and Supplementary Fig. S4 for censor-practice, corresponding bias of Cox in Supplementary Table S2).

When there is no left truncation, the truncation-related misclassification does not exist and similar conclusions from removal-practice hold for the relative performance of the four models (Supplementary Appendix SC, Supplementary Figs S5–S7, corresponding bias of Cox in Supplementary Table S2).

3.1.2. Simulation 2—baseline shifted

In Simulation 2, the relative performance of the four models is consistent with, if not more apparent than, those from Simulation 1 (see Supplementary Appendix SC, Supplementary Figs S8–S13, corresponding bias of Cox in Supplementary Table S2). We considered the settings with either low (Supplementary Appendix SC, 5–16% for Supplementary Fig. S8, 15–23% for Supplementary Fig. S10, 18–26% for Supplementary Fig. S12) or large (Supplementary Appendix SC, 46–67% for Supplementary Fig. S9, 51–74% for Supplementary Fig. S11, 51–74% for Supplementary Fig. S13) amount of data removed due to failure to diagnose before event or censoring time (i.e. $T_{\mathrm{e}}-ϵ<0$ or $T_{\mathrm{c}}-ϵ<0$). In all settings, the bias of Cox is negligible as shown in Supplementary Appendix SC, Supplementary Table S2 under Supplementary Figs S8–S13. Cox performs similarly or better than the logistic regression models in terms of statistical power, usually followed by LRM_rl. LRM_obs generally performs the worst, though it is about the same as LRM_u when the censoring distribution depends on the covariates. As in Simulation 1, when the censoring distribution depends on exposure, LRM_obs and LRM_u have inflated type I error, sometimes striking as in Supplementary Appendix SC, Supplementary Figure S12.

3.2 Genomic study application

To study the robustness of Cox and logistic regression models in the presence of delayed event time, we compared the four models with every delayed event time scenario using genetic data linked to the EHR. A cohort of 49 792 individuals of European ancestry was used, and ten phenotypes were defined from the EHR. For each model and delayed event time combination, GWAS was run on 795 850 common SNPs. The Manhattan plots for the ten phenotypes are shown in Supplementary Appendix SC, Supplementary Figures S14–S23. Cox generally detected the most significant SNPs, followed by LRM_rl, especially for common phenotypes.

Based on the results found in the simulations and Hughey et al. (2019), we calculated the true positive and true negative rates (TPRs and TNRs) of detecting associations for the models with each delayed event time scenario, using the Cox regression model with no delayed event time as the gold standard. Thus, the SNPs found to be significant at either the $P\le 5\times {10}^{-8}$ or $P\le 1\times {10}^{-5}$ significance level by Cox with no delayed event time are considered the ‘true’ associations at the respective significance level. The average TPRs and TNRs from all ten phecodes and corresponding 95% confidence intervals are reported in Supplementary Appendix SB, Supplementary Table S25. The average TNRs are very high for all the model and delayed event time combinations due to the relatively small number of significant SNPs compared to the 795 850 SNPs that were analyzed in the GWAS. The average TPRs for each model and delayed event time combination can be visualized in Figure 4. Cox and LRM_rl have the highest true positive rates, even in the presence of delayed event time. The individual TPRs and TNRs for the phecodes are provided in Supplementary Appendix SB (Supplementary Tables S3–S22).

Fig. 4.

Average true positive rates for detecting significant SNPs from all ten phecodes for each model and delayed event time combination, using Model 1 (Cox) with no delayed event time as the gold standard. This application corresponds to the delayed diagnosis set-up. *Based on Model 1 (Cox)—no delayed event time

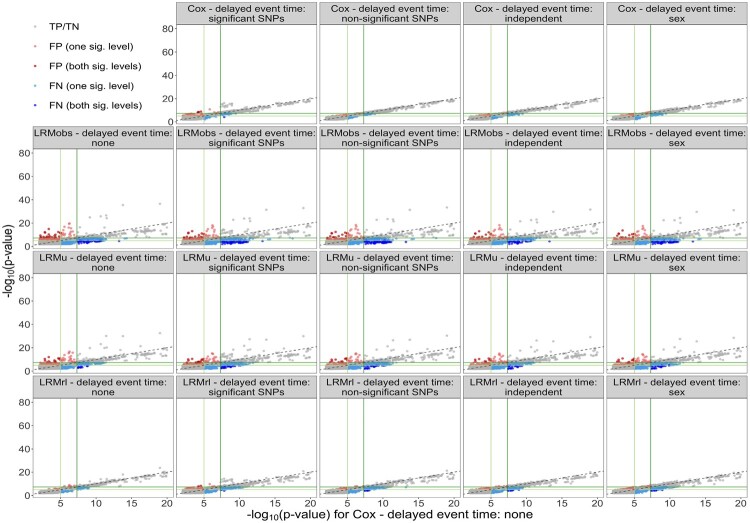
We also plotted the P-values of Cox with no delayed event time against the P-values of the remaining model and delayed event time combinations in Figure 5. The gray points indicate true positive or true negative SNPs, while the colored points represent false positive and false negative SNPs. The ideal performance of a model would be to have as few false positives (red points) and false negatives (blue points) as possible. In addition, the true negative and true positive SNPs (gray points) should follow closely along the 45° line. Cox and LRM_rl have the fewest false positive and false negative points, even in the presence of delayed event time. The true positive/true negative points follow most closely to the 45° line for Cox compared to the logistic regression models, within each respective delayed event time scenario. The corresponding figures for the individual phecodes are given in Supplementary Appendix SC (Supplementary Figs S24–S33).

Fig. 5.

False positive and false negative SNPs for each model and delayed event time combination, using Model 1 (Cox) with no delayed event time as the gold standard, for all ten phecodes. Dark green lines correspond to $P\le 5\times {10}^{-8}$ and light green lines correspond to $P\le 1\times {10}^{-5}$

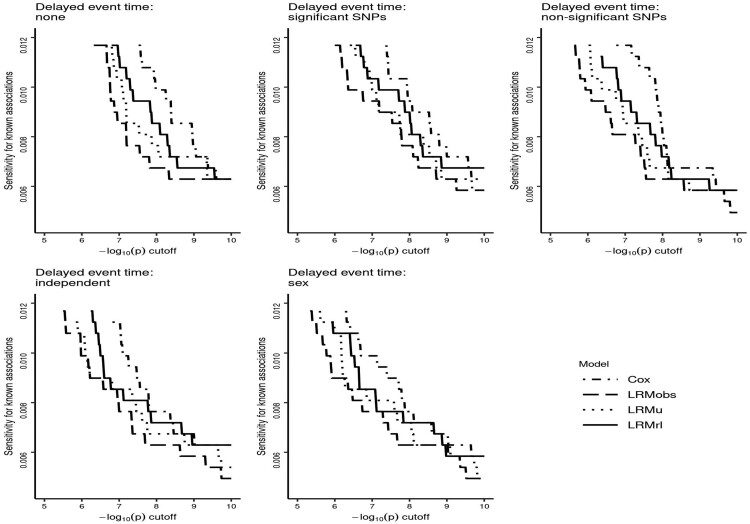
In addition, we used the GWAS results from each model/delayed event time combination for the ten phenotypes to determine each method’s ability of detecting known associations from the NHGRI-EBI GWAS Catalog (Buniello et al., 2019). The results are shown in Figure 6, where each graph shows the four models for a particular delayed event time scenario. It can be seen that Cox has the highest relative sensitivity compared to the other models across a range of P-value cutoffs. LRM_rl generally seems to perform better than Models LRM_obs and LRM_u in detecting known associations.

Fig. 6.

Sensitivity of each model and delayed event time combination for detecting known genotype–phenotype associations

4 Discussion

In this article, we sought to determine the impact of delayed event time with positive error on the performance of Cox regression and logistic regression models in simulations and for identifying genotype–phenotype associations in genetic data linked to EHR data. One Cox model and three different logistic regression models that have been used in literature were studied. We considered different types of misclassification that introduced bias into the regression parameters, including non-differentiable, conditional non-differentiable and differentiable error. In reality, delayed event time is more likely to occur for chronic diseases than acute diseases.

When left truncation is present, the general assumption is that subjects experiencing the event before truncation time can be recorded and removed from the analysis. This assumption, however, is challenging in EHR-based research. To evaluate its impact, we compared the removal-practice and censor-practice scenarios in simulation studies. This extends to the EHR application, where if patients had the phenotype of interest before entry into a healthcare site, they could be identified and then removed in removal-practice, or misclassified as controls in censor-practice if unidentified. Compared to removal-practice, when the truncation-related misclassification rate is high, potential non-negligible bias could be introduced by censor-practice even without delayed event time. In practice, researchers could focus on reviewing individuals with a diagnosis code at their first visit. Those patients are more likely referred to the current hospital for a disease that was already diagnosed at another hospital. The medical history may summarize prior diagnosed diseases, or even when the diagnosis occurred. Completely identifying those patients could be challenging, especially for whom little medical history was taken. The performance depends on the importance of the diagnosis and the quality of the medical history. This challenge highlights the significance of having a unified EHR system so that truncation is no longer a concern. It is worth noting that in the simulation, we assumed no recurrence of diagnosis codes after entering the current health system, which represents the worst scenario of misclassifying the patients with the highest risk to those with the lowest risk. With recurrence of diagnosis codes, the bias due to censor-practice in practice would be less severe than the results observed in the simulation study.

In our simulation study, we examined both independent and conditionally non-informative censoring distributions. When the censoring distribution depended on the exposure in addition to other covariates, the performance of LRM_obs and LRM_u deteriorated with inflated type I error rate and decreasing power with increased effect size (see Supplementary Appendix SC, Supplementary Fig. S12), and should be avoided.

There are limitations with the use of both Cox with no delayed event time and the GWAS Catalog as the gold standards in the GWAS application. We made the assumption that the associations found to be significant by Cox with no delayed event time were the truth based on previous work (Hughey et al., 2019) and the results of the simulation study. These associations were used to calculate the true positive and true negative rates of the other model/delayed event time combinations, which could be misleading if some of the significant associations are incorrect. In addition, the use of the GWAS Catalog as the gold standard to determine the sensitivity of the Cox models is limiting, since most of the known genotype–phenotype associations were found by logistic or linear regression. Thus, it does not apply directly to associations found by Cox regression. All of the methods showed low sensitivity due to being underpowered for detecting the associations. However, it is promising that both the simulations and the GWAS application indicated that Cox regression has the best performance in detecting genotype–phenotype associations, even with these limitations.

Lastly, we did not determine the exact magnitude of delayed event time that would be acceptable in the EHR in order for the Cox model to continue to outperform the logistic regression models, as our main goal was to explore the impact of delayed event time on the performance of the models in general. However, in the simulations, we varied the parameters when simulating the delayed event time to obtain different numbers of observations with a misclassified event status, which led to different ranges of delayed event time magnitude. For example, when there was a small number of misclassified events and confounder-dependent delayed event time, we set $c_1=20$ and $c_3=60$ days. To increase the proportion of misclassified events, we set $c_1=60$ and $c_3=1400$ days. Increasing the magnitude of the delayed event time caused all the methods to be invalid when there was exposure-dependent delayed event time, as explained in Section 3.1.1. However, for the other delayed event time scenarios, even when the magnitude of the delayed event time was large, the Cox regression model performed either the same or better as the logistic regression models in terms of statistical power, and the type I error rate was controlled. This gives some insight into the impact of the magnitude of delayed event time on the performance of the models.

5 Conclusion

Based on the use of both simulations and empirical data, we found that while logistic regression does not model the time-to-event directly, various logistic regression models used in the literature were more sensitive to delayed event time than Cox regression. The simulations highlighted the need to identify the patients having the disease of interest before entering the current healthcare system. With those patients being properly identified and excluded from analysis, Cox regression had similar or modest improvement in statistical power over logistic regression at controlled type I error with or without the presence of delayed event time. These results were supported by the empirical data, where the Cox models steadily had the highest sensitivity to detect known genotype–phenotype associations under all scenarios of delayed event time. In the presence of delayed event time scenarios that might exist in EHRs, Cox regression outperformed the logistic regression models commonly used in genomic studies. Among the three logistic regression models, the logistic regression model that adjusts for record length, LRM_rl, is the preferred modeling scheme to use. The big discrepancy in the performance of the three commonly used logistic regression models highlights the needs to clarify the model used.

As stated in the Introduction, previous work has already shown the advantages of Cox regression over logistic regression in many scenarios (Staley et al., 2017; van der Net et al., 2008), including for use in genomic studies that utilize the EHR (Hughey et al., 2019). Our primary focus in this study was to determine if Cox regression still outperformed logistic regression when the time-to-event information in the EHR was incorrect, which we found to be true. This indicates that Cox regression is the most robust modeling scheme to delayed event time. Thus, even if time-to-event information is inaccurate, Cox regression may improve our ability to determine the significant genetic constitutes for a variety of diseases.

Funding

This work was supported by National Institutes of Health/NLM [R01-LM0010685 to J.J.H., L.B., J.C.D.]; National Institutes of Health/NIGMS [R35GM124685 to J.J.H.]; and National Institutes of Health/NCI [1R01CA237895, U24 CA194215 to Q.C.]. Dr Denny’s involvement in this project was primarily while at Vanderbilt University Medical Center prior to joining the National Institutes of Health.

Conflict of Interest: none declared.