Thermodynamic characterization of naturally occurring RNA pentaloops

Abstract

RNA folding is hierarchical; therefore, predicting RNA secondary structure from sequence is an intermediate step in predicting tertiary structure. Secondary structure prediction is based on a nearest neighbor model using free energy minimization. To improve secondary structure prediction, all types of naturally occurring secondary structure motifs need to be thermodynamically characterized. However, not all secondary structure motifs are well characterized. Pentaloops, the second most abundant hairpin size, is one such uncharacterized motif. In fact, the current thermodynamic model used to predict the stability of pentaloops was derived from a small data set of pentaloops and from data for other hairpins of different sizes. Here, the most commonly occurring pentaloops were identified and optically melted. New experimental data for 22 pentaloop sequences were combined with previously published data for nine pentaloop sequences. Using linear regression, a pentaloop-specific model was derived. This new model is simpler and more accurate than the current model. The new experimental data and improved model can be incorporated into software that is used to predict RNA secondary structure from sequence.

INTRODUCTION

In addition to transcribing genetic information from DNA and translating it to protein, RNA can regulate gene expression (Tucker and Breaker 2005; Sun et al. 2018), catalyze reactions in the cell (Doudna and Cech 2002; Wilson and Lilley 2015), and act as a therapeutic target (Krützfeldt et al. 2005; Elmén et al. 2008; Esau 2008; Faghihi et al. 2008; Gupta et al. 2010; Gupta and Nandan 2017), to name a few. Due to a strong relationship between structure and function (Dyson et al. 1993; Lee et al. 1997; McCarthy 2005; Campagnola et al. 2015; Travers and Muskhelishvili 2015), determining RNA tertiary structure is the prime step in order to better understand RNA's diverse functionalities. An intermediate step in predicting tertiary structure from sequence is to predict secondary structure from sequence. The most common way to predict secondary structure from sequence is by free energy minimization using nearest neighbor parameters (Xia et al. 1998; Chen et al. 2012) derived for each secondary structure motif from optical melting experiments. However, there is still room for improving secondary structure prediction because not all secondary structure motifs have been sufficiently characterized thermodynamically.

One of the most common secondary structure motifs in RNA is a hairpin, formed when a strand of RNA folds back on itself to form a stem–loop structure. In Escherichia coli, ∼70% of rRNA nucleotides are involved in forming hairpins (Giese et al. 1998). Hairpins can act as nucleation sites for higher order folding (Uhlenbeck 1990) and recognition sites for other biomolecules (Legault et al. 1998; Wu et al. 2001; Koldobskaya et al. 2011; Koirala et al. 2018). One of the most common sizes of hairpins is a pentaloop, a hairpin containing 5 nt in the loop. In 16S rRNA of E. coli, pentaloops account for 13% of the total hairpins (Woese et al. 1990), and in large subunit rRNA, 24% of the hairpins are pentaloops (Gutell and Fox 1988). In addition to being prevalent, pentaloops can serve important biological functions. For example, pentaloops can play an important role in alternative splicing. In the transcript of the survival motor neuron, a temporary pentaloop is located at the junction of exon 7 and intron 7 and acts as a regulatory element for exon 7 inclusion (Singh et al. 2007, 2015). A pentaloop is present in the D3 and D5 domains of group II introns and facilitates tertiary interactions between domains (Jestin et al. 1997; Fedorova and Pyle 2005; Pechlaner et al. 2013). Pentaloops in spliceosomal U6 RNA can mediate tertiary folding (Cate et al. 1996) or act as a recognition site for proteins (Legault et al. 1998). In RNA crystallization experiments, pentaloops can serve as a recognition site for crystallization chaperones (Koldobskaya et al. 2011; Koirala et al. 2018). N protein of phages λ and P22 recognize boxB RNA by a pentaloop, which acts as a transcription antiterminator (Salstrom and Szybalski 1978; de Crombrugghe et al. 1979; Olson et al. 1982; Franklin 1985; Lazinski et al. 1989; Weisberg and Gottesman 1999). A pentaloop found in aptamer NEO1A can act as a recognition site for a wide range of aminoglycoside antibiotics (Ilgu et al. 2014) and can cause toxicity. In E. coli, the aminoacyl (A) site of 23S rRNA has a conserved pentaloop hairpin which is essential for the function of the peptidyltransferase center of rRNA (Samaha et al. 1995; Kim and Green 1999). Lastly, a pentaloop can mediate pre-mRNA modification; a highly conserved pentaloop at the R/G site of pre-mRNA in mammals and birds acts as a recognition site for adenosine deaminases that act on RNA (ADARs) (Aruscavage and Bass 2000; Stefl et al. 2006).

Despite the high frequency and functional importance of pentaloops, the thermodynamics of pentaloops are not well characterized. The current model (Vecenie and Serra 2004; Vecenie et al. 2006) used to predict the thermodynamic stability of pentaloops is based on a data set of experimental thermodynamic parameters from only nine pentaloop sequences (Serra et al. 1997; Giese et al. 1998) as well as data from different size hairpins. In the current model, two different equations are used based on the closing base pair of the hairpin (Vecenie and Serra 2004; Vecenie et al. 2006). The general hairpin equation for hairpins with a Watson–Crick closing base pair is:

$$\begin{array}{rl}\mathrm{\Delta }{\mathrm{G}}_{37,\mathrm{L}\left(\mathrm{n}\right)}^{\mathrm{o}}& =\mathrm{\Delta }{\mathrm{G}}_{37\mathrm{i}\left(\mathrm{n}\right)}^{\mathrm{o}}+\mathrm{\Delta }{\mathrm{G}}_{37\mathrm{MM}}^{\mathrm{o}}\\ & -0.8\mathrm{kcal}/\mathrm{mol}(\mathrm{if}\mathrm{the}\mathrm{first}\mathrm{mismatch}\mathrm{is}\mathrm{G}\cdot \mathrm{A}\mathrm{or}\\ & \mathrm{U}\cdot \mathrm{U})-0.8\mathrm{kcal}/\mathrm{mol}(\mathrm{if}\mathrm{the}\mathrm{first}\mathrm{mismatch}\mathrm{is}\\ & \mathrm{G}\cdot \mathrm{G}\mathrm{and}\mathrm{the}\mathrm{loop}\mathrm{is}\mathrm{closed}\mathrm{on}\mathrm{the}{5}^{\mathrm{\prime }}\mathrm{side}\mathrm{by}\mathrm{a}\mathrm{purine})\end{array}$$ (1)

For pentaloops, ΔG°_37i(n) 5.7 kcal/mol. ΔG°_37MM is the free energy of interaction between the first mismatch of the loop and the closing base pair (Freier et al. 1986; SantaLucia et al. 1991; Serra et al. 1994; Serra and Turner 1995; Giese et al. 1998; Vecenie and Serra 2004; Vecenie et al. 2006; Sheehy et al. 2010). For hairpins with a G-U or U-G closing base pair, the equation is:

$$\begin{array}{rl}\mathrm{\Delta }{\mathrm{G}}_{37,\mathrm{L}\left(\mathrm{n}\right)}^{\mathrm{o}}& =\mathrm{\Delta }{\mathrm{G}}_{37\mathrm{i}\left(\mathrm{n}\right)}^{\mathrm{o}}-0.8\mathrm{kcal}/\mathrm{mol}(\mathrm{if}\mathrm{the}\mathrm{first}\mathrm{mismatch}\mathrm{is}\\ & \mathrm{G}\cdot \mathrm{A})-0.8\mathrm{kcal}/\mathrm{mol}(\mathrm{if}\mathrm{the}\mathrm{first}\mathrm{mismatch}\mathrm{is}\\ & \mathrm{G}\cdot \mathrm{G}\mathrm{and}\mathrm{the}\mathrm{loop}\mathrm{is}\mathrm{closed}\mathrm{on}\mathrm{the}{5}^{\mathrm{\prime }}\mathrm{side}\mathrm{by}\mathrm{a}\mathrm{purine})\end{array}$$ (2)

Here, for pentaloops, ΔG°_37i(n) = 5.0 kcal/mol. The bonus for G·A, U·U, and G·G first mismatches in Equations 1 and 2 was included based on the thermodynamics of hexaloops (Vecenie and Serra 2004; Vecenie et al. 2006). The model was also validated by predicting the stability of hexaloops (Vecenie and Serra 2004; Vecenie et al. 2006). Therefore, we hypothesized that a thermodynamic model derived from only pentaloop data will be more accurate at predicting pentaloop stability. Here, we report the thermodynamics of 22 pentaloops. We combine this data with the data for nine pentaloops from the literature (Serra et al. 1997; Giese et al. 1998) to derive a pentaloop-specific model. This new model can be incorporated into secondary structure prediction software to improve RNA secondary structure prediction from sequence.

RESULTS

Database searching

A total of 1589 pentaloops were found in the secondary structure database described in Materials and Methods, averaging about one pentaloop in every secondary structure. Almost all of the pentaloops were found within rRNA (∼75% were found in 23S RNA and ∼18% were found in 16S RNA). Group I introns (∼4%) and tRNA (∼1%) also contributed pentaloops, with all other types of RNA contributing <1% of the total pentaloops found. A summary of these pentaloops is shown in Table 1. Data set 1 shows frequency and percent occurrence of pentaloops when specifying the loop sequence and the closing base pair. Because previous studies have shown that the stability of hairpin loops depends on both the identity of the nucleotides in the loop and the closing base pair (Vecenie and Serra 2004; Vecenie et al. 2006; Sheehy et al. 2010; Thulasi et al. 2010), this categorization is most important. A total of 545 combinations of this type were found in the database. The top 18 most frequent pentaloops each account for 1%–4% of the total number of pentaloops, and together, they account for 36.8% of the total number of pentaloops. The remaining 527 pentaloops account for 63.2% of the total number of pentaloops, but each accounts for <1% of the total number of pentaloops. Data set 2 consists of pentaloops when specifying the loop nucleotides only (closing base pair is not included). A total of 358 pentaloops were found in the database. The top 19 most frequent pentaloops each account for 1.1%–6.4% of the total number of pentaloops, and together, they account for 46.5% of the total number of pentaloops. The remaining 339 pentaloops account for 53.1% of the total number of pentaloops, but each accounts for <1% of the total number of pentaloops. Data set 3 tallies the number of pentaloops with each of the six possible canonical closing base pairs. Lastly, data set 4 lists the pentaloop sequences when purine nucleotides are represented as “R” and pyrimidine nucleotides are represented as “Y.” While all 32 possible types of pentaloops were found in the database, the top 27 most frequent pentaloops each account for 1.0%–11.6% of the total number of pentaloops, and together, they account for 97.6% of the total number of pentaloops. The remaining five pentaloops account for 2.4% of the total number of pentaloops, with each accounting for <1% of the total number of pentaloops.

TABLE 1.

Summary of the RNA pentaloops found in the secondary structure database^a

Thermodynamic parameters

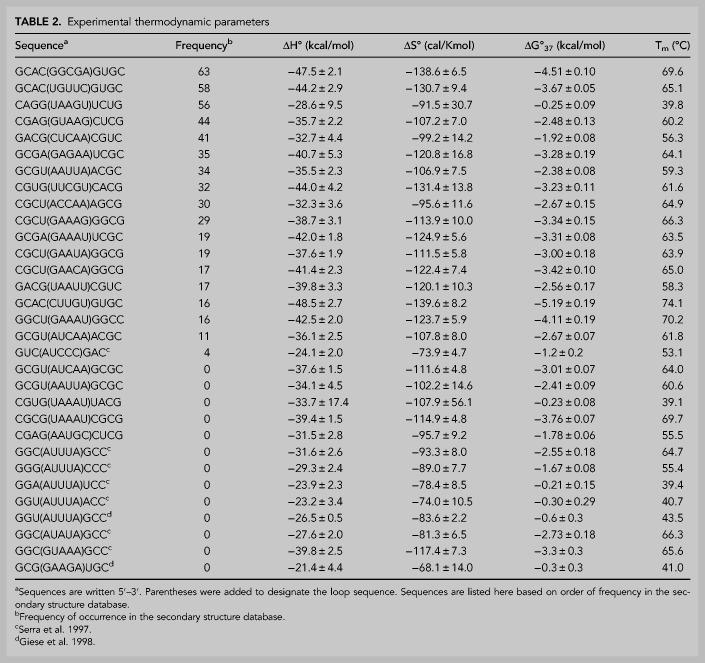
Seventeen of the most frequent pentaloops in the database were optically melted, and thermodynamic parameters were derived (Table 2). Due to possible competition from bimolecular association of strands, some frequent pentaloops were not studied here. In order to incorporate more sequence variability and to develop the most inclusive thermodynamic model, five additional pentaloop sequences that were not found in the database were also studied. These sequences were selected to fill in gaps (i.e., additional pentaloops with G-U and U-G closing pairs) in the data set and to see if frequency in the secondary structure database was related to stability.

TABLE 2.

Experimental thermodynamic parameters

Contribution of pentaloops to stem–loop free energy

Table 3 shows the thermodynamic contribution of pentaloops to stem–loop stability. In addition to the 22 pentaloops measured here, previously published data for nine additional pentaloops are included (Serra et al. 1997; Giese et al. 1998). The free energy contribution of pentaloops (ΔG°_37,pentaloop) ranges from 2.58 to 5.74 kcal/mol.

TABLE 3.

Pentaloop contribution to stem–loop thermodynamics

Updated model for predicting the free energy of previously unmeasured pentaloops

To improve prediction of pentaloop stability and reduce the complexity of the current model, a new pentaloop-specific model was derived. Many different parameters were tested, but the following equation represents the best combination of parameters for a simple model with high accuracy:

$$\begin{array}{rl}\mathrm{\Delta }{\mathrm{G}}_{37,\mathrm{pentaloop}}^{\mathrm{o}}& =4.37\mathrm{kcal}/\mathrm{mol}\\ & -1.00\mathrm{kcal}/\mathrm{mol}(\mathrm{for}\mathrm{a}\mathrm{C}-\mathrm{G}\mathrm{closing}\mathrm{pair})\\ & +0.58\mathrm{kcal}/\mathrm{mol}(\mathrm{for}\mathrm{a}\mathrm{G}-\mathrm{U}\mathrm{closing}\mathrm{pair})\\ & +0.60\mathrm{kcal}/\mathrm{mol}(\mathrm{for}\mathrm{an}A\cdot \mathrm{A}\mathrm{first}\mathrm{mismatch})\end{array}$$ (3)

Please note that the −1.00 kcal/mol bonus only applies to pentaloops closed by a C-G pair, with a C on the 5′ side of the loop (the bonus does not apply to G-C closing pairs), which is consistent with what was seen previously for triloops (Thulasi et al. 2010). Similarly, the 0.58 kcal/mol penalty only applies to pentaloops closed by a G-U pair, with a G on the 5′ side of the loop (the penalty does not apply to U-G closing pairs). Additional bonuses and/or additional penalties may be discovered with additional experiments. The standard error from the regression analysis for the pentaloop penalty, C-G closing pair bonus, G-U closing pair penalty, and A·A first mismatch penalty is 0.11, 0.18, 0.26, and 0.16 kcal/mol, respectively. For the new model, the average difference between the predicted and experimental free energy is 0.26 kcal/mol, with a range of 0.00–0.89 kcal/mol (Table 3). This can be compared to the current model (using Equations 1 and 2 for the same set of pentaloops) where the average difference between the predicted and experimental free energy is 0.42 kcal/mol, with a range of 0.04–2.32 kcal/mol (Table 3). Similar models without each of the individual parameters introduced in Equation 3 resulted in a significant decrease in accuracy.

A similar model was derived in order to predict the enthalpic contribution of pentaloops. Using the same parameters as Equation 3, the following equation resulted:

$$\mathrm{\Delta }{\mathrm{H}}_{\mathrm{pentaloop}}^{\mathrm{o}}=-4.57\mathrm{kcal}/\mathrm{mol}-2.85\mathrm{kcal}/\mathrm{mol}(\mathrm{for}\mathrm{a}\mathrm{C}-\mathrm{G}\mathrm{closing}\mathrm{pair})+0.46\mathrm{kcal}/\mathrm{mol}(\mathrm{for}\mathrm{a}\mathrm{G}-\mathrm{U}\mathrm{closing}\mathrm{pair})+3.73\mathrm{kcal}/\mathrm{mol}(\mathrm{for}\mathrm{an}\mathrm{A}\cdot \mathrm{A}\mathrm{first}\mathrm{mismatch})$$ (4)

Experimental and predicted ΔH°_pentaloop values can be found in Supplemental Table S2.

DISCUSSION

Database searching

For triloops, G(GGG)C and GGG were the most common triloop sequences in data sets 1 and 2, respectively (Thulasi et al. 2010). For tetraloops, the most common tetraloop sequences in data sets 1 and 2 were C(GAAA)G and GAAA, respectively (Sheehy et al. 2010). Note that all four of these hairpins consist of all purine nucleotides. Common pentaloop sequences are a little different. For pentaloops, C(GGCGA)G and UGUUC were the most common pentaloop sequences in data sets 1 and 2, respectively. It was not until the seventh most common sequence for data set 1, A(GAGAA)U, and the sixth most common sequence for data set 2, GAAAG, did pentaloops exhibit all purine sequences. Only 52.3% of pentaloops were closed by C-G or G-C pairs, compared to 68.6% of triloops (Thulasi et al. 2010) and 69.3% of tetraloops (Sheehy et al. 2010). More specifically, pentaloops with C-G closing pairs (28.6%) were much fewer than triloops (42.0%) and tetraloops (49.2%) with C-G closing pairs. Similar to what was observed in data sets 1 and 2, data set 4 for triloops (Thulasi et al. 2010) and tetraloops (Sheehy et al. 2010) were dominated by all purine nucleotides, 25.2% and 34.6%, respectively. However, for pentaloops, all purine hairpins were only the third most abundant at 7.1%.

Thermodynamic contributions of pentaloops to motif stability

As was the case for triloops and tetraloops, it is clear that stability is not the only determinant of pentaloop frequency in nature. For example, the third most frequent pentaloop in the secondary structure database, G(UAAGU)U, is the least stable (ΔG°_37,pentaloop = 5.74 kcal/mol) pentaloop measured in this study. On the other hand, the most stable pentaloop (2.58 kcal/mol) was only the 18th most frequent pentaloop in the secondary structure database, C(CUUGU)G. Additionally, there is very little difference in average stability between the pentaloops that were found frequently in the secondary structure database (4.3 ± 0.8 kcal/mol) and those that were not found in the secondary structure database (4.6 ± 0.5 kcal/mol).

Several trends emerged from the thermodynamic data which resulted in the updated model (Equation 3). Pentaloops with a C-G closing base pair (with the C on the 5′ side of the hairpin loop) were found to be more stable (average ΔG°_37,pentaloop of 3.5 kcal/mol) than pentaloops with other closing base pairs (average ΔG°_37,pentaloop of 4.7 kcal/mol). Pentaloops with a G-U closing base pair (with the G on the 5′ side of the hairpin loop) were found to be less stable (average ΔG°_37,pentaloop of 5.0 kcal/mol) than pentaloops with other closing base pairs (average ΔG°_37,pentaloop of 4.4 kcal/mol). Pentaloops with an A-A first mismatch were found to be less stable (average ΔG°_37,pentaloop of 4.8 kcal/mol) than pentaloops with other first mismatches (average ΔG°_37,pentaloop of 4.2 kcal/mol).

Updated model for predicting thermodynamics of pentaloops

Because we have collected thermodynamic data for 22 pentaloops that previously did not have experimental values, when predicting the free energy contributions of these pentaloops in an RNA stem–loop, the experimental values can be used. For pentaloops that still do not have experimental values, the predictive model (Equation 3) can be utilized.

The updated model for predicting thermodynamics of pentaloops is simple; the inclusion of bonuses and penalties (and the corresponding values) can be determined from sequence alone. Unlike the current model in Equations 1 and 2 (Vecenie and Serra 2004; Vecenie et al. 2006), the updated model does not require the calculated free energy change for the stacking of the first mismatch on the closing base pair. Not only is the new model simpler to use, but it also more accurately predicts the stability of the entire data set of pentaloops (0.42 vs. 0.26 kcal/mol average difference from experimental value). The higher accuracy is mostly likely due to the use of pentaloop data only, whereas the parameters of the current model were derived from several different sizes of hairpins and validated using a data set of hexaloops (Vecenie and Serra 2004; Vecenie et al. 2006). The new model is significantly better for certain subsets of the data. For example, ΔΔG°₃₇ values (difference between predicted and measured ΔG°₃₇ values) for pentaloops with a G·G first mismatch improved from 0.80 to 0.11 kcal/mol. Additional studies with more pentaloop sequences and adjacent base pairs may result in additional free energy bonuses/penalties. We recommend Equation 3 for predicting the stability of previously unmeasured pentaloops and the general Equations 1 and 2 for previously unmeasured hairpins of larger sizes.

MATERIALS AND METHODS

Compiling and searching a database for RNA pentaloops

In order to determine which pentaloop sequences to characterize thermodynamically, sequences were selected based on frequency of occurrence in a database of secondary structures. A database of 1349 RNA secondary structures, consisting of 123 small subunit rRNAs (Gutell 1994), 223 large subunit rRNAs (Gutell et al. 1993; Schnare et al. 1996), 309 5S rRNAs (Szymanski et al. 1998), 484 tRNAs (Sprinzl et al. 1998), 91 signal recognition particles (Larsen et al. 1998), 16 RNase P RNAs (Brown 1998), 100 group I introns (Waring and Davies 1984; Damberger and Gutell 1994), and three group II introns (Michel et al. 1989), was searched for pentaloops. During this search, G-U base pairs were considered canonical base pairs. Pentaloops were required to have canonical closing pairs. The number of occurrences for each type of pentaloop were tallied.

Design of sequences for optical melting studies

To be consistent with the Watson–Crick thermodynamic parameters and parameters for most other RNA secondary structure motifs, the melting buffer used in this work contained 1 M NaCl. A major limitation of a thermodynamic analysis of RNA hairpins using a high salt concentration is the possible bimolecular association of RNA strands. To ensure that unimolecular pentaloop formation out-competed bimolecular association in a 1 M NaCl solution, the following equations, derived from the equilibrium equations and ΔG° = −RT ln K (see SI for derivation of Equation 5), were utilized:

$$[\mathrm{H}]={\displaystyle \frac{-1+\sqrt{1+\left(\right(8{\mathrm{K}}_{\mathrm{D}}{\left[\mathrm{A}\right]}_{\mathrm{T}}\left)/\right({\mathrm{K}}_{\mathrm{H}}{\mathrm{K}}_{\mathrm{H}}\left)\right)}}{\left(4{\mathrm{K}}_{\mathrm{D}}\right)/({\mathrm{K}}_{\mathrm{H}}{\mathrm{K}}_{\mathrm{H}})}}$$ (5)

$$\left[\mathrm{D}\right]=({\left[\mathrm{A}\right]}_{\mathrm{T}}-[\mathrm{H}\left]\right)/2$$ (6)

$$\text{\%}H={\displaystyle \frac{\left[\mathrm{H}\right]}{\left(\left[\mathrm{H}\right]+\left[\mathrm{D}\right]\right)}\times 100}$$ (7)

Here, [H] is the concentration of hairpin, and %H is the percent hairpin in solution. [A]_T is the total concentration of strand, and [D] is the concentration of duplex. K_D and K_H are the equilibrium constants for duplex and hairpin formation, respectively. K_H and K_D values were calculated at 37°C using ΔG°₃₇ values predicted by RNAstructure (Reuter and Mathews 2010; Bellaousov et al. 2013) for hairpin and duplex formation, respectively. Calculations were done for [A]_T = 1 µM and 0.1 mM, which is the typical concentration range for the melting experiments. Due to potential competition from duplex formation, some of the most frequently occurring pentaloops were not studied here; only those that were likely to form pentaloops were used. All of the sequences studied here had %[H] > 92% at [A]_T = 0.1 mM and %[H] > 99% at [A]_T = 1 µM.

Sequences of pentaloops and closing base pairs were designed to represent those found in the database described above. Each stem contained three Watson–Crick pairs in addition to the closing base pair. The terminal base pair was always a G-C pair in order to prevent end fraying of the duplex during melting. The duplexes were also designed to have a melting temperature between 40°C and 75°C. Care was taken to design the stem–loop sequences so that the pentaloop of interest would form, with little competition from other secondary structure motifs.

RNA synthesis and purification

The oligonucleotides were ordered from Integrated DNA Technologies, Inc. and purified by column chromatography and thin-layer chromatography as described previously (Davis and Znosko 2007; Wright et al. 2007; Christiansen and Znosko 2008).

Optical melting experiments and thermodynamics

Optical melting experiments were performed in a buffer containing 1 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na₂EDTA at pH 7.0 with a Beckman-Coulter DU800 spectrophotometer from 10°C–90°C at 260 and 280 nm. All stem–loops were melted at least nine times with a ∼50-fold concentration range. Each stem–loop melting curve resulted in a single transition, and all melts of a given sequence were concentration independent, suggesting stem–loop formation. Stem–loop thermodynamics were determined by averaging the thermodynamics derived from each individual curve fit using MeltWin 3.5 (McDowell and Turner 1996) in order to derive enthalpy (ΔH°), entropy (ΔS°), melting temperature (T_m), and free energy (ΔG°₃₇) values. The free energy contribution of the pentaloop (ΔG°_37,pentaloop) was calculated by subtracting the canonical pair contribution of the stem (Xia et al. 1998; Chen et al. 2012) from the measured ΔG°₃₇ values for the stem–loops. Stem sequences in which the terminal pair of the stem (or the pentaloop closing base pair) is A-U or U-A utilize the 0.45 kcal/mol terminal A-U penalty (Xia et al. 1998) when calculating the contribution of the canonical pairs in the stem. The inclusion of this penalty here is likely the reason why no additional terminal pair bonuses or penalties emerged from the analysis of the pentaloop data.

Linear regression and pentaloop thermodynamic parameters

Experimental data for the 22 hairpins measured here were combined with data for nine previously published pentaloops (Serra et al. 1997; Giese et al. 1998), which were also melted in 1 M NaCl. A new predictive model for pentaloops was derived using the LINEST function (linear regression) in Microsoft Excel. The calculated experimental contribution of the pentaloop to stem–loop stability was used as a constant when doing linear regression. Many combinations of variables, including a parameter for a U·U, G·G, G·A, pyrimidine·pyrimidine, and purine·purine first mismatch and a parameter for pyrimidine or purine as the middle nucleotide in the loop, were tested, with the best combination of variables resulting in the simple, highly accurate model described in the “Results” section. The robustness of the predictive model was tested by removing individual pentaloops and small sets of pentaloops that were not predicted well by the original model and rederiving a new model. In the cases that we tested, removing data resulted in ΔΔG°₃₇ values that improved by <0.1 kcal/mol (data not shown). As a result, the predictive model using all of the data is presented here.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.

MEET THE FIRST AUTHOR

Md. Sharear Saon.

Meet the First Author(s) is a new editorial feature within RNA, in which the first author(s) of research-based papers in each issue have the opportunity to introduce themselves and their work to readers of RNA and the RNA research community. Sharear Saon is the first author of this paper, “Thermodynamic characterization of naturally occurring RNA pentaloops.” Sharear is a fifth-year graduate student working in Dr. Znosko's laboratory in the Department of Chemistry at Saint Louis University. His research projects are focused on the study of RNA structure and stability.

What are the major results described in your paper and how do they impact this branch of the field?

In this work, thermodynamic parameters for 22 naturally occurring sequences are reported. For previously unmeasured pentaloop sequences, the model developed here can be used. The new model can predict the stability of pentaloops more accurately than the current model proposed in Vecenie et al. The average difference between experimental and predicted free energy of pentaloop formation was 0.42 and 0.26 kcal/mol for current and new model, respectively. This improved model can be incorporated into software used to predict secondary structure from sequence.

What led you to study RNA or this aspect of RNA science?

I began studying RNA because I was fascinated with the diverse functionalities of RNA. This fascination convinced me to pursue research investigating RNA structure and stability in the hopes that this research can help explain the functionalities of RNA.

If you were able to give one piece of advice to your younger self, what would that be?

I would advise myself to read more articles from fields outside my research interest. This would broaden my knowledge and give me different perspectives.

Are there specific individuals or groups who have influenced your philosophy or approach to science?

I first learned about John Nash from the movie, A Beautiful Mind. The most important lesson I have learned from John Nash is that, regardless of the obstacles, dedication and focus can help us achieve our dreams, or in some cases, achieve beyond our dreams.

What are your subsequent near- or long-term career plans?

Right after my defense, I want to explore more in the field of RNA structure and function. Long term, through my own research group, I want to develop tools to perform predictive analyses on RNA structure and function.