Improving large‐scale estimation and inference for profiling health care providers

Abstract

Provider profiling has been recognized as a useful tool in monitoring health care quality, facilitating inter‐provider care coordination, and improving medical cost‐effectiveness. Existing methods often use generalized linear models with fixed provider effects, especially when profiling dialysis facilities. As the number of providers under evaluation escalates, the computational burden becomes formidable even for specially designed workstations. To address this challenge, we introduce a serial blockwise inversion Newton algorithm exploiting the block structure of the information matrix. A shared‐memory divide‐and‐conquer algorithm is proposed to further boost computational efficiency. In addition to the computational challenge, the current literature lacks an appropriate inferential approach to detecting providers with outlying performance especially when small providers with extreme outcomes are present. In this context, traditional score and Wald tests relying on large‐sample distributions of the test statistics lead to inaccurate approximations of the small‐sample properties. In light of the inferential issue, we develop an exact test of provider effects using exact finite‐sample distributions, with the Poisson‐binomial distribution as a special case when the outcome is binary. Simulation analyses demonstrate improved estimation and inference over existing methods. The proposed methods are applied to profiling dialysis facilities based on emergency department encounters using a dialysis patient database from the Centers for Medicare & Medicaid Services.

1. INTRODUCTION

The variable nature of the U.S. health care system has raised public concerns regarding the quality of care. ¹ In an effort to accommodate the growing demand for accountability in care delivery, provider profiling, that is, the identification of outlying care providers with particularly high or low rates, ² has been implemented in monitoring the structure, processes and outcomes of health care by regulatory organizations. ³ , ⁴ , ⁵ As one such organization, the Centers for Medicare & Medicaid Services (CMS) administers quality programs to evaluate care providers, ⁶ with the aim of assuring quality care for beneficiaries and controlling medical costs. Established by the Medicare Improvements for Patients and Providers Act, the CMS End‐Stage Renal Disease (ESRD) Quality Incentive Program (QIP) promotes high‐quality services in kidney dialysis facilities by linking payments for treating patients to facilities' performance on a spectrum of quality measures. ⁷ The QIP will reduce payments to facilities unable to meet certain standards, motivating them to improve their services. Thus, accurate provider profiling is a high‐stakes endeavor.

Among the various patient outcomes used in the ESRD QIP, emergency department (ED) encounters are an important indicator of care delivery, quality of life, and cost effectiveness. ⁸ Lovasik et al ⁹ reported that ESRD patients have on average 2.68 ED visits per patient‐year, six‐fold higher than the national mean rates for U.S. adults, with care access as a preventable cause of ED use; Zhang et al ¹⁰ showed that ED visit rates for patients on thrice‐weekly hemodialysis are highest after the interdialytic interval over the weekend, suggesting that the ED visit rate is associated with the dialysis schedule; Cohen et al ¹¹ found that missed dialysis treatments are associated with a high risk of an ED visit, suggesting an opportunity for facilities to reduce skipped treatments and ED visits through improved care coordination. Our endeavors in this article are motivated by profiling dialysis facilities on ED encounters and seek to resolve two associated statistical challenges.

Current approaches to profiling providers typically relate the outcome of interest to risk factors using generalized linear models (GLMs) with fixed ¹² , ¹³ , ¹⁴ , ¹⁵ or random provider effects. ² , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ The fixed effects approach shall be our primary focus here, since it has been used by CMS in profiling dialysis facilities, and has been recognized as less affected by shrinkage estimation than the random effects approach in handling the confounding of patient‐level risk factors with provider‐level effects when identifying outlying providers. ¹³ , ¹⁴ , ²¹ , ²²

Despite the estimation advantage, using fixed effects models poses a computational challenge to large‐scale profiling applications: existing GLM‐oriented algorithms such as Newton‐Raphson and Fisher scoring ²³ developed for general‐purpose model fitting cannot fulfill the computational task as the number of providers escalates along with the sample size (eg, 7232 dialysis facilities with 757 086 hospital discharges in our application of ED visits). When thousands of provider effects are admitted into the parameter space, the computational cost of inverting the Fisher information matrix dramatically increases, and imposes a formidable burden even on specially designed workstations. In light of this hardship, He et al ¹² introduced a block ascent Newton (BAN) algorithm, a block relaxation approach ²⁴ , ²⁵ , ²⁶ to sequentially updating provider effects and parameters of risk factors. Approximating the Fisher information by a block diagonal matrix, the BAN relieves the memory burden at the expense, however, of prolonged convergence. Some routine tasks involving resampling‐based model refitting, for example, assessing the reliability of quality measures associated with the performance of care providers, ²⁷ , ²⁸ are still computationally infeasible using the time‐consuming BAN.

To tackle the challenge of large‐scale model fitting for provider profiling, we propose a serial blockwise inversion Newton (SerBIN) algorithm. Exploiting the block structure of the Fisher information matrix, the SerBIN substantially reduces the time complexity of inverting that high‐dimensional matrix when thousands of provider effects are present. The algorithm also allows joint updating of a large number of provider effects and other parameters, leading to cost‐efficient scalability and fast convergence. Employing the divide‐and‐conquer (DAC) strategy in a shared‐memory context, a novel parallelization of the SerBIN is developed to further reduce the computational burden, especially when the sample size grows beyond one million. By splitting the intensive task of computing the information submatrix for regression coefficients into a series of lightweight inner product calculations, the computational efficiency is further improved without extra hardware requirements.

In addition to the computational issue, current literature lacks a distribution‐based inferential approach to detecting providers with outlying performance. Traditional testing procedures, including the score and Wald tests, are based on the asymptotic distribution of the test statistics. In the presence of small providers with near‐zero variation in outcomes, these large‐sample techniques can lead to poor approximations of the small‐sample distributions. ²⁹ , ³⁰ As He et al ¹² pointed out, for a small provider with invariant outcomes, its effect estimate tends to infinity with an invalid Wald test statistic.

To bypass unwarranted large‐sample approximations, we propose an exact test of provider effects using finite‐sample distributions specific to outcome types. When the outcome is binary, the tail probabilities can be calculated according to the Poisson‐binomial distribution. ³¹ , ³² Compared with the score and Wald tests, the exact test achieves improved power with controlled type I error, even if patient‐level risk factors are correlated with the corresponding provider effect. Unlike resampling‐based methods, ¹² , ¹⁴ the proposed exact test, as a distribution‐based approach, is computationally scalable to data sets of extraordinarily large sample size and provider count, and is free from resampling‐induced arbitrariness in provider flagging.

The remainder of the article is structured as follows: Section 2 introduces a GLM framework and presents the SerBIN algorithm and its shared‐memory DAC parallelization. Section 3 develops the distribution‐based exact test. Sections 4 and 5 evaluate the proposed methods through simulations and an application to a national ED visits database for Medicare beneficiaries on dialysis. Section 6 concludes with a discussion (the SerBIN, DACBIN, and exact tests are implemented as an Rpackage FEprovideR available at https://cran.r‐project.org/package=FEprovideR).

2. MODEL AND ESTIMATION

Before delving into the estimation strategy, we briefly introduce a GLM of the outcome of interest on fixed provider effects and risk factors.

2.1. Model

Let $m$ denote the total number of providers, let $n_i$ be the number of subjects from provider $i$ ($i=1,\dots ,m$), and let $n:={\sum }_{i=1}^m{n}_i$ be the total count. For subject $j$ ($j=1,\dots ,n_i$) of provider $i$, let $Y_{ij}$ denote the outcome variable, and let ${\mathbf{Z}}_{ij}$ be a $p\times 1$ vector of risk factors. We assume that given ${\mathbf{Z}}_{ij}$, outcome $Y_{ij}$ follows a distribution in the exponential family with parameters ${\omega }_{ij}$ and $\varphi$, that is,

$$\pi (Y_{ij}|{\mathbf{Z}}_{ij};{\omega }_{ij},\varphi )\propto \exp \left\{\frac{Y_{ij}{\omega }_{ij}-b({\omega }_{ij})}{a(\varphi )}\right\},$$ (1)

for known functions $a$ and $b$ with $\mathrm{E}(Y_{ij}|{\mathbf{Z}}_{ij};{\omega }_{ij})=\dot{b}({\omega }_{ij})$, where the dot notation denotes differentiation with respect to ${\omega }_{ij}:={\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta }$, a linear predictor relating to provider effect ${\gamma }_i$ and coefficients $\mathit{\beta }$ of risk factors. The specification of $a$ and $b$ is subject to the type of outcome $Y_{ij}$. In this article, we focus on the commonly encountered normal, binary, and Poisson outcomes in provider profiling, which correspond to the canonical identity, logit, and log links, respectively. Given the observed data $\{(Y_{ij},{\mathbf{Z}}_{ij}):i=1,\dots ,m,j=1,\dots ,n_i\}$, we have the log‐likelihood

$$\ell (\mathit{\gamma },\mathit{\beta })\propto \sum _{i=1}^m\sum _{j=1}^{n_i}\left\{Y_{ij}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta })-b({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta })\right\},$$ (2)

where $\mathit{\gamma }={[{\gamma }_1,\dots ,{\gamma }_m]}^{\top }$. The score and the Fisher information matrix of (2) are available in Appendix A of the Supporting Information.

2.2. Serial blockwise inversion Newton algorithm

In our application, fitting model (1) amounts to estimating 7232 facility effects and 86 regression parameters. Using the classical Newton‐Raphson algorithm, this estimation requires inverting a large information matrix with 7318 rows and columns, a computational challenge that existing software packages cannot handle. Inspired by analyses of Prentice and Gloeckler ³³ and Kalbfleisch and Prentice, ³⁴ we propose a serial blockwise inversion Newton (SerBIN) algorithm, which takes advantage of the diagonal information submatrix $ℐ(\mathit{\gamma })$ of facility effects. Let $\circ$ denote the Hadamard product, and $k\in \{0\}\cup \mathbb{N}$ index iterations. With the notation in Appendix A of the Supporting Information, we present the SerBIN as Algorithm 1, in which $\mathit{\theta }:={[{\mathit{\gamma }}^{\top },{\mathit{\beta }}^{\top }]}^{\top }$. The global convergence of the SerBIN is guaranteed with mild assumptions. Details can be found in Boyd and Vandenberghe. ³⁵

Algorithm 1. Serial blockwise inversion Newton (SerBIN).

1.

A primary advantage of SerBIN is the improved Newton step $\mathrm{\Delta }\mathit{\theta }={ℐ}^{-1}(\mathit{\theta })𝒰(\mathit{\theta })$ in Lines 8 and 9 of Algorithm 1. Let ${ℐ}_{11},{ℐ}_{12},{ℐ}_{21},{ℐ}_{22}$ denote the four blocks of $ℐ(\mathit{\theta })$. Then, from the blockwise inversion formula, ³⁵ we have

$${ℐ}^{-1}(\mathit{\theta })=\left[\begin{array}{cc}{ℐ}_{11}^{-1}+{𝒥}_1^{\top }{𝒮}^{-1}{𝒥}_2,& -{𝒥}_2^{\top }\\ -{𝒥}_2,& {𝒮}^{-1}\end{array}\right],$$ (3)

where ${𝒥}_1:={ℐ}_{21}{ℐ}_{11}^{-1}$, $𝒮:={ℐ}_{22}-{𝒥}_1{ℐ}_{12}$ is the Schur complement of ${ℐ}_{11}:=ℐ(\mathit{\gamma })$, a diagonal submatrix ($7\text{,}232\times 7\text{,}232$ in our application) of $ℐ(\mathit{\theta })$, and ${𝒥}_2:={𝒮}^{-1}{𝒥}_1$. As a space‐time trade‐off, ${𝒥}_1$, ${𝒮}^{-1}$ and ${𝒥}_2$ in Lines 5‐7 of Algorithm 1 are temporarily stored in memory to avoid repetitive computing. Specifically, ${𝒥}_1$, although defined as a matrix product, can instead be calculated by multiplying each column of ${ℐ}_{21}$ with the corresponding diagonal element of ${ℐ}_{11}^{-1}$, which reduces the cost from $O(m^{2}p)$ to $O(mp)$. With $ℐ(\mathit{\theta })$ as the input, computing $\mathrm{\Delta }\mathit{\theta }$ via (3) costs $O(m{p}^2+p^3)$, much less than $O({(m+p)}^3)$ resulting from a naive Newton‐Raphson algorithm given that $m\gg p$. Because of this efficiency gain, the SerBIN outperforms existing Newton‐Raphson implementations such as glm in R ³⁶ or the GENMOD procedure in SAS® (left panel of Figure 1), both of which result in a system crash with out‐of‐memory errors when applied to the ED visits data. Backtracking line search ³⁵ allowing flexible step size determination is introduced in Lines 10‐12 of Algorithm 1 to handle nearly singular instances of $ℐ(\mathit{\theta })$.

FIGURE 1.

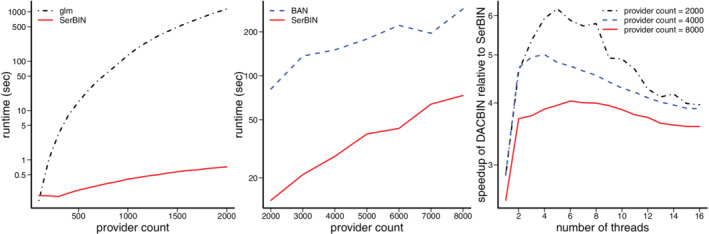
(1) Runtime of SerBIN and glm with provider counts varying from 100 to 2000 (left). To accommodate large provider counts for glm, experiments were conducted on an Intel® Xeon® Gold 6254 quad‐processor with base frequency 3.1GHz and RAM 576GB. SerBIN was implemented using Rcpp and RcppArmadillo. ³⁷ , ³⁸ , ³⁹ Three covariates were included in model fitting with $\mathit{\beta }={[1,0.5,-1]}^{\top }$. The vertical axis is set as the base‐10 log scale. (2) Runtime of SerBIN and BAN with provider counts varying from 2000 to 8000 (middle). Experiments conducted on an Intel® Core^TM i9‐9900K processor with base frequency 3.6GHz and RAM 16GB. BAN was implemented using Rcpp and RcppArmadillo. A design matrix of 100 covariates was drawn based on (6), and then dichotomized column‐wise according to the column median. Regression parameters $\mathit{\beta }$ were jointly sampled from a standard multivariate normal distribution. (3) Speedup of DACBIN relative to SerBIN with various thread and provider counts (right). Speedup with a given number of threads is defined as the ratio of the runtime of SerBIN to the runtime of DACBIN. Experiments conducted on the Intel^® Core^TM i9‐9900K processor with 100 covariates generated as in (2). DACBIN was implemented using Rcpp and RcppArmadillo

In a related setting, He et al ¹² proposed a block ascent Newton (BAN) algorithm as an instance of block relaxation methods: ²⁴ , ²⁵ , ²⁶ the information matrix $ℐ(\mathit{\theta })$ is substituted by a block diagonal matrix $\text{diag}(ℐ(\mathit{\gamma }),ℐ(\mathit{\beta }))$, and $\mathit{\gamma }$ and $\mathit{\beta }$ are sequentially updated using the Newton‐Raphson algorithm. Feasible as an alternative approach to circumventing the direct inversion of $ℐ(\mathit{\theta })$, the sequential updating scheme omitting the off‐diagonal elements of $ℐ(\mathit{\theta })$ gives rise to prolonged convergence. By contrast, SerBIN jointly updates $\mathit{\gamma }$ and $\mathit{\beta }$ and requires far fewer iterations than BAN before termination. This advantage enables SerBIN to outperform BAN in terms of time to convergence (middle panel of Figure 1), and considerably reduces the computational cost of resampling‐based reliability assessments of quality measures. ²⁷ , ²⁸

To demonstrate the advantage of the proposed algorithm via simulations, we compare SerBIN with glm and BAN in terms of runtime (time to convergence) and display the results in Figure 1. With provider counts ranging from 100 to 2000 in the left panel, SerBIN has its runtime no greater than one second, while the runtime of glm increases dramatically to over 1000 s. With larger provider counts and more covariates, the middle panel of Figure 1 suggests that on average, SerBIN is five times as fast as BAN. When applied to the ED visits data (see Section 5), the advantage of SerBIN over BAN becomes more pronounced: on an Intel® Xeon® Gold 6254 quad‐processor, the former ends within 10 s, while the latter takes nearly 40 min to converge. Although the runtime of an algorithm generally depends upon the coding decisions in the implementation as well as the characteristics of the data in question (eg, binary predictors with near‐zero variance), the marked difference in runtime adds to the computational efficiency of the SerBIN.

2.3. Shared‐memory DAC algorithm

A time‐complexity analysis reveals that at each iteration, computing ${ℐ}_{22}=ℐ(\mathit{\beta })$ (or ${𝒥}_1{ℐ}_{21}^{\top }$) in Line 6 of Algorithm 1 costs $O(n{p}^2)$, which becomes a bottleneck of SerBIN when sample size $n$ is extraordinarily large. To further boost computational efficiency, we introduce the notion of DAC to the calculation of $ℐ(\mathit{\beta })$, taking advantage of the ubiquitous shared‐memory multicore computer architecture.

Observe that the original task of computing $ℐ({\mathit{\beta }}^{(k)})$ at iteration $k$ of Algorithm 1 can be evenly divided into $p^2$ smaller tasks of computing vector inner products, as suggested by the following reformulation:

$$ℐ({\mathit{\beta }}^{(k)})=\sum _{i=1}^m\sum _{j=1}^{n_i}\ddot{b}({\gamma }_i^{(k)}+{\mathbf{Z}}_{ij}^{\top }{\mathit{\beta }}^{(k)}){\mathbf{Z}}_{ij}{\mathbf{Z}}_{ij}^{\top }=(⟨{\mathbf{Z}}^r,{\mathbf{Z}}^c\circ {ℐ}^{(k)}⟩),$$

where $⟨{\mathbf{Z}}^r,{\mathbf{Z}}^c\circ {ℐ}^{(k)}⟩$, an inner product of ${\mathbf{Z}}^r$ and ${\mathbf{Z}}^c\circ {ℐ}^{(k)}$, is the $rc$th element of $ℐ({\mathit{\beta }}^{(k)})$, with ${\mathbf{Z}}^c$ denoting the $c$th column of the $n\times p$ matrix $\mathbf{Z}$ of risk factors, and ${ℐ}^{(k)}$ denoting the vector of $\ddot{b}({\gamma }_i^{(k)}+{\mathbf{Z}}_{ij}^{\top }{\mathit{\beta }}^{(k)})$. Since $ℐ({\mathit{\beta }}^{(k)})$ is a symmetric matrix, it suffices to only compute the $p(p+1)/2$ upper triangular entries of $ℐ({\mathit{\beta }}^{(k)})$. Letting $C\le p(p+1)/2$ be the number of threads scheduled for conquering the $p(p+1)/2$ sub‐tasks in parallel, we present as Algorithm 2 the DAC algorithm of computing $ℐ({\mathit{\beta }}^{(k)})$, with $\{\ddot{b}({\gamma }_i^{(k)}+{\mathbf{Z}}_{ij}^{\top }{\mathit{\beta }}^{(k)}):i=1,\dots ,m,j=1,\dots ,n_i\}$ and $\mathbf{Z}$ as inputs at iteration $k$ of Algorithm 1. Similarly, ${𝒥}_1{ℐ}_{21}^{\top }$ can also be computed in a DAC fashion. The improved Algorithm 1, embedded with the DAC algorithm of computing $ℐ(\mathit{\beta })$ and ${𝒥}_1{ℐ}_{21}^{\top }$, is hence called a DACBIN algorithm. The computational gain of DACBIN compared to SerBIN is illustrated by simulation experiments in the right panel of Figure 1.

Algorithm 2. DAC computation of $ℐ(\mathit{\beta })$ .

1.

Before the DAC steps in Algorithm 2, Lines 1‐9 establish a one‐to‐one mapping between the one‐dimensional sub‐task index $id=1,\dots ,p(p+1)/2$, and the two‐dimensional index of the upper triangular portion of $ℐ(\mathit{\beta })$ on a row‐major basis. In practice, scheduling the $p(p+1)/2$ parallel tasks on $C$ threads can be readily achieved by most shared‐memory application programming interfaces (eg, OpenMP® and Intel® Threading Building Blocks®). Because of the memory‐efficient communication in a shared‐memory parallel computing scheme, the DACBIN, designed for large‐scale data sets, is applicable on desktop workstations with moderate hardware configurations and common operating systems.

Using three levels of provider counts, the right panel of Figure 1 shows that the optimal levels of speedup of DACBIN relative to SerBIN are achieved at different thread counts. In particular, given only 6 threads, the parallel DACBIN is 3 times faster than the serial SerBIN when 8000 providers are present.

3. EXACT‐TEST‐BASED PROVIDER PROFILING

When identifying outlying providers with extreme outcomes, it is of particular interest to know whether a provider effect is significantly different from an effect of reference. This amounts to testing the null hypothesis that $H_{0i}:{\gamma }_i={\gamma }_{\mathrm{M}}$ with a prespecified ${\gamma }_{\mathrm{M}}$. In our application of ED visits, for instance, ${\gamma }_{\mathrm{M}}$ is the provider effect of a population average provider, called population norm and defined as the median of $\mathit{\gamma }$. This median reference effect is more robust than the average and has been applied in some profiling analyses. ¹² , ¹⁴ , ¹⁵ Existing inferential procedures used for identifying outlying providers, including the score and Wald tests, largely rely on the asymptotic distribution of the test statistics. When, however, there are many small providers with few subjects and little variation in the outcomes, these large‐sample techniques can lead to poor approximations of the finite‐sample distributions. ²⁹ , ³⁰ Assuming that the outcomes $\{Y_{ij}:j=1,\dots ,n_i\}$ from provider $i$ are independent given risk factors ${\mathbf{Z}}_i={[{\mathbf{Z}}_{i1}^{\top },\dots ,{\mathbf{Z}}_{i{n}_i}^{\top }]}^{\top }$ and the provider effect ${\gamma }_i$, we propose an exact test of the null $H_{0i}$, leveraging the conditional distribution of $O_i:={\sum }_{j=1}^{n_i}{Y}_{ij}$ given ${\mathbf{Z}}_i$. Since the estimation of $\mathit{\beta }$ involves a large number of subjects according to (2), we assume that $\widehat{\mathit{\beta }}$ is sufficiently accurate to replace $\mathit{\beta }$. Ruling out the variation of $\mathit{\beta }$, this assumption validates the calculation of tail probabilities under the null. Similar treatments have been adopted in the literature. ¹² , ¹⁴ , ¹⁵ , ⁴⁰ Depending on the type of outcome $Y_{ij}$, we consider three commonly encountered scenarios of the distribution of $O_i$ given ${\mathbf{Z}}_i$:

If outcome $Y_{ij}$ is normal, we have $O_i|{\mathbf{Z}}_i\sim 𝒩({\sum }_{j=1}^{n_i}\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta }),n_i{\sigma }^2)$. With an unbiased estimator ${\widehat{\sigma }}^2:={(n-m-p)}^{-1}{\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{(Y_{ij}-{\widehat{\gamma }}_i-{\mathbf{Z}}_{ij}^{\top }\widehat{\mathit{\beta }})}^2$, we further assume that ${\sigma }^2$ is fixed at ${\widehat{\sigma }}^2$. The cumulative distribution function (CDF) of $O_i$ conditional on ${\mathbf{Z}}_i$ can be written as

$$F_i(o;{\gamma }_i,\mathit{\beta })=\frac{1}{\sqrt{2\pi n_i{\widehat{\sigma }}^2}}{\int }_{-\infty }^o\exp \left\{-\frac{1}{2n_i{\widehat{\sigma }}^2}{\left[x-\sum _{j=1}^{n_i}\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta })\right]}^2\right\}\mathrm{d}x,o\in ℝ.$$

When $Y_{ij}$ is binary, we have $Y_{ij}|{\mathbf{Z}}_i\sim \text{Bernoulli}(\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta }))$. It follows that $O_i|{\mathbf{Z}}_i$ has a Poisson‐binomial distribution. Letting $S_i:=\{1,\dots ,n_i\}$, the CDF of $O_i$ conditional on ${\mathbf{Z}}_i$ is

$$F_i(o;{\gamma }_i,\mathit{\beta })=\sum _{l=0}^o\sum _{A_i\in {𝒜}_{il}}\left\{\prod _{a\in A_i}\dot{b}({\gamma }_i+{\mathbf{Z}}_{ia}^{\top }\mathit{\beta })\prod _{q\in A_i^c}[1-\dot{b}({\gamma }_i+{\mathbf{Z}}_{iq}^{\top }\mathit{\beta })]\right\},o\in \{0\}\cup S_i,$$ (4)

where ${𝒜}_{il}:=\{A_i\subset S_i:|A_i|=l\}$, and $A_i^c:=S_i\setminus A_i$.

When $Y_{ij}$ is Poisson, that is, $Y_{ij}|{\mathbf{Z}}_i\sim \text{Poisson}(\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta }))$, we have $O_i|{\mathbf{Z}}_i\sim \text{Poisson}({\sum }_{j=1}^{n_i}\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta }))$. The CDF of $O_i$ given ${\mathbf{Z}}_i$ is

$$F_i(o;{\gamma }_i,\mathit{\beta })=\frac{1}{o!}{\left[\sum _{j=1}^{n_i}\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta })\right]}^o\exp \left\{-\sum _{j=1}^{n_i}\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta })\right\},o\in \{0\}\cup \mathbb{N}.$$

Provided the CDFs above, the mid $P$‐value $P_i$ associated with a two‐sided exact test against the null $H_{0i}$ is given by

$$P_i=2·\min \{G_i(O_i;{\gamma }_{\mathrm{M}},\widehat{\mathit{\beta }}),1-G_i(O_i;{\gamma }_{\mathrm{M}},\widehat{\mathit{\beta }})\},$$ (5)

where $G_i(o;{\gamma }_i,\mathit{\beta }):=F_i(o;{\gamma }_i,\mathit{\beta })-0.5\mathrm{Pr}(O_i=o|{\mathbf{Z}}_i;{\gamma }_i,\mathit{\beta })$ is a sub‐CDF of $F_i(o;{\gamma }_i,\mathit{\beta })$. Note that $G_i(O_i;{\gamma }_{\mathrm{M}},\widehat{\mathit{\beta }})$ is equal to $F_i(O_i;{\gamma }_{\mathrm{M}},\widehat{\mathit{\beta }})$ when $Y_{ij}$ is normal. With $\alpha \in (0,1)$, a $100(1-\alpha )\%$ confidence interval of provider effect ${\gamma }_i$ can be constructed based on Fleiss et al. ⁴¹ The lower limit ${\bar{\gamma }}_i$ and upper limit ${\bar{\gamma }}_i$ of the confidence interval are determined by $G_i(O_i;{\bar{\gamma }}_i,\widehat{\mathit{\beta }})=1-{\alpha }_1$ and $G_i(O_i;{\bar{\gamma }}_i,\widehat{\mathit{\beta }})={\alpha }_2$ where ${\alpha }_1,{\alpha }_2\in [0,1)$ with ${\alpha }_1+{\alpha }_2=\alpha$.

Since the exact tests for normal and Poisson outcomes are based on the well‐studied normal and Poisson distributions, we will exclusively focus on binary outcomes throughout the rest of this article.

4. SIMULATION STUDY

We perform simulation‐based evaluations of the proposed estimation and inference methods. In each scenario, we generate 1000 data replicates. Provider‐specific discharge counts are drawn from $\text{Poisson}(80)$ and left‐truncated by 11. Provider effects are independently drawn from a normal distribution $𝒩(\mu ,{\sigma }^2)$. With calibrations based on the ED visits data, we set $\mu =\log (4/11)$ and $\sigma =0.4$. Following Kalbfleisch and Wolfe, ¹³ subject‐specific covariates ${\mathbf{Z}}_{ij}$ are generated according to

$${\mathbf{Z}}_{ij}|{\gamma }_i\sim 𝒩\left((\rho /\sigma )({\gamma }_i-\mu )\mathbf{w},\mathbf{\Omega }-{\rho }^2\mathbf{J}\right),j=1,\dots ,n_i,$$ (6)

where $\rho \in [0,1)$, $\mathbf{\Omega }$ is a $p\times p$ matrix with diagonal ones and off‐diagonal $\rho$'s, $\mathbf{w}$ is a $p\times 1$ vector of ones, and $\mathbf{J}$ is a $p\times p$ matrix of ones. Consequently, we have $\text{Corr}({\mathbf{Z}}_{ij},{\gamma }_i)=\rho \mathbf{w}$ and ${\mathbf{Z}}_{ij}\sim 𝒩(\mathbf{0},\mathbf{\Omega })$. Regression coefficients $\mathit{\beta }$ are drawn from a standard multivariate normal distribution. The outcome $Y_{ij}$ is sampled from $\text{Bernoulli}(\dot{b}({\gamma }_i+{\mathbf{Z}}_{ij}^{\top }\mathit{\beta }))$, where $\dot{b}$ denotes the logistic function.

The proposed exact test is compared with the score and Wald tests in terms of type I error, power, and coverage probability. To compute the CDF (4), we use an R package poibin, ⁴² an implementation based on the discrete Fourier transform of the characteristic function of the Poisson‐binomial distribution. ⁴³

Panel A of Figure 2 displays left‐ and right‐tailed type I error rates associated with the three tests at varied levels of correlation $\rho$. When the provider size is small ($n_1=11$), the exact test has its two‐tailed error rates closest to the nominal level $\alpha =0.05$. By contrast, the type I error rates of the score test are consistently greater than 0.05, while those of the Wald test are less than 0.05. Regarding the difference between left‐ and right‐tailed error rates, we observe that the score and Wald tests have more skewed one‐tailed error rates than the exact test. When the provider size grows large ($n_1=50$), the score test still barely controls its overall type I error, and the Wald test remains conservative. One‐tailed error rates become more balanced for all three tests. Two‐tailed type I error rates for the three tests are available in Appendix C of the Supporting Information.

FIGURE 2.

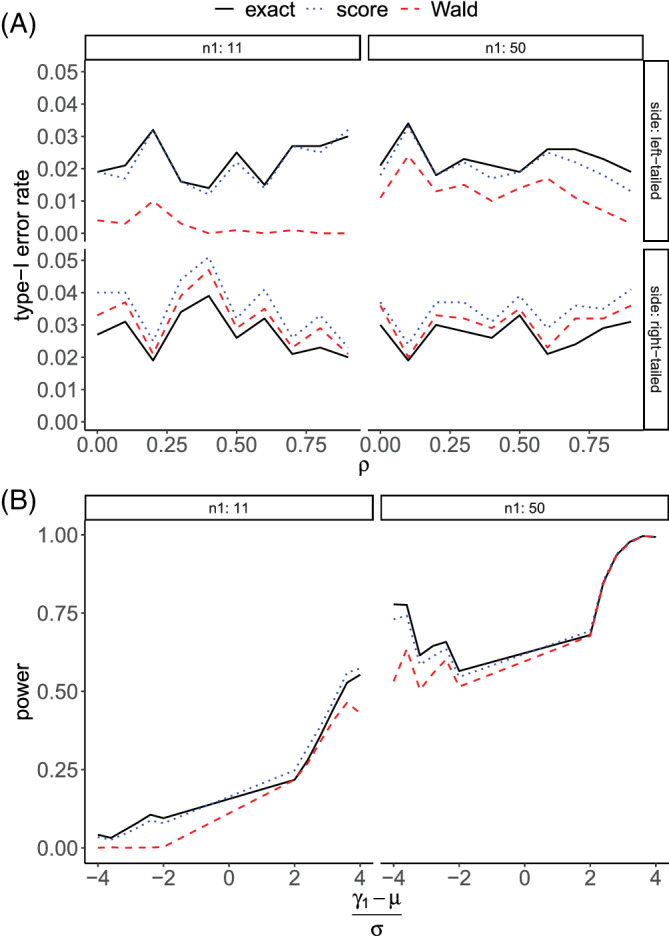
Type I error rates and powers of exact, score and Wald tests. All values were calculated based on 1000 independent replicates with $m=100$, ${\sigma }^2=0.16$, and significance level $\alpha =0.05$. With correlation $\rho$ varying from 0 to 0.9, rates in Panel A were obtained assuming ${\gamma }_1={\gamma }_{\mathrm{M}}=\mu =\log (4/11)$. In Panel B, correlation was fixed at $\rho =0.5$, whereas ${\gamma }_1$ is allowed to vary in terms of relative deviation $({\gamma }_1-\mu )/\sigma$

Panel B of Figure 2 provides power calculations at different levels of relative deviation of provider effect $({\gamma }_1-\mu )/\sigma$. Except when $n_1=11$ and the deviation is negative, the test power increases as relative deviation grows in magnitude. The exact test consistently exhibits higher power than the other two for negative relative deviation. When the deviation is positive, the power of the exact test becomes slightly lower than that of the score test, largely due to the inflated type I error shown in Panel A.

Figure 3 presents coverage probabilities of confidence intervals from test inversion with varying levels of correlation $\rho$ and relative deviation of ${\gamma }_1$, the effect of the first provider. Since the number of providers does not systematically affect testing a single facility effect, we use a fixed number of $m=100$ providers in each of the 1000 simulated data sets, and a fixed number of $n_1=11$ subjects in the first provider. The three panels in the first row indicate that when the provider effect ${\gamma }_1$ is at least $2\sigma$ smaller than $\mu$, the coverage probabilities of the score and Wald tests can be far below the nominal level of 0.95. Throughout the remaining six plots, each coverage probability curve of the score test lies between the curves of the other two tests. This confirms the liberality of the score test and the conservativeness of the Wald test.

FIGURE 3.

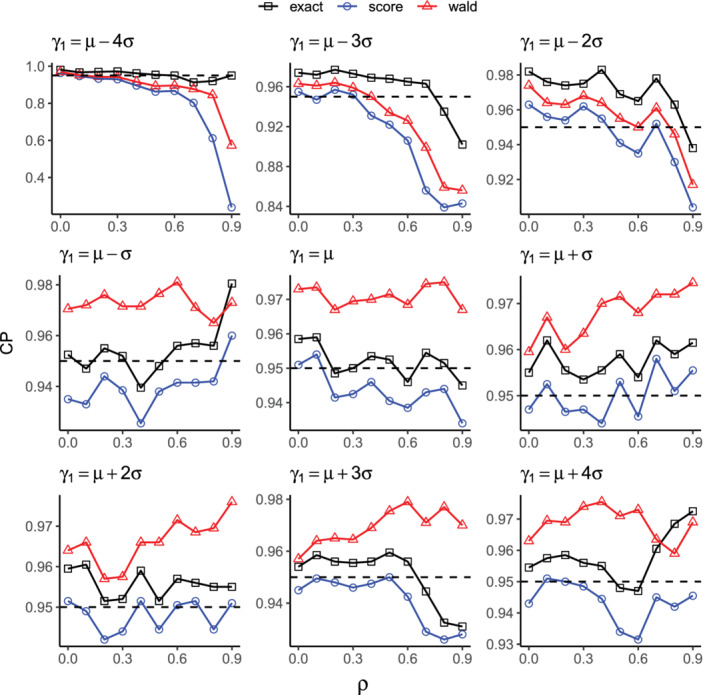
Coverage probability (CP) vs correlation $\rho$ with varying levels of provider effect ${\gamma }_1$. In each scenario, 1000 data sets are simulated with $m=100$ providers, with the first provider having $n_1=11$ subjects

5. APPLICATION

We evaluate the proposed estimation and inference methods through profiling dialysis facilities according to ED encounters within 30 days of hospital discharge. The data set was extracted from the Medicare administrative claims database for ESRD patients on dialysis. It contained 7232 Medicare‐certified dialysis facilities with 757 086 qualifying discharges in 2018 and 2019. These facilities had discharges varying from 11 to 842 (mean 104.7) and ED visits from 0 to 130 (mean 16.95). Corresponding to a hospital discharge, each record consists of patient demographics, clinical characteristics, and prevalent comorbidities as risk factors. Prevalent comorbidities were determined using the previous 12 months of Medicare Part A claims (inpatient hospital care, skilled nursing facility care, skilled home health care, and hospice care). ⁴⁴ Individual comorbidities were then grouped into categories based on the Agency for Healthcare Research and Quality Clinical Classifications Software. ⁴⁵ Each comorbidity category was included as a separate risk factor in the model. Since facilities have little opportunity to affect newly discharged patients until dialysis resumption, discharges with events over the first 3 days were excluded, following guidelines from the National Quality Forum Technical Expert Panel. Therefore, the outcome of interest is defined as an ED visit within 4 to 30 days after discharge. Additional details about the data are available in Appendix D of the Supporting Information.

Since the outcome of ED visits is binary, we fit model (1) (logit link) of 7232 facility effects and 86 covariates using the SerBIN algorithm, which takes 9.35 s to converge on the Intel^® 6254 quad‐processor. By contrast, the BAN takes 2351.59 s (0.65 h) until convergence, and the glm in R fails to accommodate the massive ED visits data. Table 1 provides a summary of counts, percents, estimated odds ratios, test statistics, $P$‐values and 95% confidence intervals for 9 risk factors. We observe that discharges with cardiogenic shocks were associated with a lower risk of ED visit than discharges without. In addition, younger patients were significantly more likely to have ED visits than older patients. Moreover, longer hospital and nursing home stays were associated with a lower risk of ED visit. A complete list of risk factors with summary statistics is available in Appendix E of the Supporting Information.

TABLE 1.

Summary of model fitting for risk factors (binary) with 2018‐2019 ED visits data (reference group in parentheses)

Risk factor	Count	Proportion	OR	SE	Z‐stat	$P$‐value	LB	UB
Year 2018	381 400	50.4%	0.970	0.007	$-$4.672	$<$0.001	0.958	0.982
Female	358 157	47.3%	1.015	0.008	1.932	0.053	1.000	1.031
Diabetes as cause of ESRD	371 643	49.1%	0.998	0.008	$-$0.273	0.785	0.983	1.013
Cardiogenic shocks	99 201	13.1%	0.879	0.010	$-$12.736	$<$0.001	0.862	0.896
Age in years (60‐74)
18‐24	4034	0.5%	1.542	0.042	10.330	$<$0.001	1.420	1.674
25‐44	87 330	11.5%	1.346	0.012	25.506	$<$0.001	1.315	1.377
45‐59	204 969	27.1%	1.176	0.008	19.025	$<$0.001	1.156	1.195
$\ge$75	154 396	20.4%	0.954	0.010	$-$4.733	$<$0.001	0.936	0.973
BMI (18.5‐25)
$\le$18.5	22 708	3.0%	1.010	0.020	0.520	0.603	0.971	1.051
25‐30	198 852	26.3%	1.002	0.009	0.214	0.831	0.984	1.020
$\ge$30	346 225	45.7%	0.982	0.009	$-$2.128	0.033	0.966	0.999
Time on ESRD (1‐2 years)
91 days to 6 months	33 355	4.4%	1.121	0.018	6.337	$<$0.001	1.082	1.162
6 months to 1 year	59 437	7.9%	1.019	0.015	1.293	0.196	0.990	1.048
2‐3 years	98 224	13.0%	1.001	0.012	0.049	0.961	0.976	1.025
3‐5 years	160 276	21.2%	1.009	0.011	0.833	0.405	0.987	1.031
$\ge$5 years	296 878	39.2%	1.007	0.010	0.626	0.531	0.986	1.027
LOHS (1st quartile)
2nd quartile	230 587	30.5%	0.945	0.009	$-$6.621	$<$0.001	0.930	0.961
3rd quartile	131 203	17.3%	0.923	0.010	$-$7.945	$<$0.001	0.905	0.942
4th quartile	196 958	26.0%	0.910	0.009	$-$10.124	$<$0.001	0.894	0.927
NHS (0 day)
1‐89 days	131 289	17.3%	0.943	0.010	$-$6.233	$<$0.001	0.925	0.960
90‐365 days	78 628	10.4%	0.859	0.012	$-$12.170	$<$0.001	0.839	0.881

Note: LB and UB stand for lower and upper bounds of the 95% confidence intervals. A complete list of risk factors with summary statistics is available in Appendix E of the Supplementary Information.

Abbreviations: BMI, body mass index; ESRD, end‐stage renal disease; LOHS, length of hospital stay; NHS, nursing home stay (past 365 days); OR, odds ratio; PC, prevalent comorbidity; SE, standard error; Z‐stat, Z‐statistics (ratio of coefficient estimate to SE).

5.1. Test comparison

The proposed exact test is compared with the score and Wald tests, with facility‐specific test statistics shown in Figure 4. To ease comparison, exact test statistics are derived by converting lower‐tail probabilities (first minimand of (5)) to quantiles according to the standard normal distribution. The diagonal histograms reveal that the distributions of the three tests are all slightly skewed right. The upper diagonal panels display a positive relationship of the test statistics and the rate of ED visits. In addition, facilities with the highest 10% ED visit rates tend to have their exact test statistics smaller than their score and Wald test statistics, while those with the lowest 10% ED visit rates have their exact test statistics greater than the score and Wald test statistics. In other words, the proposed exact test is more conservative in flagging underperforming facilities with many ED visits and more liberal in identifying overperforming facilities with few ED visits. This feature is further demonstrated in Table 2, where facilities are flagged based on the three tests given a significance level of 0.05. A facility is flagged as “better” (or “worse”) than expected if the associated facility effect is significantly less (or greater) than the national norm. Among the 7232 facilities, 426 (5.89%) and 719 (9.94%) are identified by the score test as “better” and “worse” facilities, respectively; 366 (5.06%) and 654 (9.04%) are flagged by the Wald test as “better” and “worse” facilities, respectively. By contrast, the proposed exact test leads to 489 (6.76%) “better” facilities and 637 (8.81%) “worse” facilities. These numbers also suggest that the exact test leads to less skewed outlier detection than the other two tests. As a side note, the outlying points farthest away from the 45‐degree lines shown in Figure 4 (the two right and two bottom panels of scatter plots) result from the numerical instability of the Wald test especially for small‐sized facilities with low rates of ED visit.

FIGURE 4.

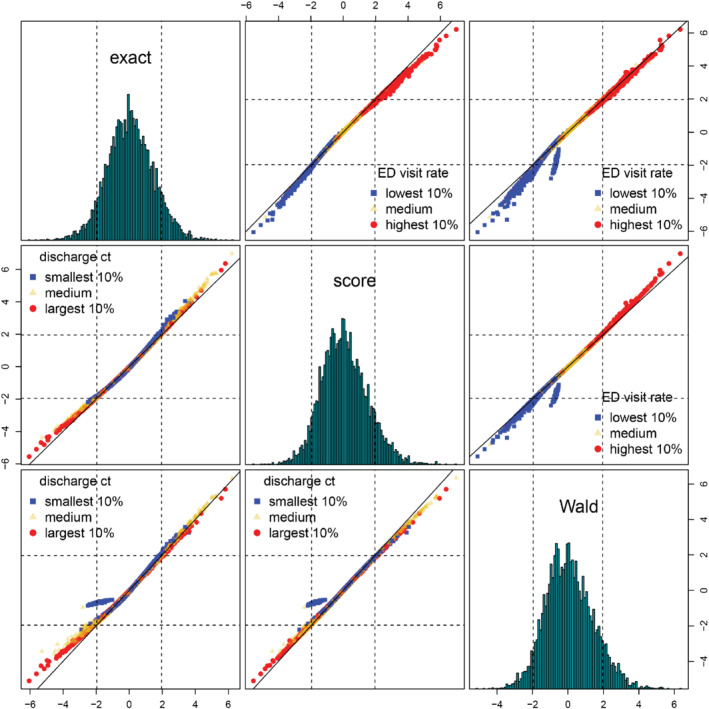
A matrix of histograms and scatter plots of test statistics using 2018‐2019 ED visits data. Facilities are stratified by ED visit rate or discharge count. Dashed lines represent 2.5% and 97.5% quantiles of the standard normal distribution. 45‐degree lines are in solid black

TABLE 2.

Facility flagging (count/proportion) based on exact, score and Wald tests at significance level $\alpha =0.05$ using 2018‐2019 ED visits data

	Score				Wald
Exact	better	expected	worse	Total	better	expected	worse
better	426/5.89%	63/0.87%	0/0%	489/6.76%	366/5.06%	123/1.70%	0/0%
expected	0/0%	6024/83.30%	82/1.13%	6106/84.43%	0/0%	6079/84.06%	27/0.37%
worse	0/0%	0/0%	637/8.81%	637/8.81%	0/0%	10/0.13%	627/8.67%
Total	426/5.89%	6087/84.17%	719/9.94%	7232/100%	366/5.06%	6212%/85.90%	654/9.04%

Note: “better” indicates that the facility effect is significantly less than the national norm; “worse” indicates that the facility effect is significantly greater than the national norm; “expected” means that the facility effect is not significantly different from the national norm.

5.2. Accounting for incomplete risk adjustment

As shown in Table 2, the proportion of dialysis facilities flagged as better or worse than expected is consistently greater than 14% by all the three tests, a much higher proportion of outliers than what is normally anticipated. This phenomenon likely indicates the presence of inadequate risk adjustment for observed or unobserved risk factors associated with the ED visit (outcome), which contributes to the substantial variation between facilities. ¹² , ¹³ , ⁴⁰ Much of the between‐facility variation is typically beyond the control of dialysis facilities, and thus should be accounted for in profiling analysis. ² , ²² To address the overdispersion, we adjust the exact test statistics in Figure 4 based on their empirical null (EN) distribution ⁴⁶ , ⁴⁷ and the corresponding facility volumes. Exact‐test based flagging results with EN adjustment and the results without EN adjustment are presented in Table 3. After EN adjustment, there are 389 (5.38%) facilities switching from “worse” to “expected,” and 349 (4.82%) facilities switching from “better” to “expected,” leading to a reduction in outlier proportion from $15.57\%$ to $5.37\%$.

TABLE 3.

Exact‐test based facility flagging (count/proportion) with and without empirical null (EN) adjustment at significance level $\alpha =0.05$ using 2018‐2019 ED visits data

Exact text with EN
Exact test without EN	better	expected	worse	Total
better	140/1.94%	349/4.82%	0/0%	489/6.76%
expected	0/0%	6106/84.43%	0/0%	6106/84.43%
worse	0/0%	389/5.38%	248/3.43%	637/8.81%
Total	140/1.94%	6844/94.63%	248/3.43%	7232/100%

Note: “better” indicates that the facility effect is significantly less than the national norm; “worse” indicates that the facility effect is significantly greater than the national norm; “expected” means that the facility effect is not significantly different from the national norm.

6. DISCUSSION

The increasing availability of massive data poses daunting challenges to existing statistical methods when comparing resource utilization and quality of care among health care providers. To facilitate large‐scale estimation and inference for provider profiling, we propose a serial blockwise inversion Newton algorithm with a shared‐memory divide‐and‐conquer parallelization, and a distribution‐based exact test of provider effects, allowing different outcome types within the framework of generalized linear models. The proposed algorithm and its parallelization achieve superior convergence speed and memory efficiency compared to existing implementations, and is scalable to massive data with a large number of providers; the exact test utilizes finite‐sample distributions to control type I error and enhance statistical power without possibly inaccurate large‐sample approximations. The advantages of the proposed methods are demonstrated by simulations and an application to profiling kidney dialysis facilities according to ED encounters among patients with end‐stage renal disease, making use of the extensive Medicare administrative claims data.

In Table 1, we observe that discharges with cardiogenic shocks were slightly less likely to result in an ED visit than discharges without. This counterintuitive evidence suggests that the higher death rate among patients with cardiogenic shocks possibly reduces their chance of getting admitted to ED. As expected, discharges with cardiogenic shocks had a death rate of 5.477%, while those without had a significantly lower death rate of 2.374%. In this case, an ED visit and a death should be viewed as competing risks to one another within 30 days of discharge: an ED visit is recorded only if it occurs before a death, if any, and a death is recorded only if there is no ED visit prior to that death. The GLM framework, although routinely used for profiling providers, ¹⁸ , ⁴⁸ does not explicitly consider competing risks (eg, post‐discharge death) and event times. Overlooking competing risks and event times may lead to less comprehensive modeling and distorted provider evaluation, especially when the rate of competing risks is nontrivial. To address this issue, we have been working on developing a discrete competing risk model based on the cause‐specific hazard approach. We will report this work as a separate article in the near future.

CONFLICT OF INTEREST

The authors declare no potential conflict of interests.

Supporting information

Data S1: Supporting Information

Wu W, Yang Y, Kang J, He K. Improving large‐scale estimation and inference for profiling health care providers. Statistics in Medicine. 2022;41(15):2840‐2853. doi: 10.1002/sim.9387

DATA AVAILABILITY STATEMENT

The data are not publicly available due to privacy or ethical restrictions.