Mapping Catalyst–Solvent Interplay in Competing Carboamination/Cyclopropanation Reactions

Abstract

Group 9 metals, in particular Rh^III complexes with cyclopentadienyl ligands, are competent C−H activation catalysts. Recently, a Cp*Rh^III‐catalyzed reaction of alkenes with N‐enoxyphthalimides showed divergent outcome based on the solvent, with carboamination favored in methanol and cyclopropanation in 2,2,2‐trifluoroethanol (TFE). Here, we create selectivity and activity maps capable of unravelling the catalyst‐solvent interplay on the outcome of these competing reactions by analyzing 42 cyclopentadienyl metal catalysts, Cp^XM^III (M=Co, Rh, Ir). These maps not only can be used to rationalize previously reported experimental results, but also capably predict the behavior of untested catalyst/solvent combinations as well as aid in identifying experimental protocols that simultaneously optimize both catalytic activity and selectivity (solutions in the Pareto front). In this regard, we demonstrate how and why the experimentally employed Cp*Rh^III catalyst represents an ideal choice to invoke a solvent‐induced change in reactivity. Additionally, the maps reveal the degree to which even perceived minor changes in the solvent (e. g., replacing methanol with ethanol) influence the ratio of carboamination and cyclopropanation products. Overall, the selectivity and activity maps presented here provide a generalizable tool to create global pictures of anticipated reaction outcome that can be used to develop new experimental protocols spanning metal, ligand, and solvent space.

What will my product be? Selectivity and activity maps can be used to predict and rationalize reaction outcomes based on catalyst and solvent choice. Here, there utility is demonstrated by examining competing carboamination/cyclopropanation reactions catalyzed by Group 9 catalysts featuring cyclopentadienyl ligands, which reveals an interesting energetic interplay involving the role of the solvent and of the catalyst.

Introduction

The functionalization of C−H bonds catalyzed by transition metal complexes is a widely used and powerful synthetic tool,[ ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ ] yet selectively activating specific C−H bonds to facilitate greater control over reaction outcome remains a key challenge. One route to improved control involves introducing directing groups coordinated to transition metals, which regulate the position of C−H functionalization by modulating the steric and electronic properties of the substrate.[ ⁹ , ¹⁰ ] The subsequent development of directing groups that also act as internal oxidants has tremendously impacted oxidative C−H functionalizations[ ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ ] by permitting the use of milder reaction conditions that result in improved selectivity and greater functional group tolerance. ^[16] For instance, Rh^III species, particularly when coupled with (chiral) Cp ligands,[ ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ ] have been shown to be capable C−H activation catalysts, as demonstrated by Glorius,[ ²¹ , ²² ] Fagnou,[ ¹⁴ , ²³ ] Liu and Lu,[ ²⁴ , ²⁵ ] as well as Cramer,[ ²⁶ , ²⁷ , ²⁸ ] amongst others. Despite the prevalence of rhodium species, catalysts based on other metals, notably cobalt[ ²⁹ , ³⁰ , ³¹ , ³² , ³³ ] and iridium,[ ³⁴ , ³⁵ , ³⁶ ] have also shown capability in activating C−H bonds.[ ³⁷ , ³⁸ ] Such advancements are particularly timely, given the ongoing shift toward the use of more abundant 3d‐metals (i. e., cobalt) for C−H activation/functionalization processes. ^[39]

In 2014, Piou and Rovis demonstrated that the product of a Cp*Rh^III catalyzed reaction of N‐enoxyphthalimides and alkenes could be modulated through a change in solvent (Scheme 1), with reactions in 2,2,2‐trifluroethanol (TFE, blue) favoring a trans‐cyclopropanation product (E), ^[40] while those in methanol (red) led to the formation of a carboamination product (C). ^[41] Cramer has expanded on these finding by employing different chiral Cp^X ligands ^[42] to achieve highly enantioselective processes for both the trans‐cyclopropanation ^[43] and carboamination ^[44] reactions. The underlying origin of the observed divergence in reaction outcome has been postulated to arise from a ring‐opening reaction where the methanol solvent cleaves the C−N bond of the phthalimide moiety, leading to the formation of an amido ester (D) ^[41] that exists in a different coordination environment to that of the phthalimide (F, Scheme 1). This altered coordination presumably influences the energetics of the competing reaction pathways to favor the carboamination product. However, this situation may not be totally generalizable, as different ligand/metal/solvent combinations potentially alter catalytic activity and/or selectivity in a very complex manner.

Scheme 1.

Cp^XRh^III‐catalyzed, solvent‐induced modulation of selectivity in the reaction of N‐enoxyphthalimides with alkenes, where TFE results in cyclopropanation and methanol in carboamination products.

Intrigued by the unique aspects of the Rh‐catalyzed cyclopropanation/carboamination reactions demonstrated by Piou and Rovis,[ ⁴⁰ , ⁴¹ ] particularly how both catalyst and solvent choice impact the reaction outcome and how this information might be harnessed to develop related processes employing other solvents as well as cobalt and iridium species, the objective of this paper is to create activity and selectivity maps that provide the anticipated reaction outcome based on catalyst and solvent choice. Such maps could then be used to predict the performance of untested catalyst/solvent pairs, rationalize previous experimental results, and identify species that simultaneously maximize activity and selectivity providing solutions in the Pareto front. ^[45] Construction of these activity and selectivity maps requires proceeding through a series of necessary steps, specifically: identifying the mechanistic pathways of the two catalytic cycles, establishing linear free energy scaling relationships, and constructing molecular volcano plots. Only after each of these steps has been completed can the final maps be created. As such, the first two subsections of the “results and discussion” cover these intermediary steps before arriving at the actual maps in the third subsection.

Results and Discussion

Mechanistic pathways

The first step in creating activity and selectivity maps requires obtaining knowledge of the reaction mechanism for both the carboamination and cyclopropanation pathways. In this respect, several proposals for each pathway exist. Liu and Chen ^[46] have elucidated both carboamination and cyclopropanation mechanisms in a DFT study of the Cp^tBuRh^III catalyst. Since that time, other proposals have been put forward, including an alternative cyclopropanation proposed by Rovis ^[47] as well as an ionic mechanism where the hydroxamate moiety is deprotonated by an acetate ion prior to metal coordination ^[48] (for the carboamination pathway). After testing multiple possibilities for both the carboamination and cyclopropanation pathways, the lowest energy catalytic cycles were identified as those depicted in Scheme 2 (see Supporting Information, Figures S1 and S2 for the relative energies of these alternative pathways).

Scheme 2.

Catalytic cycles leading to formation of the carboamination (red) and cyclopropanation (blue) products.

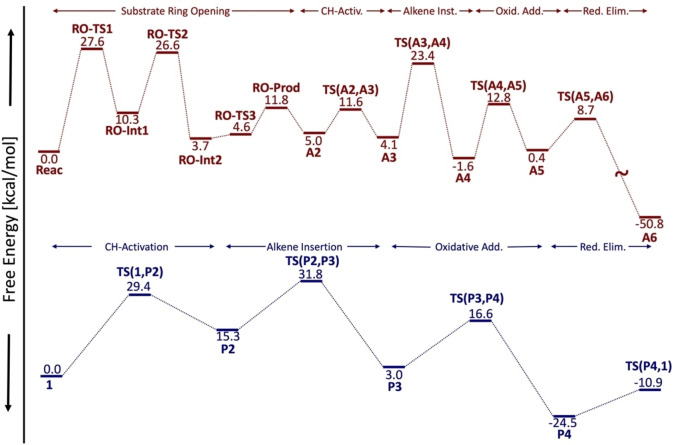
For the carboamination pathway (red, Scheme 2), phthalimide first undergoes a solvent‐assisted ring‐opening reaction through a stepwise mechanism (via RO‐TS1, RO‐Int1, and RO‐TS2) to form RO‐Int2. ^[49] Deprotonation of the nitrogen of RO_Int2 by an acetate anion from the solvent (via RO‐TS3) and coordination with the Cp^X‐M catalyst leads to A2. The catalytic cycle then proceeds by C−H activation [TS(A2,A3)], alkene insertion [TS(A3,A4)], oxidative addition [TS(A4,A5)], and finally reductive elimination [TS(A5,A6)]. Release of the modified substrate and a subsequent ring‐closing procedure yield the carboamination product (CA_prod ) via a series of low‐energy processes, ^[46] while the catalyst is regenerated by the addition of two acetate molecules. In contrast, the cyclopropanation mechanism (blue, Scheme 2) is simpler: following coordination of the Cp^XM^III catalyst with the directing group, successive C−H activation [TS(1,P2)], alkene insertion [TS(P2,P3)], oxidative addition [TS(P3,P4)], and reductive elimination [TS(P4,1)] steps give the final product (CP_prod ). Importantly, note that the cyclopropanation process does not involve substrate ring‐opening prior to entering the catalytic cycle. As such, a key element that dictates reaction outcome is the relative rates of ring‐opening followed by C−H activation on the opened substrate versus direct C−H activation of the alkene bonded to the closed phthalimide by the catalyst. An overview of the two catalytic cycles, including each of the key intermediates and transition states along with the computed free energies for Cp*Rh^III, is provided in Figure 1.

Figure 1.

Overview of the catalytic cycle steps leading to the carboamination (red) and cyclopropanation (blue) products. Free energies shown here are for the Rh−L2 (Cp*Rh^III) species in methanol (carboamination, red) and TFE (cyclopropanation, blue) computed at the B3PW91‐D3(BJ)/def2‐TZVP//M06/def2‐SVP level (see Computational Details for full protocol).

To understand the energetic factors underpinning the phthalimide ring‐opening process and the relative rates associated with traversing the two catalytic cycles, we examined a series of 42 catalysts comprised of cobalt, rhodium, or iridium metal centers along with a series of 14 different substituted cyclopentadienyl ligands possessing varying steric and electronic properties (Figure 2). The relative free energies of the catalytic cycle intermediates and transition states from this catalyst set were determined through the computational protocol given at the end of the manuscript (and subsequently used to extract linear free energy scaling relationships, LFESRs, see Supporting Information for details). These LFESRs describe the free energies of the carboamination and cyclopropanation pathways for any catalyst based on the values of two descriptor variables, ▵G(A4) (for carboamination) and ▵G(P4) (for cyclopropanation).

Figure 2.

Structures of different cyclopentadienyl ligands used in this study.

Molecular volcano plots in methanol and TFE solvents

Over the past several years our research group has used molecular volcano plots[ ⁵⁰ , ⁵¹ , ⁵² , ⁵³ , ⁵⁴ , ⁵⁵ ] to study a multitude of homogeneous catalytic reactions.[ ⁵⁶ , ⁵⁷ , ⁵⁸ , ⁵⁹ , ⁶⁰ , ⁶¹ ] These plots employ sets of scaling relationships (linear and beyond) between the various catalytic cycle intermediates and transition states to predict a measure of catalytic performance (displayed on the volcano y‐axis) based on the value of a single chosen descriptor variable (displayed on the volcano x‐axis). Here, we derive volcano plots within the context of the energy span model,[ ⁶² , ⁶³ , ⁶⁴ ] where the measure of catalytic activity is given as the negative of the catalytic cycle's energy span (‐δE), as defined by equations 1 and 2. $T_i$ and $I_j$ are the Gibbs free energies of the reaction intermediates and transition states, respectively, and $\Delta G_r$ is the total Gibbs free energy of the reaction (Equation (1) and 2).

$${\displaystyle \delta E=ma{x}_{i,j}\left(T_i-I_j+\delta G_{i,j}\right)}$$ (1)

$${\displaystyle \delta G_{i,j}=\left\{\begin{array}{c}0\mathrm{if}{T}_i\mathrm{after}{I}_j\\ \Delta G_r\mathrm{if}{T}_i\mathrm{before}{I}_j\end{array}\right\}}$$ (2)

Conceptually, the energy span represents the energy difference between two key states of the catalytic cycle, the turnover‐determining transition state (TDTS, i. e., the rate‐limiting TS) and the turnover‐determining intermediate (TDI, i. e., the most populated intermediate), and thus is the largest energetic barrier that must be overcome in the catalytic cycle. As such, catalysts that lie high on the volcano can be interpreted as being more “active” than species lying further down, as these catalysts have small energy spans. By postprocessing the LFESRs (see Supporting Information for details), we arrive at the volcanoes shown in Figure 3. ^[65]

Figure 3.

Volcano plots for (a) the carboamination pathway in methanol solvent, (b) the cyclopropanation pathway in methanol solvent, (c) the carboamination pathway in TFE solvent, (d) the cyclopropanation pathway in TFE solvent. Vertical lines delineate regions of the volcano where the energy span is controlled by different turnover determining intermediates/transition states (TDI/TDTS): for (a/c) I [TDI: A5, TDTS: TS(A5,A6)], II [TDI: Reactants, TDTS: RO‐TS1], III [TDI: Reactants, TDTS: TS(A3,A4)], for (b/d) I [TDI: P4, TDTS: TS(1,P2)], II [TDI: P4, TDTS: TS(P4,1)], III [TDI: Reactants, TDTS: TS(1,P2)], IV [TDI: Reactants, TDTS: TS(P2,P3)]. Enlargements of each volcano showing the location of the individual catalysts are given in the Supporting Information (Figure S1‐S3). Note the dotted lines in (c) are present to illustrate the change in volcano shape in moving from methanol to TFE solvent.

Figure 3a shows the volcano for the carboamination reaction in methanol. Here, nearly all rhodium (orange) and iridium (teal) catalysts, as well as many cobalt species (green), lie atop the volcano, indicative of anticipated high activity. Importantly, for the most active catalysts, phthalimide ring‐opening dictates the reaction rate and, therefore, plays a key role in defining the selectivity of the reactions (see below).

On the other hand, iridium, rhodium, and cobalt behave differently for the cyclopropanation pathway in methanol (Figure 3b). Here, cobalt species (green) are located far from the volcano peak, corresponding to prohibitively high energy barriers that would render these species inactive for cyclopropanation. Rhodium catalysts (orange) have smaller energy barriers than cobalt catalysts and should demonstrate enhanced activity, while iridium species (teal) are predicted to be the most active catalysts.

Figure 3c shows how changing the solvent from methanol to TFE influences the energetics of carboamination. In essence, the solvent‐assisted phthalimide ring‐opening is significantly more energetically costly in TFE (RO‐TS1=37.6 kcal/mol) than methanol (RO‐TS1=27.6 kcal/mol), which results in a dramatic downward shift of the volcano plateau that corresponds to much more costly energetics for carboamination in TFE compared to methanol. This ring‐opening process then becomes the rate‐determining step for the catalytic cycle (in TFE) for each of the tested catalysts, which is seen by each catalyst lying at the same height (on the plateau) of the Figure 3c volcano.

In contrast to the dramatically different volcanoes seen for the carboamination reactions in different solvents (Figures 3a and 3c), changing from methanol to TFE only minimally influences the cyclopropanation energetics (see the similar shapes of the Figures 3b and 3d volcanoes). As a result, the same trends regarding catalytic behavior seen in methanol (Figure 3b) are reproduced in TFE (Figure 3d), with iridium and rhodium catalysts anticipated to demonstrate enhanced activity over cobalt species.

Overall, it is clear that the metal, but also the ligand of the catalyst can significantly influence anticipated activity. For instance, substituting different ligands causes shifts in the energy span (y‐axis of the volcanoes) of over 10 kcal/mol (the specific energetic influence of each Cp ligand can be found in the Supporting Information, Figure S3–S5). Thus, while the metal center is clearly an important factor in establishing catalyst activity, judicious ligand choice can serve as additional route to tune overall activity.

Mapping catalytic activity and selectivity

Having completed the necessary intermediary steps in the proceeding sections, maps that provide information about the selectivity and activity of the competing carboamination/cyclopropanation reactions can now be constructed by extrapolating the Figure 3 volcano plots into three dimensions (see Supporting Information, Figure S6). ^[66] Given a catalyst/solvent pair, the Figure 4 maps quickly predict which of the two catalytic cycles is energetically preferred (carboamination or cyclopropanation) as well as provide an anticipated relative measure of activity (that can be compared with other catalyst/solvent combinations). Importantly, the maps are broadly valid and can be used to predict the expected behavior of any group 9 metal/Cp^X ligand combination in any alcoholic solvent. ^[67] They are not restricted to combinations of the 42 catalysts/2 solvents from which they are derived.

Figure 4.

(a) Selectivity map of the competing carboamination and cyclopropanation pathways. Dark blue indicates strong preference for the cyclopropanation pathway and dark red strong preference for the carboamination pathway. Note the lighter blue/red as well as white areas indicate regions of energetic competition between the different pathways. (b) Activity map indicating the energy span of the two competing pathways. Warmer colors indicate more facile catalytic process. Maps are derived from the 3D volcanoes shown in Supporting Information Figure S6. Enlargements showing the location of the individual catalysts are given in Supporting Information Figure S7 and S8.

The Figure 4 maps predict the activity and selectivity of any catalyst/solvent combination through knowledge of two descriptor variables, ▵G(P4), which provides information about the influence of the catalyst, and ▵G(RO‐TS1), which provides information about the influence of the solvent. For the selectivity map (Figure 4a), a catalyst/solvent combination falling in the dark blue area indicates energetic preference for the cyclopropanation pathway, while location in a dark red area indicates preference for the carboamination pathway. The location of a point in the brighter blue/red or white areas indicates regions of lower selectivity, where a combination of the two products may be expected. For activity (Figure 4b) the location of points in warmer colors indicates a more active catalyst/solvent combination than a corresponding point located in cooler colors.

While these maps are clearly useful for predicting the preferred reaction pathway for a given catalyst/solvent combination (as well as rationalizing the behavior of previous experimental work), it is important to note that there are limitations to their predictive ability. Specifically, they provide a comprehensive picture of selected reaction mechanisms (e. g., Scheme 2) and do not account for side reactions or off‐cycle species that have not explicitly been considered. In principle, such information could be recovered through the creation of additional maps specifically aimed at examining these alternative pathways. In this sense, one individual map is not capable of predicting reaction outcome with absolute certainty, but this objective could potentially be achieved by creating a series of similar maps. Nonetheless, even a single set of maps serves as an excellent starting point for experimentalists seeking to identify new catalyst/solvent tandems by providing knowledge of the regions of catalyst/solvent space most likely to contain highly active/selective species.

Predicting the behavior of untested catalyst/solvent combinations

One of the key features of the Figure 4 maps is predicting the results of reactions run using different catalysts and with different solvents. Aside from methanol and TFE (the solvents used to create the maps), the energetic influence arising from employing other alcoholic solvents can also be easily explored by adding new horizontal lines obtained by computing the corresponding ▵G(RO‐TS1) values to the maps. How selectivity and activity evolve with different alcoholic solvents and which new metal and ligand are ideal for maximum performance can then be assessed. In fact, the maps reveal that seemingly “innocent” changes that might be made to improve, for instance, catalyst/substrate solubility, such as replacing methanol with ethanol, considerably influence the reaction outcome. For instance, using Rh−L2 but replacing methanol with ethanol results in both diminished selectivity (e. g., shifting the catalyst from the dark red region associated with strongly favoring carboamination to the red/white area, Figure 4a) and activity (ethanol line lies in cooler colors, Figure 4b).

To confirm that our selectivity maps correctly predict the influence of the solvent on the reaction outcome, we turned to a combination of new and existing experimental results for the Rh−L2 catalyst with several alcoholic solvents. Here, a clear trend emerges regarding the experimentally observed carboamination:cyclopropanation (CA : CP) ratios. ^[68] As predicted by our maps, carboamination is found to be strongly favored in methanol (CA : CP of 3.9 : 1), which aligns well with the darker red location of the Rh−L2 catalyst on the methanol line (Figure 5). Changing the solvent from methanol to ethanol shifts the catalyst from the activity map's dark red to the light red/white area, which is expected to increase energetic competition between the cyclopropanation and carboamination pathways thereby resulting in a lower CA : CP ratio, with carboamination still being the major product. Indeed, experimental results confirm this to be the case, where a CA : CP ratio of 2.0 : 1 was observed. Finally, shifting to the TFE line in the selectivity map shows that cyclopropanation should be the major product (point falls in the dark blue area, Figure 5), in‐line with experiment (CA : CP ratio of 1 : 2.3). Clearly, the role of the solvent represents a key factor in predicting and rationalizing observed experimental outcome of these competing reactions. Assessing the ring‐opening TS values of other solvents unambiguously shows that solvent nucleophilicity plays a key role, as more nucleophilic solvents (as measured by Mayr's nucleophilicity index ^[69] ) show a linear correlation with ΔG(RO‐TS1) (see Supporting Information, Figure S11).

Figure 5.

Experimental reaction outcome as a function of solvent for the Rh−L2 catalyst. The experimentally observed decrease in carboamination:cyclopropanation (CA : CP) ratio as the solvent is changed is predicted by the selectivity map.

Rationalizing existing experimental results

The behavior observed by Piou and Rovis occurring when switching from methanol to TFE solvent can be fully rationalized using the Figure 4 maps, a second key feature of their utility. In methanol, carboamination is clearly favored (i. e., the catalyst is located in the red area of Figure 4a) and the catalytic cycle possesses ideal energetics (i. e., the catalyst is located in the orange areas of Figure 4b). In TFE, cyclopropanation becomes clearly favored (i. e., the catalyst falls in the blue area of Figure 4a). It should be noted, however, that the energetics of the cyclopropanation cycle are not ideal, as the point representing Rh−L2 lies far from the area of maximum anticipated activity (i. e., the catalyst is not in the orange‐red area of Figure 4b). Nevertheless, the use of Rh‐L2 is an intelligent choice if the desire is to alter the reaction outcome solely through a change of solvent, as this catalyst falls unmistakably in either the red (carboamination) or blue (cyclopropanation) areas of the Figure 4a map depending on the solvent used. Employing more active catalysts (in TFE), such as iridium species, would represent an inferior choice to many rhodium catalysts, as the desired switch in reaction outcome may not be observed due to poor selectivity in methanol (Ir catalysts fall in or near the white areas in Figure 4a).

Optimization of reaction conditions with selectivity/activity maps

To optimize selectivity and activity, reaction conditions including metal‐ligand combinations and solvent must be carefully considered. Generally, activity and selectivity are difficult to maximize simultaneously without deteriorating one in favor of the other (i. e., finding solutions in the Pareto front). ^[45] In this regard, tools that can help in this type of multiobjective optimization are extremely valuable. By providing a comprehensive picture of metal/ligand combinations, the maps developed in this work help to quickly identify regions of the catalyst space most likely to contain both active and selective species. Traversing a horizontal line on the Figure 4 maps and finding a position that is simultaneously in a dark area on Figure 4a and in a warm area of Figure 4b gives metal and ligand partners that are solutions in the Pareto front. For example, when running a reaction in TFE, the region on the maps that is both highly selective (dark blue, Figure 4a) and active (warm red, Figure 4b) has descriptor value [▵G(P4)] between −45 and −40 kcal/mol, which corresponds to Ir−L7 or Ir−L1.

To develop new experimental protocols beyond the Rh−L2 system and quickly identify other possible metal/ligand combinations that could lead to highly active and selective reactions, the plots shown in Figure 6, which provide a summarized version of the information contained in both the selectivity (Figure 4a) and activity (Figure 4b) maps, can be used. For carboamination in methanol, cobalt species represent the most selective and active catalysts (left side, Figure 6a). The optimization of activity and selectivity of cyclopropanation reactions in TFE is also straightforward (Figure 6b), where the most selective species (i. e., iridium catalysts) are also the most active (upper right corner, Figure 6b). To verify the predictions of iridium species being good cyclopropanation catalysts in TFE, we synthesized iridium complexes with Cp ligands L7 and L10 and subsequently tested them in the cyclopropanation reaction between N‐enoxyphthalimide and dimethyl fumarate. However, none of the anticipated cyclopropanation product was detected. Performing a similar reaction with a stoichiometric amount of IrL10 (instead of using it in a catalytic fashion), we isolated iridacycle IrL10a (Scheme 3) and unequivocally revealed its structure by single crystal X‐ray diffraction analysis. ^[70] Notably, the formation of IrL10a must have occurred by initial C−H activation of the N‐enoxyphthalimide, in line with our theoretical predictions. In contrast to the rhodium congener, iridium undergoes a previously unknown divergent pathway that energetically outcompetes the alkene insertion step [TS(P2,P3)], leading ultimately to IrL10a via N−O bond cleavage processes. Notably, this example shows both a success and a limitation of the selectivity/activity maps. This specific iridium species did undergo direct C−H activation (i. e., the cyclopropanation pathway) as opposed substrate ring‐opening (i. e., the carboamination pathway), but was subsequently diverted from the expected cyclopropanation pathway, a facet for which our maps, in their present form, cannot account.

Figure 6.

Relative activity vs. selectivity for the 42 catalysts tested in (a) methanol and (b) TFE. Catalysts favoring carboamination are colored in red, those favoring cyclopropanation are colored in blue. Species further from the dashed vertical line, which represents lack of selectivity, are predicted to be more selective for one specific product.

Scheme 3.

Formation of cyclometalated complex IrL10a. Crystal structure of IrL10a as ORTEP drawing with 50 % probability thermal ellipsoids.

Conclusion

In conclusion, we have created selectivity and activity maps that aid in unraveling catalyst/solvent interplay in competing carboamination/cyclopropanation reactions catalyzed by Group 9 Cp^XM^III species. These maps provide quantitative information regarding how specific metal, ligand, and solvent combinations influence the expected reaction outcome that can be used to both rationalize existing experimental results as well as predict the behavior of untested catalyst/solvent combinations. In this regard, our maps reveal that the Cp*‐Rh^III catalyst used by Piou and Rovis represents a nearly ideal system choice for provoking a solvent‐induced change in selectivity. This chameleon‐like behavior can be traced to the unique properties of the rhodium catalysts, where cyclopropanation energetics are sufficiently “good” to favor cyclopropanation over carboamination in TFE, yet sufficiently “bad” to favor carboamination over cyclopropanation in methanol. In essence, these rhodium species fit into a finite energetic window that delineates a “Goldilocks” zone where reaction outcome can be altered based on solvent choice, something that is unlikely to occur with either cobalt or iridium catalysts.

In addition to rationalizing previous experimental results, the selectivity maps also illustrate the degree to which (even minor) solvent changes influence the final product ratios. For example, our maps predict that even seemingly benign changes in the solvent (e. g., from methanol to ethanol) sufficiently alter the reaction energetics to considerably reduce the final carboamination to cyclopropanation product ratio. New experimental results confirmed the accuracy of our predictions, with a reduction in the ratio of carboamination to cyclopropanation products from 3.9 : 1 (methanol) to 2.0 : 1 (ethanol). These findings indicate that small changes in solvent nucleophilicity can be a viable strategy for further tuning the reaction outcome. Broadly speaking, the creation of these selectivity and activity maps serves as a revealing first step to provide a more global picture of reaction outcome simultaneously across catalyst and solvent space, as opposed to the limited information typically extracted from the individual examination of reaction profiles. While we have demonstrated the utility of these tools on an illustrative example here, the underlying methods should be applicable across a wide range of interesting chemical problems.

Experimental Section

Computational details: The geometries of all species were optimized in the gas‐phase using the M06[ ⁷¹ , ⁷² ] functional and the def2‐SVP ^[73] basis set as implemented in Gaussian16. ^[74] Species were characterized as either a minimum (zero imaginary frequencies) or a transition state (one imaginary frequency) through examination of the vibrational frequencies. Single point energies were obtained on the optimized M06/def2‐SVP geometries at the B3PW91[ ⁷⁵ , ⁷⁶ ]‐D3(BJ) ^[77] /def2‐TZVP level using the SMD ^[78] solvation model with the corresponding solvent (methanol, 2,2,2‐trifluoroethanol, ethanol, isopropanol). Free energy corrections were determined using the quasi rigid‐rotor harmonic oscillator model and corrected for translational entropy in solution ^[80] using the approach of Martin, Hay, and Pratt ^[81] (24.69 mol/L atm for methanol, 13.24 mol/L for TFE) using the GoodVibes package. ^[82] Unless otherwise indicated, reported free energies in the paper are taken as the sum of the B3PW91‐D3(BJ)/def2‐TZVP//M06/def2‐SVP electronic energies and the M06/def2‐SVP free energy corrections.

Crystal structure determination

Deposition Number 2104530 (for Ir‐L10a) contains the supplementary crystallographic data for this paper. These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Supporting Information

M. D. Wodrich, M. Chang, S. Gallarati, Ł. Woźniak, N. Cramer, C. Corminboeuf, Chem. Eur. J. 2022, 28, e202200399.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.