Live-cell fluorescence spectral imaging as a data science challenge

Abstract

Live-cell fluorescence spectral imaging is an evolving modality of microscopy that uses specific properties of fluorophores, such as excitation or emission spectra, to detect multiple molecules and structures in intact cells. The main challenge of analyzing live-cell fluorescence spectral imaging data is the precise quantification of fluorescent molecules despite the weak signals and high noise found when imaging living cells under non-phototoxic conditions. Beyond the optimization of fluorophores and microscopy setups, quantifying multiple fluorophores requires algorithms that separate or unmix the contributions of the numerous fluorescent signals recorded at the single pixel level. This review aims to provide both the experimental scientist and the data analyst with a straightforward description of the evolution of spectral unmixing algorithms for fluorescence live-cell imaging. We show how the initial systems of linear equations used to determine the concentration of fluorophores in a pixel progressively evolved into matrix factorization, clustering, and deep learning approaches. We outline potential future trends on combining fluorescence spectral imaging with label-free detection methods, fluorescence lifetime imaging, and deep learning image analysis.

Introduction

Fluorescence spectral imaging (FSI) in cell biology is an advanced type of fluorescence microscopy that generates images from a sample at different wavelengths across the electromagnetic spectrum (Hiraoka et al. 2002; Zimmermann, 2005). The set of images produced by FSI contains extensive information about the sample’s fluorescent properties, which can be used to simultaneously identify several molecules or structures, given that their fluorescence signatures are different. FSI has been used to study fixed biological samples, such as fluorescently stained tissues, fixed cells, and microarrays (Tsurui et al. 2000; Samarov et al. 2012; Fereidouni et al. 2018; Lichten et al. 2014). However, one of the most promising applications of FSI is the simultaneous visualization and quantification of the multitude of biochemical reactions and cellular structures in living cells (Valm et al. 2017; Arguello-Miranda et al. 2018; Chen et al. 2021). The further development of live-cell fluorescence spectral imaging could hold the key to tracking entire networks or intracellular structures in real-time as cells grow and divide during healthy and disease conditions (Argüello-Miranda et al. 2021; Hedde et al. 2021; Valm et al. 2017).

Spectral imaging has been implemented in a wide range of fields including biomedical diagnostics (Campos-Delgado et al., 2019; Schröck et al. 1996; Ortega et al. 2020), quality control in crop or food science (Elmasry et al. 2012; Su and Xue 2021), multidimensional cytometry (Jiménez-Sánchez et al. 2019; Schraivogel et al. 2022), and object detection in astronomy, remote sensing, and satellite imagery (Pauca et al. 2006). However, live-cell fluorescence spectral imaging has remained exceedingly challenging due to the specific requirements of working with living cells and, crucially, the lack of specific algorithms to optimize and analyze data produced from live-cell fluorescence imaging.

This work aims to introduce both the wet lab experimentalist and the dry-lab data analyst to the algorithmic approaches used to analyze live-cell fluorescence spectral data. This is a balancing act of finding a middle ground in the depth in which fluorescence microscopy or data science concepts are discussed. A general explanation of fluorescence or the design of spectral microscopes is omitted since excellent reviews already describe the principles of fluorescence microscopy (Lichtman and Conchello 2005; Rino et al. 2009) and the general design of spectral imaging systems (Hiraoka et al. 2002; Li et al. 2013). We focus instead on providing a unified description of the evolution of spectral unmixing approaches used in live-cell fluorescence spectral imaging. Using a preamble on the basics of live-cell fluorescence microscopy, we then discuss how the analysis of live-cell fluorescence spectral imaging can be understood as a data science challenge.

Basics and current limits of FSI

In cell biology, fluorescence spectral images are produced from samples containing combinations of fluorophores, which are molecules that absorb photons at a specific wavelength and then emit photons at a longer wavelength that contain less energy (Lichtman and Conchello 2005; Rino et al. 2009). Common fluorophores in cell biology include dyes (Haraguchi et al. 2002), nanostructures (Jaiswal and Simon 2015), fluorescent biomolecule analogs (Sinkeldam et al. 2010), and fluorescent proteins (Chamberlain and Hahn 2000; Lansford et al. 2001b; Shaner et al. 2005).

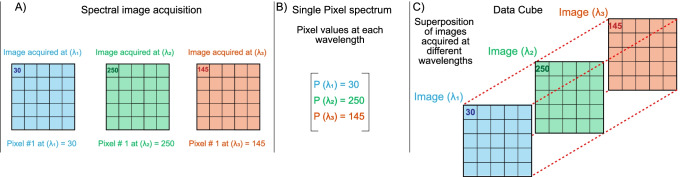
The information acquired by FSI constitutes a multidimensional data set composed of wavelength-specific images (Fig. 1A). An image in this context is an array or matrix of pixels whose values depend on the fluorescence intensity of the sample at the imaging wavelength (Waters 2009). The values of a pixel at each different imaging wavelength create a single pixel spectrum (Fig. 1B), and the array of wavelength-specific images creates a data cube that has the images’ length and width dimensions and a third dimension defined by the imaging wavelengths (Fig. 1C) (Deal et al. 2019; Chen et al. 2021; Li et al. 2013).

Fig. 1.

Schematic definition of spectral imaging, pixel spectrum, and data cube. A Schematic representation of three images acquired at different $\mathit{\lambda }$ wavelengths (colors) using a spectral imaging setup. The intensity value of pixel number one is shown to ease comparison. B Representation of the single pixel spectrum as the values of pixel number one arranged as a vector. C Schematic representation of a data cube in which, besides their length and width dimensions, the images acquire a third dimension along their $\mathit{\lambda }$ values

In samples containing two or more fluorophores, the images acquired at a specific wavelength can present pixels containing mixtures of fluorescent signals. The presence of mixed pixels in an image prevents the direct quantification of individual fluorophores, which requires calculating the proportion of each fluorophore in the mixed pixels by analyzing the information contained in the single-pixel spectra. This approach, known as spectral unmixing, processes fluorescent images with mixed pixels acquired at a certain wavelength to generate fluorophore-specific images for further quantitative analysis (Keshava and Mustard 2002; Zimmermann 2005; Lansford et al. 2001b).

By using spectral unmixing, the number of different features that can be simultaneously imaged is in principle equal to the number of fluorophores that can be unequivocally identified. Given that the available fluorophores for cell biology span the ultraviolet (UV), visible, and infrared (IR) portion of the electromagnetic spectrum (Shaner et al. 2005; Balleza et al. 2018), one could imagine that a high number of fluorophores could be used to study several processes or structures in living cells simultaneously. However, live-cell fluorescence microscopy is usually reduced to blue, green, and red detection channels (Ettinger and Wittmann 2014).

Why has live-cell fluorescence microscopy remained limited to three fluorescent channels? We consider that at least four factors have prevented live-cell imaging from using numerous fluorophores simultaneously: (1) the requirement of customized optical equipment in spectral microscopes (Favreau et al. 2013; Abuleil and Abdulhalim 2016; Hedde et al. 2021); (2) the phototoxic effects of illuminating cells with different excitation wavelengths (Ettinger and Wittmann 2014; Icha et al. 2017; Kiepas et al. 2020); (3) the complexity of stably expressing or delivering three or more fluorophores in living cells (which is feasible in organisms such as the yeast Saccharomyces cerevisiae (Arguello-Miranda et al. 2018), but remains challenging in mammalian and plant cells despite recent advances in tandem protein expression systems (Abdeladim et al. 2019; Boone et al. 2019; Cai et al. 2013; Yang et al. 2021) or CRISPR-based approaches (Kim et al. 2021; Willems et al. 2020)); and (4) the fact that algorithms for spectral unmixing of fluorophores are beyond the formal training of many cell biologists and, conversely, live-cell imaging is beyond the formal training of many data scientists (Sommer and Gerlich 2013; Noorbakhsh et al. 2019).

This review focuses on the evolution of spectral unmixing algorithms in a language that appeals to the wet lab experimental cell biologist and the computational data analyst. We emphasized the analysis of spectral fluorescence data derived from fluorescent proteins, which are the most common fluorophores used in live-cell imaging.

Fluorescent proteins used in live-cell spectral imaging

Fluorescence microscopy in cell biology heavily relies on a wide range of dyes or fluorophores that label cellular structures or biomolecules (Vida and Emr 1995). However, despite the increase of new probes, such as quantum dots (Jaiswal and Simon 2015) and organelle-specific dyes (Tamura et al. 2020), the most common class of fluorophores in live-cell imaging are genetically encoded fluorescent proteins (Tsien 1998; Zhao et al. 2021).

Genetic engineering techniques create organisms producing genetically encoded fluorescent proteins by fusing a DNA sequence carrying the information for synthesizing a protein to a DNA sequence carrying the information for synthesizing a fluorophore (Chalfie et al. 1994; Thorn 2017). Genetically encoded protein fluorophores started with the discovery of green fluorescent protein (GFP) in jellyfish (Prasher et al. 1992) and the realization that GFP’s DNA sequence could be fused to almost any protein DNA sequence (Chalfie et al. 1994).

Imaging GFP-tagged proteins in living cells quickly revealed that GFP fluorescence properties, such as intensity, spectral shape, and anisotropy, are sensitive to intracellular acidity (pH), viscosity, redox state, ionic strength, and molecular crowding (Tsien 1998; Germond et al. 2016). The performance of GFP was improved, for instance, by creating a monomeric version called mEGFP (Zacharias et al. 2002) or a “superfolder” version, called sfGFP, that reduced the time required between its initial synthesis and its proper three-dimensional folding, known as maturation time (Balleza et al. 2018; Pédelacq et al. 2006). However, these GFP variants were spectrally indistinguishable, and new fluorophores were required to answer key cell biology questions such as whether two or more proteins colocalize or act in the same biochemical pathway (Lichtman and Conchello 2005).

The search for fluorophores with a different spectral signature from GFP led to engineering GFP’s DNA sequence to generate blue (Heim et al. 1994) and yellow (Ormö et al. 1996) fluorescent proteins. Eventually, new fluorescent proteins were discovered in organisms such as corals (Matz et al. 1999), algae (Nagel et al. 2003), crustaceans (Evdokimov et al. 2006), bacteria (Bellini and Papiz 2012), lancelets (Shaner et al. 2013), fish (Kumagai et al. 2013), and plants (Rodríguez-Pulido et al., 2016). Genetic and computer-aided engineering of fluorescent proteins has now produced fluorophores spanning the UV, visible, and IR range (Ai et al. 2006; Bindels et al. 2017; Chu et al. 2016; Bajar et al. 2016; Tsutsui et al. 2008). Thus, nowadays, the major constraint to visualizing multiple processes in living cells is not the lack of different fluorophores but the capacity to accurately quantify each fluorescent protein independently.

Fluorophore properties used in FSI

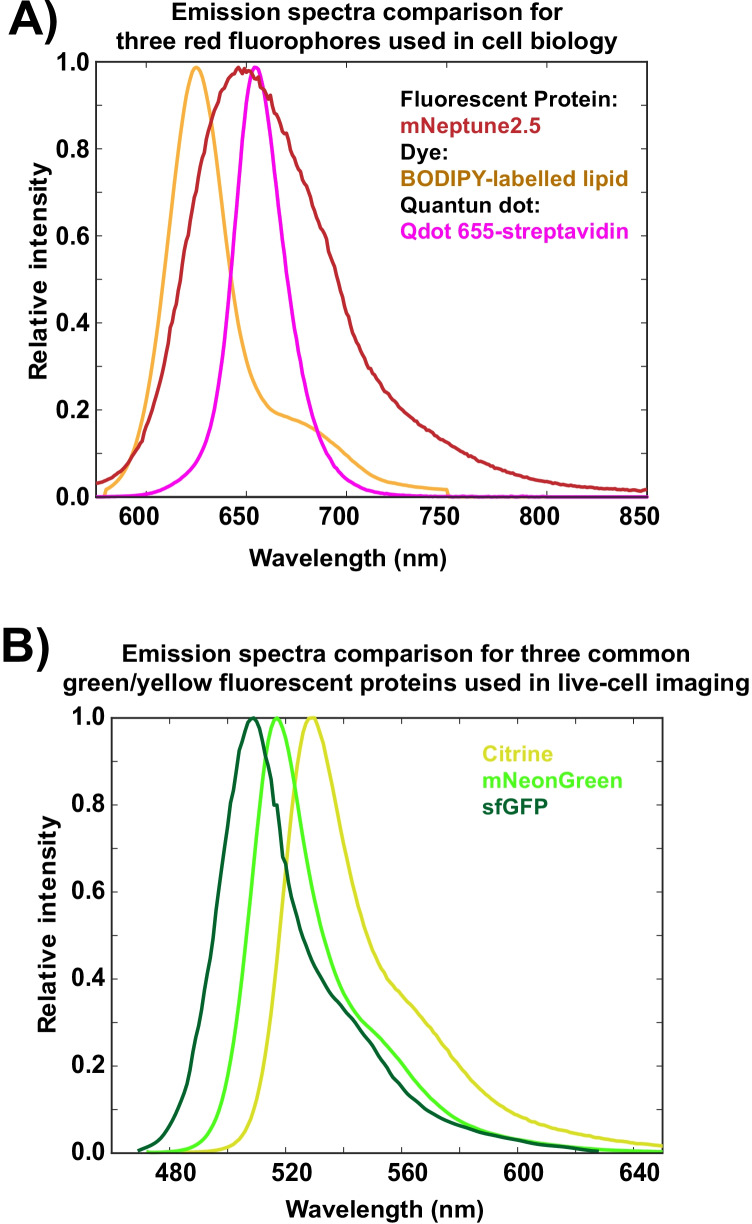
Differences in excitation and emission spectra are the most utilized properties to identify and quantify fluorophores in live-cell imaging (Deal et al., 2019). The excitation spectrum corresponds to the propensity of a fluorophore to absorb photons across multiple wavelengths. The emission spectrum corresponds to the propensity of a fluorophore to emit a photon at a certain wavelength. Fluorescence microscopy setups are usually optimized to illuminate the sample at the wavelength that matches the peak of the fluorophore’s excitation spectrum, while the detection system matches the peak of the emission spectrum. This strategy can detect several fluorophores with significantly different excitation/emission spectra; however fluorescent proteins have broad excitation/emission spectra (Chen et al. 2021; Lansford et al. 2001b; Schröck et al. 1996), especially compared with the excitation or emission spectra of other fluorophores used in cell biology, such as some BODIPY dyes or quantum dots (Fig. 2A) (Loudet and Burgess 2007). Broad excitation/emission spectra frequently overlap, leading fluorophores to be co-excited or co-detected, a problem called crosstalk or bleed-through (Fig. 2B). Co-detection of fluorescent proteins produces images with pixels that contain a mixture of fluorescent signals preventing direct quantitative analysis of individual fluorophores (Chen et al. 2021; Zimmermann et al. 2003; Haraguchi et al. 2002; Schröck et al. 1996). Thus, although the number of fluorescent proteins has expanded steadily, the overlap in their excitation/emission spectra has remained a challenge for quantifying individual fluorophores in cells expressing several fluorescent proteins.

Fig. 2.

Emission spectra comparison among common fluorophores and fluorescent proteins used in cell biology. A Reference emission spectra comparison of three fluorophores with similar emission peaks used in cell biology applications: the red fluorescent protein, mNeptune2.5 (Chu et al. 2014); the red lipid-conjugated BODIPY dye, CellTrace™ BODIPY® TR methyl ester (NCBI 2021); and Invitrogen™'s streptavidin-conjugated red quantum dot, Qdot® 655. Notice mNeptune2.5’s broader spectrum. B Reference emission spectra comparison of superfolder green fluorescent protein (sfGFP) (Pédelacq et al. 2006), mNeonGreen (Shaner et al. 2013), and Citrine (Griesbeck et al. 2001), three green/yellow fluorophores commonly used as genetically encoded tags to fluorescently label proteins. Despite the differences in their emission peaks, the fluorophores’ spectra significantly overlap, potentially leading to co-detection and preventing their simultaneous use in fluorescence microscopy. Spectra obtained from SearchLight Spectra Viewer from Semrock accessed on 11/29/2021

Beyond the identification of fluorophores based on their excitation/emission spectra, other fluorophore’s properties could be exploited for FSI including the time between the initial excitation of a fluorophore and its return to a relaxed state, known as fluorescence lifetime (Scipioni et al. 2021; Zhao et al. 2014), the capacity of a fluorophore to directly excite a second fluorophore, known as Förster resonance energy transfer (FRET) (Tsutsui et al. 2008; Haraguchi et al. 2002; Yang et al. 2021), the reduction of the fluorophore’s emission intensity under constant illumination, known as photobleaching or photostability (Orth et al. 2018), and the differential emission intensity along polarization axes, known as fluorescence anisotropy (Esposito and Venkitaraman 2019). All of the previous properties could be combined to identify multiple fluorescent targets simultaneously (Esposito and Venkitaraman 2019); however, the excitation/emission spectra are by far the most utilized fluorophore properties used in live-cell imaging.

Experimental optimization to deal with fluorophores’ spectral overlap

The detection of multiple fluorophores with overlapping excitation/emission spectra can be achieved, in part, by careful design of the spectral imaging setup (see Fig. 1 in Hiraoka et al. (2002) for schematics of FSI designs and table 3 in Li et al. (2013) for an extensive list of spectral imaging setups). Multiple fluorophores can be excited by light sources that match their excitation peaks, such as arrays of wavelength-specific LEDs (Arguello-Miranda et al. 2018), arrays of wavelength-specific lasers (Cohen et al. 2018), or tunable lasers that can generate several different wavelengths (Esposito and Venkitaraman 2019). The specificity of fluorophore excitation is also enforced by selecting wavelengths or altering light source properties using devices such as optical filters (Valm et al. 2016; Orth et al. 2018; Jeffet et al. 2021), interferometers (Schröck et al. 1996; Zhao et al. 2014), polarizers, gratings, and prisms (Valm et al. 2017; Wang et al. 2019c; Esposito and Venkitaraman 2019). Combinations of optical filters, such as bandpass filters or tunable filters, can increase the specificity of fluorophore excitation/detection by selecting specific wavelengths from the excitation or emission light source (Arguello-Miranda et al. 2018; Argüello-Miranda et al. 2022). Thin-film tunable filters (TFTF) (Favreau et al. 2013; Vissa et al. 2020), acousto-optic tunable filters (AOTF) (Chen et al. 2021; Garbacik et al. 2018), and liquid crystal tunable filters (LCTF) (Lansford et al. 2001; St-Georges-Robillard et al. 2018) are commonly used in spectral imaging because, unlike wavelength-fixed bandpass filters, several excitation wavelengths can be produced by a single tunable filter (Deal et al. 2019).

Optimized FSI setups, however, seldom prevent the co-detection of fluorescent proteins in live-cell imaging because, beyond overlapping excitation/emission spectra, the imaging process is further constrained by noise, background fluorescence, cellular autofluorescence, and phototoxicity (Icha et al. 2017; Oheim 2010; Rino et al. 2009). In most cases, even after considering the previous factors, the quantification of individual fluorophores is only possible after a proper deployment of spectral unmixing algorithms.

Image acquisition constraints in live-cell fluorescence spectral imaging

Phototoxicity

Avoiding phototoxicity is the first general challenge of live-cell fluorescence imaging (Kilian et al. 2018; Kiepas et al. 2020). For this purpose, imaging wavelengths are usually set above 400 nm to prevent UV-driven deleterious reactions in biomolecules, which can trigger stress responses and activate cell surveillance mechanisms such as the DNA damage checkpoint (Icha et al. 2017; Olivieri et al. 2020). In addition, the irremediable oxidative damage produced by light-generated free radicals, such as reactive oxygen species (ROS), must be kept in check by reducing the light source intensity and exposure times (Laissue et al. 2017).

Weak signals

The use of dim light sources and reduced exposure times to prevent phototoxicity (Kiepas et al. 2020), and the use of optical filters to achieve specific fluorophore excitation/emission, constraint live-cell fluorescent microscopy to produce weak signals (Mandracchia et al. 2020; Mafi et al. 2019). Thus, spectral unmixing algorithms for live-cell imaging can be thought of as approaches to identify weak fluorescent signals in a noisy environment affected by background fluorescence and cellular autofluorescence (Shi et al. 2020b).

A common strategy to detect weak signals in FSI setups is the use of very sensitive detectors such as electron-multiplying, intensified, or electron-bombarded charge-coupled devices (CCDs) (Gómez-García et al. 2018; Chen et al. 2021; Cubeddu et al. 2002; Hirvonen et al. 2015), complementary metal–oxide–semiconductor (CMOS) cameras coupled to image intensifiers (Görlitz et al. 2017; Yoon et al. 2009), single-photon avalanche diodes (SPADs) devices (Garbacik et al. 2018; Connolly et al. 2021), and photomultiplier tubes (PMTs) (Valm et al. 2017; Abdeladim et al. 2019; McRae et al. 2019). These devices, however, cannot control most sources of noise, background fluorescence, and cellular autofluorescence, which must be addressed experimentally or algorithmically.

Noise

Noise in fluorescence microscopy can be classified as shot noise, which is signal-dependent and follows a Poisson distribution, and read noise, which is signal-independent and follows a gaussian distribution (Foi et al. 2008). Read noise has a constant variation that depends on factors such as thermal fluctuations and inaccuracies in the detectors (Waters 2009). On the other hand, shot noise is the square root of the average detected photons (Garini et al. 1999). Both types of noise have a stronger effect on weak signals, which can be illustrated by calculating the signal-to-noise ratio (SNR) given by the total number of photons divided by the noise (Garini et al. 1999; McRae et al. 2019; Okada et al. 2016). For instance, assuming only shot noise in a pixel, a signal with an average of 4 photons has a SNR (4/$\surd$ 4) of 2, indicating that the value in the pixel is half noise, whereas a signal of 64 photons has a SNR (64/$\surd$ 64) of 8, indicating that the value in the pixel is only 12.5% noise.

Prevention of phototoxicity, however, forces live-cell spectral imaging to produce weak signals, and noise sources must be controlled by post-acquisition image filtering algorithms that model noise using Poisson/Gaussian mixtures (Foi et al. 2008), hidden Markov models (Yang and Lee 2015), or generalized threshold assessment (Luisier et al. 2011), among others.

Background fluorescence and autofluorescence

When imaging cells in vitro conditions, background fluorescence could be considered a source of noise generated by the cell culture medium, exchanges of cell culture medium, and the material of the structure used for cell culture such as glass slides, Petri dishes, and microfluidic devices (Ettinger and Wittmann 2014; Cordina et al. 2018; Gharia et al. 2020). Background fluorescence can be alleviated by using low-autofluorescence cell culture medium (Ettinger and Wittmann 2014; Cordina et al. 2018) and assessing the fluorescent properties of the device for cell culture (Shi et al. 2020b). When imaging cells in tissues, dedicated experimental and algorithmic approaches must be used to control the non-homogenous fluorescent background produced by out-of-focus cells and scattered light (Helmchen and Denk 2005; Mansfield et al. 2005).

Cellular autofluorescence could be considered another source of noise generated by fluorescent molecules in living cells such as aromatic amino acids (Monici 2005), metabolites (García-Plazaola et al. 2015), protein aggregates (Tikhonova et al. 2018), and certain enzymes and cofactors (Kolenc and Quinn 2019). Cellular autofluorescence is a double-edged sword; on the one hand, autofluorescence can be used for label-free tracking of cellular metabolism and the stress status of cells (Kolenc and Quinn 2019; Surre et al. 2018). On the other hand, autofluorescence signals can outcompete fluorescently tagged proteins and are hard to model since they are affected by the cell culture medium and the stress or differentiation status of the cell (Surre et al. 2018; Walsh et al. 2021; Bertolo et al. 2019; Miranda-Lorenzo et al. 2014). Autofluorescence can be experimentally quantified by simultaneously imaging a mixed population of blank cells (without any of the target fluorophores) and cells carrying fluorophores (Argüello-Miranda et al. 2022).

Measuring individual fluorophores in the presence of background fluorescence, autofluorescence, and Poisson/gaussian noise, while preventing phototoxicity, is the essence of live-cell spectral fluorescence microscopy. Under these conditions, identifying and unmixing the signals of single fluorophores requires data-driven or computational tools (Smith et al. 2020a; Wang et al. 2019c; Garbacik et al. 2018; St-Georges-Robillard et al. 2018; Valm et al. 2017).

The analysis of single-pixel spectra and multidimensional images or data cubes

The judicious selection of fluorophores, light sources, and optical filters can maximize the capacity of spectral microscopy to detect images corresponding to single fluorophores (Arguello-Miranda et al. 2018; Valm et al. 2017). However, even carefully designed imaging setups are unable to prevent crosstalk and bleed-through between excitation/detection channels when imaging more than five fluorophores (Argüello-Miranda et al. 2022). Once the imaging system surpasses its capacity to produce fluorophore-specific images, data-driven approaches are necessary to reveal the proportion of fluorophores contained in a pixel and reconstruct approximations of fluorophore-specific images (Orth et al. 2018; Seo et al. 2021; Rehman and Qureshi 2021; Ozkan et al. 2019).

The problem of assessing bleed-through between detection channels in fluorescence microscopy has been traditionally solved by experimentalists’ careful visual inspection of whole images taken at different wavelengths. In FSI, however, distinguishing fluorophores using single-pixel spectra at multiple wavelengths escapes a human-based approach (Sommer and Gerlich 2013), and automated strategies for single-pixel analysis are necessary (Silva et al. 2019; Noorbakhsh et al. 2019; Zhao et al. 2021; Megjhani et al. 2017).

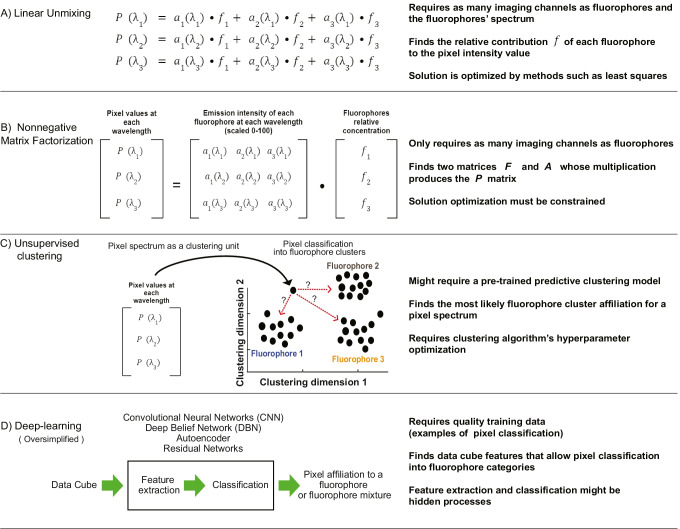
Most approaches to identify single fluorophores in spectral imaging use single-pixel spectra information to express the value registered at a single pixel as a precise mixture of different fluorophores. Such methods have evolved from linear models (Zimmermann et al. 2002; Montcuquet et al. 2010) into clustering algorithms for single-pixel classification (Rehman and Qureshi 2021; McRae et al. 2019) and deep learning approaches for spectral data cube analysis (Manifold et al. 2021; Rehman and Qureshi 2021; Smith et al. 2020a; Bhatt and Joshi 2020).

Data preprocessing

FSI often requires tailored raw data preprocessing to account for variable background fluorescence or illumination, autofluorescence, and noise (Lansford et al. 2001). Image preprocessing can include normalization or scaling pixel values (Zimmermann et al. 2002), the use of noise-canceling algorithms (Okada et al. 2016), foreground detection through thresholding (Leavesley et al. 2012), flat-field correction when uniform illumination is not possible (Waters 2009; Wolf 2003), and deconvolution of maximum intensity projections (Webb and Brown 2013). In the following sections, proper image preprocessing is assumed before the use of spectral unmixing algorithms.

Linear unmixing

The simplest model to identify the fluorophores present at a single pixel is linear unmixing (Cohen et al. 2018; Zimmermann 2005). This method assumes that the intensity value of a pixel $\mathit{p}$, in a wavelength-specific image, is the sum of the contributions of each fluorophore expressed as algebraic terms of the form ${\mathit{a}}_{\left(\mathit{\lambda }\right)}\bullet \mathit{f}+\mathit{n}$ where $\mathit{f}$ corresponds to the relative concentration of a fluorophore in the pixel, ${\mathit{a}}_{\left(\mathit{\lambda }\right)}$ corresponds to the expected intensity of a fluorophore at the imaging $\mathit{\lambda }$ wavelength, and $\mathit{n}$ represents noise (Zimmermann 2005; Hiraoka et al. 2002). For simplicity, noise terms are initially ignored in the following explanation.

A single pixel $\mathit{p}$ in an image containing three fluorophores acquired at ${\mathit{\lambda }}_1$ wavelength, can be represented as follows:

$${\mathit{p}}_{\left({\mathit{\lambda }}_1\right)}={\mathit{a}}_{1\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_1+{\mathit{a}}_{2\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_2+{\mathit{a}}_{3\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_3$$ 1

Assuming three wavelength-specific images, the pixel values at each $\lambda$ wavelength produce the following system of algebraic linear equations:

$$\begin{array}{c}{\mathit{p}}_{\left({\mathit{\lambda }}_1\right)}={\mathit{a}}_{1\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_1+{\mathit{a}}_{2\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_2+{\mathit{a}}_{3\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_3\\ {\mathit{p}}_{\left({\mathit{\lambda }}_2\right)}={\mathit{a}}_{1\left({\mathit{\lambda }}_2\right)}\bullet {\mathit{f}}_1+{\mathit{a}}_{2\left({\mathit{\lambda }}_2\right)}\bullet {\mathit{f}}_2+{\mathit{a}}_{3\left({\mathit{\lambda }}_2\right)}\bullet {\mathit{f}}_3\\ {\mathit{p}}_{\left({\mathit{\lambda }}_3\right)}={\mathit{a}}_{1\left({\mathit{\lambda }}_3\right)}\bullet {\mathit{f}}_1+{\mathit{a}}_{2\left({\mathit{\lambda }}_3\right)}\bullet {\mathit{f}}_2+{\mathit{a}}_{3\left({\mathit{\lambda }}_3\right)}\bullet {\mathit{f}}_3\end{array}$$ 2

In this equation system, the values of the pixel $\mathit{p}$ and the expected fluorophore’s intensities $\mathit{a}$ change in each $\mathit{\lambda }$ wavelength-specific image, but the relative concentration of fluorophores ${\mathit{f}}_1,{\mathit{f}}_2,{\mathit{f}}_3$ should be the same (Lansford et al. 2001). The equation system can be solved by entering the pixel values ${\mathit{p}}_{\left({\mathit{\lambda }}_1\right)},{\mathit{p}}_{\left({\mathit{\lambda }}_2\right)},{\mathit{p}}_{\left({\mathit{\lambda }}_3\right)}$ and the expected intensities of the fluorophores $\mathit{a}$ at each $\mathit{\lambda }$ imaging wavelength, which returns the relative concentration of fluorophores in the pixel (Zimmermann 2005).

Importantly, solving the linear equation system involves at least two scaling operations. First, all fluorophores’ spectra must be scaled between 0 and 1 and their expected intensities must be entered at unit concentration, that is, all expected fluorophores intensities in a pixel at a imaging wavelength must add to 1 (Lansford et al. 2001). Second, the solutions for each fluorophore’s relative concentration are also scaled so that their sum is one (Zimmermann 2005).

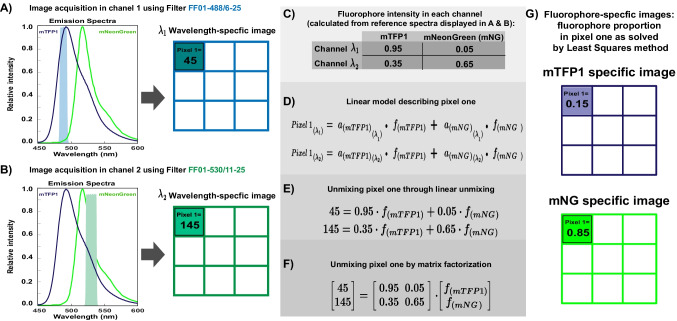
While pixel values are obtained experimentally during image acquisition (Fig. 3A and B), the expected intensity of a fluorophore at a specific wavelength must be derived from a reference spectrum (Fig. 3A–C) or by determining the fluorophore’s spectrum under experimental conditions (Valm et al. 2011; Mylle et al. 2013).

Fig. 3.

Linear unmixing model for spectral imaging data. A–B, left Schematic image acquisition showing the reference emission spectra of monomeric teal fluorescent protein one, mTFP1 (Ai et al. 2006), and the monomeric green fluorescent protein mNeonGreen (Shaner et al. 2013). The shaded area indicates the wavelength range of the detection channel generated using the bandpass filters A FF01-488/6–25 (light blue) and B FF01-530/11–25 (light green) from Semrock. A–B, right Schematic matrix representation of the mixed images collected by the wavelength-specific channels. For simplicity, only the intensity value of pixel one is shown. C Normalized fluorophores’ expected intensities at each detection channel are derived by calculating the approximated fluorophore spectrum area that falls in the wavelength range allowed by the filter set (shaded areas in A). D Linear model showing the intensity value of pixel number one as a linear combination of the multiplication of each fluorophore's expected intensity $\mathit{a}$ by each fluorophore’s relative concentration $\mathit{f}$ at the imaging wavelength range $\mathit{\lambda }$. E Linear equation system to solve the relative concentration of fluorophores $\mathit{f}$ in pixel number one. F Matrix factorization representation of the linear equation system to solve the relative concentration of fluorophores $\mathit{f}$ in pixel number one. G Schematic unmixed fluorophore-specific images showing the linear unmixing solution of pixel number one as approximated by the least squares method (Lloyd 1982a) using the Python function numpy.linalg.lstsq()

The linear unmixing equation system does not have a single solution; that is, different relative concentrations of fluorophores could produce similar pixel values, and the best approximation can be found using methods such as least squares (Lloyd 1982b). Solving the linear unmixing equation system reveals the proportions of each fluorophore contained in each pixel (Fig. 3D–F), producing fluorophore-specific images in which the original pixel intensity value is replaced by the calculated relative fluorophore concentration (Fig. 3G) (Zimmermann et al. 2003).

In linear unmixing methods, homogeneous background fluorescence can be treated as an “extra” fluorophore (Zimmermann 2005), and Gaussian or Poisson noise terms can be directly added to the linear equation terms (Wang and Chang 2006). For a pixel containing two fluorophores, homogenous spectral background and, for instance, an additive mixture of Poisson-Gaussian noise at the $\mathit{\lambda }$ imaging wavelength, the linear unmixing equation becomes:

$${\mathit{p}}_{\left({\mathit{\lambda }}_1\right)}={\mathit{a}}_{1\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_1+{\mathit{a}}_{2\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_2+{\mathit{a}}_{\mathit{b}\mathit{g}\left({\mathit{\lambda }}_1\right)}\bullet {\mathit{f}}_{\mathit{b}\mathit{g}}+\mathit{n}$$ 3

where ${\mathit{a}}_{\mathit{b}\mathit{g}}$ equals the intensity of background at $\mathit{\lambda }$ wavelength, ${\mathit{f}}_{\mathit{b}\mathit{g}}$ equals the relative proportion of spectrally homogenous background fluorescence, and the term $\mathit{n}$ is the result of adding Poisson and Gaussian noise. However, accurate treatments of autofluorescence or spectrally uniform background are seldom reported or assumed to be controlled by algorithms such as the maximum noise fraction transformation (Green et al. 1988).

Several methods have attempted to improve the efficiency of linear unmixing models, including vertex component analysis (VCA) (Nascimento and Dias 2005), the N-FINDR algorithm (Winter 1999), independent component analysis (ICA) (Wang and Chang 2006), and alternating projected subgradients (APS) (Zymnis et al. 2007). However, these methods assume that pixels’ intensities originate from linear mixtures and that reference spectra remain unchanged and independent from other fluorophores under experimental conditions, which might not always be the case (Mylle et al. 2013; Balleza et al. 2018). A solution to these limitations is to determine the spectrum of each fluorophore under experimental conditions, which is the base for methods such as spectral deconvolution (Ricard and Debarbieux 2014). Nonetheless, the experimental determination of spectra is a time-consuming task when handling large numbers of fluorophores or in time-lapse experiments (Valm et al. 2016; Zimmermann 2005). For large data sets, linear unmixing might also be computationally intensive, and its accuracy decreases due to strong spectral overlap, inaccurate spectral information, low-SNR acquisitions, and the presence of nonlinear effects such as quenching, FRET, photobleaching, or multiphoton excitation (Li et al. 2013; Smith et al. 2020a; Tsurui et al. 2000). Crucially, linear unmixing does not provide a threshold criterion to classify single pixels according to fluorophores which must be addressed by data post-processing (Lansford et al. 2001).

Nonnegative matrix factorization

The search for more computationally efficient methods to unmix fluorescent spectral imaging data led to the realization that the linear unmixing equation can be represented as a matrix multiplication problem (Pauca et al. 2006; Montcuquet et al. 2010). In fact, the terms on the right side of the linear unmixing equation system in Eq. 2 are a matrix multiplication operation in which a matrix containing the expected fluorophores’ intensities at each wavelength $\mathit{a}$ is multiplied by a vector containing the relative fluorophore concentrations $\mathit{f}$ (compare also Fig. 3E and F). Equation 2 can be written in matrix notation as follows:

$$\left[\begin{array}{c}{\mathit{p}}_{\left({\mathit{\lambda }}_1\right)}\\ {\mathit{p}}_{\left({\mathit{\lambda }}_2\right)}\\ {\mathit{p}}_{\left({\mathit{\lambda }}_3\right)}\end{array}\right]=\left[\begin{array}{ccc}{\mathit{a}}_{1\left({\mathit{\lambda }}_1\right)}& {\mathit{a}}_{2\left({\mathit{\lambda }}_1\right)}& {\mathit{a}}_{3\left({\mathit{\lambda }}_1\right)}\\ {\mathit{a}}_{1\left({\mathit{\lambda }}_2\right)}& {\mathit{a}}_{2\left({\mathit{\lambda }}_2\right)}& {\mathit{a}}_{3\left({\mathit{\lambda }}_2\right)}\\ {\mathit{a}}_{1\left({\mathit{\lambda }}_3\right)}& {\mathit{a}}_{2\left({\mathit{\lambda }}_3\right)}& {\mathit{a}}_{3\left({\mathit{\lambda }}_3\right)}\end{array}\right]\bullet \left[\begin{array}{c}{\mathit{f}}_1\\ {\mathit{f}}_2\\ {\mathit{f}}_3\end{array}\right]$$ 4

For simplicity, in the previous example (Eq. 4), the factorization of a single pixel spectrum without noise is shown. However, when dealing with multiple images acquired at multiple wavelengths, the spectra of individual pixels can be represented as the columns of a matrix $\mathit{P}$ which can be expressed as the multiplication of the matrix representing the expected intensities of each fluorophore at each wavelength $\mathit{A}$ by a matrix representing the relative concentration of the fluorophores $\mathit{F}$, or for short:

$$\mathit{P}\approx \mathit{A}\bullet \mathit{F}$$ 5

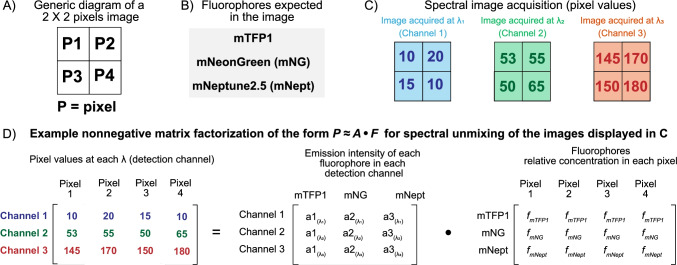
When represented as a matrix operation, spectral unmixing is equivalent to a matrix factorization problem (Fig. 4A–D) that consists in finding two matrices ( the expected spectra intensities $\mathit{A}$ and the relative fluorophore concentrations $\mathit{F}$) whose multiplication produces a good approximation of the matrix containing the $\mathit{P}$ pixel values (Wei and Wang 2020).

Fig. 4.

Schematic nonnegative matrix factorization spectral unmixing. A Generic diagram of a 2 × 2 pixels image. B Fluorophores assumed to be present in the image. C Spectral image acquisition using three different detection channels showing individual pixel values. D Example of a nonnegative matrix factorization algorithm that could calculate the relative fluorophore concentration in each pixel. Notice how, in this approach, each 2 × 2 image is “unraveled” into a 1 × 4 row vector whose concatenation creates the matrix to be factorized

As with linear unmixing models, matrix factorization can take advantage of theoretical or experimental determination of the fluorophores spectra to calculate $\mathit{P}$, a case known as semi-blind matrix factorization because the fluorophore spectra information defines matrix $\mathit{A}$ a priori (Rossetti et al. 2020). Blind matrix factorization algorithms have also been proposed, which can generate both the fluorophores’ intensities matrix and the fluorophores’ relative concentration matrix without precise a priori knowledge about the fluorophores’ spectra (Pengo et al. 2013; Montcuquet et al. 2010; Seo et al. 2021; Jiménez-Sánchez et al. 2019; Neher et al. 2009). In principle, blind matrix factorization algorithms could bypass the linear unmixing models’ need for reference spectra (which is an example of a general problem known as blind source separation (Sawada et al. 2019)). However, most blind matrix factorization algorithms tend to become less efficient as the number of fluorophores or spectral overlap increases; in addition, the number of fluorophores should not outnumber the detection channels (Wei and Wang 2020; Seo et al. 2021).

Examples of matrix factorization deployed in fluorescence spectral unmixing include approaches based on singular value decomposition (SVD) (Tsurui et al. 2000) and nonnegative matrix factorization (NMF) (Lee and Seung 1999). In general, these approaches iteratively optimize the values in the matrices of relative fluorophore concentrations $\mathit{F}$ and expected fluorophore intensity $\mathit{A}$ until their product approximates the values in the pixel spectrum matrix $\mathit{P}$ (Huang et al. 2015). However, the process to approximate $\mathit{P}$ can generate a high number of solutions, and optimization constraints must be imposed on the matrix factorization algorithms to efficiently find the best solution without creating high computational complexity or requiring large amounts of a priori knowledge (Ertürk 2020; Huck et al. 2010; Qian et al. 2011).

Nonnegative matrix factorization has arisen as the basis of a large number of spectral unmixing algorithms because it embodies natural constraints of spectral imaging, such as the fact that the intensity and concentration of a fluorophore are invariably positive numbers (Montcuquet et al. 2010; Pauca et al. 2006; Yokota et al. 2015). NMF algorithms can easily incorporate a priori optimization constraints, such as the expected abundance of the fluorophores (Ertürk 2020; Horisaki and Tanida 2010; Peharz and Pernkopf 2012), and assumptions about the structure of the matrices, such as their sparsity, which refers to the number of non-zero elements contained in a matrix (He et al. 2016; Aggarwal and Majumdar 2016). Sparsity constraints can be implemented by assuming that mixed pixels only combine a few fluorophores (He et al. 2016). For instance, in a sample containing six fluorescent markers, an NMF sparsity constraint could state that mixed pixels can only be the combination of two fluorophores, implying that the values of the remaining four fluorophores will be equated to zero. Matrices with great sparsity can be rapidly processed using algorithms derived from fields such as compressed sensing (Liu et al. 2016). In addition, spatial information from the sample can be used as a constraint by specifying the coordinates of pixels expected to contain a precise mixture of fluorophores, for instance, when fluorescently labeled proteins interact or colocalize in a specific intracellular location (Wang et al. 2019c; Megjhani et al. 2017; Horisaki and Tanida 2010).

Spectral unmixing NMF algorithms can also include noise sources, such as Poisson/Gaussian noise (Theis et al. 2009; Qin et al. 2016), by adding a noise term $\mathit{N}$ to Eq. 5:

$$\mathit{P}\approx \mathit{A}\bullet \mathit{F}+\mathit{N}$$ 6

Background fluorescence can be quantified using regularized NMF (Qin et al. 2016) or affine NMF (aNMF,(Rossetti et al. 2020)) approaches. In contrast to linear unmixing models, in aNMF background fluorescence is not treated as another fluorophore, but it is assumed to be an “offset” of the noise term (Rossetti et al. 2020) obtained by multiplying a vector composed of the background’s fluorescence spectrum $b$ by a row vector of ones $1$:

$$\mathit{P}\approx \mathit{A}\bullet \mathit{F}+\mathit{b}\bullet 1+\mathit{N}$$ 7

Autofluorescence signals can also be separated by advanced NMF approaches, such as the semi-blind sparse affine spectral unmixing (SSASU) algorithm (Rossetti et al. 2020), sparse constrained NMF (Montcuquet et al. 2011), and specific read noise considerations (Woolfe et al. 2011). However, the use of more complicated NMF algorithms to deal with fluorescent signals, noise, background, and autofluorescence can become computationally demanding (Theis et al. 2009).

Clustering algorithms

Constrained NMF is actually a widely used clustering algorithm in machine learning (Lee and Seung 1999). This insight leads to the realization that the problem of spectral unmixing is indistinguishable from clustering and classification tasks in data science. In fact, NMF applied to spectral imaging can be understood as a clustering task in which pixels are classified as belonging to different fluorophore clusters based on similarities of spectral signatures (Montcuquet et al. 2010). The interpretation of NMF unmixing as clustering (Li et al. 2017; Oh et al. 2021) bears a crucial implication: clustering algorithms could classify the pixels of spectral images into clusters corresponding to fluorophores without reference spectra information and independently of the number of imaging channels (Fig. 5C).

Fig. 5.

Evolution of spectral unmixing models. A System of linear equations to solve the relative concentration of three fluorophores in a mixed pixel $\mathit{p}$. The pixel intensity value is assumed to be the sum of terms composed of each fluorophore’s expected intensity $\mathit{a}$ multiplied by each fluorophore’s relative concentration $\mathit{f}$ at the imaging wavelength $\mathit{\lambda }$. B Matrix factorization representation of a linear equation system to solve the relative concentration of fluorophores in a pixel. The pixel values matrix $\mathit{P}$ is assumed to result from multiplying the fluorophore expected intensities matrix $\mathit{A}$ by the fluorophore relative concentrations matrix $\mathit{F}$. C A clustering approach for assigning a single pixel spectrum to a particular fluorophore that is represented as a data cluster. Notice how the single pixel spectrum could be compressed to a single value in the clustering space (solid arrow) before being affiliated to a cluster by calculating, for instance, the minimum Euclidean distance between the pixel spectrum data point and the center (centroid) of the clusters representing different fluorophores (red dotted arrows). D Deep learning approach to spectral unmixing. Instead of assuming linearity or focusing on the single pixel spectrum, deep learning approaches use the entire data cube to find relevant features or patterns for single pixel classification into fluorophores. Green arrows represent an oversimplified information flow in a deep learning architecture designed to extract features (feature extraction) from a data cube and classify pixels (classification) according to fluorophores

Learning unsupervised means of spectra (LUMoS, McRae et al. 2019) is an example of an unmixing algorithm based on clustering that does not require reference spectra or a precise number of imaging channels. LUMoS uses a staple machine learning algorithm known as k-means (Arthur and Vassilvitskii 2007) to separate pixels into clusters corresponding to fluorophores, autofluorescence, or background. “Means of Spectra” does not refer to spectral data but to the center (centroid) of the clusters corresponding to the fluorophores that are used to classify pixels. Interestingly, LUMoS assumes that neighboring pixels often belong to the same structure and applies a median filter to the raw image, fusing neighboring pixels, before clustering. Furthermore, LUMoS assumes that each pixel is occupied by a single fluorophore and classifies mixed pixels as new clusters. Although this approach makes the affiliation of a pixel to a cluster unambiguous, it could lead to the generation of many clusters when multiple fluorophores are highly colocalized (McRae et al. 2019). A solution to this problem is to generate a predictive clustering model based on previously classified data.

A trained clustering model is an algorithm that has been optimized using past clustered results that are known to be correct and constitute a “ground truth” (Sommer and Gerlich 2013). The initial algorithm is iteratively forced to improve until its results recapitulate the clustering in the ground truth data set (Chicco 2017). Assuming that the number of clusters in a spectral imaging data set is equivalent to the number of fluorophores, spectral clustering algorithms could be classified as follows: (1) supervised, if the number of fluorophores is known a priori; (2) semi-supervised, if the number of fluorophores is specified within a range, for instance, by including background fluorescence, noise, or bona fide colocalized signals as potential additional clusters; and (3) blind or unsupervised, if the number of fluorophores is not defined before the clustering task. Although blind clustering algorithms hold the promise of revealing unsuspected correlations in a spectral data set, for instance, by showing that two fluorescent signals always colocalize, there is no universal approach to determine the optimum number of clusters in a data set (Strehl and Ghosh 2003; Șenbabaoğlu et al. 2014). Although some approaches such as the silhouette method (Rousseeuw 1987), the Caliński-Harabasz criterion (Caliński and Harabasz 1974), and consensus or ensemble clustering (Monti et al. 2003) can provide an educated guess of the maximum number of clusters in a data set, the final decision can depend on empiric factors and experimental context.

A general workflow for creating a trained clustering algorithm for spectral imaging could include the following steps (Chicco 2017; Sommer and Gerlich 2013): (1) data points (pixels groups, pixel spectra) are normalized and their index randomized; (2) data points are split into three data sets: 50% for training, 30% for validation, and 20% for testing; (3) the training data set is initially clustered using different algorithms, such as k-means (McRae et al. 2019) or support vector machines (SVM) (Yang et al. 2016; Shi et al. 2020a), which in turn can be optimized by changing their specific parameters (also known as hyperparameters) such as including spatial information, number of clusters, and criterium or distance metric to determine cluster affiliation of a data point; (4) the validation data set is labeled by experienced researchers and becomes “ground truth”; (5) clustering algorithms are iteratively optimized by comparing their clustering solutions to the “ground truth” using a measure of classification quality such as a multiclass Matthews’s coefficient or a loss function; (6) the best-performing clustering model is deployed for clustering the test data set and cross-validated with orthogonal approaches if possible; and (7) the best-performing trained algorithm is used to classify future data points, which in this case correspond to pixels from new images. In this approach, the success of the clustering algorithm heavily depends on the quality of the training data and the correctness of the ground truth (Rajkomar et al. 2019; Silva et al. 2019). Since human-classified data or human-defined features usually define the ground truth, the clustering results will recapitulate subject biases (Sommer and Gerlich 2013).

Deep learning

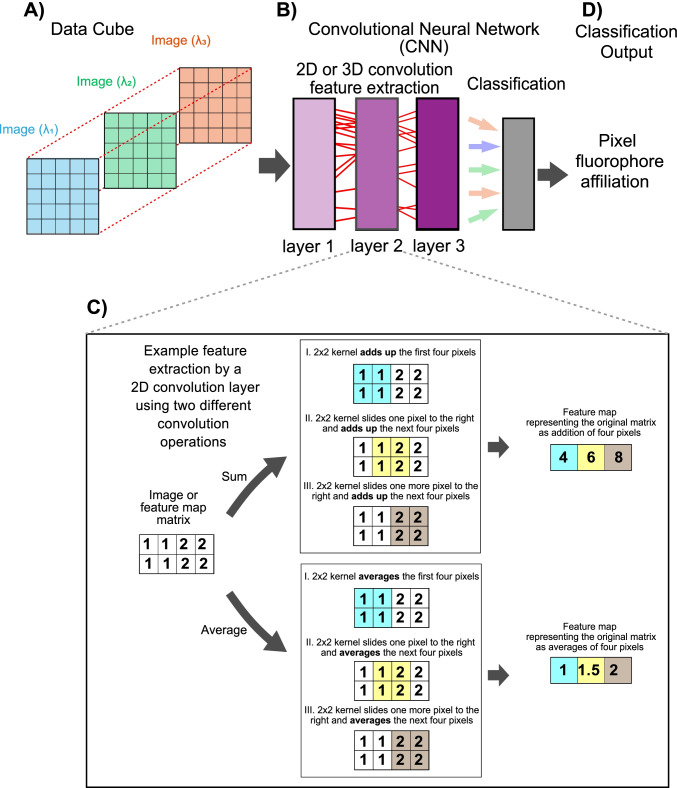
Deep learning offers a significant expansion of clustering models for spectral unmixing (Bhatt and Joshi 2020; Belthangady and Royer 2019). In contrast to most clustering algorithms that use human-defined features for data cube analysis, such as pixel intensity, deep learning automatically identifies classification-relevant features (Manifold et al. 2021). A deep learning system of algorithms, or architecture, uses a set of correctly classified training data to identify the pixel—or image—features that lead to successful classification (Fig. 5D) (Belthangady and Royer 2019; Wang et al. 2019a; Smith et al. 2020). Different types of deep learning architectures, such as convolutional neural networks (CNN) (Ochoa et al. 2020), autoencoders (Wang et al. 2019b; Ozkan et al. 2019), and deep belief networks (DBN) (Chen et al. 2015), could be potentially applied for spectral unmixing in live-cell imaging, as they have been deployed in remote-sensing applications (Aggarwal and Majumdar 2016; Bhatt and Joshi 2020; Bioucas-Dias et al. 2012; Ozkan et al. 2019).

Deep learning algorithms are composed of layers of operations that reduce the matrix representing an image or a data cube to a compressed matrix called feature map. Successful algorithms for image analysis, such as CNNs (Fig. 6A–B), are composed of layers of iterative matrix operations that reduce an image or data cube to its key features (Bhatt and Joshi 2020). Convolution refers to compressing a section of the original image to a single pixel in the feature map matrix. This operation scans the original matrix, sliding the image section, or kernel, to be compressed, for instance, one pixel at a time (Fig. 6C). The resulting “layer” comprises different feature maps resulting from different convolution operations that scanned the original matrix (Fig. 6C). The “depth” of the network depends on how many times the same process is applied to the feature maps. Deep learning algorithms first produce feature maps of the image and then feature maps of the feature maps and use this highly distilled information to predict pixel classification. By using training data to evaluate the importance, or weight, of each feature map for successful classification, this process can identify highly efficient, although also highly abstracted, features for single pixel classification (Fig. 6D). Although deep learning spectral unmixing does not require any prior information about the fluorophores or the imaging setup, it is in most cases limited by the availability of training data and the researchers’ acceptance that after the initial feature extraction layers, the feature extraction process is hard to follow and becomes “hidden” (Tajbakhsh et al. 2016).

Fig. 6.

Schematic representation of a convolutional neural network (CNN) for data cube analysis using 2D convolution. A A data cube, or any other multidimensional representation of the spectral imaging data, is used as input for deep learning approaches. B The schematic CNN uses three feature extraction layers to produce feature maps of the data cube. The feature extraction process through convolution is continued in each layer using the feature maps produced by the previous layer as input. C Minimalistic schematic of feature extraction through convolution in which a kernel, or defined area in pixels, is used to scan a feature map image using two different oversimplified operations, “sum” and “average.” Notice how the original feature map image has two rows and four columns, whereas, after convolution, it is reduced to one row of three pixels containing the result of the scanning process. The deep learning algorithms can find pixel classification-relevant features by selecting the feature maps that lead to successful pixel classification based on training data. D Based on features found to be good predictors of a pixel’s fluorophore affiliation, pixels in the data cube are assigned to fluorophores or combinations of fluorophores

Unmix multiple emissions (UNMIX-ME) (Smith et al. 2020a) exemplifies an unmixing algorithm for fluorescence microscopy that uses both spectral and fluorescence lifetime imaging microscopy (FLIM) data for fluorophore unmixing. UNMIX-ME uses a CNN architecture with 2D (for images) and 3D (for data cubes) convolution layers for feature extraction. Interestingly, UNMIX-ME was trained on simulated data sets, which overcame the need for collecting a large amount of experimental training data. The algorithm was validated by processing and unmixing in vitro and in vivo data sets, including FRET and infrared spectral imaging information.

The capacity to use any pixel-associated data to identify fluorophores is the most significant promise of deep learning for spectral unmixing (Smith et al. 2020; Rehman and Qureshi 2021). As seen in remote sensing, the classification of pixels in a data cube improves by combining features beyond the spectral information, such as spatial information (Xu et al. 2020; Chen et al. 2015). A combination of spectral information and other fluorophore properties, such as fluorescence lifetime, could result in a new generation of deep learning–driven unmixing approaches for imaging multiple fluorophores in living cells.

Outlook

We envision that future trends in live-cell fluorescence spectral imaging will include (1) the use of spectral imaging data sets to train deep learning algorithms for label-free detection of intracellular structures (Ounkomol et al. 2018; Manifold et al. 2021); (2) the use of spectral imaging to track entire biochemical pathways directly (Argüello-Miranda et al. 2022) or to in silico reconstruct biochemical pathways based on in vivo spectral fluorescence data (Yang et al. 2021); (3) the combination of spectral imaging with FLIM to enlarge the specificity, sensitivity, and combinations of fluorophores for live-cell imaging (Poland et al. 2015; Görlitz et al. 2017; Scipioni et al. 2021; Zhao et al. 2014).

Recent advances in detectors and algorithms to obtain and process FLIM data using representations such as phasors (Hedde et al. 2021; Scipioni et al. 2021; Vu et al. 2022) make this approach highly relevant for creating richer data cubes for spectral unmixing or for achieving fluorophore identification independently of spectral properties (Bruschini et al. 2019; Scipioni et al. 2021; Zhao et al. 2014; Ochoa et al. 2020; Rehman and Qureshi 2021; Smith et al. 2020). However, regardless of new fluorophores, better detectors, and the inclusion of FLIM, live-cell fluorescence spectral imaging’s crucial question of assigning pixels to their corresponding fluorophores is likely to remain a challenge for data science.

Author contribution

JAR, JPMV, and OAM conceived the idea, performed literature research, and wrote the manuscript.

Funding

This work was supported by the USA National Institute of General Medical Sciences of the National Institutes of Health (K99GM135487) and the Center for Geophysical Research (CIGEFI), University of Costa Rica, project number VI-805-B9454.

Declarations

Conflict of interest

The authors declare no competing interests.