Numerical simulation of wave propagation through interfaces using the extended finite element method for magnetic resonance elastography

Abstract

Magnetic resonance elastography (MRE) is an elasticity imaging technique for quantitatively assessing the stiffness of human tissues. In MRE, finite element method (FEM) is widely used for modeling wave propagation and stiffness reconstruction. However, in front of inclusions with complex interfaces, FEM can become burdensome in terms of the model partition and computationally expensive. In this work, we implement a formulation of FEM, known as the eXtended finite element method (XFEM), which is a method used for modeling discontinuity like crack and heterogeneity. Using a level-set method, it makes the interface independent of the mesh, thus relieving the meshing efforts. We investigate this method in two studies: wave propagation across an oblique linear interface and stiffness reconstruction of a random-shape inclusion. In the first study, numerical results by XFEM and FEM models revealing the wave conversion rules at linear interface are presented and successfully compared to the theoretical predictions. The second study, investigated in a pseudo-practical application, demonstrates further the applicability of XFEM in MRE and the convenience, accuracy, and speed of XFEM with respect to FEM. XFEM can be regarded as a promising alternative to FEM for inclusion modeling in MRE.

I. INTRODUCTION

Magnetic resonance elastography (MRE) is an elasticity imaging technique to assess quantitatively the stiffness of human tissues. It was first proposed by the Mayo Clinic¹ and has been greatly developed in the last two decades.² MRE usually contains three steps: using an external source of motion to induce shear waves within the tissue; imaging the tissue mechanical response by magnetic resonance imaging (MRI); recovering stiffness images (elastograms) from the obtained displacements.^3,4 Stiffer areas in MR elastograms could represent lesions like tumors and fibroses. It is a promising medical imaging modality partially due to the possibility of applications to numerous organs and tissues such as liver, muscle, lung, spleen, kidney, heart, brain, breast, etc.⁵

In MRE, numerical simulations have been widely used to generate displacement fields for a given model with known material properties, boundary conditions, and excitation sources. Such simulations modeling the wave propagation are helpful in understanding the effects of different parameters on MRE measurements.⁶ In addition, simulations can also serve as a tool for evaluating novel MRE inversion methods,^7,8 for assessing metric definitions,⁹ and even for reconstructing stiffness.^10,11

Stiffness reconstruction by simulation can be generally categorized into two groups: using analytical formulations or finite element methods (FEM). A number of reconstruction methods based on analytical formulations have been proposed and are commonly used.² Most of them assume linear viscoelasticity, local homogeneity, and small-amplitude excitation, with many assuming isotropy;^7,12 however, there have been a number of studies that have attempted to reconstruct transversely isotropic material properties.^8,13,14 Although it is easy to implement and efficient in producing a simulated displacement dataset, the underlying simplifications such as exponentially attenuated plane wave and independence to boundary conditions¹² may be unrealistic in some cases. In comparison, the latter one based on FEM can describe in a more realistic way more complex wave patterns, geometries, and boundary conditions. It consists in solving an elastodynamics problem by applying the variational formulation and by performing the finite element discretization.¹⁵ Either custom-developed codes^10,16 or commercial software^6,9 have been used to simulate two-dimensional (2D) or three-dimensional (3D) models subjected to different boundary conditions and FEM-based reconstruction methods have also been used for transversely isotropic materials.¹⁷

In FEM-based simulations, the spatial discretization by finite elements has to take into account the geometry boundaries of the whole model and potential inclusions. Usually, triangular elements in 2D¹⁸ and tetrahedral elements in 3D¹⁹ are employed to model the curved, nonlinear inclusion interfaces. For complex interface, this could imply a burdensome task in terms of the prerequisite model partition, and the resulting finer mesh usually leads to large computational effort. In this case, the eXtended finite element method (XFEM), which is a formulation of FEM, can be an alternative. XFEM was first developed by Moës et al.²⁰ for the domain of fracture mechanics. It extends the classical FEM solution space by discontinuous enrichment functions²¹ so that some challenging features such as discontinuity in strain or displacement can be reproduced with ease. In terms of modeling the discontinuity in strain like inclusions, a signed distance function known as the level-set function can be applied to define the interface;²² the interface can thus become independent of the mesh and no longer require a mesh refinement, and the model can dispense with the need of remeshing for a different interface. To the best of our knowledge, XFEM has not been utilized in MRE studies yet.

In terms of wave propagation, two types of harmonic waves can be generated by drivers, distinguished by the polarization direction: transverse and longitudinal. The former, also called shear wave or S-wave, is characterized by polarization direction perpendicular to the propagation direction, while the latter, also called compressional wave or P-wave, has the two directions in parallel. In soft tissues, S-wave propagates much more slowly (1–10 m/s) than P-wave (around 1540 m/s),⁵ thus allowing its detection by MRI. Besides, due to the quasi-incompressibility of soft biological tissues, the shear moduli $G$ related to shape change and measured from S-wave can vary to a much greater extent within tissues than the bulk moduli $K$, which is related to volume change and P-wave ( $G={10}^{-2}\sim {10}^{-6}K$).²³ These features explain why S-wave propagation is investigated in MRE for stiffness reconstruction.

MRE drivers can be actuated either transversely or longitudinally depending on applications.²⁴ The popular transverse drivers are able to generate planar S-waves parallel to the driver/tissue interface,¹ while the longitudinal ones can deliver S-waves with a cone-like hemispherical distribution and have better penetration depth and design flexibility.²⁵ Whatever the actuation direction is, the shear and compressional components usually coexist. It is however the former component that is really needed and can be extracted by the curl operator.¹² Note that these two components are not independent of each other, but rather connected by mode conversion taking place at interfaces such as tissue boundaries and inclusion interfaces.^12,24 Due to its complexity, the wave mode conversion in MRE is often neglected, like in the numerical model,²⁶ and has rarely been studied.²⁷

Therefore, in this work, we aim to present, in the context of MRE, our numerical model based on XFEM for simulating wave propagation within a soft tissue, and investigate wave conversion through interfaces. In what follows, we first introduce a theoretical work²⁸ developed for the problem of reflection and transmission of plane waves at an oblique plane interface between viscoelastic materials, where the formulations of mode conversion are given. Then, we present our bases of the implementation, including the viscoelasticity model, the FEM and XFEM formulations, the time integration scheme, the shear components extraction method, and the stiffness reconstruction algorithm. All of these were implemented into a homemade Fortran solver. Two applications are then proposed: one model of a heterogeneous tissue containing a linear interface, for numerically studying by XFEM/FEM the mode conversion from P to S in comparison with the analytical model; one model of a heterogeneous tissue containing a random-shape inclusion modeled by XFEM/FEM for demonstrating the advantages of XFEM, namely, its convenience, accuracy, and speed. Then, the results are shown, for a parametric study of the first model and for the extracted shear components and the reconstructed stiffness of the second model. Finally, the discussion and the conclusion are given.

II. THEORY

The characteristics of mechanical waves have been studied for a long time, while the problems of reflection and refraction at boundaries or interfaces were just resolved some decades ago. In the following, we try to concisely present the formulations developed in the work of Cooper,²⁸ which, in a relatively general way, deals with the reflection and transmission of plane waves at an oblique plane interface between two viscoelastic media. Meanwhile, some errors in the formulas in the article are found and corrected. Proof and numerical implementation are provided.²⁹ We take the subscripts $l,m,n$ to indicate different cases as done in Ref. 28. $l$ is used to denote incident wave type, as P-wave ( $l=1$) or S-wave ( $l=2$). $m$ refers to the side of the interface, i.e., $m=1$ means the incident side and $m=2$ means the transmitted side. $n$ is used to denote the resulting wave type, as P-wave ( $n=1$) or S-wave ( $n=2$). For instance, ${\zeta }_{\mathit{lmn}}$ expressed as ${\zeta }_{121}$ would describe the angle of a refracted $(m=2)$ P-wave $(n=1)$ arising from an incident P-wave $(l=1)$; similarly, $k_{mn}$ expressed as $k_{12}$ defines the wave number of a reflected $(m=1)$ S-wave $(n=2)$.

A. Plane wave representation

The basic concepts in elasticity theory, like the strain-displacement relations, the constitutive equations, and the equilibrium equations, can lead to, in the case of linearity and isotropy, the Navier equation,

$$\left(\lambda +\mu \right)\mathbf{\nabla }\left(\mathbf{\nabla }·\mathit{u}\right)+\mu {\mathbf{\nabla }}^2\mathit{u}+\mathit{F}=\rho {\partial }_{tt}\mathit{u},$$ (1)

where $\mathit{u}$ is the displacement tensor, $\lambda$ and $\mu$ are Lamé parameters, $\mathit{F}$ is the tensor of body force density, $\rho$ is the mass density, and ${\partial }_{tt}$ denotes the second derivative with respect to time, i.e., ${\partial }^2/\partial t^2$. $\mathbf{\nabla }$ denote the gradient operator and ${\mathbf{\nabla }}^2$ implies $\mathbf{\nabla }\cdot \mathbf{\nabla }$, which is the divergence of the gradient, namely, the Laplace operator $\mathbf{\Delta }$.

By further supposing that material is viscoelastic, waves are time-harmonic, and also assuming that body forces can be neglected, Eq. (1) becomes

$$\left(\lambda +\mu \right)\mathbf{\nabla }(\mathbf{\nabla }·\mathit{u})+\mu {\mathbf{\nabla }}^2\mathit{u}+\rho {\omega }^2\mathit{u}=\mathbf{0},$$ (2)

where $\omega$ is the angular frequency related to harmonic motion and $\lambda \left(\omega \right)$ and $\mu \left(\omega \right)$ are hereafter complex-valued parameters related to viscoelastic properties. Equation (2) describes the motion of harmonic (visco-)elastic waves and is widely used in the literature.^7,12,30–32

Across an interface, it can be demonstrated that the reflected and transmitted waves are in the same plane as the incident wave.³³ Thus, we consider here only the 2D motions in the $x-y$ plane with displacements $\mathit{u}=\left(u,v,0\right)$ and coordinates $\mathit{x}=\left(x,y,0\right)$. As shown in Ref. 34, the solution to Eq. (2) can be expressed conventionally in exponential form, e.g., in the $x$-direction,

$$u=u_0\mathrm{\hspace{0.17em}exp}\left[i\left(kx-\omega t\right)\right],$$ (3)

where $u_0$ is the amplitude and $k$ is the wavenumber.

Wavenumber can be calculated using its definition, with the subscripts defined previously applied, as

$$k_{mn}=\frac{\omega }{S_{mn}},$$ (4a)

$$S_{m1}^2=\frac{{\lambda }_m+2{\mu }_m}{{\rho }_m},$$ (4b)

$$S_{m2}^2=\frac{{\mu }_m}{{\rho }_m}.$$ (4c)

It can be also regarded as complex-valued and reads

$$k_{mn}=\frac{\omega }{C_{mn}}\left(1-i\text{\hspace{0.17em}tan\hspace{0.17em}}{\Omega }_{mn}\right),$$ (5)

where

$$\text{tan\hspace{0.17em}}2{\Omega }_{mn}=\frac{\text{Im}{S}_{mn}^2}{\text{Re}{S}_{mn}^2},$$ (6a)

$$C_{mn}=\left|S_{mn}\right|\text{sec\hspace{0.17em}}{\Omega }_{mn}.$$ (6b)

Unlike Ref. 28, we reverse the sign of $\text{tan\hspace{0.17em}}{\Omega }_{mn}$ and $\text{tan\hspace{0.17em}}2{\Omega }_{mn}$, which corresponds to the conventional use. Indeed, it can be proved that original signs will lead to improper results.²⁹

B. Reflection and refraction coefficients ${\mathit{R}}_{\mathit{lmn}}$

Following the notations in Ref. 28, we use ${\theta }_l$ and ${\zeta }_{\mathit{lmn}}$ to indicate incident angle and reflected/refracted angle, respectively. The angle ${\theta }_l$ is real while ${\zeta }_{\mathit{lmn}}$ is generally complex. Besides, $R_{\mathit{lmn}}$ is used to denote the ratio between reflected/refracted amplitude and incident amplitude.

As presented in Ref. 28, after introducing some potential functions for displacement components, applying the boundary conditions at the interface and combining the complex Snell's law, a system of linear equations can be obtained for each wave type $(l=1\hspace{0.17em}\mathrm{or}\hspace{0.17em}2)$,

$${\mathit{A}}_l{\mathit{R}}_l={\mathit{B}}_l,\hspace{1em}l=1 \mathrm{or} 2,$$ (7)

where

$${\mathit{A}}_l=\left[\begin{array}{cccc}\text{sin}\hspace{0.17em}{\zeta }_{l11}& \text{cos\hspace{0.17em}}{\zeta }_{l12}& -\text{sin}\hspace{0.17em}{\zeta }_{l21}& \text{cos\hspace{0.17em}}{\zeta }_{l22}\\ \text{cos\hspace{0.17em}}{\zeta }_{l11}& -\text{sin}\hspace{0.17em}{\zeta }_{l12}& \text{cos\hspace{0.17em}}{\zeta }_{l21}& \text{sin}\hspace{0.17em}{\zeta }_{l22}\\ -{\rho }_1{S}_{11}\text{\hspace{0.17em}cos\hspace{0.17em}}2{\zeta }_{l12}& {\rho }_1{S}_{12}\text{\hspace{0.17em}sin\hspace{0.17em}}2{\zeta }_{l12}& {\rho }_2{S}_{21}\text{\hspace{0.17em}cos\hspace{0.17em}}2{\zeta }_{l22}& {\rho }_2{S}_{22}\text{\hspace{0.17em}sin\hspace{0.17em}}2{\zeta }_{l22}\\ ({\rho }_1{S}_{12}^2/S_{11})\text{sin\hspace{0.17em}}2{\zeta }_{l11}& {\rho }_1{S}_{12}\text{\hspace{0.17em}cos\hspace{0.17em}}2{\zeta }_{l12}& ({\rho }_2{S}_{22}^2/S_{21})\text{sin\hspace{0.17em}}2{\zeta }_{l21}& -{\rho }_2{S}_{22}\text{\hspace{0.17em}cos\hspace{0.17em}}2{\zeta }_{l22}\end{array}\right],$$ (8)

$${\mathit{B}}_1=\left\{\begin{array}{c}-\text{sin}\hspace{0.17em}{\theta }_1\\ \text{cos\hspace{0.17em}}{\theta }_1\\ {\rho }_1{S}_{11}\text{\hspace{0.17em}cos\hspace{0.17em}}2{\zeta }_{112}\\ ({\rho }_1{S}_{12}^2/S_{11})\text{sin\hspace{0.17em}}2{\theta }_1\end{array}\right\},$$ (9a)

$${\mathit{B}}_2=\left\{\begin{array}{c}\text{cos\hspace{0.17em}}{\theta }_2\\ \text{sin}\hspace{0.17em}{\theta }_2\\ {\rho }_1{S}_{12}\text{\hspace{0.17em}sin\hspace{0.17em}}2{\theta }_2\\ -{\rho }_1{S}_{12}\text{\hspace{0.17em}cos\hspace{0.17em}}2{\theta }_2\end{array}\right\},$$ (9b)

$${\mathit{R}}_l=\left\{\begin{array}{c}{R}_{l11}\\ R_{l12}\\ R_{l21}\\ R_{l22}\end{array}\right\}.$$ (9c)

These expressions include some corrections compared to the expressions in Ref. 28, namely, ${\mathit{A}}_l\left(3,1\right)$ corrected from $-{\rho }_1{S}_{11}\text{\hspace{0.17em}cos\hspace{0.17em}}{\zeta }_{l12}$, ${\mathit{B}}_1\left(4\right)$ from ${\rho }_1{S}_{12}^2\text{\hspace{0.17em}sin\hspace{0.17em}}2{\theta }_1$, and ${\mathit{B}}_2\left(3\right)$ from $-{\rho }_1{S}_{12}\text{\hspace{0.17em}sin\hspace{0.17em}}2{\theta }_2$.

C. Reflection and refraction angles ${\mathit{\theta }}_{\mathit{lmn}}$

Solving the precedent system of equations requires the knowledge of complex angle ${\zeta }_{\mathit{lmn}}$. To this end, the angle is represented by

$${\zeta }_{\mathit{lmn}}={\alpha }_{\mathit{lmn}}+i{\beta }_{\mathit{lmn}}.$$ (10)

It can be proven that ${\beta }_{\mathit{lmn}}$ satisfies

$${\sinh }^2{\beta }_{\mathit{lmn}}=\frac{1}{2}\left\{{\Gamma }_{\mathit{lmn}}^2-1+{\left[{\left(1-{\Gamma }_{\mathit{lmn}}^2\right)}^2+4{\Gamma }_{\mathit{lmn}}^2{\text{sin}}^2{\Delta }_{\mathit{lmn}}\right]}^{1/2}\right\},$$ (11)

where

$${\Gamma }_{\mathit{lmn}}={\gamma }_{\mathit{lmn}}\text{\hspace{0.17em}cos\hspace{0.17em}}{\Omega }_{mn}/\text{cos\hspace{0.17em}}{\Omega }_{1l},$$ (12)

$${\gamma }_{\mathit{lmn}}=C_{mn}\text{\hspace{0.17em}sin}\hspace{0.17em}{\theta }_l/C_{1l},$$ (13)

$${\Delta }_{\mathit{lmn}}={\Omega }_{1l}-{\Omega }_{mn}.$$ (14)

With some derivations in terms of wavenumber, the real reflection or refraction angle ${\theta }_{\mathit{lmn}}$ can be determined by the formula

$$\text{sin}\hspace{0.17em}{\theta }_{\mathit{lmn}}={\xi }_{\mathit{lmn}}{\gamma }_{\mathit{lmn}},$$ (15)

where

$${\xi }_{\mathit{lmn}}={\left(1+{\sinh }^2{\beta }_{\mathit{lmn}}{\text{\hspace{0.17em}sec}}^2{\Omega }_{mn}\right)}^{-1/2}.$$ (16)

Finally, the real part of complex angle can be calculated by

$${\alpha }_{\mathit{lmn}}={\theta }_{\mathit{lmn}}+{\varphi }_{\mathit{lmn}},$$ (17)

where

$$\text{tan\hspace{0.17em}}{\varphi }_{\mathit{lmn}}=\text{tan\hspace{0.17em}}{\Omega }_{mn}\mathrm{\hspace{0.17em}tanh\hspace{0.17em}}{\beta }_{\mathit{lmn}}.$$ (18)

It should be noted that the sign of ${\beta }_{\mathit{lmn}}$ is determined by

$$\text{sign}\left({\beta }_{\mathit{lmn}}\right)=-\mathrm{sign}({\xi }_{\mathit{lmn}}^2\mathrm{\hspace{0.17em}tan\hspace{0.17em}}{\Omega }_{mn}-\text{tan\hspace{0.17em}}{\Omega }_{1l}).$$ (19)

III. METHODS

The behavior of plane waves at plane interface between viscoelastic materials has been formulated in the previous section. However, the reality is often more complex; for instance, the inclusion interface is likely not plane. In this context, the powerful tool of numerical methods can be used to simulate and reproduce wave fields in a more general manner.

In this section, we first introduce the bases of our numerical implementation, including the standard linear solid (SLS) model for describing viscoelasticity, the FEM and XFEM formulations, the time integration scheme for reducing numerical spurious oscillations, and the postprocessing methods for extracting S-waves and reconstructing stiffness. Then, we present two numerical models with different sample configurations and interfaces; both are 2D, viscoelastic, isotropic, locally homogeneous, and longitudinally actuated. The first one contains a linear interface and allows us to study plane wave mode conversion from P to S at plane interface. The numerical results obtained by both XFEM and FEM simulations, for various combinations of parameters, will be compared to the analytical model introduced in the previous section, in terms of the angle of refraction and amplitude of transmitted S-wave. The second one contains a random-shape inclusion and allows to investigate XFEM in a pseudo-practical application. The inclusion is modeled by XFEM or FEM; the shear component of the waves is extracted from displacement fields by the curl operator and the shear moduli are reconstructed from the extraction using an existing tool. The stiffness estimation results are then compared to the ground truth values.

A. Bases of the implementation

1. Standard linear solid (SLS) model

Several rheological models are available for describing the viscoelasticity of materials like soft tissues, and their different frequency-dependent characteristics have been investigated by MRE researchers.^4,35,36 The two simplest models with only two parameters, i.e., the Voigt and Maxwell model, may not represent well the tissue behaviors in MRE frequency range.^2,4,37 Other complex models, such as the SLS model and the generalized Maxwell model, can have better performances in fitting MRE experimental measurements at multiple frequencies.^35,36 Currently, there is no agreement regarding the choice of model, but models with the least parameters and good performance are preferred.³⁶ In view of simplicity and being representative, we have chosen to employ the SLS model. It is also a relevant choice regarding the small amplitude of the waves used in elastography.

The standard linear solid model, also known as the Zener model, is composed of springs and dashpot to represent elastic and viscous properties, respectively. Following the convention in MRE, we consider in our model the Maxwell form of SLS model, as shown in Fig. 1, which consists of two systems in parallel, one containing a spring $E_v$ and a dashpot $\eta$ in series, and the other containing only a spring $E_{\infty }$. The stress-strain ( $\sigma -\epsilon$) constitutive equation of spring and dashpot can be expressed in terms of Young's modulus $E$ and viscosity $\eta$, respectively, as

$$\sigma =E\hspace{0.17em}\epsilon ,$$ (20)

$$\sigma =\eta {\partial }_t\epsilon .$$ (21)

FIG. 1.

Maxwell form of SLS model.

For the Maxwell form, it can be demonstrated using the Fourier transformation that the complex elastic modulus $E^{*}$ under harmonic excitation is written as³⁸

$$E^{*}=E^{\prime }+i{E}^{″},$$ (22)

where

$$E^{\prime }=E_{\infty }+\frac{{\tau }^2{\omega }^2}{1+{\tau }^2{\omega }^2}{E}_v,$$ (23)

$$E^{″}=\frac{\tau \omega }{1+{\tau }^2{\omega }^2}{E}_v.$$ (24)

$E^{\prime }$ is the storage modulus and $E^{″}$ is the loss modulus. $\tau =\eta /E_v$ is the relaxation time, $\omega =2\hspace{0.17em}\pi f$ is the angular frequency, and $f$ is the ordinary excitation frequency.

2. FEM

The FEM is a numerical method based on discretization of continuum problems. It solves the discrete system and uses the obtained discrete values of each element to represent continuous fields.^14,39 We introduce here simply the basic formulation, which is a system of equations of motion after discretizing the spatial domain with finite elements,

$$\mathit{M}\ddot{\mathit{U}}+\mathit{C}\dot{\mathit{U}}+\mathit{KU}={\mathit{F}}_{\mathit{ext}},$$ (25)

where

$$\mathit{M}={\int }_{\Omega }\rho {\mathit{N}}^T\mathit{N}d\Omega ,$$ (26)

$$\mathit{C}={\int }_{\Omega }{\mathit{N}}^T\kappa \mathit{N}d\Omega ,$$ (27)

$$\mathit{K}={\int }_{\Omega }{\mathit{B}}^T\mathit{D}\mathit{B}d\Omega ,$$ (28)

$${\mathit{F}}_{\mathit{ext}}={\int }_{\Omega }{\mathit{N}}^T\mathit{f}d\Omega +{\int }_{\Gamma }{\mathit{N}}^T\overline{\mathit{t}}d\Gamma .$$ (29)

$\mathit{M}$ is the mass matrix, $\mathit{C}$ is the damping matrix especially for purely elastic case, $\mathit{K}$ is the stiffness matrix and ${\mathit{F}}_{\mathit{ext}}$ is the external force. Besides, $\rho$ is the mass density, $\kappa$ is the damping parameter, $\Omega$ is the whole integral domain and $\Gamma$ is certain boundary. $\mathit{N}$ denotes the shape functions vector, $\mathit{B}$ denotes the strain-displacement matrix and $\mathit{D}$ represents the stress-strain constitutive matrix. $\mathit{f}$ is the body force and $\overline{\mathit{t}}$ the traction vector imposed on boundary $\Gamma$. Finally, $\mathit{U},\dot{\mathit{U}},\ddot{\mathit{U}}$ denote the vector of displacement, velocity, and acceleration, respectively.

3. XFEM

The XFEM was proposed by Moës et al. in 1999.²⁰ It is based on the partition of unity method⁴⁰ and has been mainly used in fracture mechanics for crack evolution modeling. However, in addition to strong discontinuity like the displacements in cracks, this method also allows the modeling of weak discontinuity like the strains across the interface of heterogeneities, such as holes and inclusions.²² Indeed, XFEM has been incorporated into some commercial software,^41,42 but it is mainly for fracture problems. The lack of available commercial tools for inclusion modeling by XFEM and the complexity of the numerical implementation might account for the fact that this method is unknown and not yet used in MRE simulations.

In XFEM, the key idea is to enrich the elements in the vicinity of interface by adding additional degrees of freedom; the interface becomes independent of mesh and the mesh refinement in classical FEM is thus no longer required. XFEM can be formulated in terms of displacement as

$${\mathit{u}}^{\mathit{XFEM}}={\mathit{u}}^{\mathit{FEM}}+{\mathit{u}}^{\mathit{enr}}\hspace{1em}$$

with

$${\mathit{u}}^{\mathit{FEM}}=\sum _{i\in I}^{}{N}_i{\mathit{u}}_i$$

and

$${\mathit{u}}^{\mathit{enr}}=\sum _{j\in J}^{}{N}_{j}F{\mathit{a}}_j,$$ (30)

where $N_i,N_j$ are shape functions, ${\mathit{u}}_i$ is FEM classical degree of freedom, ${\mathit{a}}_j$ is the enriched degree of freedom, and $F$ is the enrichment function. ${\mathit{u}}^{\mathit{enr}}$, represented as enriched displacement, is only applied for elements around the interface and equals zero otherwise. $I$ and $J$ are the sets of regular and enriched nodes, respectively.

For the modeling of inclusions, the level set method was coupled to XFEM due to its capacity of representing the location of material interfaces.²² The level set function, which is the signed distance ${\varphi }_I$ from point $I$ to interface, was also applied to develop the enrichment function defined as the absolute value,

$$F=F_1=\left|\varphi \right|=\left|\sum _I^{}{N}_I{\varphi }_I\right|.$$ (31)

It was later proposed by Moës et al.²¹ that another enrichment function could present a better numerical convergence rate, expressed as

$$F=F_2=\sum _I^{}{N}_I\left|{\varphi }_I\right|-\left|\sum _I^{}{N}_I{\varphi }_I\right|,$$ (32)

and was thus employed in our model. For more details concerning the numerical implementation of XFEM, readers are recommended to see Refs. 43–45.

In the frame of MRE simulations, XFEM can be expected to get more attention and application, since (1) the mesh is no longer required to match the geometry of any complex, arbitrary inclusion, (2) there are no known limits for the stiffness difference and excitation frequency, and (3) it can be applied not only for modeling inclusions at macroscale²² but also for solving microstructures.²¹

4. Spurious oscillations reduction

When solving dynamic problems of wave propagation using FEM, numerical noises referred to as spurious oscillations usually occur due to the spatial and time discretizations, especially for waves with high frequency modes. These errors can alter the displacement fields, and thus the stiffness estimation results in MRE. The classical central difference (CD) scheme is non-dissipative and hence no longer appropriate in wave propagation simulations.⁴⁶ Many other explicit time integration schemes introducing numerical dissipation to reduce noise have been developed, such as the bulk viscosity method (BVM), the Tchamwa-Wielgosz (TW) scheme, and the Chung Lee (CL) algorithm.⁴⁷ Especially, BVM is based on the CD scheme and used in some commercial software including abaqus.⁴⁸ However, most dissipative explicit methods are only first-order accurate and the second-order accurate ones are not satisfyingly accurate. Recently, Noh and Bathe (NB) introduced another explicit scheme that is second-order accurate and presents better accuracy and a bigger critical time step size.⁴⁹ Later, Mirbagheri et al.⁵⁰ proposed a modified version of NB method presenting even better stability and accuracy.To take advantage of the low computational cost of explicit schemes and to reduce spurious oscillations with high accuracy, we chose to apply in our model the modified-NB scheme which is briefly presented in what follows.

In the frame of FEM [Eqs. (25)–(29)], the explicit scheme to solve these equations proceeds as:

• (a)
  First, initialize the following parameters with a predefined time step $\Delta t$:

  • (1)
    $p=0.54,$
  • (2)
    $q_1=(1-2p)/2p\left(1-p\right)$;  $q_2=0.5-p{q}_1$; $q_0=-q_1-q_2+0.5,$
  • (3)
    $a_0=q_0\left(1-p\right)\Delta t$; $a_1=\left(0.5+q_1\right)\left(1-p\right)\Delta t$; $a_2=q_2\left(1-p\right)\Delta t.$
• (b)
  Then, for each time step:

  • (1)
    First sub-step:

    • (i)
      ${\mathit{U}}_{t+p\Delta t}={\mathit{U}}_t+\left(p\Delta t\right){\dot{\mathit{U}}}_t+(\eta /2){\left(p\Delta t\right)}^2{\ddot{\mathit{U}}}_t,$
    • (ii)
      ${\mathit{F}}_{\mathit{ext},t+p\Delta t}=\left(1-p\right){\mathit{F}}_{\mathit{ext},t}+p{\mathit{F}}_{\mathit{ext},t+\Delta t},$
    • (iii)
      ${\ddot{\mathit{U}}}_{t+p\Delta t}={\mathit{M}}^{-1}\left[{\mathit{F}}_{\mathit{ext},t+p\Delta t}-\mathit{C}\left({\dot{\mathit{U}}}_t+\left(p\Delta t\right){\ddot{\mathit{U}}}_t\right)-\mathit{K}{\mathit{U}}_{t+p\Delta t}\right],$
    • (iv)
      ${\dot{\mathit{U}}}_{t+p\Delta t}={\dot{\mathit{U}}}_t+\frac{1}{2}\left(p\Delta t\right)\left[{\ddot{\mathit{U}}}_t+{\ddot{\mathit{U}}}_{t+p\Delta t}\right].$
  • (2)
    Second sub-step:

    • (i)
      ${\mathit{U}}_{t+\Delta t}={\mathit{U}}_{t+p\Delta t}+\left[\left(1-p\right)\Delta t\right]{\dot{\mathit{U}}}_{t+p\Delta t}+(\eta /2){\left[\left(1-p\right)\Delta t\right]}^2{\ddot{\mathit{U}}}_{t+p\Delta t},$
    • (ii)
      ${\ddot{\mathit{U}}}_{t+\Delta t}={\mathit{M}}^{-1}\left[{\mathit{F}}_{\mathit{ext},t+\Delta t}-\mathit{C}\left({\dot{\mathit{U}}}_{t+p\Delta t}+\left[\left(1-p\right)\Delta t\right]{\ddot{\mathit{U}}}_{t+p\Delta t}\right)-\mathit{K}{\mathit{U}}_{t+\Delta t}\right],$
    • (iii)
      ${\dot{\mathit{U}}}_{t+\Delta t}={\dot{\mathit{U}}}_{t+p\Delta t}+a_0{\ddot{\mathit{U}}}_t+a_1{\ddot{\mathit{U}}}_{t+p\Delta t}+a_2{\ddot{\mathit{U}}}_{t+\Delta t}.$

This scheme becomes the NB method when the parameter $\eta$ is set to 1 and the NB method reduces to the CD method when $p$ equals 1. Finally, as proposed in Ref. 50, $\eta =1.1$ is a good choice and compromise between accuracy and stability, and thus applied in our model.

5. S-wave extraction and stiffness reconstruction

As can be seen from the theoretical formulations describing waves behavior across interface, waves can be converted at a plane interface as long as the angle of incidence is not equal to zero. For example, plane P-waves propagating through a plane interface between two viscoelastic media with a certain angle of incidence, in addition to the reflected and transmitted P-waves, generate reflected and transmitted S-waves. This is also valid for more general cases where incident waves and interface are not plane. It means that the two kinds of waves generally coexist.

Indeed, this characteristic can be also revealed by the wave Eq. (2) that contains both the first Lamé parameter $\lambda$ and the second Lamé parameter $\mu$. The former basically has the same magnitude as the bulk modulus $K$, hence representing the compressional components. The latter is in fact the shear modulus $G$ and hence represents the shear components. In MRE, we aim to reconstruct the shear stiffness $G$ based on the wave Eq. (2). However, as there is a great difference in magnitude between $\lambda$ (GPa) and $\mu$ (kPa) in soft tissues due to quasi-incompressibility, $G$ cannot be properly recovered directly from the equation. To this end, several strategies were usually considered, such as ignoring the term containing $\lambda$ due to the divergence-free relation of displacement $\mathbf{\nabla }\cdot \mathit{u}\approx 0$ (i.e., ${\partial }_i{u}_i\approx 0$) resulting from the quasi-incompressibility property,⁷ and applying the curl operator to the wave equation [Eq. (12)]. The latter one is based on the Helmholtz theorem stating that any sufficiently smooth vector field can be decomposed into an irrotational (curl-free) vector field and a solenoidal (divergence-free) vector field. For the displacement field $\mathit{u}$, the curl-free part represents the compressional/longitudinal components ${\mathit{u}}_L$ and the divergence-free part represents the shear/transverse components ${\mathit{u}}_T$. The wave equation thus becomes a Helmohltz-type equation in terms of a new field of curl-applied displacement $\mathit{q}=\mathbf{\nabla }\times \mathit{u}$ where any contributions from ${\mathit{u}}_L$ are removed, leading to the remaining ${\mathit{u}}_T$ for reconstructing shear stiffness.

To reconstruct the stiffness, several algorithms have been developed in MRE including direct and iterative methods. As the name suggests, direct methods aim at retrieving stiffness by directly solving the wave equation, or the simplified Helmholtz equation,²

$$G^{*}=-\frac{\rho {\omega }^2\mathit{u}}{{\mathbf{\nabla }}^2\mathit{u}},$$ (33)

where $G^{*}$ is the complex shear modulus for viscoelastic materials. Note that $G^{*}=G^{\prime }+i{G}^{″}$ and the relation $G^{*}=E^{*}/2\left(1+\nu \right)$. Compared to iterative methods that are hard to implement and computationally expensive, direct methods have the advantage of being straightforward and fast despite the sensitivity to noise due to the multiple derivatives. The most frequently used direct methods may include local frequency estimation (LFE) and algebraic inversion of the differential equation (AIDE). The AIDE method, proposed by Oliphant et al.,⁷ consists in performing an inversion of a system of differential equations of mechanical motions, similar to Eq. (33). Moreover, a least-square polynomial fitting by Savitzky-Golay filter is used to compute the spatial derivatives and a regularization technique is applied to prevent division by zero. These two direct methods can be accessed, for example, through the tool MREJ, which is a Java plugin implemented in ImageJ software.⁵¹

In our work, the simulated displacement fields are postprocessed by applying the curl operator to filter out the compressional components ${\mathit{u}}_L$. The obtained fields representing shear components ${\mathit{u}}_T$ are then imported into the MREJ tool to reconstruct shear modulus (real part $G^{\prime }$) by the implemented AIDE algorithm, which means that the displacement field $\mathit{u}$ in Eq. (33) is actually regarded as the curl-based alternative $\mathit{q}$.

B. Applications

In the following, we present two models: the P-S conversion model, designed to numerically study the conversion from P-waves to S-waves at an oblique linear interface; the random-shape inclusion model, designed to investigate the convenience, accuracy, and speed of XFEM compared to FEM in a pseudo-practical application. Both models were longitudinally actuated to generate P-waves. 2D models with plane strain hypothesis were considered since (1) the first model with plane interfaces and plane waves can be reduced from 3D to 2D, and (2) for the second model, a 2D case allows us to better illustrate the mesh and facilitate the interpretation of results. For both studies, the materials interface was modeled by the two methods, XFEM or FEM. The simulations were all executed on a Linux cluster (running CentOS Linux 7.9.2009) with three CPUs Intel(R) Xeon(R) CPU Gold 5118 @ 2.30 GHz and 5GB RAM.

1. P-S conversion model

To numerically study the wave conversion from plane P-waves to plane S-waves at an oblique interface between two different viscoelastic materials, we could take a 2D finite model divided into two parts directly by an oblique linear interface. However, such a simple, intuitive model can cause some undesired reflections at boundaries which pollute the S-waves generated at the interface, rendering the interpretation of results difficult. To this end, we designed a model with a piecewise linear interface, as illustrated in Fig. 2. The rectangular P-S conversion model had dimensions of 1000 × 500 mm². The P-waves were generated from the right edge and propagated to the left. The left edge was totally embedded. Symmetric boundary conditions (SBC) were applied along the top and bottom edges to make the incident P-waves plane. The three linear segments in dashed lines represented the interface separating the materials with material 1 on the right side and material 2 on the left side. The inner oblique segment, characterized by the angle of incidence ${\alpha }_i$ of incident P-waves, served as the targeted linear interface across which S-waves would be generated from P-wave conversion and studied. The upper and lower vertical segments, across which only plane P-waves were present, protected the inner transmitted waves from being polluted by reflections at boundaries. In this manner, the measurements within the zones following the inner segment would be relatively representative of S-waves arising only from P-wave conversion at the interface, and comparable to theoretical predictions.

FIG. 2.

P-S conversion model. It contains a piecewise linear interface represented by the dashed lines separating material 1 on the right side from material 2 on the left side.

With the previos P-S conversion model, we conducted a parametric study. The transmitted S-waves were measured in terms of the angle of refraction ${\alpha }_t$ and the amplitude $A_t$. The influence of the angle of incidence ${\alpha }_i$ (from 10 to 80 degrees), the Young's modulus $E_{\infty }$ (10 to 80 kPa) of material 2, the excitation frequency $f$ (25 to 100 Hz), and the excitation amplitude $A_i$ (50 to 200 μm) on ${\alpha }_t$ and $A_t$ was evaluated. The default parameters of the model are listed in Table I.

TABLE I.

Default parameters of the P-S conversion model. $E_{\infty }$, $E_v$, and $\eta$, parameters of the SLS model; $G^{\prime }$, storage modulus; $\rho$, density; $\nu$, Poisson's ratio; $f$, frequency; $A_i$, amplitude; ${\alpha }_i$, angle of incidence.

	$E_{\infty }$ (kPa)	$E_v$ (kPa)	$\eta$ (Pa s)	$G^{\prime }$ (kPa)	$\rho$ (kg m−3)	$\nu$	$f$ (Hz)	$A_i$ (μm)	${\alpha }_i$ (de.g., )
Material 1	6	10	16	3.7	1000	0.49	—	—	—
Material 2	20	10	16	8.4
Incident P-waves	—	—	—	—	—	—	100	150	40

This parametric study was performed in two ways for interface modeling: by XFEM and by FEM. A case of ${\alpha }_i$ = 40 degrees is illustrated in Fig. 3. A regular mesh with 125 000 quadrilateral elements with size of 2 mm was used in XFEM, while in FEM mesh, 123 878 quadrilateral elements with size of 2 mm and 14 754 triangular elements with a minimum size of 0.5 mm were mixed to match the material interface. A mesh convergence study has been performed in advance for determining the mesh size.

FIG. 3.

(Color online) Illustration of mesh of the P-S conversion model by XFEM (a) and FEM (b).

The simulations were all launched for 10 harmonic periods considering the speed of incident P-wave, while the measurements of ${\alpha }_t$ and $A_t$ for each study were performed at different moments around the fifth period when fields near the oblique interface became stable, depending on the speed of transmitted S-waves. Finally, the numerical results were compared with predictions given by the analytical model of Cooper.²⁸

2. Random-shape inclusion model

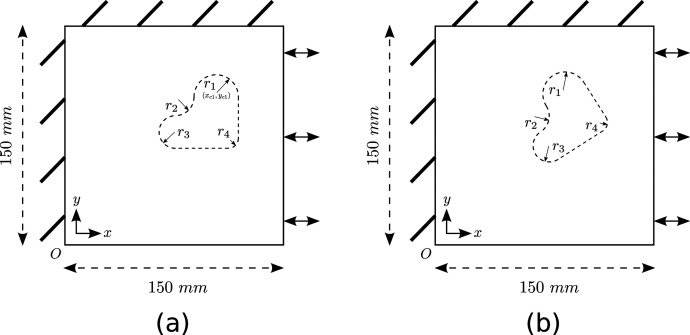
To further investigate XFEM performances in a more practical application, we developed a 2D square model containing a random-shape inclusion, as shown in Fig. 4(a). The model had dimensions of 150 × 150 mm². The inclusion was characterized by two vertical/horizontal segments and four circular arcs with radius $r_1$ = 15 mm, $r_2$ = 10 mm, $r_3$ = 8 mm, and $r_{4\hspace{0.17em}}$= 6 mm, and the first arc was centered at ( $x_{c1},y_{c1}$) = (100, 100) mm. In addition to this aligned inclusion, a tilted inclusion was also considered by rotating the aligned one in the counterclockwise direction around the point (100, 80) mm by 30 degrees, as presented in Fig. 4(b). In terms of boundary conditions, the right edge was longitudinally actuated, the left and top edges were embedded, and the bottom edge was free of restrictions. The other parameters of materials and excitation are summarized in Table II.

FIG. 4.

Random-shape inclusion model. The random-shape inclusion is represented by dashed lines. (a) aligned inclusion and (b) tilted inclusion.

TABLE II.

Parameters of the random-shape inclusion model. $E_{\infty }$, $E_v$, and $\eta$, parameters of the SLS model; $G^{\prime }$, storage modulus; $\rho$, density; $\nu$, Poisson's ratio; $f$, frequency; $A_i$, amplitude.

	$E_{\infty }$ (kPa)	$E_v$ (kPa)	$\eta$ (Pa s)	$G^{\prime }$ (kPa)	$\rho$ (kg m−3)	$\nu$	$f$ (Hz)	$A_i$ (μm)
Background	3.3	6	6.5	1.6	1000	0.49	—	—
Inclusion	10.5	2	4	3.88
Incident P-waves	—	—	—	—	—	—	84	100

As with the P-S conversion model, the previous inclusion model was also studied in two ways for the interface modeling: by XFEM and by FEM. Figure 5 presents the mesh difference between XFEM and FEM. As can be seen, in FEM triangular elements were still needed around the material boundaries to match the mesh with the interface, while in XFEM a regular mesh with only quadrilateral elements was sufficient. Concretely, 90 000 quadrilateral elements with size of 0.5 mm were employed in XFEM for modeling the aligned and tilted inclusion shown in Figs. 5(a) and 5(c), respectively. In FEM, 87 311 quadrilateral elements with size of 0.5 mm and 17 142 triangular elements with a minimum size of 0.2 mm were used for the aligned inclusion illustrated in Fig. 5(b), and 87 188 quadrilateral elements with size of 0.5 mm and 17 688 triangular elements with a minimum size of 0.2 mm were used for the tilted inclusion illustrated in Fig. 5(d). The mesh size has been determined by a mesh convergence study.

FIG. 5.

(Color online) Illustration of mesh of the random-shape inclusion model by XFEM and FEM. (a) and (c) present the regular mesh by XFEM for the aligned and tilted inclusion, respectively. (b) and (d) present the mesh by FEM for the aligned and tilted inclusion, respectively, where triangular elements are used to match the material interface.

The simulations by XFEM and FEM were both launched for 100 harmonic periods at the end of which the model was observed to reach a steady state. The displacement fields, sampled at eight snapshots evenly distributed over one period, were postprocessed by applying the curl operator to extract the shear components ${\mathit{u}}_T$. The results were then imported into the MREJ tool for reconstructing shear modulus ${\mathrm{G}}^{\prime }$ by the AIDE algorithm.

IV. RESULTS

A. Parametric study of P-S conversion

It is illustrated by the displacements fields in Figs. 6(a) and 6(b) that the incident wave is a P-wave propagating from right to left and impacts the oblique interface. Recall in Figs. 6(a) and 6(b) the displacements that the incident wave is a P-wave propagating from right to left and impacts the oblique interface. In Figs. 6(c) and 6(d), the inner oblique segment of the interface can be distinctly observed. Due to the existence of the angle between oblique and vertical segments, some undesired waves were generated from the two corners. Moreover, the spurious oscillations were produced before the shock front following the wave conversion. The measurements of the angle of refraction ${\alpha }_t$ and amplitude $A_t$ of the transmitted S-waves, on the left side, were hence performed several periods later when the displacement fields next to the oblique interface became stable. In terms of ${\alpha }_t$, the nodes respecting ${\mathit{u}}_T\approx \mathbf{0}$, corresponding to the wavefront as illustrated by the dashed line in Fig. 6(c), were chosen to determine the tilted angle and calculate ${\alpha }_t$ by the difference with ${\alpha }_i$. In terms of $A_t$, since the S-waves propagate with great attenuation, the maximum displacement picked from the zone just following the upper part of the oblique interface, as indicated by the arrow in Fig. 6(c), was considered as a good estimate of the wave amplitude $A_t$.

FIG. 6.

(Color online) Illustration of displacement fields and extracted S-waves of the P-S conversion model with the default parameters. (a) and (b), from the model by XFEM, present the displacement fields along $x$-axis and $y$-axis, respectively. (c) and (d) present the extracted S-waves from the displacements of model by XFEM and FEM, respectively.

Figure 7 presents the results of the parametric study. ${\alpha }_t$ and $A_t$ are generally in accordance between the theoretical model, the XFEM model, and the FEM model, for various values of the angle of incidence ${\alpha }_i$, the modulus $E_{\infty }$ of material 2, the frequency $f$, and the amplitude $A_i$ of excitation.

FIG. 7.

(Color online) Results of the parametric study presenting the variation of angle of refraction ${\alpha }_t$ and amplitude $A_t$ of transmitted S-waves across an oblique linear interface, in terms of the parameters, including angle of incidence ${\alpha }_i$, modulus $E_{\infty }$ of material 2, frequency $f$, and amplitude $A_i$ of incident P-waves.

For different angles of incidence ${\alpha }_i$, as shown in the first column of Fig. 7, the three models predict that the angle ${\alpha }_t$ increases with ${\alpha }_i$, while the amplitude $A_t$ reaches a maximum at around 60 degrees and then decreases as ${\alpha }_i$ tends to 90 degrees. However, we observe a discrepancy between the numerical models and the theoretical one as neither FEM nor XFEM predict the sharp increase in $A_t$ above ${\alpha }_i$ = 40 degrees.

For different moduli $E_{\infty }$ of material 2 varying from 10 to 80 kPa, we can derive the more commonly-used complex modulus using Eqs. (22)–(24). Thus, the second column of Fig. 7 also represents the influence of the storage modulus $G^{\prime }$ of material 2 from 5.04 to 28.53 kPa, or the effect of the stiffness ratio of material 2 to material 1 varying from 1.35 to 7.57. As can be seen, both ${\alpha }_t$ and $A_t$ increase with $E_{\infty }$ (or $G^{\prime }$, or the stiffness ratio). Although the numerical results by XFEM model and FEM model present the same increasing tendency, the numerical models seem to underestimate $A_t$ for $E_{\infty }$ greater than 40 kPa.

For different excitation frequencies $f$, as shown in the third column of Fig. 7, both ${\alpha }_t$ and $A_t$ decrease as the excitation frequency increases. In terms of ${\alpha }_t$, all the three models are in good agreement. Finally, for different excitation amplitudes $A_i$, the angle ${\alpha }_t$ remains constant and the amplitude $A_t$ increases linearly with $A_i$. Particularly, the XFEM model is in better agreement with the theoretical model, in comparison with the FEM model.

B. Investigation of XFEM by a random-shape inclusion

Figure 8 illustrates, for the random-shape inclusion modeled by XFEM and FEM, the extracted shear components with curl operator applied to the simulated displacement fields. For both models, only one snapshot is shown, which is indeed the first one of the last simulated period (100th). Reflected S-waves from the top and left embedded boundaries can be observed by their great amplitude. The inclusion can be also easily located due to the phase difference between the waves at the two sides of interface. Qualitatively, the two models provide very similar results.

FIG. 8.

Illustration of the first snapshot during a period in steady state (100th period) of curl-applied displacement fields ${\mathit{u}}_T$ from the model containing a random-shape inclusion. (a) and (c) correspond to the results of XFEM simulation for the aligned and tilted inclusion, respectively, while (b) and (d) correspond to the results of FEM simulation for the aligned and tilted inclusion, respectively.

Videos of the entire eight snapshots during a period (100th period) for the four cases in Fig. 8 are provided in Mm. 1, Mm. 2, Mm. 3, and Mm. 4.

Mm. 1.

8 snapshots recording of the curl-applied displacements shown in Fig. 8(a). This is a file of type “gif” (252 KB).

JASMAN-000151-003481_1-S1.gif ^{(251.7KB, gif)}

DOI: 10.1121/10.0011392.1

Mm. 2.

8 snapshots recording of the curl-applied displacements shown in Fig. 8(b). This is a file of type “gif” (254 KB).

JASMAN-000151-003481_1-S2.gif ^{(253KB, gif)}

DOI: 10.1121/10.0011392.2

Mm. 3.

8 snapshots recording of the curl-applied displacements shown in Fig. 8(c). This is a file of type “gif” (248 KB).

JASMAN-000151-003481_1-S3.gif ^{(247.6KB, gif)}

DOI: 10.1121/10.0011392.3

Mm. 4.

8 snapshots recording of the curl-applied displacements shown in Fig. 8(d). This is a file of type “gif” (246 KB).

JASMAN-000151-003481_1-S4.gif ^{(245.6KB, gif)}

DOI: 10.1121/10.0011392.4

Figures 9(a) and 9(b) present the stiffness reconstruction results for the aligned inclusion modeled by XFEM and FEM, respectively. For each model, the shear modulus $G^{\prime }$ was measured within two zones. Zone 1, represented as a circle at the top left, was used for estimating $G^{\prime }$ of the background. This area was chosen for the relatively large amplitude of the shear waves due to reflections at the boundaries. Zone 2 was used for estimating $G^{\prime }$ in the inclusion. In terms of the computation time, it took about 19.2 h of CPU time (6.4 h of real time) for the XFEM model, and 22.0 h of CPU time (7.3 h of real time) for the FEM model.

FIG. 9.

(Color online) Results of shear modulus $G^{\prime }$ reconstruction from the curl-applied displacement fields of the model containing a random-shape inclusion. (a) and (c) correspond to the results of XFEM simulation for the aligned and tilted inclusion, respectively, while (b) and (d) correspond to the results of FEM simulation for the aligned and tilted inclusion, respectively.

Figures 9(c) and 9(d) present the stiffness reconstruction results for the tilted inclusion modeled by XFEM and FEM, respectively. In terms of the computation time, it took about 19.5 h of CPU time (6.5 h of real time) for the XFEM model, and 21.6 h of CPU time (7.2 h of real time) for the FEM model.

All the stiffness estimates are summarized in Table III. Quantitatively, both XFEM and FEM have yielded stiffness estimates close to the ground truth values which were 1.60 kPa for the background and 3.88 kPa for the inclusion. We can also observe that the tilted inclusion model yields larger variance within the inclusion, the estimated modulus being more heterogeneous than that of the aligned inclusion model.

TABLE III.

Stiffness estimates of the inclusion model. The mean, standard deviation (SD), the ratio of standard deviation to the mean (as x%), and the error of the mean with respect to “True” (as x%) in each region are presented for both the XFEM and FEM methods. The “True” values indicate the known ground truth values in the simulations. All the units except those of percentages are in kPa.

	XFEM				FEM				“True”
	Mean	SD	SD/Mean %	Error %	Mean	SD	SD/Mean %	Error %
Aligned inclusion
background	1.599	0.033	2.06	0.06	1.600	0.027	1.69	0	1.60
inclusion	3.450	0.503	14.58	11.08	3.384	0.576	17.02	12.78	3.88
Tilted inclusion
background	1.597	0.016	1	0.19	1.597	0.015	0.94	0.19	1.60
inclusion	3.191	0.794	24.88	17.76	3.162	0.806	25.49	18.51	3.88

V. DISCUSSION

This paper presents an investigation of the potential of XFEM to accurately simulate wave propagation within heterogeneous viscoelastic media, with a special focus on the wave behavior at interfaces. XFEM is indeed particularly adapted to the description of complex inclusion geometries, without requiring a fine remeshing in the vicinity of the interface.

A. Wave mode conversion

A comparison between a theoretical model on the one hand, and FEM and XFEM models on the other hand was performed in the academic case of a plane P-wave impacting an oblique plane interface, to evaluate the potential of FEM and XFEM to correctly predict wave conversion at interfaces. Analytical solutions existed for this case and were considered here as the reference. Good agreement has been shown between the three models, except for some specific cases addressed in the following.

First, numerical errors have been dramatically reduced at the beginning of the simulations, due to the application of the modified-NB time integration scheme. The presence of material interface, however, resulted in the amplification of these noises. Figure 10 compares the case of ${\alpha }_i$ = 60 degrees with normal mesh size (2 mm) to another one with finer mesh (1 mm), both captured at the moment of 4.5 periods. The finer mesh leads to smoother displacement fields, while the coarser mesh yields spurious oscillations that extend much further from the interface. The measurements in the parametric study were conducted several (2 $–$ 3) periods later when the shock front had progressed far away ( $\sim$300 mm) from the region of interest, implying that the results were not likely to be impacted by these noises. However, for other studies requiring the focus on the entire domain, such as the second model with a random-shape inclusion, these numerical oscillations might be an issue and have effects on the reconstruction precision.

FIG. 10.

(Color online) Illustration of converted S-waves by the P-S conversion XFEM model with the angle of incidence ${\alpha }_i$ = 60 degrees. A central zoom is taken for illustration purpose. (a) corresponds to the model meshed with element size of 2 mm, while (b) corresponds to the model with element size of 1 mm.

Then, from the parametric study results in Fig. 7, the conclusion can be drawn that the XFEM model had a similar performance to the FEM model in modeling wave mode conversion at plane interface. For different excitation frequencies and amplitudes, XFEM could produce better results than FEM with respect to the analytical predictions. However, for different angles of incidence and moduli $E_{\infty }$ (or $G^{\prime }$, or the stiffness ratio of material 2 to 1), an offset between the numerical and analytical results was observed. Indeed, the analytical model assumes an infinite plane interface which is hard to model in reality. The interface with finite length, however, implies two extremities such as the two corners formed by the oblique segment and the vertical segments in the P-S conversion model. These two extremities can degrade the wave fields, making the theoretically plane transmitted and reflected waves become no longer plane. Greater angle of incidence and larger value of $E_{\infty }$ (which also means greater wavelength) will further amplify these effects. Moreover, as reported in Ref. 28, the interface waves, i.e., ${\theta }_{\mathit{lmn}}=\pi /2$, can exist when the parameter $\gamma$ in Eq. (13) satisfies ${\gamma }_{\mathit{lmn}}\ge 1$. It can be demonstrated that ${\gamma }_{121}\ge 1$ for an angle of incidence greater than 50 degrees. This indicates that an interface wave existed, though hard to observe, on the transmission side (material 2) for the large angles, which could probably have an influence on the measurements.

B. XFEM for inclusion modeling in MRE

Although XFEM has been developed for two decades and successfully used in modeling different heterogeneities such as cracks, holes, and inclusions, the application to the domain of MRE is not yet introduced in the literature. The second model in this work containing a random-shape inclusion was intended to illustrate the convenience of XFEM in inclusion modeling, namely, the advantage of being remeshing-free. The stiffness estimation from the simulated wave fields further helped in investigating the accuracy of XFEM, and showed that XFEM is totally likely to be integrated and applied in MRE studies. In terms of the computation time, 2 to 3 h of CPU time were gained by XFEM with respect to FEM, revealing the speed of XFEM in this rather simple case. We can imagine that the gain would be even more interesting when it comes to complex geometries of inclusions, such as the irregular ones of real tissues in three dimensions.

The mesh in the XFEM model was composed of only quadrilateral elements (QUAD4), considering the accuracy and the model shape. However, in addition to QUAD4, the triangular elements (TRI3) are also compatible with XFEM in case of complex outer boundaries.

The mesh in the FEM model was mixed with QUAD4 and TRI3. QUAD4 were used as the main elements due to the high accuracy and TRI3 were used for modeling the interface due to flexibility. Indeed, using TRI3 for the entire mesh is also feasible in spite of the potential degradation of simulated results quality.

For the stiffness estimation results, the boundary regions including the model boundaries and the material interfaces were not well reconstructed. This came from the limits of AIDE method and was probably due to the inherent homogeneity assumption as reported in Ref. 7. For the background, the regions with obvious converted S-waves were well reconstructed with $G^{\prime }$ being around the ground truth value of 1.60 kPa, such as those close to the left, top, and bottom edges of model, and those close to the interface of inclusion. The other regions were poorly reconstructed by AIDE due to the absence of S-waves.

From the results summarized in Table III, it can be found that XFEM and FEM yielded similar stiffness estimates and that XFEM performed even better than FEM in the inclusion region. This performance can be more evident by comparing Figs. 9(a) with 9(b) where the inclusion stiffness by XFEM is more homogeneous near the interface than that by FEM. However, it has to be highlighted that by the AIDE reconstruction algorithm, the stiffness estimates of inclusion here were not quite satisfying, with the ratio of standard deviation to the mean between 14.58% and 25.49% and the error of the mean with respect to the ground truth varying from 11.08% to 18.51%. Using other methods such as heterogeneous direct ones assuming stiffness heterogeneity and iterative ones independent from data quality could possibly produce better estimates.⁵²

XFEM would be particularly powerful compared to FEM for more complex geometries than those proposed in this work. Multiple inclusions could for instance be modeled by several level-set functions, without any limitation in stiffness ratio. However, if interfaces are too close, i.e., two interfaces cross the same element, the mesh should be locally refined, or a recent algorithm of multi-split XFEM could be implemented.⁵³

C. Perspectives

The work presented here applied a 2D model with a finite piecewise linear interface for investigating the P-S conversion. A more realistic model in three dimensions, containing a better designed interface, might produce results closer to the analytical predictions. In addition, other theories using different methods and assumptions for the wave behaviors at interface are also available, such as that applied decomposition and superposition of wave components⁵⁴ and that applied generalized Snell's law.⁵⁵ They could be further studied to compare with the results in this work.

The work presented here investigated XFEM by a 2D inclusion model. The 3D inclusions can be also modeled by XFEM. For its implementation, the 3D element partition and the definition of 3D interface can be a challenge. The applicability of 3D XFEM in MRE will be studied in future work.

In fact, XFEM has no known limit on the material property (non-linearity, anisotropy, etc.), problem scale and excitation frequency. It can be also applied to inclusions at microscale and subjected to higher mechanical frequency, provided that the mesh is accordingly adapted. For example, an adaptive XFEM was recently proposed which can be applied for solving the multiscale problems.⁵⁶

Recently, artificial intelligence (AI) has been applied in MRE research for stiffness estimation. Different models were used such as the deep neural network (DNN),⁵⁷ the support vector machine (SVM),⁵⁸ and the convolutional neural network (CNN).^26,59,60 To train the AI model, a great deal of sample data is generally required, in which the configuration such as the inclusion shape and size, the materials, and the boundary conditions could be different from one another. Both experimental data and simulated data have been employed in the training procedures. However, numerical simulations could be more efficient for generating massive, various, and reliable samplings in a relatively short time. For example, the CHO model has been used for this purpose in Ref. 26. Despite its efficiency, some assumptions were made in this model such as not modeling the full Navier equations of motion, neglecting longitudinal waves and mode conversion at interfaces. A more realistic model obeying the equations of motion was thus expected by the author and FEM could be a competent candidate. However, in traditional FEM, a different configuration of inclusion means a different mesh and would require a remeshing work. The data preparation prior to the AI model training could thus become burdensome, let alone the expensive computing efforts by FEM. In this context, the alternative method proposed in this work, XFEM, can be applied to overcome the previously noted difficulties. By XFEM, different inclusions can be modeled without remeshing and the calculations can be also accelerated. This could facilitate the application of AI method in MRE.

VI. CONCLUSION

In this work, XFEM has been proposed to model inclusions in MRE simulations. A 2D model containing piecewise linear interfaces was developed to study the plane wave conversion from P-waves to S-waves at a plane oblique interface. Results from numerical simulations by XFEM/FEM and theoretical predictions revealed the P-S conversion rules and also suggested that it is hard to perfectly reproduce the analytical model due to the infinite plane assumption and the undesired perturbations. The other model containing a random-shape inclusion was developed to investigate XFEM in a pseudo-practical application. By conducting the stiffness reconstruction and comparing the results of XFEM model with those of FEM model, it was demonstrated that with respect to FEM, XFEM could have similar and even better performance. XFEM can be also time-saving with the same computation device. Due to its convenience, accuracy, and speed, XFEM could be a better choice and a promising tool for inclusion modeling in MRE.