Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jun 9;7(24):20914–20926. doi: 10.1021/acsomega.2c01630

Alkaline-Earth Metal Effects on Physical Properties of Ferromagnetic AVO3 (A = Ba, Sr, Ca, and Mg): Density Functional Theory Insights

Md Mijanur Rahaman †,*, Khandaker Monower Hossain †, Mirza Humaun Kabir Rubel †,*, A K M Azharul Islam ‡,§, Seiji Kojima ∥
PMCID: PMC9219064  PMID: 35755384

Abstract

graphic file with name ao2c01630_0015.jpg

The effects of alkaline-earth metals on electronic, optical, thermodynamic, and physical properties of ferromagnetic AVO3 (A = Ba, Sr, Ca, and Mg) have been investigated by first-principles calculations within the GGA+U formalism based on density functional theory. The optimized structural parameters are in good agreement with the available experimental results that evaluate the reliability of our calculations. The cell and mechanical stability is discussed using the formation energy and Born stability criteria, respectively. The mechanical behaviors of AVO3 are discussed on the basis of the results of elastic constants, elastic moduli, Peierls stress, and Vickers hardness. The nature of the ductile–brittle transition of AVO3 compounds was confirmed by the values of Pugh’s ratio, Poisson’s ratio, and Cauchy pressure. The electronic band structures, as well as density of states, reveal the half-metallic behavior of BaVO3 and SrVO3. However, CaVO3 and MgVO3 exhibit spin-gapless and magnetic semiconductor characteristics, respectively. The microscopic origin of the transition from the half-metallic to semiconductor nature of AVO3 is rationalized using electronic properties. The presence of covalent, ionic, and metallic bonds in AVO3 compounds is found by the analysis of bonding properties. The single-band nature of half-metallic AVO3 is seen by observing hole-like Fermi surfaces in this study. Furthermore, the various thermodynamic and optical properties are calculated and analyzed. The refractive index suggests that AVO3 could be a potential candidate for applications to high-density optical data storage devices.

1. Introduction

The understanding of ABO3-type oxide perovskites is crucial not only due to their structures and properties being modified by the exchange of distinct elements into their crystallographic equivalent sites but also for investigating phase transitions. This type of material is also fundamentally interesting and bears technological importance because of its ferroelectric, multiferroic, magnetic, and superconducting properties,1−5 which originate from an interplay between the chemical composition and the structure type. Recently, the study of AVO3 (A = Ba, Sr, Ca, and Mg) has been given much attention because of the strong couplings between the lattice degrees of freedom and spin,6−8 which makes them a potential candidate for the application to spintronics devices. It has been found that few atoms at the A site in AVO3, e.g., PbVO3, showed antiferromagnetic ordering with large spontaneous polarization.9,10 Belik et al. also reported the insulator to metal transformation, induced by crystal symmetry variations from the tetragonal to cubic phase in PbVO3.11

AVO3 (A = Ba, Sr, Ca, and Mg) have been synthesized by using high-temperature and high-pressure (HTHP) conditions for investigating their structural and relevant properties.12−15 BaVO3 showed a polycrystalline phase with a cubic perovskite structure under high pressures, and it should be noted that Ba3(VO4)2 was formed instead of BaVO3 when either the pressure or temperature was insufficient.12 Notably, SrVO3 and CaVO3 have correlated Mott conductors in which SrVO3 is cubic perovskite, and their oxygen nonstoichiometric effects on the structures and electronic states are investigated extensively.13,14,16,17 Strontium vanadate has a simple cubic perovskite structure with a = 3.842 Å that exhibits Pauli paramagnetic and metallic characteristics near room temperature as well.16 Additionally, the dielectric function, the band structure, the Fermi surface, and interband optical transitions of the SrVO3 transparent conducting thin film have also been analyzed from the first-principles study.16 Moreover, this material has attracted great attention as a potential oxide electrical conductor.18,19 However, stoichiometric CaVO3 belongs to the orthorhombic phase, while nonstoichiometric CaVO3−δ (0.04 < δ < 0.08) and CaVO3−δ (δ = 0.20) show cubic and monoclinic phases, respectively.14,20 In addition, the slightly oxidized CaVO3.05 exhibits insulating behavior without any significant structural changes.21 At ambient pressure, Chamberland et al. reported the orthorhombic crystal structure of MgVO3, whereas the high-pressure adjustment of MgVO3 exhibited a triclinic structure.22 The electronic band structure with various spin arrangements for MgVO3 showed paramagnetic as well as magnetic solutions with ferro- and antiferromagnetic ordering.23 Between them, the paramagnetic solution has metallic behavior, whereas the band splits into two in the magnetic solutions with an insulator gap in ferro- and antiferromagnetic states.23 Hence, with the substitution of distinct A site cations, a perovskite may show various stable phases and correspondingly diverse material peculiarities. Therefore, it is interesting to discover the electronic, optical, and diverse physical properties of AVO3 perovskites, where A is a divalent cation.

Nowadays, the cubic phase of oxide perovskite materials is an extensive research area for the proper explanation of electronic, elastic, vibrational, thermodynamic, and optical properties for emergent applications. Recently, Kamruzzaman et al.24 reported a comparative study on the cubic phases of ATiO3 (A = Ba, Ca, Pb, and Sr) by first-principles calculations. The first-principles calculations on the cubic phase of simple and double-perovskite Bi oxide magnetic materials, which exhibited superconductivity, envisage different interesting physical properties including electronic, mechanical, and thermodynamic properties as well.3,25,26 The cubic perovskite structures of AVO3 (A = Ba, Sr, Ca, and Mg) are our point of interest in the present investigation. The cubic phase with Pm3̅m symmetry of SrVO3 and BaVO3 was reported experimentally,12,13 whereas CaVO3 and MgVO3 show an intrinsically orthorhombic phase.14,15 The cubic phase of CaVO3 and MgVO3 may be comprehended by using specifically designed growth conditions similar to those implemented for achieving hexagonal Si.27 Rashid et al.28 reported metallic behavior in both spin channels of cubic BaVO3 and LaVO3 using the GGA-PBE exchange–correlation, while the utilization of the mBJ scheme explicated a clear half-metallic ferromagnetic behavior. They discussed the electronic and thermoelectric properties of BaVO3 and LaVO3. The electronic, magnetic, and optical properties in the low-energy range (0–15 eV) of cubic AVO3 (Ba, Sr, and Ca) were studied by first-principles calculations.29 However, extensive studies on the alkaline-earth metal’s effects on physical properties (elastic constants, elastic moduli, Peierls stress, Pugh’s and Poisson’s ratio, Cauchy pressure, and Vickers hardness), the Fermi surface, electronic charge density, and population analysis are rather scarce, which are crucial for accelerating the applications and understanding of these material systems precisely.

In this study, we have investigated the structural, physical (elastic constants, Young’s, shear, and bulk moduli, Pugh’s and Poisson’s ratio, Cauchy pressure, Peierls stress, and Vickers hardness), electronic (the band structure, charge density map, DOS, and Fermi surface), optical (the dielectric function, photoconductivity, refractive index, reflectance, and absorbance), population analysis, and thermodynamic properties (melting temperature, Debye temperature, and minimum thermal conductivity) considering the cubic phase of ferromagnetic AVO3 by altering cations Ba, Sr, Ca, and Mg employing density functional theory (DFT)-based CASTEP code. The possibility of applications to high-density optical data storage devices of AVO3 has been discussed on the basis of observed optical properties.

2. Computational Methods

The present calculations based on density functional theory (DFT)30,31 were carried out with the Cambridge Serial Total Energy Package (CASTEP) code32 utilizing the GGA+U parameterization scheme. The spin-polarized scheme using formal spin as the initial state with charge neutrality conditions was implemented in the relatively high-level computation GGA+U method. The default value of Hubbard U = 2.5 eV for V 3d was set for computations in this study. The ultrasoft pseudopotential formalism of the Vanderbilt type33 was utilized for all atoms to simulate the interactions of valence electrons with ion cores. The choice of exchange–correlation functionals (XCs) was regarded as a crucial parameter for first-principles calculations. Therefore, geometry optimization of the cubic structure of BaVO3 with Pm3̅m symmetry with fully relaxed structures was performed by the Broyden–Fletcher–Goldfarb–Shannon (BFGS) algorithm34 using various XCs to search the ground state to obtain the best lattice parameters and compare them with the available experimental ones. The XC that induced the best results for BaVO3 was used to calculate all properties of AVO3 (A = Ba, Sr, Ca, and Mg) by altering the A cations. The electronic wave function with a cutoff energy of 700 eV was used for all calculations of cubic AVO3 with a ferromagnetic (FM) configuration because the FM state was relatively more stable than the antiferromagnetic (AFM) state.29 According to the Monkhorst–Pack scheme,35 12 × 12 × 12 k-point grids were employed for sampling the irreducible Brillouin zone. In the present calculations, the convergence tolerances for geometry optimization were set to be 1 × 10–6 eV/atom (total energy), 0.03 eV/Å (maximum force on atoms), 0.001 Å (maximum atom displacements), and 0.05 GPa (maximum stress).

3. Results and Discussion

3.1. Structural Parameters and Cell Stability

The oxide perovskites AVO3 (A = Ba and Sr) belong to the cubic phase with Pm3̅m (no. 221) symmetry consisting of an A atom at the corner, V in the body center, and O at the face center of the cube.12,13 The cubic phase of nonstoichiometric CaVO3−δ (0.04 < δ < 0.08) was reported experimentally by Ueda,14 while stoichiometric CaVO3 and MgVO3 showed an orthorhombic phase.14,15 To realize the cubic phase of CaVO3 and MgVO3, specifically designed growth schemes similar to those implemented for observing hexagonal Si are necessary.27 First, the crystal structure of BaVO3 was sketched using the available refinement data12 in this study. After that, the structures were absolutely relaxed with the lattice parameters and internal coordinates in order to optimize the geometry by swapping A site cations. The crystal structures of the cubic AVO3 (A = Ba, Sr, Ca, and Mg) system are depicted in Figure 1. The optimized lattice parameters of AVO3 substances, both theoretical and experimental data, are summarized in Table 1. The calculated values of lattice parameters match reasonably with the experimental results,12−14 and the relation is noted as follows: a(BaVO3) > a(SrVO3) > a(CaVO3) > a(MgVO3). The resultant interatomic distance decreases with decreasing atomic radii from the bottom to top in a group, which results in a decreasing trend in lattice parameters. Interestingly, these consequences are similar to those observed in ATiO3 (A = Ba, Ca, Pb, and Sr) compounds.24 Moreover, the chemical stability of AVO3 can be confirmed by analyzing their formation energies. The formation energy (ΔEf) is approximated by the subtraction of the total energies of pure constituent atoms from the total energy of the materials in their stable structures. The magnitude of ΔEf of AVO3 is estimated by the following expression:36

3.1. 1

Here, Etot(AVO3)fu represents the total energy per formula unit and is given by Etot(AVO3)fu = 1/N[Etot(AVO3)cell], where N denotes the number of formula units per unit cell. Es(A), Es(V), and Es(O) are the total energies per atom of the pure elements A, V, and O, respectively, in their ground-state solid phases. So, ΔEf per atom = ΔEf(AVO3)fu/Nt, where Nt denotes the total number of atoms in one formula unit. The calculated formation energies of ferromagnetic AVO3 are also displayed in Table 2. It is seen from Table 2 that the energies of AVO3 are negative, indicating that the compounds are energetically stable.

Figure 1.

Figure 1

Open in a new tab

(Color online) Unit cell of cubic perovskite AVO3 (A = Ba, Sr, Ca, and Mg).

Table 1. The Optimized Lattice Parameter, a (Å), of BaVO3 with Different XCs and Compared with the Available Experimental Results.

  exchange–correlation functions (XCs)
  
  PBE RPBE PW91 WC PBEsol expta
lattice parameter 3.97846 4.01721 3.97463 3.92674 3.92391 3.94288
Open in a new tab
a

Ref (12).

Table 2. The Calculated Lattice Constant, a, Volume, V, and Formation Energy ΔEf of AVO3 Compounds Together with Available Experimental Results.

compounds a (Å) V (Å3) ΔEf (eV/atom) refs.
BaVO3 3.927 60.547 –7.601 present calc.
  3.943(3)     (12)
SrVO3 3.830 56.185 –7.626 present calc.
  3.843(1)     (13)
CaVO3 3.774 53.752 –7.635 present calc.
CaVO3−δ 3.786(3)     (14)
MgVO3 3.741 52.358 –6.986 present calc.
Open in a new tab

3.2. Physical Properties

3.2.1. Elastic Moduli and Peierls Stress

The study of numerous physical characteristics such as elastic anisotropy, both brittle and ductile nature, and elastic moduli is crucial for industrial applications of engineering materials. The elastic constants Cij are obtained from the linear finite stress–strain approach within the CASTEP code.37 The calculated three independent elastic constants, namely, C11, C12, and C44, for cubic AVO3 are displayed in Table 2. The mechanical stability of a lattice can be determined by Born stability criteria that are commonly formulated in terms of Cij and hence based on free energy considerations.38 For a cubic crystal, the mechanical stability criteria are C11 + 2C12 > 0, C11 – C12 > 0, and C44 > 0, which stand for spinodal, shear, and Born criteria, respectively. The spinodal criterion is equivalent to insisting on a positive bulk modulus, B. Hence, the mechanical stability of a cubic crystal requires that the elastic constants B, C11 – C12, and C44 be positive. Following these stability conditions, the calculated elastic constants are presented in Table 2. Therefore, the chosen cubic phase of AVO3 in this investigation is mechanically stable. The tendency of a solid to deform non-permanently in diverse directions with applied stress is measured by its elastic property. The elastic constants provide information about the bonding behavior of solids as well. The elastic constant C11 gives the elasticity along the axial length. So, the elastic stiffness of solids against the ⟨100⟩ uniaxial strain of the (100) plane can be signified by the value of C11. The elasticity in shape is given by the elastic constants C12 and C44, where C44 denotes the shear stress in the (010) plane along the ⟨001⟩ direction and C12 indicates the pure shear stress in the (110) plane in the ⟨110⟩ direction. As can be seen in Table 3, CaVO3 has the largest value of C11 compared to others. It is worth noting that the calculated value of C11 for all perovskites is higher than C12, indicating that the bonding strength along the ⟨100⟩ direction is higher than that along the ⟨110⟩ directions in AVO3. This result indicates that the elasticity in length is stiffer than the elasticity in shape. The Kleinman parameter (ξ) measures the ease of bond bending to bond stretching. In general, the value of ξ can be between 0 and 1 (0 ≤ ξ ≤ 1) and is estimated using the following expression:39

3.2.1. 2
Table 3. The Elastic Constants, Cij (GPa), Bulk Moduli, B (GPa), Shear Moduli, G (GPa), Young’s Moduli, E (GPa), the Kleinman Parameter, ξ, the Burgers Vector, b (Å), the Interlayer Distance, d (Å), and Peierls Stress, σp (GPa), of AVO3 Compounds.
compounds C11 C12 C44 B G E ξ b d σp HV
BaVO3 300 116 134 177 115 283 0.527 3.927 1.963 2.489 16.4
SrVO3 335 113 118 187 115 287 0.482 3.830 1.915 2.380 15.2
CaVO3 351 113 98 192 106 268 0.468 3.774 1.887 1.985 12.3
MgVO3 345 124 56 198 74 197 0.502 3.741 1.871 0.990 4.9
Open in a new tab

Kleinman reported that the upper limit corresponds to a minimized bond bending term and the lower limit corresponds to a minimized bond stretching term.40 The calculated value of ξ for AVO3 compounds is shown in Table 2. The estimated value of ξ of ∼0.50 for AVO3 compounds is in good agreement with the previously reported value of ξ of ∼0.555 for perovskite LaAlO3.41 The calculated value of ξ suggests the strong bonding nature of AVO3, which is dominated by the bond bending compared to the bond stretching.

The various elastic properties such as the bulk modulus, B, shear modulus, G, Young’s modulus, E, and Poisson’s ratio, ν, are calculated from the single-crystal zero-pressure elastic constants using well-known relationships.42,43 The calculated elastic parameters are shown in Table 2. The constituent atom’s average bond strength for a given solid is assessed by the bulk modulus.44 Recently, Rahaman et al. found the moderate bonding strength in LiCuBiO4 by observing the bulk modulus of 101 GPa.47 However, Nasir et al. reported the strong bonding in ScIrP and ScRhP by the bulk moduli of 190 and 171 GPa, respectively.45 Thus, the calculated values of B in the range of 177–198 GPa (Table 2) may imply the strong bonding strength of atoms involved in AVO3. It is also seen from Table 2 that the bulk modulus improves by varying cations from Ba to Mg. The cationic size decreases the compressibility of the compounds, making the solid dense that enhances the bulk modulus of AVO3. The bond strength of atoms also gives the required resistance to volume deformation under external pressure. In contrast, the G evaluates the change of shape in a solid, which exhibits a crucial relationship with the hardness of materials. The material becomes more rigid when the value of G becomes greater. The Young’s modulus, E, exerts an influence on the thermal shock resistance of solid matter. The critical thermal shock coefficient varies inversely with respect to E.46 The greater the value of the thermal shock coefficient, the better the thermal shock resistance. A material is chosen as a thermal barrier coating (TBC) substance based on thermal shock resistance. Notably, AVO3 has a comparatively higher Young’s modulus, and hence, it might not be suitable as a TBC material. However, the calculated value of E (197–287 GPa) indicates that AVO3 is moderately stiff.47 The moduli of elasticity such as G, B, and E are not only useful to explain the mechanical properties of solids but also effective to estimate the hardness of materials. C44 is the best one to predict the hardness of solids among the observed elastic constants. Moreover, the shear modulus (G) is considered as the best hardness predictor among the moduli of elasticity as well. It is evident from Table 3 that BaVO3 is harder than the rest of the compounds in this study. These statements may be strengthened by the calculations of hardness by Chen’s formula,48 which can be expressed as HV = 2(k2G)0.585 – 3, where k is the Pugh ratio (G/B). The estimated values of HV are displayed in Table 3 and found to be consistent with the earlier predictions based on the values of C44 and G. Mazhnik and Oganov49 reveal conducive agreement between the experimental and theoretical values of hardness of different materials calculated using Chen’s formula. It is well-established that diamond (HV = 96 GPa), BC2N (HV = 76 GPa), and BC5 (HV = 71 GPa) are widely used as superhard materials.49 Thus, the much lower harness of AVO3 in comparison with superhard materials confirms that the studied compounds do not belong to superhard materials. However, the value of HV of half-metallic BaVO3, SrVO3, and CaVO3 is comparable with hard refractory materials NbC (HV = 16.0 GPa), GaN (HV = 15.1 GPa), and GaN (HV = 12.0 GPa), respectively, whereas the HV value of MgVO3 is comparable with the semiconductor AlAs (HV = 5.0 GPa).49 The relatively large value of hardness denotes that BaVO3, SrVO3, and CaVO3 are not machinable, whereas MgVO3 is machinable by conventional cutting machines.

Furthermore, the study of failure modes, i.e., the ductile or brittle nature of a material, is technologically very important. For most practical situations, a material may be classified as either brittle or ductile. Figure 2 shows the graphical representation of ductile materials from brittle materials for all considered perovskite materials. If the value of Pugh’s ratio (G/B) is higher than 0.57, then the material is said to be brittle;50 otherwise, it is ductile. It is apparent from the upper part of Figure 2a that BaVO3 and SrVO3 are brittle materials, whereas the nature of CaVO3 is at around the ductile–brittle transition line; on the other hand, MgVO3 exhibits a ductile nature. In addition to Pugh’s ratio, Frantsevich et al. also proposed a critical value of Poisson’s ratio (ν of ∼0.26) for separating the brittle and ductile nature of solids.51 The calculated values of ν (middle part of Figure 2a) again confirm that BaVO3 and SrVO3 are purely brittle, while MgVO3 is a completely ductile material. However, CaVO3 is the crossover of the brittle to ductile transition. The Cauchy pressure, defined as C12–C44, is another indicator of failure mode of materials.52 If the Cauchy pressure is negative, then the material is expected to be brittle; otherwise (having a positive Cauchy pressure), it is a ductile one.52 Hence, in this study, BaVO3 and SrVO3 are assumed to be brittle, whereas CaVO3 and MgVO3 are ductile in accordance with the aforementioned three indicators.

Figure 2.

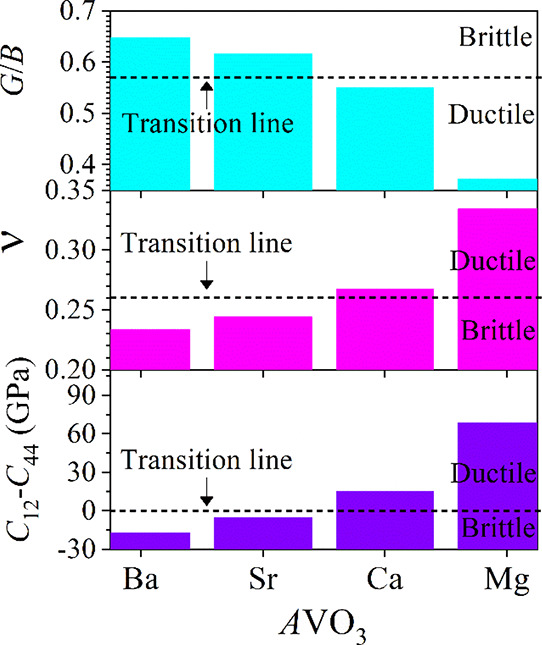
Figure 2

Open in a new tab

(Color online) Calculated Pugh’s ratio (G/B), Poisson’s ratio (ν), and Cauchy pressure (C12–C44) showing the graphical representation of ductile/brittle behavior of AVO3 (A = Ba, Sr, Ca, and Mg). The horizontal dashed lines indicate the ductile–brittle transition line.

The Peierls stress represented by σp is the force required to move a dislocation inside an atomic plane in the unit cell, which measures the strength of a crystal through displacing dislocations. Therefore, Peierls stress can provide the knowledge to accelerate dislocation in a glide plane of the synthesized cubic perovskite crystals as well. The Peierls stress can be estimated using the shear modulus (G) and the Poisson ratio (ν) as follows:53

3.2.1. 3

Herein, d and b denote the interlayer distance between the glide planes and the Burgers vector, respectively. The calculated interlayer distance (d), the Burgers vector (b), and the resulting Peierls stress (σp) of AVO3 are presented in Table 3. It is seen from Table 3 that the values of σp decrease as we follow the sequence Ba→Sr→Ca→Mg. The lowest and highest values of estimated Peierls stress are 0.990 and 2.489 GPa for MgVO3 and BaVO3, respectively. The σp values of BaVO3, SrVO3, and CaVO3 are comparable to the reported double cubic perovskite (Na0.25K0.45)Ba3Bi4O12,54 whereas the σp value of MgVO3 is comparable to the reported simple cubic perovskite (Ba0.62K0.38)(Bi0.92Mg0.08)4O12.24 The calculated values of σp for AVO3 compounds can also be compared with several inverse perovskites Sc3InX (X = B, C, and N) with σp values ranging from 3.06 to 5.31 GPa55 and those of MAX phases Y2AlC (Y = Nb, Ta, V, Cr, and Ti) ranging from 0.74 to 0.98 GPa.56 Furthermore, the reported σp values for rocksalt binary carbides TiC, VC, and CrC are between 17.46 and 22.87 GPa.56 The value of σp of AVO3 exhibits the sequence σp (MAX phases) < σp (AVO3 perovskites) < σp (selected inverse perovskites) ≪ σp (binary carbides). Hence, it is apparent that dislocations can move easily in the selected MAX phases, but the movement of dislocation is almost impossible in the case of the binary carbides. Since AVO3 (A = Ba, Sr, and Ca) perovskites in the present study show an intermediate value of σp larger than the MAX phases but smaller than the selected inverse perovskites, so, the dislocation movement may still be observed here but not as easily as in MAX phases. The value of σp for MgVO3 is similar to that of the MAX phase Ti2AlC56 and smaller than those of BaVO3, SrVO3, and CaVO3. So, the movement of dislocation in MgVO3 may occur more easily than in other perovskites and the same as in the MAX phase Ti2AlC under this study.

3.2.2. Elastic Anisotropy

Elastic anisotropy influences various types of physical processes, such as microscale cracking in ceramics, development of plastic deformation in crystals, mechanical yield points, enhanced charged defect mobility, internal friction, and elastic instability. In a cubic phase, Zener’s anisotropy index [AG = 2C44/(C11 – C12)] is one of the important parameters to determine whether the crystal is isotopic or not. The material will be isotropic only if AG becomes unity. The deviation of AG from unity measures the degree of elastic anisotropy, and more deviation means more anisotropy. Another important measure of anisotropy, namely, the universal anisotropy index AU, is defined as Inline graphic, where the subscripts denote the upper bound (Voigt, V) and the lower bound (Reuss, R) of B and G. Here, AU = 0 indicates the isotropic nature of materials, and the deviation from zero characterizes the elastic anisotropy of crystals. It is apparent from Figure 3b that the values of AG and AU of SrVO3 are close to the isotropic line, whereas values of AG and AU significantly deviate from the isotropic line in the cases of BaVO3, CaVO3, and MgVO3. These results indicate that BaVO3, CaVO3, and MgVO3 are anisotropic, but SrVO3 represents very weak or reasonably negligible anisotropy.

Figure 3.

Figure 3

Open in a new tab

(Color online) Isotropic/anisotropic nature of AVO3 shown graphically by Zener’s anisotropy index (AG) and the universal (AU) anisotropy index, where the dash-dotted lines denote the isotropic line.

The three-dimensional (3D) dependences of the shear modulus, G, Young’s modulus, E, and Poisson’s ratio, ν, of AVO3 are studied in order to depict the elastic anisotropy visually as well as quantitatively. The 3D directional dependence of G, E, and ν is depicted in Figure 4. The 3D surface should exhibit a spherical shape for a perfectly isotropic compound. It is seen in Figure 4 that the 3D surface of G, E, and ν of SrVO3 has an almost spherical shape. This result clearly indicates that BaVO3, SrVO3, and MgVO3 are anisotropic compounds, whereas SrVO3 is a compound with weak or negligible anisotropy. The minimum and maximum values of G, E, and ν of the materials are shown in Table 4 for comparison among the four compounds. The 3D plots as well as numerical values of different anisotropy indices reveal that MgVO3 is the most prominent anisotropic compound among the four compounds, and the relation MgVO3 > BaVO3 > CaVO3 > SrVO3 was observed.

Figure 4.

Figure 4

Open in a new tab

(Color online) Directional dependences of the shear modulus, G (upper curves), Young’s modulus, E (middle curves), and Poisson’s ratio, ν (lower curves), of AVO3 (A = Ba, Sr, Ca, and Mg).

Table 4. The Maximum and Minimum Limits of G, Y, and ν of AVO3 (A = Ba, Sr, Ca, and Mg).
  shear modulus (GPa)
 Young’s modulus (GPa)
 Poisson’s ratio
compounds Gmax Gmin Emax Emin νmax νmin
BaVO3 133.62 91.59 320.41 234.41 0.350 0.098
SrVO3 118.07 110.93 292.60 277.83 0.262 0.223
CaVO3 118.94 97.68 295.80 250.58 0.334 0.214
MgVO3 110.13 56.00 278.68 153.52 0.544 0.165
Open in a new tab

3.3. Electronic Properties

3.3.1. Electronic Band Structures

The calculated electronic band structures of AVO3 with a ferromagnetic configuration are depicted in Figure 5, where the horizontal dash-dotted lines denote the Fermi level, EF. The splitting of energy in the spin-polarized electronic band structure is clearly seen, which appears owing to the existence of vanadium cations in the studied perovskites. It is seen from Figure 5 that the valence and conduction bands of BaVO3 and SrVO3 appreciably overlap with each other and cross the Fermi level in the spin-up channel (Figure 5a,b), resulting in no band gap at the EF, indicating that the free carriers are available to show metallic conductivity, while the spin-down (spin-dn) channel exhibits an indirect band gap (R−Γ) semiconductor-like behavior because the Fermi level lies inside the forbidden gap. However, the valence band of CaVO3 and MgVO3 touches the Fermi level in both spin-up and spin-down channels as shown in Figure 5c,d, while the conduction band of CaVO3 touches the Fermi level in the spin-up channel, but a clear energy gap is found for the spin-down channel. In contrast, there is a tiny (Eg of ∼0.12 eV) and wide energy gap (Eg of ∼2.19 eV) between the conduction band and the Fermi level in spin-up and spin-down channels for MgO3, respectively. For the spin-up state of CaVO3, no overlapping and also a negligible energy gap (Eg of ∼0.03 eV) between the valence and conduction bands are observed (Figure 5c); this finding suggests the spin-gapless semiconductor behavior of CaVO3. Hence, the overall behavior of BaVO3 and SrVO3 is half-metallic ferromagnetic, whereas ferromagnetic CaVO3 and MgVO3 behave like spin-gapless and magnetic semiconductors, respectively. It is significant that the valence band of CaVO3 and MgVO3 is very flat just below the EF with a large dispersion from the R to M point, which may create a van Hove singularity (vHS) at both points. The presence of such a vHS in the band diagram usually denotes the enhanced electronic and electrical carriers as well as electron pairings in the case of superconducting materials.3,57 Hence, the presence of a flat band might be the possible reason for the spin-gapless and magnetic semiconductor nature of CaVO3 and MgVO3, respectively. Mahmood et al.29 reported the half-metallic ferromagnetic behavior of AVO3 (A = Ba, Sr, and Ca) as well. The electronic properties of AVO3 (A = Sr, Ba, and Pb) also revealed the half-metallic nature studied by Yan et al.58 The band gap of ferromagnetic MgVO3 was also reported at about 0.5 eV within the local spin density approximation (LSDA).22 In this study, the half-metallic nature of AVO3 (A = Ba, Sr, and Ca) is 100% spin-polarized because all the states are present in the spin-up channel, while the spin-down channel has no states. The indirect band of the studied AVO3 compounds may arise owing to the exchange splitting.29 It is significant that the indirect band gap in the spin-down channel decreases with the cation changing from Ba to Ca as shown in Figure 7. The results are similar to those observed in ref (29).

Figure 5.

Figure 5

Open in a new tab

(Color online) Spin-polarized GGA+U (U = 2.5 eV for V 3d) calculated electronic band structures of (a) BaVO3, (b) SrVO3, (c) CaVO3, and (d) MgVO3 along the high-symmetry directions in the Brillouin zone.

Figure 7.

Figure 7

Open in a new tab

(Color online) (a–d) Total density of states (TDOS) and partial density of states (PDOS) at the Fermi level (EF) of AVO3. (e) Band gap energy (Eg) of AVO3 in the spin-down channel.

3.3.2. Density of States (DOS)

In order to have a better understanding, the atomic contributions to the band formation of AVO3 compounds, the partial density of states (PDOS), and the total density of states (DOS) have been calculated and are plotted in Figure 6. It is evident from DOS that all the compounds have n-type carriers59 with a sharp peak for the crossing of electrons at EF. Among them, MgVO3 has a relatively lower class of carriers because of its semiconducting nature. The lower band of AVO3 for both spin-up and spin-down channels is situated at about −65 eV, which originated from V 4s states, whereas the lowest band of MgVO3 is located at around −75 eV, which stemmed from the Mg 3s state only. The band of BaVO3 originated from the V 3p state for both channels and is situated at around −39 eV and shifts to a little higher energy with the alteration of the cation from Ba to Mg. The bands at about −25, −34, −42, and −39 eV of BaVO3, SrVO3, CaVO3, and MgVO3 come from the Ba 6s, Sr 5s, Ca 4s, and Mg 2p states, respectively. The band at around −18 eV of BaVO3 and SrVO3 is due to the admixture of dominating O 2s along with minor contributions of V 3p and 3d, Ba 5p and 4d, and Sr 4p and 3d states, whereas the band of CaVO3 is due to the primary contribution of the Ca 3p state along with a little contribution of O 2s. Over these states, around −16 to −11 eV is demonstrated to be completely p states of Ba and Sr with the minor contributions of s and p states of O for BaVO3 and SrVO3, respectively, whereas in the case of CaVO3 and MgVO3, the band is a major contribution of O 2s with minor contributions of p and d states of V. Finally, the TDOS from −8 eV to the Fermi level (EF) has primary contributions from V 3d and O 2p states along with minor contributions of the p state of V and d and s states of Ba and Sr atoms (Figure 6).

Figure 6.

Figure 6

Open in a new tab

(Color online) Total and partial density of states of (a) BaVO3, (b) SrVO3, (c) CaVO3, and (d) MgVO3 with the spin-polarized GGA+U (U = 2.5 eV for V 3d) method.

To clarify the physical origin of half-metallic ferromagnetism of AVO3 compounds, we also studied the TDOS and PDOS at the EF for the spin-up channel, which is shown in Figure 7. It is found from Figure 7 that the PDOS value of V 3d and O 2p states decreases by changing cations from Ba to Ca, and the PDOS value of V 3d becomes very small in CaVO3 and MgVO3, while the PDOS value of the O 2p state increases in MgVO3. These results indicate that the strong hybridization between V 3d and O 2p is responsible for the half-metallic and semiconductor nature of AVO3, where the V 3d state controls the half-metallic behavior and O 2p dominates the semiconductor nature of the studied compounds.

3.3.3. Electronic Charge Density

The charge density maps of valence electrons are depicted in Figure 8 to comprehend the total electronic charge density distribution of AVO3 compounds. The scale on the right side shows the intensity of electron density. The red color denotes the high density of electrons, whereas the blue color represents the low density of electrons. It is apparent from Figure 8 that the distribution of charge density is essentially spherical around all the atoms of AVO3 compounds. This outcome indicates the ionic nature of AVO3 compounds. The ionic characteristics are also an effect of the metallic characteristics of compounds. As can be seen in Figure 4b, the O–V bonds where the electronic charge transfer from V 3d to O 2p in AVO3 (A = Ba, Ca, and Mg) manifest a half-metallic nature.

Figure 8.

Figure 8

Open in a new tab

(Color online) Electronic charge density of (upper left) BaVO3, (upper right) SrVO3, (lower left) CaVO3, and (lower right) MgVO3.

3.3.4. Fermi Surface

The Fermi surface topologies of AVO3 compounds are shown in Figure 9. The Fermi surfaces of BaVO3, SrVO3, CaVO3, and other compounds are almost similar. It is seen from the topology that there is a hole-like Fermi surface that looks like a cylindrical cross section with six windows surrounded at the Γ-point. A hole pocket is also present around the X-point connected with the hole-like Fermi surface surrounding the Γ-point. Hence, it is evident that only hole-like Fermi surfaces are present, which reveals the single-band nature of AVO3 (A = Ba, Sr, and Ca) compounds. However, the MgVO3 compound does not show the Fermi surface topology for its semiconducting nature.

Figure 9.

Figure 9

Open in a new tab

(Color online) Fermi surface topology of (a) BaVO3, (b) SrVO3, and (c) CaVO3.

3.4. Optical Properties

The material’s response to incident electromagnetic radiation can be explained by various optical properties, namely, the dielectric function, the refractive index, conductivity, the absorption coefficient, reflectivity, and the loss function. The real (ε1) and imaginary (ε2) parts of the dielectric function of AVO3 compounds are displayed in Figure 10. The damping factor of 0.05 eV and the Drude plasma frequency of 3 eV have been used to study dielectric properties because of the half-metallic nature of AVO3 in the present investigation. In this study, the position of the peak of the real part of the dielectric function is linked to the electron excitation, and the peak is primarily caused by interband transitions. It is apparent from Figure 10 that ε1(ω) shows a peak in the visible region at around 2.30 eV, which is related to the interband transitions. It is well-known that the real part of the dielectric function is dominated by intraband transformations from the conduction electrons primarily in the low-energy infrared region for metallic systems. However, the real part of the dielectric function gives rise to interband transitions because of the half-metallic or semiconductor nature of AVO3 in this study. The half-metallic behavior of AVO3 (A = Ba, Sr, and Ca) compounds and semiconductor behavior of MgVO3 are revealed on the basis of their electronic properties. It is important to note that ε2(ω) reaches zero in the ultraviolet region at around 30 eV, which demonstrates that the AVO3 compounds are transparent and optically anisotropic as well. The anisotropic behavior of AVO3 compounds was also found by the elastic properties.

Figure 10.

Figure 10

Open in a new tab

(Color online) Energy-dependent dielectric function (real part, ε1, and imaginary part, ε2) of AVO3 compounds.

The extinction coefficient (k) and the refractive index (n) represent the amount of the absorption loss and the phase velocity, respectively, when the electromagnetic wave (as light) passes through the material. The energy-dependent n and k are shown in Figure 11. The calculated values of the static refractive index n(0) of BaVO3, SrVO3, CaVO3, and MgVO3 are found to be 6.14, 5.97, 7.89, and 8.77, respectively, which changes with the applied energy, implying that AVO3 carries photorefractive effects. The relatively high value of the static refractive index suggests that AVO3 can be suited as a potential candidate for application as an ultrahigh-density optical storage device upon suitable laser irradiation.59

Figure 11.

Figure 11

Open in a new tab

(Color online) Refractive index (n) and extinction coefficient (k) of AVO3 compounds as a function of energy.

The coefficient of absorption (α) provides the measure of energy absorbed by materials and gives information about the solar energy conversion efficiency.60 From the lower part of Figure 12, the spectra of the absorption coefficient start with a zero value, and the calculated α illustrates a trend similar to ε2(ω). Generally, the peaks with the energy in the infrared range of spectra may arise due to the intraband transition. In contrast, the peaks in the high-energy region of the conductivity and absorption spectra may be from the interband transition. The maximum absorption is found at 19.54, 23.85, 27.47, and 41.02 eV for BaVO3, SrVO3, CaVO3, and MgVO3, respectively. The different high-intensity peaks in the range of 15–30 eV denote various electronic transition rates.

Figure 12.

Figure 12

Open in a new tab

(Color online) Real parts of conductivity (σ) and absorption coefficient (α) of AVO3 compounds as a function of energy.

It is worth noting that the real part of the photoconductivity (σ) spectra of AVO3 (upper part of Figure 12) begins with zero photon energy, albeit MgVO3 shows a small band gap (Eg of ∼0.12 eV) in the electronic band structure (Figure 5). Therefore, the conductivity at zero photon energy is a clear indication of the half-metallic nature of BaVO3 and SrVO3 compounds, whereas the conductivity at zero photon energy of MgVO3 denotes the degenerate-like semiconductor material. Hence, the cubic phase of MgVO3 can be a suitable candidate for photovoltaic applications. The maximum values of photoconductivity are observed at 18.62, 23.02, 26.87, and 40.46 eV for BaVO3, SrVO3, CaVO3, and MgVO3, respectively. It is noted from Figure 12 that the photoconductivity spectra vary with the absorption spectra. As a result of absorbing photons, the photoconductivity of AVO3 increases, according to this finding.61

The energy-dependent reflectivity (R) spectra of AVO3 are depicted in the upper part of Figure 13. The highest reflectivity of AVO3 (A = Ba, Sr, and Ca) is seen in the ultraviolet region, while the highest reflectivity is found in the infrared region in MgVO3. The peaks in the ultraviolet region give rise to the interband transition, whereas the peaks in the infrared region stem from the intraband transition. The zero frequency value of reflectivity R(0) is found to be 0.53, 0.52, 0.61, and 0.64 for BaVO3, SrVO3, CaVO3, and MgVO3, respectively. It is noted that the maximum reflectivity value at zero frequency is seen in the MgVO3 compound. The high-reflectivity spectra of AVO3 reflect that these materials can be a potential candidate for coating materials to diminish solar heating.

Figure 13.

Figure 13

Open in a new tab

(Color online) Energy-dependent reflectivity (R) and loss function (L) of the AVO3 compounds.

The loss spectra (L) of AVO3 as a function of energy are shown in the lower part of Figure 13. The energy loss function denotes the loss of energy of a fast electron when it passes through a material.62 The maximum loss function is connected to the plasma resonance, and the frequency associated with it is defined as the plasma frequency, ωp.63 The maximum loss function of BaVO3, SrVO3, CaVO3, and MgVO3 is found at 25.99, 27.91, 29.45, and 23.95 eV, respectively, which implies the plasma frequency of the respective compound. The results are similar to those observed in ATiO3 (A = Ba, Sr, Ca, and Pb).23 The AVO3 materials become transparent when the incident light frequency is higher than the plasma frequency. In addition, the loss function peak related to ωp corresponds to the zero-crossing of ε1 with small ε2 (Figure 10), and it correlates with the edge in the reflectivity spectrum in which a sudden reduction of the maximum reflectivity spectrum occurs (Figure 13). It is worth seeing that the value of ωp increased by varying cations from Ba to Ca, while the value of ωp significantly decreased in MgVO3. The significant decrease in ωp may be due to the semiconductor nature and/or the larger effective mass of free electrons of the MgVO3 compound.

3.5. Population Analysis

The analysis of the Mulliken atomic population provides interesting information regarding the chemical bonding nature of solids.64 The calculated Mulliken atomic populations of AVO3 are listed in Table 4 gradually. As can be seen from Table 5, A (= Ba, Sr, Ca, and Mg) and V atoms carry positive charges, while O atoms carry negative charges, implying that the sharing of charges occurs from A and V to O atoms. We also studied the bond overlap population (Pμ) in order to have a better understanding of the bonding nature of the AVO3 compounds. The zero value of the bond overlap population expresses a perfectly ionic bond, whereas the deviation from zero reflects the increasing levels of covalency.65 The deviation of Pμ from zero is clearly seen in Table 6, which reveals the covalent nature of these compounds. It is noted in Table 6 that the V–O bond in BaVO3 is more covalent than the other compounds. It is also found that the value of Pμ for the V–O bond is positive, whereas the value of Pμ is negative for the A–V (A = Ba, Sr, Ca, and Mg) and O–O bonds. The positive and negative magnitudes of Pμ denote the direct and indirect bonds of atoms involved in AVO3 compounds, respectively. The calculated values of spin (Table 5) indicate that the V atom is mainly accountable for the magnetic properties of AVO3 compounds. We have also calculated the net magnetic moments of AVO3 and summarized them in Table 5. The detailed magnetic properties of AVO3 compounds were studied by researchers earlier.29 The net magnetic moments of AVO3 under this inspection somewhat differ from the value reported in ref (29). However, the value of the net magnetic moment of BaVO3 is in good agreement with the value found in ref (66).

Table 5. Mulliken Atomic Population Analysis of AVO3 Compounds.

    Mulliken atomic population
  
compounds species s p d total charge (e) spin (hbar/2) net magnetic moment (μB)
  Ba 2.00 5.97 0.76 8.73 1.27 –0.03  
BaVO3 V 2.32 6.68 3.24 12.24 0.76 1.41 0.99
  O 1.84 4.84 0.00 6.68 –0.68 –0.13  
  Sr 2.02 5.99 0.66 8.67 1.33 –0.03  
SrVO3 V 2.31 6.69 3.26 12.27 0.73 1.31 1.01
  O 1.83 4.86 0.00 6.69 –0.69 –0.09  
  Ca 2.04 5.99 0.53 8.57 1.43 –0.02  
CaVO3 V 2.30 6.73 3.28 12.31 0.69 1.26 1.00
  O 1.83 4.88 0.00 6.71 –0.71 –0.08  
  Mg 2.30 6.36 0.00 8.65 1.35 –0.02  
MgVO3 V 2.30 6.66 3.28 12.24 0.76 1.25 0.99
  O 1.82 4.88 0.00 6.70 –0.70 –0.08  
Open in a new tab

Table 6. The Calculated Mulliken Bond Number (nμ), Bond Length (dμ), and Bond Overlap Population (Pμ) of the AVO3 Compounds.

compounds bonds nμ dμ (Å) Pμ
  V–O 3 1.96337 0.92
BaVO3 Ba–V 1 3.40065 –0.70
  O–O 3 2.77662 –0.13
  V–O 3 1.91503 0.88
SrVO3 Sr–V 1 3.31693 –0.52
  O–O 3 2.70826 –0.15
  V–O 3 1.88698 0.87
CaVO3 Ca–V 1 3.26835 –0.36
  O–O 3 2.66860 –0.17
  V–O 3 1.86655 0.85
MgVO3 Mg–V 1 3.23296 –0.34
  O–O 3 2.63970 –0.20
Open in a new tab

3.6. Thermodynamic Properties

To understand the behavior of AVO3 under high temperatures and pressures, we have investigated the various thermodynamic properties such as melting temperature, Tm, Debye temperature, θD, and minimum thermal conductivity, Kmin. θD is an essential parameter of solids to rationalize some interesting physical processes related to phonons, specific heat, melting point, thermal conductivity, etc.67 The value of θD can be estimated using the average sound velocity using the following equation:67

3.6. 4

where kB and h denote the Boltzmann and Planck constants, respectively. ρ is the density, and NA is Avogadro’s number. V, m, and M are the volume of a unit cell, the number of atoms within a unit cell, and molecular weight, respectively. vm implies the average sound velocity in the crystal, which is calculated using the following equation:

3.6. 5

Here, vt and vl denote the transverse and longitudinal sound velocities, respectively. The following expressions can be used to calculate vl and vt using the shear modulus, G, and the bulk modulus, B:

3.6. 6

The melting temperature, Tm, of the AVO3 compounds has also been calculated via the following empirical formula using elastic constants, Cij:68

3.6. 7

In a cubic structure, the axial lengths are equal; thus, C11, C22, and C33 are also equal.

Moreover, we calculated another important entity, that is, thermal conductivity, which is used to study the heat conduction of a material. It is well-established that the minimum thermal conductivity is directly concerned with the temperature. The temperature of a material gradually increases the conductivity of the material and, after that, gradually decreases to a certain value.69

Albeit many similar equations are available to predict the minimum thermal conductivity, in this report, the minimum thermal conductivity, Kmin has been calculated by using the Clarke expression70 and can be defined as follows:

3.6. 8

where kB is the Boltzmann constant, vm is the average sound velocity, M is the molecular mass, n is the number of atoms per molecule, and NA is Avogadro’s number used for the calculation.

The Grüneisen parameter (γ) provides information regarding anharmonic effects, i.e., the temperature-dependent phonon dampings and frequencies as well as the thermal expansion effects. The Grüneisen parameter is explained by the following:

3.6. 9

where ωn and Φ are the angular frequency and the packing fraction of crystals, respectively.71 The value of γ can be estimated by a simple expression related to Poisson’s ratio71 as follows:

3.6. 10

The calculated values of Debye temperature, θD, along with different sound velocities (vl, vt, and vm), melting temperature, Tm, the Grüneisen parameter, γ, and minimum thermal conductivity, Kmin, of AVO3 under this study are listed in Table 7. In general, a higher Debye temperature is associated with a higher phonon thermal conductivity and vice-versa. The relatively high values of θD and Kmin of AVO3 imply high thermal conductivity, and they might not be suitable for use as thermal barrier coating (TBC) materials.

Table 7. The Calculated Density, (ρ), Debye Temperature, (θD), Longitudinal, Transverse, and Average Sound Velocities (vl, vt, and vm), Minimum Thermal Conductivity (Kmin), and Melting Temperature (Tm) of AVO3 Compounds.

compounds ρ (g/cm3) vl (km/s) vt (km/s) vm (km/s) θD (K) Tm (K) Kmin (W m–1 K–1) γ
BaVO3 6.479 7140 4213 4668 605 1704 1.22 1.42
SrVO3 5.514 7856 4567 5067 673 1861 1.39 1.47
CaVO3 4.295 8810 4968 5526 745 1933 1.57 1.59
MgVO3 3.909 8712 4351 4881 664 1906 1.41 2.01
Open in a new tab

4. Conclusions

In this study, we have investigated various physical properties of the cubic phase of AVO3 (A = Ba, Sr, Ca, and Mg) compounds. The calculated lattice parameters show very fair agreement with the available experimental data, implying the reliability of these computational calculations. The mechanical stability of AVO3 is confirmed by the Born stability criteria. The Poisson’s and Pugh’s ratios reveal the ductile behavior of CaVO3 and MgVO3, whereas a brittle nature is exhibited by BaVO3 and SrVO3. The analysis of various anisotropy indices shows that BaVO3, CaVO3, and MgVO3 are anisotropic, whereas SrVO3 exhibits insignificant anisotropy. The intermediate values of Peierls stress were found in AVO3. The AVO3 (A = Ba, Sr) compounds exhibit half-metallic character, whereas CaVO3 and MgVO3 show spin-glass and magnetic semiconductor-like behavior alongwith n-type carriers, respectively. The half-metallic nature of AVO3 stems mainly from p–d hybridization between O and V atoms. The single-band nature and the presence of hole-like Fermi surfaces are seen. The bonding properties reveal that AVO3 possesses intra-atomic bonding with a mixture of covalent, ionic, and metallic interactions. Numerous thermodynamic behaviors of AVO3 are calculated using relevant equations and analyzed properly based on the obtained results. The study of optical properties, especially the refractive index of these compounds, indicates that all the materials could be used as promising high-density optical data storage.

Acknowledgments

This research work was supported in part by the JSPS KAKENHI Grant Number JP17K05030 and the (no. 106/5/52/R.U./Eng.) from the Faculty of Engineering, University of Rajshahi, Rajshahi 6205, Bangladesh.

The authors declare no competing financial interest.

References

  1. Rahaman M. M.; Imai T.; Sakamoto T.; Tsukada S.; Kojima S. Fano resonance of Li-doped KTa1–xNbxO3 single crystals studied by Raman scattering. Sci. Rep. 2016, 6, 23898. 10.1038/srep23898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Rubel M. H. K.; Takei T.; Kumada N.; Ali M. M.; Miura A.; Tadanaga K.; Oka K.; Azuma M.; Magome E.; Moriyoshi C.; Kuroiwa Y. Hydrothermal synthesis, structure, and superconductivity of simple cubic perovskite (Ba0.62K0.38)(Bi0.92Mg0.08)O3 with Tc ∼ 30 K. Inorg. Chem. 2017, 56, 3174–3181. 10.1021/acs.inorgchem.6b01853. [DOI] [PubMed] [Google Scholar]
  3. Rubel M. H. K.; Ali M. M.; Ali M. S.; Parvin R.; Rahaman M. M.; Hossain K. M.; Hossain M. I.; Islam A. K. M. A.; Kumada N. First–principles study: Structural, mechanical, electronic and thermodynamic properties of simple-cubic-perovskite (Ba0.62K0.38)(Bi0.92Mg0.08)O3. Solid State Commun. 2019, 288, 22–27. 10.1016/j.ssc.2018.11.008. [DOI] [Google Scholar]
  4. Wei Y.; Gui H.; Zhao Z.; Li J.; Liu Y.; Xin S.; Li X.; Xie W. Structure and magnetic properties of the perovskite YCo0.5Fe0.5O3. AIP Adv. 2014, 4, 127134. 10.1063/1.4904811. [DOI] [Google Scholar]
  5. Pradhan D. K.; Mohanty H. S.; Kumari S.; Bhoi K.; Tang N.; Ravikant; Rahaman M. M.; Pradhan D. K.; Kumar A.; Gilbertah D. A.; Rack P. D. Ferroic phase transitions and magnetoelectric coupling in cobalt doped BaTiO3. J. Mater. Chem. C 2021, 9, 12694–12711. 10.1039/D1TC02961D. [DOI] [Google Scholar]
  6. Varignon J.; Bristowe N. C.; Bousquet E.; Ghosez P. Coupling and electrical control of structural, orbital and magnetic orders in perovskites. Sci. Rep. 2015, 5, 15364. 10.1038/srep15364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Blake G. R.; Palstra T. T. M.; Ren Y.; Nugroho A. A.; Menovsky A. A. Transition between Orbital Orderings in YVO3. Phys. Rev. Lett. 2001, 87, 245501 10.1103/PhysRevLett.87.245501. [DOI] [PubMed] [Google Scholar]
  8. Mossanek R. J. O.; Abbate M.; Fonseca P. T.; Fujimori A.; Eisaki H.; Uchida S.; Tokura Y. Optical conductivity and x-ray absorption spectra of the Mott-Hubbard compounds RVO3 (R=Sr, Ca, La, and Y). Phys. Rev. B 2009, 80, 195107. 10.1103/PhysRevB.80.195107. [DOI] [Google Scholar]
  9. Uratani Y.; Shishidou T.; Ishii F.; Oguchi T. First-Principles Predictions of Giant Electric Polarization. Jpn. J. Appl. Phys. 2005, 44, 7130. 10.1143/JJAP.44.7130. [DOI] [Google Scholar]
  10. Okos A.; Colin C.; Darie C.; Raita O.; Bordet P.; Pop A. Structure and magnetic properties of the layered perovskite PbVO3. J. Alloys Compd. 2014, 602, 265–268. 10.1016/j.jallcom.2014.02.144. [DOI] [Google Scholar]
  11. Belik A. A.; Azuma M.; Saito T.; Shimakawa Y.; Takano M. Crystallographic features and tetragonal phase stability of PbVO3, a new member of PbTiO3 family. Chem. Mater. 2005, 17, 269–273. 10.1021/cm048387i. [DOI] [Google Scholar]
  12. Nishimura K.; Yamada I.; Oka K.; Shimakawa Y.; Azuma M. High-pressure synthesis of BaVO3: A new cubic perovskite. J. Phys. Chem. Solids 2014, 75, 710–712. 10.1016/j.jpcs.2014.02.001. [DOI] [Google Scholar]
  13. Lan Y. C.; Chen X. L.; He M. Structure, magnetic susceptibility and resistivity properties of SrVO3. J. Alloys Compd. 2003, 354, 95–98. 10.1016/S0925-8388(02)01349-X. [DOI] [Google Scholar]
  14. Ueda Y. Oxygen nonstoichiometry, structures, and physical properties of CaVO3–δ: I. A series of new oxygen-deficient phases. J. Solid State Chem. 1998, 135, 36–42. 10.1006/jssc.1997.7587. [DOI] [Google Scholar]
  15. Bouloux J.-C.; Milosevic I.; Galy J. Les hypovanadates de magnésium MgVO3 et MgV2O5. Structure cristalline de MgVO3. J. Solid State Chem. 1976, 16, 393–398. 10.1016/0022-4596(76)90056-6. [DOI] [Google Scholar]
  16. Zhang L.; Zhou Y.; Guo L.; Zhao W.; Barnes A.; Zhang H. T.; Eaton C.; Zheng Y.; Brahlek M.; Haneef H. F.; Podraza N. J.; Chan M. H. W.; Gopalan V.; Rabe K. M.; Engel-Herbert R. Correlated metals as transparent conductors. Nat. Mater. 2016, 15, 204–210. 10.1038/nmat4493. [DOI] [PubMed] [Google Scholar]
  17. Falcón H.; Alonso J. A.; Casais M. T.; Martínez-Lope M. J.; Sánchez-Benítez J. Neutron diffraction study, magnetism and magnetotransport of stoichiometric CaVO3 perovskite with positive magnetoresistance. J. Solid State Chem. 2004, 177, 3099–3104. 10.1016/j.jssc.2004.05.010. [DOI] [Google Scholar]
  18. Chamberland B. L.; Danielson P. S. Alkaline-earth vanadium (IV) oxides having the AVO3 composition. J. Solid State Chem. 1971, 3, 243–247. 10.1016/0022-4596(71)90035-1. [DOI] [Google Scholar]
  19. Giannakopoulou V.; Odier P.; Bassat J. M.; Loup J. P. SrVO3 and Sr2VO4, electrical properties below and above room T. Solid State Commun. 1995, 93, 579–583. 10.1016/0038-1098(94)00834-Y. [DOI] [Google Scholar]
  20. Shirakawa N.; Murata K.; Makino H.; Iga F.; Nishihara Y. Scaling of negative magnetoresistance and extraordinary Hall Effect in CaVO3-δ. J. Phys. Soc. Jpn. 1995, 64, 4824–4833. 10.1143/JPSJ.64.4824. [DOI] [Google Scholar]
  21. Inoue I. H.; Morikawa K.; Fukuchi H.; Tsujii T.; Iga F.; Nishihara Y. Metal-to-insulator transitions in CaVOy. Phys. B 1994, 194-196, 1067–1068. 10.1016/0921-4526(94)90863-X. [DOI] [Google Scholar]
  22. Chamberland B. L.; Danielson P. S.; Moeller C. W. A high-pressure modification of MgVO3. J. Solid State Chem. 1978, 26, 377–382. 10.1016/0022-4596(78)90172-X. [DOI] [Google Scholar]
  23. Chaplygin I.; Hayn R.; Koepernik K. Electronic structure of the spin-1/2 chain compound MgVO3. Phys. Rev. B 1999, 60, R12557–R12560. 10.1103/PhysRevB.60.R12557. [DOI] [Google Scholar]
  24. Kamruzzaman M.; Helal M. A.; Ara I. E.; Farid Ul Islam A. K. M.; Rahaman M. M. A comparative study based on the first principles calculations of ATiO3 (A = Ba, Ca, Pb and Sr) perovskite structure. Indian J. Phys. 2016, 90, 1105–1113. 10.1007/s12648-016-0848-3. [DOI] [Google Scholar]
  25. Rubel M. H. K.; Mitro S. K.; Mondal B. K.; Rahaman M. M.; Saiduzzaman M.; Hossain J.; Islam A. K. M. A.; Kumada N. Newly synthesized A-site ordered cubic-perovskite superconductor (Ba0.54K0.46)4Bi4O12: A DFT investigation. Phys. C 2020, 574, 1353669. 10.1016/j.physc.2020.1353669. [DOI] [Google Scholar]
  26. Rubel M. H. K.; Hadi M. A.; Rahaman M. M.; Ali M. S.; Aftabuzzaman M.; Parvin R.; Islam A. K. M. A.; Kumada N. Density functional theory study of a new Bi-based (K1.00)(Ba1.00)3(Bi0.89Na0.11)4O12 double perovskite superconductor. Comput. Mater. Sci. 2017, 138, 160–165. 10.1016/j.commatsci.2017.06.030. [DOI] [Google Scholar]
  27. Hauge H. I. T.; Verheijen M. A.; Conesa-Boj S.; Etzelstorfer T.; Watzinger M.; Kriegner D.; Zardo I.; Fasolato C.; Capitani F.; Postorino P.; Kölling S.; Li A.; Assali S.; Stangl J.; Bakkers E. P. A. M. Hexagonal silicon realized. Nano Lett. 2015, 15, 5855–5860. 10.1021/acs.nanolett.5b01939. [DOI] [PubMed] [Google Scholar]
  28. Rashid M.; Abbas Z.; Yaseen M.; Afzal Q.; Mahmood A.; Ramay S. M. Theoretical investigation of cubic BaVO3 and LaVO3 perovskites via Tran–Blaha-Modified Becke–Johnson exchange potential approach. J. Supercond. Novel Magn. 2017, 30, 3129–3136. 10.1007/s10948-017-4099-0. [DOI] [Google Scholar]
  29. Mahmood Q.; Ali S. A.; Hassan M.; Laref A. First principles study of ferromagnetism, optical and thermoelectric behaviours of AVO3 (A = Ca, Sr, Ba) perovskites. Mater. Chem. Phys. 2018, 211, 428–437. 10.1016/j.matchemphys.2018.03.019. [DOI] [Google Scholar]
  30. Hohenberg P.; Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  31. Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  32. Clark S. J.; Segall M. D.; Probert M. J.; Pickard C. J.; Hasnip P. J.; Payne M. C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567. 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
  33. Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. 10.1103/PhysRevB.41.7892. [DOI] [PubMed] [Google Scholar]
  34. Head J. D.; Zerner M. C. A Broyden-fletcher-goldfarb-shanno optimization procedure for molecular geometries. Chem. Phys. Lett. 1985, 122, 264–270. 10.1016/0009-2614(85)80574-1. [DOI] [Google Scholar]
  35. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  36. Rubel M. H. K.; Hossain K. M.; Mitro S. K.; Rahaman M. M.; Hadi M. A.; Islam A. K. M. A. Comprehensive first-principles calculations on physical properties of ScV2Ga4 and ZrV2Ga4 in comparison with superconducting HfV2Ga4. Mater. Today Commun. 2020, 24, 100935. 10.1016/j.mtcomm.2020.100935. [DOI] [Google Scholar]
  37. Murnaghan F. D.Finite deformation of an elastic solid; Wiley: New York, 1951. [Google Scholar]
  38. Born M. Thermodynamics of crystals and melting. J. Chem. Phys. 1939, 7, 591–603. 10.1063/1.1750497. [DOI] [Google Scholar]
  39. Jamal M.; Asadabadi S. J.; Ahmad I.; Aliabad H. A. R. Elastic constants of cubic crystals. Comput. Mater. Sci. 2014, 95, 592–599. 10.1016/j.commatsci.2014.08.027. [DOI] [Google Scholar]
  40. Kleinman L. Deformation potentials in silicon. I. Uniaxial strain. Phys. Rev. 1962, 128, 2614–2621. 10.1103/PhysRev.128.2614. [DOI] [Google Scholar]
  41. Elias B. H.; Ilyas B. M.; Saadi N. S. A first principle study of the perovskite lanthanum Aluminate. Mater. Res. Express 2018, 5, 086302. 10.1088/2053-1591/aad15f. [DOI] [Google Scholar]
  42. Hill R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc., A 1952, 65, 349–354. 10.1088/0370-1298/65/5/307. [DOI] [Google Scholar]
  43. Bouhemadou A. First-principles study of structural, electronic and elastic properties of Nb4AlC3. Braz. J. Phys. 2010, 40, 52–57. 10.1590/S0103-97332010000100009. [DOI] [Google Scholar]
  44. Maradudin A. A.; Montroll E. W.; Weiss G. H.; Ipatova I. P.. Theory of lattice dynamics in the harmonic approximation; Academic Press: New York, 1971. [Google Scholar]
  45. Nasir M. T.; Hadi M. A.; Rayhan M. A.; Ali M. A.; Hossain M. M.; Roknuzzaman M.; Naqib S. H.; Islam A. K. M. A.; Uddin M. M.; Ostrikov K. First-Principles Study of Superconducting ScRhP and ScIrP pnictides. Phys. Status Solidi B 2017, 254, 1700336. 10.1002/pssb.201700336. [DOI] [Google Scholar]
  46. Wang X.; Xiang H.; Sum X.; Liu J.; Hou F.; Zhou Y. Mechanical properties and damage tolerance of bulk Yb3Al5O12 ceramic. J. Mater. Sci. Technol. 2015, 31, 369–374. 10.1016/j.jmst.2015.01.002. [DOI] [Google Scholar]
  47. Rahaman M. M.; Rubel M. H. K.; Rashid M. A.; Alam M. A.; Hossain K. M.; Hossain M. I.; Khatun A. A.; Hossain M. M.; Islam A. K. M. A.; Kojima S.; Kumada N. Mechanical, electronic, optical, and thermodynamic properties of orthorhombic LiCuBiO4 crystal: a first-principles study. J. Mater. Res. Technol. 2019, 8, 3783–3794. 10.1016/j.jmrt.2019.06.039. [DOI] [Google Scholar]
  48. Chen X.-Q.; Niu H.; Li D.; Li Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. 10.1016/j.intermet.2011.03.026. [DOI] [Google Scholar]
  49. Mazhnik E.; Oganov A. R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. 10.1063/1.5113622. [DOI] [Google Scholar]
  50. Pugh S. F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. 10.1080/14786440808520496. [DOI] [Google Scholar]
  51. Frantsevich I. N.; Voronov F. F.; Bokuta S. A.. Elastic constants and elastic moduli of metals and insulators; Handbook, edited by Frantsevich I. N. (Naukova Dumka: Kiev, (1983) pp.60–180. [Google Scholar]
  52. Pettifor D. G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. 10.1179/mst.1992.8.4.345. [DOI] [Google Scholar]
  53. Wang J. N. A new modification of the formulation of Peierls stress. Acta Metall. 1996, 44, 1541–1546. 10.1016/1359-6454(95)00273-1. [DOI] [Google Scholar]
  54. Ali M. S.; Aftabuzzaman M.; Roknuzzaman M.; Rayhan M. A.; Parvin F.; Ali M. M.; Rubel M. H. K.; Islam A. K. M. A. New superconductor (Na0.25K0.45) Ba3Bi4O12: A first-principles study. Phys. C 2014, 506, 53–58. 10.1016/j.physc.2014.08.010. [DOI] [Google Scholar]
  55. Hossain M. A.; Ali M. S.; Parvin F.; Islam A. K. M. A. Mechanical and optical properties of inverse-perovskites Sc3InX (X = B, C, N). Comput. Mater. Sci. 2013, 73, 1–8. 10.1016/j.commatsci.2013.02.017. [DOI] [Google Scholar]
  56. Music D.; Schneider J. M. Elastic properties of Srn+1TinO3n+1 phases (n = 1–3,∞). J. Phys.: Condens. Matter 2008, 20, 055224 10.1088/0953-8984/20/5/055224. [DOI] [Google Scholar]
  57. Rubel M. H. K.; Takei T.; Kumada N.; Ali M. M.; Miura A.; Tadanaga K.; Oka K.; Azuma M.; Magomae E.; Moriyoshi C.; Kuroiwa Y. Hydrothermal synthesis of a new Bi-based (Ba0.82K0.18)(Bi0.53Pb0.47)O3 superconductor. J. Alloys Compd. 2015, 634, 208–214. 10.1016/j.jallcom.2014.12.274. [DOI] [Google Scholar]
  58. Yan S.-Y.; Xie Y.; Liu T.; Yu H.-T. Electronic structures and ferroelectric instabilities of cubic AVO3 (A = Sr, Ba, and Pb) perovskites by first-principles calculations. J. Phys.: Condens. Matter 2010, 22, 125501. 10.1088/0953-8984/22/12/125501. [DOI] [PubMed] [Google Scholar]
  59. Rubel M. H. K.; Islam M. S.; Mahmuda U. S. M.; Rahaman M. M.; Hossain M. E.; Parvez M. S.; Hossain K. M.; Hossain M. I.; Hossain J.; Yamanaka J.; Kumada N.; Kojima S. CaxBa1–xNb2O6 ferroelectric nanopowders for ultrahigh-density optical data storage. ACS Appl. Nano Mater. 2018, 1, 6289–6300. [Google Scholar]
  60. Li S.; Ahuja R.; Barsoum M. W.; Jena P.; Johansson B. Optical properties of Ti3SiC2 and Ti4AlN3. Appl. Phys. Lett. 2008, 92, 221907. 10.1063/1.2938862. [DOI] [Google Scholar]
  61. Sun J.; Zhou X.-F.; Fan Y.-X.; Chen J.; Wang H.-T.; Guo X.; He J.; Wang Y. First-principles study of electronic structure and optical properties of heterodiamond BC2N. Phys. Rev. B 2006, 73, 045108. 10.1103/PhysRevB.73.045108. [DOI] [Google Scholar]
  62. Parvin F.; Hossain M. A.; Ali M. S.; Islam A. K. M. A. Mechanical, electronic, optical, thermodynamic properties and superconductivity of ScGa3. Phys. B 2015, 457, 320–325. 10.1016/j.physb.2014.10.007. [DOI] [Google Scholar]
  63. Fox M.Optical properties of solids; Academic Press: New York, 1972. [Google Scholar]
  64. Mulliken R. S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I. J. Chem. Phys. 1955, 23, 1833–1840. 10.1063/1.1740588. [DOI] [Google Scholar]
  65. Segall M. D.; Shah R.; Pickard C. J.; Payne M. C. Population analysis of plane-wave electronic structure calculations of bulk materials. Phys. Rev. B 1996, 54, 16317–16320. 10.1103/PhysRevB.54.16317. [DOI] [PubMed] [Google Scholar]
  66. The Materials Project. Materials Data on BaVO3 by Materials Project; U.S. Department of Energy: United States: N. p., 2020. Web. doi: 10.17188/1349744. [DOI] [Google Scholar]
  67. Anderson O. L. A simplified method for calculating the debye temperature from elastic Constants. J. Phys. Chem. Solids 1963, 24, 909–917. 10.1016/0022-3697(63)90067-2. [DOI] [Google Scholar]
  68. Fine M. E.; Brown L. D.; Marcus H. L. Elastic constants versus melting temperature in metals. Scr. Metall. 1984, 18, 951–956. 10.1016/0036-9748(84)90267-9. [DOI] [Google Scholar]
  69. Shen Y.; Clarke D. R.; Fuierer P. A. Anisotropic thermal conductivity of the Aurivillus phase, bismuth titanate (Bi4Ti3O12): A natural nanostructured superlattice. Appl. Phys. Lett. 2008, 93, 102907. 10.1063/1.2975163. [DOI] [Google Scholar]
  70. Clarke D. R. Materials selection guidelines for low thermal conductivity thermal barrier coatings. Surf. Coat. Technol. 2003, 163-164, 67–74. 10.1016/S0257-8972(02)00593-5. [DOI] [Google Scholar]
  71. Belomestnykh V. N.; Tesleva E. P. Interrelation between anharmonicity and lateral strain in quasiisotropic polycrystalline solids. Tech. Phys. 2004, 49, 1098–1100. 10.1134/1.1787679. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES