Interplay between traveling wave propagation and amplification at the apex of the mouse cochlea

Abstract

Sounds entering the mammalian ear produce waves that travel from the base to the apex of the cochlea. An electromechanical active process amplifies traveling wave motions and enables sound processing over a broad range of frequencies and intensities. The cochlear amplifier requires combining the global traveling wave with the local cellular processes that change along the length of the cochlea given the gradual changes in hair cell and supporting cell anatomy and physiology. Thus, we measured basilar membrane (BM) traveling waves in vivo along the apical turn of the mouse cochlea using volumetric optical coherence tomography and vibrometry. We found that there was a gradual reduction in key features of the active process toward the apex. For example, the gain decreased from 23 to 19 dB and tuning sharpness decreased from 2.5 to 1.4. Furthermore, we measured the frequency and intensity dependence of traveling wave properties. The phase velocity was larger than the group velocity, and both quantities gradually decrease from the base to the apex denoting a strong dispersion characteristic near the helicotrema. Moreover, we found that the spatial wavelength along the BM was highly level dependent in vivo, such that increasing the sound intensity from 30 to 90 dB sound pressure level increased the wavelength from 504 to 874 μm, a factor of 1.73. We hypothesize that this wavelength variation with sound intensity gives rise to an increase of the fluid-loaded mass on the BM and tunes its local resonance frequency. Together, these data demonstrate a strong interplay between the traveling wave propagation and amplification along the length of the cochlea.

Significance

Our understating of the sense of hearing in mammals is impeded by inadequate measurements of the traveling waves, specifically at the apex of the cochlea. Herein, we present spatial waveform measurements along the apex of the unopened mouse cochlea. We found that traveling wave mechanical properties are highly dependent on the stimulus frequency and intensity. One important implication of this observation is that the fluid-loaded mass on the BM increases as the sound intensity increases, consequently shifting the peak of the tuning curves toward lower frequencies. This level-dependent fluid mass impacts the local impedance of the BM and thus the active power transmission from OHCs. Our data provide a better understanding of the interplay between the cochlear traveling wave and the amplification that is necessary for nonlinear sound encoding.

Introduction

The mammalian auditory system comprises a series of coupled acoustical, mechanical, and electrochemical components that transduce sounds and convey the neural information to the brain. The input sound pressure propagates along the cochlea as a fluid-borne wave that travels from the base to the apex, while growing in magnitude until it attains a peak at the place specific for the frequency of stimulation (1). This creates maximal vibration of the basilar membrane (BM) and stimulates the hair cells at that location. Thus, according to the traveling wave theory of cochlear mechanics (2), complex sounds are decomposed into their constitute frequencies at different longitudinal locations along the cochlea. An active electromechanical process, mediated by outer hair cells (OHCs) (3), amplifies the traveling wave so that the vibrations become larger and more sharply tuned.

Understanding of the spatiotemporal mechanics of the cochlea is impeded by the fact that most vibration measurements to date have been performed locally at one point. This has been largely due to technical limitations in accessing multiple locations along the spiral-shaped structure of the cochlea. Interestingly, the very first traveling wave measurements were performed longitudinally. Von Bekesy (1) demonstrated traveling waves by visualizing opened cadaveric cochleae using stroboscopic illumination. Von Bekesy’s observations were pioneering and countered the resonance theory of Helmholtz (4). However, the results were confined to the passive, postmortem cochlea. Since then, nearly all measurements have been made using techniques that provide more sensitivity, but which are performed at a single location. Thus, experiments changed from playing one pure tone and visualizing the wave travel down the length of the cochlea to sweeping the frequency of sound while measuring the vibration at one spot. Single-point measurements can be extrapolated to estimate what happens outside of the measurement spot under the assumption of scaling symmetry (5). In its strictest form, this assumption means that the pattern of cochlear vibrations is identical at all points along the length of the cochlea, but that the frequency response is adjusted to fit the cochlear tonotopic map. Although the scaling symmetry assumption simplifies the interpretation of the cochlear responses significantly, multiple reports have demonstrated that this theory is not valid when comparing the cochlear base, middle, and apical regions (6, 7, 8, 9, 10, 11).

The cochlea achieves its astonishingly sharp frequency selectivity by combining a nonlinearly amplified traveling wave on the BM with a local resonance that arises from the interplay of mass and stiffness to set the impedance. The exact underlying mechanisms are still widely debated (12, 13, 14, 15, 16), but they are important given that they give rise to important clinical measurements, including auditory brainstem responses and otoacoustic emissions (17). Furthermore, understanding the dispersion of the BM traveling wave may help to better represent pitch and temporal fine structure in cochlear implant stimulation paradigms (18). These properties are particularly important for speech and music perception, which occurs within the low-frequency region of the cochlea, where helicotrema mechanics can significantly affect cochlear responses (19). Recently, the spatial pattern of cochlear vibrations has begun to receive more attention (20, 21, 22, 23, 24, 25, 26). However, the full characteristics of the cochlear traveling waves and their interactions with the local active process are still not well understood. Therefore, we sought to make detailed measurements of the BM traveling wave along the apical turn of the mouse cochlea. We recorded along ∼20% of the BM length (∼1200 μm), within 350–1500 μm (10–30% of the BM length) from the helicotrema. Our measurements cover a significantly larger proportion of the BM length compared with the previous studies (e.g., 5% of the BM length in (20,21)), with a fine longitudinal step size of 25 μm. This enabled us to accurately calculate critical traveling wave properties, including wavelength, propagation velocity, and spatial dispersion, over a range of frequencies and intensities.

Materials and methods

In this study we used our previously reported volumetric optical coherence tomography and vibrometry (VOCTV) system to noninvasively measure mouse cochlear mechanical responses to pure tone stimuli (26, 27, 28, 29, 30). The experimental protocols were approved by the Institutional Animal Care and Use Committee of University of Southern California. CBA/CaJ mice (P42–P47) of either sex were anesthetized with ketamine (80–100 mg/kg) and xylazine (5–10 mg/kg), placed on a heating pad, and the skull was fixed to a custom head-holder with dental cement. A ventrolateral surgical approach was then used to access the left middle ear bulla, which was widely opened so that the otic capsule bone and middle ear ossicles could be visualized. VOCTV was performed using a custom-built system, utilizing a broadband swept-laser source (Insight Photonic Solutions, Lafayette, CO, USA) with a 1310 nm center wavelength, 90 nm bandwidth, and 100 kHz sweep rate, as well as a dual-balanced photodetector (BPD-1, Insight Photonic Solution), and a high-speed digitizer (ATS9373, Alazar Technologies, Point-Claire, QC, Canada). The VOCTV system is integrated into a dissecting stereomicroscope (Discovery.V8, Zeiss, White Plains, NY, USA). Cross-sectional images of the apical cochlear turn were acquired by sweeping the laser beam across the otic capsule bone using a 2D voice coil mirror. These are collected at 5–10 frames per second. At each cross section, the organ of Corti (OoC) was identified and sound-evoked vibrations were then measured from the center of the BM with 100 ms pure tones presented via a speaker (Fostex FT17H) positioned close to the eardrum. Sound stimuli were calibrated inside the ear canal over the frequency range of 2–15 kHz and the intensity range of 10–90 dB SPL (sound pressure level). Cochlear sensitivity was calculated by normalizing the displacement magnitudes to the stimulus SPL inside the ear canal.

BM vibration measurements were repeated every 25 μm for a length of 1000–1200 μm along the cochlea. There is some variation between experiments on the exact position of the recorded data relative to the base of the cochlea. Hence, we have used the characteristic frequency (CF) at the measurement spot to estimate the corresponding longitudinal location using the tonotopic map by Müller et al. (31). Moreover, the term “longitudinal distance” in this paper refers to the relative distance between recorded longitudinal locations with respect to the most basal spot in each individual animal. Care was taken to measure vibrations at the center of the BM for each longitudinal position. After sacrificing the mouse via anesthetic overdose, the vibration measurements were repeated postmortem. The vibration phase values are reported with respect to the sound pressure in the ear canal. The sensitivity of our system to vibrations is a function of the signal-to-noise of the interferometric signal. As in our previous publications, we used the noise mean plus 3 standard deviations as a threshold (32); hence, any signal below this threshold was considered to be within the noise. This threshold is calculated for each measurement by analyzing the noise at frequencies adjacent to the stimulus frequency. To further remove physiological noise resulting from cardiac and respiratory fluctuations, the spatial phase profiles were smoothed by fitting them with parabolas using a moving average filter before calculating the wavelength.

Results

Longitudinal pattern of basilar-membrane vibrations

Fig. 1A illustrates a representative cross-sectional OCT image of the apical cochlear turn. The key structures of the OoC including BM, OHC, tectorial membrane, and Reissner’s membrane are labeled. We selected a point in roughly the midpoint of the BM and measured vibrations in response to sound stimuli. Fig. 1 B shows a representative set of BM vibratory responses at one cross-sectional location. In the living mouse, responses demonstrate the hallmarks of active, OHC-mediated amplification: (1) sensitive and sharply tuned responses for low sound intensities and (2) compressive, nonlinear response growth near the frequency of best response (here ∼8.5 kHz). At high sound levels, the response becomes more broadly tuned and the frequency of the peak (called the best frequency [BF]) decreases. After death (gray curves), amplification is lost and the responses become less sensitive, are broadly tuned, and grow linearly with the intensity of the sound stimulus. These observations are all consistent with our previous vibration measurements in normal mice (26,27).

Figure 1.

Vibration measurements of the mouse cochlea using VOCTV. (A) cross-sectional OCT image of the mouse organ of Corti; RM, Reissner’s membrane; TM, tectorial membrane; OHC, outer hair cells; BM, basilar membrane. (B) BM vibration magnitude (first row), sensitivity (second row), and phase (third row) at a single longitudinal location (8.5 kHz best place) for a range of frequencies and stimulation levels (10–80 dB SPL). The postmortem response is shown in gray (60–80 dB SPL). (C) Schematic of the cochlear spiral shape illustrating the locations of our measurements, which was about half of the apical turn. (D and F) BM responses at three representative longitudinal locations for 40, 60, and 80 dB SPL stimuli. The best frequencies of 40 dB SPL are 5.5 kHz (D), 8 kHz (E), and 10.5 kHz (F) as denoted by dashed lines. (G and H) families of frequency tuning curves measured at sequential longitudinal locations along the BM for a representative live (G) and dead (H) mouse at 80 dB SPL sound. The displacement amplitudes are normalized to the peak values and phases are relative to the sound pressure inside the ear canal. (I) The place-frequency map for a live (40, 60, and 80 dB SPL) mouse. Locations are expressed as the fraction of the distance along the basilar membrane from stapes (using a tonotopic map by Müller et al. (31), with BM length L = 5.1 mm). The solid red line demonstrates the neural place-frequency map for a CBA/CAJ mouse (31). All data in this figure are from one representative mouse. To see this figure in color, go online.

We then measured BM vibrations along a 1200 μm segment (Fig. 1 C). This region had characteristic frequencies between 5 and 11 kHz. Tuning curves measured at three different locations using 40, 60, and 80 dB SPL stimuli from one representative mouse are presented in Fig. 1, D and F. All measured tuning curves of 80 dB SPL are shown in Fig. 1, G and H for the same mouse, both living and dead. In these figures, amplitudes are normalized to the maximum value of each individual tuning curve for the sake of visual clarity and phase values are referenced to the sound pressure in the ear canal. The vibratory responses underwent a gradual change in BF, decreasing from base to apex. The change was greater in live mice (∼4 to ∼9 kHz) than in dead mice (∼4 to ∼5 kHz).

We calculated the BF using tuning curve data for 40, 60, and 80 dB SPL stimuli to obtain the mechanical frequency-place map at the apex of the mouse cochlea (Fig. 1 I). The tonotopic map from previously published neural recordings (31) described a pure logarithmic place-frequency relation over the frequency range that was measured. These data are included in this figure for comparison as a straight line in the semilog plot. It is evident that the slope of the neural map (1.25 mm/octave) is similar but not identical to that of the mechanical vibrations. To compare frequency-place maps of different sound levels, we fit the data from Fig. 1 I to the generalized form of the mammalian reception cochlear map described by the Greenwood relation: $BF\left(x\right)=A\left({10}^{a\left(1-x/L\right)}-\text{Κ}\right)$. In this relation, $BF$ is the best frequency in kHz, $x$ is the distance from the stapes, and $L$ the total BM length. Moreover, $A$ is a scale factor and $a$ is a constant describing the steepness of the curve when it is plotted on a logarithmic frequency scale. The $\text{Κ}$ constant quantifies the deviation from exponential behavior at low frequencies. The parameters $A$, $a$, and $\text{Κ}$ are fitting coefficients (33), which are calculated for 40 dB SPL ($A$ = 85.27 kHz, $\text{Κ}$= 0.087, $A$= 0.94), 60 dB SPL ($a$ = 26.29 kHz, = 0.252, $\text{Κ}$= 0.81), and 80 dB SPL ($A$ = 5.86 kHz, $a$ = 0.966, $\text{Κ}$= 0.29) using our vibration data. The slope of the line fit to the vibration data is flatter in the more basal region of the cochlea, and then has a sharp roll off ($\text{Κ}\ne 0$) when approaching the helicotrema. Even though the neural frequency map in mice does not show this roll-off, this deviation from exponential behavior near the helicotrema is consistent with the Greenwood map in other animals (33). We were able to detect this finding in mice because we were able to measure to lower vibratory BFs than the previously published neural CFs (31). Thus, it appears that the mechanical properties of the mouse helicotrema are like that of other mammals. It is noted that our fitted coefficients are only valid for the apical part of the mouse cochlea where the vibration measurements were performed (0.7 < $x/L$ < 0.95).

Cochlear active wave propagation

The dependence of BM motion on time ($t$) and longitudinal location ($x$) can be described using a quantity of the form $W\left(x,t\right)=A\left(x,\omega \right)e^{i\theta \left(x,t\right)}$, where $A\left(x,\omega \right)$ represents the wave amplitude and $\theta \left(x,t\right)=\omega t-\underset{0}{\overset{x}{\int }}k\left(x\right)dx$ is the phase of the wave. The wave phase depends on the excitation frequency$\omega$, and longitudinal location. Traveling wave properties, such as group delay (${\tau }_g=-d\theta /d\omega )$ and wavenumber ($k=-d\theta /dx)$, can be calculated from derivatives of the wave phase with respect to excitation frequency and longitudinal location, respectively. Wavenumber is proportional to the reciprocal of the wavelength $\left[\lambda \left(\omega ,x\right)=2\pi /k\right]$ and varies by excitation frequency and longitudinal location. The frequency and location dependence stems from interactions between fluid inertia and spatially varying structural properties of the OoC and the BM (34, 35, 36).

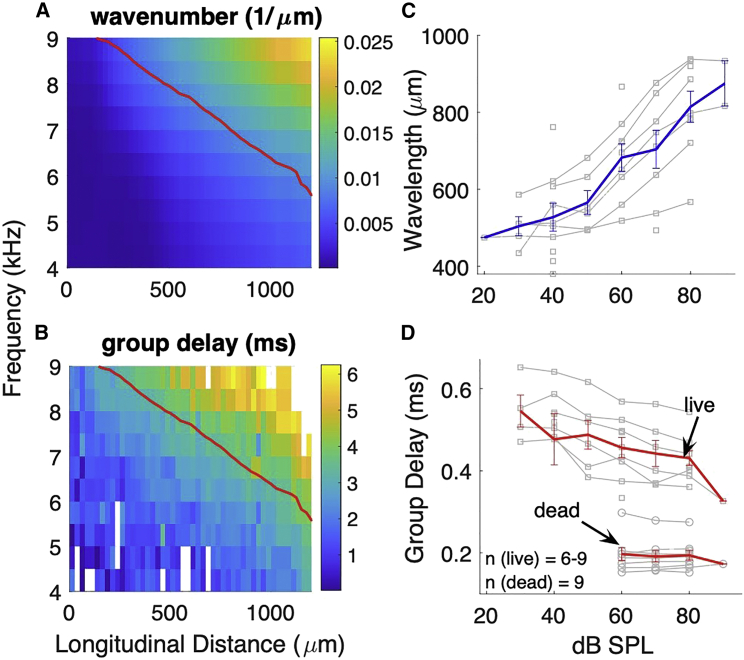
Availability of the spatial phase profiles enables us to quantify the traveling wave properties, such as wavelength (wavenumber), phase and group velocities, and propagation delay along the cochlea, as shown in Fig. 2. The frequency-location pattern of the BM wavenumber and group delay are shown in Fig. 2, A and B, respectively. Both wavenumber and group delay increase monotonically with increased stimulation frequency or with distance from the base. There is no abrupt change near the BF (red curves), which disagrees with some cochlear model predictions that the wavenumber and group delay decrease beyond traveling wave peak (37).

Figure 2.

Traveling wave properties. (A and B) BM wavenumber and group delay patterns plotted as a function of longitudinal location and stimulation frequency. Sound level was 60 dB SPL and red curves denote the best frequency versus best place (redrawn from Fig. 4, B and E). Both wavenumber and group delay increase from base to apex as well as by increasing stimulation frequency. (C and D) Wavelength (C) and group delay (D) of the 9 kHz traveling wave at the 9 kHz location plotted as a function of the stimulus level. Data from each individual mouse is plotted (gray curves) together with the averaged data (blue in C and red in D). Square and circle markers in (D) denote live and dead data, respectively. Error bars are the mean ± SE. To see this figure in color, go online.

To investigate the interplay between the cochlear active process and the traveling wave, we examined level dependence of the waveform properties, as shown in Fig. 2, C and D. Fig. 2 C shows the level dependence of the wavelength at the 9 kHz tonotopic location. The excitation frequency was 9 kHz and the stimulus intensity was varied from 30 to 90 dB SPL. The wavelength data from each individual animal are plotted (gray) along with the averaged values (blue), showing a systematic growth with increasing SPL; from 504 ± 24 μm (mean ± SD) at 30 dB SPL to 874 ± 58 μm at 90 dB SPL. The group delay (Fig. 2 D) also shows a strong level dependence for live data, changing from 0.55 ± 0.03 to 0.39 ± 0.06 ms. The level dependence of these traveling wave properties disappeared after death, indicating that active process contributes significantly to normal traveling wave mechanics in living mice.

Level dependence of the fluid-loaded mass

Complex mechanisms of signal transformations in the cochlea can only be understood if they are split up into parts that are sufficiently simple for analysis using theoretical principles. In this section we use the Wentzel-Kramers-Brillouin (WKB) analysis of cochlear hydrodynamics, developed by Steele and Taber (34), to interpret our in vivo vibration measurements and investigate the interplay between the active process and BM traveling wave.

The simplicity of this analytical technique allows us to find a closed-form relation that relates the BM mechanical responses (simplified as a flexible plate) to the cochlear fluid dynamics. Their 3D-WKB model predicts that the fluid-loaded mass ($M_f=\rho \times h_{eq}$, $\rho$ and $h_{eq}$ being fluid density and effective height, respectively) increases monotonically by increasing BM spatial wavelength (see Eq. 14 b of (34)). Consistent with this, a simpler 2D model demonstrates that the $h_{eq}$ relation gets the form $h_{eq}^{2d}\left(\lambda \right)=\frac{\lambda }{2\pi tanh\left(2\pi L_2/\lambda \right)}$ (38), which relates the effective fluid height to the cochlear duct height ($L_2$ in Fig. 3 a) and the wavelength of the BM traveling wave ($\lambda$). Thus, both the 2D and 3D relations indicate that fluid-loaded mass increases as the BM wavelength gets longer.

Figure 3.

Modeling the effect of a variable fluid-loaded mass on best frequency. (A) Cross section of the cochlear duct of a representative mouse. The duct dimensions were measured to be L₁ = 475 μm and L₂ = 215 μm and b = 220 μm at the 9 kHz location. (B) Level dependence of the best frequency (BF). The BF decreases monotonically with increasing sound intensity in both direct in vivo measurements (red) and estimations using added mass calculation (black and blue). The nonlinear SHO estimation ($B{F}_{nl}$ relation, blue curve) works better than linear SHO estimation ($B{F}_{lin}$ relation, black curve). The fluid added mass $\left(M_f\right)$ for both models is calculated from Eq. 14 b of (34), using geometries shown in (A). The constant $\alpha$ in the nonlinear SHO is fitted for each individual animal (with the average value of $\alpha =$ 1.05 ± 1.03 ${\left(\text{mm s}\right)}^{-2}$), using the least-squares method. Error bars show the mean ± SE (n = 10). To see this figure in color, go online.

These theoretical predictions of a montonic relationship between the fluid-loaded mass and the BM wavelength are consistent with our in vivo observation of a level dependence to the spatial wavelength of the BM traveling wave (Fig. 2 C). This would produce dynamic changes in fluid mass, which would contribute to the BM mechanical response by shifting its resonance frequency. Therefore, we hypothesize that shifting of the BF with sound intensity (as shown in Fig. 1 B) is mainly controlled by the local fluid-loaded mass variation, which stems from interplay between the cochlear active process and traveling wave.

We tested this hypothesis using our experimental data. The fluid added mass ($M_f$) for different stimulus intensities and frequencies were estimated by inserting the corresponding BM wavelength (Fig. 2 C) and duct geometry values (Fig. 3 A) into the $h_{eq}$ equation (Eq. 14b of (34)). Then, by applying the estimated added masses and measured BFs (red curve in Fig. 3 b) into the linear resonance relation of a simple harmonic oscillator (SHO), $B{F}_{lin}=1/2\pi \sqrt{k_{bm}/M_f}$, the BM effective stiffness ($k_{bm}$) was estimated. The effective stiffness using the 30 dB SPL data is calculated to be $k_{bm}=$ 1.18 ± 0.18 N/m. This point stiffness is consistent with the in vitro recording of 0.5 ± 0.5 N/m measured at the region 4 mm from the base (39).

To further probe our hypothesis, we then fixed the $k_{bm}$ to the value estimated for the 30 dB SPL and investigated how the BF varies by increasing the sound intensity (and $M_f$). For each SPL we used the corresponding $M_f$ value along with the constant $k_{bm}$ into the SHO model ($B{F}_{lin}$) and estimated BFs. Fig. 3 B shows the BFs measured directly from in vivo tuning curves (red) overlapped with those estimated by the SHO assumption (black). It is noted that we used the first data point (30 dB SPL) to estimate the constant $k_{bm}$; hence, the estimated and measured BFs are the same at the 30 dB SPL. The linear SHO model predicts the variations of the BFs at lower levels well; however, predictions at higher levels are not as good. This behavior is expected due to contributions from the cochlear nonlinearity associated with the active process. In nonlinear oscillators, the resonance frequency is often level dependent and normally is described as a nonlinear stiffness (for instance, Duffing-type resonator (40)). It has been shown that the level-dependent resonance frequency of a nonlinear system can be estimated by including a correction factor in the form of a square of the oscillation amplitude (40). To consider this effect we modified the linear SHO equation and included the nonlinearity correction, $B{F}_{nl}=1/2\pi \sqrt{k_{bm}/M_f+\alpha u_{bm}^2}$. In this equation $u_{bm}$ is the BM displacement at the BF and $\alpha$ is constant of the anharmonic coefficients and it is computed using the least-squares fitting. Fig. 3 B shows that using this nonlinear resonance relation the BF estimation is improved (blue) at higher levels. It is noted that the small error in the BF estimation is partially related to the simplified duct geometry considered for the WKB calculations. A more physiologically realistic duct geometry (e.g., finite element calculation) has been shown to impact the fluid-loaded mass (9).

Cochlear Tonotopicity

We examined tonotopic variations of key features from tuning curves measured along the cochlea. The BM traveling wave amplitudes and phases for one representative mouse are presented in Fig. 4, A–F as 2D frequency-location profiles. To quantify the gain of cochlear amplification, we calculated the difference in sensitivity between the responses at 40 and 80 dB SPL stimuli (BM gain or $G_{40}^{80}$). Fig. 4 G shows $G_{40}^{80}$ as a function of longitudinal distance and excitation frequency in the same representative mouse. The solid black curve denotes the BM BF for 40 dB SPL.

Figure 4.

Cochlear tonotopicity (A–F), BM displacement magnitude (A–C), and phase (D–F) as a function of excitation frequency (y axis) and longitudinal location (x axis) for 40 dB SPL (A and D), 60 dB SPL (B and E), and 80 dB SPL (C and F) stimuli. Values for the amplitude are normalized with respect to the frequency tuning curve at each location. The red solid curves in each panel indicate the best frequency versus best place. (G) BM gain variation with frequency and longitudinal location. The pseudocolor map represents the sensitivity difference between 40 and 80 dB SPL ($G_{40}^{80}$) responses at all measured locations (x axis) and frequencies (y axis). Solid black line denotes the best frequency of 40 dB SPL versus location. (H) Gain ($G_{40}^{80}$) at the 40 dB SPL best place (i.e., along the solid line denoted in G) as a function of the best frequency (n = 7–10). I, $Q_{10dB}$ of mechanical frequency tuning curves for the 60 dB SPL response (n = 7–10) as function of the best frequency. Error bars are the mean ± SE. To see this figure in color, go online.

To assess gain at the peak of the traveling wave, characterized by the highest sensitivity, longitudinal variation of the $G_{40}^{80}$ along the BF-best place of 40 dB SPL (black curve in Fig. 4 G) is plotted in Fig. 4 H. The averaged data show a progressive decrease toward the apex with a slope of −1.1 dB/kHz. This longitudinal gain reduction toward the mouse apex is consistent with the published data from the apex of the guinea pig cochlea (6). We then plotted the $Q_{10dB}$ of BM vibrations in response to 60 dB SPL against the BF of the measurement location (Fig 2 I). The averaged data show a progressive decrease toward the apex with a slope of −0.19 (1/kHz). This finding is consistent with the neural data measurements showing a spatial dependence of the tuning sharpness (41) that decreases from base to apex. Thus, both the gain and the sharpness of tuning conferred by cochlear amplification are larger at higher-frequency regions of the cochlea than lower frequency regions.

We then investigated the longitudinal profile of BM vibration along the cochlea. Fig. 5 shows the BM spatial profiles of displacement magnitude (Fig. 5, A–C), sensitivity (Fig. 5, D–F), and phase profile (Fig. 5, G–I) for 7, 8, and 9 kHz sounds and three different SPLs (40, 60, and 80 dB SPL) in one representative mouse. The peak of the traveling wave shifted toward the base as the stimulation frequency was increased. This observation is consistent with data measured at a single point in which the BF decreases as the sound intensity is increased (see Fig. 1 B). The sensitivity plots (Fig. 5, D–F) demonstrate nonlinear gain over the entire segment length (1200 μm). The spatial phase profiles are shown in Fig. 5, G–I. A level-dependent phase accumulation toward the apex is evident such that lower SPLs undergo larger phase lags near the peak location. This level dependency of the amplitude and phase are evident from the spatial waveforms constructed in Fig. 5, J–L. As the SPL increased from 40 to 80 dB, wave amplitudes and wavelengths increased nonlinearly (further quantified in Fig. 2).

Figure 5.

Traveling wave profiles. Longitudinal pattern of the BM response to tones at 7 kHz (first column), 8 kHz (second column), and 9 kHz (third column); displacement magnitude (A–C), sensitivity (D–F), phase (G–I), and instantaneous waveforms (J–L) for 40, 60, and 80 dB SPL stimuli from one representative mouse. To see this figure in color, go online

Traveling wave dispersion

In the cochlea, dispersion causes the frequency components of an impulse sound at the base of the cochlea to become separated in space as they travel toward the apex. The dispersion characteristics of waves can be analyzed by comparing phase velocity with the group velocity. With no dispersion, the phase velocity equals the group velocity (i.e., the propagation of sound pressure waves in air). The group velocity ($C_g\left(x,k\right)=\partial \omega \left(x,k\right)/\partial k$) and the phase velocity ($C_p\left(x,k\right)=\omega \left(x,k\right)/k\left(x\right)$) are calculated from the dispersion relation that relates the spatial wavelength of a wave to its temporal frequency (42).

Using our BM vibration magnitude and phase profiles, we calculated the dispersion relationship for a range of locations, excitation frequencies, and intensities. Fig. 6 A shows that the spatial wavelength of the traveling wave along the BM decreased monotonically from basal to apical locations. The dispersion diagram of the BM traveling wave at the 9 kHz best place (denoted by a vertical line in Fig. 6 A) is shown in Fig. 6 B. Any deviation from a straight line indicates dispersion, that is, a frequency dependence of the group velocity. Fig. 6 B shows that the BM dispersion is level dependent for frequencies above 7 kHz, which is consistent with the onset of the BM nonlinearity (43). It is noted that, in contrast to the BM response, other OoC structures, such as RL, show nonlinear characteristics at much lower frequencies (29). Using the dispersion relation at different locations, the phase and group velocities were calculated for a range of stimulation intensities, as shown in Fig. 6 C for a representative mouse.

Figure 6.

Cochlear dispersion. (A) BM wavelength for 9 kHz sound and 30–90 dB SPL intensities versus longitudinal location. (B) BM dispersion diagram (frequency versus wavenumber) for different sound intensities at the 9 kHz best place of 40 dB SPL. (C) BM phase velocity and group velocity as a function of the longitudinal location. The color key for different sound levels is presented in (B). (D) Group velocity and phase velocity for 9 kHz, 60 dB SPL stimulation against best frequency of different longitudinal locations along the cochlea. Error bars are the mean ± SE. To see this figure in color, go online.

Fig. 6D illustrates the averaged group velocity and phase velocity of 9 kHz sound stimulation along different BF locations. These velocities are much lower than the speed of sound in water (1500 m/s), hence BM waves are called “slow waves” compared with the “fast wave” of the fluid compression. Both group and phase velocities decreased with increasing distance from the stapes toward the apex. This effect has mainly been attributed to the gradations of structural stiffness and mass along the BM (39,44). The phase velocities were larger than the group velocities and values increased with increasing sound level. The ratio of the phase velocity to the group velocity quantifies the degree of dispersion (1 being nondispersive). In our measurements, this ratio increased with distance from the base, changing from 2.5 at the 9.5 kHz BF location to 3.5 at the 7.5 kHz BF location, implying a larger dispersion near the helicotrema.

Testing the scaling symmetry approximation near the helicotrema

Scaling symmetry assumptions have been employed extensively to predict the spatial profile of the BM vibrations using single-point frequency response measurements (see, for instance, (45, 46, 47)). However, experimental validation of this approach is lacking. To test the validity of the scaling symmetry hypothesis in the apical section of the mouse cochlea, we compared our in vivo spatial measurements with those estimated using scaling symmetry from single-point recordings (Fig. 7). Fig. 7, A–F show a comparison between direct spatial measurements (black curves) with those estimated using the scaling symmetry method (gray curves). The assumption of the scaling symmetry approach is that the pattern of cochlear vibrations is identical at all points along the length of the cochlea, while the frequency response is adjusted to fit the cochlear tonotopic map. Hence, we used single-point frequency response recordings (at the locations denoted by the red vertical lines in Fig. 7, A–F) to extrapolate vibratory responses at nearby locations.

Figure 7.

Testing for scaling symmetry. Spatial profiles of displacement magnitude (A–C) and phase (D–F) for three different stimulus levels (40, 60, and 80 dB SPL) from one representative mouse. The stimulus frequencies were 6 kHz (A and D), 7 kHz (B and E), and 9 kHz (C and F). The thin black curves are the actual in vivo measurements from multiple points. The thick gray curves represent scaling symmetry extrapolations based on single-point measurements, made at the sites of the red vertical lines. (G and H) Tuning curve magnitudes (G) and phases (H) for 46 different longitudinal locations along the BM. Stimulation is 60 dB SPL for (G–L) and frequencies in the x axes are normalized to the BF of each tuning curve. (I and J) The coefficient of variation (CV) of the normalized tuning curves. (K and L) Averaged CV (n = 5) for displacement (K) and phase (L) against normalized frequency. Error bars are the mean ± SE. To see this figure in color, go online.

It is observed that the scaling symmetry approximation fails to fully describe spatial wave profiles. When a single-point recording was used to predict vibratory responses at nearby locations, the results were in good agreement with the direct wave measurements. For example, using a tuning curve from the middle of our measured region accurately predicted responses over the entire region (Fig. 7, B and E). However, using a tuning curve from either end did not accurately predict the measurements made at the other end (Fig. 7, A, D and C, F). In our dataset, this may reflect the fact that the most apical measurements were made very close to the helicotrema.

The scaling symmetry hypothesis predicts that frequency responses at different locations along the BM depend primarily on the ratio between the characteristic frequency and the stimulation frequency (48). While it is still not possible to measure vibrations along the entire cochlea noninvasively, our measurements over a confined region can be used to quantify spatial variation of mechanical tuning curves. Fig. 7, G and H show the family of BM frequency tuning curve magnitudes and phases for 60 dB SPL, while the frequencies along the x axes are normalized to the corresponding BFs. Spatial variation of the frequency tuning curves was assessed using the coefficient of variation (CV), a statistical metric defined as the standard deviation divided by mean. The CV curves for the magnitude and phase data of Fig. 7, G and H are presented in Fig. 7, I and J. The CV curves show a minimum near the BF for both amplitude and phase, indicating that cochlear scaling is local, with the best performance near the BF. Averaged data for five mice shows similar patterns (Fig. 7, K and L).

Discussion

A comprehensive analysis of the cochlear traveling wave permits a better understanding of sound processing within the peripheral auditory system. In this study, we measured BM traveling waves in the apical region of the mouse cochlea. The vibration data obtained from a dense array of longitudinally spaced locations for a range of frequencies and intensities enabled us to accurately measure critical features of the traveling waves, including wavelength, phase velocity, group velocity, and spatial gradient of displacement magnitude in the passive and active cochlea. Our data shed new light into the interplay between the active process and the traveling wave mechanics by adding quantitative details to some previously reported phenomena and testing widely used assumption of scaling symmetry, and demonstrating that the logarithmic tonotopic map is altered near the helicotrema in the mouse, as in other mammals.

More importantly, our data support the concept that the local fluid loading mass on the BM grows with sound intensity, and that this mechanism is responsible for creating the intensity-dependent shift in BF. The fluid loading mass adds to the BM physical mass and decreases its local resonance frequency (Fig. 3 b). The effect of the fluid added mass is expected to be dominant relative to the BM structural mass given that the density of the BM and cochlear fluid are similar. Using the simple equation of $h_{eq}^{2d}\left(\lambda \right)$ and our in vivo wavelength measurements (Fig. 2 C), along with duct geometry values (see Fig. 3 A), we estimate the effective fluid heights to be 80 and 152 μm for 30 and 90 dB SPLs, respectively. These values are much larger than the BM thickness (∼1 μm at the apex (49)).

Interestingly, the phase data do not show the same frequency shift associated with an isolated spring-mass-damper oscillatory system (see Fig. 1 B). In a pure resonance system, we expect the amplitude and phase components to shift concomitantly by changing the corresponding mass or stiffness. These results suggest that the cochlear partition at each longitudinal location is not responding to the input sound as a pure resonance system. Instead, there is a hybrid of traveling wave and resonance effects (50). This interpretation is also in line with the intensity invariance of the zero crossing of the BM response (51), implying that the displacement phases are mainly set by the global traveling wave and not the local resonance system.

A complete understanding of the cochlear nonlinear mechanics requires precise measurements of the traveling wave spatial profiles. However, due to lack of in vivo traveling wave data with fine spatial resolution, the scaling symmetry approximation (5) has been mostly utilized to translate single spot frequency tuning curves into the spatial vibration profiles (5,45,52, 53, 54). In this study we show that this approximation fails to fully describe spatial wave profiles at the apex of the mouse cochlea (Fig. 7). In particular, the propagation velocity of the traveling wave, its wavelength, and the extent of compressive growth with increasing sound level were different from those expected from scaling symmetry. Different mechanisms may contribute to the deviations observed from scaling symmetry, including cochlear reflection and wave-interference, spatial variation of cochlear gain (Fig. 4 H), and, perhaps most importantly, proximity to the helicotrema on the tonotopic map near the apex (within 350–1500 μm from the helicotrema as shown in Fig. 1 I).

Cochlear wave dispersion

Dispersion causes different frequencies to travel at different speeds along the cochlea while phase and group velocities are not equal. The phase velocities in our data were larger in amplitude than the group velocities and values were increased by increasing the SPLs. The group velocity at the 9 kHz CF location was ∼2 m/s, which is comparable with the 3.2 m/s measured for gerbil at 16 kHz CF location (20). It has been predicted in cochlear models (36), (42) that traveling wave dispersion should occur because of the fluid-structure coupling between the scala fluids and the BM. It has also been predicted that cochlear amplification should produce additional dispersion of the traveling wave (42). In our recordings, we experimentally proved that both predicted findings are correct. First, the spatial wavelength of the traveling wave along the BM decreased from basal to apical locations. Second, the wavelength also decreased as the stimulus intensity was decreased. These dispersive characteristics at the apical region of the mouse cochlea are consistent with those measured at the basal region of the gerbil (20). Moreover, our data show that BM wavelength is highly level dependent in vivo, such that increasing the sound level from 30 to 90 dB SPL increases the wavelength by a factor of 1.73 (from 504 to 874 μm). Our wavelength values at 9 kHz CF location of mouse cochlea are larger than the single value of 200 μm reported for gerbil at 16 kHz CF location (20).

The other important feature of the traveling wave affected by dispersion characteristics is the group delay, which represents the time for acoustical energy of a given frequency to propagate from the base to the apex. The traveling wave group delay in mice has been previously estimated as 1.12 ms/decade over the entire range of cochlear best frequencies (55). In that study, the first-spike latencies to clicks measured in auditory nerve fibers were used to estimate the delay. In our study, we measured mechanical group delay of the BF along the apical region of the mouse cochlea. As shown in Fig. S1, the group delay was 2.4 ± 0.14 ms/decade for 60 dB SPL intensity. Moreover, we found that traveling wave group delay in vivo is highly level dependent such that it decreased systematically as the sound level increased (i.e., from 0.55 ± 0.03 ms at 30 dB SPL to 0.39 ± 0.06 ms at 90 dB SPL). This complex processing of the auditory spectrum, which includes frequency- and level-dependent dispersion, is compensated for by brainstem circuitry, a process that is just beginning to be understood (55).

Together, our data support the hypothesis that there is a strong interplay between the cochlear active process and the mechanics of the traveling wave. Variation of the cochlear amplification by sound intensity impacts the traveling wave properties that in turn add a level-dependent mass to the BM. This fluid mass changes the local impedance (resonance) of the cochlear partition and thus impacts the active power transmission from the OHCs to the BM.

Author contributions

A.N. and J.S.O. designed the research and analyzed data. A.N. performed the experiments, applied mathematical tools, and drafted the paper. A.N., J.S.O., B.E.A., and C.A.S. interpreted results of experiments and edited the manuscript. All authors read and approved the final manuscript.

Editor: Guy Genin.