Abstract
Fluorescence recovery after photobleaching (FRAP) is a common technique to analyze the turnover of molecules in living cells. Numerous physicochemical models have been developed to quantitatively evaluate the rate of turnover driven by chemical reaction and diffusion that occurs in a few seconds to minutes. On the other hand, they have limitations in interpreting long-term FRAP responses where intracellular active movement inevitably provides target molecular architectures with additional effects other than chemical reaction and diffusion, namely directed transport and structural deformation. To overcome the limitations, we develop a continuum mechanics-based model that allows for decoupling FRAP response into the intrinsic turnover rate and subcellular mechanical characteristics such as displacement vector and strain tensor. Our approach was validated using fluorescently labeled β-actin in an actomyosin-mediated contractile apparatus called stress fibers, revealing spatially distinct patterns of the multi-physicochemical events, in which the turnover rate, which represents effective off-rate of β-actin, was significantly higher at the center of the cell. We also found that the turnover rate is negatively correlated with the rate of displacement or velocity along stress fibers but, interestingly, not with the absolute magnitude of strain. Moreover, stress fibers are subjected to centripetal flow that is facilitated by the circulation of actin molecules. Taken together, this novel framework for long-term FRAP analysis allows for unveiling the contribution of overlooked microscopic mechanics to molecular turnover in living cells.
Significance
Fluorescence recovery after photobleaching (FRAP) is a common technique to analyze the turnover of molecules in living cells. Numerous physicochemical models have been developed, but they have limitations in interpreting long-term FRAP responses where multi-physicochemical factors affect intracellular active transport of target molecules. To overcome these limitations, we develop a continuum mechanics-based model that allows for decoupling FRAP response into multiple factors, including the intrinsic turnover rate and subcellular mechanical characteristics. We apply this technique to β-actin in stress fibers to find spatially distinct patterns of the multi-physicochemical events. This novel framework for long-term FRAP analysis allows for unveiling the contribution of overlooked microscopic mechanics to molecular turnover in living cells.
Introduction
Fluorescence recovery after photobleaching (FRAP) is a widely used technique to evaluate molecular dynamics in living cells (1,2). Time recovery of fluorescence intensity of target molecules within a bleached region is often fitted by a single exponential function to determine the characteristic time (3). The characteristic time estimates the involvement of individual physicochemical factors in the FRAP response. In chemical reaction-driven molecular turnover, for example, the fluorescence intensity is recovered without exhibiting diffusive gradients in space. Reaction rate equation-based models have been used in these cases to determine the kinetics (4,5), in which the time constant in the single exponential function as a characteristic time gives the dissociation rate (4,6). In diffusion-driven case where the Brownian motion-based pure-diffusion transports molecules, fluorescence distribution within the bleached region exhibits spatial gradients, meaning that the characteristic time depends on the size of the bleached region (7). The diffusion coefficient is then pragmatically estimated by considering the size of the bleached region and the time constant (8) or more accurately by analyzing the spatiotemporal fluorescence profile with a diffusion equation instead of single exponential functions (9, 10, 11, 12). For more complicated cases with anomalous diffusion, fractional diffusion equation (13), alternative point FRAP (14), computational framework (15), and Fourier transform-FRAP with patterned photobleaching (16) have been developed to evaluate the effect of intracellular molecular crowding. Moreover, in a mixed case where diffusive molecules associate and dissociate with their reaction partners, mathematical models considering reaction-diffusion equations (4,17,18), FRAP combined with fluorescence correlation spectroscopy (19), and FRAP combined with genetic manipulation (7) have been developed to separately determine the diffusion coefficient and binding kinetics.
While many approaches have thus contributed to analyzing complex FRAP responses, long-term responses remain to be characterized. Specifically, the time course of intensity recovery inevitably displays an abnormal curve distinct from simple exponential functions because of the presence of intracellular directed movements. To analyze such abnormal curves, double exponential functions are instead used for determining two independent characteristic times (20,21). However, the interpretation of the two characteristic times in terms of the actual physicochemical properties such as diffusion, directed movements, structural deformation, and chemical reaction is difficult. Regarding the involvement of directed movements in FRAP response, advection-reaction-diffusion models were developed to analyze one-dimensional movements of motor proteins in relatively short-term recovery curves of <3 min (22,23). In addition, advection-reaction models were developed to analyze two-dimensional directed movements of actin molecules observed in long-term FRAP experiments of >10 min where fast diffusion process is ignorable (24). However, these models assumed constant velocities of the movement, and therefore more general nonlinearly and temporarily changing movements were beyond the scope of the analysis. Besides, intracellular structures are subjected to mechanical deformations or distortions, which are also not accessible with existing models. Consequently, it remains unclear how these unprobed effects, namely intracellular directed movements and structural deformations, affect the turnover within cells, which would be critical to understanding mechanotransduction at the organelle level to which these effects are related.
Here we develop a continuum mechanics-based approach to simultaneously determine the molecular turnover and active movements that inevitably appear in long-term FRAP responses. Analyses for such long-term behaviors are indispensable, particularly for analyzing the dynamics of actin molecules associated with stress fibers, a contractile apparatus consisting of actin filaments, myosin II, and other cross-linking and actin-binding proteins, given its long lifetime that exceeds 10 min (24, 25, 26, 27). Because of the absence of appropriate FRAP analysis models for long-term behaviors, actin dynamics has not accurately been decomposed to evaluate the individual contribution of the two factors. Specifically, with the aid of a continuum mechanics-based approach, we obtain strain tensors of and turnover rate in moving photobleached areas, providing a basic framework to evaluate the turnover of molecules undergoing spatial movements and structural deformations.
Materials and methods
Cell culture, plasmids, transfection, and reagents
Rat aortic smooth muscle cell lines (A7r5, ATCC) that express non-muscle β-actin and myosin II (25) were cultured with low-glucose (1.0 g/L) Dulbecco’s modified Eagle’s medium (Wako) containing 10% (v/v) heat-inactivated fetal bovine serum (SAFC Biosciences) and 1% penicillin-streptomycin (Wako) in a humidified 5% CO2 incubator at 37°C. An expression plasmid encoding mClover2-tagged β-actin was constructed by inserting a human β-actin gene, which was digested with XhoI and BamHI restriction enzymes from the EYFP-actin vector (#6902-1, Clontech) into the mClover2-C1 vector (Addgene plasmid #54577, a gift from Michael Davidson). The plasmid was transfected to cells using Lipofectamine LTX and Plus Reagent (Thermo Fisher Science) according to the manufacturer’s instruction. Actin polymerization inhibitor Latrunculin A (Wako) was used at 10 nM concentration.
FRAP measurements
Cells were cultured on a glass-bottom dish with no coating and transfected with the plasmid for 24 h for FRAP experiments. FRAP experiments were performed by using a confocal laser scanning microscope (FV1000, Olympus) with a 60× oil immersion objective lens (NA = 1.42). Fluorescence images were acquired every 10 s for 20 min using a 488-nm wavelength laser. For each imaging, 1024 × 1024 pixels were scanned at a speed of 8 μs/pixel, thus taking ∼8.4 s, which is within 10 s; here, the physical size of each pixel is 0.197 μm. Pre-bleach images were acquired for the first two time frames (namely 20 s), and then photobleaching was carried out onto stress fibers by using a 405-nm and 440-nm wavelength laser. For photobleaching, a rectangular region with a size of 500 (length) × 50 (width) pixels was scanned three times at a speed of 10 μs/pixel for a total of 30 μs for each pixel, while having a spacing of 100 pixels in between the adjacent stripes. The photobleaching laser was applied at 100%, and the power was low enough not to induce severing of stress fibers.
Image analysis
Images were analyzed by using ImageJ (NIH) and MATLAB (MathWorks). Images were cropped to a tetragon to include a labeled region in single stress fibers. For the cropping, we set a threshold of intensity that automatically recognizes unbleached regions in the cropped pre-bleach frames, and thus the vertices of the labeled region were obtained in every time frame. For FRAP analysis, an intensity profile of the labeled region surrounded by the vertex points was spatially averaged over the area of , i.e.,
| (1) |
To describe the recovery curve, Eq. 1 was normalized by,
| (2) |
where and represent the spatially averaged intensities in pre-bleach and bleached frames, respectively. The time course of normalized average intensity was fitted by using a least-squares method with a single exponential function
| (3) |
where and represent the mobile fraction and the turnover rate, respectively.
Continuum mechanics-based model of stress fibers
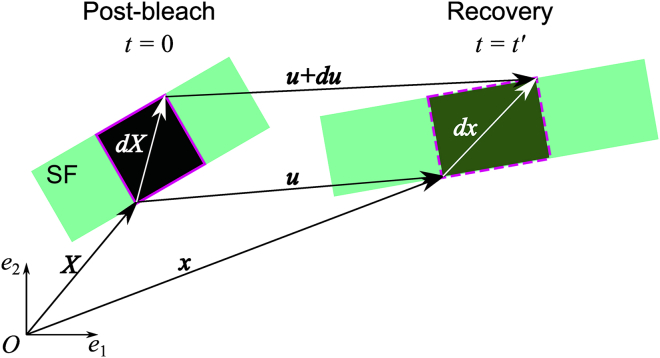
Continuum mechanics allows for analysis of solid deformation and fluid flow, in which the physical properties are represented by tensors; i.e., a mathematical form being independent of coordinate systems. This approach is valid at the continuum level with length scales much greater than that of individual molecules. Given that stress fibers are composed of a large number of actin molecules, they are often regarded to be a continuum for mechanical analysis (24, 25, 26, 27). To evaluate mechanical properties of a labeled region by photobleaching on individual stress fibers, we define position vectors corresponding to the vertex points forming the labeled region in cropped images (Fig. 1). The displacement vector between (post bleach) and is described as
| (4) |
where and represent the position vectors at and , respectively. The deformation of the labeled region is evaluated from the change in the displacement vectors to determine the displacement gradient Eij (Green’s strain tensors) and (Almansi’s strain tensors), which are described by
| (5) |
respectively. In the case of infinitesimal deformations, we can assume that , and the second order of the displacement gradient is negligible. The strain tensor is then reduced to
| (6) |
Figure 1.
Schematic of the continuum mechanics-based FRAP model to analyze the chemomechanical properties within the region labeled by photobleaching. SF represents a part of a single stress fiber. See the text for details of the variables and coordinates. To see this figure in color, go online.
As the strain tensor is symmetric, coordinate-independent principal invariants are reduced to
| (7) |
where is the volumetric strain. Substituting of the displacement rate for of the displacement describes the strain rate tensor as
| (8) |
In the same manner, of the volumetric strain rate is obtained.
To distinguish between the deformations parallel and perpendicular to stress fibers, vectors and tensors are transformed according to
| (9) |
where and represent arbitrary vector and tensor, respectively, and represents the transformation matrix determined by of the orientation of a single stress fiber within cropped images. The displacement and strain parallel and perpendicular to a stress fiber are then rewritten as
| (10) |
where the subscripts and represent parallel and perpendicular to the stress fiber, respectively.
Orientation analysis of stress fibers
Images were analyzed using ImageJ (NIH) and MATLAB (MathWorks). The orientation index between vectors is defined as
| (11) |
where represents the orientation vector of a stress fiber. Here, indicates that the displacement vector is perpendicularly oriented to the stress fiber, while means the displacement vector is parallel with the stress fiber.
Statistical analysis
Unless otherwise stated, data are expressed as the mean ± standard deviation. Differences were calculated based on the Mann-Whitney U-test for variables with a non-Gaussian distribution, or the unpaired Student's t-test for variables with a Gaussian distribution, with a significance level of (∗), (∗∗), or (∗∗∗).
Results
Continuum mechanics-based FRAP model determines both molecular turnover and mechanical properties in cells
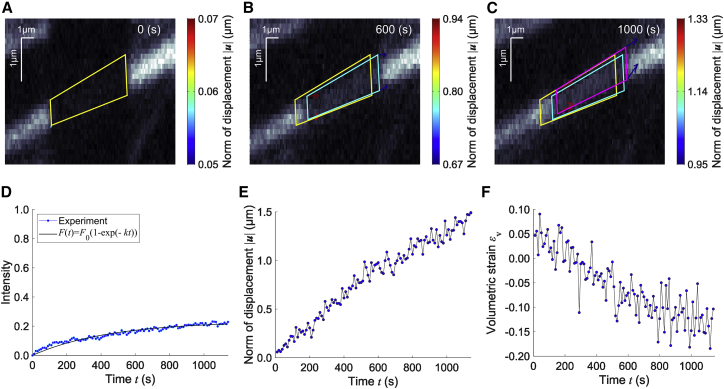
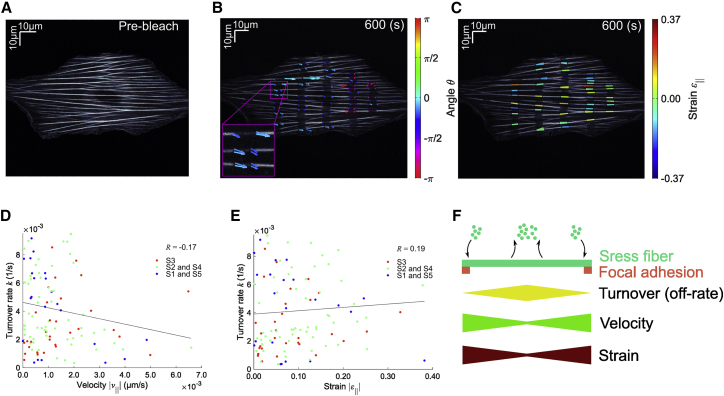
Photobleaching was carried out onto mClover2-actin localized in stress fibers in A7r5 cells (Fig. 2 A); in this cell line, stress fibers tend to align along the long axis of the cell. The labeled region was automatically extracted based on an intensity threshold that distinguishes between bleached and unbleached regions in cropped images (Fig. 2 A–C; Video S1). The actin molecular turnover recovered the intensity within the region. Meanwhile, the bleached square regions were subjected to spatial movements. To separately evaluate the molecular turnover and subcellular mechanical properties, first, the time evolution of the intensity within the tracked bleached region was normalized by Eq. 2 and then fitted by the least-squares method with Eq. 3 (Fig. 2 D), determining of the turnover rate (Table 1). Second, the analysis of the spatial movement provides the displacement vector at given time points (Fig. 2 B and C). The magnitude of the displacement, namely the norm of the displacement vector, was increased over time (Fig. 2 E). To evaluate spontaneous deformations of the tracked region, the Green’s and Almansi’s strain tensors were obtained by using the rate change in the displacement vectors according to Eq. 5 (Fig. S1 A and B). The error between these stain tensors, defined by , was within a range of for both and and of for (Fig. S1 C). This result allows us to assume that the strain is infinitesimal and use the simplified form of the strain tensor shown in Eq. 6. Notably, , , and are dependent on the coordinate system, meaning that individual components of these tensors in a certain region are unable to be compared with those in other labeled regions of stress fibers having different orientations in cells. To overcome this limitation, the volumetric strain corresponding to the first principal invariant of the strain tensor was finally evaluated according to Eq. 7 (Fig. 2 F).
Figure 2.
Determination of actin molecular turnover and mechanical properties (displacement and strain) of stress fibers in A7r5 cells. (A) The region of interest (ROI), automatically detected as shown in yellow, is labeled by photobleaching ( s). (B, C) The ROI, shown in cyan ( s) and magenta ( s), is often spatially transported in a long-term observation (see Video S1). Arrows represent the tracked displacement vectors. (D) Time course of the fluorescence intensity within the ROI. The regression curve based on Eq. 3 determines the molecular turnover rate. (E) Time course of the norm of representative displacement vector. (F) Time course of the coordinate-independent volumetric strain. To see this figure in color, go online.
Table 1.
Turnover rate, displacement rate, and volumetric strain rate simultaneously determined
| Turnover Rate | Displacement Rate | Volumetric Strain Rate |
|---|---|---|
| (1/s) | (μm/s) | (1/s) |
Mapping the distribution of mechanical behaviors in cells
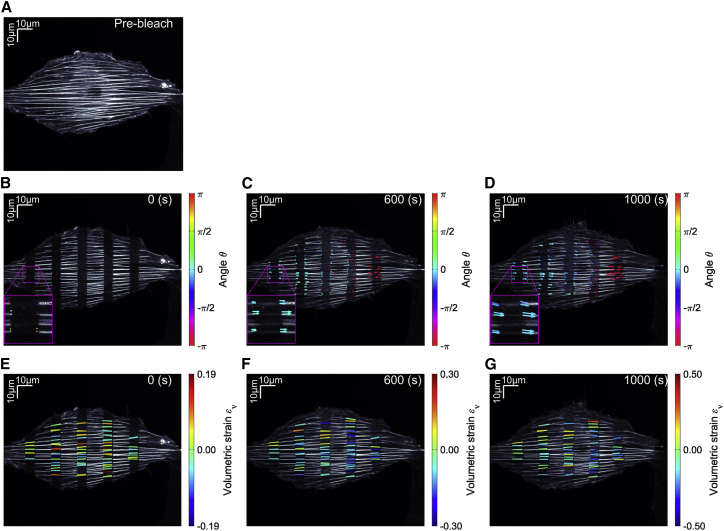
To obtain the distribution of mechanical properties or, more specifically, intrinsic strain in cells, the displacement vector was calculated for multiple bleached regions on stress fibers (Fig. 3 A–D; Video S2). Following this process, the volumetric strain, which is the most general definition of strain independent of the coordinates, was evaluated for these regions according to Eqs. 6 and 7, providing the strain distribution in the cell (Fig. 3 E–G; Video S3). The turnover rate of actin molecules was also determined by fitting Eq. 3 to fluorescence recovery curves of those regions (Fig. 2 D). Our approach thus unveiled the mechanical properties as well as the molecular turnover along stress fibers in living cells (Table 1).
Figure 3.
Multiple bleached regions on stress fibers in a single cell with the displacement and deformation distribution. Arrows and overlaid rectangular regions represent the displacement vectors and volumetric strain, respectively. (A) Pre-bleach image. (B–D) Displacement vectors at t = 0 s (B), t = 600 s (C), and t = 1000 s (D). Color bar represents the angle of the displacement vectors (see Video S2). Insets of the indicated regions are magnified 3×. (E–G) Volumetric strains at t = 0 s (E), t = 600 s (F), and t = 1000 s (G). Color bar represents the value of the volumetric strain (see Video S3). To see this figure in color, go online.
Anisotropic mechanical properties distinct between parallel with and perpendicular to stress fibers
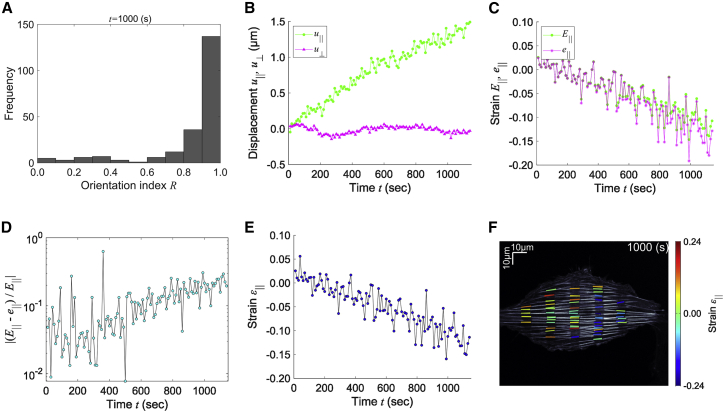
Stress fibers are subjected to myosin II-dependent sustained contraction (28,29). Probably because of this activity along the longitudinal direction of stress fibers, we found an anisotropic displacement that differs between the parallel and perpendicular directions (Fig. 3 B–D). To evaluate the anisotropy, the orientation index , which describes the correlation between displacement and orientation vectors of stress fibers, was calculated for multiple bleached regions according to Eq. 11, where and indicate the parallel and perpendicular correlation, respectively (Fig. 4 A). The result showed that the displacement vector was predominantly parallel with the orientation of stress fibers as expected. The displacement vector was converted into the dominant coordinate system determined by the local orientation of single stress fibers in cropped images according to Eqs. 9 and 10. The transformed vector parallel with stress fibers was more dominant than the perpendicular one (Fig. 4 B), consistent with the tendency of the orientation index.
Figure 4.
Long-term strain analysis of stress fibers. The displacement vectors and strain tensors are transformed to either parallel with or perpendicular to stress fibers. The subscripts and represent parallel with and perpendicular to stress fibers, respectively. (A) The orientation index defined in Eq. 11 at s. (B) Time course of the displacement vectors parallel with (green) and perpendicular to (magenta) stress fibers. (C) Time course of the parallel components of the Green’s (green) and Almansi’s (magenta) strain tensors. (D) Time course of the error defined as . (E) Time course of strain parallel with stress fibers. (F) The values of strain parallel with stress fibers in the reference frame are overlaid in the cell image (see Video S4). To see this figure in color, go online.
Next, Green’s and Almansi’s strain tensors were likewise converted to conform to the dominant coordinate system, providing the deformation parallel with (Fig. 4 C) and perpendicular to stress fibers (Fig. S2 A). To assess whether the deformation of labeled regions is infinitesimal, we analyzed the error defined by either or . The difference between the Green’s and Almansi’s strains parallel with stress fibers remained below the magnitude of their values (Fig. 4 D), while the magnitude of the displacement was increased over time (Fig. 4 B). In contrast, the difference between their perpendicular components was almost the same as the magnitude of strains (Fig. S2 B), probably because the small width of stress fibers, i.e., the perpendicular component of transformed and , would include inevitable observation errors that could be comparable with the actual deformation. The strains along the width direction may therefore be affected particularly regarding the third term in Eq. 5, even though the displacement along the width of stress fibers remained within a range (Fig. 4 B). Contrary to the behavior of the Green’s strain, the Almansi’s strain along the width of stress fibers was decreased with increasing time due to the opposite sign of the third term in Eq. 5 (Fig. S2 A). On the other hand, by considering of the small displacement compared with (Fig. 4 B) in addition to the small difference between Green’s and Almansi’s strains parallel with stress fibers (Fig. 4 C and D), we found that the deformation of labeled regions was infinitesimal, which allowed us to use of the transformed strain tensor. The strains parallel with (Fig. 4 E) and perpendicular to stress fibers (Fig. S3 A) were then recalculated according to Eqs. 9 and 10. We also obtained the ratio of the error between the strains parallel with and perpendicular to stress fibers defined by , resulting in the strain parallel with stress fibers being dominant (Fig. S3 B), which agrees with the displacement vectors (Fig. 4 A). The strain parallel with stress fibers was then overlaid onto the multiple regions to visualize the anisotropic mechanical properties of the cell (Fig. 4 F; Video S4).
Actin molecular turnover increases at the cell center as opposed to mechanical behavior
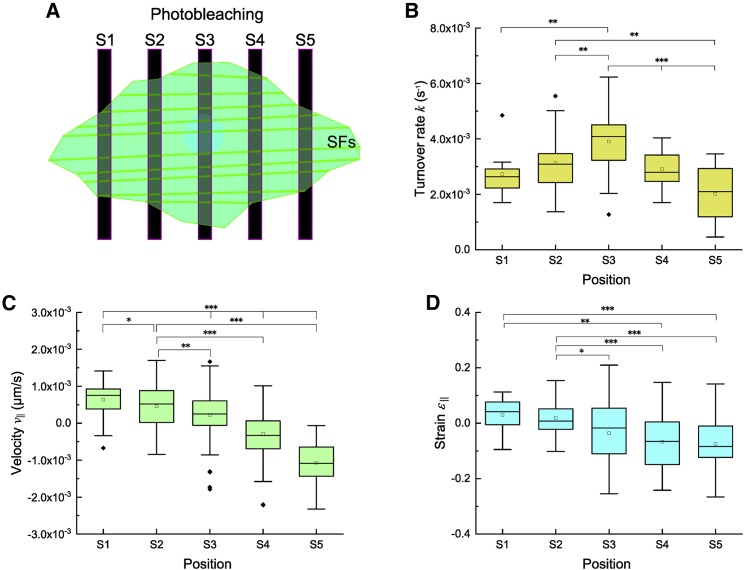
Our results indicated that stress fibers are indeed subjected to the deformation that occurs predominantly along their longitudinal direction (Fig. 4 A and B). However, it has remained an open question whether there is a cooperative or competitive effect between such mechanical behavior and actin molecular turnover on stress fibers. To decipher this complex process, we performed the FRAP experiments with the stripe bleach pattern that is approximately perpendicular to the dominant orientation of stress fibers in A7r5 cells (Fig 5 A). FRAP responses within multiple bleached regions were analyzed at all the stripes from S1 to S5 to determine of the turnover rate (Fig. 5 B), of the velocity (Fig. 5 C), and of the strain (Fig. 5 D). The turnover rate of actin in peripheral stripes of S1 and S5 was ~2-fold slower than that of S3, increasing at the center of the cell (Fig. 5 B). By contrast, the magnitude of velocity and strain along the stress fibers decreased at the center of the cell. Moreover, negative sign of the velocity on either side of the cell appeared while positive sign did on the other side, suggesting the presence of a centripetal flow (Fig. 5 C). In a similar manner to the velocity, approximately one-half of cells tend to possess compressive strains, whereas the others tend to possess tensile strains (Fig. 5 D).
Figure 5.
The chemical turnover and mechanical strain are high at the cell center and periphery, respectively. (A) Schematic of stripe pattern of photobleaching in a cell. (B–D) Actin turnover rate (B), of the displacement rate (C), and strain (D) along stress fibers are shown by mean SD analyzed at each stripe ( from independent experiments of cells for S1, S2, S3, S4, and S5, respectively); different numbers of photobleached regions (namely stress fibers) are included in each of the stripes, and consequently values could differ among the experiments. Asterisks represent a statistically significant difference among the stripes: ∗; ∗∗; ∗∗∗. To see this figure in color, go online.
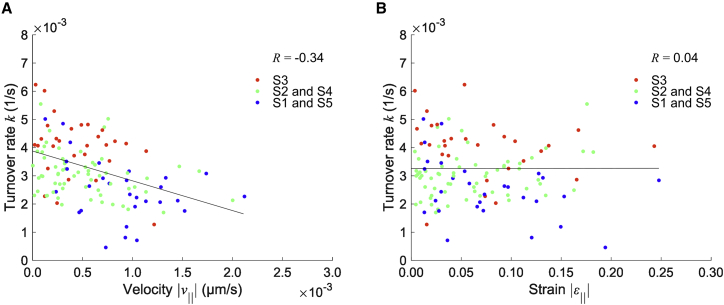
We analyzed the Pearson correlation coefficient between the actin molecular turnover rate and the magnitude of either the velocity of spatial displacement or the strain of microscopic structural deformation. We found a negative correlation with (Fig. 6 A), and no correlation with (Fig. 6 B). Since the turnover rate in the chemical reaction-driven case is known to be involved in the off-rate (4,6), the negative correlation of suggests that the dissociation of actin molecules with stress fibers is reduced by the mobility of stress fibers. Regarding the specific spatial distribution (Fig. 5 B and C), it is likely that actin polymerization at the cell periphery may directly facilitate the spatial transport of stress fibers toward the cell center as is often observed in the retrograde flow (30, 31). Thus, turnover is rather suppressed to end up having locally stabilized stress fibers when they are under fast movement within cells.
Figure 6.
Correlation analysis represents the relationship between the molecular turnover and mechanical behaviors. The actin molecular turnover is negatively correlated with the magnitude of velocity parallel with stress fibers (; ; from independent cells) (A) but not with the magnitude of strain parallel with stress fibers (; from independent cells) (B). Lines represent the regression fitting for variables of S1 and S5 (blue), S2 and S4 (green), and S3 (red), where the definition of S1–S5 is shown in Fig. 5A. To see this figure in color, go online.
Actin polymerization facilitates the spatial transport of stress fibers toward the cell center
To evaluate the effect of actin polymerization, we carried out FRAP experiments in A7r5 cells treated with an actin polymerization inhibitor, Latrunculin A (LatA, 10 nM) (Fig. 7 A–C). We found that there is no correlation ( with ) between the actin turnover rate and the magnitude of velocity (Fig. 7 D). Comparing this inhibitor experiment with the above control experiment having the negative correlation (Fig. 6 A), these results suggest that there is a circulation of actin molecules from and to the free actin pool in the cytoplasm that occurs along stress fibers at the periphery and center, respectively, and resulting flow observed along stress fibers is correlated with the rate of disassembly at the center. We also observed no correlation between the turnover rate and the strain along stress fibers in cells treated with LatA ( with ; Fig. 7 E).
Figure 7.
Continuum mechanics-based FRAP onto mClover2-actin in stress fibers of A7r5 cells treated with 10-nM Latrunculin A. (A) Pre-bleach image. (B) The displacement vectors. Color bar represents the angle of the displacement vectors. Insets of the indicated regions are magnified 3×. (C) The values of strain parallel with stress fibers in the reference frame are overlaid in the cell image. (D) The actin molecular turnover results in no correlation with the magnitude of velocity parallel with stress fibers (; ; = 119 from independent = 3 cells). (E) The actin molecular turnover is not correlated with the magnitude of strain parallel with stress fibers (; ; = 119 from independent = 3 cells). Lines represent the regression fitting for variables of S1 and S5 (blue), S2 and S4 (green), and S3 (red), where the definition of S1–S5 is shown in Fig. 5A. (F) Model of chemomechanical behavior of stress fibers in cells. To see this figure in color, go online.
Discussion
Numerous FRAP methods have been proposed to evaluate the complex turnover in a normal diffusion-driven case (8, 9, 10, 11, 12), anomalous diffusion-driven case (13, 14, 15, 16), chemical reaction-driven case (4,5), and diffusion-reaction case (4,7,17). However, because of the current lack of appropriate FRAP methods, the long-term turnover driven by stress fiber-associated active dynamics, which include both intracellular bulk-like flow and microscopic structural deformation, remains highly elusive. The main difficulty is that fluorescence recovery curves exhibit abnormal curves, unlike the conventional single exponential form due to spatial movements of labeled regions. To overcome this problem, double exponential functions are alternatively used to determine two independent characteristic times (20,21). However, it is difficult to interpret such independent characteristic times in terms of the real physicochemical factors such as chemical reaction, spatial movements, and/or structural deformation that potentially all affect the long-term turnover. We here provided the continuum mechanics-based FRAP framework to reveal the multi-physicochemical contributions to the long-term turnover.
To demonstrate our approach, FRAP experiments were carried out for mClover2-tagged actin molecules on stress fibers in A7r5 cells. The material points forming the region of interest provide the position and displacement vectors at given time points (Figs. 1 and 2 A–C). The rate change in displacement vector gives us the strain tensors, , , and . Notably, intracellular fibrous structures such as stress fibers exist with respective orientations in cells, meaning that the coordinate-dependent form is not adequate to extract vectors and tensors in multiple bleached regions. To circumvent this situation, the coordinate-independent volumetric strain, one of the principal invariants of the strain tensor, is determined (Fig. 2 F). Meanwhile, the time evolution of intensity within the labeled region determines the molecular turnover rate that represents the effective off-rate (4, 6) (Fig. 2 D). Taken together, our approach enables us to evaluate comprehensive physicochemical properties, namely the chemical reaction-driven molecular turnover rate and the subcellular mechanical displacement and deformation.
Furthermore, we performed FRAP experiments with the stripe photobleaching pattern to evaluate the distribution of chemomechanical properties on stress fibers in A7r5 cells (Fig. 5). By analyzing spatiotemporal profiles of multiple bleached regions, we made the following novel findings: 1) the actin turnover rate in central regions of cells is twofold faster than that at the periphery of the cell, which is consistent with the previous study reporting the faster turnover of actin cross-linking proteins in stress fibers (myosin regulatory light chain and α-actinin) at the cell center (32), and 2) both the velocity and the strain are decreased at the center of the cell in an opposite manner to the turnover rate (Fig. 5 C and D).
It was an open question whether there is a cooperative or competitive interaction between the actin molecular turnover and such microscopic dynamics on stress fibers. To decipher this complex process, we analyzed the Pearson correlation coefficient between the actin molecular turnover rate and the velocity of spatial displacement with or without LatA-induced inhibition of actin polymerization. We found a negative correlation with actin polymerization (Fig. 6 A), whereas no correlation is observed with the inhibition of actin polymerization (Fig. 7 D). These results collectively suggest that actin polymerization facilitates the spatial transport of stress fibers from the cell periphery toward the cell center.
In contrast, no correlation between the turnover rate and the strain along stress fibers was observed both with and without LatA-induced inhibition of actin polymerization, suggesting that the microscopic deformation is not a measure to evaluate the actin molecular turnover. Considering the microscopic structure of the contractile unit of stress fibers known as non-muscle sarcomere (27), actin filaments are basically only sliding to change the relative position with another stress fiber constituent, myosin II (28), in a manner similar to the actomyosin-mediated contraction in cytokinesis (33,34). Thus, the net strain of individual actin filaments would not necessarily be comparable in magnitude to, or even be associated with, the microscopic strain observed at the whole-cell level. Altogether, our findings made with the quantitative decoupling of the multiple-physicochemical phenomena suggest that stress fibers are transported toward the cell center where the turnover of actin molecules is accelerated, and stress fibers under such fast transportation are stabilized (Fig. 7 F), while the macroscopic deformation or the absolute strain magnitude does not actually reflect the extent of the chemical reaction or turnover, thus giving novel insights into the complex cellular mechanism of how stress fiber-associated molecules respond to mechanical factors.
Author contributions
T.S. and S.D. conceived research. T.S. designed and conducted research with feedback from S.D. D.M. provided support in analysis. T.S. and S.D. wrote the manuscript. All authors read and approved the final manuscript.
Acknowledgments
T.S. is supported by the Japan Society for the Promotion of Science (JSPS). This study was partly supported by JSPS KAKENHI grants (18H03518, 19K22967, and 20J10828).
Declaration of interests
The authors declare no competing interests.
Editor: Baohua Ji.
Footnotes
Takumi Saito, JSPS Research Fellowship for Young Scientists.
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.06.032.
Contributor Information
Takumi Saito, Email: takumi.saitou.b2@tohoku.ac.jp.
Shinji Deguchi, Email: deguchi.shinji.es@osaka-u.ac.jp.
Supporting material
References
- 1.Lorén N., Hagman J., et al. Braeckmans K. Fluorescence recovery after photobleaching in material and life sciences: putting theory into practice. Q. Rev. Biophys. 2015;48:323–387. doi: 10.1017/s0033583515000013. [DOI] [PubMed] [Google Scholar]
- 2.Moud A.A. Fluorescence recovery after photobleaching in colloidal science: introduction and application. ACS Biomater. Sci. Eng. 2022;8:1028–1048. doi: 10.1021/acsbiomaterials.1c01422. [DOI] [PubMed] [Google Scholar]
- 3.Kapitza H.G., McGregor G., Jacobson K.A. Direct measurement of lateral transport in membranes by using time-resolved spatial photometry. Proc. Natl. Acad. Sci. USA. 1985;82:4122–4126. doi: 10.1073/pnas.82.12.4122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sprague B.L., Pego R.L., et al. McNally J.G. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys. J. 2004;86:3473–3495. doi: 10.1529/biophysj.103.026765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kamnev A., Palani S., et al. Balasubramanian M.K. Time-varying mobility and turnover of actomyosin ring components during cytokinesis in Schizosaccharomyces pombe. Mol. Biol. Cell. 2021;32:237–246. doi: 10.1091/mbc.e20-09-0588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bulinski J.C., Odde D.J., et al. Waterman-Storer C.M. Rapid dynamics of the microtubule binding of ensconsin in vivo. J. Cell Sci. 2001;114:3885–3897. doi: 10.1242/jcs.114.21.3885. [DOI] [PubMed] [Google Scholar]
- 7.Saito T., Matsunaga D., et al. Deguchi S. Determining the domain-level reaction-diffusion properties of an actin-binding protein transgelin-2 within cells. Exp. Cell Res. 2021;404:112619. doi: 10.1016/j.yexcr.2021.112619. [DOI] [PubMed] [Google Scholar]
- 8.Axelrod D., Koppel D.E., et al. Webb W.W. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 1976;16:1055–1069. doi: 10.1016/s0006-3495(76)85755-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dayel M.J., Hom E.F., Verkman A.S. Diffusion of green fluorescent protein in the aqueous-phase lumen of endoplasmic reticulum. Biophys. J. 1999;76:2843–2851. doi: 10.1016/s0006-3495(99)77438-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jönsson P., Jonsson M.P., et al. Höök F. A method improving the accuracy of fluorescence recovery after photobleaching analysis. Biophys. J. 2008;95:5334–5348. doi: 10.1529/biophysj.108.134874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Deschout H., Hagman J., et al. Braeckmans K. Straightforward FRAP for quantitative diffusion measurements with a laser scanning microscope. Opt. Express. 2010;18:22886–22905. doi: 10.1364/OE.18.022886. [DOI] [PubMed] [Google Scholar]
- 12.Berk D.A., Yuan F., et al. Jain R.K. Fluorescence photobleaching with spatial Fourier analysis: measurement of diffusion in light-scattering media. Biophys. J. 1993;65:2428–2436. doi: 10.1016/s0006-3495(93)81326-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lubelski A., Klafter J. Fluorescence correlation spectroscopy: the case of subdiffusion. Biophys. J. 2009;96:2055–2063. doi: 10.1016/j.bpj.2008.10.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Daddysman M.K., Fecko C.J. Revisiting point FRAP to quantitatively characterize anomalous diffusion in live cells. J. Phys. Chem. B. 2013;117:1241–1251. doi: 10.1021/jp310348s. [DOI] [PubMed] [Google Scholar]
- 15.Leung W.K.C., Ching A.K.K., et al. Wong N. A novel interplay between oncogenic PFTK1 protein kinase and tumor suppressor TAGLN2 in the control of liver cancer cell motility. Oncogene. 2011;30:4464–4475. doi: 10.1038/onc.2011.161. [DOI] [PubMed] [Google Scholar]
- 16.Geiger A.C., Smith C.J., et al. Simpson G.J. Anomalous diffusion characterization by fourier transform-FRAP with patterned illumination. Biophys. J. 2020;119:737–748. doi: 10.1016/j.bpj.2020.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sprague B.L., Müller F., et al. McNally J.G. Analysis of binding at a single spatially localized cluster of binding sites by fluorescence recovery after photobleaching. Biophys. J. 2006;91:1169–1191. doi: 10.1529/biophysj.105.073676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ait-Haddou R., Kurachi Y., Nomura T. On calcium-buffer dynamics within the excess buffer regime. J. Theor. Biol. 2010;264:55–65. doi: 10.1016/j.jtbi.2010.01.017. [DOI] [PubMed] [Google Scholar]
- 19.Im K.-B., Schmidt U., et al. Wachsmuth M. Diffusion and binding analyzed with combined point FRAP and FCS. Cytometry. 2013;83:876–889. doi: 10.1002/cyto.a.22316. [DOI] [PubMed] [Google Scholar]
- 20.Campbell J.J., Knight M.M. An improved confocal FRAP technique for the measurement of long-term actin dynamics in individual stress fibers. Microsc. Res. Tech. 2007;70:1034–1040. doi: 10.1002/jemt.20513. [DOI] [PubMed] [Google Scholar]
- 21.Sakurai-Yageta M., Maruyama T., et al. Murakami Y. Dynamic regulation of a cell adhesion protein complex including CADM1 by combinatorial analysis of FRAP with exponential curve-fitting. PLoS One. 2015;10:e0116637. doi: 10.1371/journal.pone.0116637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ciocanel M.V., Kreiling J.A., et al. Sandstede B. Analysis of active transport by fluorescence recovery after photobleaching. Biophys. J. 2017;112:1714–1725. doi: 10.1016/j.bpj.2017.02.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hallen M.A., Liang Z.Y., Endow S.A. Ncd motor binding and transport in the spindle. J. Cell Sci. 2008;121:3834–3841. doi: 10.1242/jcs.038497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Saito T., Matsunaga D., et al. Deguchi S. Long-term molecular turnover of actin stress fibers revealed by advection-reaction analysis in fluorescence recovery after photobleaching. bioRxiv. 2021 doi: 10.1101/2021.06.19.449123. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Matsui T.S., Kaunas R., et al. Deguchi S. Non-muscle myosin II induces disassembly of actin stress fibres independently of myosin light chain dephosphorylation. Interface Focus. 2011;1:754–766. doi: 10.1098/rsfs.2011.0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Okamoto T., Matsui T.S., et al. Deguchi S. Helical structure of actin stress fibers and its possible contribution to inducing their direction-selective disassembly upon cell shortening. Biomech. Model. Mechanobiol. 2020;19:543–555. doi: 10.1007/s10237-019-01228-z. [DOI] [PubMed] [Google Scholar]
- 27.Kaunas R., Hsu H.J., Deguchi S. Sarcomeric model of stretch-induced stress fiber reorganization. Cell Health Cytoskeleton. 2010;3:13. doi: 10.2147/chc.s14984. [DOI] [Google Scholar]
- 28.Saito T., Huang W., et al. Deguchi S. What factors determine the number of nonmuscle myosin II in the sarcomeric unit of stress fibers? Biomech. Model. Mechanobiol. 2020;20:155–166. doi: 10.1007/s10237-020-01375-8. [DOI] [PubMed] [Google Scholar]
- 29.Kaunas R., Deguchi S. Multiple roles for myosin II in tensional homeostasis under mechanical loading. Cell. Mol. Bioeng. 2011;4:182–191. doi: 10.1007/s12195-011-0175-x. [DOI] [Google Scholar]
- 30.Yamashiro S., Watanabe N. A new link between the retrograde actin flow and focal adhesions. J. Biochem. 2014;156:239–248. doi: 10.1093/jb/mvu053. [DOI] [PubMed] [Google Scholar]
- 31.Gardel M.L., Sabass B., et al. Waterman C.M. Traction stress in focal adhesions correlates biphasically with actin retrograde fl ow speed. J. Cell Biol. 2008;183:999–1005. doi: 10.1083/jcb.200810060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Peterson L.J., Rajfur Z., et al. Burridge K. Simultaneous stretching and contraction of stress fibers in vivo. Mol. Biol. Cell. 2004;15:3497–3508. doi: 10.1091/mbc.e03-09-0696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Alonso-Matilla R., Thiyagarajan S., O’Shaughnessy B. Sliding filament and fixed filament mechanisms contribute to ring tension in the cytokinetic contractile ring. Cytoskeleton. 2019;76:611–625. doi: 10.1002/cm.21558. [DOI] [PubMed] [Google Scholar]
- 34.Mcdargh Z., Wang S., et al. O’shaughnessy B. Myosins generate contractile force and maintain organization in the cytokinetic contractile ring. bioRxiv. 2021 doi: 10.1101/2021.05.02.442363. Preprint at. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.