Collective Variables for Crystallization Simulations—from Early Developments to Recent Advances

Abstract

Crystallization is an important physicochemical process which has relevance in material science, biology, and the environment. Decades of experimental and theoretical efforts have been made to understand this fundamental symmetry-breaking transition. While experiments provide equilibrium structures and shapes of crystals, they are limited to unraveling how molecules aggregate to form crystal nuclei that subsequently transform into bulk crystals. Computer simulations, mainly molecular dynamics (MD), can provide such microscopic details during the early stage of a crystallization event. Crystallization is a rare event that takes place in time scales much longer than a typical equilibrium MD simulation can sample. This inadequate sampling of the MD method can be easily circumvented by the use of enhanced sampling (ES) simulations. In most of the ES methods, the fluctuations of a system’s slow degrees of freedom, called collective variables (CVs), are enhanced by applying a bias potential. This transforms the system from one state to the other within a short time scale. The most crucial part of such CV-based ES methods is to find suitable CVs, which often needs intuition and several trial-and-error optimization steps. Over the years, a plethora of CVs has been developed and applied in the study of crystallization. In this review, we provide a brief overview of CVs that have been developed and used in ES simulations to study crystallization from melt or solution. These CVs can be categorized mainly into four types: (i) spherical particle-based, (ii) molecular template-based, (iii) physical property-based, and (iv) CVs obtained from dimensionality reduction techniques. We present the context-based evolution of CVs, discuss the current challenges, and propose future directions to further develop effective CVs for the study of crystallization of complex systems.

1. Introduction

Understanding phase transition using computer simulations has been a prime focus of the simulators—starting from the early method developers to the current community. Alongside the enrichment of our fundamental understanding of the symmetry-breaking transition from a nonsymmetric liquid state to a symmetric crystalline phase, this process is of great interest and bears relevance to the pharmaceutical industry as well as the environment. Investigation of the crystallization mechanism, optimizing crystallization conditions, predicting crystal shape, and obtaining thermodynamics and kinetics of crystal growth/dissolution processes require significant time investment as well as monetary resources.

Computer simulations, especially the molecular dynamics (MD) methods, have been probably the most convenient way to delineate microscopic details of the early stage of the crystallization process and calculate the thermodynamics and kinetics of the process. Unfortunately, in the context of computer simulations, crystallization is a rare event that, in most cases, takes place in a time scale ranging from milliseconds to seconds. The brute-force MD simulations are limited by short time scales in the range of nano- to microseconds that are inadequate to study crystallization. To circumvent this issue, several enhanced sampling (ES) simulation methods have been developed over the years.¹⁻¹⁶ The central aspect of most of these methods (collective variable-based, discussed later) is to define one or more variables that are functions of atomic coordinates and describe the system’s slow degrees of freedom. These variables are called collective variables (CVs) or order parameters (OPs). (Note that there are subtle differences between these two nomenclatures. A CV is defined as a function of atom coordinates, while an OP is a special type of CV which distinguishes between a system’s states.)¹⁷ In ES simulations, the fluctuations of these CVs are enhanced to sample the metastable states. In the context of crystallization, the CVs are designed such a way that they can distinguish between the particles in the crystal and liquid or dispersed in solution phases.

The CVs that are routinely used in crystallization simulations can be majorly divided into four categories: (i) spherical particle-based CVs such as the most popular Steinhardt parameters that are useful in simulating spherical particles (atomic, metallic, and colloids systems); (ii) molecular CVs (template-based, root-mean-square deviation-based, local crystallinity) that are used to crystallize molecular systems in predefined structures; (iii) physical property-based CVs such as volume/density, pair correlation functions, structure factor and X-ray diffraction peaks, and entropy-enthalpy; and (iv) CVs that are derived from linear and nonlinear (machine learning) dimensionality reduction of basic OPs (distance, coordination number, angles, etc.).

In this review, we provide a systematic overview of the CVs that are used specifically in ES simulations of crystallization. We might have missed many other important developments including those CVs that are used as classifiers (fingerprints) to characterize disordered and various crystal polymorphs. Discussion on these topics can be found in the literature.¹⁸⁻²⁹ We conclude this review with a discussion on the current challenges and future directions in the development of efficient CVs for the study of crystallization of complex molecular systems.

2. Collective Variables (CVs)

2.1. Spherical-Particle-Based

2.1.1. Steinhardt Parameters

In 1983, Steinhardt et al. proposed bond-orientational order parameters (OPs) to characterize and distinguish between solid and liquid states.³⁰ These OPs identify the system’s states by measuring the symmetries of the clusters formed during simulation. In their approach, a central atom i is considered which forms “virtual bonds” with its neighbors that are found within the radial distance of 1.2r₀ around i, where r₀ is the minimum distance in the Lennard-Jones (LJ) potential. Here these virtual bonds do not imply any chemical bonds, rather they are imaginary lines that connect the central atom with its neighbors. The atoms’ connectivity is defined by spherical harmonic function, and the OP, q̅_lm(r⃗) for particle i is defined by taking an average of these spherical harmonics over a suitable set of neighbors around the particle i,

1

Here N_b(i) is number of virtual bonds of particles i with its neighbors, Y_lm(θ, ϕ) are the spherical harmonics, and θ(r_ij) and ϕ(r_ij) are polar angles made by bonds with respect to some reference coordinate system. The value of Y_lm(θ, ϕ) depends upon two integers l and m and for a given value of l there are 2l + 1 values of m. Hence, q_lm(i) will have different values for a particular value of l. Therefore, a particular structure will have different values of q_lm(i) for a particular value of m for a given l. Therefore, rotationally invariant combinations of bond order parameters are defined as

where

2

The matrix 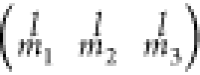is called Wigner 3j symbols. The q_lm and W_l are called as quadratic and third order invariants, respectively. Figure 1 shows the histogram of q_lm and W_l for five clusters at l = 2, 4, 6, 8, 10. Nonzero averages appear at l ≥ 4 for clusters having hcp and cubic symmetry. For icosahedral clusters, nonzero averages occur at l = 6. All the values are calculated for clusters corresponding to the unit cell.

Figure 1.

Histogram of q_lm and W_l for 13 atom icosahedral, fcc, and hcp clusters, as well for 15 atom bcc and 7 atom sc cluster. Figure reproduced from ref (30) with permission. Copyright 1983 APS.

In 1996, ten Wolde et al.³¹ studied the crystallization of the LJ system using MD simulations. They computed nucleation barrier, and nucleation rate and identified precritical, critical, and postcritical nuclei for the LJ system. They calculated the free energy surface for nucleation by using the umbrella sampling method.² In order to calculate the nucleation barrier, they defined an OP (reaction coordinate) which measures the degree of crystallinity of a system during phase transition. They found that the local OPs introduced by Steinhardt (eq 1) have almost the same values in both solid and liquid phases. Therefore, they introduced the global Steinhardt parameter q₆ which vanishes in liquid and has high values in the crystalline phase. The generalized global orientational OP, q_lm is defined as

3

In q̅_lm, the average is taken over all N particles present in the system. The values of global orientational OPs for different crystal systems can be seen in the Table 1,

Table 1. Global Orientational Order Parameters for fcc, hcp, bcc, sc, and Icosahedral Structures^a.

	Q4	Q6	Ŵ4	Ŵ6
fcc	0.191	0.575	–0.159	–0.013
hcp	0.097	0.485	0.134	–0.012
bcc	0.036	0.511	0.159	0.013
sc	0.764	0.354	0.159	0.013
icosahedral	0	0.663	0	–0.170
liquid	0	0	0	0

^aData taken from ref (31).

Subsequently, ten Wolde, Frenkel, and co-workers³² introduced the scalar product of the normalized bond orientational vectors, q_lm(i) and q_lm(j) between neighboring particles i and j, used to differentiate between solid and liquid clusters as described below:

4

Here, q_lm(j)* is the complex conjugate of q_lm(j), and q_lm(i)·q_lm(i) is equal to 1. Two neighbors, i and j are connected if the dot product is greater than a threshold, say 0.5. According to this criterion all particles in solid state are found to be connected to each other. However, this is not a sufficient condition to call a cluster as solid-like or liquid-like because the liquid-like cluster can also be connected frequently because of the presence of local order in liquids. Therefore, an additional condition has been included that if the number of “connections” are above some threshold, say 6 or 8 then the particles are solid-like, and if less, then they are liquid-like. Using this criterion, the solid-like particles can be distinguished from the liquid-like particles as the former will have more number of connections (coordination) than the latter. Distribution of number of connections per particle in LJ system for liquid, bcc, and fcc structures is shown in Figure 2.

Figure 2.

Distribution of number of connections per particles for liquid, bcc, and fcc structure. Figure reprinted from ref (31) with permission. Copyright 1996 AIP.

The approach of Steinhardt, ten Wolde, Frenkel, and co-workers has been further extended by Eslami et al.³³ who have defined a local OP as follows,

5

The q_l(i) OP includes contributions from the first and second coordination shell neighbors of the particle i averaged over all its neighbors.

Lenchner and Dellago proposed a variant of the Steinhardt OPs which is more accurate to determine specific crystal structures.³⁴ They introduced the OPs that are obtained by averaging the bond orientation orders over all neighbors,

6

where q̅_lm(i) is defined as

7

where the index k goes from 0 to all N_b(i) neighbors of i including itself. The advantages of this definition are that these OPs are not restricted to including only the first coordination shell but they can take into account the second shell neighbors, and the solidlike and liquidlike particles can be distinguished better due to the decreased overlap between the OPs distributions belonging to the two states.

They have calculated the mean of the probability distributions of q̅₄ and q̅₆ for fcc, bcc, and hcp crystals in undercooled liquid in which particles are interacting via LJ and Gaussian potential (Tables 2 and 3). Due to the averaging procedure, the OPs distributions get narrower, which reduces the overlap between different phases (Figure 3) and a clear distinction between different phases is obtained. However, even in the averaged OPs, the bcc and liquid phases are not well-separated. This issue can be solved by considering a two-dimensional (q4 – q6) space with two bond OPs.

Table 2. Global Orientational Order Parameters for fcc, hcp, bcc, sc, and Icosahedral Structure^a.

	q4	q̅4	q6	q̅6
bcc	0.089988	0.033406	–0.440526	0.408018
fcc	0.170880	0.158180	0.507298	0.491385
hcp	0.107923	0.084052	0.445384	0.421813
liq	0.109049	0.031246	0.360012	0.161962

^aData taken from ref (34).

Table 3. Average of the Distributions of q4, q̅4, q6, and q̅6 for the bcc, fcc, and hcp Crystals in System Interacting via Gaussian Potential^a.

	q4	q̅4	q6	q̅6
bcc	0.085581	0.031728	0.437129	0.407515
fcc	0.155336	0.134388	0.474079	0.447782
hcp	0.109723	0.073369	0.424627	0.385720
liq	0.126950	0.040297	0.375121	0.158913

^aData taken from ref (34).

Figure 3.

(a) Probability distributions of q̅₄ (solid lines) and q₄ (dashed lines) for the fcc, bcc, and hcp crystals and for the undercooled liquid (LIQ) in the Lennard-Jones system. (b) Probability distributions of q̅₆ (solid lines) and q̅₆ (dashed lines) for the same phases. Figure reprinted from ref (31) with permission. Copyright 1996 AIP.

In 2014, Tang et al. used as CVs the local and average Steinhardt OPs with or without supercell parameters included in the CVs definition to predict the polymorphism of xenon crystal at high temperature and pressure.³⁵ As expected, fcc and bcc structures were obtained when Q4 and Q6 were used as CVs (see Figure 4), and along with it, the new structures including fcc with hcp stacking faults were also obtained when the supercell parameters were included in the CVs definition.

Figure 4.

Free energy surface when only Q4 and Q6 were used as CVs. Figure reprinted from ref (34) with permission. Copyright 2008 AIP.

The structures obtained by using local and average order parameters as CV were compared (see Figure 5). The fcc structure with stacking faults shows two types of structures with the local OPs being used as CV, and the fcc structure with stacking faults was found to split into more types of structures when the average OP was used as CV.

Figure 5.

Local (q6, q4, and w4) and the average (q̅6, q̅4, and w̅4) bond OPs of various solid forms are plotted for comparison. Figure reprinted from ref (35) with permission. Copyright 2014 AIP.

Very recently, Rozanov et al. studied the phase transition of a LJ system from its metastable liquid to crystalline state using MetaD simulations.³⁶ The Q6 along with the systems potential energy (U) was used as CVs. The free energy landscape associated with this phase transformation process is shown in Figure 6.

Figure 6.

(a) Free energy landscape for the system. (b) Projection of the same landscape in the Q6-U space. Figure reprinted from ref (36) with permission. Copyright 2022 Springer.

The free energy barrier of crystallization at constant pressure obtained from the Metadynamic(MetaD) simulations is in good agreement with those obtained from experiments. This manifests the CVs effectiveness in sampling the actual nucleation process and reproducing the experimental observations.³⁶

2.2. SOAP Kernel

2.2.1. SOAP Kernel Method

A crucial property of a variable representing atomic environments is its invariance with respect to the basic symmetries like rotation, reflection, translation, and permutation of atoms. Steinhardt OPs are one of the invariants used to describe atomic environments. These parameters are useful in identification of different crystalline phases and clusters, like fcc, hcp, bcc, icosahedral nuclei. These can be used to study melting transitions, nucleation processes and interfaces in systems containing atomic, metallic and colloidal particles. But these OPs have certain limitations.³⁷ These parameters are not suitable to identify the order in molecular crystals as molecular crystals have orientational symmetry and Steinhardt parameters do not take orientation of nonspherical molecules into account. The other hurdle is about the qualitative trend of the Steinhardt OPs that is influenced by the choice of neighborhood, and due to the discrete nature of neighborhood definition, the neighborhood of a particle is not a continuous function of particles coordinates. This discontinuous nature of q_l leads to the lack of robustness of these OPs as structure metrics. Bartok et al. has shown that the descriptors like Steinhardt parameters are the special cases of some general approach in which the atomic environment is defined by neighborhood density.³⁸ This approach is called Smooth Overlap Of Atomic Positions (SOAP). In the SOAP Kernel method, each atom in a given environment is defined as the sum of Gaussian functions centered on the neighborhood of an atom and including that atom itself. These parameters fulfill the criteria of being invariant and continuous functions of atomic coordinates. The SOAP kernel and its variants have been used in many applications for identifying crystal structures and polymorphs.^39,40

2.2.2. Environment Similarity CV

Piaggi and Parrinello utilized a reduced definition of the SOAP kernel approach to design a CV, called environment similarity CV (Env-CV).⁴¹ This method is based on the local ordering of n neighbors (i) around a central atom (r) in a crystalline environment (Figure 7). As done in the SOAP kernel approach, the local density ρ_χ(r) of the central atom in a given environment χ is written as the sum of Gaussian functions,

8

where r_i’s are the coordinates of the neighbors relative to the central atom, and σ² is the variance of the Gaussian functions. The n nearest neighbors positions {r_j⁰} of the central atom in a reference crystal environment (χ₀) are chosen. The difference between the two environments χ and χ₀ is obtained from the following integral,

9

where ρ_χ0(r) is the local density of the atom in the reference crystal environment (χ₀).

Figure 7.

(a) The particles positions with respect to a central atom (black sphere) in the reference crystal environment χ₀ and in an instantaneous configuration χ are shown in gray and orange spheres, respectively. The configuration was extracted from a trajectory of bcc sodium simulated at T = 300 K and P = 1 bar. (b) Distributions of the kernel k̅_χ0(χ) (eq 11)) for the liquid (blue) and bcc (orange) sodium at 375 K and 1 atm pressure. Figure reprinted from ref (41) with permission. Copyright 2019 AIP.

Unlike in the SOAP’s actual definition,³⁸ in this approach, only the spatial part has been considered. This results in a simple analytical expression of the CV in the form of a kernel function, k_χ0(χ) which can be calculated efficiently.

10

The kernel function in eq 10 is then normalized such that similarities between identical environments k̅_χ0(χ₀) are equal to one.

11

In a system of N particles, for each particle (i = 1, .., N) the kernel function, k̅_χ0(χ_i) is calculated using eq 11. The particles having k̅_χ0(χ_i) > k₀, where k₀ = 0.5, are classified as crystalline or liquid by a continuous and differentiable switching function (s_i) as follows,

12

The variable s_i has values in the range from 0 to 1, for atoms in the solution s_i ≈ 0, while those in a perfect crystalline environment, s_i ≈ 1 (Figure 7(b)). The parameters p and q control the steepness and the range of the switching function. The kernel function defined in eq 10 is in the similar spirit as that of the local metric order by Martelli, Car, and co-workers.⁴²

The Env-CV has been successfully used in the study of the phase diagram of sodium and aluminum using a multithermal–multibaric enhanced sampling simulation approach.⁴¹ The nonrotationally invariant nature of the CV facilitates the crystallization of a defect-free crystal. Niu et al. extended the application of this CV to calculate the phase diagram of gallium modeled using a DeepNN potential.⁴³ Recently, Piaggi et al. used the Env-CV to study the molecular system, in particular, ice nucleation from water modeled using a deep learning based potential model. The Env-CV’s use was not restricted to single-component systems crystallizations. Karmakar et al. used this CV to nucleate NaCl from its supersaturated aqueous solution using a combination of MetaD and constant chemical potential MD approaches.⁴⁴

2.3. Molecular Ordering

2.3.1. A Generalized Set of OPs

For highly symmetric systems consisting of atoms or spherical particles (colloids), Steinhardt bond OPs are found effective. However, for complex low symmetric systems extending such OPs is very difficult to execute.

To define OPs for complex crystals, preliminary information can be generated from a normal unbiased MD simulation of the crystal. An OP to define complex crystallization is to take advantage of the structural properties of the given crystal or consider the atomic coordinates relevant to a specific molecular arrangement in a crystal. A new method to design an OP to study complex crystal systems is presented here.⁴⁵

To build OPs for molecular crystals, a generalized pair correlation function consisting of all relevant variables that represent the crystal structure is introduced by Santiso et al.⁴⁶ Before moving ahead with pair correlation functions, it is important to understand the idea of point molecule representation (Figure 8). In point molecule representation, the crystal system is reduced to defining (i) position (the center of mass of each molecule in the crystal), (ii) absolute orientation (containing a set of molecule-centered coordinate axes), and (iii) internal degrees of freedom (define the internal structure of the original molecule). The OPs are then defined as the product of the probability density functions f as

13

where r is the distance between the center of mass of two molecules, r̂ is the bond orientation, and the relative orientation of first molecule with respect to the second molecule is represented by q, and ψ′ is the relative internal degrees of freedom with respect to ψ (the internal degrees of freedom for the first molecule). Now, we can define the pair distribution function as the probability that a molecule has internal degrees of freedom between ψ and ψ + dψ with a neighbor with internal degrees of freedom between ψ′ and ψ′ + dψ′, relative orientation between q and q + dq at a position between r and r + dr with respect to the first molecule. The values r, q, ψ, and ψ′ uniquely represent the peaks in the pair distribution function and define the crystal structure. In order to define an OP, there is a need to choose models for each function appearing in the probability density function, G(r, q, ψ, ψ′) in eq 13 (Figure 8(b)). Parameters are estimated for the models using an unbiased simulation. The distribution of distance between center of mass of the molecules, f_α^r(r) is approximated using a Gaussian function,

14

where σ_α is the standard deviation, α is the peak corresponding to the mean center of mass distance r_α. For each of the peaks in the pair distribution function, the distribution of bond orientation, f_α^(r̂)(r̂) is approximated using the Fisher distribution,

15

where κ_α is the concentration parameter, and α is the peak corresponding to the mean bond orientation r_α̂. For the relative orientation distribution, f_α^q(q), 4D Bingham distribution can be used, as the orientation vectors are directionless on a 4D unit sphere. However, whatever studies have been done so far, bipolar Watson distribution can be a good approximation around each peak in the pair distribution function G(r, q, ψ, ψ^′):

16

where ξ_α is the concentration parameter, qα is the mean relative orientation, ₁F₁(1/2, 2, x)) is the confluent hypergeometric function, and the 4D dot product is denoted by the ‘·’ symbol. Finally, the accurate model for the internal degrees of freedom is chosen on a case by case basis. When describing a crystal structure, the internal degrees of freedom that are considered are atom distances, angles, and dihedrals. For distance between two atoms, a Gaussian distribution model is used, and for angles and dihedrals, the von Mises distribution is generally used.

17

where i is the central molecule, and r_ij is the center-of-mass separation between molecule i and its neighbors, j. Similar to this, one can define OPs that consider both bond distances and bond orientations,

18

where r̂_ij represents the bond orientation vector projected onto the frame with the molecule i at its center. Additional order criteria that are sensitive to relative orientations of molecules include

19

where, ₁F₁(1/2,2,ξ_α) is the confluent hypergeometric function, q_α is the relative orientation, ξ_α is a concentration parameter, and ‘·’ indicates a 4D dot product. Likewise, OPs that take into account a molecule’s internal configuration can be defined.

Figure 8.

(a) A “point molecule” representation of glycine: r is the center of mass (COM) of the molecule, q (quaternion) indicates the absolute orientation of the molecule in the reference coordinate frame (bottom left), ψ is the (N–C–C–O) dihedral angle. (b) Construction of the pair distribution function: r is the distance vector along the COM–COM positions of the two glycine molecules projected on the first molecular coordinate frame q₁, and ψ₁ and ψ₂ are the internal degrees of freedom that are included in the pair distribution function’s definition, eq 13. Figure reprinted from ref (46) with permission. Copyright 2011 Springer.

The “local” or per-molecule and per-peak, OPs mentioned above can be used to quantify which molecule initiates the process of ordering as well as its extent. However, it is impractical for use in complex system, instead, a “global” OP obtained by adding up either or both of the indices i and α in eqs 17–19 would be more convenient to use. The design and application of this order parameters is presented in the study of (i) crystallization of α-glycine from solution which demonstrates how to cope with a nonsymmetric molecule with adaptable internal degrees of freedom, (ii) the crystallization (nucleation)⁴⁷ of benzene from the melt, which serves as an example of how the OPs for a relatively high symmetric molecule are constructed, and (iii) solid–solid polymorph transformation of terephthalic acid.

2.3.2. Local Crystallinity Order

Giberti, Salvalaglio, and Parrinello have developed CVs based on local crystallinity order for studying molecular crystals.⁴⁸⁻⁵² The synergistic effect of local density fluctuations and molecular orientational ordering has been embedded in the CVs definition. The advantages of this CV are 2-fold: (i) It allows the system to explore the free energy surface without the prior knowledge about the global crystal symmetry, and (ii) its use can be extended to crystallization in multicomponent systems such as solution crystallization.^49,52

The global CV is defined as the sum of individual molecules crystallinity order (Γ_i) in a system containing N molecules,

20

Local density of a central i^th molecule is calculated by calculating its coordination number (CN) with respect to its neighbors, j. From the central atom, distances (r_ij) from its j neighbors within a cutoff distance, r_cut are calculated. To decide weather j^th particle will be considered as neighbor of i^th particle a switching function (Fermi), f(r_ij) is used,

The summation of f(r_ij) defines the neighbor density as

21

Another switching function, ρ_i, is defined to calculate the local density as a function of coordination number as

22

where a and b are used to tune the slope of exponential functions in the switching functions.

To calculate the orientation between molecules i and j, a function θ_ij which is a function of the angle between two molecular vectors is defined (Figure 9a). Due to the effect of temperature the orientation between molecules fluctuates around an average value (θ̅_k). Therefore, the fluctuation is expressed in terms of Gaussian functions centered around the (θ̅_k) between two molecular vectors,

23

Here k_max is the maximum number of angles that define the local molecular orientations. Based on these spatial and local molecular orientational OPs, the molecular crystallinity is defined as

24

A CV based on the total number of crystalline molecules is obtained by summing over the individual crystallinity orders,

25

In ref (50), the fraction of molecules that are in a crystalline environment has been used as a global CV,

26

Figure 9.

(a) Molecular vectors along C=O and N–N directions in a single urea molecule. (b) A representative urea crystal structure (polymorph I) extracted from well tempered metadynamics (WTMetaD) simulation trajectory in ref (50). Figure reprinted from ref (50) with permission. Copyright 2015 Elsevier.

The molecular crystallinity CV has been used in our recent studies either to characterize crystal-like molecules in a multicomponent system or to construct the bias potential in WTMetaD simulations studying crystallization from melt or solution.^49,52−54

2.3.3. Molecular RMSD

Inspired by the shape matching OP by Keys et al.⁵⁵ and the pattern matching variables by Shetty et al.,⁵⁶ Duff and Peters introduced the template based polymorph specific OP which computes root-mean-square deviation (RMSD) between a tagged crystal molecule in a simulation system and a molecular template in a perfect crystal.⁵⁷ The RMSD-based OP can audibly differentiate between different polymorphs of a crystal structure.

Though theoretically comparable to the OPs proposed by Shetty et al., this order parameter is computationally simpler. By using a template of the crystal structure and the environment of a tagged molecule in a simulation, the method calculates the desired RMSDs. For the purpose of showcasing the new technique, Peters et al. carried out the same order parameter diagnostics as Lechner and Dellago³⁴ here for molecular crystal polymorphs. They showed that their technique is capable of differentiating between the bulk crystal structures of the three glycine polymorphs without any overlap in the order parameter distributions. Additionally, in solvated glycine crystallites, the α, β, and γ glycine polymorph structures may be distinguished using the local RMSD based OPs. The approach offers a broad framework that makes it simple to design OPs for a range of molecular crystals.

The local molecular order is obtained by matching a tagged solute in the crystal and its simulated microenvironment (SME) comprising neighboring solutes to its corresponding “central” template molecule and its neighbors present in a perfect crystal (from Cambridge Crystallographic Database or a modeled equilibrium lattice structure). If the crystal has m solutes, there will be m distinct templates to build the crystal structure. If one deals with k number of crystal polymorphs, for each polymorph (k) one needs to define m_k molecular templates. Figure 10 shows the template-matching procedure.

Figure 10.

Gray and red ellipses represent molecules in the (SME) and in a crystal template, respectively. The core molecule in the template and the marked atom in the SME almost perfectly coincide after step (ii). The closest molecules in the SME are given the template molecules in step (iii). The closest of the two template molecules is preserved if two template molecules are assigned to the same SME molecule (as indicated by the dotted line). Unmatched SME molecules are also not kept if no template molecule is associated with a particular SME molecule. The unshaded template and SME molecules are “deleted” as a consequence of these criteria prior to the RMSD reduction in step (iv). Figure reprinted from ref (57) with permission. Copyright 2011 AIP.

Here we briefly mention the steps involved in the RMSD OPs development. To reduce the computational cost, the hydrogen atoms are not considered in the RMSD calculations, and the functional groups that can adopt degenerate configurations are replaced with nondegenerate surrogate functional groups. After this “molecular pruning” step, the RMSD OP calculation is initiated. The overall process has the following steps: (i) At first, a solute molecule is tagged and the solutes surrounding it within a cutoff radius are used to define the SME. (ii) This is followed by the rotation and translation of the central molecule in the crystal template to minimize the RMSD between the tagged and the central molecule. The same amount of rotation and translation is performed with the entire template. (iii) Subsequently, each molecule in the SME is matched with its nearest template molecule. (iv) Finally, all molecules in the SME are matched with the molecules in the crystal (polymorph) template. The final step’s reduced RMSD value serves as an OP for the tagged molecule that is particular to unit-cell-member and polymorph. For each member of the polymorph k unit cell, repeat steps (i–iv). Then choose the k^th polymorph’s smallest minimized RMSD value.

Both for bulk crystallites and a small crystal in solution, the RMSD OPs can differentiate between various polymorphs with clarity. The new OPs should make it possible to simulate small molecules, something that was previously only achievable for supercooled simple liquids. The template-based RMSD OP compares a collection of templates of the known polymorphs to each molecule’s local environment during simulation; however, it provides no information regarding the likelihood and stability of an unknown polymorph that might be present during simulation.

2.4. Physical-Property-Based

Recently, the use of CVs related to a system’s physical properties that can be calculated experimentally has become a preferred choice for studying crystallization using simulations. This is because, in general, the value of a particular physical property is known experimentally for all the states of a system, and it can be directly used to construct a useful CV. An important aspect of using the physical property as a CV is that it does not require prior knowledge of a system’s crystalline state. The physical properties that have been utilized to construct a CV are radial distribution functions, XRD peak intensities, entropy and enthalpy, and system’s volume (density).

2.4.1. Radial Distribution Function

Nada in 2020 proposed a method in which the radial distribution functions (RDFs) can be utilized as a CV for the formation of water polymorphs.⁵⁸ They performed MetaD simulations using two CVs defined as two discrete oxygen–oxygen RDFs represented by Gaussian window functions. Different polymorphs of ice such as cubic, stacking disorder⁵⁹ (consists of cubic and hexagonal), high pressure ice VII, layered ice with an ice VII, and layered ice with an unknown structure were identified from the MetaD simulation trajectory (Figure 11).

Figure 11.

MetaD simulation snapshots of low density water (LDW) structures and ice structures (I_c = cubic ice, I_sd = stacking disorder ice). On the right free-energy landscape is shown plotted using CV1 and CV2, where color pallet shows free energy in kJ/mol. Figure reprinted from ref (58) with permission. Copyright 2011 Nature.

2.4.2. Entropy and Enthalpy

The CVs discussed in sections 2.1 and 2.2 were constructed based on known crystal structures, and thus they are not effective in discovering other possible polymorphic phases of the crystal. Hence, there was a need to construct CVs that can sample the states without any prior knowledge of the crystal structure. Keeping this in mind, in 2017, Piaggi et al. proposed the use of enthalpy and entropy surrogates as CVs.⁴⁰ This choice was based on two simple facts: (i) “enthalpy and entropy” that do not predict any feature of the crystal structure a priori, and (ii) there is a trade-off between “enthalpy” and “entropy” during the crystallization which, in turn, describes the transitions between metastable states. Although “enthalpy” is easy to estimate, the “entropy” calculation is a nontrivial task. However, in the context of crystallization, we do not require an exact definition of entropy to bias the system; an approximate equation involving only two body correlations, derived from an expression where excess entropy per atom is expressed as an infinite series of terms involving multiparticle correlation functions suffices the need.⁶⁰

The two CVs constructed using enthalpy and entropy are defined below:

27

28

where g_m(r) is the modified version of the radial distribution function to ensure the function’s continuity.

29

where σ is the broadening parameter, r_ij is the distance between i^th and j^th particle, and ρ is the system’s density. These CVs were used to study the crystallization of Na and Al from their molten states (Figure 12).

Figure 12.

FES projected on the s_H and s_S variables for (a) Na at 350 K and (b) Al at 800 K. Figure reprinted from ref (40) with permission. Copyright 2017 AIP.

Mendels et al. in 2018, extended the applicability of these CVs to study a multicomponent system, silver iodide (AgI).⁶¹ In this work, they have predicted the existence of an α phase of AgI which is stabilized by strong entropic contributions in comparison to the enthalpically favored β phase.

Although, these CVs were successful in predicting polymorphism in atomic crystals like Na and Al, they cannot be used for molecular crystals because the molecules do not have a spherical symmetry. Hence they can have different orientations in space, and depending on the orientation, they can exist in different polymorphic forms. The above-defined CVs do not take into account these orientations and thus are less efficient in the case of molecular crystals.

To tackle this problem, in 2018 Piaggi et al. proposed the use of orientational entropy as a CV for predicting polymorphisms in molecular crystals.⁶² In this case, along with the spatial distances they included molecular orientations (s_θ).

30

where θ is the angle between two vectors v_i and v_j describing the orientation of molecules i and j.

31

In principle, at least three angles are required to define the relative orientation of a molecule in space, for example, Euler angles ϕ, θ, ψ. Hence, our function would look like g(r, ϕ, θ, ψ) which is not very convenient to work with, as this function has four variables making our simulations complicated and less efficient. So, instead of taking one CV with 4 variables, the better alternative is to take 2 CVs s_θ1 and s_θ2 defining two different relative orientations of molecules using two angles θ₁ and θ₂. To understand the behavior of g(r, θ) for liquid and solid phases we can see an example of urea at 450 K (Figure 13). Here, θ represents the direction of dipole moment in urea. From Figure 13 we can observe that the liquid exhibits some structure at very short distances, whereas, in polymorph I, a well-defined structure exists at long distances. One of the main characteristics of polymorph I revealed by g(r, θ) is that molecules have parallel and antiparallel dipole moments.

Figure 13.

g(r, θ) for the liquid and polymorph I of urea at 450 K with snapshots of system in both phases. Figure reprinted from ref (62) with permission. Copyright 2018 National Academy of Sciences.

Further, using these CVs WTMetaD simulations were performed for urea and naphthalene at 450 and 300 K, respectively. These temperatures are close to the melting temperatures of both substances. A large number of transitions to different crystal forms have been observed. To identify and classify the polymorphs formed during the simulation, a similarity finding strategy has been adopted in ref (63). and⁶⁴. between two given configurations. The distance between two g(r, θ)’s i.e., the divergence is calculated as

32

This is Kullback–Leibler divergence for non-normalized functions with a minima at g₁ = g₂.⁶⁵ As D(g₁ ∥ g₂) is not symmetric, it cannot be used as distance, hence distance is given by

33

Using hierarchical clustering and average distance between points in two clusters the trajectory of urea was analyzed and different crystalline forms and liquid form were successfully distinguished.

Amodea et al. used this entropy surrogate CV along with the potential energy CV to study the effect of cooling rate during Ni₃Al nanoparticle freezing.⁶⁶ In that work, they found that by adjusting the cooling rate of Ni₃Al nanoparticles one can stabilize an out of equilibrium polymorph, BCC DO-3 structure.

2.4.3. Information Entropy

In another work, Gobbo et al. used a CV based on the relative information entropy along with the Santiso and Trout’s pair-distribution function based CVs to study crystallization of benzene and paracetamol.⁶⁷ The point molecule representation⁴⁶ which is characterized by the position of its molecular center (r) and two orientation vectors (v₁ and v₂) has been used. The per-molecule OP is written as

34

where M is the number of peaks in the joint distribution of distances and angles, θ_α and d_α are the peak centers, and σ is the width of the Gaussian. s(r) is a switching function.

The global average of these OPs is given as

35

These CVs discussed above have some major limitations such as they are (i) not able to distinguish between different polymorphs, (ii) prone to have degeneracies (different configurations giving same value of CVs), and (iii) not able to describe more complex structures such as paracetamol. Hence to overcome these limitations, the authors of ref (67) used a similar approach of utilizing entropy based CVs as first proposed in ref (62). Here instead of using the entropy surrogate as a CV, they used its distributions to differentiate the ordered state from the disordered state taking into account the long-range correlations which can give better resolution of the states. To construct the CV, relevant quantities can be selected and the relative probability density p is built on-the-fly and compared with the suitable reference distribution, q. The relative entropy is calculated using the Kullback–Leibler divergence (KLD) method,⁶⁸

36

From the above equation it is clear that the value of KLD can only be positive, and it is zero only when q(x) = p(x). The probability density (p(x)) is given by

37

where the sum runs over all elements, g is the normalized Gaussian function, and w is the weights. To avoid numerical instability due to very small values of p, eq 36 is modified as follows,

38

Kernel density estimate (KDE)⁶⁹ must be evaluated on a grid to compute integrals numerically. Hence the OP takes the final form as

39

m runs over all the grid points and dS is the measure of the volume element associated with every grid point.

Using this approach, one can construct CVs of increasing complexity that can help understand the crystallization of molecular systems. In ref (67), the authors have constructed a CV, KL^r̂ where a set of distance vectors between centers of molecules is considered. For every normalized distance vector, an azimuthal angle (θ) and a dihedral angle (ϕ) are calculated. The value of the CV, KL^r̂ is calculated using eq 39 using uniform distribution as the reference distribution, q.

For benzene, a good separation between the liquid and crystal states was observed, and additionally, another ordered structure C₂ (possibly a polymorph) was observed as well. MetaD simulations gave two different pathways of form I crystal formation when the KL^r̂ CV was used alone or used together with the pair-function based CV (Γ^rv). In the first pathway, orientational ordering is followed by form I crystal formation, whereas, in the second pathway, positional ordering is followed by transition to form I crystal.

In the case of paracetamol, when both CVs, KL^r̂ and Γ^rv, were biased, the system efficiently sampled multiple ordered and disordered states (Figure 14). A few of the ordered states resemble the form I crystal of paracetamol; however, the obtained structures showed defects and unmatched lattice parameters.

Figure 14.

MetaD simulation of the paracetamol system obtained biasing both KL^r̂ and Γ^rv. Figure reprinted from ref (67) with permission. Copyright 2018 ACS.

So to further improve the results, the authors constructed OPs using only KLD framework because use of pair-function OPs was not able to define the complexity of paracetamol molecules. To compensate orientational contribution which was previously described by pair-function OPs, new KLD based OPs were constructed using orientational vectors of molecules namely KL_c^v₁ and KL_c. Instead of using them separately which will increase computational cost due to multidimensionality, they were combined to give one OP given as KL_c^v₁,v₂ = (KL_c + KL_c^v₂)/2. To incorporate the effect of hydrogen bonding during form I crystal formation, KL_c was modified as KL_c^{r̂,r̂_OO,r̂_ON} = (KL_c + KL_c^r̂_OO + KL_c)/3. Where the last two terms take care of hydrogen bonds formed from I crystal according to Figure 15. In the metadynamics simulation it was observed that the nucleation event starts around 20 ns with the formation of dimers, after this the system rapidly orders to form a full crystal in 60 ns simulation (Figure 16. After analysis it was observed that KL_c^r̂_OO and KL_c) were the slowest evolving OPs which tells that hydrogen-bond formation is the rate-determining step in this nucleation process. Once the hydrogen bonds are formed in proper direction and orientation, it stabilizes the complex leading to drive the nucleation mechanism forward. Despite success of these CVs, no hydrogen bonds were found to be present in the dimeric species formed at first in the nucleation mechanism and left this mechanism unclear which leaves room for further research to understand the complexity of nucleation mechanism.

Figure 15.

Example of the two unique hydrogen bonds between molecules in the form 1 crystal. Figure reprinted from ref (67) with permission. Copyright 2018 ACS.

Figure 16.

Nucleation trajectory obtained from a multiple walkers metadynamics simulation biasing the positional and orientational OPs, KL_c^{r̂,r̂_OO,r̂_ON} and KL_c. Figure reprinted from ref (67) with permission. Copyright 2018 ACS.

In 2020, Song et al. used the concept of Shannon information entropy based CVs to predict polymorphism in 1:1 cocrystal of resorcinol and urea using adiabatic free energy dynamics (AFED).⁷⁰

2.4.4. Structure Factor and XRD

Recently, Invernizzi and Niu used the concepts of structure factor and X-ray diffraction (XRD-peaks), respectively, to design suitable CVs for the enhanced sampling simulation of crystallization.^71,72 One of the most important properties of a crystal is its X-ray diffraction pattern which is easily obtained from experiments. In an XRD experiment, the scattering intensity is derived as a function of scattering vectors as follows

40

where, R_i and R_j are the positions of i^th and j^th particle, f(Q) is a function of magnitude of scattering vector (Q) known as the scattering form factor.

In ref (72), the spherically averaged Debye scattering function has been used as a CV,

41

where R_ij is the distance between the atoms i and j. A window function W(R_ij)^73–74 is used to define a soft cutoff R_c for R_ij to avoid numerical instability while dealing with a finite-size system.

In general, it is obvious to choose low-theta high intensity peaks as CVs as they provide long-range crystalline order. Ramakrishnan-Yussouff theory of crystallization also suggests to use highest peak of the structure factor as freezing order parameter.⁷⁵Figure 17 shows XRD patterns for β-cristobalite silica which shows most intense peak at {111} and {022} and the liquid silica where the peaks loose sharp features. The two CVs, s₁ and s₂ were therefore defined as follows,

42

43

Using these CVs, the FES for silica crystallization was obtained. Successful implementation of the XRD peak as CV has opened a new and better class of CVs which can be used for studying crystallization without any prior knowledge of the crystalline structure. Further to this development, Bonati et al. used the local structure factor as a CV to study the nucleation of silicon from its melt using a deep neural network potential for Si.⁷⁶

Figure 17.

Simulated XRD patterns for β-cristobalite and liquid silica at 2,400 K with system containing 1536 atoms. Figure reprinted from ref (72) with permission. Copyright 2018 National Academy of Sciences.

The Debye formula has been modified into individual atomic contributions,

44

Here, every atom is assigned to its own structure factor S_i(q) (Figure 18) defined as

45

where the sum is over all N_n neighbors of atom i which are in a cutoff distance of r_c.

Figure 18.

Distribution of the local structure factor S_i(q₁) in the liquid and the solid phase. Figure reprinted from ref (76) with permission. Copyright 2018 APS.

In another work by Niu et al. in 2019, both XRD peak intensities and surrogate of translational entropy were used to study ice nucleation from water and their temperature dependence.⁷⁷

In their work, the CV based on scattering peak intensities was constructed using a linear combination of seven descriptors

46

Here the first three peaks have high intensity, next two correspond to intensities of two main peaks of one single honeycomb bilayer which is projected into the XY plane, and the last two are the first main peak of the layers that are vertical to the honeycomb bilayer in a x–z and y–z plane, respectively. α, β, and γ are the weights for corresponding descriptors which have the values 2, 1, and 1, respectively, in this work.

The use of XRD peaks as CVs has gained popularity in recent times for the investigation of crystallization processes. There are many articles published recently where XRD peaks have been utilized as CVs.⁷⁸⁻⁸² In 2021, Ahlawat et al. used XRD peaks as CVs to study phase transitions in methylammonium lead iodide (MAPbI₃) and formamidinium lead iodide (FAPbI₃).⁸⁰ They also found a low temperature crystallization pathway for the α-FAPbI₃. In another work by Deng et al. 1^st and 2^nd XRD peak intensities were chosen as CVs to study crystallization of silica using enhanced sampling method and further combined with machine learning method to find out the relationship of structure and mechanical properties of silica.⁷⁹ In 2021, Lodesani et al. also utilized these CVs to study the crystallization path of lithium disilicate through metadynamics simulations where they modified eq 41 to take only silicon atoms to calculate XRD peak intensities for the purpose of reducing computational cost.⁸¹ In another recent work, they used XRD peak intensity based CVs to study thermodynamics of silica crystallization into β-cristobalite.⁸²

2.4.5. Coordination Number and Volume as CVs

More recently, Badin et al. studied pressure induced B1–B2 phase transition in NaCl using metadynamics where they used coordination number (CN) and volume (V) as 2D collective variables.⁸³ The choice of CN as CV was motivated by the generic rule of high pressure chemistry which states that pressure induced transitions are accompanied by an increase of CN in the first coordination sphere. Also there is a significant change in the volume of the system during the pressure induced structural transition. In pressure induced phase transitions, it was a smart choice to utilize very basic properties, i.e., CN and V as the CVs to study the B1–B2 transitions in NaCl which is accompanied by transfer of ions from the second to the first coordination shell. The average coordination number between Na⁺ and Cl^– is calculated using the following switching function

47

where r_ij is the distance between i^th cation and j^th anion and N is the total number of ions. d₀ and r₀ are the parameters of the switching function which can be chosen according to the need. Using these, CVs free energy surface was obtained for the B1–B2 transition of NaCl crystal (Figure 19).

Figure 19.

FES from 100 ns MetaD simulation of a 512-atom system (NaCl), using CN and V as CVs, at T = 300 K and P = 20 GPa. Figure reprinted from ref (83) with permission. Copyright 2021 APS.

2.5. Dimensionality Reduction Based

In the previous sections, we presented a large number of CVs that have been developed and used to carry out crystallization simulations. While they are effective on their own merits, for practical use, in enhanced sampling simulations, only a small number of such CVs can be used. However, as Russo and Tanaka⁸⁴ pointed out, crystallization involves the ordering of multiple OPs, and to study such a process, one needs to deal with a large number of CVs/OPs. To alleviate this problem, various dimensionality reduction techniques have been used that condense a large number of CVs into one or two-dimensional ones. Here we briefly discuss some of those dimensionality methods that have been used to design CVs for crystallization simulations.

2.5.1. Harmonic Linear Discriminant Analysis (HLDA)

Mendels et al. developed a method, Harmonic Linear Discriminant Analysis (HLDA) to find CVs from a set of descriptors d(R) collected from metastable states of a system. In general to construct HLDA CVs, a set of descriptors d(R) is calculated from unbiased simulations of a system’s metastable phases. Subsequently, the averages and variances are used to define the ‘between class’ (S_b = (μ_A – μ_B)(μ_A – μ_B)^T) and ‘within class’ (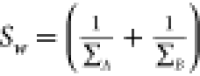) matrices, respectively. The highest separation between the two states is obtained by maximizing the Fischer’s ratio, 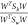, with respect to an N_d-dimensional projection vector, W. The value of W* that maximizes the Fischer’s ratio is obtained as,

48

Finally, the HLDA CV is obtained as,

49

This method has been applied in the study chemical reaction⁸⁵ and folding of a mini-protein.⁸⁶ Recently, Zhang et al. used this approach to find out suitable CVs for crystallization of Na and Al from their molten states.⁷⁸ They have used a set of high intense XRD peaks (see eq 41) of crystalline Na (d₁ = Ĩ⁰¹¹, d₂ = Ĩ⁰⁰², d₃ = Ĩ¹¹², and d₄ = Ĩ⁰²²) and Al (d₁ = Ĩ¹¹¹, d₂ = Ĩ⁰⁰², d₃ = Ĩ⁰²², and d₄ = Ĩ¹¹³) as descriptors to derive the HLDA CVs. Two sets of WTMetaD simulations were carried out: in the first, a single peak of the XRD was biased, and in the second set, the HLDA CV, s^H. From Figure 20, it is clear that the HLDA CV, s^H, outperforms the single peak-based CV in sampling the solid and liquid states.

Figure 20.

A comparison among three CV profiles: (a) XRD intensity CV s⁰¹¹ for Na, (b) HLDA CV s^H, (c) VAC CV s^V for Na. Figure reprinted from ref (78) with permission. Copyright 2019 AIP.

2.5.2. Time-lagged Independent Component Analysis (TICA) and Variational Approach to Conformational Dynamics (VAC)

The time-lagged independent component analysis (TICA) linearly combines a set of input descriptors, d_k(R_t), k = 1···N_d to construct a CV as, s_i(R) = ∑_k = 1^N_db_ikd_k. The TICA variant developed by Pande and Noè provides a way to optimally choose the expansion coefficients, b_i by solving the eigenvalue problem,

50

where C̃(0) is the covariance matrix at time 0, and C̃(τ) is the time lagged covariance matrix obtained as C_mn(τ) = ⟨r_m(0),r_n(τ)⟩ where r_k(τ) = d_k(τ) – d_k. λ_i is the i^th eigenvalue. The eigenvalues are arranged in descending order, and the eigenvector having the largest eigenvalue corresponding to the slowest degree of freedom is used as a CV.

Usually, TICA components are obtained from a long unbiased simulation in which the system visits metastable states multiple times as done in refs (87−89). McCarty and Parrinello⁹⁰ showed that a WTMetaD (biased) trajectory in which frequent transitions between the system’s metastable states are obtained can also be used to obtain the TICA components. However, in the latter case, one has to obtain the scaled time from the biased simulation time,

51

Zhang et al.⁷⁸ used this idea to develop a VAC CV, s^V, which was based on the linear combination of a selected set of XRD peaks, I⁰¹¹, I⁰⁰², I¹¹², and I⁰²². Both HLDA CV, s^H, and the VAC CV, s^V, exhibited improved efficiency compared to that of the single XRD peak-based CV, s⁰¹¹ (Figure 20).

2.5.3. Spectral Gap Optimization of Order Parameters (SGOOP)

Tiwary and co-workers used the spectral gap optimization of order parameters (SGOOP) approach to construct an one-dimensional reaction coordinate (RC) to study nucleation of urea crystals.⁹¹ In SGOOP,⁹² at first, a short MetaD simulation is performed by taking a trial CV (f = c₁ψ₁ + c₂ψ₂ + ... + c_dψ_d) to estimate the stationary density. Postprocessing optimization is performed in the space of mixing coefficients (c₁, c₂, ..., c_d) to find out the best CVs with maximum spectral gap.

In ref (91), to study urea nucleation, the RC has been defined as a linear combination of six different OPs, entropy (S), enthalpy(H), coordination number, averaged angles 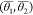, and pair orientational entropy (S_θ1, S_θ2).

52

It is clear from the coefficients of the RC defined in eq 52 that the pair orientational entropy (S_θ1,S_θ2), specifically S_θ1, has maximum weight to the RC indicating its dominant role in nucleation events. The CV profile obtained from the WTMetaD simulations with the SGOOP 1d-RC shows multiple transitions of the system to various metastable states (Figure 21(a)). These states correspond to different polymorphs of urea. The calculated FE profile (Figure 21(b)) indicates greater stability of polymorph I than the polymorph-IV which is in agreement with the experiments.

Figure 21.

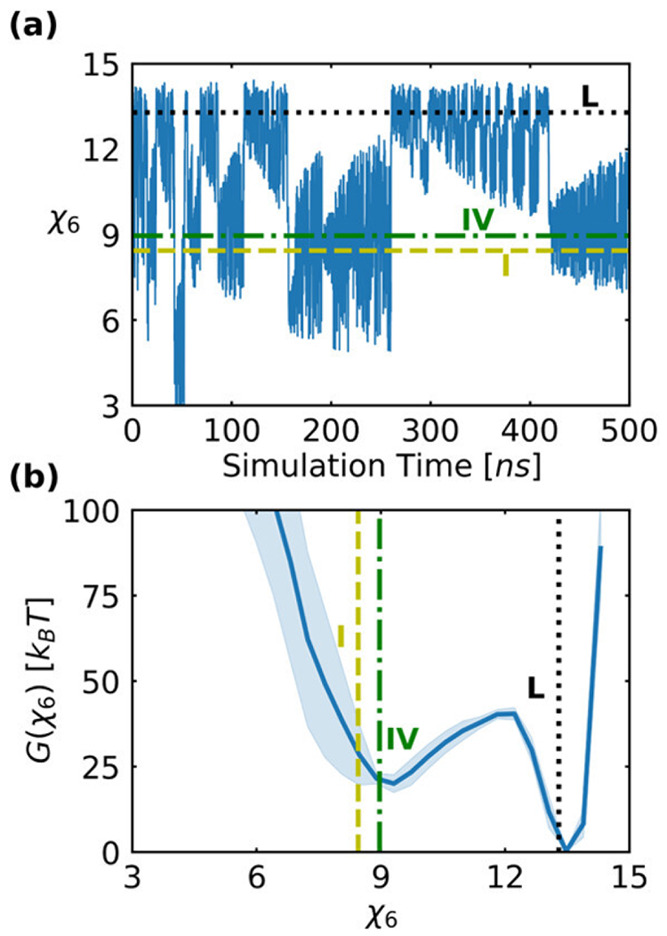
(a) Evolution of χ₆ profile with time, (b) reweighted free energy profile of WTMetaD. Polymorph I (in yellow) and IV (in green) in (a,b) figure. Multiple transitions are visible from Polymorph I to IV. Error bar is shown in shaded blue color. Figure reprinted from ref (91) with permission. Copyright 2021 ACS.

2.5.4. Neural-Network-Based Path Collective Variable (NN-PCV)

Rogal et al.⁹³ have used Behler-Parrinello symmetry functions^94,95 and Steinhardt parameters (Q_l, l = 6, 7, 8, see section 2.1.1) as input descriptors for a feed-forward NN to obtain per-atom CVs (q_i^α) corresponding to a particular crystal structure (α = A15, fcc, bcc, hcp, disordered structure). Subsequently, these atomic CVs were used to define the global CVs as Q^bcc = (1/N)∑_i = 1q_i^α. Finally, the path CV between two states, say A15 and bcc is defined as,

53

where Q(r) is a point on the two-dimensional {Q^A15, Q^bcc} space, Q_k, k = 1··· P are the nodal points along the path of transformation from A15 to bcc states, |Q(r) – Q_k(r)|² is the square distance, and λ is a parameter. Starting from the A15 phase, the value of the Path-CV increases from 0 to 1 reaching the bcc phase. Another Path-CV, z(Q(r)) perpendicular to f(Q(r)), is defined to measure the distance from the path of transformation. One can use z(Q(r)) either to construct bias or as a restraint potential. This Path-CV was then used in d-AFED/TAMD and MetaD simulations to enhance the phase transition between the A15 to bcc phases of molybdenum and calculate the associated free energy profile (not shown, Figure 22).

Figure 22.

Path-CV, f(Q(r)) as a function of d-AFED (top) and MetaD (bottom) simulation time. The red and blue spheres indicate Mo atoms in bcc and A15 phases, respectively. Figure reprinted from ref (93) with permission. Copyright 2019 AIP.

2.5.5. Deep-LDA

So far we have discussed a few methods that are used to linearly combine a set of descriptors to construct low dimensional CVs. Recently, a few nonlinear methods based on deep learning have been developed and used in the context of crystallization. Deep-LDA developed by Bonati et al. is one such method in which a deep NN is appended with a LDA layer in the penultimate step of the dimension reduction setup.⁹⁶

In the LDA method, one uses N_d number of descriptors, d(R) which are the functions of atom coordinates and calculate ‘within class’, , and ‘between class, S_b = ((d_S – d_L)(d_S – d_L)^T matrices. Here in the context of crystallization, the subscript S and L refer to the “Solid” and “Liquid” states, respectively. The maximum separation between the two states is obtained by maximizing the Fisher’s ratio, 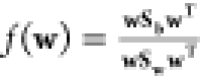. The value of the projection vector, w* that maximizes f(w) is obtained from the generalized eigenvalue problem, S_bw_i = ν_iS_ww_i. The LDA CV finally takes the form, s = w*^Td(R).

In the Deep-LDA method, the d(R) are fed to a feed-forward deep NN which results in an N_h dimension output h (hidden layer). The ‘within class’ and ‘between class’ matrices of dimension N_h × N_h are then calculated in the h basis. The eigenvalue of the lowest eigenvector from the Fisher’s generalized equation is used as the loss function to optimize the NN weights. Finally, the deep-LDA CV is obtained as, s = w^Th.

The efficiency of a Deep-LDA CV depends on the quality of the input descriptors. As common descriptors, one can use atom coordinates, distances, and coordination numbers. However, most of these order parameters are localized and include short-range orders. To study crystallization which involves long-range ordering of molecules in a periodic lattice, Karmakar et al.⁹⁷ used the square root of the three-dimensional structure factor peaks as input descriptors for Deep-LDA.

54

where k is the 3D scattering vector, and R_i, i = 1··· N, is N atoms coordinates. An appropriate choice of the k vectors results in the formation of a particular crystal lattice. The CV by its construction is not rotationally invariant; however, this feature favors the growth of the crystal aligned with the MD box.

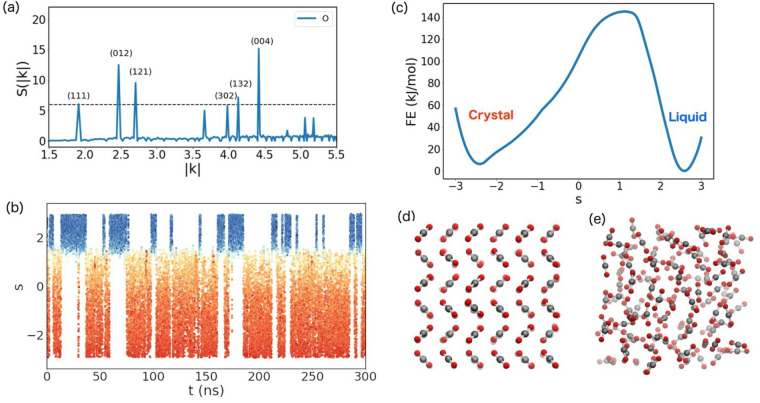
This approach has been applied in study of NaCl and CO₂ crystallization from their molten/fluid phase. In particular, for the case of CO₂, the s(k) peaks with Miller indices, (111), (012), (121), (302), (132), and (004) were used to describe the input descriptors (eq 54). The Deep-LDA CV was used in the OPES simulations to study the phase transitions.

A large number reversible transitions between the solid to liquid phase is clearly visible from Figure 23(b) manifesting the effectiveness of the Deep-LDA CV. Similar sampling efficiency has been observed in the case of NaCl crystallization (figure not shown). In both cases, the Deep-LDA-based CVs gave better separation among the different states than in the single peak-based CVs. Deep-LDA based CVs give new route to efficient study of crystallization and find out the stability of crystal phase relative to its liquid phase.

Figure 23.

(a) S(k) plot of CO₂ crystal is shown with respective Miller indices. (b) The evolution of CVs profile with time obtained from OPES MetaD. The color is based on value of the Miller index (111) which is the first descriptor of Deep-LDA. Red color represents the crystal, and blue color represents the liquid, (c) Free energy profile of CO₂ crystallization, and (d) crystal and liquid structure of CO₂ are shown. Figure reprinted from ref (97) with permission. Copyright 2021 Taylor and Francis.

There are, however, a few technical limitations to using the Deep-LDA CV; the current version works best for a process involving two adjacent states. Intermediate states, if any, can be included either by implementing an iterative two-class Deep-LDA method for each pair of states or its multiclass variant. Additionally, the Deep-LDA CV, by its construction, is built upon the information on the system in its metastable states and does not include any information on transition times between the states or any relaxation modes involved therein.

2.5.6. DeepTICA

In section 2.5.2, we have discussed TICA and VAC approaches to construct CVs from unbiased and biased simulation trajectories having multiple transitions between metastable states. Recently, Bonati et al. extended the VAC approach and developed its nonlinear variant using a deep NN.⁹⁸

The NN of Deep-TICA takes a set of descriptors, d(R_t) and d(R_t+τ) as input features and returns a set of latent variables, h_θ(d(R_t) and h_θ(d(R_t+τ). Subsequently, the covariance matrices are calculated using these latent variables,

The eigenvalues (λ_i) are then obtained from the generalized eigenvalue equation,

55

The Deep-NN is optimized by minimizing the loss function (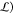 defined as a sum of the first N eigenvalues,

56

In this way, the Deep-TICA network provides as output a set of eigenfunctions that are used as Deep-TICA CVs in OPES simulations.

This approach has been applied to the study of prototypical processes: alanine dipeptide conformational dynamics, folding of a mini protein (chignolin), and crystallization of liquid Si. To fit the context of this review, here we discuss only the case of Si crystallization. A Deep-LDA CV was developed from a set of three-dimensional structure factor peaks, S(k) (discussed in Section 2.4.4), and used in OPES simulations to sample the phase transitions. From this trajectory, the Deep-TICA CVs were obtained. Compared to the Deep-LDA CV, the Deep-TICA CV exhibited improved sampling between the two states (Figure 24) manifesting the importance of incorporation of dynamical information in the development of an efficient CV.

Figure 24.

Comparative study between Deep-LDA and Deep-TICA driven simulation: Time evolution CV profile of (A) Deep-LDA and (B) Deep-TICA. (C) and (D) indicate the correlation between Deep-LDA and Deep-TICA CVs with the fraction of diamond atoms. White circles represent the average values of two CVs in liquid and solid phases while the dotted gray lines interpolate between them. Figure reprinted from ref (98) with permission. Copyright 2021 National Academy of Sciences.

3. Discussion

In this review, we discussed some of the important order parameters or collective variables that have been developed and used in enhanced sampling simulations to study crystallization. The early OPs developments were based on spherical particles that were mostly used to study atomic or metallic systems. Attempts have been made to extend their application in complex multicomponent materials and molecular systems. However, later studies revealed that the spherical particle-based OPs: the Steinhardt’s parameters and their variants are not sufficient to capture molecular orientation in periodic crystals. The atoms’ density fluctuations alone cannot fully describe the crystallinity order. The development of local molecular OPs provided a leap toward this goal, and these CVs have been used to sample the nucleation and growth of organic crystals. So far, most of the systems in which these CVs were tested consist of small, mostly rigid organic molecules. Their application in large flexible organic crystals is, however, scarce. This is due to the fact that for a large flexible molecular system, one needs to define a large number of CVs that describe molecular ordering. In ES simulation, one cannot use so many CVs, and in fact, the use of more than three variables is already a tedious task. Dimensionality reduction-based methods are useful in such a context. In this review, we have briefly discussed a few linear and nonlinear (NN) methods that can help construct low-dimensional CVs from a large set of descriptors. It is important to note that the success of any dimensionality reduction-based CV development method relies on the quality of the input descriptors, and we have seen in a few examples that the linear combinations of either XRD peak intensities^78,80,99 or entropy-based descriptors⁹¹ are found effective, while in another set of examples, the three-dimensional structure factor-based CVs were nonlinearly combined to develop efficient NN CVs.^97,98

Despite the enormous success of the above-mentioned approaches, the development of effective CVs for large fluxional molecules such as active pharmaceutical ingredients and biomolecules (peptides) is far from reality. The large conformational space intrinsic to these systems makes it challenging to design efficient CVs. ML-based dimensionality reduction methods^93,96−98 with RMSDs as effective descriptors can be tested for such systems. Among other possibilities, one can combine local atoms contacts combined with systems properties such as configurational entropy and enthalpy as possible CVs. The multicanonical approaches^14,41,98 along with NN-based CVs^{28,93,94,96,98,100,101} may open up new possibilities for the study of phase transitions of complex systems.

Author Contributions

^† N., V.T., S.M., and N.K have contributed to the review equally. T. K. has conceived the idea and designed the framework of the review. All authors wrote and approved the review article.

The authors declare no competing financial interest.