Theoretical study on the radical scavenging activity of gallic acid

Abstract

The global descriptors of the chemical activity: ionization potential IP, electron affinity EA, chemical potential μ, absolute electronegativity χ, molecular hardness η and softness S, electrophilicity index ω, electro-donating ω^-, electro-accepting ω⁺ powers as well as Ra and Rd indexes for gallic acid (GA) in the gas phase and water medium have been determined. To this aim, the HOMO and LUMO energies were calculated using the DFT method at the B3LYP, M06–2X, LC-ωPBE, BHandLYP, ωB97XD/cc-pVQZ theory levels using C-PCM, IEF-PCM and SMD solvation models, enabling more accurate descriptor calculations than those carried out so far. Quantum-chemical computations were also applied to investigate the GA structure and thermodynamic parameters characterizing its radical scavenging properties. To this aim, the full optimization of the neutral GA and its radical, cationic and anionic forms in vacuum and water medium has been performed, and then the bond dissociation enthalpy BDE, adiabatic ionization potential AIP, proton dissociation enthalpy PDE, proton affinity PA, electron transfer enthalpy ETE, gas phase acidity H_acidity and free Gibbs acidity G_acidity in water have been determined. The calculations revealed that GA in vacuum scavenges free radicals via hydrogen atom transfer (HAT), whereas in water (polar) medium by sequential proton loss electron transfer (SPLET). Analysis of the global activity descriptors of GA indicates that only B3LYP method combined with different solvation models satisfactory reproduces LUMO-HOMO energies and provides the smallest value of the total electron energy of GA. Among the parameters of chemical activity, the indexes Ra and Rd are the most independent of the computational method and the solvation model used. They can be recommended as a reliable source of information on the antioxidant activity of chemical compounds.

1. Introduction

Polyphenols belong to the most important class of naturally occurring antioxidants, characterized by a broad spectrum of bioactivity including: antibacterial, anticancer, antifungal, antilipemic, antiviral, and antiulcer properties mentioned as examples [1,2,3,4,5,6,7,8]. Among various polyphenols, gallic acid (3,4,5-trihydroxybenzoic acid, CAS-149-91-7, Fig. 1) deserves special attention due to its presence in many plants of nutritional, pharmacological and cosmetic importance [7]. For example, it has been identified in the free, ester, depside and depsidone forms in bark of various oak species, gallnuts, fruits (e.g. bananas, cherry, grapes, pomegranate, strawberries), spices [9] (e.g. bay leaves, marjoram, oregano, rosemary, sage, sumac), green tee [10] and wine [11].

Fig. 1.

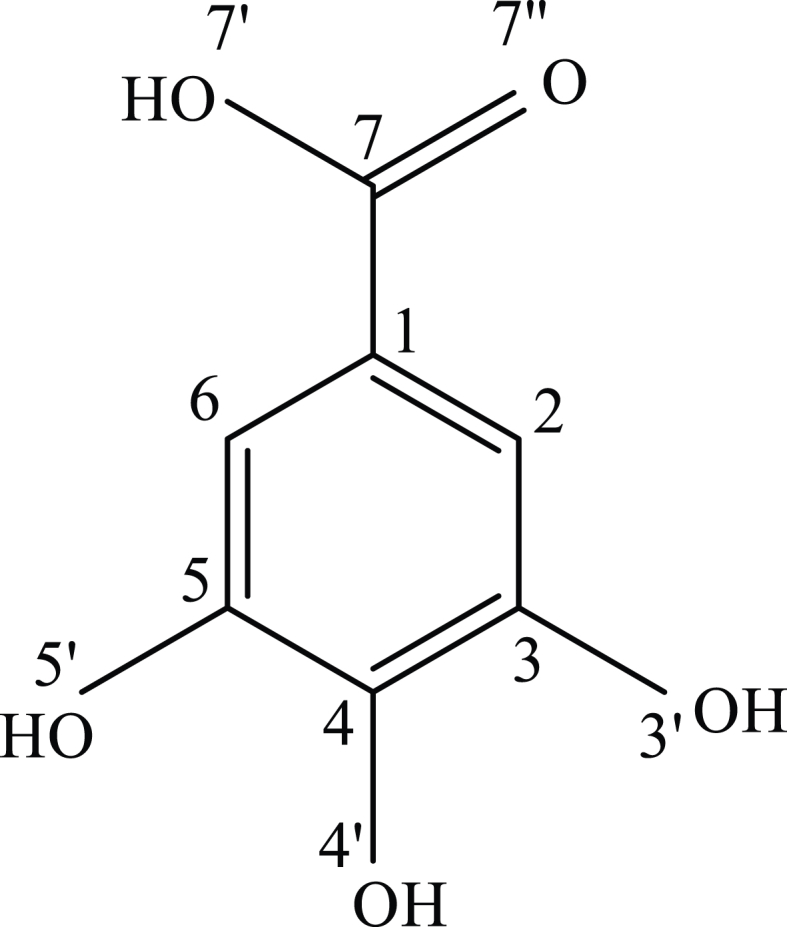
Gallic acid, 3,4,5-trihydroxybenzoic acid, CAS-149-91-7.

Due to its prevalence in the kingdom of plants GA has been employed as a standard for determining the polyphenols content of various analytes by taking advantage of the Folin-Ciocalteau assay; the results are specified in the GAE units (Gallic Acid Equivalent). This concise characteristics of GA explain why this compound has become the object of intense in vitro, in vivo and in silico studies aiming, for instance, at radical scavenging activity, metal ion chelation, ability to inhibit lipid peroxidation, maintenance of endogenous defense systems, cell signaling pathways, apoptosis of cancer cells and other [7,12]. Investigations are focused, among others, on the employing of antiradical and antimicrobial properties of GA in the food packaging and storage, including GA encapsulation in natural biopolymers as zein fibres [13] and covering food with chitosan microfilm containing active GA particles [14]. The first method is an efficient and effective for the preparation of sub-micron structured encapsulated functional ingredient that may find uses in food industry, whereas the second one provides a practical method in applying GA/chitosan coatings on preservation of meat, improving its quality and consumer safety. Additionally, the antimicrobial and antioxidant activity of the active coating has been shown to increase with the concentration of GA resulting in lower oxidation of lipids and myoglobin. Removing of oxygen from the package headspace is necessary for quality preservation of oxygen-sensitive products e.g. vitamins, nutrients, and bioactive compounds. To control of oxygen concentration the bio-based plastic containing GA and linear-low-density polyethylene has been proposed [15]. The authors demonstrated that the rates of oxygen scavenging increased whereas the residual oxygen decreased linearly with GA content. Recently, GA-benzylidenehydrazine hybrids were synthesized by Peng et al. [16]. They exhibit anti-tyrosinase, antioxidant, and antibacterial (against Vibrio parahaemolyticu and Staphylococcus aureus) activities, hence they can be used in the development of novel food preservatives.

The ability of GA to scavenge free radicals has been theoretically investigated by many authors [17,18,19,20,21,22,23,24,25,26] usually applying the DFT method and different hybrid functionals including B3LYP, B3LYP-D2, M052X, ωB97XD, LC-ωPBE taken as examples. The calculations have been performed using the basis sets 6-31G(d,p) [21], 6–311++G(df,p) [23], 6–311++G(d,p) [24] and various solvation models, preferably C-PCM, SMD and IEF-CPM ones. In the most advanced approach, Sousa and Peterson [26] analyzed antioxidant-related GA properties using not only DFT, but also MP2, CCSD, CCSD(T) approaches and more advanced basis sets cc-pVDZ, aug-cc-pVDZ, cc-pVTZ, aug-cc-pVTZ. The calculations revealed that the DFT/M06–2X method provided the most accurate antioxidant descriptors of neutral GA when compared to the CCSD(T)/aug-cc-pVTZ theory level, while in the case of deprotonated GA, the most reliable results were obtained using DFT/LC-ωPBE approach. Apart from thermodynamic studies, the kinetic characteristic of GA radical scavenging activity has been determined using the M05–2X functional at the 6-31+G(d,p) theory level [20]. The calculations proved that GA belongs to the best peroxyl radical scavengers identified so far in nonpolar (lipid) media, which is capable to deactivate hydroperoxyl radicals at the rate constant in the order of 10⁵ [M⁻¹ s⁻¹].

The variety of DFT methods used in thermodynamic [17,18,19,20,21,22,23,24,25,26,27] and kinetic [20] calculations is a consequence of the fact that the most popular B3LYP functional has serious disadvantages [28]. In particular: (i) it cannot be used in the investigation of transition metals and their compounds, (ii) it systematically underestimates reaction barrier heights by an average of 4.4 kcal mol⁻¹ for a database of 76 barriers analyzed, and (iii) it is inaccurate to study interactions dominated by van der Waals attraction, aromatic−aromatic stacking, and alkane isomerization energies [28]. In light of these facts, the main goal of this work is to check the impact of alternative to B3LYP methods on the values of chemical activity parameters that characterize GA in the gas phase and the water medium. To this aim the B3LYP, M06–2X, LC-ωPBE, BHandLYP, ωB97XD methods and the Dunning correlation consistent basis set cc-pVQZ [29] combined with C-PCM, IEF-PCM, SMD solvation models have been taken into account. An additional goal of the present work is to perform a comparative analysis of the GA antioxidant descriptors by taking advantage of the B3LYP and M06–2X methods, as well as the basic set cc-pVQZ, which guarantees a high accuracy of the calculations. This approach makes it possible to verify the correctness of the antioxidant parameters so far determined and examines the influence of the methods and models applied on the GA activity descriptors necessary to explain its chemical activity in general, and the preferred mechanism of the radicals scavenging in particular. To this purpose, global descriptors: ionization potential IP, electron affinity EA, chemical potential μ, absolute electronegativity χ, molecular hardness η and softness S, energy gap ΔE, electrophilicity index ω, electro-donating ω^- and electro-accepting ω⁺ powers, Ra and Rd indexes for GA, as well as antioxidant descriptors: bond dissociation enthalpy BDE, adiabatic ionization potential AIP, proton dissociation enthalpy PDE, proton affinity PA, electron transfer enthalpy ETE, gas phase acidity H_acidity and total free solvation energies G_acidity have been calculated in the gas phase and the water medium. They are indispensable to characterize the ability of GA to scavenge the free radicals and chelate transition metals ions (especially Fe⁺² and Cu⁺²), which participate in the radicals creation. The identification of sites of high and low GA activity enables the introduction of modifications in GA structure aimed at enhancing the power of scavenging free radicals and reducing its toxicity and side effects [30].

2. Materials and methodology

In this work, a computational approach to the structure-radical scavenging activity of GA has been employed. The input structures were constructed by taking advantage of the Gauss View-6.1 graphical interface whereas the calculations were carried out through Gaussian 16 W software package in Supercomputing and Networking Center via PL-Grid Infrastructure. The values of the global and antioxidant descriptors were calculated using Maple vs 16 processor for symbolic computations.

2.1. Antioxidant descriptors and scavenging mechanisms

It is well known that free radicals can be deactivated in interactions with antioxidant R─H, particularly with polyphenolic compounds (R = ArO) through three fundamental mechanisms specified below.

2.1.1. HAT (Hydrogen atom transfer)

$$\mathrm{R}─\mathrm{H}+{\mathrm{X}}^{●}\to {\mathrm{R}}^{●}+\mathrm{X}─\mathrm{H}$$

This mechanism is widely applied in investigation of phenomena such as combustion, halogenation, free radical scavenging, and other processes in which the hydrogen atom is transferred from the basic compound to the reactive intermediate. The antioxidant potency of a compound is related to a low bond dissociation enthalpy (BDE) of the N–H bond in amines, S–H in organosulfur compounds, or O–H in polyphenols. Hence, crucial for calculating the BDE parameter is reaction

$$\mathrm{R}─\mathrm{H}\to {\mathrm{R}}^{●}+{\mathrm{H}}^{●}$$

initiating the HAT process, which allows defining the BDE parameter [31,32].

$$\mathrm{B}\mathrm{D}\mathrm{E}=\mathrm{H}\left({\mathrm{R}}^{●}\right)+\mathrm{H}\left({\mathrm{H}}^{●}\right)–\mathrm{H}(\mathrm{R}─\mathrm{H})$$

in which H(R^●), H(H^●) and H (R─H) denote enthalpies of the antioxidant radical, hydrogen atom, and neutral molecule.

2.1.1.1. SET-PT (single electron transfer followed by proton transfer)

$$\mathrm{R}─\mathrm{H}+{\mathrm{X}}^{●}\to \mathrm{R}─{\mathrm{H}}^{●+}+{\mathrm{X}}^{-}$$

$$\mathrm{R}─{\mathrm{H}}^{●+}\to {\mathrm{R}}^{●}+{\mathrm{H}}^{+}$$

This scenario involves in the first step the transfer of an electron from the parent compound

$$\mathrm{R}─\mathrm{H}\to \mathrm{R}─{\mathrm{H}}^{●+}+{\mathrm{e}}^{-}$$

generating a cation radical R─H^●+ and then the proton transfer from the cation radical producing parent antioxidant in the radical form R^●. These two stages are described by the adiabatic ionization potential (AIP) and the proton dissociation enthalpy (PDE) calculated from the formulae [31,32].

$$\mathrm{A}\mathrm{I}\mathrm{P}=\mathrm{H}(\mathrm{R}─{\mathrm{H}}^{●+})+\mathrm{H}\left({\mathrm{e}}^{-}\right)–\mathrm{H}(\mathrm{R}─\mathrm{H})$$

$$\mathrm{P}\mathrm{D}\mathrm{E}=\mathrm{H}\left({\mathrm{R}}^{●}\right)+\mathrm{H}\left({\mathrm{H}}^{+}\right)–\mathrm{H}(\mathrm{H}─{\mathrm{R}}^{●+})$$

Here, H(R─H^●+), H(e^-), H(H⁺) and H(R─H) represent the enthalpies of the cation radical, electron, proton, and the parent compound.

SPLET (sequential proton loss electron transfer)

$$\mathrm{R}─\mathrm{H}\to {\mathrm{R}}^{-}+{\mathrm{H}}^{+}$$

$$\mathrm{R}ˆ(-)+\mathrm{X}ˆ(●)+\mathrm{H}ˆ(+)\to \mathrm{R}ˆ(●)+\mathrm{X}─\mathrm{H}$$

The second step specified above is initiated by the reaction

$${\mathrm{R}}^{-}\to {\mathrm{R}}^{●}+{\mathrm{e}}^{-}$$

Therefore, the SPLET process is characterized by the proton affinity (PA) and electron transfer enthalpy (ETE) calculated according to the formulae [31,32].

$$\mathrm{P}\mathrm{A}=\mathrm{H}\backslash \left({\mathrm{R}}^{-}\right)+\mathrm{H}\left({\mathrm{H}}^{+}\right)–\mathrm{H}(\mathrm{R}─\mathrm{H})$$

$$\mathrm{E}\mathrm{T}\mathrm{E}=\mathrm{H}\left({\mathrm{R}}^{●}\right)+\mathrm{H}\left({\mathrm{e}}^{-}\right)–\mathrm{H}\left({\mathrm{R}}^{-}\right)$$

2.1.1.3. TMC (transition metals chelation)

Another antioxidant mechanism is related to the ability to chelate transition metal ions (especially Fe⁺² and Cu⁺²), producing stable complexes that remove them from the reaction medium and participate in the slowdown of radical cascade reactions. The vital for this process is a dissociation decay

$$\mathrm{R}─\mathrm{H}\to \mathrm{R}-+\mathrm{H}+$$

exactly the same as for the first stage of the SPLET scenario. The numerical parameter related to this mechanism is the gas phase acidity H_acidity [24]

$${\mathrm{H}}_{\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{y}}=\mathrm{H}\left({\mathrm{R}}^{-}\right)–\mathrm{H}(\mathrm{R}─\mathrm{H})$$

whereas for the calculations performed in solvents - the free Gibbs accidity G_acidity [24]

$${\mathrm{G}}_{\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{y}}=\mathrm{G}\left({\mathrm{R}}^{-}\right)–\mathrm{G}(\mathrm{R}─\mathrm{H})$$

in which G(R^-) and G(R─H) denote the Gibbs free energy of the anion and its parent compound, respectively. Their values are usually applied together with zero-point energy corrections and conversion factor 1.89 [kcal mol⁻¹] due to the passing from pressure 1 [Atm] to molar 1 [Mol] unit as the standard state [33]. A lower value of this parameter indicates a greater ability to chelate metals and, consequently, to slow down radical processes.

2.1.1.4. RAF (radical adduct formation)

In this scenario [34], radicals are deactivated in the reaction

$$\mathrm{R}─\mathrm{H}+{\mathrm{X}}^{●}\to \mathrm{R}─{\mathrm{X}\mathrm{H}}^{●}$$

which is characterized by the enthalpy or Gibbs free energies formation calculated for a radical specified and an antioxidant considered [34]. Hence, this pathway is not characterized by a descriptor independent of the radical type, as these presented above, consequently, it will not be considered here.

2.1.1.5. pKa (acid dissociation constant)

Having calculated the G_acidity one may determine a useful descriptor pKa specifying the pH value at which chemical species will accept or donate a proton. The lower pKa means a stronger acid and greater ability to donate a proton in aqueous solution. pKa can be calculated using the following relationship [33].

$$pKa=\frac{\Delta G_{sol}}{TR\ln \left(10\right)}=\frac{\Delta G_{sol}}{1.364}\Delta G_{sol}=G{\left(R^{-}\right)}_{sol}+\mathrm{G}{\left(H^{+}\right)}_{sol}-\mathrm{G}{\left(R-H\right)}_{sol}$$

Here, R is the gas constant, T = 298.15 K is the absolute temperature. For the water solvent G(H⁺)_sol = G(H⁺)_gas+Δ_aqG(H⁺) = -6.28-265.62 [kcal mol⁻¹] includes free Gibbs energy of proton in the gas phase and proton hydration recommended by Ref. [33] as the most reliable value of this parameter corrected to the standard condition of 1 M by 1.89 [kcal mol⁻¹].

2.1.1.6. Test of correctness

Taking into account the formulae defining the antioxidant descriptors BDE, AIP, PDE, PA, and ETE, one may prove that they satisfy the following identities valid in the gas phase:

$$\mathrm{A}\mathrm{I}\mathrm{P}+\mathrm{P}\mathrm{D}\mathrm{E}-\mathrm{B}\mathrm{D}\mathrm{E}=\mathrm{H}\left({\mathrm{e}}^{-}\right)+\mathrm{H}\left({\mathrm{H}}^{+}\right)-\mathrm{H}\left({\mathrm{H}}^{●}\right)$$

$$\mathrm{P}\mathrm{A}+\mathrm{E}\mathrm{T}\mathrm{E}–\mathrm{B}\mathrm{D}\mathrm{E}=\mathrm{H}\left({\mathrm{e}}^{-}\right)+\mathrm{H}\left({\mathrm{H}}^{+}\right)-\mathrm{H}\left({\mathrm{H}}^{●}\right)$$

$$\mathrm{A}\mathrm{I}\mathrm{P}+\mathrm{P}\mathrm{D}\mathrm{E}=\mathrm{P}\mathrm{A}+\mathrm{E}\mathrm{T}\mathrm{E}$$

$$\mathrm{P}\mathrm{A}-{\mathrm{H}}_{\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{y}}=\mathrm{H}\left({\mathrm{H}}^{+}\right)$$

and the condensed phase (water or other solvents):

$${\mathrm{A}\mathrm{I}\mathrm{P}}_{\mathrm{a}\mathrm{q}}+{\mathrm{P}\mathrm{D}\mathrm{E}}_{\mathrm{a}\mathrm{q}}–{\mathrm{B}\mathrm{D}\mathrm{E}}_{\mathrm{a}\mathrm{q}}=\mathrm{H}{\left({\mathrm{e}}^{-}\right)}_{\mathrm{a}\mathrm{q}}+\mathrm{H}{\left({\mathrm{H}}^{+}\right)}_{\mathrm{a}\mathrm{q}}-\mathrm{H}{\left({\mathrm{H}}^{●}\right)}_{\mathrm{a}\mathrm{q}}$$

$${\mathrm{P}\mathrm{A}}_{\mathrm{a}\mathrm{q}}+{\mathrm{E}\mathrm{T}\mathrm{E}}_{\mathrm{a}\mathrm{q}}–{\mathrm{B}\mathrm{D}\mathrm{E}}_{\mathrm{a}\mathrm{q}}=\mathrm{H}{\left({\mathrm{e}}^{-}\right)}_{\mathrm{a}\mathrm{q}}+\mathrm{H}{\left({\mathrm{H}}^{+}\right)}_{\mathrm{a}\mathrm{q}}-\mathrm{H}{\left({\mathrm{H}}^{●}\right)}_{\mathrm{a}\mathrm{q}}$$

$${\mathrm{A}\mathrm{I}\mathrm{P}}_{\mathrm{a}\mathrm{q}}+{\mathrm{P}\mathrm{D}\mathrm{E}}_{\mathrm{a}\mathrm{q}}={\mathrm{P}\mathrm{A}}_{\mathrm{a}\mathrm{q}}+{\mathrm{E}\mathrm{T}\mathrm{E}}_{\mathrm{a}\mathrm{q}}$$

The relationships specified above are extremely useful in checking the correctness of the descriptors, enthalpies, and Gibbs energies used in the calculations. In calculations of the BDE, PDE, AIP, ETE, PA, H_acidity, G_acidity parameters the following values of the electron, proton and hydrogen enthalpies in the gas phase and water medium have been used [31] H(e^-) = 0.001198 [Ha], H(H⁺) = 0.002363 [Ha], H(H^●) = -0.497640 [Ha], H(e^-)_aq = -0.03879545 [Ha], H(H⁺)_aq = -0.38690658 [Ha], H(H^●)_aq = -0.49916356 [Ha]. The last three values can be calculated using the following relationships:

$$\mathrm{H}{\left({\mathrm{e}}^{-}\right)}_{\mathrm{a}\mathrm{q}}=\mathrm{H}\left({\mathrm{e}}^{-}\right)+{\Delta }_{\mathrm{a}\mathrm{q}}\mathrm{H}\left({\mathrm{e}}^{-}\right),\mathrm{H}{\left({\mathrm{H}}^{+}\right)}_{\mathrm{a}\mathrm{q}}=\mathrm{H}\left({\mathrm{H}}^{+}\right)+{\Delta }_{\mathrm{a}\mathrm{q}}\mathrm{H}\left({\mathrm{H}}^{+}\right),\mathrm{H}{\left({\mathrm{H}}^{●}\right)}_{\mathrm{a}\mathrm{q}}=\mathrm{H}\left({\mathrm{H}}^{●}\right)+{\Delta }_{\mathrm{a}\mathrm{q}}\mathrm{H}\left({\mathrm{H}}^{●}\right)$$

in which Δ_aqH(e^-) = -105 [kJ mol⁻¹], Δ_aqH(H⁺) = -1022 [kJ mol⁻¹] and Δ_aqH(H^●) = -4.0 [kJ mol⁻¹] are the solvation corrections recommended by Rimarčik et al. [31].

2.2. Global chemical descriptors

An important source of information on the reactivity of chemical compounds is the difference between the energies of the HOMO and LUMO orbitals (usually expressed in electron volts [eV])

$$\Delta E=E_{LUMO}-E_{HOMO}$$

A large energy gap defines a hard molecule that is more stable and less active, while a small energy gap defines a soft molecule that is less stable and more reactive. Using the energy of LUMO and HOMO orbitals, as well as the Koopmans’ theorem for closed-shell molecules, the global activity descriptors [35,36], which model the physicochemical properties of the compounds [37] can be defined. The most important activity descriptors are [38].

2.3. Ionization potential

$$IP=-E_{HOMO}$$

This is the minimum energy indispensable to detach the electron away from the molecule's HOMO orbital and bring it to infinity. The smaller IP value indicates a greater tendency to electron transfer. The best antioxidants are endowed with low IP values denoting the easier electron abstraction.

2.4. Electron affinity

$$EA=-E_{LUMO}$$

It expresses the ability of a molecule to attach an electron and form an anion. Because radicals deactivation might act either via donating or accepting electrons, the EA descriptor is useful to characterize the capacity of the compound to accept electrons.

2.5. Chemical hardness and softness

Chemical hardness

$$\eta \approx \frac{E_{LUMO}-E_{HOMO}}{2}$$

characterizes the low susceptibility of a molecule to deformation or polarization of the electron cloud under the influence of external factors, e.g., reagents or forces. The chemical softness

$$S\approx \frac{1}{E_{LUMO}-E_{HOMO}}$$

is the inverse of chemical hardness and characterizes molecules with high susceptibility to deformation and polarization of the electron cloud.

2.6. Chemical potential

$$\mu \approx \frac{E_{LUMO}+E_{HOMO}}{2}$$

It describes the thermodynamic activity of substances and is used in the derivation of phase equilibrium constants and chemical reactions.

2.7. Electronegativity

$$\chi =-\mu \approx -\frac{E_{LUMO}+E_{HOMO}}{2}=\frac{EA+IP}{2}$$

Characterizes a tendency to attract the electrons during the bond forming. When the EA and IP values are comparable, the common electron pair is shifted toward the functional group (atom) that has a higher value of χ, and a polarized bond is formed. In the case when IP < EA the bond created between atoms or groups of atoms is of the ionic type.

Electrophilicity index

$$\omega \approx \frac{{\chi }^2}{2\eta }=\frac{{\left(E_{LUMO}+E_{HOMO}\right)}^2}{4\left(E_{LUMO}-E_{HOMO}\right)}$$

It determines the energy change of an electrophilic reagent (acceptor) when it is saturated with electrons provided by the donor [39]. The higher value of ω implies that the compound can be considered a strong electrophile, whereas a strong nucleophile is described by lower values of ω.

Electro-donating and electro-accepting power

Taking into account the fact that a radical scavenger (RS) can act in two ways: either by donating electrons to or accepting electrons from a radical (R)

$$\mathrm{R}\mathrm{S}+\mathrm{R}\to {\mathrm{R}\mathrm{S}}^{+}+{\mathrm{R}}^{-}\mathrm{R}\mathrm{S}+\mathrm{R}\to {\mathrm{R}\mathrm{S}}^{-}+{\mathrm{R}}^{+}$$

Gázquez et al. [40] introduced the new descriptors characterizing the electro-donating ω^- and electro-accepting ω⁺ power of RS, defined in the following manner

$${\omega }^{-}=\frac{{\left(3IP+EA\right)}^2}{16\left(IP-EA\right)}{\omega }^{+}=\frac{{\left(IP+3EA\right)}^2}{16\left(IP-EA\right)}$$

To define the relative electro-accepting(donating) power of an arbitrary radical scavenger X, Martinez [41] introduced acceptance Ra and donation Rd indexes

$$Ra=\frac{{\omega }_X^{+}}{{\omega }_F^{+}}Rd=\frac{{\omega }_X^{-}}{{\omega }_{Na}^{-}}$$

defined by the IP and EA for F and Na atoms, which represent a good electron acceptor (F) and donor (Na), respectively. In the calculations we use the well-known experimental values for F: IP = 17.42282, EA = 3.4011898 [eV], and for Na: IP = 5.1391, EA = 0.547926 [eV]. The descriptors Ra and Rd are useful for classifying any substance X in terms of its electron donating (accepting) capacity. As the electron transfer represents the first step of the SET-PT mechanism of the radical scavenging, Ra and Rd can be applied to characterize the antiradical capacity of any substance X. In this way, an arbitrary molecule can be classified in terms of its electron donating-accepting capacity with respect to F and Na, taken as the reference points [41].

3. Results and discussion

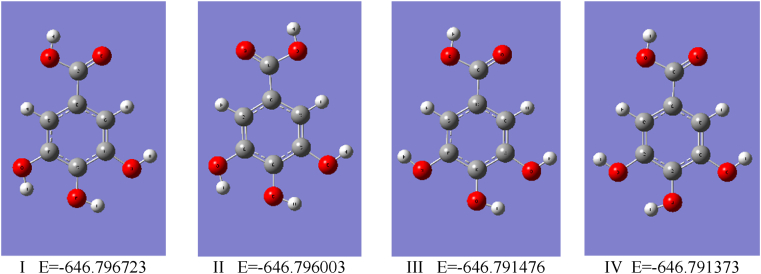
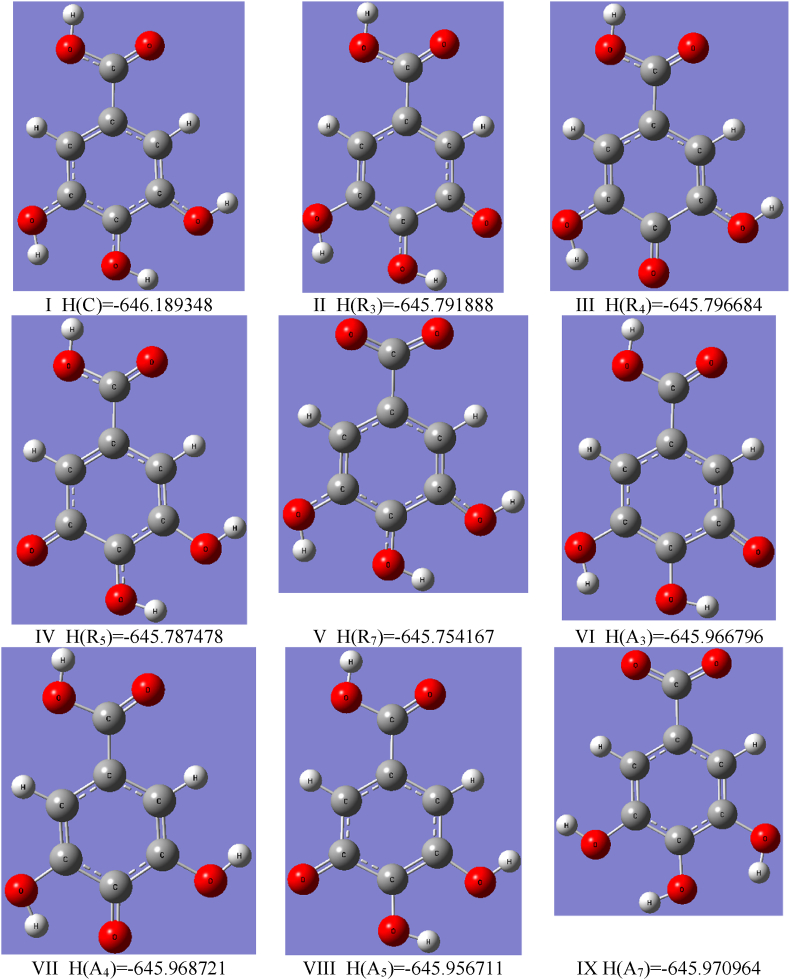
To calculate the specified GA descriptors and to perform GA structural analysis, we used the DFT method implemented in Gaussian vs. 16 software. At the first stage of the calculations, the B3LYP approach, consisting of the Becke's [42] exchange functional in conjunction with the correlational LYP functional of Lee, Yang and Parr [43], has been taken into account. The geometry optimization and enthalpy calculation were performed using B3LYP/cc-pVQZ level of the theory including the correlation consistent polarized valence quadruple zeta basis set (cc-pVQZ) introduced by Dunning [29]. The basis set used is a compromise between the expensive calculation time and the accuracy of the generated results, which may increase for basis sets, e.g. aug-cc-pVQZ, cc-PV5Z, cc-PV6Z taken into consideration. The test calculations showed that such extensive basis sets do not significantly affect the values of the geometric parameters, the calculated descriptors, and the interpretation of the results obtained. To generate the GA energy in the global minimum, the three-dimensional potential energy surfaces (3D PES) was generated using procedure of scanning of dihedral angles α = H_7’ - O_7’ - C₇ -C₁ and β = H_4’ - O_4’ - C₄ - C₃ in the ranges 180^o ≤ α ≤ 360^o, 180^o ≤ β ≤ 360^o. The α and β describe the rotation around the single bonds of the carboxyl and hydroxyl O_4’–H_4’ groups, respectively. The calculations allowed selecting four conformers I – IV presented in Fig. 2, with the lowest energy values E(I) = -646.796723, E(II) = -646.796003, E(III) = -646.791476 and E(IV) = -646.791373 [Ha] slightly differing from each other, of which I represents GA in the “absolute” global minimum. This form of GA was considered by Rajan and Muraleedharan [23], whereas form II by Saqib et al. [21] as the base structures for the calculation of antioxidant descriptors. From all points on PES the GA conformer I has been endowed with the smallest energy (stationary point); hence it has been used as the input data for calculating enthalpies of the anions, cation and radicals, as well as optimizing the geometry of GA at the B3LYP/cc-pVQZ level of the theory in the gas phase and water medium employing the C-PCM (Conductor–like Polarizable Continuum Model) [44]. Consequently, no imaginary frequencies were reported during computations. The calculated HOMO-LUMO energies and enthalpies have been applied to calculate GA activity descriptors presented in Tables 1–3.

Fig. 2.

Optimized geometries of the selected conformers of GA with the lowest energy values E [Ha]. Conformer I was considered theoretically by Rajan and Muraleedharan [23], while II by Saqib et al. [21]. Conformers III-IV were analyzed by crystallographic means [46,47].

Table 1.

The values of total electronic energy [Ha] and global descriptors [eV] of GA in the gas phase and water medium, calculated from the energies E_LUMO = -EA and E_HOMO = -IP determined at different DFT/cc-pVQZ theory levels using C-PCM, IEF-PCM, and SMD solvation models.

Method	Model	Energy	EA	IP	ΔEa	η	S	μ = -χ	ω	ω+	ω-	Ra	Rd
B3LYP	–	-646.796723	1.4536	6.4162	4.9625	2.4813	0.2015	-3.9349	3.1201	1.4628	5.3977	0.4300	1.5556
B3LYPb	–	–	1.5851	6.5147	4.9296	2.4663	0.2027.	-4.0484	3.3227	–	–	–	–
M06–2X	–	-646.551040	0.3929	7.7669	7.3740	3.6870	0.1356	-4.0799	2.2574	0.6783	4.7582	0.1994	1.3713
BHandHLYP	–	-646.441732	0.1475	7.5256	7.3781	3.6890	0.1355	-3.8365	1.9950	0.5378	4.3744	0.1581	1.2607
LC-ωPBE	–	-646.375284	-0.9021	9.0285	9.9305	4.9653	0.1007	-4.0632	1.6625	0.2516	4.3148	0.0739	1.2435
ωB97XD	–	-646.580221	-0.5393	8.2951	8.8344	4.4172	0.1132	-3.8779	1.7022	0.3154	4.1933	0.0927	1.2085
ωB97XD	IEF-PCM	-646.388483	-0.7788	9.0679	9.8467	4.9234	0.1016	-4.1446	1.7475	0.2876	4.4322	0.0845	1.2774
B3LYP	C-PCM	-646.809859	1.5682	6.4317	4.8635	2.4317	0.2056	-3.9999	3.2897	1.5937	5.5936	0.4685	1.6121
B3LYP	IEF-PCM	-646.809777	1.5679	6.4306	4.8627	2.4313	0.2056	-3.9993	3.2891	1.5934	5.5927	0.4684	1.6118
B3LYP	SMD	-646.818956	1.5121	6.3247	4.8126	2.4063	0.2078	-3.9184	3.1904	1.5320	5.4504	0.4503	1.5708
M06–2X	IEF-PCM	-646.584299	0.5211	7.8075	7.2864	3.6532	0.1372	-4.1643	2.3800	0.7532	4.9175	0.2214	1.4172
BHandHLYP	IEF-PCM	-646.455204	0.2629	7.5588	7.2959	3.6480	0.1371	-3.9108	2.0963	0.5969	4.5077	0.1755	1.2991

^aThe experimental values of ΔE = 4.6786 and 4.5920 [eV] evaluated in the gas phase and water medium correspond to λ = 265 and 270 [nm] UV absorption of neutral GA molecule reported by Cappelli et al. [51].

^bParameters calculated by Rajan and Muraleedharan [23] using the B3LYP/6–311++G(df,p) theory level.

Table 3.

The values of descriptors [kcal mol⁻¹] characterizing antioxidant activity of the hydroxyl groups in GA determined at the M06–2X/cc-pVQZ level of the theory in water using IEF-PCM solvation model. The values calculated by Škorňa et al. [22] employing the B3LYP/6–311++G(d,p) method and the IEF-PCM solvation model are given in parentheses.

Descriptor	Water
	3′O–H	4′O–H	5′O–H	7′O–H
BDE	83.06(78.58)	80.05(75.93)	85.83(81.45)	106.73
PA	43.75(39.41)	42.54(37.26)	50.07(45.62)	41.13
ETE	85.41(83.83)	83.61(82.88)	81.85(80.25)	111.70
PA + ETE	129.16(123.24)	126.15(120.14)	131.92(125.87)	152.83
PDE	6.62(4.30)	3.61(1.43)	9.38(7.17)	30.29
AIP		122.54(118.71)
PDE + AIP	129.16(123.01)	126.15(120.14))	131.92(125.87)	152.83
Gacidity	278.76	277.75	284.60	275.26
pKa	5.02	4.28	9.30	2.46

In the second stage of the calculations, we examined the influence of different DFT methods, including M06–2X, LC-ωPBE, BHandLYP, ωB97XD ones on the values of total electronic energy and IP, EA, μ, χ, η, S, ΔE, ω, ω^-, ω⁺, Ra, Rd parameters by taking advantage of the basis set cc-pVQZ combined with C-PCM, IEF-PCM, SMD solvation models. In the case of BDE, PDE, AIP, ETE, PA, TMC descriptors the calculations have been performed at the M06–2X/cc-pVQZ levels of the theory in the water medium employing the IEF-PCM (Integral Equation Formalism Polarizable Continuum Model) [45] solvation model. Both the M06–2X method and the IEF-PCM model are recommended as the optimal combined approach to calculate the antioxidant descriptors of GA [26] (Sousa and Peterson, 2021). In calculations, the values of vacuum (gas phase) and solvation enthalpies of H^●, H⁺ and e^- reported by Rimarčik et al. [31] have been taken into account. Calculations of the descriptors were performed for all –OH groups present in GA to select those that are the most active in the radical scavenging processes. The results of the calculations are graphically displayed in Figs. 2, 4–7 and presented in Tables 1–4.

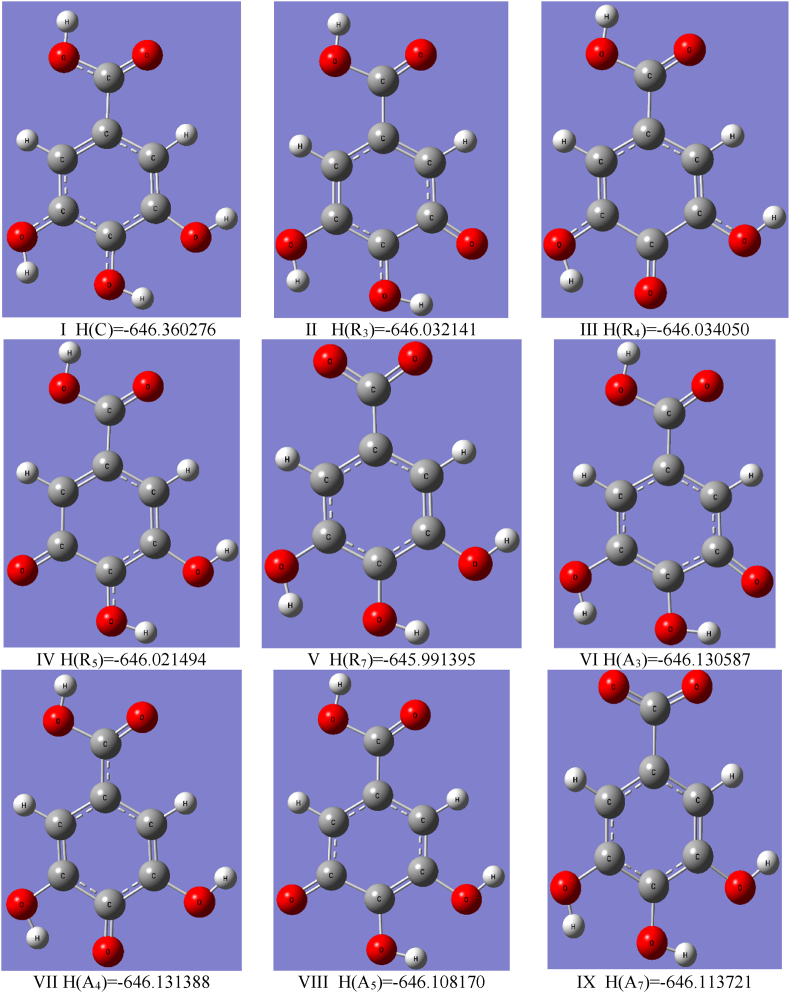
Fig. 5.

Optimized geometries of the GA cation I (x = C), radicals II-V (x = R_n), anions VI – IX (x = A_n) in vacuum and values of the enthalpies H(x) [Ha] determined using the B3LYP/cc-pVQZ level of the theory. The subscript n corresponds to the number of carbons in GA according to Fig. 1. The reported enthalpy values have been used in the calculations of the antioxidant descriptors presented in Table 2.

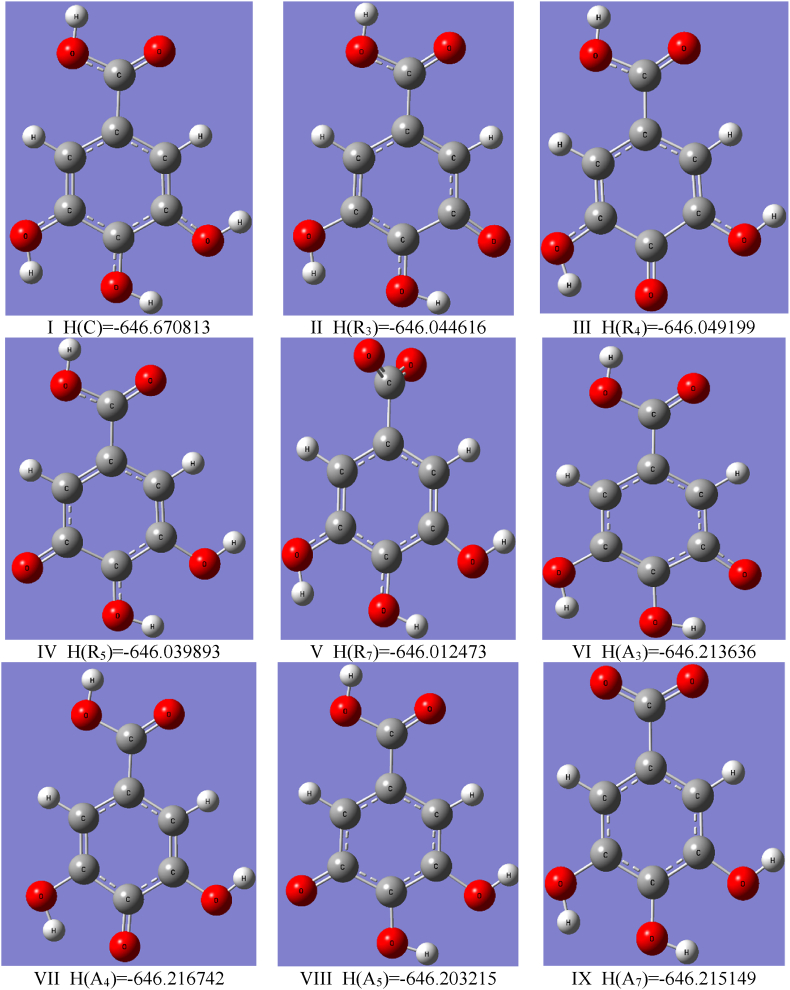
Fig. 6.

Optimized geometries of the GA cation I (x = C), radicals II-V (x = R_n), anions VI-IX (x = A_n) in water and values of the enthalpies H(x) [Ha] determined using the B3LYP/cc-pVQZ level of the theory and C-PCM solvation model. The subscript n corresponds to the number of carbons in GA according to Fig. 1. The reported enthalpy values have been used in the calculations of the antioxidant descriptors presented in Table 2.

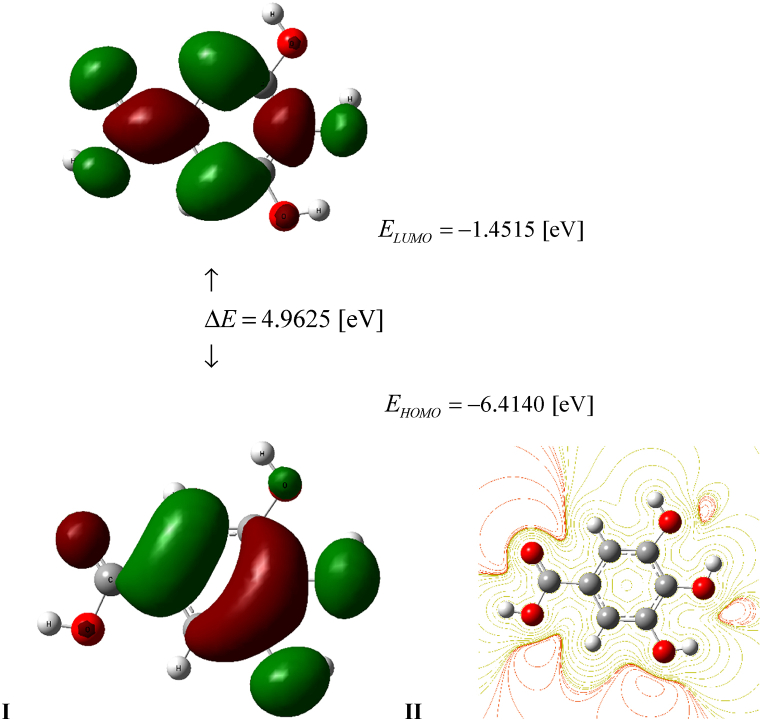
Fig. 4.

I. HOMO and LUMO GA frontier orbitals and energy levels calculated using DFT B3LYP/cc-pVQZ level of the theory. II. Contour surface of electrostatic potential of GA.

Fig. 7.

Optimized geometries of the GA cation I (x = C), radicals II-V(x = R_n), anions VI-IX (x = A_n) in water and values of the enthalpies H(x) [Ha] determined at the M06–2X/cc-pVQZ level of the theory in water using the IEF-PCM solvation model. The subscript n corresponds to the number of carbons in GA according to Fig. 1. The reported enthalpy values have been used in the calculations of the antioxidant descriptors presented in Table 3.

Table 4.

Bond length values [Å], angles and dihedral angles [deg] determined at B3LYP/cc-pVQZ level of the theory in vacuum and water using the C-PCM solvation model. The experimental values of the GA geometric parameters obtained from crystallographic analysis (I [46], II [47]) are also presented.

Geometry	Vacuum	Water	Experiment I	Experiment II
Bond
C1–C2	1.3972	1.3980	1.3984	1.391(2)
C2–C3	1.3812	1.3831	1.3880	1.378(2)
C3–C4	1.3936	1.3965	1.3947	1.387(2)
C4–C5	1.3944	1.3953	1.4025	1.388(2)
C5–C6	1.3870	1.3861	1.3885	1.382(2)
C6–C1	1.3940	1.3958	1.4025	1.388(2)
C1–C7	1.4804	1.4785	1.4737	1.488(2)
C3–O3′	1.3726	1.3654	1.3732	1.368(2)
C4–O4′	1.3634	1.3589	1.3575	1.372(2)
C5–O5′	1.3590	1.3614	1.3624	1.372(2)
C7–O7′	1.3531	1.3492	1.3163	1.317(2)
C7–O7″	1.2076	1.2129	1.2429	1.212(2)
O3′-H3′	0.9607	0.9626	0.8810	0.8200
O4′-H4′	0.9641	0.9654	0.8380	0.8200
O5′-H5′	0.9639	0.9649	0.8930	0.8200
O7′-H7′	0.9662	0.9674	0.9100	0.8200
Angle
C1C2C3	119.3427	119.5356	119.6700	119.61(16)
C2C3C4	120.4123	120.2186	120.0200	120.01(15)
C3C4C5	120.0827	120.0335	119.9900	120.05(14)
C4C5C6	119.8938	120.0614	120.5600	120.48(15)
C5C6C1	119.6437	119.6328	118.8200	118.99(15)
C6C1C2	120.6248	120.5181	120.9100	120.83(15)
C2C1C7	117.3692	117.8438	119.4200	118.32(15)
O7″C7O7′	121.8607	121.7555	121.7800	122.82(15)
C7O7′H7′	106.3743	107.6125	111.7000	109.50
C3O3′H3′	110.2035	110.9506	110.1000	109.50
C4O4′H4′	108.9291	109.5470	108.0000	109.50
C5O5′H5′	108.8386	109.2035	111.0000	109.50
Dihedral Angle
C1C6C5O5′	180.00	180.00	179.54(7)	178.97(16)
O4′C4C5O5′	-0.01	0.00	1.35(10)	-0.50(2)
O3′C3C2C1	180.00	180.00	178.27(6)	178.56(18)
O4′C4C5C6	180.00	180.00	178.08(7)	178.51(16)
O4′C4C3O3′	0.00	0.00	0.35(10)	2.4(3)
C3C2C1C6	0.00	0.00	0.95(11)	-0.5(3)
C3C2C1C7	-180.00	-180.00	-179.03(6)	-179.08(17)

Analysis of Table 4 reveals that the geometric parameters characterizing the conformer I agree acceptably with those determined by crystallographic analysis [46,47]. The important exceptions are the bond lengths 0.9607, 0.9641, 0.9639, 0.9662 [Å] of the O_n′-H n = 3,4,5,7 hydroxyl groups, compared to the experimental values 0.8810, 0.8380, 0.8930, 0.9100 [Å] (Table 4). The differences can be explained by the fact that molecules are susceptible to intermolecular interactions in the crystal lattice, which may modify the bond lengths and angles of external groups relative to those in the isolated molecule. The calculations predict that the weakest (longest) bonds are present in the O₄′-H and O₇′-H hydroxyl groups, which, compared to the rest of the OH groups, are the most susceptible to proton detachment. The calculations performed for the more extensive basis set aug-cc-pVQZ provided similar results 0.9606, 0.9639, 0.9638, 0.9662 [Å] to those obtained for the cc-pVQZ one. The determined values of phenolic OH bond lengths coincide acceptably with the bond orders 0.7506, 0.7322, 0.7455 calculated by Rajan and Muraleedharan [23], indicating that the O₄′-H bond is the weakest one and breaks easily in the radical deactivation process.

The antioxidant descriptors presented in Table 2 are significantly different (except for the BDE) from those determined by Rajan and Muraleedharan [23] and completely change their interpretation of the antioxidant activity of GA in the water medium. Although the BDE in the water environment changes insignificantly, the values of PA and ETE decrease radically and are definitely lower than those of the BDE in water. This indicates that the dominant free radical scavenging mechanism predicted for GA in water solution is sequential proton loss electron transfer (SPLET), with the most active group in this regard, O_4′-H. The energy value of PA = 42 [kcal mol⁻¹] is required for the activation of the first stage of SPLET, and for the second stage ET = 81 [kcal mol⁻¹], which is comparable to the BDE of the other OH phenolic groups. On the other hand, in vacuum, the hydrogen atom transfer (HAT) mechanism dominates, with the participation of the most active O_4′-H group having the lowest value of BDE = 79 [kcal mol⁻¹]. The remaining phenolic hydroxyl groups show various susceptibility to hydrogen detachment as evidenced by the BDE = 80 and 87 [kcal mol⁻¹], respectively. A detailed analysis of Table 2 reveals additional differences in the results obtained by Rajan and Muraleedharan [23]. From a physical point of view, antioxidant parameters describe the energy needed to activate a given radical scavenging mechanism. Therefore, they cannot be negative as in the case of PA = -4 [kcal mol⁻¹] and PA_aq = -49 [kcal mol⁻¹] evaluated by the authors mentioned. In the calculations carried out by Škorňa et al. [22] by making use of the similar B3LYP/6–311++G(d,p) theory level and IEF-PCM solvation model, all the parameters determined assume positive values reported in Table 3. Furthermore, all antioxidant descriptors determined in this work and presented in Tables 2 and 3 assume positive values and differ significantly from those calculated by Rajan and Muraleedharan [23]. The differences appear probably due to the use of an inaccurate value of the hydrogen cation enthalpy in the water and gas phase, as well as approximate formulas for AIP and ETE parameters, which do not take into account the enthalpy of the electron [31]. This thesis is supported by the correctness test that yields PA-H_acidity = 1 [kcal mol⁻¹], which, according to the correct value of the proton enthalpy in vacuum H(H⁺) = 0.002363 [Ha], should be equal to 1.48 and not 1.0 [kcal mol⁻¹]. The values of H_acidity related to the TMC mechanism take the large values for all hydroxyl groups in GA, indicating that this mechanism is not preferred in vacuum. The situation changes under the influence of the water polar medium, which activates especially the O_4′-H and O_7′-H groups having the lowest G_acidity = 278 [kcal mol⁻¹] and the strongest chelating property. The calculated values of pKa indicate that the tendency to deprotonation of hydroxyl groups in GA is arranged as follows: pKa(O_7′-H, 4.11)> pKa(O_4′-H, 4.67)> pKa(O_3′-H, 5.45)> pKa(O_5′-H, 9.72)>, confirming Marino et al. [20], finding that GA in the water solution is deprotonated first from the O_7′-H (in carboxylic group) and then the site O_4′-H. This conclusion is also consistent with the bond lengths of the hydroxyl groups presented in Table 4. The value of pKa(O_7′-H) = pKa₁ = 4.11 determined for neutral GA (at pH = 1.9) agrees acceptably with the experimental values of pKa₁ = <4.24,4.40> determined at physiological pH = 7.4 [20]. The application of M06–2X method and IEF-PCM solvation model underestimates this parameter yielding approximate value of pKa₁ = 2.46. The results presented in Table 3 show that all BDE(B3LYP)<BDE(M06–2X), confirming that the B3LYP method underestimates the value of this descriptor compared to the M06–2X one. The same result has been obtained for AIP(B3LYP)<AIP(MO6-2X) and ETE(B3LYP)<ETE(MO6-2X), whereas PA(B3LYP)> PA(MO6-2X) excluding the O_4′-H site and PDE(B3LYP)>PDE(MO6-2X) besides O_7′-H site. The application of the B3LYP/cc-pVQZ level of the theory decreases the values of phenolic BDE's in water about 1 [kcal mol⁻¹] in comparison to the results obtained by Škorňa et al. [22] by taking advantage of the B3LYP/6-311G(d,p) theory level. On the other hand, the reported phenolic BDE's are only about 0.4 [kcal mol⁻¹] higher than the BDS's in water calculated by Sousa and Peterson [26] by using the B3LYP/aug-cc-pVTZ theory level and the IEF-PCM solvation model. In the case of the M06–2X method, the difference is much larger, averaging 2 [kcal mol⁻¹] for all phenolic OH groups. It should be noted that phenolic BDS's in water (83.06, 80.05, 85.83 [kcal mol⁻¹]) obtained at the M06–2X/cc-pVQZ level of the theory agrees acceptably with those (83.5, 80.3, 86.4 [kcal mol⁻¹]) generated by the U-CCSD method combined with the cc-pVTZ basis set [26].

Table 2.

The values of descriptors [kcal mol⁻¹] characterizing antioxidant activity of the hydroxyl groups in GA determined at the B3LYP/cc-pVQZ level of the theory in vacuum and water medium. The values calculated by Rajan and Muraleedharan [23] employing the method B3LYP/6–311++G(df,p) are given in parentheses. In the calculations, the enthalpy values presented in Figs. 5 and 6, as well as the enthalpies of the neutral GA molecule in vacuum H = -646.657042 [Ha] and in water H_aq = -646.670813 [Ha] were taken into account.

Descriptor	Vacuum				Water
	3′O–H	4′O–H	5′O–H	7′O–H	3′O–H	4′O–H	5′O–H	7′O–H
BDE	79.86	78.66(78)	86.54	105.43	79.71	76.84(77)	82.68	99.88
PA	331.84	331.33(-4)	345.90	342.42	44.10	42.14(-49)	50.63	43.14
ETE	62.53	61.83(396)	55.14	77.51	81.71	80.79(441)	78.14	102.84
PA + ETE	394.37	393.16(392)	401.05	419.93	125.81	122.93(392)	128.77	145.98
PDE	207.39	206.18(204)	214.07	232.95	8.47	5.59(247)	11.43	28.64
AIP		186.98(188)				117.34(143)
PDE + AIP	394.37	393.16(392)	401.05	419.93	125.81	122.93(390)	128.77	145.98
Hacidity	330.36	329.85(-5)	344.42	340.94
Gacidity					279.34	277.42(-53)	285.17	277.51
PA-Hacidity	1.48	1.48(1)	1.48	1.48
pKa					5.45	4.67	9.72	4.11

The different activity of all hydroxyl groups attached to the benzene ring in GA explains the strong antioxidant potency [48,49] of ellagic acid (dimeric GA derivative) - a secondary metabolite that naturally occurs in many plant taxa, especially in strawberries (Fragaria ananassa), Jamun berry (Eugenia jambolana), and pomegranate (Punica granatum) fruits, as well as in wood and bark of some tree species. This dilactone is formed by intramolecular double esterification of the hydroxyl group O_5′-H in the first GA molecule by the carboxylic group containing O_7′-H in the second GA molecule and vice versa (“head to tail” assemblage presented in Fig. 3). According to our analysis, these groups show the weakest antioxidant activity in both vacuum and in water medium as compared to the remaining O_3′-H and O_4′-H groups, which, in a double amount, are responsible for the unusual ability of ellagic acid to scavenge free radicals and, consequently, its bioactivity, including, for example, cardio, hepato, nephron, and neuroprotective properties [50].

Fig. 3.

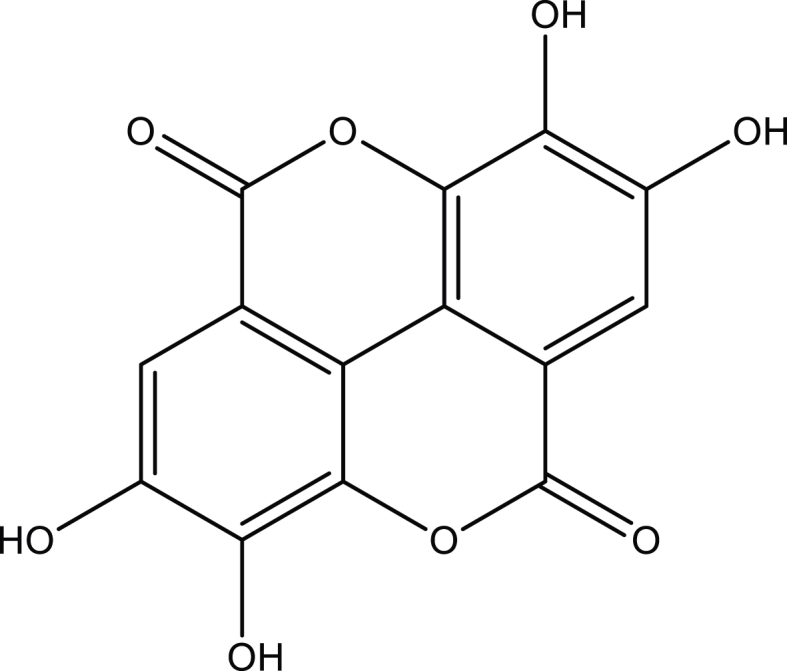
Ellagic acid, CAS: 476-66-4.

The values of the global descriptors of GA in the gas phase presented in Table 1, differ slightly from those obtained by Rajan and Muraleedharan [23]. It shows that the application of the B3LYP/6–311++G(df,p) theory level in the calculations has a minimal impact on the value of ΔE and other global parameters determined. Also, the HOMO and LUMO frontier orbitals as well as the ESP contours presented in Fig. 4 are qualitatively identical to those generated by Rajan and Muraleedharan [23], confirming the correctness of their Natural Bond Orbital analysis. An inspection of Table 1 reveals that the methods M052X, ωB97XD, LC-ωPBE recommended by various authors as optimal in the study of GA activity in particular, and in the calculation of antioxidant descriptors in general reproduce the HOMO-LUMO energy gap with much less accuracy when compared to the B3LYP. The experimental values of ΔE = 4.6786 and 4.5920 [eV] evaluated in the gas phase and water medium, correspond to λ = 265 and 270 [nm] UV absorption reported by Cappelli et al. [51]. They conform acceptably with ΔE = 4.9625 and 4.8126 obtained using B3LYP approach and significantly differ from those generated by the methods alternative to B3LYP. Moreover, the latter approach, in conjunction with the basis set cc-pVQZ, enables the calculation of the global energy minimum with the lowest value compared to the energies produced by the remaining methods. The solvent models C-PCM, IEF-PCM, and SMD have only a slight impact on lowering the energy gap value. Because the IP, EA, μ, χ, η, S, ΔE, ω, ω^-, ω⁺, Ra, Rd parameters depend on the HOMO-LUMO energies, only those calculated taking advantage of the B3LYP method can be considered reliable from a physical point of view. Analysis of Ra and Rd indexes calculated at this theory level shows that their values increase in the water solution. Because Ra = 0.4293(0.4685) whereas Rd = 1.5543(1.6121) in the gas(water) phase, GA is a less effective electron acceptor than F and a more effective electron donor than Na atom, respectively. Hence, GA scavenging activity is similar to β-carotene and tetradecahexenal (psittacofulvin pigment found in parrot feathers) characterized by Ra = 0.46, Rd = 1.40 and Ra = 0.43, Rd = 1.62, respectively [41]. The parameter ω^- = 5.3931 allows us to compare the ability of GA to oxidation with other known substances that exhibit activity in this respect. A comparison of the ω^- and ω⁺ values, reported by Martinez [41] reveals that GA is weaker antioxidant than vitamins A, C, E, anthocyanins, β-carotene and stronger than psittacofulvins and astaxanthin. Another conclusion can be drawn from the analysis of the ω⁺ = 1.4604 parameter, which characterizes the tendency of an antireductant to eliminate free radicals by electron capture. In this sense, GA is weaker antireductant than astaxanthin, psittacofulvins, β-carotene and stronger than anthocyanins and vitamins A, C, and E [41].

The ability of GA to scavenge free radicals through the HAT mechanism can also be compared with other antioxidants theoretically investigated, using their BDE (in [kcal mol⁻¹]) and the GA BDE = 79(77) [kcal mol⁻¹] in vacuum (water). For example: α-lipoic acid enantiomers and their natural metabolites bisnorlipoic and tetranorlipoic acids in oxidized and reduced forms have BDE = 85–87 in vacuum and 95–97 in water [52]; trans(cis)-resveratrol and its derivatives – BDE = 69–82 in vacuum and 70–86 in water [53,54]; trans-resveratrol analogs – BDE = 69–83 in vacuum [55,56]; trans-p-coumaric acid – BDE = 83 in vacuum, 85 in water and trans-sinapinic acid – BDE = 77 in vacuum and 78 in water [57]; trans-ferulic acid – BDE = 323–330 in vacuum and 338–342 in water [58]. Comparison of the BDE values confirms that GA is one of the most powerful antioxidants found in nature, and this fact explains its common occurrence in herbaceous materials and food products, especially fruits [8].

4. Conclusions

A detailed analysis of the results obtained indicates that the B3LYP and M06–2X methods combined with the basis set cc-pVQZ provide a useful tool to gain insight into GA's structure and the free radical scavenging mechanisms attributed to this compound. The extremely high ability of GA to eliminate free radicals encourages researches to conduct research aimed at theoretical modeling new derivatives of GA that will increase their antioxidant potency and decrease their toxicity [30]. In this way, GA-based compounds could be applied as dietary supplements, preservatives, and antioxidants of food, as well as cosmetic and medicine ingredients. The results obtained clearly demonstrate that the B3LYP method, recently replaced by M06–2X, LC-ωPBE, BHandLYP, ωB97XD ones and recommended in thermodynamic and kinetic calculations, should not be banished, and can be restored to its rightful place in the field of DFT calculations. However, to obtain reliable results concerning the activity characteristics of chemical compounds, the approach presented by Sousa and Peterson [26] should be applied. They used in calculations various methods (DFT, CCSD, CCSD(T), MP2, MP4), models (M06–2X, LC-ωPBE, ωB97XD), basis sets (6–311++G(df,p), cc-pVDZ, aug-cc-pVDZ, cc-pVTZ, aug-cc-pVTZ etc.), and finally confronted the theoretical and experimental results. For this purpose, a broad spectrum of activity descriptors should be employed, and their theoretical and experimental consistency should be the basic criterion for selecting the optimal calculation approach.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.