A statistical framework for tracking the time-varying superspreading potential of COVID-19 epidemic

Abstract

Timely detection of an evolving event of an infectious disease with superspreading potential is imperative for territory-wide disease control as well as preventing future outbreaks. While the reproduction number (R) is a commonly-adopted metric for disease transmissibility, the transmission heterogeneity quantified by dispersion parameter k, a metric for superspreading potential is seldom tracked. In this study, we developed an estimation framework to track the time-varying risk of superspreading events (SSEs) and demonstrated the method using the three epidemic waves of COVID-19 in Hong Kong. Epidemiological contact tracing data of the confirmed COVID-19 cases from 23 January 2020 to 30 September 2021 were obtained. By applying branching process models, we jointly estimated the time-varying R and k. Individual-based outbreak simulations were conducted to compare the time-varying assessment of the superspreading potential with the typical non-time-varying estimate of k over a period of time. We found that the COVID-19 transmission in Hong Kong exhibited substantial superspreading during the initial phase of the epidemics, with only 1 % (95 % Credible interval [CrI]: 0.6–2 %), 5 % (95 % CrI: 3–7 %) and 10 % (95 % CrI: 8–14 %) of the most infectious cases generated 80 % of all transmission for the first, second and third epidemic waves, respectively. After implementing local public health interventions, R estimates dropped gradually and k estimates increased thereby reducing the risk of SSEs to approaching zero. Outbreak simulations indicated that the non-time-varying estimate of k may overlook the possibility of large outbreaks. Hence, an estimation of the time-varying k as a compliment of R as a monitoring of both disease transmissibility and superspreading potential, particularly when public health interventions were relaxed is crucial for minimizing the risk of future outbreaks.

1. Introduction

Coronavirus disease 2019 (COVID-19) has been continuously spreading around the world since its first detection in late December 2019. As of 23 January 2023, the disease has incurred more than 660 million cases and over 6.7 million associated deaths (WHO Coronavirus (COVID-19) dashboard, n.d.), aggravating the public health burden and bringing substantial health threats worldwide.

The effective reproduction number (R), defined as the average number of secondary cases generated by a typical infectious individual (Heesterbeek, 2002), is a crucial biological parameter that measures the transmissibility of an infectious disease. R fluctuates dynamically as the transmissibility and population susceptibility to the infection changes (Flaxman et al., 2020). Intuitively, when the value of R is below unity, the disease cannot persist and would eventually die out in the population. Monitoring the R during the epidemic is therefore of crucial importance to provide a timely understanding of the disease transmissibility and thus to evaluate the effectiveness of the current public health control measures (Yeoh et al., 2021). Nevertheless, R only reflects the average transmission potential across the whole case population. When solely focusing on R, one fails to appreciate the importance of another parameter in pandemic progression, the transmission heterogeneity, which has been widely observed in the current pandemic (Bauch, 2021). Disease outbreaks involving unusually large numbers of secondary cases seeded by one source case were recorded in many settings like Japan (Koizumi et al., 2020), Hong Kong (Adam et al., 2020) and European countries (Quinn, 2020, Correa-Martínez et al., 2020). These phenomena are known as superspreading events (SSEs), in which the source case is known as a super-spreader. Superspreading has also been observed in other types of coronavirus including the SARS-CoV and the MERS-CoV (Wang et al., 2021).

Although the key driver of SSEs has not been well-established, relevant biological and human behavioral factors were found from epidemiological investigations. Broadly, individual heterogeneity in virus shedding and social contact patterns are major contributing factors toward the occurrence of the COVID-19 SSEs (Lewis, 2021, Frieden and Lee, 2020). Statistical analysis has shown that SSEs were equivalent to the “fat-tail event”, meaning that the occurrence of the SSEs was extremely infrequent but still likely (Wong and Collins, 2020). More importantly, if an ongoing epidemic is characterized by SSEs, the underlying transmission pattern is highly likely to be heterogeneous – a small number of infectious individuals is able to generate a large number of cases. Public health interventions that target potential super-spreaders or high superspreading potential settings (e.g. contact tracing, social distancing) would control the epidemics more efficiently (Lewis, 2021, Woolhouse et al., 1997, Althouse et al., 2020).

In Hong Kong, large clusters of cases were persistently observed even under rigorous public health interventions (Adam et al., 2020, Westbrook, 2020, Lee, 2021). Previous modeling studies indicated that the local transmission exhibited significant superspreading potential during the early phase of the epidemics, with 80 % of all transmissions generated by less than 20 % of the most infectious cases (Adam et al., 2020). Given that the superspreading potential can change over the course of the outbreaks as public health interventions conducted (Lim et al., 2021, Adam et al.,). In this paper, we extended a previous estimation approach to jointly estimate the time-varying superspreading potential and transmissibility of COVID-19 and demonstrated our method using the three epidemic waves of COVID-19 in Hong Kong. In addition, we compared our time-varying estimate method with the traditional grand estimation approach using an individual-based outbreak simulation.

2. Methods

2.1. Data

The line listing of infected cases from 23 January 2020 to 30 September 2021 covering the three epidemic waves was collected from the Center for Health Protection (CHP) in Hong Kong. Individual information including demography, illness onset date, case confirmation (reporting) date, and epidemiological linkage were available from the dataset. Each case was classified by the following categories: imported case (infector, case got infected outside Hong Kong), local case (infector, case infected locally with unknown source), close contact with imported/local cases (infectee, case had an epidemiological link with known infector). Hong Kong has implemented a series of public health interventions including border control, personal protective measures, physical distancing with restriction of socio-economic activities, and contact tracing followed by case isolation. These interventions were carried out in a “suppress and lift” manner (Han et al., 2020) and different phases of interventions were captured from government press releases, reports, and websites (GovHk, n.d.). To account for the intensity of the implemented interventions by the Hong Kong government, we employed the stringency index which is a composite measure based on public health response indicators such as physical distancing, closure of public facilities, and travel bans (Hale et al., 2021). A higher score indicates a stricter response (i.e. 100 = strictest response). The stringency index and captured intervention phases were used only for aiding the comparison and interpretation of the results.

For analysis and interpretation, we denoted any infector and infectee that had an epidemiological link between each other as a transmission pair, and we denoted a cluster of cases as a transmission cluster if all secondary cases had the same source cases or if all offspring cases were associated with a same exposure (same infector/source cases or contact settings) but the epidemiological links between cases were unknown. In our study, we defined different types of transmission clusters. A transmission cluster could encompass single or multiple sources of infections, and involve a single generation of infections (i.e., secondary cases directly generated by the source cases) or a chain of infections (i.e., the epidemiological linkage and number of generations for cases within the cluster were unknown). Cases that led to no secondary cases were also counted as a cluster with a size equal to one.

We re-categorized the cases into 6 mutually exclusive types of clusters based on the settings where the primary infections occurred. They included household (initiated by local cases between family members), workplace (initiated by local cases in workplaces), social (initiated by local cases in social settings such as entertainment, restaurants, social gatherings, and healthcare facilities), clusters initiated by imported cases, sporadic local (local cases that have no secondary cases), and sporadic imported (imported cases that had no secondary cases). Twelve infectees without any information on the exposure history and source cases in the analysis.

2.2. Data analysis

2.2.1. Transmission patterns in Hong Kong

Descriptive statistics were drawn to delineate the dynamics of the transmission patterns characterized by different types of transmission clusters during three epidemic waves. The temporal distributions of the secondary infections as well as the observed SSEs, defined as an event with at least 6 secondary cases with respect to a source case were displayed graphically.

2.2.2. Joint estimation of time-varying R and k

Given the stochastic effect of the transmission events, the transmission process can be described by a secondary case distribution of the source cases, the mean of which represents the population transmissibility of an infection. According to Lloyd-Smith et al. (2005), the transmission heterogeneity can be quantified by a dispersion parameter k originated from the Gamma distribution, which describes the variations in individual case transmissibility. We assumed the transmission events are modeled by the Poisson process, the resultant secondary case distribution is thereby a Poisson-Gamma mixture, which is also called Negative Binomial distribution (NBD) (Lloyd-Smith et al., 2005). Sufficiently small value of k (k < 1) of the NBD indicates a substantial heterogeneous transmission pattern (VanderWaal and Ezenwa, 2016, Lloyd-Smith, 2007). NBD is not qualitatively different from a Poisson distribution when k = 10 or larger but is quite dissimilar to one with k = 1 or smaller (Lloyd-Smith, 2007). In order to jointly estimate R and k by using different types of transmission cluster data, we first followed previous works (Blumberg et al., 2014, Endo et al., 2020, Farrington et al., 2003) to construct the likelihood functions. When a transmission cluster of size j contains a single generation of cases that are infected by $i$ cases, according to the branching process theory and the property of the generating function, the likelihood that $i$ source cases (jointly) directly generated a total of $\left(\mathit{j}-\mathit{i}\right)$ cases is given by Blumberg et al. (2014):

$$P_1(J=j\mathrm{;}i)=\frac{\mathrm{\Gamma }(j-i+\mathit{ki})}{\mathrm{\Gamma }(j-i+1)\mathrm{\Gamma }(\mathit{ki})}{(\frac{R}{R+k})}^{j-i}{(\frac{k}{R+k})}^{\mathit{ki}}$$

When a transmission cluster involves unknown number of generations of infection, that is, only knowing the total size of the cluster (chain of infections) $j$ and the number of source infection $i$, then the likelihood of observing such transmission cluster is given by Blumberg et al. (2014) and Endo et al. (2020):

$$P_2\left(J=j\mathrm{;}i\right)=(\frac{i}{j})\frac{\mathrm{\Gamma }(j-i+\mathit{kj})}{\mathrm{\Gamma }(j-i+1)\mathrm{\Gamma }(\mathit{kj})}{(\frac{R}{R+k})}^{j-i}{(\frac{k}{R+k})}^{\mathit{kj}}$$

Here, $\frac{i}{j}$ is the normalization factor for the requirement of the extinction of the cluster (Blumberg et al., 2014).

For an ongoing epidemic, clusters’ sizes are likely to grow after the time of estimation, which would result in censored cluster data. To address this issue, we adjusted the above likelihood function as per (Endo et al., 2020, Farrington et al., 2003):

$$L_1\left(R,k\right)={P_1\left(J=j\mathrm{;}i\right)}^c{(1-{\sum }_{j=i}^{j-i-1}{P}_1\left(J=j\mathrm{;}i\right))}^{1-c}$$

$$L_2\left(R,k\right)={P_2\left(J=j\mathrm{;}i\right)}^c{(1-{\sum }_{j=i}^{j-1}{P}_2\left(J=j\mathrm{;}i\right))}^{1-c}$$

Here, $c$ is an indicator of censoring. $c=0$ if the cluster is censored and $\mathit{c}=1$ if the cluster is considered self-limited. A cluster is censored if it has new confirmed cases within 11 days before the time of estimation. We chose 11 days as this is the 99th percentile of the serial interval distribution that was estimated from our identified local transmission pairs (See Supplementary materials for details). The 11-day is also consistent with the upper bound of a generation interval estimated from a previous study (around 10 days derived by calculating the 99th percentile of their estimated distribution) (Ferretti et al., 2020). The likelihood is formed as the product of $L_1\left(R,k\right)$ and $L_2\left(R,k\right)$ over all transmission clusetrs. Sporadic local/imported cases were counted as clusters with sizes equal to one.

We estimated the R and k through a weekly sliding window process. In each window, R and k were jointly estimated by the Markov chain Monte Carlo (MCMC) method. Within each window, we only used those new transmission clusters for estimation and dropped those clusters without known source cases as the window is moving. The Normal and Half-Normal distributions were chosen as weakly-informative prior distributions for R and k, respectively. Followed by Endo et al., (2020), we employed a Hit and Run Metropolis algorithm and obtained 2000 thinned samples from 100,000 MCMC iterations. The convergence of each MCMC chain was checked by using the trace plot and Gelman-Rubin-Brooks convergence diagnostic (Gu and Li, 2022). We discarded the first half of the thinned samples as burn-in and the 95 % credible intervals for each parameter were sampled from the marginal posterior distributions. As our unit of observation is transmission cluster, we set the window size to be around 30 days as the main result to avoid covering a small sample size in some windows. We also examined the effect of a relatively short window size (21 days) as a sensitivity analysis of our estimation framework. To mimic a nearly real-time estimation, we excluded asymptomatic cases in the analysis as the main results and applied our estimation framework based on the illness onset date of cases from 16 February 2020 to 25 July 2021, since then no local symptomatic transmission has been reported by the end of the study period (30 September 2021). We also performed our framework on all cases observed during the study period (including both symptomatic and asymptomatic cases) as sensitivity analysis. We imputed the symptom onset date as the case confirmation date for asymptomatic cases during each window. The time-varying R and k estimates were reported at the end of each window.

2.2.3. Superspreading potential

All SSEs occurred during the study period were identified and were described by the size of the SSEs, and the time interval between the illness onset date of the super-spreaders and the reporting date of the last cases relevant to the SSEs. Armed with the R and k estimates, we calculated the expected proportion of the most infectious cases that generated the majority (80 %) of all transmissions (Endo et al., 2020). The risk of SSEs was quantified as the expected probability of the occurrence of SSEs from the assumed Negative-Binomial secondary case distributions, given the predefined SSEs threshold. The SSEs threshold was defined as the 99 % quantile of the Poisson distribution of the basic reproduction number of SARS-CoV-2 (Adam et al., 2020, Lloyd-Smith et al., 2005). Thus, based on the current consensus estimations of the basic reproduction number (i.e., 2–3) of the wild-type strains (Zhao et al., 2020, Zhang et al., 2020), the SSEs threshold was determined to be 6–8, and we used 6 here as a lower bound definition. A single generation of spread of the infections that initiated by one source case would be counted as SSEs if the number of secondary cases is equal to or above the threshold.

2.2.4. Outbreak simulations

We used individual-based branching process models to compare the time-varying estimate of k in identifying the outbreaks with the traditional non-time-varying grand estimate. We also compared our estimated time-varying R values with the widely-adopted method (the R package “EpiEstim”) (Cori et al., 2013). We applied the branching process model provided by Hellewell et al. (2020) but made some changes to the model structure to adapt it to our simulation setting (Supplementary materials). In summary, we assumed the number of new cases of the next generation was sampled from the NBD of each source case of the current generation. Outbreaks were simulated under three scenarios, which were defined as follows: 1) Dynamic R and Dynamic k: The NBD of source cases in each generation were parametrized by our time-varying (30-day window size) R and k estimates. 2) Dynamic R and Fixed k: The NBD of source cases of each generation were parametrized by the same R values used in 1) and a fixed value of k based on the traditional non-time-varying estimation method using all the transmission clusters observed during the study period (Supplementary materials). 3) EpiEstim R and Fixed k: The NBD of source cases of each generation were parametrized by R estimates generated from the R package “EpiEstim” (Cori et al., 2013, Thompson et al., 2019) (Supplementary materials) and same k value used in 2). Fifty outbreaks under each scenario were simulated and the epidemic curves by generation, outbreak size distributions, and secondary case distributions were obtained from the simulated outbreaks. In addition, by applying the classic branching process theory (Harris, 1990), we examined the relationships between the k and the number of generations to the extinction of outbreaks when R is less than one (Supplementary materials).

All analysis were conducted in R version 4.0.2 (R Foundation for Statistical Computing).

3. Results

3.1. Descriptive statistics of the local epidemics

There have been a total of 12,221 confirmed cases recorded from 23 January 2020 to 30 September 2021 by Hong Kong CHP, among which, female (6355, 52 %) and younger people (8799, 76 %) made up of a higher proportion than male and elderly cases, and approximately one-third of all cases were asymptomatic (3971, 33 %). The outbreak with the largest peak size (N = 149) was reported in the second wave and the longest outbreak duration (approximately 5 months, November 2020–March 2021) was observed in the third wave.

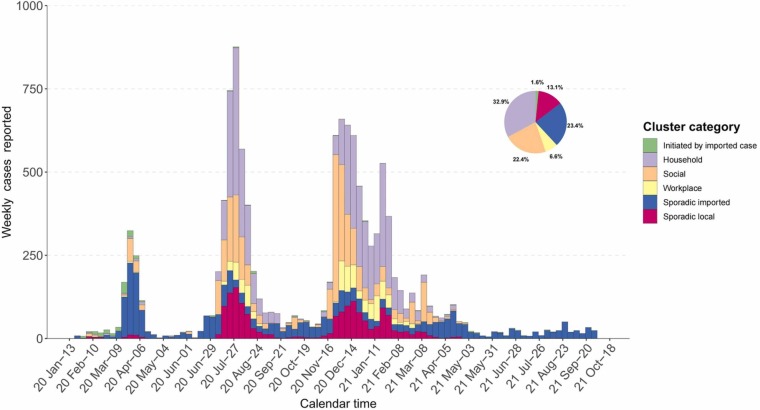
After removing 12 cases whose contact history was missing, we categorized all cases according to the transmission clusters. The COVID-19 epidemic curve by the reporting date, stratified for the size of local transmission clusters is displayed in Fig. 1. It shows that local transmissions were most likely to occur in households (32.9 %), followed by social settings (22.4 %) and workplace (6.6 %). Specifically, a larger proportion of the transmissions were initiated by import cases (10.3 %) during the first wave than in other epidemic waves. Besides, household and social transmissions dominated the local epidemics during the second and third waves ( Table 1).

Fig. 1.

Epidemic curve of confirmed cases in Hong Kong by week (n = 12,209). All cases were categorized into transmission clusters by colors based on the settings where the infections occurred.

Table 1.

No. of clusters and cases by epidemic waves in Hong Kong.

	First wave (Jan–Apr 2020)		Second wave (Jul–Sep 2020)		Third wave (Nov–Mar 2021)		Total
	Clusters (N = 698)	Cases (N = 923)	Clusters (N = 172)	Cases (N = 3824)	Clusters (N = 2350)	Cases (N = 6029)	Clusters (N = 6011)	Cases (N = 12,209)
Household	12 (1.7)	33 (3.6)	453 (26.3)	1586 (41.5)	633 (26.9)	2340 (38.8)	1111 (18.5)	4015 (32.9)
Social	9 (1.3)	138 (15.0)	117 (6.8)	888 (23.2)	136 (5.8)	1617 (26.8)	271 (4.5)	2737 (22.4)
Workplace	2 (0.3)	10 (1.0)	38 (2.2)	227 (5.9)	82 (3.5)	568 (9.4)	123 (2.0)	807 (6.6)
Initiated by imported cases	28 (4)	95 (10.3)	5 (0.3)	15 (0.4)	4 (0.2)	9 (0.2)	49 (0.8)	193 (1.6)
Sporadic imported	607 (87.0)	607 (65.8)	453 (26.3)	453 (11.8)	635 (27.0)	635 (10.5)	2860 (47.6)	2860 (23.4)
Sporadic local	40 (5.7)	40 (4.3)	655 (38.1)	655 (17.2)	860 (36.6)	860 (14.3)	1597 (26.6)	1597 (13.1)

Statistics are presented as no. of clusters (%) and cases (%).

The percentage was obtained by dividing the cells’ number by the column total.

3.2. Secondary case distributions and observed SSEs

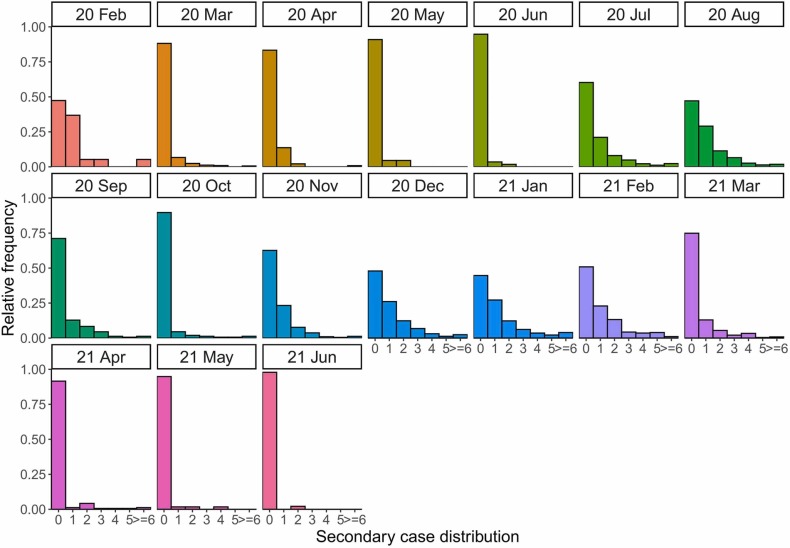
A total of 5686 unique transmission pairs with 2130 infectors were identified by 30 September 2021 ( Fig. 2). More than 90 % of cases led to zero secondary infection after the end of the first and third waves (May–June 2020 and May-June 2021). We identified 64 SSEs throughout the three epidemic waves. Of the identified SSEs, nearly half occurred in social settings (47 %, 30/64), with a few initiated by asymptomatic cases (9 %, 6/64). We found that majority of the SSEs occurred during the second and third waves, and were heavily concentrated during the initial growth phase ( Fig. 3).

Fig. 2.

Observed secondary case distributions by month in Hong Kong. Secondary case distributions of identified 2130 infectors and 5689 infectees in Hong Kong during study period. No transmission pairs were detected in January 2020 and from July to September 2021.

Fig. 3.

Identified SSEs by 30 September 2021 in Hong Kong. The SSEs were defined with as a single generation of spread from the source case, who had at least 6 secondary cases. The size of the bubble represents the number of the secondary cases of a superspreading event. The bubbles were colored by transmission settings, shaped by asymptomatic or symptomatic super-spreaders. The location of the bubble is the report date of the first infectee and the error bar represents the duration of the SSEs from the illness onset date of the super-spreaders to the report date of the last infectee. The labeled SSEs were the three largest among others and were suspected as the key initiators of the subsequent new outbreaks (Adam et al., 2020, Westbrook, 2020, Lee, 2021).

3.3. Superspreading potential of COVID-19

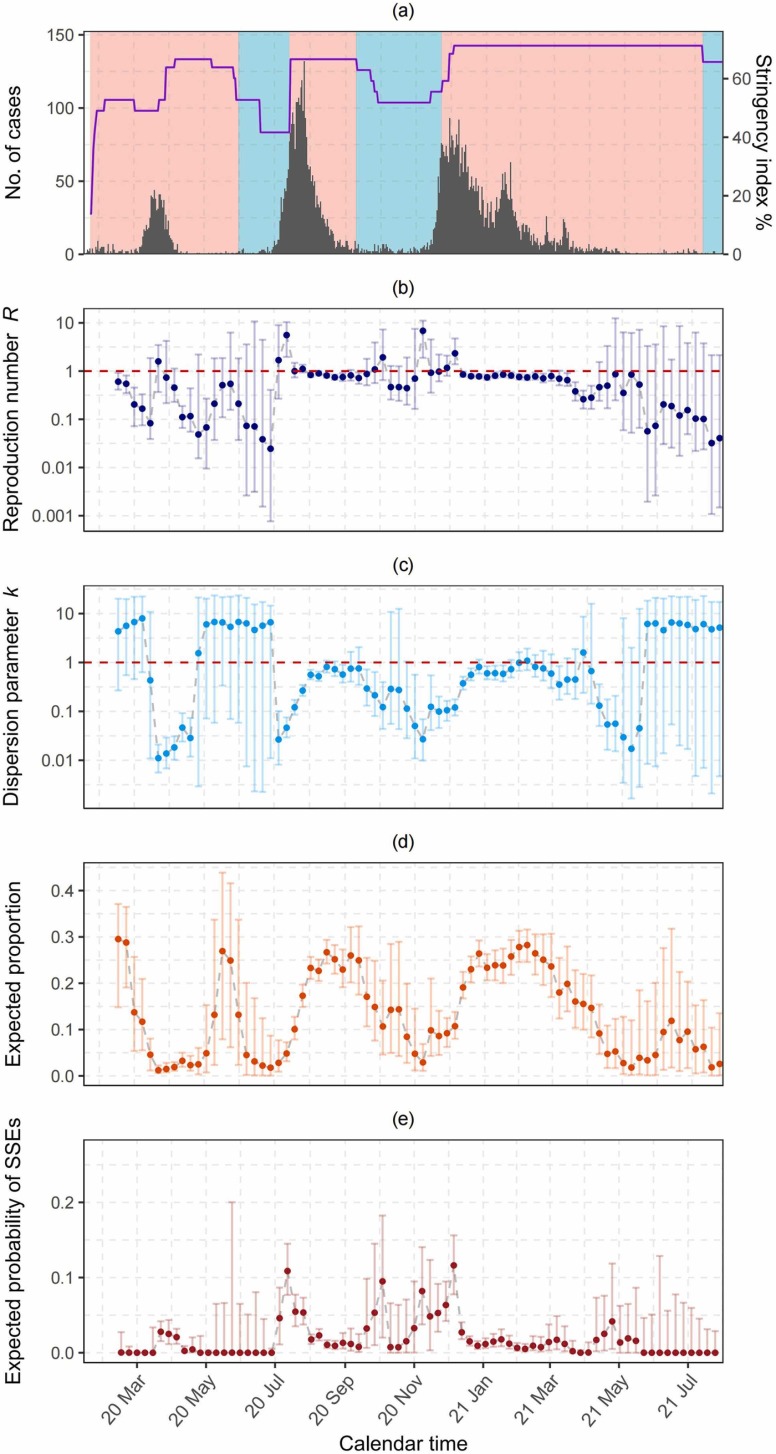
The superspreading potential of COVID-19 characterized by the time-varying R and k estimates unfolded throughout local epidemics ( Fig. 4). During the initial growth phase (i.e., first month) of the local epidemic waves, only 1 % (95 % CrI: 0.6–2 %), 5 % (95 % CrI: 3–7 %) and 10 % (95 % CrI: 8–14 %) of the most infectious cases generated 80 % of all transmission for the first, second and third waves, respectively. (Fig. 4d). The risks of observing SSEs were high with elevated R values and substantial low k values for the first [R = 1.59, (95 % CrI: 0.37–3.47); k = 0.01, (95 % CrI: 0.006–0.02)], second [R = 5.59, (95 %CrI: 1.97–10.35); k = 0.05, (95 % CrI: 0.03–0.08)] and third waves [R = 2.34, (95 % CrI: 1.39–4.75); k = 0.12, (95 % CrI: 0.08–0.18)] (Figs. 4b and 4c), with respectively around 3 %, 11 % and 12 % of total transmission events expected to be SSEs (Fig. 4e). During a short period (around two weeks) after the public health interventions were escalated, the risks of SSEs were approaching to zero, with the time-varying R estimates dropping to 0.45 (95 % CrI: 0.23–1.13), 0.83 (95 % CrI: 0.75–0.91) and 0.78 (95 % CrI: 0.72–0.86), and k rising to 0.02 (95 % CrI: 0.01–0.03), 0.56 (95 % CrI: 0.45–0.71) and 0.56 (95 % CrI: 0.43–0.76) for the first, second and third waves, respectively (Figs. 4b, 4c and 4e). It should be noted that during the relaxation phase before the third wave (from mid-Sep to mid-Nov 2020), although the incidence was low with R values hovering around 1, the superspreading potential was still high due to low k values (around 0.1) with 80 % of all transmissions generated by only 8–14 % of the most infectious cases (Fig. 4c). Sensitivity analysis on the length of the sliding window were shown in Fig. S1. The time-varying estimates were similar when narrowing the window size to be 21 days though the credible intervals were relatively wider, as compared to the main results. The time-varying estimates were also similar to the main results when including asymptomatic cases into the analysis (30 day window), while the credible intervals were narrower, as shown in Fig. S2.

Fig. 4.

Time-varying estimations by illness onset date. (a) Epidemic curve by illness onset date in Hong Kong by 25 July 2021. The shaded area represents the intervention (red) and relaxation (blue) phases, respectively. The black bar denotes the incidence, and the purple solid line represents the Hong Kong government stringency index reflecting the intensity of implemented public health interventions, which was displayed in the scale of 7-day moving averages in percentage. (b) Time-varying estimation of R. (c) Time-varying estimation of k. (d) Estimated time-varying proportion of cases that generates 80 % of all transmissions. (e) Estimated time-varying risks of SSEs, which is the expected probability of SSEs obtained from the NBD secondary case distributions for given R and k estimates. The solid points represent the median estimates and the error bars in (b), (c), (d) and (e) denote the 95 % credible intervals. The red horizontal dashed lines in (b) and (c) denote values of estimates equal to 1. The y-axis in (b) and (c) were log10 transformed though the values on the ticks remained untransformed.

3.4. Outbreak simulations and generations to the extinction of minor outbreaks

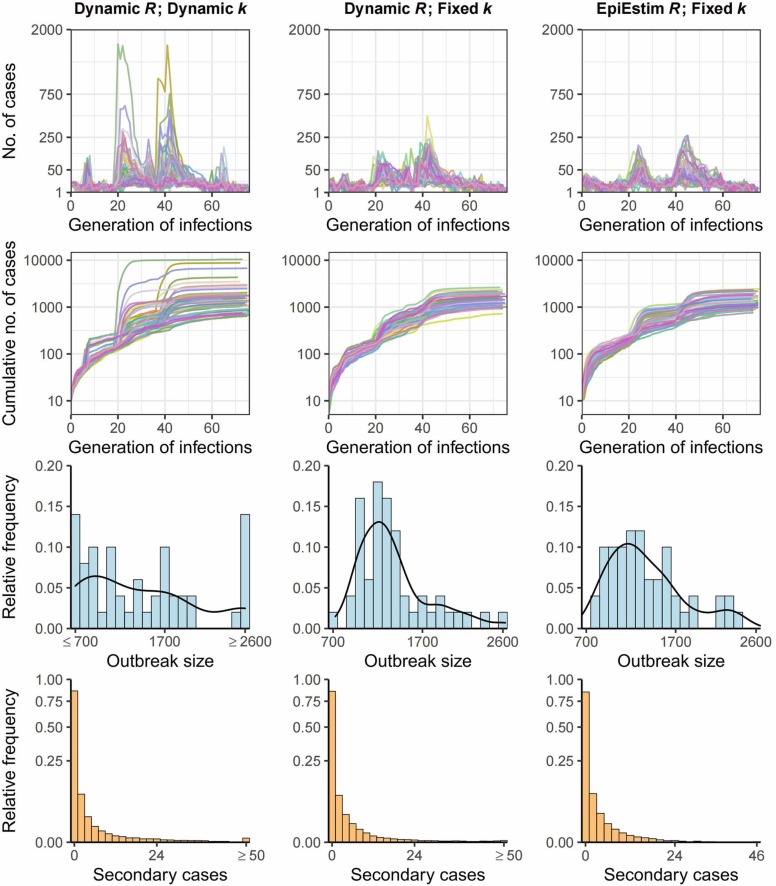
The simulated outbreaks generally captured the patterns of the real-world epidemics ( Fig. 5). In the scenarios of using the dynamic R values (i.e., time-varying estimates using the Hong Kong data), the outbreaks simulated under dynamic k and fixed k value (k = 0.3) differed substantially. The simulated epidemic curves using dynamic k appeared to be more explosive, with a surge of cases occurring within only a few generations during the growth phase of the second and third waves of outbreaks, resulting from a much smaller time-varying k value (< 0.1) compared to the fixed one. The smaller k value gives rise to the probability of observing more extreme SSEs (see the secondary case distribution in Fig. 5, and the large SSEs observed in Fig. 3), and thereby is likely to result in a larger epidemic size. On the other hand, a smaller k value also increases the probability of extinction of clusters, which could downsize the outbreak size. As shown in the simulated outbreak size distributions in Fig. 5, compared to other scenarios, the distribution in the dynamic k scenario is more dispersed and had a larger proportion of much smaller and larger outbreaks. It is worth noting that given the same fixed k value, the simulated outbreaks under our dynamic R value were similar to the outbreaks simulated by the EpiEstim R. The relationship between the k and the number of generations to the extinction of outbreaks with a R value less than one was intricate (Fig. S3). Given the same k value, decreasing R may cause minor outbreaks to go extinct more quickly (i.e., a smaller number of generations), and this effect is especially evident when k becomes larger. On the other hand, for a given value of R, an increase in k value could lead to minor outbreaks go extinct more slowly (i.e., more generations), and such effect becomes evident when k is between 0.1 and 1.

Fig. 5.

Outbreaks simulations by branching process. Fifty outbreaks initiated by 5 cases were simulated under different scenarios of R and k values. First two rows of figures represented the epidemic curve and cumulative cases by generation of infections, and the last two rows represented the distributions of simulated outbreak sizes and distributions of secondary cases by the source cases over the course of the 50 simulated outbreaks. The solid black curve in the distributions of simulated outbreak sizes plots represented the kernel density. The y-axis in the epidemic curve and cumulative cases plots were square root transformed though the values on the ticks remained untransformed. The y-axis in the secondary case distribution were log transformed though the values on the ticks remained untransformed.

4. Discussion

A timely understanding of COVID-19 transmissibility and superspreading potential is pivotal for formulating disease control policies. In this study, we developed an estimation framework to characterize the time-varying potential of superspreading and applied it to the three COVID-19 epidemic waves in Hong Kong. The data application showed the potential of SSEs was modified by the public health interventions, with a declined risk during the intervention phase but an elevated risk when interventions were eased. Although the local epidemics exhibited significant transmission heterogeneity most of the time (i.e., k < 1), the simulation results demonstrated that the traditional non-time-varying estimate of k may not well characterize the transmission heterogeneity at certain stages of the epidemics where the superspreading potential is considerably high, and thereby may overlook the possibility of an even larger outbreak size. The identified transmission patterns and the corresponding estimations help to give a picture of the local transmission dynamics and superspreading potential and inform the formulation of the public health policy in adjusting social restrictions.

While numerous studies have been conducted for estimating the dynamic of the effective reproduction number R (Cori et al., 2013, Thompson et al., 2019, Wallinga and Teunis, 2004, Tariq et al., 2020) during epidemics, few studies investigated the dynamic pattern of k value. Adam et al. also estimated the time-varying k during the third epidemics waves in Hong Kong by applying a different approach from ours. In their study, instead of joint estimation, the k in each dynamic window was univariately estimated by fitting identified transmission pairs to the NBD, with R fixed as an input parameter that were separately estimated from the R package “EpiNow2” (Abbott et al., 2020). This package, however, required the knowledge of generation interval, which is relatively hard to be estimated from contact tracing data. Moreover, as the generation interval could change over the course of an outbreak, a single fixed generational interval distribution may lead to an upward or downward bias on real-time R estimates, which depends on the epidemic phases where the contact tracing data comes from Ali et al. (2020). The methodology framework of jointly estimating R and k can be generally categorized into two branches based on the type of data used. One can use epidemiological contact tracing data to infer R and k of the secondary case distribution (Adam et al., 2020, Endo et al., 2020, Sun et al., 2021, Shi et al., 2021). Alternatively, phylogenetic analysis can be performed for parameter estimations when genome sequencing data is available (Wang et al., 2020). We chose to use epidemiological data here because it is easily accessible for timely analysis purposes when compared to genomic data. When contact tracing data is available, previous studies mainly used reconstructed transmission pairs to directly infer the secondary case distribution (Adam et al., 2020, Sun et al., 2021, Shi et al., 2021). This method, however, only uses partial information from the epidemiological data since not all cases can be epidemiologically linked into transmission pairs by contact tracing alone. As a result, large transmission clusters are likely to be missed (Lloyd-Smith, 2007, Endo et al., 2020). As indicated by Adam et al., when using transmission pair data, imperfect case detections could lead to an overestimation of k. By applying the branching process theory, we constructed the likelihood function of observing transmission cluster to infer the parameters of the secondary case distribution (i.e., R and k), such that our unit of observation for analysis was transmission cluster rather than the number of secondary cases from each source case. Cluster-based analysis could provide timely information on the local transmission pattern, especially for an ongoing epidemic where the implementation of contact tracing is limited (Yuan and Blakemore, 2022). A previous study conducted in Hong Kong during the early epidemic phase analyzed the local transmission clusters, indicating sustained transmissibility and significant transmission heterogeneity characterized the local outbreak (Wong et al., 2020).

The observed dynamics of local transmission patterns indicated a possible order of the occurrence of the transmission events that made up the large outbreaks, that is, a large proportion of household transmissions followed by a relatively small proportion of transmissions occurring in the workplace and social settings, which was also consistently found in other modeling study conducted in Hong Kong (Liu et al., 2021), indicating that the outbreaks which began in social settings were largely responsible for the subsequent widespread transmissions in the community. This pattern could inform the efficient implementation of public health interventions, that is, once new outbreaks started from social settings, the closure of relevant social places should be followed immediately by contact tracing for timely identification and isolation of household cases (Chong et al., 2021). Although the potential role of SSEs played in local epidemics cannot be confirmed by our data, given the occurrence of SSEs that were particularly concentrated during the early phase of local waves, we thus speculated that SSEs might be the initiator of the subsequent local outbreaks, which was also suggested by an earlier modeling study (Kochańczyk et al., 2020).

Our analysis highlights the importance of tracking the dispersion parameter k along with R for a better understanding of the transmission dynamics. When the R estimate was greater than one, on one hand, the transmission would be highly heterogeneous if the k estimate was significantly low (e.g., below one), and the epidemics are explosive (as seen from the left corner plot of Fig. 5) yet controllable with rapid case finding and isolation, as a result of the higher probability of extinction for most of the transmissions (Lloyd-Smith et al., 2005). On the other hand, if the time-varying k value increased, the transmission would become homogeneous, favoring the risk of sustained outbreaks (Harris, 1990). This pattern was observed during the intervention phase of the second and third waves, though R is around one, the duration of the outbreaks last for a long time since the k value increased (around one). This was also consistent with the findings from Fig. S3, which suggests that even with an R value equals to 0.9, the small outbreaks may still persist for a long time when the time-varying k is around one. Therefore, planning control strategies that tailored the time-varying transmission pattern (both R and k values) is crucial for efficient outbreaks mitigation. Targeted public health measures including the closure of entertainment facilities, social distancing in eateries, and limitation on social gatherings were imposed during the intervention phases in Hong Kong (GovHk, n.d.), which potentially reduced R and enlarged the k, indicating the extreme events (SSEs) were trimmed from the (long) right tail of the secondary case distribution, where the zero class (cases lead to no secondary cases) increased. This pattern is conformed with a previous study conducted in South Korea, showing that the k value increased during the latter epidemic phases, possibly as a result of the escalated control measures (Lim et al., 2021). Early mathematical modeling studies indicated mitigation measures that curb SSEs would be effective to control epidemics (Nielsen et al., 2021, Kain et al., 2021), with a greater impact when a specific type of social contact was reduced (Sneppen et al., 2021). What is less certain is the timing to implement these measures. Although we cannot identify super-spreading settings preceding the occurrence of transmissions, the time-varying k estimates can be a complement of the R to timely indicate both transmissibility and superspreading potentials of the virus in context, which could guide targeted public health measures to quickly curb the SSEs and cut the scale of subsequent outbreaks.

Our study has the following limitations. First, as our time-varying estimates rely on contact tracing data, it is expected that any degree of case under-detection and recall bias would bias our results. In particular, an upward bias on both R and k would be expected when the sporadic cases (i.e., cases led to zero secondary infections) were more likely to be under-detected by contact tracing. On the other hand, if each case was detected with the same probability, only a downward bias on R would be expected (Lloyd-Smith, 2007, Blumberg and Lloyd-Smith, 2013). Nonetheless, the probability of detecting each case was assumed to be high in Hong Kong during the study period because each epidemic wave was mitigated quickly as a result of stringent case contact tracing, isolation, and mass testing (GovHk, n.d.). In addition, the outbreaks simulated from our R estimates were similar to that from the R estimates generated from the standard method (i.e., EpiEstim) which is less subjected to the case-detection bias. Second, although our sensitivity analysis on window size showed similar results to our main analysis, we found that the credible intervals of the estimates become too wide to inform policy when we set the window size to 7 days or 14 days (we did not show the result). Additionally, there was considerable uncertainty surrounding our R and k estimates when the sample sizes of the clusters were quite small. Further modeling studies are warranted to investigate the relationship between the window size and the accuracy of the estimates. Third, our time-varying estimates should be interpreted with caution, given that a transmission cluster could involve possibly multiple generations, possibly crossing different public health intervention phases. In our framework, the effect of interventions in the context was averaged within each estimation window, such that effective interventions may cause a smoother change in our time-varying estimates, as opposed to a sudden change in estimates obtained from the standard method (i.e., EpiEstim) (Cori et al., 2013). Fourth, we used the serial interval distribution that was inferred from our identified transmission pairs when determining the censoring of a cluster. The serial interval estimates may be biased during an increase (more likely to be shorter) and decrease (more likely to be longer) of the incidence. However, as our data were collected from entire epidemic waves, such bias would be minimal (Kang et al., 2022). A previous study (Sender et al., 2022) indicated a larger upper bound of generation interval (theoretically had the same mean as serial interval) (around 17 days derived by calculating the 99th percentile of their estimated generation interval distribution) during the unmitigated phase of an epidemic (before any public health interventions were implemented). However, a series of strict control policies were imposed in Hong Kong since the detection of the first imported case locally, which trimmed down the unmitigated serial interval distributions (Ali et al., 2020). Therefore, the realized serial interval is expected to be shorter. Finally, although our estimation framework provided a possible way to jointly estimate the time-varying R and k in nearly real-time by using the transmission cluster data, contact tracing measures were limited especially during an ongoing epidemic, such that the transmission cluster data would not be timely available to enable the real-time estimates. Nonetheless, our analysis highlighted the importance of monitoring the k value, as a complement of R in characterizing the epidemics and informing control policies. We thus recommended proactive joint surveillance on R and k as long as enough transmission cluster data were available.

5. Conclusions

In summary, our study demonstrated a joint estimation of the time-varying R and k values is essential for the monitoring of disease transmissibility as well as superspreading potential, particularly during a period when public health interventions are relaxed in order to minimize a risk of outbreak resurgence. Our proposed estimation framework could be adapted in other settings to guide decisions in lifting restrictions to socio-economic activities wherever the transmission cluster data is available.

CRediT authorship contribution statement

Conceptualization: ZG, SZ and KCC. Data curation: TYC and CHKY. Formal analysis: ZG. Funding acquisition: KCC and EKY. Investigation: ZG and SZ. Methodology: ZG and SZ. Project administration: KCC, CHKY and EKY. Resources: KCC and EKY. Software: ZG and SZ. Supervision: KCC and EKY. Validation: KCC and EKY. Visualization: ZG. Writing – original draft: ZG and SZ. Writing – review & editing: SSL, CTH, NSW, MHW, JW, KCC, and EKY. All authors contributed to the revision of the manuscript. All authors read and approved the final manuscript.

Ethics approval and consent to participate

Ethics approval was obtained from the Joint Chinese University of Hong Kong – New Territories East Cluster Clinical Research Ethics Committee.

Funding

This work was supported by Health and Medical Research Fund [Grant nos. COVID190105, COVID19F03, INF-CUHK-1]; Collaborative Research Fund of University Grants Committee [Grant no. C4139-20G]; and National Natural Science Foundation of China (NSFC) [71974165], and Group Research Scheme from The Chinese University of Hong Kong.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

Data Availability

The authors do not have permission to share data.