Assessing sustainable operational conditions of a bottoming organic Rankine cycle using zeotropic mixtures: An energy-emergy approach

Abstract

In this work, an Organic Rankine Cycle system is used to produce electricity from the waste heat of an internal combustion engine (ICE). The toluene, and cyclohexane, are the selected pure fluids to be compared with the zeotropic mixtures. The zeotropic mixtures used as working fluids are cyclohexane/R11 (0.2/0.8), cyclohexane/R11 (0.25/0.75), and cyclohexane/R11 (0.3/0.7). An energy, exergy and emergy analysis was conducted to assess the sustainability of the whole system and the viability of the zeotropic mixture from the environmental point of view. Finally, a multi-objective optimization was carried out. The results showed that the zeotropic mixtures have better performance compared with the selected pure fluids when the net power and the exergy efficiency are considered. The pure fluids had a better Emergy Sustainability Index (ESI) index by 10% on average, there is not a big difference on this parameter so the advantages of using zeotropic mixtures as working fluids for this type of system cannot t be ignored. However, using the mixture the system obtained a lower Environmental load Ratio (ELR) value compared to cyclohexane and toluene. Finally, the multi-objective optimization was able to maximize the exergy efficiency for the working fluids by about 9.7% and reduce the ESI by 50.94%. This study intends to show the advantage and disadvantage of using zeotropic mixtures as working fluid on waste heat recovery systems that uses Organic Rankine cycle from the environmental point of view and using emergy as a way to asses the sustainability of the whole system.

Highlights

• •Energy-emergy performance comparison between pure fluids and zeotropic mixtures for bottoming ORC.
• •Sustainable operational condition for a waste heat recovery system using an ORC operating with zeotropic mixtures.
• •Parametric analysis to an Organic Rankine Cycle with emergy indexes as study variables.

energy-emergy approach; ORC; zeotropic mixtures; sustainability; waste heat recovery.

1. Introduction

The engine is one of the most widely used mechanical elements globally, given its versatility to perform different tasks, mainly used in the area of transportation or power generation [1]. However, this has several disadvantages. First, the emission of substances into the environment intensifies global warming. Second, the low efficiency in the production of useful energy. Therefore, reducing the emission of polluting gases and increasing efficiency in energy generation is a consolidated task in the scientific community [2]. Part of these studies has focused on changing the composition of the fuel in search of more environmentally friendly components, in addition to maximizing fuel efficiency [3,4,5,6].

The organic Rankine cycle (ORC) is a promising technology in waste heat recovery for power generation or cogeneration [7,8,9]. One of the advantages of the ORC over conventional steam cycles is the use of organic fluids with a low boiling point, which makes them more adaptable to systems with low-temperature in the heat source compared to water. Moreover, the ORC has a simple structure, low cost, and good applicability for different types of heat sources [10]. When designing an ORC, there are three fundamental challenges the selection of the working fluid, the sizing of the components, and the system’s design. This has allowed the ORC cycle to become an important alternative for increasing the overall efficiency of internal combustion engines [11].

Depending on the type of fluid, these can be classified according to the slope of the T-s saturation curve diagram in three categories: dry, wet, and isentropic. Among these three categories, it is suggested that isentropic substances provide better performance when used as working fluids [12]. The effect that produces the use of zeotropic mixtures over the ORC’ performance has been extensively studied, the mixtures have a temperature sliding during the phase change, which reduces the difference in temperature profiles in the evaporator and condenser, and therefore, the irreversibilities associated with heat transfer decrease, increasing the exegetic efficiency of the system [13]. Another characteristic of the mixtures is their low global warming potential (GWP), which reduces CO₂ emissions [10,[14], [15], [16]].

Several researches have conducted investigations on the implementation of zeotropic mixtures in ORC. Zhang et al. [16] designed an ORC system to recover residual energy for a diesel engine. The effect of eight types of zeotropic mixtures on the performance of the ORC system was analyzed. The authors concluded that each zeotropic mixture requires different degrees of superheating at particular evaporation pressures. Zhang et al. [17] adopted a regenerative organic Rankine cycle (RORC) to recover waste heat from a diesel engine. The authors considered isopentane/R245fa (0.7/0.3) as zeotropic mixture and R245fa as a pure fluid. The authors concluded that the use of the zeotropic mixture isopentane/R245fa (0.7/0.3) increases the net power output (10.54%) and improves the brake specific fuel consumption (9.55%).

Zhou et al. [18] presented a dual-loop Rankine system cycle to recover waste heat from an internal combustion engine. The authors used RC138/R1234yf, butane/R1234yf, and RC318/R245fa as zeotropic mixtures in the low-temperature loop (LTL). The results revealed that the use of RC318/R1234yf mixture can improve engine output by 11–12% compared to pure fluids. Collings et al. [19] proposed a novel study of an ORC system using a binary zeotropic mixture as the working fluid. The results obtained with these design changes show a substantial improvement of 23% in thermal efficiency over a conventional ORC when the heat source is 100 °C. The increase in capital cost is less than 7%.

Tian et al. [20] conducted a thermo-economic analysis using zeotropic mixtures based on siloxanes and R123 in a dual-loop organic Rankine cycle (DORC) to recover heat from an engine. The authors proposed three types of binary mixtures and concluded that the D4/R123 (0.3/0.7) mixture had the highest performance in terms of energy efficiency (22.84%), exergy (48.6%), and the lowest total exergy destruction rate (19.64 kW). In economic terms, the MD2M/R123 (0.35/0.65) mixture represents the most economical system. Similar work was carried out by Ge et al. [21] who coupled a dual-loop organic Rankine cycle (DORC) to recover heat from an internal combustion engine. The researchers analyzed the effect of the molar fraction of different zeotropic mixtures cyclopentane/cyclohexane, and benzene/toluene for the high-temperature loop (HTL), and isobutane/isopentane for the low-temperature loop (LTL) of DORC. The results showed that with the use of zeotropic mixtures for HTL and LTL, the net power output of the system increases compared to the use of pure fluids. The relative increase was 2.5–9.0% and 1.4–4.3% for cyclopentane/cyclohexane, and benzene/toluene, respectively.

Tian et al. [22] carried out energy, exergy, and thermo-economic analysis of a Rankine cycle using zeotropic mixtures from an internal combustion engine of a marine engine. In thermo-economic terms, the authors concluded that the best performances were achieved with R170/R1270 (0.9/0.1).

Based on the previous works, it is evident that the use of zeotropic mixtures can partially increase the system’s performance. However, the working fluid selection is a challenge due to the lack of selection criteria. Therefore, research has been conducted to determine a suitable route for fluid selection, with as little complexity as possible. Some of these investigations have taken into account the effects of molar composition, the effect of the mating temperature between the working fluid and the thermal source on the overall performance of the system, and the effect of the thermal source on the overall performance of the system [23,24,25]. Performing optimization studies when using zeotropic mixtures as working fluids in ORC systems to wasted heat recovery on internal combustion engines is essential to determine the operating ranges where the best performance is achieved for particular operating conditions.

The optimizations tools play a fundamental role when making decisions involving more than one variable subject to certain restrictions. In this sense, research has been carried out to optimize parameters of the organic Rankine cycle to maximize or minimize objective functions. Among them is Tiwari et al. [26] who conducted a multi-objective optimization of an ORC-solar system considering hexane/pentane, isohexane/pentane, and butane/pentane mixtures. The results showed that the application of the optimization achieved a 20% maximization of the exergetic efficiency. Hajabdollahi et al. [27] carried out an optimization of a regenerative solar organic Rankine cycle (RORC). The results revealed that isobutane and R245fa were the best economic performers. Similar work was presented by Petrollese & Cocco [28] who minimized the levelized cost of energy (LCOE) of a solar-based ORC power plant. Garg & Orosz [29] performed an optimization of an organic Rankine cycle with pure fluids and azeotropic mixtures for solar applications using Particle Swarm Optimization (PSO). The results showed that R134a and R152a were the fluids that allowed the highest enthalpy recovery from the thermal source at a minimum investment cost. Other works have focused on optimization taking into account environmental, energy, and exergy aspects, such as those presented by Herrera et al. [30]. In this work, the authors minimized the environmental impact by maximizing energy and exergy indicators. Other works have focused on the study of different optimization algorithms as reported by Duarte et al. [31]. In this study, the authors evaluated the performance of three optimization algorithms (PSO, RPSO, and GA) using an organic Rankine cycle. The results showed that PSO-based algorithms have better performance compared to GA.

On the other hand, determine quantitatively the impact of energy generation to the environment is crucial. Emergy analysis is a widely accepted and currently used method for this purpose [32,33,34]. In that context, there is the study conducted by Sha et al. [35] who performed an emergy analysis to evaluate the sustainability and the effect on the biosphere of CHP (combined heat and power plants) using biomass and coal as energy source. The results showed that CHP using biomass is at least 3.3 times more energy efficient than those based on coal.

Converting low-grade energy into electric power can effectively reduce environmental pollution and increase the efficiency of energy utilization. Therefore Zhang et al. [36] performed a sustainability analysis to an ORC for waste heat recovery using the emergy method and a life cycle analysis, using R134a as the working fluid. The results showed that the emergy ratio and emergy sustainability index of an ORC is 197.52 and 3.97 respectively, which proves to be lower than that from wind, water, and geothermal plants, but much higher than fossil fuel-based power plants.

Previous studies indicate that the use of zeotropic mixtures can improve the thermal system efficiency. However, the vast majority of these works have only considered an energetic, exergy, and economic approach. For this reason, this manuscript introduces the emergy concept to evaluate the environmental impact of the ORC-engine system. The main contribution of the manuscript is to apply a methodology to evaluate the environmental impact of a simple organic Rankine system (SORC) using zeotropic mixtures as working fluid and to quantify the effect on system performance and environmental impact using emergy analysis. In this work is compared the system’s performance when pure fluids and zeotropic mixtures are used as working fluid, also a multi-objective optimization is performed.

2. Methodology

The analysis of the system was carried out using Matlab and Refprop. The energetic, exegetic, and emergy models necessary for the analysis of the system are presented, as well as the results obtained from them.

2.1. System description

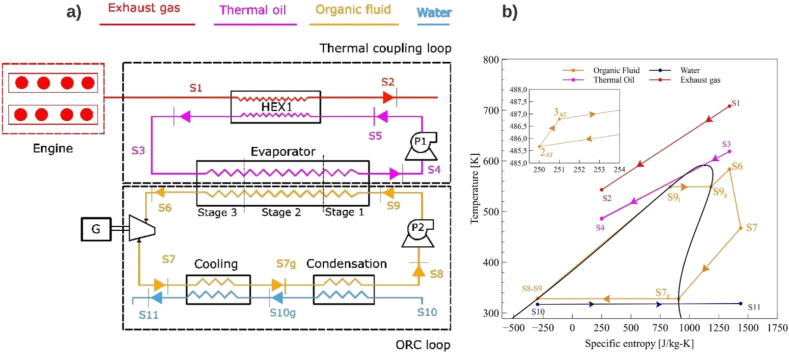
The configuration proposed for this case study is the so-called simple configuration shown in Figure 1.

Figure 1.

Design layout: a) waste heat recovery system, b) T-s diagram.

Figure 1a shows the Engine-ORC process. Initially, the exhaust gases are expanded by a turbocharger (state S1) transferring energy through heat exchanger 1 (HEX1) to the thermal oil (state S5) to be released to the environment (state S2). The thermal oil flows through the thermal circuit driven by the pump (P1). The hot fluid leaving HEX1 (state S3) enters the evaporator to preheat, evaporate and reheat the working fluid. The superheated working fluid (state S6) is sent to the turbine to be expanded in the turbine (T1) and generate electrical power through a generator. The low steam at the turbine outlet (state S7) is fed to the condenser to be cooled and then condensed. Finally, the pump (P2) drives the working fluid to the high pressure of the system completing the cycle. Figure 1b shows the thermodynamic points of the cycle considering toluene as working fluid.

2.2. Thermodynamic modeling

The assumptions for the thermodynamic modeling are established, which helps to define the scope of the analysis to be carried out.

• •The system works in steady-state conditions.
• •Equipment belonging to the heat cycle does not thermally interact with the environment.
• •Pressure drops in the pipelines are ignored.
• •The pressure drop in the heat exchangers is a function of the geometry and hydraulic characteristics of the flow.

2.2.1. ORC energy balance

Each component that is part of the waste heat recovery system is considered as an open system operating at a steady-state, the mass and energy balance are shown in equations (1), and equation (2).

$$\begin{array}{c}\sum {\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}-\sum {\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=\frac{\mathrm{d}\mathrm{m}}{\mathrm{d}\mathrm{t}}\end{array}$$ (1)

$$\begin{array}{c}\sum {\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}\bullet {\mathrm{h}}_{\mathrm{i}\mathrm{n}}-\sum {\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\bullet {\mathrm{h}}_{\mathrm{o}\mathrm{u}\mathrm{t}}-\sum \dot{\mathrm{Q}}+\sum \dot{\mathrm{W}}=\frac{\mathrm{d}\mathrm{E}}{\mathrm{d}\mathrm{t}}\end{array}$$ (2)

where E the energy within the control volume, $\dot{\mathrm{m}}$ is the mass flow, h is the enthalpy, $\dot{\mathrm{Q}}$ is the heat transferred during the process, and $\dot{\mathrm{W}}$ is the power. The energy balance of each component is shown in Table 1.

Table 1.

Energy balance for system components.

Component	Equation
Heat Exchanger (HEX1)	${\dot{\mathrm{Q}}}_{\mathrm{H}\mathrm{E}\mathrm{X}1}={\dot{\mathrm{m}}}_{\mathrm{r}0}\bullet {\mathrm{C}}_{\mathrm{p}\mathrm{T}0}\bullet \left({\mathrm{T}}_{\mathrm{s}3}-{\mathrm{T}}_{\mathrm{s}5}\right)$
Pump 1 (P1)	$\dot{{\dot{\mathrm{W}}}_{\mathrm{p}1}}={\dot{\mathrm{m}}}_{\mathrm{r}\mathrm{o}}\bullet \left({\mathrm{h}}_{\mathrm{s}5}-{\mathrm{h}}_{\mathrm{s}4}\right)$
Pump 2 (P2)	$\dot{{\dot{\mathrm{W}}}_{\mathrm{p}2}}={\dot{\mathrm{m}}}_{\mathrm{r}\mathrm{o}}\bullet \left({\mathrm{h}}_{\mathrm{s}9}-{\mathrm{h}}_{\mathrm{s}8}\right)$
Turbine	$\dot{{\dot{\mathrm{W}}}_{\mathrm{t}}}={\dot{\mathrm{m}}}_{\mathrm{O}\mathrm{R}\mathrm{C}}\bullet \left({\mathrm{h}}_{\mathrm{s}6}-{\mathrm{h}}_{\mathrm{s}7}\right)$
Condenser	${\dot{\mathrm{Q}}}_{\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}}={\dot{\mathrm{m}}}_{\mathrm{O}\mathrm{R}\mathrm{C}}\bullet \left({\mathrm{h}}_{\mathrm{s}7}-{\mathrm{h}}_{\mathrm{s}8}\right)$
Evaporator	${\dot{\mathrm{Q}}}_{\mathrm{E}\mathrm{v}\mathrm{a}\mathrm{p}}={\dot{\mathrm{m}}}_{\mathrm{O}\mathrm{R}\mathrm{C}}\bullet \left({\mathrm{h}}_{\mathrm{s}6}-{\mathrm{h}}_{\mathrm{s}9}\right)$

2.2.2. System exergy balance

The exergy for each component is calculated ignoring the variation of kinetic and potential energy. The calculation of the states is made following Eq. (3).

$$\begin{array}{c}\mathrm{x}=\left(\mathrm{h}-{\mathrm{h}}_0\right)-{\mathrm{T}}_0\bullet \left(\mathrm{s}-{\mathrm{s}}_0\right)\end{array}$$ (3)

Where x is the exergy for the specific state, h is the enthalpy, $h_0$ is the enthalpy at reference conditions, $T_0$ is the reference temperature, s is the entropy and $s_0$ is the entropy at reference conditions.

However, for the exhaust gases circulating in the S1 stream, the chemical exergy produced by the inherent combustion of the process must be calculated. Eq. (4) shows the mathematical simplification for the calculation of the chemical exergy in the working fluid.

$$\begin{array}{c}{\mathrm{x}}_{\mathrm{c}\mathrm{h}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{X}}_{\mathrm{i}}\bullet \mathrm{e}{\mathrm{x}}_{\mathrm{c}\mathrm{h}\mathrm{i}}+\mathrm{R}\bullet {\mathrm{T}}_0\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{X}}_{\mathrm{i}}\bullet \ln {\mathrm{X}}_{\mathrm{i}}\end{array}$$ (4)

where $\mathrm{R}$ is the universal gas constant, ${\mathrm{X}}_{\mathrm{i}}$ expresses the mole fraction of the gas, $\mathrm{e}{\mathrm{x}}_{\mathrm{c}\mathrm{h}\mathrm{i}}$ is the mole fraction per gas.

Therefore, the total exergy of the exhaust gases is the flow exergy ($\mathrm{x}$) plus the chemical exergy, according to Eq. (5).

$$\begin{array}{c}{\mathrm{x}}_{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\mathrm{x}+{\mathrm{x}}_{\mathrm{c}\mathrm{h}}\end{array}$$ (5)

On the other hand, the exergy balance of each component as shown in Eq. (6).

$$\begin{array}{c}\sum {\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}\bullet {\mathrm{x}}_{\mathrm{i}\mathrm{n}}-\sum {\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\bullet {\mathrm{x}}_{\mathrm{o}\mathrm{u}\mathrm{t}}+\dot{\mathrm{Q}}\bullet \left(1-\frac{{\mathrm{T}}_0}{\mathrm{T}}\right)-\dot{\mathrm{W}}-{\dot{\mathrm{X}}}_{\mathrm{D}}=\frac{\mathrm{d}{\mathrm{x}}_{\mathrm{v}\mathrm{c}}}{\mathrm{d}\mathrm{t}}\end{array}$$ (6)

where the term ${\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}\bullet {\mathrm{x}}_{\mathrm{i}\mathrm{n}}$ refers to the incoming input exergy, the term ${\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\bullet {\mathrm{x}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$ is the output exergy, ${\dot{\mathrm{X}}}_{\mathrm{D}}$ is the destroyed exergy and $\frac{\mathrm{d}{\mathrm{x}}_{\mathrm{v}\mathrm{c}}}{\mathrm{d}\mathrm{t}}$ to the change of exergy within the control volume with respect to time.

The exergy fuel (${\dot{X}}_F$) for each component, is equal to the product exergy (${\dot{\mathrm{X}}}_{\mathrm{P}}$) plus the exergy destroyed (${\dot{\mathrm{X}}}_{\mathrm{D}}$), plus losses (${\dot{\mathrm{X}}}_{\mathrm{L}}$) as shown in Eq. (7).

$$\begin{array}{c}{\dot{\mathrm{X}}}_{\mathrm{F}}={\dot{\mathrm{X}}}_{\mathrm{P}}+{\dot{\mathrm{X}}}_{\mathrm{D}}+{\dot{\mathrm{X}}}_{\mathrm{L}}\end{array}$$ (7)

Following the same principle, the exergy destroyed for each component is calculated according to Eq. (8).

$$\begin{array}{c}{\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{k}}={\dot{\mathrm{X}}}_{\mathrm{F},\mathrm{k}}-{\dot{\mathrm{X}}}_{\mathrm{P},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}-{\dot{\mathrm{X}}}_{\mathrm{L},\mathrm{k}}\end{array}$$ (8)

Based on Eq. (8), the exergy balance was applied to each of the components of the system. The results are shown in Table 2.

Table 2.

Exergy balance for system components.

Component	Exergetic balance
Evaporator	$({\dot{\mathrm{E}}}_{\mathrm{s}3}-{\dot{\mathrm{E}\mathrm{s}}}_4)-({\dot{\mathrm{E}}}_{\mathrm{s}6}-{\dot{\mathrm{E}\mathrm{s}}}_9={\dot{\mathrm{E}}}_{\mathrm{D},\mathrm{E}\mathrm{v}\mathrm{a}\mathrm{p}}$
Condenser	$({\dot{\mathrm{E}}}_{\mathrm{s}7}-{\dot{\mathrm{E}}}_{\mathrm{s}8})-({\dot{\mathrm{E}}}_{\mathrm{s}11}-{\dot{\mathrm{E}}}_{\mathrm{s}10}={\dot{\mathrm{E}}}_{\mathrm{D},\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}}$
Heat Exchanger (HEX1)	$({\dot{\mathrm{E}}}_{\mathrm{s}1}-{\dot{\mathrm{E}}}_{\mathrm{s}2})-({\dot{\mathrm{E}}}_{\mathrm{s}3}-{\dot{\mathrm{E}}}_{\mathrm{s}5}={\dot{\mathrm{E}}}_{\mathrm{D},\mathrm{H}\mathrm{E}\mathrm{X}1}$
Turbine	$\left({\dot{\mathrm{E}}}_{\mathrm{s}6}-{\dot{\mathrm{E}}}_{\mathrm{s}7}\right)-{\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{E}}}_{\mathrm{D},\mathrm{T}\mathrm{u}\mathrm{r}}$
Pump 1	${\dot{\mathrm{W}}}_{\mathrm{p}2}-\left({\dot{\mathrm{E}}}_{\mathrm{s}5}-{\dot{\mathrm{E}}}_{\mathrm{s}4}\right)={\dot{\mathrm{E}}}_{\mathrm{D},\mathrm{P}\mathrm{u}\mathrm{m}\mathrm{p}2}$
Pump 2	${\dot{\mathrm{W}}}_{\mathrm{p}1}-\left({\dot{\mathrm{E}}}_{\mathrm{s}9}-{\dot{\mathrm{E}}}_{\mathrm{s}8}\right)={\dot{\mathrm{E}}}_{\mathrm{D},\mathrm{P}\mathrm{u}\mathrm{m}\mathrm{p}1}$

2.2.3. Emergy analysis

Emergy consider all the work that has been made to produce something, the energy used to generate that product is only lost once the process is at the end of its life [37].

The emergy can be considered a property that evaluate a system and its surroundings. Because of this it is recommended to divide the analysis into two systems, the first would be the system being evaluated and the second representing how the system affects and is affected by its surroundings [38].

The resources needed to start a production process can be described as renewable resources (R), non-renewable resources (N), goods (G), and services (S).

One of the most important indexes to consider on a Emergy synthesis is the imported emergy (F), which is the emergey imported to the system in the form of good and services, such as: fuels, minerals and raw materials; another indicator to consider is the exported emergy (Y), that is the emergy exported as good and services [32], determined from Eq. (9).

$$\begin{array}{c}\mathrm{Y}=\mathrm{R}+\mathrm{N}+{\mathrm{F}}_{\mathrm{R}}+{\mathrm{F}}_{\mathrm{N}}\end{array}$$ (9)

The Emergy yield ratio (EYR) is the emergy generated by the system divided by imported energy [32], obtained by Eq. (10).

$$\begin{array}{c}\mathrm{E}\mathrm{Y}\mathrm{R}=\mathrm{Y}/\left({\mathrm{F}}_{\mathrm{R}}+{\mathrm{F}}_{\mathrm{N}}\right)\end{array}$$ (10)

The Environmental Load Ratio (ELR) is the ratio of non-renewable energy plus imported energy divided by renewable energy [32], defined according to Eq. (11).

$$\begin{array}{c}\mathrm{E}\mathrm{L}\mathrm{R}=\left(\mathrm{N}+{\mathrm{F}}_{\mathrm{N}}\right)/\left(\mathrm{R}+{\mathrm{F}}_{\mathrm{R}}\right)\end{array}$$ (11)

Finally, the Emergy Sustainability Index (ESI) is the ratio of EYR to ELR [32], given by Eq. (12)

$$\begin{array}{c}\mathrm{E}\mathrm{S}\mathrm{I}=\mathrm{E}\mathrm{Y}\mathrm{R}/\mathrm{E}\mathrm{L}\mathrm{R}\end{array}$$ (12)

ESI can help to determine the sustainability that a system has; if ESI >1, this can show a contribution to the system energy, and imply an increment, an ESI less than one represents a loss of system energy. However, measuring the sustainability of a system based on ESI alone may reveal very little about its true sustainability, because this indicator alone, given that sustainability is determined by various social, economic, and ecological factors, cannot reveal the relative contribution of each of these factors [32,39,40].

Emergy indices offer an advantage over others economics and environmental indices, because the former considered all kinds of resources that were utilized, thus having a common ground for these types of resources [37].

The emergy analysis is a method focused on the energy that measures all the inputs and outputs of a system in a unified unit of measurement having a fairly large scale of time and space is a good measure of sustainability. For the development of an emergy synthesis, the following steps were followed [35].

• 1.Define the system boundaries.
• 2.Make a list of all external and internal units.
• 3.Link all objects according to process flows, relationships, and interactions.
• 4.Calculate the energy and mass balance of the whole process.
• 5.Identify if the system produces more than one product.
• 6.Create an emergy evaluation table and calculate the transformity of the final product.

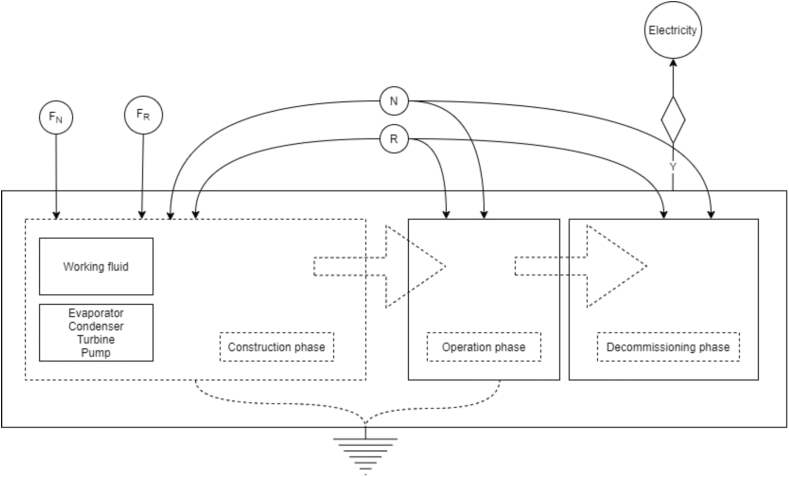
In addition to the previous steps to develop this type of analysis, it is necessary to make a diagram as shown in Figure 2 to help visualize how every stage interact with each other and what kind of resources are used to produce the expected product. The input and output flows of the emergy diagram are divided into renewable resources (R), non-renewable resources (N), purchased products (F) which in turn are divided into renewable (FR) and non-renewable (FN) purchased products.

Figure 2.

Emergy flow diagram.

Three stages of the system are taken into account for the emergy analysis: construction, operation and decommissioning. For the first phase, the steel used for the construction of the turbine and pumps, copper for the evaporator piping, condenser, and heat exchanger coupling are listed. In the operation phase, the heat source is considered, the water used for the condensation stage of the working fluid, and heat absorption. Finally, in the dismantling phase, the cost of transportation of the components and the product of the heat recovery system are considered.

The heat transfer area for heat exchangers is determined using Eq. (13) [41].

$$\begin{array}{c}{\mathrm{A}}_{\mathrm{k}}=\frac{\dot{{\mathrm{Q}}_{\mathrm{k}}}}{{\mathrm{U}}_{\mathrm{k}}\bullet \Delta {\mathrm{T}}_{\mathrm{k}}}\end{array}$$ (13)

where ${\mathrm{A}}_{\mathrm{k}}$ is the heat exchanger area, $\dot{{\mathrm{Q}}_{\mathrm{k}}}$ is the equipment heat flux, ${\mathrm{U}}_{\mathrm{k}}$ is the heat exchange coefficient and $\Delta {\mathrm{T}}_{\mathrm{k}}$ is the logarithmic mean difference.

From this, the mass of the heat exchangers is calculated using Eq. (14) [41].

$$\begin{array}{c}{\mathrm{M}}_{\mathrm{k}}=\rho \bullet {\mathrm{A}}_{\mathrm{k}}\bullet \delta \end{array}$$ (14)

where, ${\mathrm{M}}_{\mathrm{k}}$ is the mass of the kth heat exchanger, $\rho$ is the material density and $\delta$ is the thickness of the material (2 mm) [41].

Based on previous work [42,43], the mass of the turbine and the pump can be obtained using the power generated by the turbine and the power consumed by the pump, determined for Eq. (15).

$$\begin{array}{c}{\mathrm{M}}_{\mathrm{k}}=\alpha \bullet {\mathrm{W}}_{\mathrm{k}}\end{array}$$ (15)

where, $\alpha$ is the mass required per 1-kW of power; ${\mathrm{W}}_{\mathrm{k}}$ is the power generated and consumed by the turbine and pump respectively, $\alpha$ has a value of 14 kg/kW for the pump and 31.22 for the turbine that are made of steel [36].

The waste heat transformity of the exhaust gases can be calculated by Eq. (16) [44].

$$\begin{array}{c}\mathrm{T}{\mathrm{r}}_{\mathrm{w}\mathrm{h}}=\frac{\mathrm{T}{\mathrm{r}}_{\mathrm{c}\mathrm{f}}\bullet \Delta \mathrm{T}}{{\eta }_{\mathrm{c}\mathrm{f}}\bullet \mathrm{T}}\end{array}$$ (16)

where $\mathrm{T}{\mathrm{r}}_{\mathrm{w}\mathrm{h}}$, and $\mathrm{T}{\mathrm{r}}_{\mathrm{c}\mathrm{f}}$ is the heat transformer in the exhaust gases and heat source, respectively, $\mathrm{T}{\mathrm{r}}_{\mathrm{c}\mathrm{f}}=1.62{\bullet 10}^{15}\mathrm{s}\mathrm{e}\mathrm{j}/\mathrm{J}$ [45]. $\Delta \mathrm{T}$ is the temperature difference of the working fluid in the condenser and evaporator, ${\eta }_{\mathrm{c}\mathrm{f}}$ is the second law efficiency, and T is the temperature of the working fluid at the evaporator.

2.3. Multi-objective optimization and decision making

The Multi-objective optimization tool is a model which represents more than one objective. In this study, two objectives have been considered: the exergetic efficiency (${\eta }_{\mathrm{I}\mathrm{I}}$) and Emergy Sustainability Index (ESI). The objective is to achieve the highest possible exergetic efficiency at the lowest environmental impact (ESI). Therefore, the multi-objective optimization problem can be expressed according to Eq. (19) together with its constraints shown in Eqs. (17), (18), (19), and (20) [30].

$$\begin{array}{c}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{F}\left(\mathrm{x}\right)={\left[{\mathrm{f}\mathrm{o}\mathrm{b}\mathrm{j}}_1\left(\mathrm{X}\right),{\mathrm{f}\mathrm{o}\mathrm{b}\mathrm{j}}_2\left(\mathrm{X}\right),{\mathrm{f}\mathrm{o}\mathrm{b}\mathrm{j}}_3\left(\mathrm{X}\right),\dots {\mathrm{f}\mathrm{o}\mathrm{b}\mathrm{j}}_{\mathrm{n}}\left(\mathrm{X}\right)\right]}^{\mathrm{T}}\end{array}$$ (17)

$$\begin{array}{c}\mathrm{x}\in \mathrm{S}\text{,}\end{array}$$ (18)

$$\begin{array}{c}\mathrm{S}=\left\{\mathrm{x}\in {\mathrm{R}}^{\mathrm{m}}:{\rm M}\left(\mathrm{x}\right)=0,{\rm N}\left(\mathrm{x}\right)\ge 0\right\}\end{array}$$ (19)

$$\begin{array}{c}\mathrm{C}=\left\{\mathrm{y}\in {\mathrm{R}}^{\mathrm{n}}:\mathrm{y}=\mathrm{f}\mathrm{o}\mathrm{b}\mathrm{j}\left(\mathrm{x}\right),\mathrm{x}\in \mathrm{S}\right\}\end{array}$$ (20)

where ${\mathrm{f}\mathrm{o}\mathrm{b}\mathrm{j}}_{\mathrm{n}}$ are the objective functions considered in the study, ${\rm M}\left(\mathrm{x}\right)$, and ${\rm N}\left(\mathrm{x}\right)$ are the constraints of the problem. In these cases, no solution globally maximizes or minimizes all the objective functions.

This tool seeks to generate a set of Pareto points for each of the objective functions considered in the study. A Pareto optimal solution is optimal if and only if it is not dominated by any other solution. In that case, all the Pareto optimal solutions form the set of solutions called Pareto front [46].

The decision variables used in the study were: condenser pinch point, evaporator pinch point, turbine efficiency, pump efficiency, and condensing temperature. Each of these variables is defined in a search range in the form of a vector, whose values are shown in Table 3.

Table 3.

Lower and upper boundary of the decision variables.

Decision Variables	Lower bound	Upper bound	Unit
Condenser pinch point	5	15	°C
Evaporator pinch point	30	34	°C
Turbine efficiency	80	85	%
Pump efficiency	75	80	%
Condensing temperature	39.8	41	°C

For this study, optimization was carried out using the Non-Dominated Sorting Genetic Algorithm (NGSA)-II using Matlab optimization environment, which is a technique based on evolutionary theory. This technique is based on six steps: population, selection, reproduction, mutation, crossover, and migration. Table 4 shows the values used for the optimization process.

Table 4.

Input parameters of NSGA II.

Parameters	Value	Reference
Population size	200	[47]
Generation size	400	[47]
Crossover fraction	0.8	[47]
Migration fraction	0.2	[47]
Selection process	Tournament	[47]

Taking a two-objective minimization problem as an example, all feasible solutions are distributed in the solution space, including the Pareto optimal solution (in blue) and the Pareto non-optimal solutions (in black) as shown in Figure 3. The selection technique used is TOPSIS (Technique for Order Preference by Similarity to Ideal Solution). Within the search space, the solution with the highest value of the objective function is called the non-ideal solution; while the solution with the lowest value is called the ideal solution. Therefore, a solution should be found as far away from the non-ideal and as close to the ideal as possible [46].

Figure 3.

Illustration decision making approaches.

Therefore, the Euclidean distance (${\mathrm{D}}_{\mathrm{i}}$) between each point on the Pareto and the ideal and non-ideal point can be calculated according to Eqs. (21) and (22).

$$\begin{array}{c}{\mathrm{D}}_{\mathrm{i}+}=\sqrt{\sum _{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{F}}_{\mathrm{i}\mathrm{j}}-{\mathrm{F}}_{\mathrm{j}}^{\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}\right)}^2}\end{array}$$ (21)

$$\begin{array}{c}{\mathrm{D}}_{\mathrm{i}-}=\sqrt{\sum _{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{F}}_{\mathrm{i}\mathrm{j}}-{\mathrm{F}}_{\mathrm{j}}^{\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}\right)}^2}\end{array}$$ (22)

where, ${\mathrm{F}}_{\mathrm{j}}^{\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}$ is the positive ideal solution, and ${\mathrm{F}}_{\mathrm{j}}^{\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}$ is the no-ideal solution, $\mathrm{i}$ denotes the index of each solution of the Pareto frontier, and $\mathrm{j}$ is the index of the objective functions considered in the study.

The final selection is given by Eq. (23).

$$\begin{array}{c}{\mathrm{Y}}_{\mathrm{i}}=\frac{{\mathrm{D}}_{\mathrm{i}-}}{{\mathrm{D}}_{\mathrm{i}-}+{\mathrm{D}}_{\mathrm{i}+}}\end{array}$$ (23)

3. Results and discussion

To obtain results, it is necessary to establish the operational conditions for the system, for this purpose, a usual engine operating condition was selected, described in Table 5.

Table 5.

Values of the main parameters considered in the study.

Parameters	Value	Unit
Ambient temperature	30	°C
Ambient pressure	101.3	kPa
Isentropic turbine efficiency	80	%
Isentropic pump efficiency	75	%
Temperature cooling water	20	°C
Pinch-point on evaporator	30	°C
Pinch-point on the condenser	15	°C
Exhaust gas temperature	435	°C
Exhaust gas outlet temperature	270	°C
Pump 1 pressure ratio	2
Pump 2 pressure ratio	30
Fuel mass flow rate	9986.04	kg/h
Operation period	20	Year
Annual working hours	2080	Hours

Based on the values of the parameters shown in Table 5, the values in base conditions, are shown in Table 6. Two things can be noticed when comparing the exegetic efficiency of the system by changing the working fluid. The first is that cyclohexane is the pure fluid with the highest efficiency. The second is that the exergy efficiency is significantly increased by the use of zeotropic mixtures, this because mixtures present a variable temperature profile during the phase change process, which can reduce the mismatch between the heat sources and the working fluid, that contrast with the constant temperature of evaporation and condensation. Additionally, the exergy efficiency of the mixture increases with the increasing mass fraction of cyclohexane. This can be explained by the fact that the mass flow of zeotropic mixtures is about 60% higher compared to pure fluids. Zeotropic mixtures have the advantage of following the temperature profile of the thermal source, which offers a higher availability of heat that can be absorbed in the evaporator. As a result, the system increases the mass flow to gain all that energy. In addition, the temperature increase of the mixture throughout the evaporation process causes the irreversibility in the evaporator to decrease, which is evidenced by the increase in net power and energy efficiency of the system. The opposite behavior occurs with the cooling water consumption, which is lower compared to cyclohexane, favoring the pumping requirements for cooling.

Table 6.

Results of the main indicators evaluated in base conditions.

Fluid	T[K]	${\dot{\mathbf{W}}}_{\mathbf{N}\mathbf{e}\mathbf{t}}\left[\mathbf{k}\mathbf{W}\right]$	${\mathbf{\eta }}_{\mathit{t}\mathit{h}}[\%]$	${\mathbf{\eta }}_{\mathbf{I}\mathbf{I}}[\%]$	$\mathbf{E}\mathbf{S}\mathbf{I}$	${\dot{\mathbf{Q}}}_{\mathbf{E}\mathbf{v}\mathbf{a}\mathbf{p}}\left[\mathbf{k}\mathbf{W}\right]$	${\dot{\mathbf{m}}}_{\mathbf{O}\mathbf{R}\mathbf{C}}$ [kg/s]	${\dot{\mathbf{m}}}_{\mathbf{w}\mathbf{a}\mathbf{t}\mathbf{e}\mathbf{r}}$ [kg/s]	${\dot{\mathbf{x}}}_{\mathbf{D}}$ [kW]
Toluene	549.20	97.024	18.85	39.66	7.85	832.52	0.79	15.31	137.29
Cyclohexane	564.53	103.27	20.76	42.21	7.90	866.73	0.756	17.29	123.23
Cyclohexane/R11 (0.2/0.8)	604.51	158.57	30.81	64.82	7.19	894.86	1.81	16.52	95.61
Cyclohexane/R11 (0.25/0.75)	616.67	161.48	31.38	66.01	7.33	618.81	1.71	16.07	88.90
Cyclohexane/R11 (0.3/0.7)	628.17	162.40	32.54	66.38	7.45	665.89	1.61	16.09	84.65

As for the exergy destroyed, the results show that the use of zeotropic mixtures considerably reduces the exergy destroyed in the heat transfer equipment, as shown in Table 7. As mentioned, the zeotropic mixtures give a better match in the source temperature throughout the heat transfer process. This causes a reduction in internal irreversibility, increasing the exergy efficiency, as shown in Table 6. However, the opposite behavior is exhibited by pumps and turbines, whose destroyed exergies are higher for zeotropic mixtures compared with pure fluids. This is due to the higher mass flow required by the ORC to operate when using mixtures which result in increased irreversibility. However, the significant decrease over the destroyed exergy in heat transfer equipment compensates for the slight increase on the turbomachinery. The thermal efficiency for the ORC is also increased when using zeotropic mixtures as working fluids.

Table 7.

Exergy destruction by component.

Fluid	HEX1 [kW]	Pump 1 [kW]	Turbine [kW]	Pump 2 [kW]	Evaporator [kW]	Condenser [kW]	Total [kW]
Toluene	42.81	0.25	15.63	0.07	47.98	30.55	137.30
Cyclohexane	33.57	0.25	16.01	0.23	39.76	33.42	123.23
Cyclohexane/R11 (0.2/0.8)	13.04	3.12	26.39	1.86	25.48	25.72	95.61
Cyclohexane/R11 (0.25/0.75)	7.76	0.21	25.66	1.71	27.46	26.10	88.90
Cyclohexane/R11 (0.3/0.7)	3.98	0.21	24.85	1.57	26.61	27.42	84.65

The sizing of the components depends on the working fluid. The heavier the working fluid, the greater the amount of material to be used in the construction stage of the system. Table 8 shows the quantities of material required in the equipment, which were estimated according to the areas (heat exchangers) and power (turbine and pumps). The largest differences are found in heat exchanger 1 (HEX1) where approximately 66% more copper is needed when using cyclohexane than when using toluene as working fluid. Also, there is a difference that varies from 3% to 36%, approximately when using zeotropic mixtures. Similar behavior is observed on the turbines, where using mixtures generates more power and, therefore, the amount of material required in this machinery increases.

Table 8.

Power, area, and mass of system equipment.

Item	HEX1	Evaporator	Condenser	Pump 1	Pump 2	Turbine	System
Toluene
Power (kW)	571.45	618.81	400.73	0.30	0.29	97.61	97.02
Area (${\mathrm{m}}^2)$	30.17	21.74	36.33				88.25
Mass (kg)	540.64	389.64	651.11	4.20	3.99	3048.36	4637.95
Cyclohexane
Power (kW)	564.02	665.89	389.46	0.29	2.42	107.46	104.76
Area (${\mathrm{m}}^2)$	50.30	22.32	32.31				104.94
Mass (kg)	901.45	400.04	578.95	4.08	33.82	3356.08	5274.42
Cyclohexane/R11 (0.2/0.8)
Power (kW)	568.04	832.52	345.59	4.14	7.72	167.20	158.57
Area (${\mathrm{m}}^2)$	51.93	26.06	30.10				108.08
Mass (kg)	930.52	466.91	539.40	58.02	108.08	5221.66	7324.59
Cyclohexane/R11 (0.25/0.75)
Power (kW)	561.64	866.73	336.13	0.29	7.12	168.89	161.48
Area (${\mathrm{m}}^2)$	63.73	26.88	27.54				118.15
Mass (kg)	1141.97	481.74	493.51	4.06	99.65	5274.43	7495.37
Cyclohexane/R11 (0.3/0.7)
Power (kW)	558.84	894.86	336.46	0.29	6.53	169.22	162.40
Area (${\mathrm{m}}^2)$	78.51	219.57	26.16				324.25
Mass (kg)	1406.97	486.88	468.79	4.03	91.43	5284.63	7742.73

For the raw steel data, data from the research conducted by Pan et al. [48] was used. A correction factor was applied due to the different amounts of material to be used. The exhaust heat input value was considered equal to the heat dissipated in HEX1. A total of 2080 h of operation per year, over 20 years, was considered to determine the contribution in joule (J). Similar considerations were made to estimate the absorption heat using the condenser as the base case.

The emergy contribution of the working fluid cannot be neglected. However, it was not possible to find the necessary information for the emergy calculation for each working fluid used. An estimate of 13% was used, as reported by Zhang et al., [36]. Thus, partial total emergy was calculated for the system and the percentage contribution of the working fluid was added to it to have a more accurate estimate.

Table 9 shows the emergy values by category for each fluid considered in the study. These results are categorized according to their contribution of emergy to the system, between imported renewable and non-renewable resources, non-renewable and renewable resources used, and the total emergy used by each system. Toluene is the working fluid that presents the greatest environmental load, taking into consideration that it is the working fluid that requires the greatest amount of emergy. There is no significant difference between the other working fluids. Regarding the environmental performance demarcated by the transformity, the mixtures offer better performance, it could be concluded that the mixtures make better use of the resources invested in these for the production of electricity, the difference between the performance of these is quite remarkable, however, the transformity does not offer a complete picture of the sustainability of a system.

Table 9.

Total emergy values divided into categories for different fluids.

Item	Toluene	Cyclohexane	Cyclohexane/R11 (0.2/0.8)	Cyclohexane/R11 (0.25/0.75)	Cyclohexane/R11 (0.3/0.7)
$\mathit{F}\mathit{n}$	8.52 ${\bullet 10}^{15}$	8.62 ${\bullet 10}^{15}$	1.03 ${\bullet 10}^{16}$	9.88 ${\bullet 10}^{15}$	9.77 ${\bullet 10}^{15}$
$\mathit{N}$	2.88 ${\bullet 10}^{18}$	2.36 ${\bullet 10}^{18}$	2.48 ${\bullet 10}^{18}$	2.31 ${\bullet 10}^{18}$	2.18 ${\bullet 10}^{18}$
${\mathit{F}}_{\mathit{R}}$	1.74 ${\bullet 10}^{15}$	1.52 ${\bullet 10}^{15}$	1.81 ${\bullet 10}^{15}$	1.73 ${\bullet 10}^{15}$	1.67 ${\bullet 10}^{15}$
$\mathit{R}$	7.66 ${\bullet 10}^{16}$	7.61 ${\bullet 10}^{16}$	8.27 ${\bullet 10}^{16}$	8.05 ${\bullet 10}^{16}$	8.06 ${\bullet 10}^{16}$
$\mathit{Y}$	2.96 ${\bullet 10}^{18}$	2.45 ${\bullet 10}^{18}$	2.58 ${\bullet 10}^{18}$	2.40 ${\bullet 10}^{18}$	2.28 ${\bullet 10}^{18}$
${\mathit{T}}_{\mathit{R}}$	2.04 ${\bullet 10}^5$	1.58 ${\bullet 10}^{15}$	1.09 ${\bullet 10}^5$	9.93 ${\bullet 10}^{14}$	9.36 ${\bullet 10}^4$
$\mathit{E}\mathit{Y}\mathit{R}$	288.97	241.59	212.16	206.83	198.92
$\mathit{E}\mathit{L}\mathit{R}$	36.80	30.55	29.50	28.21	26.68
$\mathit{E}\mathit{S}\mathit{I}$	7.85	7.91	7.19	7.33	7.46

To have a better perception of the contribution for each category to the system's total energy output, a pie chart is presented in Figure 4. This behavior is to be expected, considering that the greatest energy contribution was from non-renewable resources, specifically the contribution of heat from the exhaust gases during the operation of the heat recovery system.

Figure 4.

Percentage distribution of emergy for: a) Toluene; b) Cyclohexane; c) Cyclohexane/R11 (0.2/0.8); d) Cyclohexane/R11 (0.25/0.75); e) Cyclohexane/R11 (0.3/0.7).

The difference in the contributions does not have a significant variation, it should be noted that there is a greater change in the contribution of renewable resources comparing the pure fluids with the mixtures in this regard. The minimal variation in this aspect is due to the greater use of water in the operation stage used to condensate the working fluid. In addition, it should be taken into account that the use of heavier working fluids increases the use of raw materials. Therefore, there will be an increase in the number of resources imported into the system (renewable and non-renewable), this difference is not difficult to appreciate.

The next parameter to be analyzed is transformity, which is a ratio between the emergy needed to produce something and the product generated by the system. That is, the lower the value, the better the use of the emergy inherent in the process. Therefore, less emergy will be necessary to generate a product. In this sense, a low value of transformity is desirable when evaluating alternatives. However, it should be kept in mind that this parameter is not enough to evaluate the system’s sustainability, so it should usually be complemented with different parameters to get a wider view.

Figure 5 shows the transformity obtained by evaluating the results gotten through numerical simulation completed in Matlab and other energy generating systems. Figure 5 shows that the use of mixtures provides a higher emergy utilization compared to the ORC taken as a reference, while pure mixtures offer a higher transformity. Wind and methane are the systems with the best performance in this aspect.

Figure 5.

Transformity for several generation systems.

The EYR is an index that relates the system's energy efficiency to the external investments in the process. In this sense, a high value implies a lower need for the purchase of external resources, for the ORC this value is particularly low in the construction stage and the energy investment is high in comparison. This means that the ORC as a form of waste heat recovery has a high return on investment over the long term, this is most notorious when the time of operation increases. It is worth noting that the systems analyzed in this project offer higher overall performance than the alternatives proposed in Table 10, which shows that the oil offers the worst performance among all the options.

Table 10.

Emergy indexes for different systems.

System	${\mathbf{T}}_{\mathbf{r}}$	$\mathbf{E}\mathbf{Y}\mathbf{R}$	$\mathbf{E}\mathbf{L}\mathbf{R}$	$\mathbf{E}\mathbf{S}\mathbf{I}$	Reference
ORC Cyclohexane/R11 (0.2/0.8)	1.09 ${\bullet 10}^5$	212.16	29.50	7.19
ORC Cyclohexane/R11 (0.25/0.75)	9.93 ${\bullet 10}^4$	206.83	28.21	7.33
ORC Cyclohexane/R11 (0.3/0.7)	9.36 ${\bullet 10}^4$	198.92	26.68	7.46
ORC Cyclohexane	1.58 ${\bullet 10}^5$	241.59	30.55	7.91
ORC Toluene	2.04 ${\bullet 10}^5$	288.97	36.80	7.85
ORC R134a	4.31 ${\bullet 10}^5$	197.52	49.71	3.97	[36]
Wind	5.89 ${\bullet 10}^4$	7.47	0.15	49.80	[49]
Geothermal	1.42 ${\bullet 10}^5$	4.81	0.44	10.93	[49]
Hydraulic	5.87 ${\bullet 10}^4$	7.65	0.45	17.00	[49]
Methane	1.60 ${\bullet 10}^4$	6.60	11.78	0.56	[49]
Oil	1.87 ${\bullet 10}^5$	4.21	14.24	0.30	[49]
Coal	1.62 ${\bullet 10}^5$	5.48	10.37	0.53	[49]

The next parameter used to evaluate the system was ELR, which expresses the relationship between the eco-economics of the system and the environment. A high value implies a high intensity of emergy on the environment, which makes the system unviable for a long period. In this aspect, it can be considered that keeping the system in operation for a very long time could be counterproductive given the high value of the ORCs in this parameter. Following this order of ideas, hydro, wind and geothermal energies offer the lowest emergy load on the environment where they are located. The mixture of cyclohexane/R11 (0.2/0.8) offers the best in terms of ELR. As the mass fraction of cyclohexane in the mixture increases there is a considerable difference. The gap becomes even larger when comparing pure fluids, making them highly unfeasible for long periods of use such as this case.

The next parameter, ESI, is a ratio between EYR and ELR where if EYR is high and ELR is relatively low, it can be inferred that the system is sustainable. Generally, a value of ESI in a range between 1 and 10 implies a system with potential for improvement and that the system is evolving to have better sustainability. A value higher than 10 indicates stagnation and a value lower than 1 implies that the system consumes more than it contributes [50,51]. Based on this index ORC offers an economic contribution in the medium term, where energy from wind offers a performance well above this range which implies that there is not much development or the presence of stagnation, on the other hand, methane, oil, and coal as a source of energy from oil offer a rather deplorable performance in this aspect and it could be considered that its use is not recommended in the long or medium term.

3.1. Parametric analysis

To improve the performance of the system, it is necessary to know which parameter has more effects over this, it was decided to perform a parametric analysis by changing 5 variables in an allowed range of values for each working fluid that were previously selected, to measure their individual impact over the system’s performance.

3.1.1. Influence of the pump efficiency

In Figure 6 abbreviations were used for the name of the working fluids. Where A refers to Toluene, B to cyclohexane, C to the mixture cyclohexane/R11 (0.2/0.8), D to the mixture cyclohexane/R11 (0.25/0.75), and E to the mixture with composition cyclohexane/R11 (0.3/0.7). From this section onwards this nomenclature will be used as a simplification.

Figure 6.

Variation of system performance as a function of the pump efficiency (${\eta }_{\mathrm{p}}$): a) net power, b) Exergetic efficiency, c) Transformity

The results show no significant change in the system’s transformity, taking into consideration that, although increasing the efficiency of the pump increases the net power generate, this increase is not enough to be considered significant.

As for the other indexes studied, the variation is quite minimal, where it practically does not exceed 0.22% in general, so that, if the process is to be optimized, this variable should not have priority in such purpose.

Table 11 shows the values of the emergy indexes considered in the study. These indicators do not vary significantly as pump efficiency increases.

Table 11.

Emergy indexes as a function of the pump efficiency.

Toluene
$\mathbf{E}\mathbf{Y}\mathbf{R}$	${\mathbf{n}}_{\mathbf{p}}=\mathbf{70}\%$	${\mathbf{n}}_{\mathbf{p}}=\mathbf{75}\%$	${\mathbf{n}}_{\mathbf{p}}=\mathbf{80}\%$
$\mathbf{E}\mathbf{Y}\mathbf{R}$	288.99	288.97	288.96
$\mathbf{E}\mathbf{L}\mathbf{R}$	36.81	36.80	36.80
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.85	7.85	7.85
Cyclohexane
$\mathbf{E}\mathbf{Y}\mathbf{R}$	241.55	241.59	241.62
$\mathbf{E}\mathbf{L}\mathbf{R}$	30.55	30.55	30.55
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.91	7.91	7.91
Cyclohexane/R11 (0.2/0.8)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	212.24	212.16	212.09
$\mathbf{E}\mathbf{L}\mathbf{R}$	29.49	29.50	29.50
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.20	7.19	7.19
Cyclohexane/R11 (0.25/0.75)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	206.76	206.83	206.89
$\mathbf{E}\mathbf{L}\mathbf{R}$	28.18	28.21	28.24
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.34	7.33	7.33
Cyclohexane/R11 (0.3/0.7)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	198.85	198.92	198.98
$\mathbf{E}\mathbf{L}\mathbf{R}$	26.65	26.68	26.70
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.46	7.46	7.45

3.1.2. Influence of the turbine efficiency

The results observed on Figure 7, we can see that by increasing the efficiency of the turbine, a decrease in the system transformity can be seen for all working fluids except fluid C. This is due to the fact that by increasing this parameter there is an increase in the exergy efficiency of the system and the net power. The emergy is a parameter that depends on the exergy, while the transformity depends directly on the generated power of the system. For fluid C it is observed that with an efficiency of 85% there is an increase of 13.94% in transformity with respect to the base condition and a decrease of 4.25% in efficiency and net power. The best performance for this fluid occurs with an efficiency of 82.5% since the transformity decreases by 4.5%. In addition, there is an increase in the net power and exergy efficiency by 3.7%. For the rest of the fluids, there is an inverse proportionality in the transformity.

Figure 7.

System performance as a function of the turbine efficiency (${\eta }_{\mathrm{t}}$): a) net power, b) Exergetic efficiency, c) Transformity

The emergy indexes are shown in Table 12 it is observed that the EYR increases as the turbine efficiency increases. This implies that most of the emergy used in the process should not be imported. However, the ELR also increases indicating a higher environmental load for the system. Using pure fluids, the variation does not exceed 2%; while the others experience an increase for fluids C (22.8%), D (4.5%), and E (3.4%).

Table 12.

Emergy indexes as a function of the turbine efficiency.

Toluene
Index	${\mathbf{\eta }}_{\mathbf{t}}=\mathbf{80}\%$	${\mathbf{\eta }}_{\mathbf{t}}=\mathbf{80.2}\%$	${\mathbf{\eta }}_{\mathbf{t}}=\mathbf{85}\%$
$\mathbf{E}\mathbf{Y}\mathbf{R}$	288.97	291.87	291.33
$\mathbf{E}\mathbf{L}\mathbf{R}$	36.80	37.06	37.32
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.85	7.88	7.81
Cyclohexane
$\mathbf{E}\mathbf{Y}\mathbf{R}$	241.59	240.89	240.25
$\mathbf{E}\mathbf{L}\mathbf{R}$	30.55	30.74	30.93
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.91	7.84	7.77
Cyclohexane/R11 (0.2/0.8)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	212.16	207.20	233.43
$\mathbf{E}\mathbf{L}\mathbf{R}$	29.50	29.20	36.22
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.19	7.10	6.44
Cyclohexane/R11 (0.25/0.75)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	206.83	204.86	208.43
$\mathbf{E}\mathbf{L}\mathbf{R}$	28.21	28.77	29.46
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.33	7.12	7.07
Cyclohexane/R11 (0.3/0.7)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	198.92	197.94	197.84
$\mathbf{E}\mathbf{L}\mathbf{R}$	26.68	27.12	27.59
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.46	7.30	7.17

Although the ESI decreases with increasing turbine efficiency, the process is still considered to be sustainable for all case studies. The decrease in the parameter is because increasing the power generated increases the raw material requirements for the turbine, which increases the environmental load of the system and the emergy used by the system, which directly affects the ESI parameter.

3.1.3. Influence of the pinch point evaporator temperature

The analysis of the influence of the evaporator pinch point temperature (Ap) on the system's emergy indexes is shown in Figure 8. It is observed that there is no difference between the transformity obtained for each working fluid, but in general, a decrease in this parameter is obtained when using the lowest value allowed by the system. This variation does not exceed 5%. For fluid C, decreasing the pinch point the transformity increases. This increase is 3% over the base value of the study. For fluid D, and E there is a decrease of 4%, and 1.4%, respectively.

Figure 8.

System performance as a function of the evaporator pinch point temperature ($\mathrm{A}\mathrm{p}$): a) net power, b) Exergetic efficiency, c) Transformity

From the results shown in Table 13 it can be observed that when the pinch point evaporator decreases, the EYR value decreases. It can be inferred that there is a greater dependence on external resources with greater temperature differences in the evaporator. The opposite behavior was found for the ELR, which increases with decreasing evaporator pinch temperature. This implies greater use of non-renewable resources. For the ESI index, there is a fairly minimal variation that does not exceed 1% in all the cases studied; however, it tends to decrease as the pinch point decreases, the net power and the energy efficiency tend to decrease the similar ways.

Table 13.

Emergy indexes as a function of the evaporator pinch point temperature.

Toluene
Index	$\mathbf{A}\mathbf{p}=\mathbf{34}°\mathbf{C}$	$\mathbf{A}\mathbf{p}=\mathbf{31}°\mathbf{C}$	$\mathbf{A}\mathbf{p}=\mathbf{30}°\mathbf{C}$
$\mathbf{E}\mathbf{Y}\mathbf{R}$	293.74	289.31	288.97
$\mathbf{E}\mathbf{L}\mathbf{R}$	36.57	36.75	36.80
$\mathbf{E}\mathbf{S}\mathbf{I}$	8.03	7.87	7.85
Cyclohexane
$\mathbf{E}\mathbf{Y}\mathbf{R}$	242.99	241.94	241.59
$\mathbf{E}\mathbf{L}\mathbf{R}$	30.33	30.49	30.55
$\mathbf{E}\mathbf{S}\mathbf{I}$	8.01	7.93	7.91
Cyclohexane/R11 (0.2/0.8)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	207.47	210.99	212.16
$\mathbf{E}\mathbf{L}\mathbf{R}$	28.50	29.24	29.50
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.28	7.22	7.19
Cyclohexane/R11 (0.25/0.75)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	208.63	205.61	206.83
$\mathbf{E}\mathbf{L}\mathbf{R}$	28.60	28.28	28.21
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.29	7.27	7.33
Cyclohexane/R11 (0.3/0.7)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	201.05	199.28	198.92
$\mathbf{E}\mathbf{L}\mathbf{R}$	26.82	26.71	26.68
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.50	7.46	7.46

3.1.4. Influence of the condensing temperature

For this analysis, the inlet temperature of the cooling water in the condenser was kept constant and the outlet temperature of the working fluid in the condenser was changed, which changes the pinch point of the component in Figure 9. There are two cases for this parameter: in the pure fluids, as the condensation temperature of the working fluid decreases, a higher transformity is obtained; for mixture C, the same tendency is observed, but as the concentration of cyclohexane increases, a decrease in the transformity of the system is observed. This is due to an increase in the net production of the system; and the opposite case for the rest of the working fluids.

Figure 9.

System performance as a function of the condensing temperature (${\mathrm{T}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}$): a) net power, b) Exergetic efficiency, c) Transformity

The results indicate that by decreasing the temperature at which condensation occurs in the working fluid a better environmental performance is obtained, however, the maximum increase for each parameter does not exceed 3%. For pure fluids, there is a decrease in the net power generated which is quite minimal, approximately 0.04% for toluene and 0.02% for cyclohexane, for mixtures this change can reach up to 0.12%, see Table 14.

Table 14.

Emergy indexes as a function of the condensing temperature.

Toluene
Index	${\mathbf{T}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{d}}=\mathbf{41}°\mathbf{C}$	${\mathbf{T}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{d}}=\mathbf{40}°\mathbf{C}$	${\mathbf{T}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{d}}=\mathbf{39.8}°\mathbf{C}$
$\mathbf{E}\mathbf{Y}\mathbf{R}$	286.88	288.97	289.42
$\mathbf{E}\mathbf{L}\mathbf{R}$	39.22	36.80	36.24
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.31	7.85	7.99
Cyclohexane
$\mathbf{E}\mathbf{Y}\mathbf{R}$	239.72	241.59	242.01
$\mathbf{E}\mathbf{L}\mathbf{R}$	33.45	30.55	29.87
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.17	7.91	8.10
Cyclohexane/R11 (0.2/0.8)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	207.04	212.16	213.43
$\mathbf{E}\mathbf{L}\mathbf{R}$	30.64	29.50	29.19
$\mathbf{E}\mathbf{S}\mathbf{I}$	6.76	7.19	7.31
Cyclohexane/R11 (0.25/0.75)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	207.94	206.83	206.76
$\mathbf{E}\mathbf{L}\mathbf{R}$	30.48	28.21	27.72
$\mathbf{E}\mathbf{S}\mathbf{I}$	6.82	7.33	7.46
Cyclohexane/R11 (0.3/0.7)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	198.49	198.92	199.05
$\mathbf{E}\mathbf{L}\mathbf{R}$	28.63	26.68	26.24
$\mathbf{E}\mathbf{S}\mathbf{I}$	6.93	7.46	7.59

3.1.5. Influence of the condenser pinch point temperature

The analysis of the condenser pinch point temperature is shown in Figure 10. If the behavior of the system is measured merely by the transformer, a desired environmental performance is obtained, since decreasing the transformer implies that less energy is needed to generate a product, also an increase in net power generated and exergetic efficiency is observed when using the lowest permissible value, this increase is approximately 7% for all cases of study, which directly affects the transformity, whose range of variation goes from approximately 12% to a decrease of 36%.

Figure 10.

Emergy and exergy performance as a function of the condenser pinch point temperature (Pinch), a) net power, b) Exergetic efficiency, c) Transformity

With the results shown in Table 15, a clearer representation of the system’s behavior can be obtained. Observing the EYR it can be concluded a reduction in the system's energy and an increase in the same way of resources imported to the system, more precisely of non-renewable resources, since the use of renewable resources was reduced. This can be read implicitly in an increase of the ELR index by decreasing the temperature difference in the condenser, so there are systems with a greater load over the environment. The decrease in the ESI index also indicates that the system, although sustainable, have a greater opportunity for improvement, it should be taken into consideration that among all the variables studied, the one that has the greatest impact on these environmental indexes has been the pinch point of the condenser, since it has had a maximum deviation among all indexes of 65%, which makes this parameter of high interest.

Table 15.

Emergy indexes as a function of the condenser pinch point temperature.

	Toluene
Index	$\mathbf{P}\mathbf{i}\mathbf{n}\mathbf{c}\mathbf{h}=\mathbf{15}°\mathbf{C}$	$\mathbf{P}\mathbf{i}\mathbf{n}\mathbf{c}\mathbf{h}=\mathbf{10}°\mathbf{C}$	$\mathbf{P}\mathbf{i}\mathbf{n}\mathbf{c}\mathbf{h}=\mathbf{5}°\mathbf{C}$
$\mathbf{E}\mathbf{Y}\mathbf{R}$	288.97	268.64	239.92
$\mathbf{E}\mathbf{L}\mathbf{R}$	36.80	42.78	43.70
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.85	6.28	5.49
Cyclohexane
$\mathbf{E}\mathbf{Y}\mathbf{R}$	241.59	221.86	197.09
$\mathbf{E}\mathbf{L}\mathbf{R}$	30.55	37.84	39.09
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.91	5.86	5.04
Cyclohexane/R11 (0.2/0.8)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	212.16	188.56	87.31
$\mathbf{E}\mathbf{L}\mathbf{R}$	29.50	34.06	34.67
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.19	5.54	2.51
Cyclohexane/R11 (0.25/0.75)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	206.83	187.54	162.83
$\mathbf{E}\mathbf{L}\mathbf{R}$	28.21	32.78	33.47
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.33	5.72	4.86
Cyclohexane/R11 (0.3/0.7)
$\mathbf{E}\mathbf{Y}\mathbf{R}$	198.92	185.46	168.29
$\mathbf{E}\mathbf{L}\mathbf{R}$	26.68	31.15	31.94
$\mathbf{E}\mathbf{S}\mathbf{I}$	7.46	5.95	5.27

3.2. Multi-objective optimization

Figures 11a to 11e shows the Pareto points obtained through the application of the Non-Dominated Sorting Genetic Algorithm (NGSA)-II. The objective of this analysis is to find the values of the decision variables that maximize the energy efficiency with the lowest environmental impact (ESI), within a search space for each of the study fluids.

Figure 11.

Pareto frontier for objective variable: a) toluene; b) cyclohexane; c) cyclohexane [0.2] R11[0.8]; d) cyclohexane [0.25] R11 [0.75]; e) cyclohexane [0.30] R11[0.70].

The TOPSIS selection criterion was applied to each of the fluid solution sets to determine the most appropriate value within the solution set. The results are shown in Table 16, where the values of the decision variables in the base case and the new values obtained for each working fluid (value Multi-Objective Optimization) are observed. The objective is to determine the percentage increase or reduction obtained by comparing the values of the objective functions (Emergy Sustainability Index, and exergetic efficiency) derived from the optimization process (Table 16) concerning those reported in the base condition (Table 6). The results show that under the defined search space the exergetic efficiency of toluene was maximized from 39% to 44.15%, which represents an increase of 11.39%, and a reduction of the Emergy Sustainability Index from 7.85 to 4.80 (38.83%). Similarly, the values of the decision variables that maximize the exergetic efficiency and reduce the Emergy Sustainability Index were obtained for cyclohexane (${\eta }_{\mathrm{I}\mathrm{I}}=47.40\%,\mathrm{E}\mathrm{S}\mathrm{I}=3.97$), cyclohexane/R11 (0.2/0.8) (${\eta }_{\mathrm{I}\mathrm{I}}=68.97\%,\mathrm{E}\mathrm{S}\mathrm{I}=1.61$), cyclohexane/R11 (0.25/0.75) (${\eta }_{\mathrm{I}\mathrm{I}}=70.06\%,\mathrm{E}\mathrm{S}\mathrm{I}=3.93$), and cyclohexane/R11 (0.30/0.70) (${\eta }_{\mathrm{I}\mathrm{I}}=72.97\%,\mathrm{E}\mathrm{S}\mathrm{I}=4.32$).

Table 16.

Optimized values for decision variables and objective function.

Parameters	Case base		Multi-objective Optimization
	Units	Value	A	B	C	D	E
Pump efficiency, ${\eta }_{\mathrm{p}}$	%	75	75	74	79	79	78
Turbine efficiency, ${\eta }_{\mathrm{t}}$	%	80	84	85	85	85	85
Evaporator pinch, $\mathrm{A}\mathrm{P}$	°C	30	30.21	30.05	30.01	33.84	30.27
Condensing temperature, ${\mathrm{T}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}$	°C	40	41.00	41.00	40.99	40.99	41.00
Condenser pinch, $\mathrm{P}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{h}$	°C	15	5.02	5.04	5.02	5.01	5.01
Emergy Sustainability Index, $\mathrm{E}\mathrm{S}\mathrm{I}$	%	-	4.80	3.97	1.61	3.93	4.32
Exergetic efficiency, ${\eta }_{\mathrm{I}\mathrm{I}}$	-	-	44.18	47.49	68.97	70.06	72.97

A = toluene; B = cyclohexane; C = cyclohexane/R11 (0.2/0.8); D = cyclohexane/R11 (0.25/0.75); E = cyclohexane/R11 (0.30/0.70).

The behavior of the design variables throughout the optimization process is presented in Figure 12. The distribution of the variables in the optimization process of the cycle using working fluid is observed. In this case, toluene achieves better performance at high values of turbine efficiency, although much of the behavior of this variable was close to the 80% zone as shown in Figure 12b. In the case of blends, the best results are obtained with an efficiency of 85%. A similar case was found for the pump efficiency shown in Figure 12a. The behavior of this variable is more dispersed throughout the optimization process; however, for pure fluids the efficiency found was 75% and 74% for toluene and cyclohexane, respectively. While for the blends there was a greater increase in this variable, being around 79% as shown in Table 16.

Figure 12.

Multi-objective optimization decision variables: a) pump efficiency; b) turbine efficiency; c) evaporator pinch point; d) condenser pinch point; e) condensing temperature.

4. Conclusions

The working fluid has a fundamental role in the performance of an ORC, so the selection process of this is quite difficult, for this study a mixture of R11 and Cyclohexane was proposed as working fluid. The effect that the mass fraction has on the behavior of the system was studied, in addition to comparing the performance obtained by using two pure fluids.

It is concluded that the use of zeotropic mixtures (cyclohexane/R11) increases the power generated by about 50% concerning pure fluid (cyclohexane). Also, the system’s energy efficiency increases due to the use of zeotropic mixtures above 50%.

Using the emergy aspect as reference it can be noted that the pure fluids had a better ESI index, but this difference comparing it with the mixtures does not exceed 10%, the use of mixtures can also offer a sustainable system.

However, the mixture offered a lower ELR value, this means that they have a lower environmental impact, toluene and cyclohexane obtained values of 36.8 and 30.55, the mixture cyclohexane/R11 (0.2/0.8) obtained an ELR of 29.5, that is, a difference of approximately 3%, while the mixture with mole fraction 0.3 of cyclohexane obtained 26.68, a difference of at least 13% between the pure fluid with lower environmental load and the mixture.

In addition, a parametric analysis was performed with different study variables, the exergetic efficiency of the pump and turbine, the pinch point of the evaporator and condenser, also the effect of varying the temperature at which condensation occurs with the working fluid was analyzed. It was found that the parameters that directly affect the thermodynamic properties of the working fluid have a greater effect on the behavior of the system than the change in the efficiencies of the pump and turbine. However, increasing the turbine efficiency too much can be counterproductive, since this value directly affects the amount of raw material used for the turbine, which can increase the environmental load of the system and decrease the sustainability of the system. Finally, the multi-objective optimization was able to maximize the exergy efficiency for the working fluids by about 9.7% and reduce the ESI by 50.94%.

Declarations

Author contribution statement

Guillermo Valencia Ochoa: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Andres Pedraza Caballero: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Dora Villada Castilla: Conceived and designed the experiments; Performed the experiments.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of interest’s statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.