Autonomous optimization of neuroprosthetic stimulation parameters that drive the motor cortex and spinal cord outputs in rats and monkeys

Summary

Neural stimulation can alleviate paralysis and sensory deficits. Novel high-density neural interfaces can enable refined and multipronged neurostimulation interventions. To achieve this, it is essential to develop algorithmic frameworks capable of handling optimization in large parameter spaces. Here, we leveraged an algorithmic class, Gaussian-process (GP)-based Bayesian optimization (BO), to solve this problem. We show that GP-BO efficiently explores the neurostimulation space, outperforming other search strategies after testing only a fraction of the possible combinations. Through a series of real-time multi-dimensional neurostimulation experiments, we demonstrate optimization across diverse biological targets (brain, spinal cord), animal models (rats, non-human primates), in healthy subjects, and in neuroprosthetic intervention after injury, for both immediate and continual learning over multiple sessions. GP-BO can embed and improve “prior” expert/clinical knowledge to dramatically enhance its performance. These results advocate for broader establishment of learning agents as structural elements of neuroprosthetic design, enabling personalization and maximization of therapeutic effectiveness.

Graphical abstract

Highlights

• •Autonomous learning algorithm optimizes complex neuromodulation patterns in vivo
• •It enables “intelligent” neuroprostheses, immediately alleviating motor deficits
• •The application is robust to changes, e.g., due to plasticity or interface failure
• •Knowledge transfer to experts/clinicians is supported with an open-source framework

Bonizzato et al. develop intelligent neuroprostheses leveraging a self-driving algorithm. It autonomously explores and selects the best parameters of stimulation delivered to the nervous system to evoke movements in real time in living subjects. The algorithm can rapidly solve high-dimensionality problems faced in clinical settings, increasing neuromodulation treatment time and efficacy.

Introduction

Neuroprostheses interfacing with the brain, spinal cord, and peripheral nerves are being applied to clinical treatment of paralysis after spinal cord injury,^1,2,3,4,5 stroke,^6,7,8,9 and other neurological disorders.^10,11 Electrical neurostimulation can immediately promote movement execution and enable users to engage in effective motor training,⁴ which is fundamental for neurorehabilitation.¹² Ideally, neuroprosthetic systems will have to provide selective circuit recruitment and precise timing of delivery. However, beyond our advances in general design of therapies, our way to handle user-specific personalization of neurostimulation in real time is largely outdated. Cutting-edge demonstrations of neuroprosthetic technology still rely on relatively simple, hand-tuned, and thus time-consuming, stimulation strategies.^13,14,15,16 A closed-loop optimization framework that determines stimulation parameters based on evoked responses in real time would relieve the experimental and clinical burden of user-specific implementation.

To date, real-time solutions have been limited to “adaptive” regulation of stimulation dosage, deployed in selected clinical trials.^17,18,19 This adaptive regulation is a single-input single-output problem that has exclusively been solved with simple mathematical methods. Conversely, neurostimulation programming across multiple parameters is a complex multivariate problem that requires a tailored autonomous learning framework. Machine learning provides the opportunity to design such algorithmic infrastructure to perform complex, online personalization and optimization of neuroprosthetic systems.^20,21,22 To accomplish this goal, a first challenge is handling the increasing number of tunable stimulation parameters (i.e., the dimensionality of input space), with considerations of time constraints. Recent technological improvements have brought high-throughput neural interfaces with hundreds of implantable electrodes.^23,24,25 While they dramatically increase flexibility for electrode selection (i.e., spatial parameters), empirical tuning for these large interfaces is already not practical. If other stimulation parameters are added (timing, duration, frequency, etc.), the complexity grows exponentially. This challenge is further amplified by the fact that optimization cannot impede treatment delivery and thus it must rely on limited data to maximize treatment time. The second challenge is the non-stationarity of neural interfaces and brain circuits. Physiological responses are noisy and time-varying.^26,27 After injury, neuroplasticity accelerates changes of connectivity in neural circuits.^28,29,30 Optimizing strategies needs to be flexible, handle unpredictable noise, and track non-stationarities.

To date, genetic algorithms and other learning agents (e.g., artificial neural networks) have been elegantly applied to optimize neurostimulation patterns.^31,32,33,34 However, these approaches rely on pre-training and require many iterations to generate performant solutions, making them mostly suited for offline optimization and applications that are standardized in time and across subjects.²¹ In contrast, neural implants are subject-specific. Treatment delivery requires personalization since each user features unique anatomic features,³⁵ tissue-electrode interface properties and positioning,^36,37 network excitability, and injury/disease profile.^38,39

In order to address these two challenges and design an online learning agent for neuroprosthetic applications, we focus on a class of algorithms that rely on parametric models of stimulation properties, namely Gaussian-Process (GP)-based Bayesian Optimization (BO).^40,41 GP-BO algorithms iteratively test single-input parameter combinations (“queries”), leveraging responses to build an evidence-based approximation (“surrogate” function) that describes how stimulus choices affect the desired output.⁴² GP-BO could directly address the unmet neuromodulation challenges, by optimizing stimulation within a limited number of queries, purely online, starting with no previous knowledge over a new neural interface. It could also maintain continual learning, allowing to evolve the intervention strategy over ever-changing scenarios. Moreover, GP-BO offers principled ways to inform future queries, and track uncertainty surrounding predictions.

Previous work supported the applicability of BO to selected neuromodulation problems to facilitate parameters selection. Nevertheless, these results have mostly been limited to offline simulations.^41,43,44 Recently, few online demonstrations of GP-BO application in neurostimulation problems have successfully tackled selected in vivo problems. For example, GP-BO was used to optimize stimulation of peripheral nerves to generate hand movements in an anesthetized non-human primate (NHP),⁴⁵ to drive cerebellar stimulation to minimize seizure in mice,⁴⁶ and to optimize non-invasive transcranial alternating current stimulation (tACS) to generate visual phosphenes in humans.⁴⁷ These studies have opened a door to allow future applications of GP-BO in real-world operational environments. However, the versatility and large-scale applicability of the approach are still elusive. For example, the robustness of GP-BO across noise levels and to spurious responses, its efficacy across parameter smoothness and large, multi-dimensional search spaces in reasonable time are still unclear. Moreover, there are still no demonstrations that GP-BO can optimize neurostimulation in awake and behaving animals, with stimulation integrated and adapting to behavior.

Here, we provide an array of in silico experiments, real-time multi-dimensional experimental validations of GP-BO neurostimulation optimization, and demonstration of online autonomous optimization in clinically relevant contexts. Our work leverages GP-BO-based stimulation optimization to achieve a learning neuromodulation agent capable of autonomously improving movement after paralysis. To help neurostimulation scientists and clinicians adopting performant online optimization in their own experimental practice, we provide a conceptual demonstration with comprehensive instructive material. This will further contribute to and accelerate the development of a next generation of intelligent neural prostheses.

Results

We implemented a GP-BO-based algorithm to identify optimal stimulation parameters for desired motor output (Figures 1A–1C), defined as a scalar value function (Figure 1D) subject to optimization. For automation, responses can be captured with a variety of sensing techniques. We used recordings of electromyographic (EMG) activity and movement kinematics with cameras. In this operations research problem, there is a trade-off between exploration and exploitation. “Exploration” refers to the ability to visit a large portion of the input space, thereby proposing solutions that are expected to be globally optimal (see STAR Methods). This metric reports the efficacy, or performance, of the input (e.g., given electrode or stimulation frequency, etc.) considered optimal by the algorithm in proportion to the true best. For example, if an algorithm’s exploration performance is 80% after 10 queries, it means that the stimulation parameters currently considered best elicit a response that is 80% of the highest response achieved across all parameters for this subject. “Exploitation” is the capability of targeting effective regions of the input space early and persistently, a likely indication for an effective therapy. This metric reports the efficacy, or performance, of the current input choice in proportion to the true best. For instance, if an algorithm’s exploitation performance is 80% after 10 queries, it means that the stimulation delivered at query 10 would elicit a response that is 80% of the highest response achieved across all parameters for this subject.

Figure 1.

A versatile learning agent for neurostimulation optimization

(A) Neurostimulation of motor regions such as M1 causes muscle responses. These controllable electrical signals delivered to the brain can feature complex spatiotemporal patterns.

(B) A GP-BO-based algorithm iteratively searches for the most effective input x, capable of eliciting a desirable output y. In doing so, it balances “exploration” (testing unknown inputs) and “exploitation” (pursuing performant solutions). The trade-off between the two is determined by the hyper-parameter k.

(C) Intracortical microstimulation (ICMS) evokes selective movements, each featuring a characteristic pattern of EMG activity. Left, stimulus causing a flexion movement and EMG pattern associated. Center, stimulus causing an extension movement and EMG pattern associated. Right, pictures of both evoked movements.

(D) An objective function can be cast over the movement, represented as a scalar value. This number encodes one representative feature of EMG activation or kinematic output (f: X → Y, where X is a multi-dimensional space of stimulation parameters and Y is a movement feature, such as peak EMG or a step height), or an arbitrary combination of several biomarkers. The example shows a linear combination using weights w_i. BO has the objective of maximizing (or minimizing) this value.

(E) Typical operation of the proposed algorithm consists in a sequence of queries following a pattern that gradually converges over “hotspots.” These are locations in the input space where the objective function is maximal. Two weighted maps of estimated value and uncertainty take part in the acquisition process.

(F) GP-BO is a flexible class of learning agents, which features the possibility to inject prior knowledge (e.g., known effective range of values) to further accelerate the search, as well as extracting posterior understanding of the neurostimulation problem (i.e., after testing several subjects, the most effective range of value is explicitly accessible to the user and can be used as prior). See also Figures S1–S3.

GP-BO simultaneously maintains (1) a map of the estimated performance of each point in the input space and (2) a map of the degree of uncertainty of the performance of different values of the parameter, as depicted in Figure 1E. An “Acquisition function”—the Upper Confidence Bound (UCB)⁴⁸—solves the optimization problem while addressing the trade-off between acquiring new information and sticking to performant parameters. This trade-off is mediated by a hyper-parameter k (Figure 1B). In practice, UCB-driven GP-BO often results in an initially broad search for viable parameter options, followed by local intensification over high-performing areas. It concludes by adopting the putative optimal solution with sporadic informative tests (Figure 1E). An enticing feature of BO is the transparency by which “prior” information can be injected in the model and “posterior” information can be extracted (Figure 1F), allowing the artificial learning agent to exchange prior/posterior information with the experimenter with an explicit representation.

Implementations of GP-BO, as most other machine learning methods, feature “hyper-parameters,” which can be tuned to control the learning process.⁴² These include a choice for the exploration-exploitation trade-off parameter k, kernel geometric properties, and a predetermined number of random queries used to start the algorithmic search. To tune the algorithm to address the specific problem of evoking movements using electrical stimulation in the central nervous system, we first characterized the effects of hyper-parameters selection on algorithmic performance using offline analysis (Figure S1). These simulations informed the hyper-parameters values used for online testing and real-time experimental demonstrations.

To evaluate the performance of GP-BO, we have chosen two benchmark strategies, extensive and greedy search (see Figure S2 and STAR Methods). We defined extensive search as the testing of all points in the input space in an arbitrary predetermined sequence. The predetermined sequence can be proposed in random order when no prior information is available or ranked by decreasing probability of high performance when prior information is available. Extensive search requires dedicating equal attention to all parts of the input space, with a high risk of false positives and negatives. Greedy search, which optimizes one input parameter at a time, partially responds to this limitation, and is arguably more human-like.¹⁶ However, greedy search features limited ability of freely chasing gradients in the input space, and cannot co-vary two or more inputs together. Conversely, UCB-driven GP-BO purposely navigates and repeatedly queries the best responding regions of the input space. This flexibility allows retaining robust decision capacity across different ranges of signal-to-noise ratios (Figure S3) and always outperforms our two benchmark strategies. The targeted exploration capabilities and hallmark resilience of BO in noisy scenarios are extremely valuable to solve the problem of stimulation parameter selection for neuromuscular responses, which are highly variable.²⁷

GP-BO-based algorithm efficiently discovers cortical movement representations

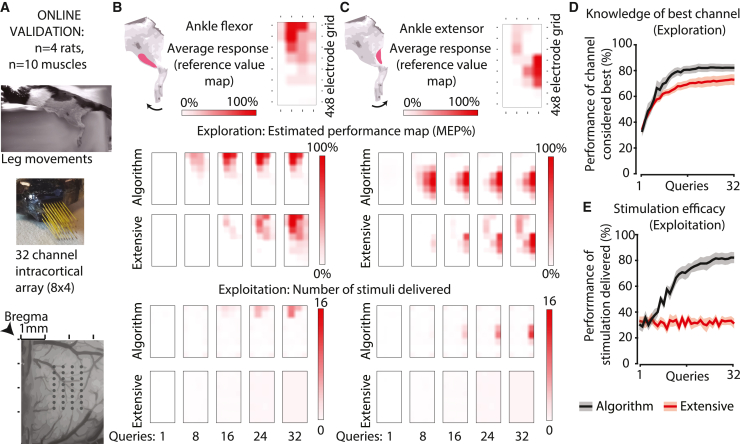
We implanted 32-microelectrode arrays (MEAs) in the hindlimb sensorimotor cortex of sedated rats (Figure 2A) and searched for the stimulus location that would evoke the strongest activation of selected muscles (Figures 2B and 2C). In real-time trials, GP-BO was compared with the extensive (random) search. Performance curves were measured on a [0–100]% scale and the absolute difference between the two curves calculated, which we refer to as a difference in performance points (see STAR Methods). After 16 trials (50% of the array), the algorithm already surpassed the extensive (random) search (Figures 2D and 2E) by an average of 12.6 points in exploration (p = 0.005) and 40.8 points in exploitation (p = 0.001). Only 9 queries (∼25% of extensive [random] search) were sufficient for the algorithm to attain average exploration performance of 70.8%, the mean score for extensive (random) search.

Figure 2.

Online cortical search for the most performant electrodes to evoke hindlimb EMG responses in rats

(A) In sedated rats, we searched for the most performant electrode evoking leg movements using a 32-channel electrode array implanted in the leg sensorimotor cortex using algorithmic hyper-parameters previously optimized offline (see Figure S1).

(B and C) The algorithm efficiently determined an estimated performance map across active sites of the implant for two antagonist muscles. Top: average response (reference value map), an empirical reference built by pooling all trials acquired during the entire recording session (i.e., data acquired during all repetitions of the GP-BO, extensive [random] and greedy searches). The value metric was the size of the motor evoked potential (MEP), reported as % of maximal EMG response (average response from the best electrode). Middle: Average estimated performance map (exploration) and comparison with the extensive (random) search. GP-BO search intensified over optimal solutions. The GP-BO algorithm developed an earlier knowledge of the position of performant hotspots. This advantage was maintained throughout the execution of the search. Bottom: Average number of stimuli delivered from each electrode (exploitation) and comparison with the extensive (random) search. The algorithm intensified stimulation of performant hotspots, while the extensive (random) search equally sampled the whole search space. This means that by the end of the 32 queries, in addition to a better knowledge of the hotspots, the algorithm used approximately half of its queries to deliver an effective intervention.

(D and E) Average performance for exploration (D) and exploitation (E) over all n = 10 experiments collected in four rats. Data displayed as mean ± SEM. During a series of 32 queries, the algorithm ranked above the extensive (random) search both in exploration and exploitation performance. Because of the random query procedure, the extensive search exploitation performance consists of a flat line. The ripple along this line is due to this performance being estimated using a finite number of experiments (32.5 ± 6.3 runs). See also Figures S4 and S5.

We next implanted a 96-electrode MEA in the hand area of the primary motor cortex (M1) of a capuchin monkey (Figure 3A) and replicated these results (Figures 3B and 3C). As expected, based on previous studies of movement representations in M1 of primates,^{49,50,51,52,53} the M1 arrays featured a relatively sparse and granular representation of movement (Figures 3D and 3E), two characteristics that might favor extensive search. GP-BO is expected to perform much better when the input-output relation for the stimulation parameter is smooth and much information can be extrapolated by neighboring points. With unsmooth response patterns such as the spatial representation of evoked movements from M1, the algorithm could wallow over local maxima, failing to visit global maxima. Albeit these challenging conditions, GP-BO took an early lead in knowledge and continued performing above extensive (random) searches. It displayed a final average gain of 6.7 performance points in exploration (p = 0.007) and 78.5 points in exploitation (p = 3 × 10⁻⁵).

Figure 3.

Online cortical search for the most performant electrodes to evoke arm muscles EMG responses in NHP

(A) We tested the efficacy of the GP-BO algorithm in a sedated capuchin monkey. We searched for the most performant electrode to evoke EMG responses in muscles driving hand/wrist movements using a 96-channel electrode array chronically implanted in M1. The value metric was the size of the motor evoked potential (MEP).

(B and C) During a series of 96 queries, the algorithm ranked above the extensive (random) search both in exploration and exploitation performance. Data displayed as mean ± SEM over all n = 4 experiments collected in 1 NHP.

(D and E) The algorithm efficiently determined an estimated performance map across active sites of the implant for two antagonist muscles. Left: Average response (reference value map). Top right: Average estimated performance map (exploration) and comparison with extensive (random) search. The algorithm features an earlier knowledge of the position of performant hotspots, and this better knowledge was maintained throughout execution. Bottom right: Number of stimuli delivered to performant hotspots (exploitation) and comparison with extensive (random) search. Algorithmic search intensified over optimal hotspots, while the extensive search evenly queried the entire space. This meant better knowledge of the true optima (exploration) and earlier access to effective intervention (exploitation).

(F) We tested the efficacy of the algorithm in two awake macaque monkeys sitting quietly. A 96-channel electrode array was chronically implanted in the hand representation of M1.

(G and H) During series of 96 queries targeting n = 4 muscles, the algorithm performed similarly to what was obtained in the sedated capuchin, ranking above the extensive (random) search both in exploration and exploitation performance. Data displayed as mean ± SEM. See also Figures S4–S6.

We finally validated these results in two non-sedated macaques (Figure 3F). In the awake state, EMG responses to stimulation are particularly susceptible to contamination by spontaneous movements and other sources of noise. Nevertheless, our algorithm maintained a performance comparable to what was obtained in sedated animals (Figures 3G and 3H). It outperformed the extensive (random) search by an average of 17.1 points for exploration (p = 0.02) and 65.0 points for exploitation (p = 0.008). Merging all NHP experiments in sedated capuchins (Figures 3A–3C) and awake macaques (Figures 3F–3H), on average only 32 queries (one-third of extensive search) were sufficient for the algorithm to attain exploration performance of 71.4%, the mean score for extensive (random) search.

We conducted complementary offline experiments for both the rat hindlimb cortex (Figure S4A) and the NHP M1 (Figure S4B), adding our alternative “benchmark” strategy, the greedy search, to compare algorithmic results. Again, GP-BO outperformed both search strategies.

Leveraging input-output relationships with diverse smoothness

In our first neuroprosthetic application, we considered cortical representations of movement (i.e., solving the spatial cortical representation problem at the length-scale of electrode spacing) to be close to a worst-case scenario for neurostimulation optimization. Other parameters, such as stimulus frequency or intensity, are characterized by smoother, but potentially noisy, input-output relationships (e.g., intracortical microstimulation using 200 or 300 Hz evoke relatively similar EMG responses).⁵⁴ To evaluate how GP-BO performance would generalize across parameters with different smoothness, we conducted an extensive offline computational analysis (Figure S5A) that consisted of creating synthetic 4-D models featuring diverse input-output relationship smoothness. Generated models also featured variable smoothness heterogeneity across search dimensions, simulating systems where certain parameters (e.g., frequency) are smoother than others (e.g., electrode location). GP-BO outperformed both extensive (random) and greedy searches across the entire dataset, both in exploration and exploitation performance (Figure S5B). We also found that having an estimation over dataset smoothness may help inform the choice of the exploration-exploitation hyper-parameter k (Figures S5C and S5D).

BO creates an explicit representation of how different inputs are related to effective outputs, which can result in a useful contribution to the experimenter’s knowledge (e.g., the 2D cortical representation in Figures 2C, 2D, 3D, and 3E) and that can be fed back in the form of prior to further improve the performance of the algorithm. Input-output mapping capacities are dependent on the Matérn kernel geometric parameter ρ (“length-scale,” see STAR Methods), which specifies how smooth the input space is. We tested an additional GP-BO feature allowing variable-ρ across the search dimensions, overcoming the necessity to estimate ρ before operating. Length-scales are optimized incrementally using BO after each new query, fitting ρ on the smoothness of acquired data. This property enabled decoupling separate input axes, for accurate mapping of functions with uneven smoothness (Figure S6A). This advantage came with the new requirement to learn ρ for each input dimension, which is a cost in terms of performance. Combining offline and online experiments in NHP, we showed that variable-ρ GP-BO performed equivalently to the fixed-ρ version in both exploration and exploitation (Figures S6B–S6D). The variable-ρ GP-BO, however, held a better representation of the objective function. The accuracy (explained variance, r²) in input-output mapping was +11.2 additional performance points (p = 4 × 10⁻⁵, Figure S6B). Thus, this variant is better suited to represent a landscape of the objective function, rather than just focusing on its maximum.

GP-BO-based algorithm embeds prior knowledge

BO’s execution can be informed of existing knowledge by injecting “priors” (Figure 1F). For instance, an expert may know that a certain stimulation location is more likely to produce a performant output. It may be desirable to make such information available to the artificial learning agent before starting the search. To explore this concept, we performed an experiment where we searched for the electrode evoking the strongest ankle flexion in rats implanted in the leg area of the sensorimotor cortex. We initialized the GP kernel with a prior suggesting where stimulation is most likely to be effective. The prior consisted of a composite topographic 2D map of evoked ankle flexion movements based on data of 25 rats previously collected (Figure 4A). We then conducted an online validation experiment to estimate the impact of this prior knowledge on the performance of the algorithm. The individual maps of the experimental subjects showed high inter-subject variability (Figure 4B), a well-described feature of cortical movement representation,³⁰ that should weaken the impact of prior knowledge. Nevertheless, even in this challenging context, performance was instantly improved by the prior, with a gain of 31.8 points in exploration by the third query (p = 0.039). This held long-lasting benefits; after 16 queries (half of an extensive search) using injected knowledge, the algorithm had reached 74.9% exploration performance (Figure 4C). The “tabula rasa” approach required the entire run to attain similar results. Note that in these experiments, both alternative search methods were also provided with the same prior information (Figure S2B), meaning that searches started from points that were highly likely to be performant, based on the prior. These extensive (prior-ranked) and greedy searches never reached GP-BO’s 74.9% exploration performance level (last query: gap of 31.9 and 26.8 points respectively in exploration, p = 0.0078 and 0.02, gap of 58.9 and 44.6 point in exploitation, p = 0.0039 for both, Figures 4C and 4D).

Figure 4.

Injecting prior knowledge immediately increases performance

(A) GP-BO strategies can incorporate existing expertise provided by the user, in this case embodied as a prior on the process mean. A “tabula rasa” approach refers to an empty mean prior. In this experiment, a prior was derived from indirect knowledge obtained from a previous study. Cortical motor maps of ankle flexion movements were collected using visual inspection of responses evoked with intracortical microstimulation (ICMS) in 25 rats. Average results were compiled in a 2D map of estimated probability of evoking ankle flexion (normalized 0%–100%). Across all these maps, the rostral (top) part of the of the array was more likely to generate ankle flexion.

(B) We performed online experiments in seven rats in which the algorithm had to find the electrode that evoked the greatest response in the ankle flexor muscle. The value metric was the size of the motor evoked potential (MEP). In one rat, an additional experiment was done for the knee flexor muscle (muscle number 8). These maps had high inter-subject variability.

(C and D) In an online demonstration, injecting priors immediately boosted exploration and exploitation performance. GP-BO outperformed extensive and greedy searches, which were provided with the same prior information. Data displayed as mean ± SEM over n = 8 experiments. See also Figure S7.

Further offline work (Figure S7) allowed us to depict a global picture of the effects of prior knowledge quality and quantity over neurostimulation optimization search performance. Both increasing quality (higher correlation to ground truth) of transferred information and quantity (number of dimensions disposing of a prior) facilitated the search for the optimal stimulation solution (Figure S7B). Moreover, GP-BO also proved robust to conflicting low-quality or erroneous prior information, being able to rapidly recover high performance. In all tested cases, GP-BO outperformed extensive (prior-ranked) and greedy searches (Figure S7C). Disposing of an estimation over prior quality/quantity may inform a choice of the exploration-exploitation hyper-parameter k (Figure S7D). When prior information is well established and precise, the algorithm benefits from “trusting” the prior and having an acquisition function that favors exploitation rather than exploration (lower k).

Continual learning adapts to neuroplasticity or neural interface non-stationarities to deliver constantly optimized stimulation throughout treatment duration

The GP-BO’s iterative optimization process is not bound to a fixed number of queries, but instead can continually probe the parameter space and increase its knowledge over time and sessions. This property is particularly enticing for neuromodulation, during which the electrical properties of the interface and the brain change with time, and the intervention itself can alter the input-output relationship. To demonstrate the capacity of GP-BO framework in these real-life conditions, we perform an experiment in which we induced thoracic spinal cord injury (SCI) in rats and stimulation optimization was carried over multiple weeks after injury, during the period of most rapid recovery and brain plasticity. Rats, when recovering motor function after SCI, experience a progressive upregulation of cortical outputs efficacy over 3 weeks.⁵ The cortical representation of movement consistently changes during this time, meaning that a neurostimulation device should require regular re-tuning. The algorithm was deployed to identify, out of a 32-channel cortical array, the one electrode whose stimulation produced the strongest leg flexion, measured with the amplitude of EMG response. At each testing day (i.e., 3 times/week), we used the previous session findings as the new priors (Figures 5A and 5B), and let the algorithm learn the new session’s novelties in a quick, 8 queries tuning session. At the end of each day, on average, the algorithm held a 17.5-point advantage in exploration over the extensive (prior-ranked) search and 16.6 over greedy search (each p = 0.0039, Figure 5C).

Figure 5.

Continual learning over an evolving neuroprosthetic scenario

(A) Schematic representation of the continual learning framework. GP-BO features an explicit representation of prior (before optimizing) and posterior (after optimizing) knowledge, which allows designing continual learning frameworks, where posterior information from a previous session is injected as prior information for a new one.

(B) From the first to the third week after SCI, in repeated sessions we sought to identify the electrode providing the most effective activation of leg flexor muscles within a cortical array. The value metric was the size of the motor evoked potential (MEP). The panels show the average response (reference value map) for one rat. As expected, in this post-SCI scenario, neuroplasticity and recovery caused a continuous evolution of cortical representation of movements.

(C) We tested the capacity of GP-BO to find the best electrode along recovery, using a very limited number of eight queries in each session, for a quick tuning of electrode choice that would maximize the duration of treatment time. On the first session we provided an initial prior consisting of the average responses across the arrays of the 25 rats of Figure 4A collected 1 week post-SCI. In subsequent sessions, the output of the previous session was used as prior. In this evolving scenario and with such a limited number of queries, GP-BO steadily maintained higher performance than extensive (prior-ranked) and greedy searches.

(D) In the same rats we ran an additional online experiment in parallel during the third week post-SCI. To simulate the loss of the best electrode in the array, one of the stimulator outputs was removed and we ran another series of eight queries in these conditions.

(E) The loss caused an immediate drop of performance, where GP-BO allowed a rapid recovery of baseline performance.

(F) Although, due to the very limited number of queries, this experimental scenario was not designed to study exploitation properties, GP-BO displayed a better exploitation than all alternative methods.

All data displayed as mean ± SEM over n = 8 experiments.

We then assessed the GP-BO robustness to unpredicted interface faults with an in vivo experiment in which we simulated the loss of the best active site by turning off one of the stimulator outputs (Figure 5D). The loss caused an immediate drop of performance, identical for all learning methods (Figure 5E). Yet, GP-BO alone proved its robustness by rapidly recovering and maintaining baseline performance for all following sessions. At the end of each day, on average, the algorithm had 16.9 points advantage in exploration over the extensive (prior-ranked) and 18.9 over greedy search (each p = 0.0039). Although these quick tuning protocols were not designed to evaluate exploitation, GP-BO did perform better in this metric (Figure 5F).

Taken together, results in Figure 5 illustrate the learning agent’s capacity to autonomously adapt to drifts in neural interface properties along extended periods of time, as well as reacting unpredictable interface faults. GP-BO quickly updated its inner model to exclude formerly performant solutions when they failed to maintain the established standard. This provides convincing evidence that the approach can effectively handle two key challenges featured in real-world neuroprosthetic problems.

Learning agent optimizes spatial features of cortical neuroprosthetic intervention to alleviate motor deficits in injured animals

We investigated the effectiveness of GP-BO-based algorithms to optimize neuroprosthetic systems and improve motor function in injured animals. We embedded the algorithm within a real-time neurostimulation system, whose objective is to track (using cameras) and condition (using cortical stimulation) the foot lift movement during locomotion (Figure 6A).⁵

Figure 6.

Intelligent intracortical neuroprosthesis optimizes spatial features of stimulation to alleviate SCI locomotor deficits

(A) Rats with SCI were engaged in treadmill walking. Inner loop: EMG activity was processed online with pattern recognition to determine gait phases and trigger phase-coherent cortical stimulation at the onset of foot lift. Outer loop: A red foot marker was real-time tracked to determine step height at each gait cycle. This information was fed to the fixed-ρ learning algorithm, which searched for the optimal cortical stimulation channel (maximizing foot clearance). The value metric was the step height.

(B and C) During a series of 32 queries, the algorithm ranked above extensive (random) search both in exploration and exploitation performance. Data displayed as mean ± SEM over n = 4 rats.

(D) Improved exploitation performance means delivering effective intervention while still fine-tuning the search: neurostimulation alleviated foot dragging during active optimization, a clear benefit over extensive search.

(E) Example trial. Top: Stepwise estimation of performance. Middle: Foot vertical trajectory. Bottom: EMG traces and stimulation timing. +, one step was not detected by real-time tracking, therefore it was ignored and repeated. Initial wide search phases correspond to low exploitation, meaning low foot clearance and presence of dragging. Steps 10–12 corresponded to the first approach to the most performant area of the cortical implant (top right corner). Subsequently, search intensified in the neighboring region and step height was quite consistently close to the 2-cm range. The algorithm converged (star symbol in figure) on the site considered optimal by average response (reference value map): in the final steps dragging was completely alleviated and the rat displayed foot clearance stably above 2 cm in height.

(F) The algorithm efficiently determined an estimated performance map for the cortical array. Left: Average response (reference value map). Top right: Average estimated performance map develops earlier (exploration). Bottom right: Average number of stimuli delivered (exploitation). See also Figure S4.

While rats with incomplete SCI were walking on a treadmill, EMG activity was monitored to determine the onset of foot lift. With no intervention, SCI resulted in consistent paw dragging (Video S1). We used intracortical microstimulation to potentiate motor outputs to alleviate foot-drop and promote ground clearance. Stimulation was delivered through a 32-electrode array implanted in the sensorimotor cortex. At each gait cycle, our algorithm queried one electrode of the cortical implant in search for the maximum stimulation efficacy, as measured by step height. This measure is associated with improvement of lift strength and reduction of foot-drop.⁵ This optimization search, like what was presented above, is here embedded in locomotor behavior and directly conditions locomotor performance. After 32 queries, the algorithm performed on average 89.8% of the maximum step height, with a gain of 12.4 points (corresponding to +0.3 cm efficacy in step height, p = 0.0005) in exploration and 39.4 points (or +1.2 cm, p = 0.007) in exploitation (Figures 6B and 6C). Only 20 queries (⅝ of extensive [random] search) were sufficient for the GP-BO based algorithm to attain average performance of 76.4%, the mean score for extensive (random) search. As stimulation intensified around “hotspots,” foot trajectory progressively increased and walking performance improved (Figures 6D–6F and Video S1). Because of GP-BO exploitation, the algorithm delivered effective neuroprosthetic intervention while fine-tuning the identification of the best electrode, and foot-drop was consistently alleviated (Figures 6D and 6E). The algorithmic run in Figure 6E shows that GP-BO is generally robust to suboptimal local maxima, which can attract optimization algorithms, thanks to a balance between exploration and exploitation behaviors. While the aleatory component of realistic neurostimulation responses implies that perfect solutions are theoretically impossible to achieve in finite time (Figure S3), GP-BO’s exploration-exploitation trade-off is performant if the parameter k is well-dimensioned (Figures S1A and S1C), allowing to exceed the results obtained by benchmark algorithms (Figure S4).

Video S1. Autonomous optimization of cortical stimulation, related to Figure 6

Video demonstration of the experimental setup, methods, and results displayed in Figure 6. Rats with SCI were engaged in treadmill walking. EMG activity was processed online with pattern recognition to determine gait phases and trigger phase-coherent cortical stimulation at the onset of foot lift. A red foot marker was real-time tracked to determine step height at each gait cycle. This information was fed to the learning algorithm, which searched for the optimal cortical stimulation channel. Optimality was defined as maximizing foot clearance with the aim to alleviate leg dragging. An example trial is presented along with stepwise estimation of performance (scheme in the bottom right of the screen) and foot vertical trajectory (trace in the bottom left of the screen).

Learning agent optimizes spatiotemporal spinal neuroprosthetic intervention alleviating motor deficits in injured animals

We sought to demonstrate that our variable-ρ GP-BO algorithm can be embodied in alternative neurostimulation techniques. To do so, we implemented it to optimize spinal cord stimulation and improve locomotion after SCI. Furthermore, we wanted to evaluate the efficacy of the GP-BO approach in solving large input space problems. We thus proposed a general application on a 4D spatiotemporal input space, including location, timing, stimulus frequency, and duration. We attempted to obtain meaningful mappings of this 672-combinations 4D space within 30 queries, corresponding to a −95.5% subsampling.

While the rats walked on a treadmill, stimulation was delivered on two epidural spinal stimulation sites (lumbar L2 and sacral S1) with various combinations of stimulus frequency, timing, and duration (Figures 7A and 7B). To enrich the search space, we imposed realistic operational constraints, using a cap in stimulus amplitude and total charge delivered on both GP-BO and extensive (random) searches (Figure 7C). Such specifications can be clinically desirable to extend battery life and avoid high stimulus amplitudes that might damage neural tissue.

Figure 7.

Intelligent neuroprosthesis optimizes multi-dimensional spinal stimulation parameters and alleviates SCI locomotor deficits

(A) Rats with SCI were engaged in treadmill walking. Inner loop: Online gait phases detection triggered phase-specific spinal stimulation. Stimulation trains were delivered at one of seven possible timings in relation to foot lift. Outer loop: The variable-ρ learning algorithm optimized spinal stimulation parameters to maximize step height (the value metric), which was real-time tracked using a camera.

(B) A 4D input space was searched, including spinal site and stimulus timing, duration, and frequency. The space featured 672 possible combinations, while the algorithm and the extensive (random) search were given 30 steps to optimize parameters.

(C) Caps in amplitude and charge were set as operational constraints to both GP-BO and extensive (random) search. As a result, top frequencies are not allowed full amplitude. Longer durations would also be associated with high charges, further reducing the stimulus amplitude available, due to the charge cap (light blue arrow).

(D) Maps from online validation. Each of the two submaps is a 2D average projection, corresponding to the region marked with a square on the complementary submap. The darker regions identified by the algorithm correspond to known spatiotemporal characteristics of spinal stimulation and to the imposed operational constraints.

(E) Example trial. Top: Stepwise optimization, progressively intensifying over performance “hotspot.” Bottom: Foot trajectory increased over time with algorithmic learning.

(F and G) Exploration and exploitation indicators evolution during a series of 30 queries. Data displayed as mean ± SEM over n = 4 rats.

(H) Neurostimulation optimization alleviated foot dragging. Bars, means and individual replicates.

(I) Top: Average estimated performance map for spinal stimulation (exploration). An accurate representation of spatiotemporal characteristics of spinal stimulation rapidly emerges during algorithmic searches. Bottom: Average density of stimuli delivered (exploitation). See also Figure S4.

The algorithm determined effective parameter combinations in the input space (Figures 7D–7I and Video S2). Although we used an extremely small number of queries, the algorithm outperformed the extensive (random) search by 10.6 points (p = 0.004) in exploration and 7.0 in exploitation (p = 0.14) and succeeded in obtaining realistic maps of the search space (Figures 7D–7I). Only 16 queries (about half extensive [random] search) were sufficient for the algorithm to attain average performance of 68.5%, the mean score for extensive searches after 30 steps. In previous lower-dimensional experiments (Figures 2 and 3), we had access to a robustly estimated ground truth, due to the large number of queries collected during each entire session (see STAR Methods). In a large search space such as the 4D one presented here, a ground truth for the objective function is harder to empirically define due to a high cost for repeated sampling. Nevertheless, the experiment was crafted to evaluate GP-BO’s solutions in light of well-defined spatiotemporal characteristics of spinal cord stimulation for locomotion. Without any prior information, the algorithm converged (Figure 7D) on known properties, such as (1) lumbar stimulation being more effective than sacral for leg flexion,^55,56 (2) optimal stimulation timing around foot lift and early swing,⁵⁶ (3) stimulus efficacy increasing with its frequency and duration,⁵⁷ and (4) best performance around the values located at the notch defined by the enforced amplitude and charge caps. In all animals, the algorithm effectively discovered stimulation patterns resulting in elevated foot trajectory (Figure 7E) and improved walking performance, drastically reducing foot-drop deficits (Figure 7H and Video S2).

Video S2. Autonomous optimization of spinal stimulation, related to Figure 7

Video demonstration of the experimental setup, methods, and results displayed in Figure 7. Rats with SCI were engaged in treadmill walking. EMG activity was processed online with pattern recognition to determine gait phases and trigger phase-specific spinal stimulation. A red foot marker was real-time tracked to determine step height at each gait cycle. This information was fed to the learning algorithm, which searched for the optimal spinal stimulation channel (lumbar or sacral), stimulus timing, duration, and frequency. The search space featured 672 possible combinations, while the algorithm was given 30 steps to optimize parameters. Optimality was defined as maximizing foot clearance with the aim to alleviate leg dragging. An example trial is presented along with stepwise estimation of performance (bottom right of the screen) and foot vertical trajectory (trace in the bottom left of the screen). Each of the two submaps is a 2D average projection, corresponding to the region marked with a square on the complementary submap.

GP-BO optimizes functional neurostimulation in very large, multi-dimensional parameter spaces

As a final demonstration of the scalability of the GP-BO approach, we tackled the problem of obtaining a meaningful characterization and optimization of neurostimulation parameters’ properties in a 5D search space with 10,976 individual input combinations. We required GP-BO, extensive (random) and greedy search to perform only 100 queries, corresponding to a 0.9% sampling of the entire space. The five dimensions consisted in a bidimensional cortical array, which was used to deliver stimuli of varied frequency, pulse-width, and duration (Figure 8A). After 100 queries, the algorithm achieved a gain of 19.4 and 14.5 points in exploration with respect to extensive (random) and greedy search, respectively (p = 0.016 in both cases), and 13.6 and 7.4 points (p = 0.078 and p = 0.156) in exploitation (Figures 8B and 8C). The GP-BO allowed identification of both similarities and differences in stimulation parameters across subjects (Figure 8D). For instance, the frequency profile was highly correlated, or stable across subjects (r = 83.0% ± 7.2%), whereas the pulse-width profile much less (r = 38.4% ± 17.3%). GP-BO captured the differences in these parameters across subjects within single 100-query runs (Figures 8E–8G), successfully personalizing neurostimulation delivery for each individual implant.

Figure 8.

Online optimization in a large, high dimensions, input space

(A) In sedated rats (n = 6), we searched for the most performant stimulus pattern to evoke responses in the ankle flexor muscle in a 5D space: stimulus position within a bidimensional (2D) 32-channel electrode array implanted in the leg sensorimotor cortex, stimulus frequency, pulse-width, and duration. In total, the input space featured 10,976 options. We compare the performance of GP-BO to benchmark searches when given the opportunity to search only <1% of this space (100 queries). The value metric was the size of the motor evoked potential (MEP) measured at the end of the stimulation burst.

(B and C) Exploration and exploitation indicators evolution for spatial parameters during the series of 100 queries. Data displayed as mean ± SEM over n = 6 rats.

(D) Optimal choices for frequency and duration are less subject-dependent than pulse-width and stimulus location. Thus, highly variable parameters cannot be well predicted without optimization. Data displayed as mean ± SEM.

(E and G) GP-BO was able to infer reliable estimations of subject-specific properties of 5D neurostimulation after a single run of 100 queries. The inferred posterior distributions after a representative single run reliably approximate the body of information collected throughout the entire session.

(E) GP-BO personalized cortical location selection (2D) in rats having diverse hotspots.

(F) GP-BO correctly identified optimal pulse-width, which highly varied between subjects.

(G) GP-BO identified optimal stimulus duration and frequency. Although the two parameters were less variable across subjects, finer details (broader frequency range in rat #2, shift in optimal duration between rats) were correctly modeled. See also Figure S8.

We finally sought to certify that solving large parameter space problem with GP-BO is manageable by commonly available computer resources. To do so, we evaluated how increasing input space sizes (Figure S8A), dimensionality (Figure S8B), and query history size (Figure S8C) affect the algorithmic execution time. We found that a GPU-based implementation on a standard workstation can evaluate million-point search spaces within a few seconds per algorithmic query (Figure S8A), thus supporting the potential for scalability far beyond the proof-of-concept applications provided in the present article.

Discussion

We demonstrated the efficacy of a versatile GP-BO-based framework for online, closed-loop neurostimulation optimization of motor outputs. The algorithm provided a solution to the requirement of personalized tuning of stimulation parameters of electrode implants in a variety of experiments: (1) across species, (2) in sedated and awake animals, (3) in intact and injured subjects, (4) continually learning and evolving over multiple days, (5) in small and large input spaces optimization, and (6) in both cortical and spinal neurostimulation interventions. It showed similar performance when used to optimize muscular or kinematic measures, and across various behaviors (i.e., hand/wrist or hindlimb function and locomotion). It can leverage properties such as sparsity (large portions of the input space may lead to negligible outputs) and smoothness (nearby inputs give similar outputs) of the search space. In summary, the algorithm displays the key qualities we highlighted for a desirable autonomous, online control framework: robustness to noise, clear outperformance of human search capacity, the ability to handle increasing complexity of parameter spaces.

In several experiments, designed to reveal the performance of the algorithm in realistic and clinically relevant contexts (i.e., finding solution in large dimensional problems while minimizing queries and maximizing treatment delivery time, successfully adapting to post-injury plasticity or equipment failure), our results provide unprecedented in vivo support and preclinical demonstration of the potential of GP-BO for neuroprosthetic applications. Our experiments demonstrate technology readiness, leveraging autonomous multivariate neuromodulation optimization in several functional environments, online and in vivo, including delivery of effective neuroprosthetic therapy after paralysis. To facilitate the translation of knowledge, we provide companion libraries in Python and MATLAB, as well as educational notebooks for the reader who seeks to implement these techniques in their own scientific or clinical practice (see STAR Methods).

Medical devices featuring autonomous adaptations can result in challenging regulatory approval paths and the agencies involved are experiencing increased industry interest in substantial involvement of machine learning. In this context, the sheer interpretability of GP-BO results and the related possibilities to define specific boundaries to the adaptive optimization procedure (e.g., limit the current increase by fixed steps) will be an advantage with respect to many other new machine learning applications in healthcare, especially when based on artificial neural networks.

Currently, a substantial portion of the research tackling the problem of spatiotemporal control of neuroprosthetic stimulation is constituted by modeling works.^32,55,58 Computational models are the favored strategy to understand and generalize during neural interfaces development.⁵⁹ Yet, computational model-based neurostimulation design is a feedforward approach, performed offline before implementation. It is generally not designed to account for individual differences and to adapt to the changes that can occur in the brain with time after the implantation. However, modification of stimulation outputs are expected with the progression of pathological processes in degenerative diseases,⁶⁰ recovery after brain injury,³⁰ and as a result of the stimulation protocols themselves.^5,61 To obtain complex and adaptive neuroprosthetic stimulation delivery, the strategic design will need to account for both computational modeling⁵⁹ and machine learning. At one end of the pipeline, models help generalize, understand, and prune down complexity. At the other end, autonomous learning allows us to personalize and optimize intervention, relieving the experimental and clinical burden of the user-specific implementation. Future theoretical novelties to GP-BO strategies, such as hierarchical GP-BO optimization (HGP)⁴¹ can further empower our online approach and offer additional modular solutions for exponentially harder control of multi-targeted distributed neuroprostheses. Longitudinal learning approaches could tailor neurostimulation intervention amid life-long changes in interface properties and co-learn user adaptation⁶² and neuroplasticity.

A key observation across our experiments is that the smoothness of the input-output relationship has a profound impact on the algorithm’s performance. High granularity and idiosyncratic responses from neighboring inputs (i.e., low smoothness) require a more detailed search to reach desirable performance. The cortical output maps, with unique responses often evoked from neighboring electrodes, fall in this category. Remarkably, the algorithm still clearly outperformed extensive searches in this challenging context (query of 30%–50% of the input space needed for equal precision). In contrast, if small changes of inputs have little impact on the outputs (i.e., high smoothness), the outcome of a given query propagates valuable information to the input space. This was the case for the spinal stimulation optimization, in which the investigated parameters had smooth properties (e.g., small changes of frequency have little impact on step height). In these conditions, our algorithm performance was greatly improved (query of 5% of the input space needed). As shown in our 5D optimization demonstration (Figure 8), GP-BO-based algorithms can solve dimensionality problems in applications that have a wide range of smoothness for the input-output relationship and will be particularly performant for parameters with high smoothness.

While we focused on motor function and recovery of movement after paralysis, the GP-BO approach is flexible. It could be applied to virtually any neuroprosthetic optimization problem. For example, deep-brain stimulation in Parkinson’s patients could be complemented with a feedback loop evaluating the immediate neurostimulation effects on tremor reduction. The GP-BO approach could also be used for sensory neuroprostheses, such as peripheral nerve stimulation for touch sensations^14,63 or spinal stimulation for chronic pain treatment.⁶⁴ In both cases, a GP-BO-based algorithm could optimize multichannel stimulation using, for example, a scalar of verbal feedback from the user.⁶³ Another application is the shaping of stimuli in autonomic neurostimulation, such as vagus nerve stimulation to regulate heart rate.^65,66 Nevertheless, because of the iterative nature of BO, it is fundamental to assess the timescale of the interaction between neurostimulation and available biomarkers of intervention efficacy. The time required to perform the optimization will be affected by the number of queries but also the time needed to evaluate the response. We showed an explicit link between the reliability of the recorded biomarker output (noise in the response) and the duration of the optimization procedure (number of queries to attain the same performance) when very fast biomarkers are used (i.e., evoked movements). In other potential applications in which longer response delays are expected (e.g., pain, addiction, depression), the performance of any optimization strategy will be affected, proportionally to the delay. In these cases, the dimension of the search space will need to be carefully engineered so that the time required for the optimization remains acceptable.

GP-BO is an iterative trial-and-error approach founded on the dialogue between query and response. Future research could progress beyond these results by mastering sequences of stimuli and dynamic output patterns, perhaps combining system identification strategies⁶⁷ to estimate the dynamic response of the neural system to varying patterns of continuous microstimulation. Reinforcement learning (RL) could also be studied as a solution to drive sequences of motor commands, although a dedicated RL framework for neuromodulation does not yet exist and it typically would require extensive offline and online training availability, which we reduced to minimal amounts in the applications presented here. Promising avenues can also emerge by integrating computational modeling approaches pre-implantation, bringing mechanistic understanding and generalization, and autonomous learning post-implantation, which is necessary for optimization and personalization.

Neural technology improvements have already begun offering access to highly refined interfaces that can enable the emergence of complex neurostimulation control, a capability that is currently untapped. In this evolving landscape, stimulation optimization assumes a core position in treatment design. We therefore believe there is no alternative solution than establishing autonomous learning as a cornerstone of neuroprosthetic design. Our work represents an initial first step toward this goal, which offers unprecedented promises for the treatment of neurological disorders. We propose that this “intelligent neuroprosthesis” approach is translationally mature and clinically viable.

Limitations of the study

GP-BO and autonomous learning agents will have to prove direct clinical and research adoption. Societal impact will be measured with the creation of commercial medical technology, by widespread automatization of research and via scientific discovery enabled by these techniques. These factors will need to be established and measured, and this study only addresses the bases of this development.

In all experiments we targeted single-output learning and we have not assessed how designing objective functions for the optimization of stimulation can play a major role. Clinical applications will have to balance on-target effects with minimizing off-target, side effects. This will require multiplexing several outcome measures and engineering multi-target objective functions and should be addressed in future studies.

Finally, the number of alternative “benchmark” algorithms to perform online neurostimulation optimization tested in our study was limited. This reflects the reality that manual optimization procedures are still currently widely adopted in research and clinical work. As new methods emerge, it will be important to compare their worth to the present GP-BO benchmark performance.

STAR★Methods

Key resources table

REAGENT or RESOURCES	SOURCE	IDENTIFIER
Experimental models: Organisms/strains
Long-Evans rats	Charles River	Line 006
Sapajus Apella NHP	Alpha Genesis, Inc.	N/A
Macaca Mulatta NHP	Envigo Global Services Inc. (formerly Covance Research Products)	N/A
Deposited data
Cortical maps data	This paper	[Database]: https://osf.io/54vhx/ as an Open Science Framework repository.
Software and algorithms
GP-BO algorithm and optimization procedures	This paper	GitHub: https://github.com/mbonizzato/EduOptimNeurostim/ https://github.com/mbonizzato/OptimizeNeurostim/
OpenEx (Data acquisition software on Tucker-Davis Technology Bioamp)	Tucker-Davis Technologies	2.31
MATLAB	Mathworks	R2018b

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Numa Dancause (numa.dancause@umontreal.ca).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •The complete cortical mapping dataset consisting of 4 NHP and 6 rats is publicly available as of the date of publication at the following Open Science Framework repository Database: https://osf.io/54vhx/
• •All original code has been deposited at GitHub and is publicly available with a variety of tutorials. See: https://github.com/mbonizzato/EduOptimNeurostim for a Python-based library and educational material (Jupiter Notebook tutorials) or: https://github.com/mbonizzato/OptimizeNeurostim/
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contacts upon request.

Experimental model and subject details

Rats

All rat experiments followed the guidelines of the Canadian Council on Animal Care and were approved by the Comité de déontologie de l’expérimentation sur les animaux (CDEA, animal ethics committee) at Université de Montréal.

Twenty-six adult (250-350g) female Long–Evans rats were used in this study. Rats were housed in solid-bottom cages with bedding, nesting material, tubes and chewing toys, in groups of 3 before implantation and individually thereafter. They received food and water at libitum and were subject to a 12:12-h light-dark cycles.

Capuchin NHP

All NHP experiments followed the guidelines of the Canadian Council on Animal Care and were approved by the Comité de déontologie de l’expérimentation sur les animaux (CDEA, animal ethics committee) at Université de Montréal.

Two adult male capuchin monkeys [sapajus apella; Subject K (dob: 04/26/2016, 2.1 kg) and Subject D (05/13/2016, 2.1 kg)] purchased from Alpha Genesis, Inc. (Yemassee, SC) were used in this study. They were housed together with two other male capuchins. They received food and water ad libitum.

Rhesus NHP

All NHP experiments followed the guidelines of the Canadian Council on Animal Care and were approved by the Comité de déontologie de l’expérimentation sur les animaux (CDEA, animal ethics committee) at Université de Montréal.

Two adult male rhesus monkeys [macaca mulatta; Subjects B (11 years old, 10.4 kg and Subjects H (11 years old, 10.0 kg)] purchased from Envigo Global Services Inc. (formerly Covance Research Products), were used in this study. Animals were housed in individual cages. Their access to water was controlled according to a protocol approved by the CDEA. They received food ad libitum.

Method details

Algorithmic implementation

We proposed a GP-BO-based approach controlling neurostimulation parameters and leveraging acquired knowledge to determine a map between said parameters (input) and motor output. For neurostimulation, in some embodiments, exploring input parameters corresponds to finding the best electrode or combination of electrodes; in other embodiments, a combination of a) electrode choice (spatial) and b) timing properties (frequency of stimulation, duration, etc.).

BO is a sequential optimization framework based on Bayes Theorem, employed to maximize value functions that are ‘expensive’ to evaluate. For an in-depth look on its mathematical foundations, several excellent tutorials are available.⁶⁸ BO leverages iterated ‘queries’ to collect responses from the investigated (biological) system. A query is the delivery of a single episode of stimulation using a contingent choice of spatial or temporal parameters (e.g., one or more activated electrodes, stimulus timing, duration, frequency, etc.). At each iteration, BO builds a probabilistic surrogate of the function being optimized, which we chose to model using GPs.⁴² Thus, for each input space point x, a GP defines the probability distribution of the possible values f (x) given x, through a normal distribution (N) of mean μ and standard deviation ζ:

P(f (x)|x) = N (μ(x), ζ²(x)).

Iterative optimization

BO makes real-time operational choices, such as (at time t) acquiring x_t+1. These decisions are taken by evaluating an acquisition function, which we selected as the Upper Confidence Bound (Figure 1B):

x_t+1 = argmax _x (μ_t(x)+k ζ_t(x)).

This choice embodies an explicit trade-off between exploration and exploitation: low values of k will privilege queries of high mean value μ_t(x), high values of k will privilege queries where uncertainty ζ_t(x) is high.

Sequential optimization was performed through the following procedure.

• 1.Initialize kernel K hyper-parameters (see next subsection for details on our specific kernel choice).
• 2.
  Select a first query:

  • 2a.
    If no prior available: pick an initial random query.
  • 2b.
    If a prior is available: the initial query is set to the input space point most likely to produce a maximal output, based on prior knowledge.
• 3.
  Repeat T times:

  • 3a.
    Test a new query (apply neurostimulation with selected parameters),
  • 3b.
    Acquire response (readout stimulation efficacy quantified as motor output),
  • 3c.
    Fit GP to current dataset (GP regression, see next subsection), integrating a prior to the mean if available,
  • 3d.
    Use the regression to compute the estimated mean value μ_t+1(x) and uncertainty ζ_t+1(x).
  • 3e.
    Compute the acquisition function (μ_t+1(x)+k ζ_t+1(x)) to select the next query.

T was set to 96 for NHP experiments and 32 for rat experiments, the respective number of available electrodes in the implanted arrays.

In the companion code we provide examples allowing to appreciate the sequential optimization procedure in a step-by-step fashion.

Fixed-ρ and variable-ρ

A kernel K specifies the covariance function of the GP. Mathematically, given a kernel K, the associated covariance matrix C is obtained with C = K(x, x’) This can be seen as the bond that keeps f (x) estimation relatively smooth for nearby input space points. Dually, for a given x it defines how far information acquired will propagate to its neighborhood. We selected the standard Matérn kernel function,⁴² which has two hyper-parameters ν (which we fixed ν = 5/2) and ρ. The latter geometric parameter (“length-scale”) directly influences information propagation. In the fixed-ρ version of the algorithm, ρ was learnt through offline optimization (Figure S1). In the variable-ρ one, ρ was optimized online during operation. Furthermore, in the latter version, we allowed for independent optimization across the input dimensions. In the companion code, we provide three different implementations of this algorithmic framework. A common ground is the creation of a GP model, the assignation of a kernel, data and information on system noise. Algorithmic details, including the exact procedure for GP regression (a tutorial available online⁶⁹), differ between implementations with consequences on execution times (Figure S8). All implementations provided in the companion code are open-source.^42,70

Benchmark comparison to quantify GP-PO performance

A. extensive search

This alternative search strategy replicates our common practice of testing all possible options in a neural implant to determine which one is the most performant. Algorithmically, it indicates extensively testing all points in the input space in a sequence determined before the experiment (Figure S2). In 2D spatial optimization experiments, it entails testing all individual electrodes. In multi-dimensional spatiotemporal optimizations, it involves testing each available parameter combination (e.g., 4D: electrode, frequency, duration and timing of stimulation). When no prior information is available, the predetermined sequence is a random permutation. When, as in Figures 4 and 5, priors are available, the sequence is ranked in descending order of expected efficacy, testing first the inputs that are expected to produce high-performant outputs. In this case, queries of the extensive search are ranked based on priors (prior-ranked).

B. Greedy search

This alternative search strategy replicates a ‘human-like’ practice of optimizing one parameter at a time. Algorithmically, it proceeds by fixating all parameters to a predetermined initial value, selecting one of these search dimensions and testing all possibilities along this dimension. The best option is retained, the parameter is fixated, and search continues along one other selected dimension, until all dimensions are tested. The search process is continued from the current best option. All dimensions are then searched again, until the process reaches a maximum number of queries. When no prior information is available, the search starts from a random point of the input space. When, as in Figures 4 and 5, priors are available, the process starts from the point of the input space which is expected to perform best, the same exact area which is tested first by GP-BO and extensive search. Thus, all algorithms have identical performance at query 1.

Algorithmic evaluation

In all Results, “ground truth” (offline simulated experiments) or its equivalent “reference value map” (online in vivo experiments) refer to the average output response (i.e., EMG or kinematic response) associated with each possible input (i.e., electrode or stimulation parameters selection) mean[f(x)] when considering all iterations collected during the whole recording session, all conditions confounded. In offline experiments, the ground truth is explicitly available. When empirically estimated (in vivo experiments), this estimation was based on the average response of a large number of queries per subject to obtain mean[f(x)]: Figure 2: 1,848 ± 268, Figure 3: 2,720 ± 693, Figure 4: 492 ± 12, Figure 5: 480 ± 0, Figure 6: 232 ± 50, Figure 7: 578 ± 35, Figure 8: 1,500 ± 78.

We defined exploration as the knowledge of the best stimulating electrode. The algorithm holds an internal representation of input-output mapping (Figure 1E: Estimated map) and will attempt to estimate which input is associated with the maximum expected output. The extensive search produces a similar map by testing all inputs without attempting to deliver effective stimulation (i.e., treatment); the input choice corresponding to the maximum recorded output is considered best. Exploration performance was computed as the EMG or kinematic output of this “best” electrode divided by the true maximum, as defined by the ground truth map or the average response (or the reference value map for in vivo experiments where the ground truth can only be estimated). Exploitation was calculated as the EMG or kinematic output associated with the input selected at each query, divided by the true maximum.

Explicitly, at time t, we defined exploration as:

f(b_t)/max_∀x(mean[f(x)]).

where b_t is the point in the input space considered best by the algorithm at time t,

and exploitation as:

f(x_t)/max_∀x(mean[f(x)]).

where x_t is the last query.

Exploration and exploitation were each reported as [0–100]% values and jointly referred to as the algorithmic performance.

It is also important to note that if algorithmic evaluation were interrupted at any given time point (for example after 20 queries) and the best value was imposed thereafter, then exploitation performance will immediately ‘jump’ to match the exploration one. This “convergence” would correspond to terminating the algorithmic exploration phase and entering a pure exploitation one.

When comparatively evaluating algorithmic gains to the extensive search performance, we used a metric which we refer to as an increase in “performance points”. We preferred the term ‘performance point’ to highlight that changes we report are absolute differences in the [0–100]% performance scale and avoid confusion with relative increases, which we thought could overamplify the algorithm’s performance. As an example, we show that our algorithmic implementation, searching for arm EMG responses in awake macaques (Figures 3F–3H), outperformed the extensive (random) search. The exploration curves peak at 78.3% and 61.2% for the algorithm and the extensive search, respectively. In this scenario, our metric reports an increase of 17.1 performance points, while the relative increase would be 27.9% (i.e., 17.1% increase of a 61.2% performance).

Offline optimization

Selection of the following hyper-parameters: 1) exploration-exploitation trade-off parameter k, 2) number of random initial queries, 3–4) minimum and maximum length-scale ρ, 5) expectation on model noise σ_max, was performed using datasets of EMG responses to cortical stimulation obtained with extensive (random) search in previous subjects. Data and codes are reported in the Data Availability statement. Each hyper-parameter was varied in turn as shown in Figure S1 and during this process all other parameters were kept to the known optimum. Each turn, the parameter being tested was updated to the argmax of the search results. The optimization continued until no improvements were made for an entire round. Figure S1 shows the final results.

Offline evaluation of the effects of noise

In Figure S3 we evaluate algorithmic performance in increasingly noisy optimization scenarios. For this analysis we pooled all the muscle responses available in four NHP datasets (n = 22 muscles). We tested GP-BO, extensive (random) and greedy searches on a simulated artificial system, whereby the response of each electrode is the average response recorded for that electrode/muscle combination (ground truth) plus injected Gaussian noise (and a lower bound at zero after noise injection). We tested noise intensities with a standard deviation σ range between [0–100] % of the maximum EMG response.

Offline evaluation of the effects of input-output relationship smoothness

In Figure S5 we evaluated algorithmic performance in optimization scenarios featuring varied dataset smoothness. We were also interested in determining the effect of smoothness heterogeneity across dimensions. For this analysis we created n = 5 virtual subjects featuring 4-Dimensional parameter spaces. The input-output relationship for each parameter was synthetized independently using gamma distribution probability density functions (SciPy gamma.pdf) with fixed α, selected β (smoothness) and random peak displacement. Each parameter had 7 possible values. We controlled the smoothness of the distribution by tuning β, since the variance of the gamma distribution is inversely proportional to β².

We thus varied β values for each parameter between β = 0.01 (corresponding to the smoothest space, where the second-best input holds 99% of the value of the first) and β = 3.95 (second input holds 1% of the best value). The smoothness of 4D spaces is parametrized by a set of four values B = [β₁, … β₄]. Random sets of B were generated, and each set was assigned to a specific quantification of “mean smoothness” and “smoothness variance” by simply calculating mean(B) and variance(B). We tested GP-BO, extensive (random) search and greedy searches on this synthetic controlled dataset. Results were computed by averaging 15 repetitions of 200 queries (−91.7% subsampling over a search space containing 2,401 options).

Algorithmic evaluation design

Algorithmic performance was compared to extensive (random or prior-ranked) and greedy searches. The exact control used is indicated in Table S1. In most experiments, algorithm, extensive and greedy search trials were alternated. In experiments in which either extensive and/or greedy search were not performed, the notion “simulated” indicates that the extensive search has been performed offline by drafting from the information collected in real-time. Since the extensive search does not require real-time feedback-based decisions, we suggest a substantial equivalency for this strategy. During online evaluations, we defined that the algorithm has “converged” on a solution after 5 consecutive selections of the same input combination.

Injecting prior knowledge, extracting posterior knowledge

In experiments when we injected “prior knowledge” (Figures 4, 5, S7), the objective function was EMG activation. We designed previous knowledge from intracortical microstimulation (ICMS) threshold values obtained when mapping the leg motor cortex of 25 rats from a previous study,⁵ using the same methods of the present study (see electrophysiological procedures below), but applying a heterogeneous metric (ICMS thresholds vs peak EMG response). Thresholds were inversely associated with excitability (scaled 1–10), so that a low ICMS threshold would represent high excitability. In each rat, stimulation was delivered through 32-electrode arrays implanted in the hindlimb motor cortex. Maps were averaged across subjects and then normalized between 0 and 100% (min to max). At the beginning of each run of the algorithm, this average map was declared a prior to the GP mean, and BO would continue normally, integrating this prior with future acquired evidence, following Bayes’ rule. The 25 rats were recorded both in the healthy state and one week post-SCI. In this study, we used aggregated data from healthy and SCI rats in experiments with healthy (Figure 4) and SCI animals (Figure 5), respectively. In experiments featuring priors, this bootstrap information was made available to all procedures, including extensive and greedy searches.

Since the algorithm maintains an explicit representation of the input-output relationship, extracting posterior knowledge consisted of directly reading the current average of the surrogate function μ_t(x) (‘estimated map’, Figure 1E), which is also used to evaluate the acquisition function. In continual learning experiments (Figure 5), the previous session’s posterior μ_{s, t=8}(x) was fed as a prior to the GP mean in the next session μ_{s+1, t=0}(x). The subscript ‘s’ and ‘s+1’ indicate two consecutive sessions.

In Figure S7 we evaluated algorithmic performance in scenarios featuring different quality and quantity of available prior information. For this analysis we created n = 6 virtual subjects featuring 6-Dimensional parameter spaces. Each subject was created starting from one of the 6 rat datasets (4 × 8 cortical maps) and additional 4 dimensions synthetized from gamma distribution probability density functions (SciPy gamma.pdf) with fixed α, random β (smoothness) and random peak displacement. This configuration simulates leg responses obtained from a 2D cortical electrode array and 4 other stimulation parameters (e.g., amplitude, frequency, pulse width and pulse duration). We tested GP-BO, extensive and greedy searches on this simulated system with different values of prior quantity and quality. Quantity: we randomly selected 0–6 dimensions and provided them a prior to the mean. Quality: the prior was modulated with additive Gaussian noise, until the correlation with the ground truth was brought to r = [0 0.33 0.66 1], where r = 1 indicates lack of noise. Negative correlations were obtained by inverting the ground truth and adding noise until r = −0.0.5 or no noise for r = −1. We tested noise intensities with a standard deviation σ range between [0–100] % of the maximum EMG response.

In the continual learning experiment every prior was faded (removed) after 3 queries, while in the offline experiment on prior quantity and quality (Figure S7) it was faded after 50 queries (25%). All priors were injected with a 75% scaling factor.

Evaluation of execution time

We studied how execution time depends on the total number of points in the input space, the number of input dimensions and the number of previous queries collected in the optimization history (Figure S8). When one parameter was varied, the others were kept constant to 10,000 points, a 3D space and 1,000 queries, respectively. This experiment was run on an Intel i7-9700K @3.60GHz CPU and an NVIDIA GeForce RTX 2080 Ti GPU, a very common setup, of broad commercial accessibility and replicability.

Surgical procedures

Surgical procedures were conducted as previously described for NHP^71,72 and rats.^2,5,73,74 Briefly, anesthesia was induced with a single dose of ketamine hydrochloride (NHP 15 mg/kg IM; rats 80 mg/kg IP). The animals were transitioned to ∼2% isoflurane general anesthesia (Furane; Baxter) in 100% oxygen and remained under general anesthesia for the duration of the surgical procedures. Animals’ vital signs, temperature and hydration were monitored. All procedures included antibiotic and analgesic treatment for 3 to 7 days post-surgery.

EMG implants

Pairs of EMG microwires (Cooner Wire, Chatsworth, CA) were inserted into upper or lower limb muscles. In NHP we targeted wrist, intrinsic hand and finger muscles. In rats we implanted leg muscles. See Table S1 for EMG available on each subject. For each muscle, the accurate placement of the EMG wires was confirmed using electrical stimulations through the implanted wires and visual inspection of the evoked movements. Wires were routed subcutaneously and chronically attached to a connector fixed on an acrylic cap above the cranium. In acute experiments in rats, wires were instead inserted transcutaneously.

Cortical implants

We performed a craniectomy to expose the motor cortex. A portion of the dura was opened and intracortical electrode arrays were inserted. In NHP, a 96-electrode array (Blackrock, US) was placed into the hand representation of M1 (Figure 3A). Three additional implanted electrodes, targeting ventral and dorsal premotor cortex (PMv, PMd) and area 5 respectively, were not considered for this study. The craniotomy was closed with artificial dura (DuraGen, Integra Lifesciences, US) and covered with bone cement. The connectors of the arrays were placed on top of the head in an acrylic box embedded in the in the bone cement. In rats, we inserted a 32-electrode array (Tucker-Davis Technology, US) onto the leg representation. The most antero-medial site was positioned stereotaxically at coordinates AP -1.1mm, ML +1.3 mm from bregma. The electrodes were lowered to a depth of 1.5 mm.^5,75

Spinal cord injury

Two groups of rats were part of the online implementation of the algorithm for neuroprosthetic intervention in the context of spinal cord injury. In one group (n = 4), the animals received an incomplete spinal cord injury^76,77 2 weeks after the cortical electrodes implant. We performed a thoracic (T9) laminectomy and durectomy. A droplet of lidocaine was delivered on the dorsal part of the cord to decrease spinal reflexes. A lateral hemisection of the left spinal cord was performed under microscope visualization using a surgical micro-knife and iridectomy scissors. One week after the lesion, we used the algorithm to optimize the cortical stimulation site (electrode selection) to increase foot height during swing. In another group (n = 4), two weeks prior to spinal cord injury, we performed two laminectomies to expose spinal levels L2 and S1². On each segment, a single Teflon-coated wire was sutured to the dura mater. A 1mm-long portion of the insulation was removed to create an electrical interface with the spinal cord and deliver epidural stimulation. Wires were routed subcutaneously and attached to a connector fixed on the head cap. One week after the lesion, we used the algorithm to optimize the spinal cord stimulation site, timing, frequency and duration, with the objective to increase foot height during swing (see Figure 7).

Electrophysiological procedures

Acute anesthetized experiments

In a subgroup of rats (n = 4; Figure 2), we tested the capacity of the algorithm to find and exploit the cortical stimulation site (electrode selection) evoking the maximal EMG response of a target muscle in acute experiments. Immediately after EMG and cortical arrays implantation, isoflurane was turned off and deep sedation was maintained with intraperitoneal injections of ketamine hydrochloride (∼3–5 mg/kg/10 min).⁷⁸ The cortical implant was connected to a neurostimulator (Tucker–Davis Technologies, US) to perform neurostimulation experiments. In turn, all active sites were tested with 40ms ICMS trains (biphasic squared pulses, cathodic first, 300 μA, 330 Hz, 200 μs/phase), following the algorithmic protocols described below.

Chronic experiments

In some rats and monkeys, the experiments were conducted chronically, after the implantation procedures. In rats (n = 7, Figure 4; n = 5, Figure 5; n = 6 Figure S1) and in macaque monkeys (n = 2; Figures 3F–3H), chronic experiments were conducted in the awake state. Rats were habituated to be hand-held for prolonged periods of time (∼5-10min). During experiments, they were held in forelimb and trunk support, leg free. NHPs were sitting quietly in a monkey chair, arm relaxed along the side or resting on a tablet. In the two sapajus apella, testing was always under ketamine sedation (Figures 3A–3E and S6C and S6D), administered intravenously and maintained on a stable plane throughout acquisition by subsequent injections (10 mg/kg per ∼10 min). They were maintained in a sitting position in a primate chair with both arms resting. Additional experiments in n = 6 rats (Figure 8) involved chronic implants and temporary ketamine sedation (120 mg/kg, in a single intraperitoneal dose).

In chronic experiments, the cortical implant was connected to a neurostimulator (Tucker-Davis Technologies, US). Motor maps were obtained following a previously established protocol.⁵ In turn, all active sites were tested with 40ms ICMS trains (either biphasic squared pulses or cathodic only pulses, 330 Hz, 200 μs/phase, with 30 μA for subjects K and B, 40μA for subject H and 100μA for subject D), following the algorithmic protocols described below. The same parameters were used for rats, and a stimulation amplitude of 100 μA for all subjects.

Continual learning experiments (Figure 5) were conducted over 8 recording sessions. A total of five repetitions were performed for each rat and each optimization method. To test robustness from potential optimization drifts, each repetition was treated independently from the other four, meaning that repetition #1 of day two only depended on the posterior results of repetition #1 after day one (not from repetition #2–5). In summary, we maintained 5 separate lineages of continual learning for each optimization method.

In a variation of the continual learning experiment (Figures 5D–5F), we simulated the loss of an electrode. This was simply obtained by turning off one of the 32 stimulator outputs, corresponding to the most effective active site. The in vivo experiment was then continued normally. These additional five repetitions (for each optimization methods) were run in parallel to the five ‘standard’ ones (i.e., no electrode loss, Figures 5A–5C).

In the 5-Dimensional optimization experiment (Figure 8), in addition to the bidimensional stimulation site coordinates within the cortical implant, 3 other stimulation parameters were varied: stimulation train duration [20, 40, 80, 100, 150, 200, 250] ms, frequency [25 50 100 200 300 400 500] Hz and pulse-width [50, 100, 150, 200, 300, 400. 500] μs. Stimulation amplitude was selected before the experiment to guarantee a clear leg movement, then kept constant. Its value varied between animals (100–600 μA).

Online algorithm-driven stimulation

During stimulation sessions, selected EMG channels were sampled at ∼12 kHz, band-pass filtered 30–3000 Hz, rectified and smoothed with a window filter (τ = 50ms) online. The cumulative muscle response was estimated by sampling this summation signal 60ms after the beginning of the 40 ms stimulus train (Figure 2, Figure 3, Figure 4, Figure 5) (or 20 ms after the end of the stimulus train in Figure 8, having diverse durations). This information was fed back to the optimization algorithm, which was in control of stimulation parameters and updated them according to the GP-BO strategy.

Cortical or spinal stimulation during locomotion

Two groups of n = 4 rats were trained to perform treadmill walking (23 cm/s) using food rewards (Figures 6 and 7). One week after SCI, they were engaged in the recording sessions. A red marker was positioned over the foot. EMG signals were digitized at 6 kHz (anti-aliasing filter at 45% of the frequency range). They were filtered online (bandpass, 70–700 Hz) and rectified using a real-time BioAmp processor (Tucker–Davis Technologies, US). An EMG pattern recognition algorithm, which we thoroughly characterized before, was used to detect gait phase.⁵ Briefly, threshold-crossing from a selected muscle, the contralateral ankle flexor, was used as a gait synchronization event. Detections were followed by a refractory period of 200-300ms to prevent eliciting multiple triggers within a single EMG burst. Synchronization events triggered delivery of cortical or spinal stimulation with a specified delay. The delay was designed to synchronize stimulation with foot lift. Cortical stimulation consisted of an ICMS train on one of 32 cortical sites (40ms train with 330Hz pulse frequency, biphasic, cathodic first, 200μs/phase, 50-100μA/phase 140-200ms from trigger). Electrical epidural spinal stimulation (EES) consisted of a train of pulses delivered on one of two available spinal sites (variable duration, variable frequency, biphasic, cathodic first, 200 μs/phase, variable amplitude, variable timing from trigger). Variable parameters were selected by the search algorithm (or at random). Possible sites were [lumbar, sacral]; durations [20, 40, 60, 80, 100, 120] ms; frequencies [20 40 60 80 150 220 330 500] Hz; timing [140, 170, 200, 230, 260, 290, 320] ms from contralateral ankle flexion. EES amplitude depended on selected duration and frequency: it was univocally determined through the amplitude and charge cap rules. EMG-based phase detection ran in hard-real-time at cycles of 24kHz. To allow feedback control of leg kinematics, an additional soft-real-time system (Simulink, Mathworks, US) was added. A color camera (50 Hz) detected the position of the red marker located on the rat’s foot, allowing determining the step height at each gait cycle. This information was fed-back to the optimization algorithm, which was in control of stimulation parameters and updated them according to the GP-BO strategy.

Quantification and statistical analysis

All data are displayed as mean values ± SEM. Paired statistical evaluations were performed using Student’s t test or the non-parametric Wilcoxon signed-rank test when at least one of the populations could not be assumed to be normally distributed. Tests are one-sided, as our hypotheses were always strictly defined toward the direction of performance improvement. We applied a threshold for statistical significance at p = 0.05.

Published: April 11, 2023