CFD analysis on blood flow inside a symmetric stenosed artery: Physiology of a coronary artery disease

Abstract

This research article interprets the computational fluid dynamics analysis on blood flow inside a symmetric stenosed artery. The current problem models the blood flow inside the left coronary artery as having a symmetric stenosis in the central region. A comprehensive physiological examination of coronary artery disease is numerically evaluated by using the computational fluid dynamics toolbox Open-Field Operation And Manipulation. There are no assumptions of mild stenosis taken into account since the considered stenosis has an exactly measured length, height and position, etc. The blood flow problem is modeled for the non-Newtonian Casson fluid with unsteady, laminar, and incompressible flow assumptions. The underlying problem is solved numerically in its dimensional form. A thorough graphical analysis is provided on the blood flow simulations, pressure profile, velocity line graphs, pressure line graphs, and streamlines for the left coronary artery having a symmetric stenosis formation. The considered artery is divided into three sections, i.e. pre-stenosis, post-stenosis, and stenosis region, and the velocity and pressure line graphs are plotted for these considered regions. The graphical illustrations provide a detailed analysis of how the blood flow is affected inside the left coronary artery due to coronary artery disease. These pre- and post-stenosis velocity line graphs reveal two intriguing results: In the pre-stenosis zone, the velocity increases with increasing axial coordinate length, whereas in the post-stenosis region, the velocity decreases with rising axial coordinate length. It is evident that as the flow moves toward the stenosis region, the flow profile rises; yet, after passing through the stenosis zone, the flow profile begins to fall as the flow moves away from the stenosis region.

Introduction

Stenosis mostly occurs in the left coronary artery due to plaque collection on the inside walls of the artery. The prime reasons for plaque collection are lack of physical activities like exercise, eating fats and oils, smoking and high cholesterol, etc. This is termed coronary artery disease (CAD). CAD can cause blood clots and stenosis inside the artery that can result in a stroke or heart attack in severe cases. The treatments used for CAD include balloon/laser angioplasty, atherectomy, and stent placement. Heart disease is a prime reason for death all around the world. The statistical data ¹ shows that cardiovascular disease is the major death cause in the United States and one patient dies every 34 s due to CAD. In 2020, ² the statistical data shows that CAD is the most common heart disease, and more than 20 million adults have CAD. United States ³ has spent more than 229 billion dollars on cardiovascular diseases from 2017 to 2018. The left coronary artery has a diameter of 3–4 mm which is slightly smaller as compared to the drinking straw width and it has a length of 10.5   $\pm$   4 mm.^4,5 The coronary artery blood flow rate and velocity ranges from 2.00 to 2.50 ml/s and 15.9 to 19.9 cm/s. ⁶

Haldar ⁷ modeled the arterial blood flow by considering the distinct formations of stenosis with their effect on flow resistance. He revealed in his study that the highest flow resistance is observed for the symmetric formation of stenosis. Ku ⁸ presented a theoretical model of blood flow that reveals the unsteady flow in arteries with turbulence phenomenon near stenosis regions. In most of the cases, many researchers have considered the non-Newtonian models to discuss the blood flow in arteries, since the non-Newtonian models provide a more realistic approach to model hemodynamics. Mandal ⁹ modeled the arterial blood flow issue with a mild formation of stenosis. He interpreted numerical solutions for this blood flow issue by considering the non-Newtonian Power law fluid model. Siddiqui et al. ¹⁰ mathematically modeled the arterial blood flow issue for a stenosed artery by using the Casson non-Newtonian model. Venkatesan et al. ¹¹ numerically interpreted the non-Newtonian Casson model as blood flow inside a narrow stenosed region of an artery in comparison to the non-Newtonian Bingham and Herschel Bulkley fluid. Carvalho et al. ¹² modeled the review issue on the blood flow analysis in a coronary artery. Some recent studies on the blood flow analysis for stenosed arteries are referred to as.^13–15 Further, some more relevant scientific literature on blood flow through a stenosed segment with endoscopic catheter applications are provided.^16–22 Akhtar et al. ²³ already modeled the steady Casson fluid blood flow problem for a multiple stenosed artery considering cases of both symmetric addition to non-symmetric stenosis and provided an exact solution for the problem. In the current study, we have modeled the unsteady Casson fluid blood flow problem for a single symmetric formation of stenosis and provided numerical solutions for the problem.

This issue provides the blood flow analysis for the left coronary artery having a symmetric formation of stenosis at the center. The problem is modeled for the non-Newtonian Casson fluid which provides a better approximation to consider the non-Newtonian nature of blood. There is no assumption of mild stenosis formation used in this study as the considered stenosis has a fixed length, height and position, etc. The problem is modeled for an unsteady, laminar, incompressible, non-Newtonian Casson fluid flow. The present problem is solved numerically by using the computational fluid dynamics (CFD) toolbox Open Field Operation And Manipulation (FOAM) which interprets the governing partial differential equations in their dimensional form. This is a theoretical study model, and it is the first research article that models the numerical simulation work on blood flow inside a symmetric stenosed coronary artery. There is no experimental study present on this topic to provide a comparative analysis. We are already working on some more similar models. In future work, we will provide a comparative study of this theoretical model. An intensive graphical analysis is provided on the blood flow profile, and pressure profile for this stenosed left coronary artery. The flow iterations are added for a detailed analysis that incorporates an extensive graphical analysis for $t=1$ to $t=10$ (iterations).

Mathematical formulation

The present problem is modeled for an unsteady, incompressible, laminar, non-Newtonian blood flow inside a stenosed left coronary artery. The geometry of the model is given in Figure (1a) and (1b) shows the pre, post, and main stenosis regions with $\overline{z}$ locations from $\overline{z}=-5$ to $\overline{z}=5$ . We have considered the left main coronary artery as having a diameter of 4 mm and a length of 10 mm. The stenosis has a length of 2 mm with a height of 0.82 mm. There are no assumptions of mild stenosis considered in this issue and the exact values for height, length, and position of stenosis are considered. The velocity for this computation is considered from 15.9 to 19.9 cm/s.

Figure 1.

(a) Geometrical model of left coronary artery with a symmetric stenosis at center. (b) Pre-stenosis, stenosis and post-stenosis locations with different $\overline{z}$ locations. (c) Arbitrary control volume (CV).

The wall of the artery with a symmetric formation of stenosis in the central region is considered by the following mathematical expression given as

$$\overline{\eta }(\overline{z})=\{\begin{array}{c}R[1-\kappa \{b^{n-1}(\overline{z}-a)-{(\overline{z}-a)}^n\}],a\le \overline{z}\le a+b;\\ R\mathrm{otherwise}\end{array}$$ (1)

where $\kappa =\left(\frac{{\delta }^{*}}{R{b}^n}\right)\frac{{(n)}^{\left(\frac{n}{n-1}\right)}}{(n-1)}.$ Here $n=2$ for the symmetric formation of stenosis. The condition on n is $n\ge 2.$

The existing blood flow problem is modeled for the non-Newtonian Casson fluid since it is the most extensively used model for blood flow and we can have more realistic simulation results. The governing equations for a non-Newtonian flow problem in cylindrical coordinates are given as ²³

$${\displaystyle \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}+{\displaystyle \frac{\overline{u}}{\overline{r}}+{\displaystyle \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}=0,}}}$$ (2)

$$\rho \left({\displaystyle \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{t}}+\overline{u}{\displaystyle \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}+\overline{w}{\displaystyle \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}}}}}\right)=-{\displaystyle \frac{\mathrm{\partial }\overline{p}}{\mathrm{\partial }\overline{r}}+{\displaystyle \frac{1}{\overline{r}}{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }\overline{r}}(\overline{r}{\overline{S}}_{rr})+{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }\overline{z}}({\overline{S}}_{rz}),}}}}$$ (3)

$$\rho \left({\displaystyle \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{t}}+\overline{u}{\displaystyle \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}+\overline{w}{\displaystyle \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}}}}\right)=-{\displaystyle \frac{\mathrm{\partial }\overline{p}}{\mathrm{\partial }\overline{z}}+{\displaystyle \frac{1}{\overline{r}}{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }\overline{r}}(\overline{r}{\overline{S}}_{rz})+{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }\overline{z}}({\overline{S}}_{zz}),}}}}$$ (4)

The extra stress tensor for non-Newtonian Casson fluid is given as

$$\sqrt{\zeta }=\sqrt{{\displaystyle \frac{{\overline{S}}_{ij}}{{\overline{\dot{\gamma }}}_{ij}}}}+\sqrt{m},$$ (5)

The values of extra stress tensors ${\overline{S}}_{rr},{\overline{S}}_{rz}$ and ${\overline{S}}_{zz}$ are provided as follows.

$${\overline{S}}_{rr}={\displaystyle \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{r}}\left(\zeta +m-2\sqrt{\zeta m}\right),}$$

$${\overline{S}}_{zz}={\displaystyle \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{z}}\left(\zeta +m-2\sqrt{\zeta m}\right),{\overline{S}}_{rz}={\displaystyle \frac{1}{2}\left({\displaystyle \frac{\mathrm{\partial }\overline{u}}{\mathrm{\partial }\overline{z}}+{\displaystyle \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}}}\right)\left(\zeta +m-2\sqrt{\zeta m}\right),}}$$

The boundary conditions are set for an axially symmetric flow with no slip at walls. The mathematical equations used for this set of boundary conditions are as follows.

$${\displaystyle \frac{\mathrm{\partial }\overline{w}}{\mathrm{\partial }\overline{r}}=0at\overline{r}=0\mathrm{and}\overline{w}=0\mathrm{at}\overline{r}=\overline{\eta },}$$ (6)

Numerical solution

The partial differential equations that govern this blood flow problem are solved numerically. The basic working principle of this program is the finite volume Method in which the entire domain volume is discretized into small volume elements. Then the considered differential equation is integrated over these small-volume element cells. The present problem case is coded for an unsteady, incompressible, non-Newtonian Casson fluid using the C + + toolbox in Open-FOAM. The partial differential equations are solved in their dimensional form. The mesh diagrams of the left coronary artery are given by Figures (2a) to (2c). Figure 2(a) shows the three-dimensional (3D)-mesh diagram of the considered artery. More precise refinement of mesh is used in the central stenosed region and around the corners of the artery. Figure 2(b), the two-dimensional (2D) slice mesh diagram also shows a more precise meshing of the central stenosed region and corners as well. Figure 2(c) is the clip or side view of the arterial mesh diagram. The case is set up for $t=1$ to $t=10$ with a courant number less than 0.5 and $\mathrm{\Delta }t=0.001$ . The write interval of the program is set to 0.1 and data is presented for each $t=1$ to $t=10$ .

Figure 2.

(a) 3D-Mesh representation of symmetric stenosis. (b) 2D-Mesh representation of symmetric stenosis (a slice view). (c) Mesh representation of symmetric stenosis (a clip view). 3D: three-dimensional; 2D: two-dimensional.

Finite volume method

The prime physical models and their practical engineering applications require the handling of complex partial differential equations numerically. Open-FOAM provides the facility to solve such complex models numerically by utilizing the finite volume method. To solve complex PDE's, the FVM is a reasonable choice. FVM provides a better approach to deal with non-linear conservation laws, to handle complex curve geometries, etc. The discretization via finite volume method is provided in detail by Jasak and Tukovic, ²⁴ in which the complex set of partial differential equations that models the physical problem is transformed into a set of algebraic equations at the discrete set of small-scale volume elements in time and space. An arbitrary polyhedral control volume (CV) is given in Figure 1(c).

Point P is assumed to be located at the centroid of CV. We consider the following equation over a CV as

$$\int (X-X_p)dV=0,$$ (7)

The continuity equation can be discretized over a CV $V_p$ in the following way for an incompressible flow by using divergence theorem.

$$\int \mathrm{\nabla }.udV=\int u.\overline{n}dS=0,$$ (8)

Since the CV is not only bounded by a single flat face so we can have the following equation for the collective flat surfaces

$$\int u.\overline{n}dS=\sum _f\left[\int u.\overline{n}\right]dS,$$ (9)

Now by using the linear variation assumptions, we get the following for a face f.

$$\int u.\overline{n}dS\approx u_f.\int \overline{n}dS=u_f.S,$$ (10)

Equation (8) $\int u.\overline{n}dS=0,$ after using equations (9) and (10) and simplification provides the following result.

$$\sum _{f}S.u_f\approx 0,$$ (11)

Results and discussion

The partial differential equations are evaluated numerically using the CFD toolbox in Open-FOAM. The graphical simulations are presented here to interpret the blood flow inside the left coronary artery having symmetric shape stenosis in the central region. The governing equations, flow simulations, and geometries are provided for a 2D flow profile. Figures (2a) and (2c) are just the 3D mesh diagram views of the considered geometry. Figure (3) depicts the graphical simulations of the blood flow profile for data ranging from $t=1$ to $t=10$ . Figure (4) represents the pressure profiles for this CAD flow problem. The data range for the pressure profile is also taken from $t=1$ to $t=10.$ Figure (5) refers to the line graphs of the velocity profile against the radial $\overline{r}-\mathrm{axis}$ . These velocity line graphs are plotted at different locations along the axial coordinate $\overline{z}$ and the different $\overline{z}$ locations divide these velocity line graphs into three regions, i.e. Pre-stenosis velocity line graphs (region −5 $<\overline{z}<$ −1), post-stenosis velocity line graphs (region 1 $<\overline{z}<$ 5) and stenosis region velocity line graphs (region −1 $<\overline{z}<$ 1). In Figure (6), the pressure line graphs are plotted at different $\overline{z}$ locations against $\overline{r}-\mathrm{axis}$ and three regions pre-stenosis, post-stenosis and stenosis region pressure line graphs are obtained. These velocity and pressure line graphs are plotted at a data range time $t=10.$ Figure (7) represents the streamlined graphs at time $t=1,3,8,10.$

Figure 3.

(a) $\overline{w}$ flow profile at t  =  1. (b) $\overline{w}$ flow profile at t  =  2. (c) $\overline{w}$ flow profile at t  =  3. (d) $\overline{w}$ flow profile at t  =  4. (e) $\overline{w}$ flow profile at t  =  5. (f) $\overline{w}$ flow profile at t  =  6. (g) $\overline{w}$ flow profile at t  =  7. (h) $\overline{w}$ flow profile at t  =  8. (i) $\overline{w}$ flow profile at t  =  9. (j) $\overline{w}$ flow profile at t  =  10.

Figure 4.

(a) Pressure profile at t  =  1. (b) Pressure profile at t  =  2. (c) Pressure profile at t  =  3. (d) Pressure profile at t  =  4. (e) Pressure profile at t  =  5. (f) Pressure profile at t  =  6. (g) Pressure profile at t  =  7. (h) pressure profile at t  =  8. (i) Pressure profile at t  =  9. (j) Pressure profile at t  =  10.

Figure 5.

(a) Pre-stenosis region velocity profile at t  =  10. (b) Post-stenosis region velocity profile at t  =  10. (c) Stenosis region velocity profile at t  =  10.

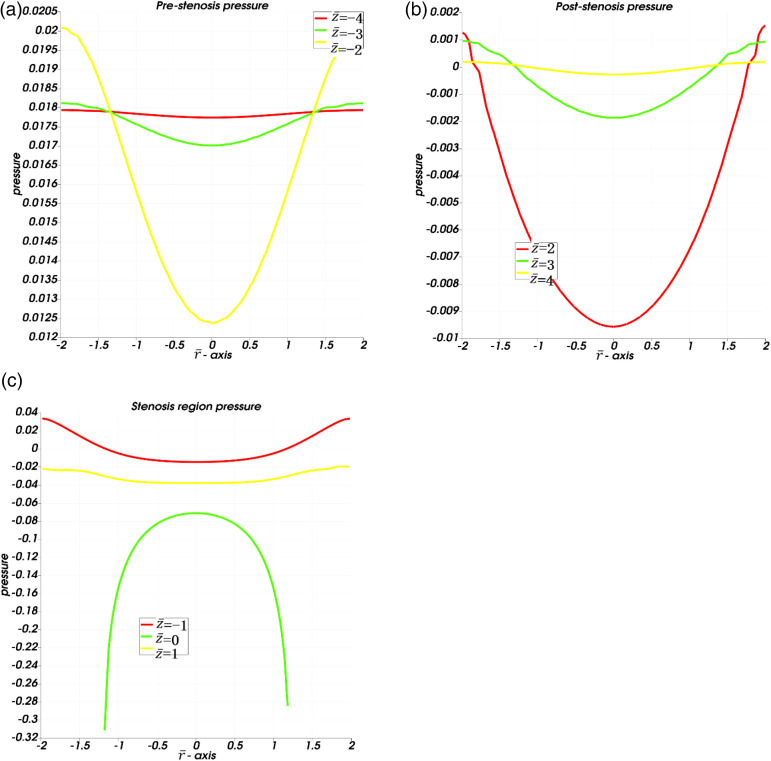
Figure 6.

(a) Pre-stenosis pressure profile at t  =  10. (b) Post-stenosis pressure profile at t  =  10. (c) Stenosis region pressure profile at t  =  10.

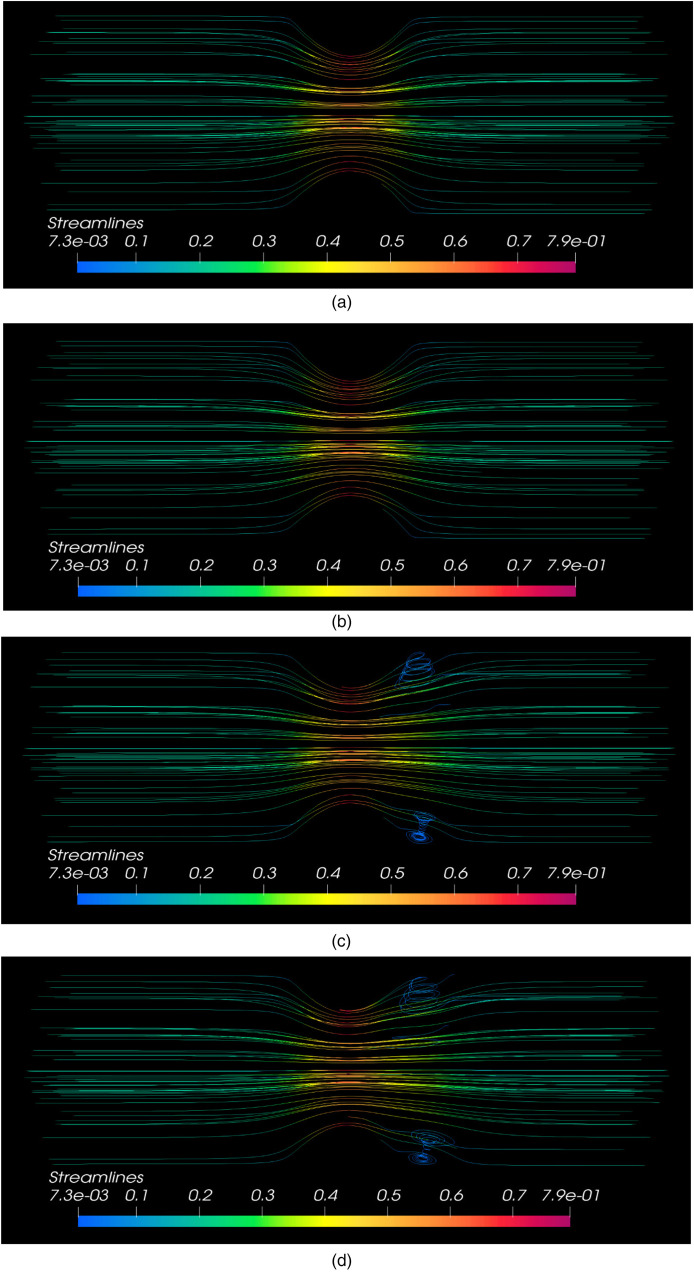
Figure 7.

(a) Streamlines at t  =  1. (b) Streamlines at t  =  3. (c) Streamlines at t  =  8. (d) Streamlines at t  =  10.

In Figures 3(a) to (j), the blood flow simulations inside the stenosed left coronary artery are presented for time $t=1$ to $t=10.$ All these blood flow simulations show an axially symmetric blood flow since the considered stenosis in the central region is symmetric in shape. The flow gains a more developed profile with varying time $t=1$ to $t=10$ . The movement of blood flow from the left to the right side of the artery is evident with varying times $t=1$ to $t=10.$ The graphical simulations of blood flow clearly show that the flow velocity is almost the same with a range of $0.1$ to $0.2$ $\mathrm{m}/\mathrm{s}$ throughout the artery except the central region featuring the symmetric stenosis. Since only disturbance in the flow profile is noted inside the stenosed region of the artery where the velocity of blood flow ranges from $0.25$ to $0.7$ $\mathrm{m}/\mathrm{s}$ . Although the experimental data shows that the normal left coronary artery has a velocity range from 0.159 to 0.199 $\mathrm{m}/\mathrm{s}$ but the occurrence of a symmetric stenosis inside that left coronary artery has increased the velocity to a range of $0.25$ to $0.7$ $\mathrm{m}/\mathrm{s}$ inside the stenosis region. A higher velocity range is observed inside the stenosis region as compared to pre or post-stenosis regions. If we observe the central region of the artery at the location $\overline{z}=0$ , a maximum velocity is observed with stenosed walls of the artery and this velocity declines towards the center of the artery at the location $\overline{z}=0.$ Thus, the blood flow velocity has a high value at the stenosed walls as compared to the central region at the location $\overline{z}=0.$ Although the velocity has increased inside the stenosed region as compared to the pre-stenosis region velocity but once the blood passes through the stenosed region the velocity again gains almost the same values in the post-stenosis region as it has in pre-stenosis region. Thus, the flow velocity has nearly the same values before passing the stenosis region or after passing the stenosis region and the stenosis has only increased the velocity values inside the stenosis region. Hence the stenosed walls only resulted in an increased velocity magnitude inside the stenosis region but the overall flow profile declined due to narrowed walls of the artery.

In Figures 4(a)–(j), the pressure profile for this flow inside the left coronary artery is provided for time $t=1$ to $t=10.$ A maximum pressure is observed on the left side of the artery which indicates a higher pressure at the inlet. As the flow moves from left to right (inlet to outlet), a higher pressure is observed at the inlet as compared to the pressure at the outlet from time $t=1$ to $t=10.$ A slightly lower pressure is observed at the outlet as compared to the inlet pressure. As we observe the pressure profile from $t=1$ to $t=10$ , the pressure profile shows an interesting manner inside the stenosis region. It is seen that the pressure profile has the lowest values inside the stenosis region as compared to pre- or post-stenosis regions. The presence of stenosis results in a declined pressure at the stenosis region. In the stenosis region, the pressure has a range from $-0.25$ to $0$ . The lowest pressure is observed at the highest point (tip) of stenosis at the location $\overline{z}=0$ and it increases towards the center at the line $\overline{z}=0$ . The pressure gains slightly higher values at locations $\overline{z}=-1$ and $\overline{z}=1$ as compared to the stenosis region $-1<\overline{z}<1$ .

Figures 5(a) to (c) provide the line graphs of the velocity profile for pre-stenosis, post-stenosis, and stenosis regions, respectively. These results are presented for the final time value $t=10$ . Figure 5(a) pre-stenosis velocity graph is plotted against the radial coordinate $\overline{r}$ at different $\overline{z}=-4,-3,-2$ locations. This velocity plot shows that the velocity of blood flow increases with an increasing length of axial coordinate $\overline{z}$ and a parabolic flow profile is attained at $\overline{z}=-2.$ Thus the blood flow velocity is increasing in the pre-stenosis region as the flow moves toward the stenosis region. Figure 5(b) post-stenosis velocity graph is plotted against the radial coordinate $\overline{r}$ at different $\overline{z}=2,3,4$ locations. This graph clearly shows that the velocity profile is declining with an increasing length of axial coordinate $\overline{z},$ since the flow velocity has a maximum value at $\overline{z}=2$ and minimum value $\overline{z}=4$ in the post-stenosis region. Two interesting outcomes are observed through these pre and post-stenosis velocity line graphs that the velocity is increasing with the increasing length of the axial coordinate in the pre-stenosis region, but the velocity is declining with the increasing length of the axial coordinate in the post-stenosis region. It clearly indicates that the flow profile increases as the flow moves toward the stenosis region but after passing through the stenosis region the flow profile starts declining as the flow moves away from the stenosis region. Figure 5(c) stenosis region velocity graph is plotted against the $\overline{r}\text{-}\mathrm{axis}$ at different $\overline{z}=-1,0,1$ locations. This graph depicts that the velocity has a lower value at $\overline{z}=-1$ that is the flow entrance region of stenosis, but it has a comparatively high value at $\overline{z}=1$ that is the flow exit region of stenosis. That is the velocity has increased due to narrowing of the artery as the fluid enters and leaves the stenosis region. At both these locations $\overline{z}=-1$ and $\overline{z}=1$ , the velocity has highest value in the center and minimum value towards walls of artery. But a completely opposite scenario is observed at the core region $\overline{z}=0$ , where the velocity is minimum at center and increases towards the walls of the artery. At location $\overline{z}=0$ , the blood flow has a maximum velocity at the highest point (tip) of stenosis at walls but this velocity declines as we move towards the central region along line $\overline{z}=0.$ This velocity at $\overline{z}=0$ has a higher value as compared to location $\overline{z}=-1$ (where flow is entering the stenosis) and $\overline{z}=1$ (where flow is leaving the stenosis). But if we compare the three considered region's velocities, that is pre-stenosis, post-stenosis and stenosis region velocities, it is evident that the maximum velocity attained by blood flow in the pre-stenosis region is more than $0.225\mathrm{m}/\mathrm{s}$ and in post-stenosis region is more than $0.265\mathrm{m}/\mathrm{s}$ and in the stenosis region the highest velocity attained is more than $0.7\mathrm{m}/\mathrm{s}$ . Although the average value for blood flow velocity inside a normal left coronary artery is about $0.15-0.2\mathrm{m}/\mathrm{s}$ but this stenosis occurrence has increased the velocity specifically in the central core region of stenosis to $0.7\mathrm{m}/\mathrm{s}$ at location $\overline{z}=0.$ But after the flow passes through the stenosis region and moves towards the end of the post-stenosis region the velocity again starts declining gaining a lower value as compared to the higher values attained in the core stenosis region.

Figure 6(a) to (c) present the pressure profile line graphs for pre-stenosis, post-stenosis, and stenosis regions respectively. In Figure 6(a), the pre-stenosis pressure profile line graphs are plotted against $\overline{r}\text{-}\mathrm{axis}$ at different $\overline{z}=-4,-3,-2$ locations. The pressure profile is declining with the increasing length of axial coordinate $\overline{z}$ and pressure is minimum at the center that increases towards the walls. In Figure 6(b), the post-stenosis pressure is plotted against the radial coordinate $\overline{r}\text{-}\mathrm{axis}$ at different $\overline{z}=2,3,4$ locations. The pressure profile is increasing with the increasing length of the axial coordinate $\overline{z}$ in the post-stenosis region. Figure 6(c) presents the pressure profile plotted against $\overline{r}\text{-}\mathrm{axis}$ for the stenosis region, −1 $\le \overline{z}\le 1.$ The pressure profile is higher at the entering region of stenosis at $\overline{z}=-1$ as compared to the exit region of stenosis at $\overline{z}=1.$ The pressure profile has the lowest value at the core region of stenosis along location $\overline{z}=0$ , where it is maximum in the center and declines toward stenosis walls. Negative pressure values mean flow will be much attracted towards the region as compared to the other section of geometry. Pressure is a push to fluid volume and when this push is positive it will repel fluid away from this region while if it is negative then it attracts. In Figures 6(b) and (c), the negative values of pressure mean that more fluid is attracted towards the central region of the artery in the post-stenosis and stenosis region.

Figure 7(a) to (d) provide streamlined graphs for blood flow inside the stenosed left coronary artery. The streamline graphs are plotted for time values $t=1,3,8,10.$ These graphs show a 3D view of streamlines for blood flow inside this stenosed left coronary artery. At $t=1$ and $t=3$ , it is observed that the streamlines do not cross each other, and a laminar flow profile is observed exactly according to the modeled problem. But in most of the real-life stenosed arteries blood flow problems, turbulence is observed near the stenosis region. In our study case, the turbulence caused due to the stenosed region can be observed in time at $t=8$ and $t=10.$ At $t=8$ and $t=10$ , when the flow becomes fully developed, one can observe that the streamlines are now crossing each other just after the stenosis region. Although the problem is modeled for a laminar flow, turbulence occurs since the blood flow inside stenosed arteries shows turbulence phenomenon in real-life problems. Thus, just like real-life stenosed arteries blood flow problems, a turbulent flow phenomenon was expected near the stenosed region that exactly matches our obtained results.

Conclusions

The blood flow issue is modeled for the left coronary artery featuring a symmetric stenosis formation due to plaque collection at the central region. The non-Newtonian nature of blood is tackled via the non-Newtonian Casson model in this study. The major outcomes are given as

• The interpretation of blood flow numerical simulations on this arterial stenosis segment provides the necessary data for the surgical purposes of these stenosis segments like the location of stenosis, shape, and formation of stenosis can be evaluated through this study.

• Once the severeness, shape, location, and formation of the stenosis segment is known then the method that can be used for the removal of this CAD can be decided like whether an angioplasty or a bypass is required. Angioplasty is good for a mild case of stenosis, otherwise a bypass is required for a severe stenosis.

• The flow problem is modeled for a laminar non-Newtonian model, but a mild turbulent phenomenon can be seen in the streamlined graphs. This turbulence is occurring just ahead of the stenosis segment. The reason for this turbulence flow occurrence is the presence of a stenosis segment. Since a slight turbulence phenomenon is observed in real-life blood flow problems of stenosed arteries. Thus, our results also verify this real-life turbulence phenomena for blood flow through the stenosis segment.

• Since the stenosis in the center region under consideration is symmetrical in shape, all these blood flow simulations display an axially symmetric blood flow. When compared to the pre- or post-stenosis sections, a greater velocity range is seen inside the stenosis zone.

• Only the velocity magnitude within the stenosis region increased as a result of the stenosed walls; nevertheless, the overall flow profile decreased as a result of the constricted artery walls. When compared to the pre- or post-stenosis regions, the pressure profile is lowest inside the stenosis region.

Nomenclature

$a$

Position of stenosis

$b$

Length of stenosis

$d_f$

Vector positioned between N and p.

$f$

Face of any CV.

$L$

Length of artery

$m$

Consistency index

$n$

Stenosis shape parameter

$n_f$

Face unit vector

$N$

Computational point

$\overline{n}$

Unit Normal Vector

$\overline{p}$

pressure

$R$

Radius of normal artery

$r_f$

Vector between point p and center.

$(\overline{r},\overline{z})$

Cylindrical system of coordinates

$S_f$

Face area

${\overline{S}}_{ij}$

Yield stress

$\overline{t}$

time

$(\overline{u},\overline{w})$

Velocity components

$V_p$

Volume of considered control volume

$X_p$

Centroid

$\overline{z}$

Axial length

${\overline{\dot{\gamma }}}_{ij}$

Shear strain rate

$\zeta$

Viscosity

$\rho$

density

$*$

$\delta$

Height of stenosis

Author biographies

Salman Akhtar has his part in the mathematical modeling of physical problem, finite volume solution section, Open-FOAM software and graphical simulations, diagrams, writing original draft, and interpretation of data used for the article.

Zahir Hussain has his role in the supervision, analysis, review, and validation of results.

Sohail Nadeem has his part in supervision, analysis, review, and validation of results.

I. M. R Najjar has his role in analysis, critical revision of manuscript, validation of results, and interpretation of data for the article.

A.M Sadoun has his role in the critical revision of manuscript, validation of results, and methods, analysis, and interpretation of data.