Bilateral arm movements are coordinated via task-dependent negotiations between independent and codependent control, but not by a “coupling” control policy

Abstract

Prior research has shown that coordination of bilateral arm movements might be attributed to either control policies that minimize performance and control costs regardless of bilateral symmetry or by control coupling, which activates bilaterally homologous muscles as a single unit to achieve symmetric performance. We hypothesize that independent bimanual control (movements of one arm are performed without influence on the other) and codependent bimanual control (two arms are constrained to move together with high spatiotemporal symmetry) are two extremes on a coordination spectrum that can be negotiated to meet infinite variations in task demands. To better understand and distinguish between these views, we designed a task where minimization of either control costs or asymmetry would yield different patterns of coordination. Participants made bilateral reaches with a shared visual cursor to a midline target. We then covertly varied the gain contribution of either hand to the shared cursor’s horizontal position. Across two experiments, we show that bilateral coordination retains high task-dependent sensitivity to subtle visual feedback gain asymmetries applied to the shared cursor. Specifically, we found a change from strong spatial covariation between hands during equal gains to more independent control during asymmetric gains, which occurred rapidly and with high specificity to the dimension of gain manipulation. Furthermore, the extent of spatial covariation was graded to the magnitude of perpendicular gain asymmetry between hands. These findings suggest coordination of bilateral arm movements flexibly maneuvers along a continuous coordination spectrum in a task-dependent manner that cannot be explained by bilateral control coupling.

NEW & NOTEWORTHY Minimization of performance and control costs and efferent coupling between bilaterally homologous muscle groups have been separately hypothesized to describe patterns of bimanual coordination. Here, we address whether the mechanisms mediating independent and codependent control between limbs can be weighted for successful task performance. Using bilaterally asymmetric visuomotor gain perturbations, we show bimanual coordination can be characterized as a negotiation along a spectrum between extremes of independent and codependent control, but not efferent control coupling.

Listen to this article’s corresponding podcast at https://jneurophysiol.podbean.com/e/jnp-micro-podcasts-four-questions-task-dependent-negotiations-of-bimanual-coordination/.

INTRODUCTION

A wide range of daily activities recruit the coordinated use of both hands, such as opening a bottle or steering a car. These types of tasks are normally performed without conscious recognition of the timing and amplitude of each arm’s contribution to the manipulated objects. However, when we try to perform some bilateral movements, such as patting the head with one hand while rubbing the stomach with circular movements of the other hand, limitations in coordination become evident; we find ourselves switching between patting with both hands or rubbing with both hands. Similarly, when we try to draw a square and a circle at the same time with different hands, both drawings often end up as a merged output of the two intended shapes. Conversely, coordination of symmetrical movements, such as drawing circles with both hands, are performed more easily. The fact that some bilateral arm movements interfere with each other while others are performed independently with ease suggests that more than one mode of coordination may exist, ranging from completely codependent to completely independent. We envision that these extremes represent the ends of a spectrum of bilateral coordination that can be negotiated depending on task demands. The neurophysiological underpinnings of such coordination have been studied for decades (for a detailed review see Ref. 1), yet the nature of the constraints on coordination are still not well understood.

Early research on bimanual coordination emphasized the strong spatiotemporal symmetry between arms. For example, discrete movements made to targets of different amplitudes can show highly correlated initiation and termination times between arms (2, 3) and continuous circle tracing with mirror symmetry between arms has reduced trajectory errors and increased phase stability compared with asymmetric movements, particularly at higher speeds (4–6). The nature of this tight spatiotemporal bimanual coordination is such that it can cause interference effects between arms if trajectories are not mirror symmetrical, or otherwise incongruent. This has been demonstrated when tracing trajectories of different shapes with either arm gradually become more similar (7, 8) or when one arm overshoots a near target when the other arm is required to reach one further away (9, 10). Taken together, these findings have been interpreted by some researchers as evidence that upper limb movements can be controlled by a common or shared motor command that activates functional groups of homologous muscles across both arms to act as a “single unit” (2). Thus, this hypothesis characterizes coordination of bilateral arm movements in a purely codependent manner when movements are mirror symmetrical, and hence can recruit symmetrical activation of bilaterally homologous muscles. In this way, there is an underlying assumption that these movements are mediated by a control policy that seeks to minimize a cost of spatial asymmetry between limbs. As a consequence, bilateral coupling should be robust to changes in perceptual context. It should be noted that this coupling view of coordination does not extend to movements that are not bilaterally homologous with respect to muscles and joints, and thus its utility in coordinating daily tasks appears limited because such tasks rarely, if ever, require or sustain such symmetry.

Other work exploring bilateral coordination has demonstrated that the extent of codependent or independent control that is expressed in a given task is largely influenced by task demands. When separate visual hand position cursors are provided for each limb during symmetrical bilateral reaching, participants can compensate for both visual (i.e., a misaligned hand position cursor) and physical (i.e., novel force environments) trajectory perturbations applied to one limb independently from the other. This includes unilateral perturbations applied on unexpected trials that evoke movement corrections based on sensory feedback mechanisms (11, 12), as well as perturbations applied consistently over repeated trials that lead to gradual adjustments in early movement trajectory, reflecting changes in feedforward control (11, 13, 14). Thus, coordination of bilateral arm movements is likely modulated by the sensory feedback from our moving limbs in relation to the intended movement goal.

Conversely, when the nature of the task is changed so that the same symmetrical bilateral movements are required to transport a single, shared visual feedback cursor (or virtual object) toward a target, movements of the two arms seem to covary with each other more closely. Spatial deviations of the left and right hands typically show a strong, negative correlation, such that errors arising from one hand appear to be effectively compensated by the other hand (15–18). The strength of this codependent mode of control is such that when a visual or physical trajectory perturbation is applied to one arm, feedback and feedforward mechanisms of movement control are recruited bilaterally in both the perturbed and unperturbed limb (11, 19, 20). Shared transport tasks also modulate reflex activity of both limbs in response to unpredictable trajectory perturbations (12, 21, 22). Modulation of muscle activity in the unperturbed arm occurs within 50–115 ms after perturbation onset (12, 22) and can alter kinematics in a way that helps correct the deviation of the shared cursor back toward the target (12). Importantly, these reflex responses are task-dependent, in that they only occur when the perturbation acts to deviate the shared cursor or object from its intended goal (12, 22). Task-dependent flexibility of the covariance relationship between limbs during shared transport tasks has also been shown elsewhere. Using a virtual rectangular object, Diedrichsen and Gush (20) demonstrated that specifying the end goal as either the length or position of the rectangle could partially reverse the direction of corrections made from one limb in response to a force perturbation applied to the other. Thus, although shared transport tasks evoke highly codependent modes of bilateral coordination, the nature of this codependent relationship is dependent on task demands. Contrary to the hypothesis of bilateral coupling, observations of task-dependent flexibility and strong codependent control during shared transport tasks has been described by a control policy of bimanual coordination that primarily seeks to minimize costs associated with task error and motor effort (23). This type of task-dependent control has also been described by a controller that constrains variability in only those elements of performance which define task success, while allowing task-redundant aspects of performance to vary in a more unconstrained manner (24–26).

Collectively, these results show that bilateral arm movements can be controlled both independently and codependently according to task conditions, which include the required movements, sensory feedback conditions, and task goal. In this study, we examine the hypothesis that coordination of bilateral arm movements reflects a spectrum of possible combinations of independent and codependent modes of control that are negotiated with respect to task conditions. Importantly, this view does not necessarily prescribe both independent and codependent control as equally likely or stable modes for a given task. Instead, we use the term “negotiation” to reflect a hypothetical computation that might underlie the resolution of the relative contributions of each arm for a given task condition.

Accordingly, this study was designed to examine the fluency with which the nervous system might negotiate coordination along a spectrum between independent and codependent control, in response to covert changes in task conditions. To examine this, we designed a task in which participants made symmetrical bilateral reaching movements to transport a shared cursor toward a target, which we expected to evoke a highly codependent mode of bilateral coordination (2, 11, 12, 15, 19, 27). However, we also introduced a subtle visual feedback manipulation, in which the gain of either hand’s contribution to the shared cursor’s horizontal (medial-lateral axis, perpendicular to target direction) position was altered asymmetrically, whereas each hand’s contribution to movement along the target direction axis remained equal (1:1). The perpendicular gain asymmetry was such that one hand’s contribution to the cursor’s lateral displacement was increased (high gain hand) and the other hand’s contribution was made negligible (low gain hand). Thus, under these asymmetric gain conditions, control of the low gain hand in the perpendicular direction becomes largely irrelevant to task success, potentially leading to a more independent mode of control to emerge. We measured changes in the covariance relationship of left- and right-hand spatial deviations under different perpendicular gain asymmetries to examine whether a spectrum between these two modes of bilateral coordination could be negotiated according to these task conditions. Under the framework of the bilateral coupling hypothesis, we would predict no change in the predominantly codependent control between arms across all visual feedback gain asymmetries, as activation requirements of homologous muscle groups could remain unchanged for all gain conditions. Conversely, a task-dependent model of bilateral coordination would predict more independent control under visual feedback gain asymmetries, and hence changes in the covariation relationship between left- and right-hand perpendicular deviations across these feedback gain conditions. We therefore measure the degree of covariation under different asymmetric gain conditions, using a series of regression analyses, to provide insight into the flexibility of this type of control for variations in sensorimotor conditions.

METHODS

Participants

A total of 21 volunteers aged 18–30 yr participated in the experiment, with 10 in Experiment 1 (5 females/5 males) and 11 in Experiment 2 (6 females/5 males). All participants self-reported as right-handed and provided written consent for the study, which was approved by the institutional review board of Pennsylvania State University.

Experimental Setup

Participants were seated in front of a two-dimensional (2-D) virtual environment where visual stimuli were projected from a large horizontally mounted TV onto a mirror placed directly beneath it (Fig. 1A). The mirror was positioned so that the reflected images appeared to the participant as incidental to the surface of a glass tabletop below it where the arms were placed. The mirror also occluded any direct vision of the arms, which were both placed in splints that fixed the position of joints below the elbow. The splints were then secured onto air sleds that discharged pressurized air onto the tabletop and reduced the friction of movements made across it. Two 6-degree-of-freedom (DOF) magnetic sensors (Ascension TrakStar) were attached to each arm (one on the back of the hand and one on the upper arm), which sampled data at a frequency of 130 Hz. Before task performance, the position of the proximal interphalangeal (PIP) joint of the index finger and other landmarks on the hand and upper arm were digitally registered, making it possible to estimate positions of the wrist, elbow, and shoulder joints.

Figure 1.

Experimental setup of Kinereach system and the task design for Experiments 1 and 2. A: Kinereach system from a lateral view. B: a top-down view with visual stimuli. Dashed circles show start positions for the left and right hands, the green circle shows start location for the shared cursor (small black circle with crosshair) whose position was determined by the unseen left and right finger tips according to the equation shown in the top right corner. C: task design for Experiment 1 (10 participants) according to changes in perpendicular (x-axis) position gains of the left (GL) and right (GR) hands. These values correspond to Eq. 1b that defines shared cursor position (also shown in B). Gain asymmetry conditions are labeled as LH High and RH High to denote whether the left or right hand had high perpendicular gain contribution to the shared cursor, respectively. D: task design for Experiment 2 (11 participants), which included additional intermediate (Int.) gain asymmetry conditions for the left and right hands. Perpendicular position gain values of the left (GL) and right (GR) hands correspond to the shared cursor position defined in Eq. 1b (also shown in B) in the same manner as the Experiment 1 design.

A black 1-cm-diameter circular cursor with a black crosshair (Fig. 1B) was used to display near real-time (17-ms delay) position of the digitally registered index finger PIP joint from each hand (between trials) or a single “shared” cursor representing the average position of both finger PIP joints (during trials). Deviations in the x and y coordinates of the shared cursor position (x_c and y_c, respectively) during reaches were calculated using physical spatial coordinates of the left (x_L and y_L) and right hand (x_R and y_R) relative to the initial position of either hand on each trial when the shared cursor appeared (see Procedure for details), as in Eqs. 1a and 1b:

$$y_{\text{c}}=\left(y_{\text{L}}+y_{\text{R}}\right)/2$$ (1a)

$$x_{\text{c}}=\left(\text{GL}·x_{\text{L}}+\text{GR}·x_{\text{R}}\right)/2$$ (1b)

GL and GR represent the left- and right-hand gain parameters, respectively, that were manipulated on some trials to create either symmetric or asymmetric contributions of the left and right hands to the x-axis position of the cursor. We term this “perpendicular gain,” as the gain manipulation occurs perpendicular to the reaching direction in the Cartesian, visually perceived space of cursor motion. Critically, the left- and right-hand gains on the shared cursor’s y-axis position (i.e., those along the reaching direction) remained at a ratio of 1:1 throughout the experiment (see Fig. 1B). Start positions were displayed as 2.5-cm circles and the target was shown as a 3-cm diameter gray circle with smaller gray and blue circles inside it to form a bullseye.

For Experiment 1, left- and right-hand start positions were located 26 cm from the table edge closest to the participant’s torso and 10 cm to either side of the midline. The shared cursor start position was located between the left- and right-hand start positions at the midline, with the target located 20 cm directly anteriorward to it. To ensure findings from Experiment 1 were not due to any between-subjects variation in range of reaching movement, left- and right-hand start positions in Experiment 2 were defined on an individual participant basis as the location where the external shoulder angle was 20° and internal elbow angle was 70°. The linear distance from these start positions to shoulder and elbow angles of 50° and 120°, respectively, was then used as the distance to the target. As in Experiment 1, the target was located along the midline, directly anteriorward from the shared cursor start position. Overall, for Experiment 2, the average left- and right-hand start positions [mean = 23.69 cm (SD = 2.42 cm) from table edge, mean = 12.14 cm (SD = 3.07 cm) either side of midline] and reach distance (mean = 19.12 cm, SD = 1.95 cm) were similar to those of Experiment 1.

Procedure

To start a trial, participants had to move both cursors (one for each hand) to their respective start positions on the left- and right-hand sides of the workspace. Once they had remained there for 1 s, the cursors and start positions for the left and right hands disappeared and were replaced with a single, shared cursor and start position located centrally between them, with the target directly ahead. At this cue, participants were instructed to make a fast, bilateral reaching movement to transport the shared cursor from its start position onto the target as accurately as possible. The trial was terminated 1 s after the participant moved outside the start circle, at which point, participants saw score feedback that was fixed at 10 points for every trial to maintain motivation and minimize awareness of sudden changes in performance due to asymmetric gain conditions. In Experiment 2, participants were also provided with feedback regarding the shared cursor hand path following trial termination. After the performance feedback disappeared, the separate hand position cursor and start positions reappeared for the next trial.

Experimental Design

An overview of the task design for Experiment 1 is shown in Fig. 1C. Participants performed 300 trials in total that were broken into six blocks of 50 trials with varying left- and right-hand perpendicular gain conditions. This task started with a familiarization block in which the gain of the left and right hands was equal at 1:1. The perpendicular gain was then increased to a ratio of 2:2 for the next block of 50 trials, which permitted larger gain asymmetries in the following blocks without altering the overall combined gain on the shared cursor (this was intended to minimize awareness of the changing gain manipulations). Participants then performed a further four blocks of 50 trials where the conditions alternated between an asymmetric ratio of 0.2:3.8 and an equal ratio of 2:2. We refer to the asymmetric gain conditions as either RH High (0.2:3.8 ratio of left to right hand) or LH High (3.8:0.2 ratio of left to right hand) to indicate whether the right hand (RH) or left hand (LH) was experiencing the high perpendicular gain in that block of trials. Performance order of the RH High and LH High conditions was counterbalanced between participants. The different 2:2 gain blocks are labeled as 2:2a, 2:2b, and 2:2c to distinguish their performed order. However, for the majority of the analysis, we used only the trials for the first (2:2a) block to compare with asymmetric conditions, which we refer to as the “Equal” block. This way the number of trials included for analysis was balanced between the equal and asymmetric gain conditions.

The task design for Experiment 2 is shown in Fig. 1D. Participants began with a brief 20-trial familiarization block of 1:1 perpendicular gain. The task then proceeded in blocks of 40 trials, which alternated between equal (2:2 ratio) conditions and the asymmetric gain conditions in the following order, RH High (0:4), RH Intermediate (1:3), LH High (4:0), and LH Intermediate (3:1). As in Experiment 1, we used the first performed block of equal (2:2a) trials for comparisons with the other asymmetric gain conditions. Participants performed a total of 380 trials in this experiment.

In both Experiments 1 and 2, the left- and right-hand gain contributions to the shared cursor’s position along the start-target axis (i.e., parallel to reach direction) remained equal at 1:1 throughout the experiment. Furthermore, informal verbal reports obtained after the experiment indicated that participants were unaware of any changes in visual feedback conditions, confirming the implicit nature of the experimental manipulation.

Kinematic Analysis

Using the digitized landmarks, we calculated inverse kinematics with 10 degrees of freedom per arm. However, for the purposes of this study (and as the task was constrained to a horizontal plane), we analyzed only the 2-D planar movements of the left and right index fingers. The kinematic data were low-pass filtered at 8 Hz (3rd-order, dual-pass Butterworth) and differentiated to obtain velocity and acceleration profiles. Movement onset was determined by an algorithm that identified the time of peak tangential velocity and working backward from that point to identify either a local minimum below 8% of this peak value or a zero velocity, whichever came first. Movement offset (end position) was identified via a similar method working forward from the time of peak velocity. Movement time was then calculated as the duration between movement onset and movement offset.

To ensure that measurements recorded for the left and right hands were time-locked—which was important for the covariation analysis described in Statistical Hypothesis Testing—we averaged the detected peak velocity and movement offset sample numbers between the two hands to use as time points for recording positions in each trial. In this way, we time-locked measures of left- and right-hand positions that approximately corresponded to their respective peak velocity and movement offsets. We then recorded perpendicular (x-axis) deviations of both hands at these shared time points in each trial to use in further covariation analysis. Measurements at peak velocity and end-position were recorded to explore the predominantly planned or feedforward components of the movement trajectory versus those influenced more by sensory feedback-mediated online corrections, respectively (28–31). The cursor error was calculated as the Euclidean distance between the cursor and the target at the shared end-position time point and was used as a measure of task performance accuracy. Kinematic data from each trial were visually inspected to make occasional manual corrections to detect movement onset and offset positions as needed, as well as to identify and remove rare cases of trials where a movement was not attempted or only partially completed (this accounted for less than 0.5% of trials).

Conceptual Model

Our experimental goal was to investigate adaptive changes in bimanual coordination due to changes in how each hand’s movements contribute to the motion of a common controlled endpoint (the screen cursor). Figure 2 presents a simplified conceptualization of the experimental task and its control requirements to coordinate motion of the two hands to bring the cursor [x_c, y_c]^T to a desired position [x_{c_desired}, y_{c_desired}]^T as quickly and accurately as possible. At any given time, the position and velocity of the two hands in the horizontal plane may be obtained from the N-element vector representing the state of the left and right arms [q_L, … q_R, …]^T, which we organize into two parts—a set of state variables pertaining to the left arm and hand (q_L) and another pertaining to the right arm and hand (q_R). We defined the hand-to-cursor projection C as in Eqs. 1a and 1b. To perform the task, subjects must learn how to effectively invert the hand-to-cursor projection (i.e., they must learn a map C⁻¹) to transform deviations of the cursor from its desired position on the display screen (ε₂) into limb positioning errors impacting hand position in the horizontal plane (ε_N). Given those estimates of hand-positioning errors, a well-designed feedback controller K can generate a set of motor commands u that will drive the (nonlinear) limb dynamics such that hand-positioning errors are reduced over time. Our model considers the combination of transformations C⁻¹K to be the adaptive task controller. This conceptualization is useful because it can promote understanding of how the experimental task influences the inherent structure of the requisite controller and how that structure can provide insight into bimanual coordination.

Figure 2.

Conceptual model of the bimanual task and its control requirements. [x_c, y_c]^T: cursor position; [x_{c_desired}, y_{c_desired}]^T: desired cursor position; [q_L, … q_R, …]^T: instantaneous state of the two hands; [$\dot{q}$_L, … $\dot{q}$_R, …]^T: time rate of change of hand states; C: experimentally defined hand-to-cursor projection matrix; A and B: matrices modeling the limb dynamics (limb-state transition matrix and control input matrix, respectively); C⁻¹ and K: comprise the adaptive task controller.

For simplicity, consider a set of N neural commands [u_L, …, u_R, …]^T that are capable of influencing each hand’s motion in the {x,y} plane independently. Accordingly:

$$\mathit{u}=\mathit{K}{\mathit{\epsilon }}_{\mathit{N}}=\left[\begin{array}{cc}\left[\begin{array}{cc}{\mathit{K}}^{LL}& \cdots \\ \cdots & \cdots \end{array}\right]& \left[\begin{array}{cc}{\mathit{K}}^{RL}& \cdots \\ \cdots & \cdots \end{array}\right]\\ \left[\begin{array}{cc}{\mathit{K}}^{LR}& \cdots \\ \cdots & \cdots \end{array}\right]& \left[\begin{array}{cc}{\mathit{K}}^{RR}& \cdots \\ \cdots & \cdots \end{array}\right]\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\epsilon }_L\\ :\end{array}\\ \begin{array}{c}{\epsilon }_R\\ :\end{array}\end{array}\right],$$ (2)

where the partitions [K^LL] and [K^RR] of block matrix K represent the independent influences of left- and right-hand positioning errors on motor commands driving the left and right hands, respectively, whereas [K^RL] and [K^LR] represent the codependent influence of one hand’s errors on motor commands of the other hand. These codependent influences are negligible when the left and right hands are controlled independently; when they are nonnegligible, they give rise to codependent (correlated) motions of the left and right arms and hands. Accordingly, this model conceptually outlines that one can have both within-hand corrections ([K^LL] and [K^RR]) and between-hand corrections ([K^RL] and [K^LR]) that could vary in contribution to overall task performance. However, for the purposes of this study, we only quantify between-hand corrections, which we infer from changes in patterns of covariance between the motions of the two hands. From this analysis, we assume that a reduction or loss of covariance between hands reflects a reciprocal increase in independent, within-hand control. This would be consistent with a shift along a spectrum between the two modes of bilateral coordination. Our experimental goal was to investigate how experimental manipulation of the hand-to-cursor projection C would impact bimanual coordination, as measured by adaptive changes to the codependent feedback parameters.

Statistical Hypothesis Testing

To address this goal, our primary analysis investigated adaptive patterns of bimanual coordination reflected in covariation between left- and right-hand perpendicular deviations at peak tangential velocity and end position, which we characterized using orthogonal linear regression models (equal variances assumed). Orthogonal regression models (also known as Deming regression) fit the data by minimizing the sum of squared differences perpendicular to the linear model, whereas ordinary least squared regression assumes all errors arise from the y-axis variable and subsequently minimizes the sum of squared differences along the y-axis, or dependent variable, alone (32). In this study, we expect the imposed visual perturbations to modulate the extent of lateral deviation in both hands and hence errors on both axes (see Fig. 5A). Accordingly, we chose orthogonal regression models to fit left- and right-hand deviations. From these models, we obtained a slope angle (in degrees) that we used to describe any changes in the covariation during exposure to the asymmetric perpendicular gain conditions. Considering we expected slope angle values to vary close to both the vertical and horizontal axes as a result of the imposed visual feedback manipulations, we applied a transformation to the raw slope angles to ensure continuity in the computed slope angles when the regressions spanned across either the vertical or horizontal axis. Specifically, we subtracted 180° from slope angles that were between +45° to +90° so that they would continue to decrease incrementally after crossing the vertical (−90°) axis. In this way, we had a continuous range of slope angles (i.e., from +45 to −135) for values that deviated from the line of equivalence where raw slope was 1. The 95% confidence intervals reported for regression slope angles were calculated using the method described by Tan and Iglewicz (33). All regression analyses were performed using JMP Pro 14.

Figure 5.

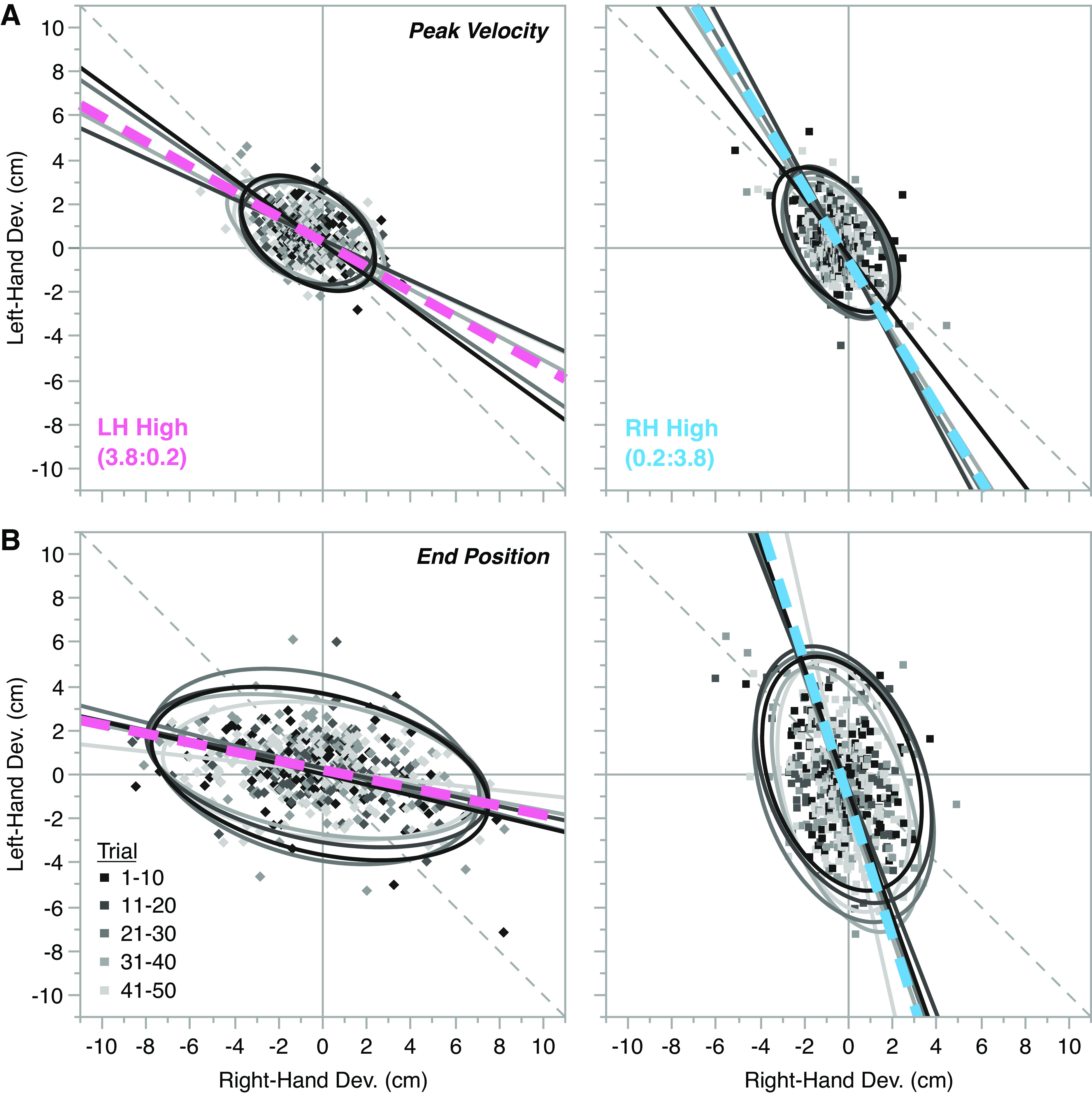
Theoretical and measured group-level covariance relationships (orthogonal regression lines and 95% confidence ellipses) of left- and right-hand perpendicular deviations for LH High (pink diamonds, left), Equal (2:2a; black circles, middle), and RH High (light blue squares, right) conditions in Experiment 1. The top row (A) shows theoretical covariance relationships and their associated regression slope angles (in degrees) that might be observed if the mode of bilateral coordination was to adjust completely to the different visual feedback conditions. The middle row (B) and bottom row (C) show empirical perpendicular deviations measured at peak velocity and end position, respectively, with annotations of measured slope angles and associated 95% confidence intervals in square brackets. The data points represent all trials from all participants combined on the same axes with 95% confidence ellipses and fitted regression models shown as solid colored lines. Individual participant 95% confidence ellipses are shown as superimposed faintly colored lines. The change in regression slopes observed for the asymmetric gain conditions are consistent in direction with the theoretical task-dependent covariance relationships shown in A, but do not completely align with those predictions due to some residual covariance between hands.

The group design of this study yielded a large amount of data across a substantial range of left- and right-hand perpendicular displacements, which we leveraged by fitting orthogonal regression models at the group level with data from all participants combined on the same axes for both experiments. In addition to examining the consistency of spatial covariance across this wider range of perpendicular displacements, we also fitted individual participant data with independent orthogonal regression models to confirm that any patterns observed at the group level were consistent across each individual’s observed range of spatial deviations. We then subjected the regression slope angles to statistical analysis with linear mixed-effects models. For this analysis, we modeled the gain condition as a continuous fixed factor by converting the gain asymmetries to a numerical value between 0 and 1, representing the extent of contribution from the right hand to the medial-lateral position of the shared cursor (e.g., a left- to right-hand gain ratio of 1:3 would be coded as 0.75). This way, it was possible to express the change in slope angle per unit step-wise change in the gain asymmetry between hands. In addition to the fixed, continuous factor of the gain condition, the model included random intercepts and slopes for each participant as this was found to be the most parsimonious model design (consistently lowest Akaike information criterion scores vs. models with random intercept or random slope only) across both experiments and measurement points of peak velocity and end position. Importantly, we used this analysis for the individually fitted slope angles due to the expected linear relationship between slope angle and gain asymmetry conditions. This linear mixed-effects model analysis was not possible to perform at the group level as there is no established method of modeling random slopes with orthogonal regression in a repeated-measures design which, as we outline here, is a critical aspect of modeling our data given the expected error in both the left- and right-hand deviations that were analyzed.

As we did not predict a linear relation between other outcomes and gain conditions a priori, we used repeated-measures analysis of variance (ANOVA) to analyze shared cursor error, absolute hand deviation, and kinematic data (peak tangential velocity and movement time). Post hoc comparisons for significant effects were then computed with a Bonferroni adjustment (obtained by multiplying the raw P value by the number of comparisons, listed as P_adj), to account for the familywise error rate associated with multiple comparisons. In cases where the assumption of sphericity was violated, a Greenhouse-Geisser correction was used. Partial eta squared (η_p²) and Cohen’s d were used for estimates of effect size for significant effects from ANOVAs and post hoc comparisons, respectively. Descriptive statistics are presented as means (standard errors) and as model estimates [95% confidence intervals], unless stated otherwise. All statistical tests were performed in JASP (34) and assessed for significance using a two-tailed α threshold of 0.05.

RESULTS

Experiment 1

Kinematic performance.

Figure 3 shows kinematics of the left-hand, right-hand, and shared cursor for one representative subject on a single trial under the Equal (Fig. 3A), LH High (Fig. 3B), and RH High (Fig. 3C) gain conditions. Covariance between the perpendicular deviation of left and right hands was assessed across the different gain conditions at two time points; one early in the movement at peak velocity and one later in the movement at end position, shown in Fig. 3 as red cross and open circle symbols, respectively.

Figure 3.

Example velocity profiles and trajectories of one representative participant in the Equal (2:2a; A), LH High (B), and RH High (C) conditions of Experiment 1. The velocity profiles and trajectories for the left hand are shown on the left column of the figure and data for the right hand is shown on the right. Shared cursor trajectories are shown down the center. Red cross and open circle symbols indicate the shared peak velocity and end position time points, respectively, where deviations in hand position were recorded for analysis. D and E show the group mean (error bars represent 1 standard error) and individual participant values for peak tangential velocity and movement time, respectively, for the left and right hands in the LH High, Equal (2:2a), and RH High conditions.

To examine potential kinematic differences between hands during exposure to the different visual gain conditions, we submitted left- and right-hand peak tangential velocity (Fig. 3D) and movement time (Fig. 3E) to separate repeated-measures ANOVA with a 2 (hand: left or right) × 3 (gain condition: LH High, Equal, and RH High) design. These analyses revealed no main effect of hand, gain condition, or their interaction on peak velocity (all P > 0.109) or movement time (all P > 0.193). These results suggest the left and right hands performed with similar kinematic profiles across the different gain conditions.

Shared cursor accuracy.

Cursor error at end position is presented as group means of 10 trial epochs in Fig. 4A. There were no marked improvements in cursor accuracy over the course of the block for any of the three gain conditions. There was, however, a clear increase in end position errors for both asymmetric gain conditions that remained high throughout the block. A significant one-way ANOVA confirmed an effect of gain condition on mean cursor error [Fig. 4B; F(2,18) = 12.79, P < 0.001, η_p² = 0.59], and post hoc comparisons indicated that errors were increased in both the RH High [t(18) = 4.02, P_adj = 0.002, d = 1.19] and LH High [t(18) = 4.67, P_adj < 0.001, d = 1.39] conditions compared with the Equal gain condition.

Figure 4.

Summary of shared cursor end-position (EP) accuracy measures for the LH High (pink), Equal (2:2a; black), and RH High (light blue) conditions from Experiment 1. Top row shows the group mean cursor error at end position in 10 trial epochs (A) and averaged across the whole 50 trial block (B). Group cursor error variability (measured by coefficient of variation) is shown in the bottom row, calculated in 10 trial epochs (C) and across the whole block of trials (D). Errors bars in A and C represent 1 standard error. The P values annotated on the boxplots in B and D reflect significant Bonferroni-adjusted post hoc comparisons, with individual subject values shown as separate data points.

Cursor error variability (measured as coefficient of variation; standard deviation as percentage of mean) was initially highest in the LH High condition and lowest in the RH High condition, but all gain conditions converged to roughly similar levels of error variability by the end of the block (Fig. 4C). Taken across the whole block, there was a difference between gain conditions in the variation of cursor error [Fig. 4D; F(2,18) = 7.98, P = 0.003, η_p² = 0.47) where variability was increased in the LH High compared with the Equal [t(18) = 2.78, P_adj = 0.037, d = 0.99] and RH High conditions [t(18) = 3.87, P_adj = 0.003, d = 1.38].

Thus, mean end-position errors of the shared cursor were increased under asymmetric gain conditions regardless of which hand had the high gain contribution, but variation in errors was only increased when gain of the left hand was high (and gain of the right hand was low), a finding consistent with reports of interlimb differences in unilateral reaching between the right and left hands (35).

Bimanual spatial covariance.

During shared bilateral reaching tasks, left and right hands typically show strong spatial covariance, reflecting a codependent mode of bilateral coordination. Accordingly, we predicted a strong, negative relationship between perpendicular deviations made by the left and right hands under equal gain conditions (i.e., relatively large values for [K^RL] and [K^LR] in Eq. 2), falling roughly along the line of equivalence. If we follow a bilateral coupling hypothesis of coordination, we would expect that this relationship would remain unchanged under asymmetric gains. Conversely, a task-dependent model of bilateral coordination predicts negligible covariation in spatial deviations of the two hands for asymmetric gain conditions, reflecting a more independent mode of control (i.e., very small values of [K^RL] and [K^LR] in Eq. 2) and hence, an adjustment of coordination to the changing task demands. Figure 5A shows predictions consistent with a task-dependent hypothesis that bilateral coordination will be adjusted in response to changing task demands. In the LH High condition (left panel), spatial variance would be tightly constrained in the left hand, but vary more freely in the right hand, with a 0° (horizontal) regression slope angle indicating no covariation between deviations of the two hands. Under the Equal gain conditions (middle panel), spatial deviations of the two hands would be expected to covary strongly, with negative covariation along the line of equivalence (i.e., slope angle of −45°). Finally, for the RH High condition (right panel), variance would be expected to be tightly constrained in the right hand, but allowed to vary more freely in the left hand, with no covariation and hence a regression slope angle of −90° (vertical). Thus, under a task-dependent hypothesis, we would predict that the mode of bimanual coordination will be responsive to changes in task conditions in the sense that an independent mode of bilateral control may emerge under perpendicular gain asymmetries where spatial covariance between the two hands no longer offers significant benefit to task performance.

To examine how bilateral coordination was negotiated under these different task conditions for the empirical data collected, we plotted left- and right-hand perpendicular deviations measured at peak velocity (Fig. 5B) and end position (Fig. 5C) for all participants in the three different gain conditions (LH High—left panel; Equal—center panel; RH High—right panel). These plots include all trials from all participants and are fitted with orthogonal regression lines and 95% confidence limit ellipses to compare with theoretical examples shown in Fig. 5A. As we expected, this group level analysis demonstrates that equal gain conditions evoked a highly codependent mode of bilateral coordination with regression slopes aligning closely to the line of equivalence. Inspection of the plots for asymmetric conditions, however, show a clear change in the group level regression slope. These changes begin to emerge early in the movement at peak velocity (Fig. 5B), but they are most striking when measured later in the movement at end position (Fig. 5C).

These changes in regression slope angle are consistent with a shift toward the more independent mode of bilateral control in the asymmetric gain conditions, similar to the theoretical examples shown for the LH High and RH High conditions in Fig. 5A. However, it is important to note that even at movement end where this effect is strongest, there is still some residual covariation between hands (the regression lines approach, but do not completely align with, the vertical and horizontal axes as in Fig. 5A). Hence, although we observed adjustments of bilateral coordination to changing task demands for this group level analysis, the shift along the theoretical spectrum of bilateral coordination from codependent to independent control was incomplete. That is, both modes of control contributed to performance under asymmetric gain conditions, which could theoretically be described as positive gains on all partitions of the K-matrix in Eq. 2.

To further explore these initial group-level observations, we fitted each individual participants data with an orthogonal regression model, then calculated its slope angle (in degrees), which are presented as group boxplots for measurements recorded at peak velocity (left) and end position (right) in Fig. 6. Here, values of 0°, −45°, and −90° correspond to regression lines, which are parallel with the x-axis, line of equivalence, and y-axis, respectively (see Fig. 5A for reference). A linear mixed-effects model revealed no effect of gain condition on the slope angle measured at peak velocity (−10.19°, [−22.85°, 2.48°], P = 0.150). However, there was a significant effect of gain condition on slope angle measured at end position (−33.99°, [−54.83°, −13.15°], P = 0.011), as reflected by the progressive increase in slope angle negativity, from left-hand high gain, to equal gain, to right-hand high gain conditions in Fig. 6 (right). Furthermore, as we modeled gain condition as a continuous fixed effect (coded proportionally to increasing gain contribution of the right hand, see Statistical Hypothesis Testing for details), this effect corresponded to a −15.30° [−24.68°, −5.92°] change in individually fitted slope angle between gain conditions, as gain contribution of the right hand increases. Although significant, it is worth noting that this step-wise change is less than the average difference in slope angle measured at end position for all group data combined (30.35° between asymmetric and equal gain conditions; Fig. 5C). Moreover, although the asymmetric gains modulated the end position regression slope angle, both conditions were considerably below the 0° (LH High; Fig. 5A, left) and −90° (RH High, Fig. 5A, right) angles, which would indicate a complete shift to independent bilateral control. That is, there was some residual covariation between hands for asymmetric gain conditions, which is consistent with the combined participant plots shown for end position measures in Fig. 5C.

Figure 6.

Boxplots and individual participant values of covariance regression slope angle measured at peak velocity (left) and end position (right) in Experiment 1. Corresponding raw slope values for 0°, −45°, and −90° slopes are shown on the right y-axis. A linear mixed-effects model indicated a significant effect of gain condition on slope angle at end position (P = 0.011), corresponding to a −15.30° [−24.68°,−5.92°] change between gain conditions, as right-hand gain contribution increases.

Between-hand comparisons of perpendicular deviations.

Although the covariation analysis shows that there is change in the relationship of spatial deviations between the high- and low-gain hand, we were also interested to see if there were differences between hands when exposed to the same gain conditions. That is, whether perpendicular deviations differ between hands when under low-gain, equal gain, or high-gain conditions. To examine this, we took the mean absolute perpendicular deviations at end position for the left and right hands and then compared by hand gain condition in a repeated-measures ANOVA with a 2 (hand: left or right) × 3 (hand gain condition: low, equal, and high) design. The ANOVA revealed a significant effect of hand gain condition on absolute end position deviations [F(2,18) = 9.876, P = 0.001, η_p² = 0.52] where deviations made under high-gain conditions were lower than both equal gain [t(18) = 2.98, P_adj = 0.024, d = 0.83] and low-gain [t(18) = 4.35, P_adj = 0.001, d = 1.21] conditions (Supplemental Fig. S1). However, neither the main effect of hand nor the hand × hand gain condition interaction was significant (both P > 0.251). Taken together, this suggests that the reduction of deviations in the high-gain hand may have been driving the change in covariation between hands during gain asymmetries, but that both the left and right hands modulated deviations similarly when exposed to the same gain conditions.

Timescale of adjustment to asymmetric gains.

Given the notable changes in bimanual coordination we observed in response to asymmetric perpendicular gain conditions, we next asked the question over what timescale this adjustment occurred throughout the block of trials. To examine this, we performed orthogonal regression analyses of the group data separately for 10 trial intervals across the 50 trial asymmetric gain blocks. The result of this analysis can be seen in Fig. 7 (peak velocity and end position measures shown in panels A and B, respectively), where the grayscale data points, regression lines, and 95% confidence ellipses indicate the separate 10 trial intervals of data throughout the block and the colored dashed lines represent the regression of all block data combined (i.e., the same regression lines shown for corresponding conditions in Fig. 5). Corresponding slope angles and 95% confidence intervals of these fitted orthogonal regression models are shown in Table 1. From inspection of Fig. 7, it can be seen that the covariance relationship rapidly adjusts to the new task conditions within the first 10 trials (black data), as evidenced by the regression lines for these data aligning near the dashed colored regression lines that were fitted to all block data combined. Similar to the group data shown in Fig. 5, this effect seems to be most striking for the end position measures (Fig. 7B), though peak velocity data (Fig. 7A) still shows convergence toward the whole block regression line within the first 10 trials. The regression lines of the remaining sets of 10 trial interval data also appear to be reasonably close to that which was fitted to the whole block data (though again with more consistency in the end position measures), suggesting a rapid but relatively stable adjustment in coordination of bilateral arm movements in response to asymmetric perpendicular gain conditions. It is interesting to note, however, that the regression for the final 10 trials of the block (lightest gray) for end position data appears to deviate toward the x- and y-axis in the LH High and RH High conditions, respectively. This suggests there may also be a slower process occurring in which a more complete adjustment to the ideal independent mode of control for these conditions (i.e., similar to the hypothesized covariance relationships shown in Fig. 5A) could be achieved with extended practice. Further research is warranted to examine this phenomenon in more detail.

Figure 7.

Covariance relationships (orthogonal regression lines and 95% confidence ellipses) of left- and right-hand perpendicular deviations grouped into intervals of 10 trials (grayscale key inset in lower left) for measures recorded at peak velocity (A) and end position (B) in Experiment 1. Data for the LH High and RH High conditions are shown in the left and right columns, respectively, with colored dashed lines representing orthogonal regression fitted to all data combined (i.e., identical to those for corresponding conditions shown in Fig. 5).

Table 1.

Orthogonal regression slope angles for incremental groups of 10 trials in Experiment 1

Trials	Slope Angle at Peak Velocity [95% CIs]		Slope Angle at End Position [95% CIs]
	LH High	RH High	LH High	RH High
1–10	−36.0° [−47.2°, −24.9°]	−52.6° [−62.1°, −43.1°]	−13.5° [−20.3°, −6.6°]	−70.5° [−81.5°, −59.4°]
11–20	−24.7° [−39.5°, −10.0°]	−61.8° [−69.2°, −54.5°]	−12.1° [−18.0°, −6.2°]	−68.8° [−79.2°, −58.3°]
21–30	−34.0° [−45.5°, −22.6°]	−59.9° [−69.6°, −50.2°]	−14.5° [−23.5°, −5.6°]	−70.6° [−81.0°, −60.2°]
31–40	−28.1° [−35.1°, −21.1°]	−57.7° [−67.0°, −48.3°]	−10.9° [−16.1°, −5.7°]	−71.3° [−78.0°, −64.7°]
41–50	−24.9° [−36.1°, −13.6°]	−61.6° [−70.8°, −52.4°]	−6.3° [−12.2°, −0.4°]	−77.3° [−84.6°, −70.1°]

Slope angles and 95% confidence intervals (square brackets) of orthogonal regression models fitted to left- and right-hand perpendicular deviations shown in Fig. 7, where all participant data were grouped into 10 trial intervals across the 50 trials blocks for the LH High and RH High conditions.

Repeat exposure to equal (2:2) gain.

Given that the asymmetric gain conditions were interleaved with blocks of equal (2:2 ratio) gain trials, we also examined whether there were any learned improvements or changes in covariance over the repeated exposure to these conditions. Accordingly, we fitted left- and right-hand deviations of all trials from all participants combined with separate orthogonal regression models for each of the equal gain conditions (2:2a, 2:2b, and 2:2c) for measurements made at peak velocity and end position (Supplemental Fig. S2). Although there appeared to be some small variations in the regression slope angle between conditions for peak velocity (Supplemental Fig. S2A; 2:2a: −50.4° [−53.0°, −47.7°]; 2:2b: −40.0°, [−43.6°, −36.3°]; 2:2c: −46.3°, [−49.2°, −43.5°]), the changes do not progress in a systematic manner from 2:2a to 2:2c that might indicate systematic changes associated with repeated practice. Moreover, there is very little difference between the regression slope angles of the different conditions for the end position measurements (Supplemental Fig. S2-B; 2:2a: −45.8°, [−47.9°, −43.6°]; 2:2b: −44.3°, [−47.3°, −41.2°]; 2:2c: −47.5°, [−50.2°, −44.8°]), which collectively suggest there were no notable or learned changes in the left- and right-hand covariance relationship with repeated performance of 2:2 gain conditions.

Specificity of bimanual covariation to different spatial axes of movement.

The data presented so far demonstrate a rapid modulation in bilateral coordination of shared cursor lateral displacements (i.e., x-axis, perpendicular to reach direction) in response to visual feedback gain modulations along the same axis. However, it is unclear whether these effects are specific to this reach axis or are also evident parallel to the reach direction (i.e., along the y-axis), where gains remained symmetric at a ratio of 1:1 between hands throughout the task. To examine this, we performed additional orthogonal regression analyses on the end-position parallel axis deviations (i.e., relative to the 20 cm target distance in the y-axis) for each of the perpendicular gain conditions in Experiment 1 (Fig. 8).

Figure 8.

Covariance relationships (orthogonal regression and 95% confidence ellipses) of left- and right-hand parallel deviations (y-axis) at end position for LH High (left, light pink), Equal (middle, black), and RH High (right, light blue) gain conditions in Experiment 1. Positive deviation values represent an overshoot of the y-axis target location (20 cm along y-axis from start position) and negative values represent undershoot. Pearson’s correlation coefficient denoted in each panel next to regression lines (n.s. = nonsignificant).

Interestingly, none of the left- and right-hand relationships for parallel deviations presented in Fig. 8 demonstrate the strong, negative covariation—and hence codependent control—we might have expected given the results from perpendicular deviation analysis of the analogous equal gain condition shown in Fig. 5. Both the Equal (Fig. 8, middle; slope angle = −84.1° [−99.3°, −69.0°], Pearson’s r = −0.03, P = 0.428) and RH High (Fig. 8, right; slope angle = −80.0° [−91.8°, −68.3°], Pearson’s r = −0.08, P = 0.093) conditions show similar regression angles and nonsignificant correlations. The LH High condition shows a modest correlation between the corrective responses of the two hands along the direction of motion, but the slope of this relationship was only slightly biased toward the line of equivalence at −45° (Fig. 8, left; slope = −62.9° [−73.6°, −52.2°]; Pearson’s r = −0.19, P < 0.001). In all conditions, the control of movement extent appears to be more tightly constrained in the right hand (with slopes steeper than −45°), though visual inspection of the plots suggests largely similar variation is permitted for both hands. Taken together, these findings show that the relationship between left- and right-hand y-axis cursor deviations remained relatively unchanged across the different perpendicular (x-axis) gain conditions, contrasting considerably from the task-specific modulations of coordination along the perpendicular axis shown in Fig. 5C. That is, the rapid reorganization of bimanual coordination observed here exhibited remarkable specificity to those degrees of freedom subject to experimental manipulation in an extrinsic frame of reference.

Experiment 2

The results from Experiment 1 demonstrated that coordination of bilateral movements was remarkably sensitive and specific to subtle and implicit changes in task demands. However, with only one asymmetric perpendicular gain ratio, it is unclear whether the extent of this task-dependent flexibility is graded to the gain asymmetry or if it represents a systematic, fixed magnitude response to gain asymmetries per se. To investigate further, we conducted a second experiment that included two asymmetric perpendicular gain conditions of 0:4 (LH/RH High) and 1:3 (LH/RH Intermediate) gain ratios. If the task-dependent change in bilateral coordination is graded with respect to gain asymmetries, we should observe a change in regression slope angle for the Intermediate (1:3) condition that lies somewhere between the Equal (2:2a) and High (0:4) conditions.

Bimanual spatial covariance.

The left- and right-hand perpendicular deviations at peak velocity and end position are shown in Fig. 9, A and B, respectively. All trials from all participants are included on the same axes and fitted with separate orthogonal regression models and 95% confidence ellipses for each gain condition. Details of calculated slope angles and their 95% confidence intervals for each gain condition are also shown in Table 2. Consistent with Experiment 1, this group-level analysis shows a clear shift toward more independent bilateral control in response to the asymmetric perpendicular gains of the LH High (light pink, filled diamonds) and RH High (light blue, filled squares) conditions while still retaining some residual covariation. Thus, a small contribution of codependent control persisted despite its negligible benefit to task performance. Interestingly, these observations appear to be roughly equal in magnitude between peak velocity (Fig. 9A) and end position (Fig. 9B) measurements, which contrasts from Experiment 1 where these effects were less pronounced at peak velocity (Fig. 5). Most importantly, however, there was a graded effect of the intermediate asymmetric gain conditions on bilateral coordination—the change in regression slope angle for the LH Intermediate (dark pink, open diamonds) and RH Intermediate (dark blue, open squares) conditions lies between the Equal (2:2a) condition and the more extreme angles of the high asymmetric gain conditions. We found a stronger contribution of codependent control for the intermediate than high gain asymmetries, consistent with this mode of control offering a small benefit to task performance under those conditions. With reference to the conceptual model outlined in Fig. 2, we can describe this as a vigilance of the adaptive task controller to the imposed changes in visual feedback gains (C); an updated transformation of cursor to hand position errors (C⁻¹) appears to be computed to make appropriate changes to the off-diagonal components of the feedback controller K that alters the relative weights of codependent (i.e., [K^LR] and [K^RL]) influences on subsequently generated motor commands impacting cursor motion. In other words, the apparent weighting of codependent bilateral control contributions was graded to the magnitude and direction of visual feedback gain asymmetry between hands. To confirm the rapid nature in which these adjustments in bimanual coordination are made, we also performed a spatial covariance analysis of the data segregated into 10 trial intervals for high and intermediate gain asymmetry blocks in a similar manner to the data presented in Fig. 7. Although we do not present the data here, we found similarly rapid adjustments (i.e., within the first 10 trials) of the bilateral covariance relationships in response to the changing visual feedback conditions.

Figure 9.

Covariance relationships (orthogonal regression and 95% confidence ellipses) for different gain asymmetry conditions in Experiment 2 (see Fig. 1D for details of task design). The data are presented as all trials from all participants combined on the same axes for measurements made at peak velocity (A) and end position (B), with the annotations of the associated regression slope angles in degrees. Boxplots of slope angles obtained from orthogonal regression models fitted to individual participant data are shown for measurements at peak velocity (C) and end position (D). Raw slope values corresponding to slope angle in degrees are shown in gray near the right axis, as in Fig. 6. A linear mixed-effects model revealed a significant effect of gain condition on slope angle at end position (P = 0.024), corresponding to an estimated −5.59° [−9.72°,−1.46°] change in slope angle between gain conditions, as contribution of the right hand increases.

Table 2.

Orthogonal regression slope angles for different gain asymmetry conditions in Experiment 2

Gain Condition	Slope Angle at Peak Velocity [95% CIs]	Slope Angle at End Position [95% CIs]
LH High (4:0)	−21.1° [−26.0°, −16.3°]	−15.3° [−18.9°, −11.8°]
LH Int. (3:1)	−36.9° [−39.8°, −33.9°]	−33.2° [−36.4°, −30.0°]
Equal (2:2a)	−49.0° [−50.8°, −47.4°]	−47.7° [−49.1°, −46.2°]
RH Int. (1:3)	−66.0° [−68.3°, −63.8°]	−66.3° [−68.5°, −64.7°]
RH High (0:4)	−75.6° [−78.3°, −72.9°]	−82.0° [−84.3°, −79.6°]

Slope angles and 95% confidence intervals (square brackets) of orthogonal regression models fitted to left- and right-hand perpendicular deviations of all group data combined for different gain conditions in Experiment 2, as shown in Fig. 9A (peak velocity) and B (end position).

As with Experiment 1, we followed up these initial group-level observations with individual participant-level analyses, where each participant’s data were fitted with orthogonal regression models for each of the five different gain conditions. The regression slope angles (in degrees) were then compared between gain conditions using a linear mixed-effects model with gain condition modeled as a continuous fixed factor, where a value between 0 and 1 was assigned to each condition to reflect the proportional contribution of the right hand to lateral deviations of the shared cursor [e.g., RH Intermediate (1:3) = 0.75]. Group boxplots of the slope angles from measurements recorded at peak velocity and end position can be seen in Fig. 9, C and D, respectively. There was no effect of gain condition on slope angle at peak velocity (13.26° [−34.29°, 7.77°], P = 0.245). However, there was a significant effect of gain condition on slope angle measured at end position (−22.37° [−38.90°, −5.86°], P = 0.024), which corresponded to an estimated change of −5.59° [−9.72°, −1.46°] in slope angle between separate gain conditions, as right hand gain contribution increased. As with Experiment 1, it is worth highlighting that this estimated change in individually fitted slope angle between gain conditions is still less than the average difference between slopes fitted at the group level (16.68°; Fig. 9B). However, the finding that asymmetric perpendicular gains significantly modulate individually fitted regression slope angles measured at end position was consistent across both experiments.

Collectively, we suggest this provides evidence for a system of bimanual coordination and control that is highly vigilant to incoming afferent feedback, seeming to adjust coordination along a spectrum between extremes of codependent and independent bilateral control in a task-dependent manner.

DISCUSSION

Summary

Previously, it has been shown that coordination of bilateral arm movements can adjust to task demands by switching between modes of control that either constrain the hands to move together or allow them to move independently of each other. Here, we explored the idea that these two modes of bimanual control might represent two extremes on a spectrum of possible combinations of codependent and independent coordination, whose relative weights are determined based on task conditions. We describe this conceptually using a simplified model (Fig. 2) that includes a task controller C^− 1K that integrates an inverse hand-to-screen map C⁻¹ and a feedback control matrix K (Eq. 2), containing adjustable components that control weighting of bilaterally codependent (e.g., [K^RL] and [K^LR]) and bilaterally independent (e.g., [K^LL] and [K^RR]) corrective limb responses to shared cursor errors. This study was designed to examine the fluency with which the nervous system might negotiate patterns of coordination along this spectrum when task demands are designed such that varying levels of contribution between codependent and independent control can achieve accurate task performance. To examine this, we used a bilateral shared transport task that included sets of trials where either arm’s contribution to the horizontal (medial-lateral axis, perpendicular to target direction) position of the shared cursor was altered asymmetrically. Specifically, we increased one hand’s contribution to the cursor’s lateral displacements and made the other hand’s contribution negligible while each hand’s contribution to movement along the target direction axis remained equal (1:1). By measuring changes in the perpendicular spatial covariation between hands, we showed that coordination was remarkably flexible in response to the asymmetric gain conditions. That is, there were notable changes from the strong codependent control observed for equal gain conditions to more independent spatial coordination that was consistent with the direction of gain asymmetry between hands. However, even when unnecessary for accurate task performance, small residual covariation between hands persisted. Furthermore, variations in bimanual coordination were largely specific to the structure of the experimentally imposed hand-to-screen cursor projection C, in that we observed minimal effects of perpendicular gain manipulations on the covariation of left- and right-hand motion along the direction of movement. In a second experiment, we then extended these findings by showing that the extent of bimanual spatial covariation was graded with respect to the magnitude and direction of perpendicular gain asymmetry between the hands when data were fitted at the group level. Taken together, our findings indicate that the nervous system is able to resolve task-dependent requirements for codependent and independent control when coordinating bilateral arm movements. Importantly, task-dependent coordination changes appear to occur rapidly (i.e., within 10 trials) and do not require explicit awareness of changes in task conditions, indicating high vigilance to incoming afferent feedback that signals changes in task demands. Yet conversely, this form of task-dependent feedback control also appears to be limited, as some covariation between arms persisted even after it no longer offered any benefit to performance.

Evidence against the Hypothesis of Bilateral Coupling

Early studies of bimanual coordination that emphasized a tight spatiotemporal symmetry and synchrony between arms led some researchers to conclude that movements of the two arms were controlled by a single, shared motor command that activated or “coupled” functional groups of homologous muscles (2, 27). This hypothesis predicts that coupling should be robust to changes in peripheral sensory feedback conditions, such as those imposed in our experiment. In this study, we modified peripheral feedback conditions by asymmetrically altering the gain contribution of either hand to the shared cursor’s position along the medial-lateral axis (perpendicular to reach direction). Under these altered feedback conditions, it was possible to maintain task success without making changes to the required mirror symmetric movements and associated bilateral activation of homologous muscle groups. Hence, the coupling hypothesis predicts that high spatial symmetry between arms should be maintained across all visual feedback conditions. However, while we do report strong covariation of perpendicular spatial deviations between the left and right hand under equal gain conditions, there was notably weaker spatial covariation between deviations of the two arms during asymmetric visual feedback gains. This calls into question the coupling hypothesis of bilateral coordination in which homologous pairs of muscles between the two arms are controlled by an integrated motor command. The fact that we also observed persistent covariation between the two arms when it no longer offered any benefit for task performance suggests there may be some obligatory or involuntary constraint imposed on the two arms to move with some degree of spatial symmetry during these type of mirror symmetric movements. However, because of the contrast in covariation and thus asymmetry between the arms under unequal feedback conditions in our experiment, such covariation cannot be attributed to bilaterally coupled motor command symmetrically activating homologous muscles as a single unit.

Bimanual Coordination Characterized as Interactions between Different Movement Costs

More recently, it has been suggested that some observations attributed to coupling may actually represent higher levels of task planning (36–39) (for extended discussion see Ref. 40). For example, direct spatial cues and perception of spatial movement symmetry have been shown to be powerful determinants of bilateral interference in both discrete and continuous movement tasks (37–39) and other forms of task-dependent visual feedback impose strong influences on coordination of bilateral arm movements too (11, 12, 19–22, 41). These observations and others have been attributed to hypothetical motor control policies, which might minimize costs associated with task errors, as well as neurocomputational, mechanical, or metabolic energetics (23, 24, 42, 43). This has also been described as a control system that only imposes constraints on elements of performance that directly impact task outcome while allowing those elements of performance that are redundant for task outcome to vary freely without constraint (24–26). Minimization of motor costs has been conceptualized for bilateral shared transport tasks through observations that one hand can effectively compensate for errors made by the other, reducing the net motor effort across the two hands (11, 15, 23). This hypothesis should predict a complete loss of covariation between hands under extreme gain asymmetries, as continuing to covary would lead to wasted motor costs of the low-gain hand given it can no longer compensate for errors made by the high-gain hand. However, the small but persistent covariation we observed between hands under extreme gain asymmetries seems to contradict this. The finding that shared cursor errors was systematically higher in the asymmetric than equal gain conditions (see Fig. 4) also suggests there may be some limits in the minimization of task error as a cost for bimanual control. Violations of this type of optimality in motor behavior have been reported previously in experiments where the task conditions change frequently and hence there is uncertainty about what is required for the upcoming movement (44, 45). Although this “switching” cost seems to be most prevalent when task structure randomly changes from trial to trial, it is possible that the relatively frequent changes in visual feedback gain conditions used here (every 40–50 trials) led to a switching cost in selecting an optimized mode of bimanual coordination that was best adapted to current task conditions. That is, participants may not have adopted a fully independent mode of control under asymmetric gains if there is uncertainty about whether the next movement may require a subsequent switch back to codependent bimanual coordination, possibly at the expense of slightly increased task error. Accordingly, we might expect that with extended periods of practice under asymmetric gains, and hence more consistency in task conditions, the small persistent covariation we observed would be eradicated, but further research is required to test this prediction. In any case, we suggest these findings reflect an interplay of performance costs that are resolved according to specific task conditions, the result of which determines the relative contributions of independent and codependent bimanual control along a spectrum of possible coordination modes. Based on this, future models of coordination should consider task-specific trade-offs between the various costs associated with movement, such as performance errors, mechanical and/or metabolic costs, and neurocomputational costs of changing motor commands (42, 43).

Limitations

A key aspect of this discussion addresses the observed increase in shared cursor errors for asymmetric gain conditions and its relation to a performance cost of task error. The increase in shared cursor errors may be due to a number of possible factors, including the residual spatial covariation between hands or a result of the increase in visual feedback gain for one of the hands. However, it is also important to note that it may also be due in part to the methodological decision to award participants maximum points for all trials in an effort to minimize awareness of sudden changes in performance due to the introduction of asymmetric gains. This may have consequently reduced the salience of the task error signal to drive the minimization of its control cost during performance. Nevertheless, participants averaged less than 1 cm increase in shared cursor error for asymmetric versus equal gain conditions, and these errors remained relatively consistent across blocks of trials. Taken together, this suggests that participants remained engaged in the maintenance of task performance throughout the experiment.

We also note that although we found significant effects of gain condition on individually fitted slope angles in Experiments 1 and 2, the overall differences in slope angle between conditions for the individually fitted data were notably smaller than for the group fitted data. Of course, with fewer data points to fit regression models to, it may not be surprising to see more varied slope angles for individual participant fits. Furthermore, given that the relatively subtle visual perturbation we imposed seemed to drive reduction in variability of the high gain hand without a significant increase in variability of the low gain hand (Supplemental Fig. S1), it is possible that limited range of deviations across the axes may have also placed limits on the reliability of the individual participant fits. As a result, we suggest that for this type of visual perturbation, the group analysis may be more reliable. Nevertheless, we acknowledge that further research is warranted, possibly with increased trials per condition and less frequent changes between them [i.e., to minimize potential switching costs that could violate expected “optimal” performance (44, 45)] to explore the strength of the effects we observe at the group level in this study are robust for within-subject measurements.

Clinical Relevance

In addition to examining bilateral coordination in neurotypical individuals, studies in populations with neurological damage could help with identifying potential neural substrates underlying some of the different performance costs involved in bimanual coordination discussed here. For example, patients with Parkinson’s disease have been reported as less willing to exert physical effort than healthy controls (46, 47), which can subsequently impact loss aversion behavior (48). Studying patients with basal ganglia pathologies could therefore reveal the role of this region in mediating trade-offs between costs of motor effort and task error on bimanual coordination. The ability to use codependent control to stabilize bimanual task performance may also be dependent on lateralized brain regions, as stroke patients with left-hemisphere damage exhibit weaker codependent control during shared virtual object transport, with an inability to exploit the task-redundant space to minimize task errors (49). Moreover, proprioceptive deafferentation has been shown to disrupt bimanual coordination during shared transport of virtual objects, as evidenced by larger distance and orientation errors and a reduction in codependent control (50). Given that unimanual reaching control and adaptation in deafferented individuals is relatively intact when relying solely on visual feedback (51–55), this highlights a specific role of proprioceptive feedback in the coordination of bilateral arm movements.

Bimanual tasks have also been suggested as a possible approach for rehabilitation from upper limb motor impairments associated with neurological injuries such as stroke (15, 56, 57). Specifically, leveraging the codependent nature of cooperative transport tasks may provide a promising method of promoting recovery (15), particularly with the use of sensory feedback asymmetries that could gradually adjust the involvement of the paretic limb with recovery. Although this remains to be examined in detail, this notion is supported by evidence that chronic stroke survivors may retain the ability to modulate movement variability of both limbs in a task-dependent fashion when reaching to control a shared cursor with asymmetric visual feedback gains, similar to those used here (58). Furthermore, when applying loads to either limb during bilateral reaches in three-dimensional virtual reality, neurotypical participants have been shown to generate proportional changes in coordination of muscle activation and spatial deviations (43). Although this has not yet been tested in a stroke population specifically, Brunfeldt et al. (43) suggested that variations of this task could act as an alternative intervention to constraint-induced movement therapy, which could be used at home and scaled progressively with recovery. The current work characterizing the flexible weighting of contributions from codependent and independent bilateral control for task performance together with previous research suggests promise for applications to rehabilitation. However, the efficacy of these paradigms for the promotion of recovery after stroke clearly requires further examination.

Conclusion

In conclusion, we demonstrated that coordination of bilateral arm movements can be characterized along a spectrum of possible combinations between two extremes of predominantly codependent and independent bilateral control. We describe this through a simple conceptual model in which an adaptive feedback controller can adjust the gains on neural commands that determine both codependent and independent control of the left and right arms. We found that this feedback controller can rapidly adjust the weights of independent and codependent control to overall performance as task conditions change, with high sensitivity to the nature of the visual task feedback manipulations. Furthermore, this covariation was modulated along only those degrees of freedom subject to experimental manipulation, suggesting a robust representation of movement-to-task mapping in our conceptual model. Yet, we also show that the combined output of coordination included contributions of codependent control even when it offered no substantial contribution to task performance. Importantly, these findings provide evidence against a bilateral coupling hypothesis that would predict no change to the tight spatial symmetry between arms when peripheral feedback conditions are manipulated. Furthermore, we suggest this seeming contradiction between “high sensitivity” but “limited extent” in the influence of task-dependent feedback control may result from a complex trade-off between different performance costs. This results in an interactive process of minimizing superfluous motor effort with costs of adjusting motor commands when they have negligible influence on task error and/or when there is uncertainty about the consistency of upcoming task conditions. Further research is warranted to explore this interpretation.

DATA AVAILABILITY

The supplementary material and data used to present the findings of this study are openly available on an Open Science Framework (OSF) repository at https://doi.org/10.17605/OSF.IO/9EM43.

SUPPLEMENTAL DATA

Supplemental Figs. S1 and S2: https://doi.org/10.17605/OSF.IO/9EM43.

GRANTS

This work was supported by NIH Grant R01HD059783 and Dorothy Foehr Huck and J. Lloyd Huck Distinguished Chair Endowment awarded to R. L. Sainburg. R. A. Scheidt's contributions were supported by NIH grants R15HD093086 and R21NS121624.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.P. and R.L.S. conceived and designed research; A.P. performed experiments; N.M.K., A.P., and R.L.S. analyzed data; N.M.K., J.Y., A.P., R.A.S., and R.L.S. interpreted results of experiments; N.M.K. prepared figures; N.M.K. drafted manuscript; N.M.K., J.Y., A.P., R.A.S., and R.L.S. edited and revised manuscript; N.M.K., J.Y., A.P., R.A.S., and R.L.S. approved final version of manuscript.