Abstract.
Significance
Among the available polarimetric techniques, backscattering Mueller matrix (MM) polarimetry provides a promising non-contact and quantitative tool for in vivo tissue detection and clinical diagnosis. To eliminate the surface reflection from the sample cost-effectively, the non-collinear backscattering MM imaging setup always has an oblique incidence. Meanwhile, for practical organ cavities imaged using polarimetric gastrointestinal endoscopy, the uneven tissue surfaces can induce various relative oblique incidences inevitably, which can affect the polarimetry in a complicated manner and needs to be considered for detailed study.
Aim
The purpose of this study is to systematically analyze the influence of oblique incidence on backscattering tissue polarimetry.
Approach
We measured the MMs of experimental phantom and ex vivo tissues with different incident angles and adopted a Monte Carlo simulation program based on cylindrical scattering model for further verification and analysis. Meanwhile, the results were quantitatively evaluated using the Fourier transform, basic statistics, and frequency distribution histograms.
Results
Oblique incidence can induce different changes on non-periodic, two-periodic, and four-periodic MM elements, leading to false-positive and false-negative polarization information for tissue polarimetry. Moreover, a prominent oblique incidence can bring more dramatic signal variations, such as phase retardance and element transposition.
Conclusions
The findings presented in this study give some crucial criterions of appropriate incident angle selections for in vivo polarimetric endoscopy and other applications and can also be valuable references for studying how to minimize the influence further.
Keywords: polarimetry, Mueller matrix, scattering imaging, endoscopy, Monte Carlo simulation
1. Introduction
Polarimetry is attracting increasing attention nowadays, due to its unique ability to obtain microstructural and optical information of tissue samples label-free.1–4 Among the available polarimetric techniques, Mueller matrix (MM) imaging can comprehensively characterize the polarization-related properties of media, including diattenuation, retardance, and depolarization, which are of great importance in biomedical studies and clinical trials.5–7 Recently, transmission MM microscopy has shown potential in detection of various abnormal and pathological tissues, such as breast cancer,8 cervical cancer,9 colon cancer,10 skin cancer,11,12 liver cirrhosis,13,14 gastrointestinal cancer,15,16 thyroid cancer,17 and lung cancer.18 Meanwhile, the backscattering MM polarimetry provides a promising non-contact and quantitative tool for ex-vivo measurement of bulk tissue samples,6,7,19–22 in-vivo imaging of skin tissue,23–26 and endoscopic detection of internal organs.27–31
Specifically, for the measurement of bulk tissue specimens, a backscattering MM polarimetry setup whose polarization state generator (PSG) and polarization state analyzer (PSA) are located at the same side of the sample is necessary. Currently, there are two backscattering polarimetry schemes, namely the collinear reflection mode with normal incidence32 and the non-collinear reflection one with obliquely incident illumination.5,19–26,33 For MM imaging, ideal collinear reflection equipment can provide accurate measurement results, avoiding the influence from the spatial orientation of the sample. However, in practice, the collinear reflection mode brings other side effects, including direct back-reflection signals from the sample and intrinsic residual polarization effect induced from the polarization components, which require more efforts and cost to deal with.34 In contrast, the non-collinear reflection MM equipment has the ability to eliminate the surface reflection from the sample cost-effectively using an oblique incidence. Thus, it has been increasingly used in biomedical studies and applications.5 On the other hand, for practical organ cavities imaged using polarimetric gastrointestinal endoscopy, the uneven tissue surfaces can induce various relative oblique incidences inevitably, which needs to be considered for detailed study.
Some recent studies have noted that the obliquely incident illumination can affect the MM measurement in a complicated manner,35,36 which hinders the effectiveness for distinguishing different sources of anisotropies. For instance, a Monte Carlo simulation based on the sphere–cylinder scattering model showed that the residue rotation dependence of MM increases with the oblique incidence angle.37 Thus, for real applications, a systematic analysis of the influence of oblique incidence on backscattering MM polarimetry is needed.
In this study, we measure the MMs of an anisotropic tissue phantom, a porcine liver tissue, and a human gastric muscularis tissue sample under different obliquely incident illuminations. The ex vivo experimental results demonstrate that oblique incidence of backscattering polarimetry can induce different changes on non-periodic, two-periodic, and four-periodic MM elements, which are comprehensively evaluated using the Fourier transform, basic statistics, and frequency distribution histograms (FDHs). Moreover, we adopt a Monte Carlo simulation program based on cylindrical scattering model for further analysis. Both the experiments and simulations confirm that a prominent oblique incidence can bring more dramatic signal variations, such as phase retardance and element transposition to MM. The findings presented in this study give some crucial confidence boundaries of appropriate incident angle selections for MM imaging based on specific properties extraction. It also indicates that some important structural information of the tissue sample may be obtained through the symmetry breaking and period degeneracy of MM elements, as the incident angle modulated.
2. Methods and Materials
2.1. Sample and Experimental Setup
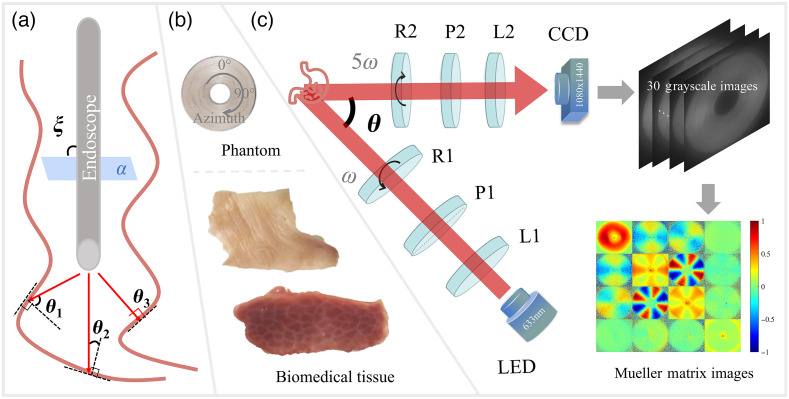
For practical in vivo tissue polarimetry, such as polarization gastrointestinal endoscopy, even though it is at a normal incidence with the incident plane shown in Fig. 1(a), a variety of relatively oblique incident angles exist according to the uneven tissue interfaces at different locations. For instance, , , and are prominent oblique incidence, moderate oblique incidence, and normal incidence, respectively. Such a kind of oblique incidence induced by tissue sample’s surface is inevitably and brings influence on polarization measurement quantitatively.
Fig. 1.
Schematics of setups and samples: (a) oblique incidence induced by tissue surface in gastrointestinal endoscopy; (b) concentrically aligned silk phantom, porcine liver, and human gastric muscularis tissues; and (c) backscattering DRR experimental setup and flowchart of MM imaging acquisition. L1 and L2, lenses; P1 and P2, polarizers; R1 and R2, rotating quarter-wave plates; , the oblique incident illumination angle. During each measurement, R1 and R2 rotate with constant rates ( for R1 and for R2).
To investigate its influence, as shown in Fig. 1(b), we designed an anisotropic phantom consisted of concentrically aligned silk fibers, adopted a porcine liver tissue sample and a human gastric muscularis tissue sample for ex vivo polarimetric imaging. The human gastric muscularis tissue was prepared and provided by Shenzhen Sixth People’s Hospital (Nanshan Hospital) Huazhong University of Science and Technology Union Shenzhen Hospital. This work was approved by the Ethics Committee of Tsinghua Shenzhen International Graduate School, Tsinghua University. In particular, the phantom generated the MMs of cylindrical scatterers along all directions in the imaging plane in single measurement,35,36,38 whereas the porcine liver tissue was used for distinctive observation of depolarization and retardance, and the human gastric muscularis sample was analyzed for diattenuation and total anisotropy.
The experimental setup used in this study is a typical backscattering MM polarimetric system based on a dual-rotating retarder (DRR) scheme.39,40 As shown in Fig. 1(c), the obliquely incident illumination light from an LED (3 W, 633 nm, , Daheng Optic, Beijing, China) passes through the PSG, which consists of an objective lens L1 (Hengyang Optic, Guangzhou, China) to produce parallel beam, a fixed polarizer P1, and a rotatable quarter-wave plate R1 to generate light with different polarization states. Then, the polarized light scattered by the sample transmits through the PSA, which consists of a rotatable quarter-wave plate R2, a fixed linear polarizer P2, and a lens L2 (Hengyang Optic, Guangzhou, China), correspondingly. Both the polarizers P1 and P2 (extinction ratio > 1000:1, Thorlabs, New Jersey, United States) are fixed in horizontal direction, and the rotatable quarter-wave plates R1 and R2 (Daheng Optic, Beijing, China) are controlled by the servo motor drivers (PRM1Z8, Thorlabs, New Jersey, United States) with a fixed angular rotating rate for 30 times ( for R1 and for R2). Then, the photons are received by the CMOS camera (MV-CA016-10UM, , 12-bit, Hikvision, China) to calculate the MM elements of the sample, and the single frame acquisition time is . Here, all the intensity matrix elements extracted from the 30 grayscale images are related to the as inputs. Considering the repetition of polarization states during each acquisition cycle, we rewrite the coefficient of angular rotating rate to , and the Fourier coefficients and can be calculated as41
| (1) |
Before measurement, the backscattering MM polarimetric setup was calibrated using air as the standard sample to make sure that the system error is within 1%. More details of the calibration procedure can be found in Ref. 42. Here, by varying the angle between the PSG and PSA arms, all the MMs of the sample are obtained as the raw data for further analysis of the relationship between oblique incident illuminations and the elements.
2.2. Analysis Methods
For quantitative analysis, a ring area with radius of 200 pixels of each MM element is taken by the interpolation method to calculate its averaged value and aims to construct the azimuthal dependent curves of the MM elements from 0 deg to 360 deg. Then, some basic statistics, such as the mean and kurtosis, are used to evaluate the influence of incidence on the azimuthal dependent curves of MM elements. In details, the mean reveals the variation in the distribution of the overall value for element pixels, whereas the kurtosis reveals how outlier-prone a distribution is. Specifically, a normal distribution has a kurtosis value of 3, and the peak with larger kurtosis preferentially represents the whole azimuthal dependent curves for multi-peaks. The statistics used in this study are given as and as follows:
| (2) |
| (3) |
where is the pixel value and is the number of interpolated pixels for azimuthal dependent curves.
Our previous studies have demonstrated that the azimuthal dependent curves of the MM elements can be fitted to some trigonometric functions with different periods.5,35 To quantitatively evaluate the variations of the curve’s intensity and period under oblique incidences, we extracted the curve’s peak and valley values marked as and . Then, we calculated the differences between adjacent peak–peak and peak–valley values marked as and values, respectively. Meanwhile, the distance between the twin peaks is recorded as the gap, which can reveal the period degeneracy of azimuthal dependent curve.
For the quantitative analysis of ex vivo tissues, we calculate the light intensity distributions for the sample to transform the 2D images into 1D FDHs. The horizontal shift of the FDH curves can reflect the overall variations (decrease or increase) of the MM elements’ values, whereas the shape can reflect the distribution changes of the MM elements, which can be used to evaluate the influence of oblique incidence.
Since the periodic signal can be treated as a sum of the baseline and a series of harmonics, here, we adopt the fast Fourier transform (FFT) method to analyze such periodic variation. After FFT, the amplitudes of each harmonic component are given as in Eq. (4), which can be calculated according to Eq. (5) related to Eq. (1)
| (4) |
| (5) |
where is the baseline called direct-current component as well, is the harmonic frequency of components. The proportion of different harmonic components reflects the periodic variations of the MM elements comprehensively. It should also be noted that taking the FFT for an asymmetric periodic square wave with amplitude , as , the amplitudes of each harmonic component can be calculated as
| (6) |
Thus, square wave signal has more odd harmonic components than even harmonic components, especially with a certain coefficient ratio for ideal results in Eq. (7). Then, based on three main harmonic components, we defined a coefficient to describe this square wave characteristic in Eq. (8), which can be used to verify the period degeneracy in Secs. 3.2–3.4 when is close to 0
| (7) |
| (8) |
2.3. Monte Carlo Simulation
For further study and verification, we also adopt a Monte Carlo simulation based on the cylinder scattering model, in which the concentrically aligned silks are simplified as infinitely long cylindrical scatterers along different directions. In the simulation, trajectories and polarization states of scattered photons are tracked synchronously as they propagate in the medium. Detailed settings of simulation parameters have been presented in our previous study.35
3. Results and Discussions
3.1. Azimuthal Dependent Curves of MM Elements Under Different Oblique Incidences
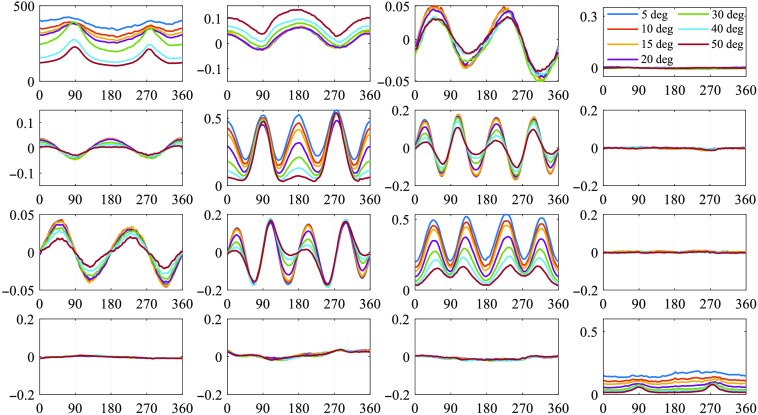
The azimuthal dependent curves of full MM elements under different oblique incidences between 5 deg and 50 deg are shown in Fig. 2. It can be observed that different oblique incidences bring specific changes on different elements, which can be divided into three categories: (1) the non-periodic diagonal elements M11 and M44, whose variations can be quantified using mean and kurtosis values; (2) the two-periodic off-diagonal elements M12, M21, M13, and M31, which are related to linear diattenuation and polarizance properties of the medium, representing symmetry breaking; and (3) the four-periodic central-block elements M22, M33, M23, and M32, which are related to linear depolarization and anisotropy of the medium, representing period degeneracy. Hence, in the following sections, we will discuss the detailed influence of oblique incidence on the three groups of MM elements.
Fig. 2.
Azimuthal dependent curves of MM elements under oblique incidences of 5 deg, 10 deg, 15 deg, 20 deg, 30 deg, 40 deg, and 50 deg, respectively. The horizontal axis shows the azimuth angle of the silk fibers, the vertical axis is the value of MM elements. All the elements are normalized by M11.
It also should be noted from Fig. 2 that the M14, M24, M34, M41, M42, and M43 elements do not change significantly under different obliquely incident illuminations. These elements mainly reflect the retardance, circular diattenuation, and polarizance properties, which are limited in backscattering imaging results of silk phantom.35,36,38 In fact, for backscattering tissue polarimetry, the MM is often adopted to provide main structural features of bulk tissues conveniently.43 For a demonstration, Fig. 3 shows the robustness of the corresponding elements for characterizing the retardance property of the porcine liver tissue sample under different oblique incidences. It can be seen that the changes of the M24, M34, M42, and M43 elements are limited as the incident angle increases within 20 deg to 30 deg.
Fig. 3.
M24, M34, M42, and M43 images of porcine liver tissue under obliquely incident illuminations of 10 deg, 20 deg, and 30 deg, respectively.
3.2. Variation of the Mean and Kurtosis in Non-Periodic Diagonal Elements
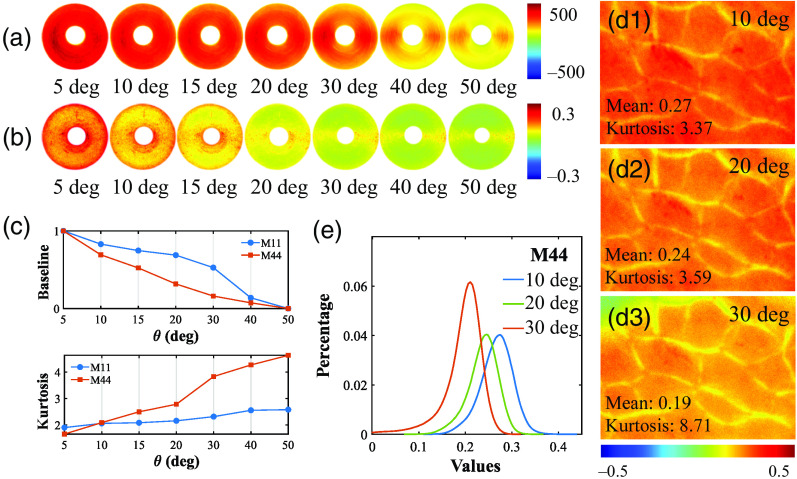
The diagonal elements M11 and M44 reflect the unpolarized backscattering intensity and circular depolarization, respectively.44,45 Ideally, the M11 and M44 elements intensities should be azimuthal independent.35,46,47 However, from Figs. 4(a) and 4(b), it can be noticed that as increased, the intensity values of M11 and M44 decrease, and the silk fibers along vertical direction (90 deg and 270 deg) show stronger signals compared to those along the horizontal direction, which can also be observed from Fig. 2. To quantify such intensity changes, we calculated the mean and kurtosis of the M11 and M44 curves according to Eqs. (2) and (3) shown in Fig. 4(c). Specifically, when becomes larger than 20 deg, the kurtosis of M44 increases sharply from 2.78 to 3.84, which suggests that within 20 deg would be considered preferably to extract reliable circular depolarization information from the M44.
Fig. 4.
MM images and analysis of concentrically aligned silk phantom and porcine liver tissue sample under different obliquely incident illuminations: (a) M11 of the silk phantom; (b) M44 of the silk phantom; (c) mean and kurtosis of the silk phantom. (d1) M44 of porcine liver tissue at 10 deg incidence; (d2) M44 of porcine liver tissue at 20 deg incidence; (d3) M44 of porcine liver tissue at 30 deg incidence. (e) FDH for the M44 of porcine liver tissue.
For an ex vivo tissue verification, we calculated the basic statistics of M44 images of porcine liver tissue sample with increasing from 10 deg to 30 deg, as shown in Figs. 4(d1)–4(d3), which reveals the enhancement and annihilation of the photons scattered from the tissue at specific azimuths. The finding is also supported by the leftward shift of the M44 intensity distribution curve of porcine liver tissue shown in Fig. 4(e). In summary, we should be aware of and minimize such false-positive circular depolarization induced by incidence to avoid inaccurate conclusions in tissue polarimetry, especially when becomes larger than 20 deg.
3.3. Symmetry Breaking in Two-Periodic Off-Diagonal Elements
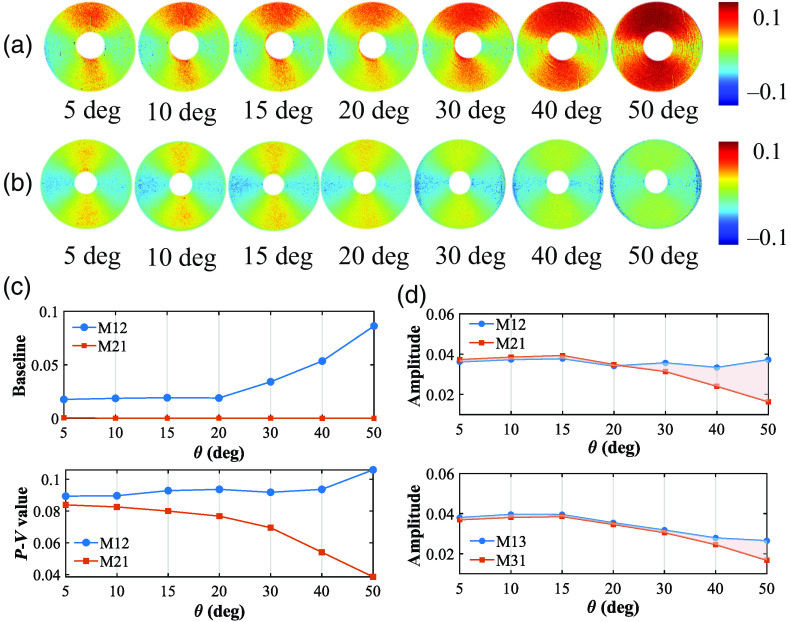
The symmetric properties between different elements tell us abundant optical and structural information of the sample.18 Ideally, the azimuthal dependent curves of M12 and M21, M13 and M31, which represent the linear diattenuation and polarizance properties of the silks, should be perfect trigonometric functions with two periods.5 Moreover, the M12 and M21 pairs, together with the M13 and M31 pairs, should both be symmetric.35 However, Fig. 2 shows that such kind of symmetry can be broken. We can see it more clearly from the MM images of concentrically aligned silk in Figs. 5(a) and 5(b). The opposite trend of both the baseline and the value in Fig. 5(c) verifies such a symmetry breaking, as well.
Fig. 5.
MM images and analysis of concentrically aligned silk phantom under different obliquely incident illuminations: (a) M12; (b) M21; (c) baseline and peak-to-valley value, calculated by the M12 and M21 in 1 period between 0 deg and 180 deg; and (d) amplitude of the third harmonic component after FFT, calculated by the M12 and M21, M13, and M31, respectively.
Moreover, we took FFT to analyze the baseline to the eighth harmonic component in sequence of these two-periodic off-diagonal elements. Among the harmonic components, the third harmonic accounts for the largest proportion, which were separately shown in Fig. 5(d) to confirm such a symmetry breaking. In addition, compared to the M13 and M31 pair shown in Fig. 5(d) (bottom), the symmetry breaking between the M12 and M21 pair presented in Fig. 5(d) (top) is much more significant after 20 deg incidence, whereas the M12 grow abnormally large at special azimuths. It may be relevant to the obliquely incident illumination scheme. For instance, an oblique incident illumination (oblique PSG arm) generates influence particularly on the linearly diattenuation elements, whereas an oblique analyzing arm (oblique PSA arm) generates influence particularly on linearly polarizance elements.
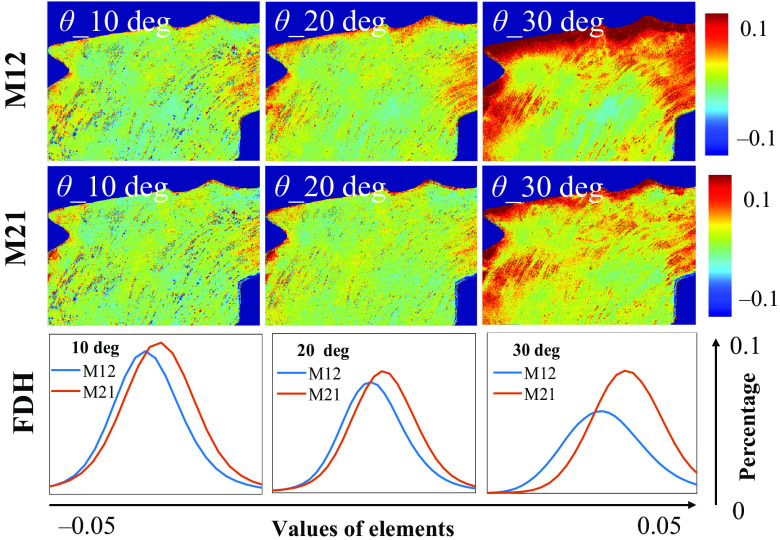
For an ex vivo tissue verification, we measured the M12 and M21 elements of human gastric muscularis tissue sample, as shown in Fig. 6. It can be observed that as increases, the elements’ values of specific areas change prominently, which can induce false-positive linear diattenuation. Meanwhile, Fig. 6 also indicates that the shapes between the FDHs of M12 and M21 varying from each other with increasing. In summary, an incident angle within 20 deg can be considered preferably for oblique incidence, set to extract reliable linear diattenuation.
Fig. 6.
M12 and M21 images, and the corresponding FDH curves of human gastric muscularis tissue sample under obliquely incident angles at 10 deg, 20 deg, and 30 deg.
3.4. Period Degeneracy in Four-Periodic Central-Block Elements
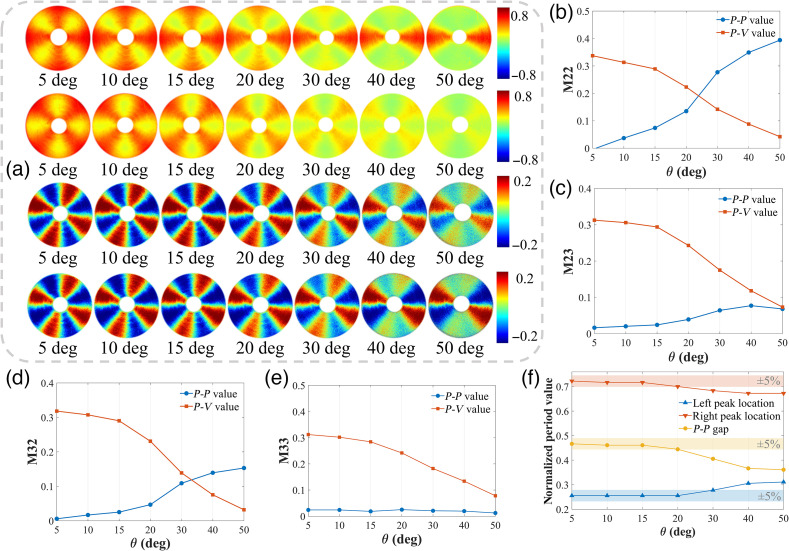
The central-block MM elements M22, M33, M23, and M32, which are related to linear depolarization and the overall linear anisotropy properties, ideally should have trigonometric functions with four periods under normal incidence.5,35 However, Fig. 2 indicates that as increased, the four periods degenerated. Figure 7(a) further visualizes the period degeneracy of the central-block elements, gradually from four to two periods with different features.
Fig. 7.
MM images and analysis of concentrically aligned silk phantom under different obliquely incident illuminations. (a) Images of M22, M33, M23, and M32 from above to below, respectively. (b)–(e) Comparison of value represented by blue dots and value represented by red squares of M22, M23, M32, and M33. The peak and valley values are taken from the first 2 periods of 0 deg to 180 deg. (f) Relative locations and gap between peak and valley in the 0 deg to 180 deg period of M33. The period length has been normalized.
For a more detailed observation of the diagonal M22 and M33 elements in the first 2 periods from 0 deg to 180 deg, we can see from Fig. 2 that as increases: (1) the M22, which is related to the 0 deg and 90 deg linear polarization components of both input and output Stokes vectors, has a sharp single-peak collapse at the special azimuth locations of 0 deg and 180 deg and (2) the M33, which is related to the 45 deg and 135 deg linear polarization components of both input and output Stokes vectors, has a sharp double-peak collapse at the special azimuth locations of 45 deg and 135 deg. Such different forms of period degeneracy make the curves of M22 and M33 under larger oblique incidences tend to be more similar as impulse and square wave signals, respectively. Hence, we list all the amplitudes of each harmonic component for M33 after FFT in Table 1. It can be seen that the odd harmonic components account more proportion than the even harmonic components, and the coefficient of square wave signal tends to 0 as increases, which is precisely the characteristics of square wave signal in Eq. (8).
Table 1.
Amplitude of harmonic components of M33 under different oblique incidences. Bold values are intended to make odd harmonic components more observable.
| (deg) | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 0.361 | 0.013 | 0.016 | 0.023 | 0.149 | 0.020 | 0.011 | 0.004 | 0.981 |
| 10 | 0.320 | 0.008 | 0.020 | 0.023 | 0.148 | 0.019 | 0.012 | 0.005 | 0.916 |
| 15 | 0.292 | 0.007 | 0.025 | 0.022 | 0.143 | 0.018 | 0.012 | 0.004 | 0.848 |
| 20 | 0.237 | 0.005 | 0.032 | 0.023 | 0.120 | 0.022 | 0.012 | 0.004 | 0.657 |
| 30 | 0.184 | 0.006 | 0.039 | 0.016 | 0.092 | 0.017 | 0.015 | 0.003 | 0.422 |
| 40 | 0.143 | 0.006 | 0.043 | 0.012 | 0.066 | 0.014 | 0.015 | 0.004 | 0.239 |
| 50 | 0.106 | 0.006 | 0.041 | 0.007 | 0.041 | 0.007 | 0.012 | 0.003 | 0.138 |
For further demonstrations of the period degeneracy, Figs. 7(b)–7(e) show the changes of (blue dots) and (red squares) values for the M22, M23, M32, and M33 elements. The opposite changing trends confirm the existences of period degeneracy. It is worth mentioning that, as increases, the characteristic of double-peak collapse for the M33 period degeneracy makes its value vary little, as shown in Fig. 5(e), but the locations of the twin peaks get closer and closer. Figure 5(f) illustrates such kind of peaks convergence, whereas the gap (yellow dots) is the distance between twin peaks accordingly. Obviously, the gap gradually becomes smaller as the incident angle becomes larger than 15 deg. Thus, the results shown in Table 1 and Fig. 5 indicate that an incident angle within 15 deg should be considered preferably, set to extract reliable linear depolarization and anisotropy information from the central-block MM elements.
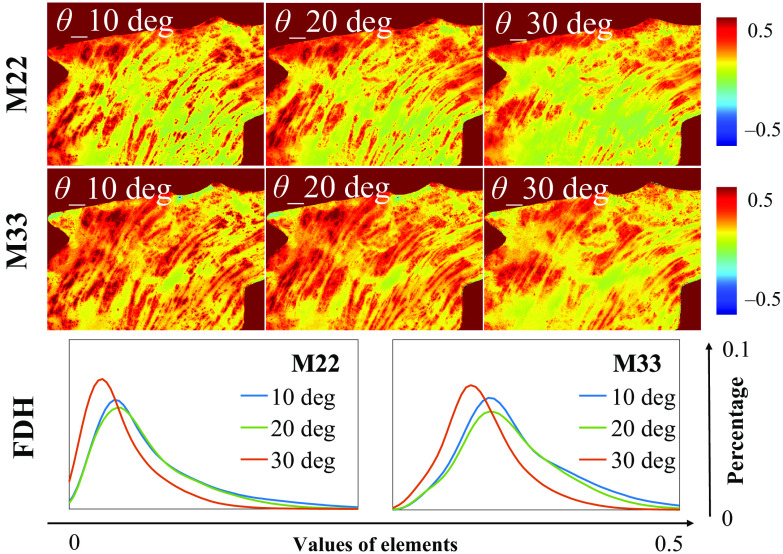
Moreover, such a kind of periodic degeneracy may lead to an annihilation of polarization information at particular azimuths, such as to 45 deg, which can result in false-negative linear anisotropy in tissue polarimetry when the incident angle increased beyond a confidence boundary. For an ex vivo tissue demonstration, we observed the M22 and M33 of human gastric muscularis tissue sample experimentally shown in Fig. 8, from which the decrease of some pixel values can be seen in both the images and FDHs.
Fig. 8.
M22 and M33 images, and the corresponding FDH curves of human gastric muscularis tissue sample under obliquely incident angles at 10 deg, 20 deg, and 30 deg.
3.5. Dramatic Curve Variations with Prominent Oblique Incidence
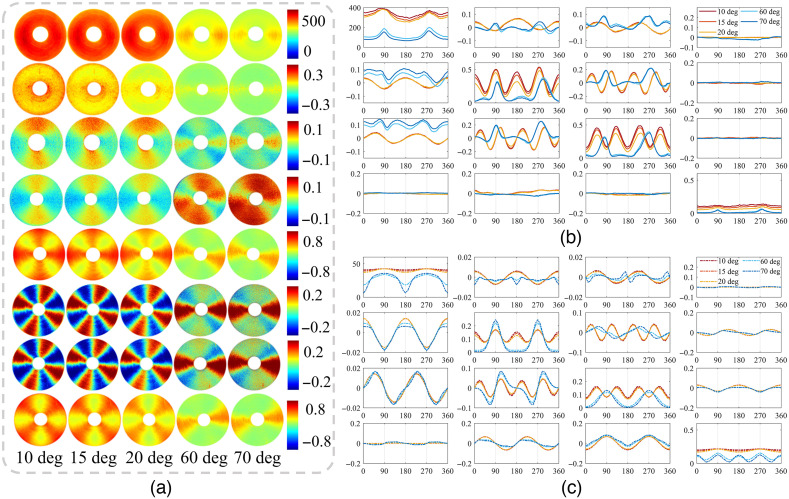
As increased beyond 50 deg, dramatic variations can happen for all the MM elements. It can be observed from Figs. 9(a) and 9(b) that there are great discrepancies of the element characteristics between prominent oblique incidence and moderate oblique incidence. In details, besides the various effects mentioned above, we can see that: (1) the two-periodic elements additionally transposed their values and (2) the baseline of the four-periodic elements decreases additionally accompanied by a certain phase retardance. For example, Fig. 9(c) shows the Monte Carlo simulated curves, which are consistent with the experimental results. Moreover, when the incident angle is modulated, some important structural information of the sample may be obtained through the characteristics of MM elements, such as symmetry breaking and period degeneracy.
Fig. 9.
MM images and analysis of concentrically aligned silk phantom under different obliquely incident illuminations. (a) Images of the M11, M44, M12, M21, M22, M23, M32, and M33 under oblique incidences of 10 deg, 15 deg, 20 deg, 60 deg, and 70 deg from above to below, respectively. (b) and (c) Experimental and Monte Carlo simulated azimuthal dependent curves of MM elements under oblique incidences of 10 deg, 15 deg, 20 deg, 60 deg, and 70 deg, respectively. All the elements are normalized by M11.
4. Conclusions
In this study, we analyzed the influence of oblique incidence on quantitative backscattering tissue polarimetry. The different changes induced by oblique incidence on MM elements include: (1) variation of the mean and kurtosis in non-periodic diagonal elements M11 and M44; (2) symmetry breaking of the two-periodic off-diagonal elements M12, M21, M13, and M31; and (3) period degeneracy of the four-periodic central-block elements M22, M33, M23, and M32. Both ex vivo experimental images and quantitative analysis revealed the variation of depolarization information, false-positive linear diattenuation, and false-negative anisotropy resulted from incidence. It also indicated that some important structural information of the sample may be obtained through the symmetry breaking and period degeneracy of MM elements, as the incident angle modulated prominently. Moreover, the phase retardance and element transposition induced by an oblique incidence larger than 50 deg deserve to be noticed and carefully avoided. The findings presented in this study give some crucial criterions of appropriate incident angle selections for in vivo polarimetric endoscopy and other applications, and can be valuable references for studying how to minimize the influence further.
Acknowledgments
This work has been supported by the Shenzhen Key Fundamental Research Project (Grant No. JCYJ20210324120012035).
Biographies
Zheng Zhang received his BEng degree in agricultural electrification from Nanjing Agricultural University, Nanjing, China, in 2021. He is now a postgraduate candidate in biomedical engineering at Tsinghua Shenzhen International Graduate School, Shenzhen, China. His research focuses on polarization imaging and calibration methods.
Honghui He received his PhD in physics from Tsinghua University, Beijing, China, in 2011. He is currently an associate professor at Tsinghua Shenzhen International Graduate School, Shenzhen, China. His current research interests include Mueller matrix polarimetric techniques and their applications in biomedical diagnosis, especially the detection of cancerous tissues.
Biographies of the other authors are not available.
Disclosures
The authors declare that there are no conflicts of interest related to this paper.
Contributor Information
Zheng Zhang, Email: zhangzhe21@mails.tsinghua.edu.cn.
Conghui Shao, Email: sch18@mails.tsinghua.edu.cn.
Honghui He, Email: he.honghui@sz.tsinghua.edu.cn.
Chao He, Email: chao.he@eng.ox.ac.uk.
Shaoxiong Liu, Email: liusx20088@sina.com.
Hui Ma, Email: mahui@tsinghua.edu.cn.
Code, Data, and Materials Availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Ghosh N., Vitkin I., “Tissue polarimetry: concepts, challenges, applications, and outlook,” J. Biomed. Opt. 16(11), 110801 (2011). 10.1117/1.3652896 [DOI] [PubMed] [Google Scholar]
- 2.Tuchin V., “Polarized light interaction with tissues,” J. Biomed. Opt. 21(7), 071114 (2016). 10.1117/1.JBO.21.7.071114 [DOI] [PubMed] [Google Scholar]
- 3.Ramella-Roman J. C., Saytashev I., Piccini M., “A review of polarization-based imaging technologies for clinical and preclinical applications,” J. Opt. 22(12), 123001 (2020). 10.1088/2040-8986/abbf8a [DOI] [Google Scholar]
- 4.He C., et al. , “Polarisation optics for biomedical and clinical applications: a review,” Light Sci. Appl. 10(1), 194 (2021). 10.1038/s41377-021-00639-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.He H., et al. , “Mueller matrix polarimetry—an emerging new tool for characterizing the microstructural feature of complex biological specimen,” J. Light. Technol. 37(11), 2534–2548 (2019). 10.1109/JLT.2018.2868845 [DOI] [Google Scholar]
- 6.Qi J., Elson D., “Mueller polarimetric imaging for surgical and diagnostic applications: a review,” J. Biophotonics 10(8), 950–982 (2017). 10.1002/jbio.201600152 [DOI] [PubMed] [Google Scholar]
- 7.Zhai H., et al. , “Distinguishing tissue structures via polarization staining images based on different combinations of Mueller matrix polar decomposition parameters,” Opt. Lasers Eng. 152, 106955 (2022). 10.1016/j.optlaseng.2022.106955 [DOI] [Google Scholar]
- 8.Dong Y., et al. , “Deriving polarimetry feature parameters to characterize microstructural features in histological sections of breast tissues,” IEEE Trans. Biomed. Eng. 68(3), 881–892 (2021). 10.1109/TBME.2020.3019755 [DOI] [PubMed] [Google Scholar]
- 9.Zaffar M., Pradhan A., “Assessment of anisotropy of collagen structures through spatial frequencies of Mueller matrix images for cervical pre-cancer detection,” Appl. Opt. 59(4), 1237–1248 (2020). 10.1364/AO.377105 [DOI] [PubMed] [Google Scholar]
- 10.Ahmad I., et al. , “Ex vivo characterization of normal and adenocarcinoma colon samples by Mueller matrix polarimetry,” J. Biomed. Opt. 20(5), 056012 (2015). 10.1117/1.JBO.20.5.056012 [DOI] [PubMed] [Google Scholar]
- 11.Le D., et al. , “Characterization of healthy and cancerous human skin tissue utilizing Stokes-Mueller polarimetry technique,” Opt. Commun. 480, 126460 (2021). 10.1016/j.optcom.2020.126460 [DOI] [Google Scholar]
- 12.Ushenko Y. A., Dubolazov O. V., Karachevtsev A. O., “Statistical structure of skin derma Mueller matrix images in the process of cancer changes,” Opt. Mem. Neural Networks 20(2), 145–154 (2011). 10.3103/S1060992X1102010X [DOI] [Google Scholar]
- 13.Dubreuil M., et al. , “Mueller matrix polarimetry for improved liver fibrosis diagnosis,” Opt. Lett. 37(6), 1061–1063 (2012). 10.1364/OL.37.001061 [DOI] [PubMed] [Google Scholar]
- 14.Chen B., et al. , “Analysis and calibration of linear birefringence orientation parameters derived from Mueller matrix for multi-layered tissues,” Opt. Lasers Eng. 146, 106690 (2021). 10.1016/j.optlaseng.2021.106690 [DOI] [Google Scholar]
- 15.Kim M., et al. , “Optical diagnosis of gastric tissue biopsies with Mueller microscopy and statistical analysis,” J. Eur. Opt. Soc. Rapid Publ. 18(2), 10 (2022). 10.1051/jeos/2022011 [DOI] [Google Scholar]
- 16.Wang W., et al. , “Investigation on the potential of Mueller matrix imaging for digital staining,” J. Biophotonics 9(4), 364–375 (2016). 10.1002/jbio.201500006 [DOI] [PubMed] [Google Scholar]
- 17.Kodela R., Vanagala P., “Polarimetric parameters to categorize normal and malignant thyroid tissue,” IETE J. Res. 63(6), 893–897 (2017). 10.1080/03772063.2017.1323562 [DOI] [Google Scholar]
- 18.He C., et al. , “Revealing complex optical phenomena through vectorial metrics,” Adv. Photonics 4(2), 026001 (2022). 10.1117/1.AP.4.2.026001 [DOI] [Google Scholar]
- 19.Pierangelo A., et al. , “Polarimetric imaging of uterine cervix: a case study,” Opt. Express 21(12), 14120–14130 (2013). 10.1364/OE.21.014120 [DOI] [PubMed] [Google Scholar]
- 20.Pierangelo A., et al. , “Multispectral Mueller polarimetric imaging detecting residual cancer and cancer regression after neoadjuvant treatment for colorectal carcinomas,” J. Biomed. Opt. 18(4), 046014 (2013). 10.1117/1.JBO.18.4.046014 [DOI] [PubMed] [Google Scholar]
- 21.Rodriguez-Nunez O., et al. , “Polarimetric visualization of healthy brain fiber tracts under adverse conditions: ex vivo studies,” Biomed. Opt. Express 12(10), 6674–6685 (2021). 10.1364/BOE.439754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Borovkova M., et al. , “Evaluating beta-amyloidosis progression in Alzheimer’s disease with Mueller polarimetry,” Biomed. Opt. Express 11(8), 4509–4519 (2020). 10.1364/BOE.396294 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mora-Nunez A., et al. , “Texture analysis applied to polarimetric images of healthy in vivo murine skin,” Opt. Eng. 57(5), 054106 (2018). 10.1117/1.OE.57.5.054106 [DOI] [Google Scholar]
- 24.Juette L., et al. , “Registration of polarimetric images for in vivo skin diagnostics,” J. Biomed. Opt. 27(9), 096001 (2022). 10.1117/1.JBO.27.9.096001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jutte L., Roth B., “Mueller matrix microscopy for in vivo scar tissue diagnostics and treatment evaluation,” Sensors 22(23), 9349 (2022). 10.3390/s22239349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Louie D., et al. , “Constructing a portable optical polarimetry probe for in-vivo skin cancer detection,” J. Biomed. Opt. 26(3), 035001 (2021). 10.1117/1.JBO.26.3.035001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Manhas S., et al. , “Demonstration of full 4 × 4 Mueller polarimetry through an optical fiber for endoscopic applications,” Opt. Express 23(3), 3047–3054 (2015). 10.1364/OE.23.003047 [DOI] [PubMed] [Google Scholar]
- 28.Clancy N. T., et al. , “Polarised stereo endoscope and narrowband detection for minimal access surgery,” Biomed. Opt. Express 5(12), 4108–4117 (2014). 10.1364/BOE.5.004108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vizet J., et al. , “In vivo imaging of uterine cervix with a Mueller polarimetric colposcope,” Sci. Rep. 7, 2471 (2017). 10.1038/s41598-017-02645-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vizet J., et al. , “Optical fiber-based full Mueller polarimeter for endoscopic imaging using a two-wavelength simultaneous measurement method,” J. Biomed. Opt. 21(7), 071106 (2016). 10.1117/1.JBO.21.7.071106 [DOI] [PubMed] [Google Scholar]
- 31.Chue-Sang J., et al. , “Use of Mueller matrix colposcopy in the characterization of cervical collagen anisotropy,” J. Biomed. Opt. 23(12), 121605 (2018). 10.1117/1.JBO.23.12.121605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen Z., et al. , “A collinear reflection Mueller matrix microscope for backscattering Mueller matrix imaging,” Opt. Lasers Eng. 129, 106055 (2020). 10.1016/j.optlaseng.2020.106055 [DOI] [Google Scholar]
- 33.Fathima A., Sharma B., Sujatha N., “Selective sensitivity of Mueller imaging for tissue scattering over absorption changes in cancer mimicking phantoms,” Opt. Lasers Eng. 102, 112–118 (2018). 10.1016/j.optlaseng.2017.10.016 [DOI] [Google Scholar]
- 34.Chen Z., et al. , “Removing the dichroism and retardance artifacts in a collinear backscattering Mueller matrix imaging system,” Opt. Express 26(22), 28288–28301 (2018). 10.1364/OE.26.028288 [DOI] [PubMed] [Google Scholar]
- 35.He H., et al. , “A possible quantitative Mueller matrix transformation technique for anisotropic scattering media,” Photonics Lasers Med. 2(2), 129–137 (2013). 10.1515/plm-2012-0052 [DOI] [Google Scholar]
- 36.Sheng W., et al. , “Quantitative analysis of 4 × 4 Mueller matrix transformation parameters for biomedical imaging,” Photonics 6(1), 34 (2019). 10.3390/photonics6010034 [DOI] [Google Scholar]
- 37.Sun M., et al. , “Probing microstructural information of anisotropic scattering media using rotation-independent polarization parameters,” Appl. Opt. 53(14), 2949–2955 (2014). 10.1364/AO.53.002949 [DOI] [PubMed] [Google Scholar]
- 38.He H., et al. , “Mapping local orientation of aligned fibrous scatterers for cancerous tissues using backscattering Mueller matrix imaging,” J. Biomed. Opt. 19(10), 106007 (2014). 10.1117/1.JBO.19.10.106007 [DOI] [PubMed] [Google Scholar]
- 39.Azzam R., “Photopolarimetric measurement of Mueller matrix by Fourier-analysis of a single detected signal,” Opt. Lett. 2(6), 148–150 (1978). 10.1364/OL.2.000148 [DOI] [PubMed] [Google Scholar]
- 40.Goldstein D., “Mueller matrix dual-rotating retarder polarimeter,” Appl. Opt. 31(31), 6676–6683 (1992). 10.1364/AO.31.006676 [DOI] [PubMed] [Google Scholar]
- 41.Chenault D. B., Pezzaniti J. L., Chipman R. A., “Mueller matrix algorithms,” Proc. SPIE 1746, 231–246 (1992). 10.1117/12.138793 [DOI] [Google Scholar]
- 42.Goldstein D., Chipman R. A., “Error analysis of a Mueller matrix polarimeter,” J. Opt. Soc. Am. A 7(4), 693–700 (1990). 10.1364/JOSAA.7.000693 [DOI] [Google Scholar]
- 43.Qi J., et al. , “Narrow band 3 × 3 Mueller polarimetric endoscopy,” Biomed. Opt. Express 4(11), 2433–2449 (2013). 10.1364/BOE.4.002433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lu S., Chipman R., “Interpretation of Mueller matrices based on polar decomposition,” J. Opt. Soc. Am. A 13(5), 1106–1113 (1996). 10.1364/JOSAA.13.001106 [DOI] [Google Scholar]
- 45.Gil J., Ossikovski R., Polarized Light and the Mueller Matrix Approach, CRC Press; (2022). [Google Scholar]
- 46.Gil J., “Invariant quantities of a Mueller matrix under rotation and retarder transformations,” J. Opt. Soc. Am. A 33(1), 52–58 (2016). 10.1364/JOSAA.33.000052 [DOI] [PubMed] [Google Scholar]
- 47.Li P., et al. , “Polaromics: deriving polarization parameters from a Mueller matrix for quantitative characterization of biomedical specimen,” J. Phys. D Appl. Phys. 55(3), 034002 (2022). 10.1088/1361-6463/ac292f [DOI] [Google Scholar]